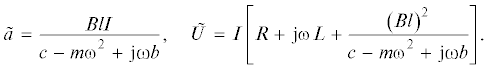Проблемы машиностроения и надежности машин, 2021, № 1, стр. 15-24

Электродинамические возбудители колебаний [1, 2], используемые в испытательных стендах, находят применение и в разнообразных вибрационных и виброударных машинах и устройствах в качестве привода рабочих органов [3–5], особенно при взаимодействии рабочего органа с нелинейной технологической нагрузкой, возникающей при выполнении рабочего процесса. В статье выполнен анализ динамических характеристик машины при ее работе, как на холостом ходу, так и в рабочих режимах при питании возбудителя колебаний от источника тока и источника напряжения.

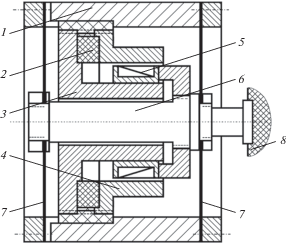
На рис. 1 показана схема вибрационной машины с электродинамическим возбудителем колебаний. В корпусе 1 жестко закреплена магнитная система, кольцевой магнит 2, который зажат между магнитопроводами 3 и 4. В кольцевом зазоре магнитопроводов размещена катушка 5 с возможностью перемещения вдоль оси устройства. Катушка жестко установлена на центральном стержне 6, который связан с корпусом упругими мембранами 7. На конце стержня установлен инструмент, взаимодействующий с обрабатываемым изделием или средой 8. Инструмент поджимается к изделию статической силой P, приложенной к корпусу машины.

Катушки получают питание от источника переменного тока. Проходящий через обмотку катушки переменный ток $i(t)$ создает переменную силу $f(t)$ возбуждения колебаний катушки [1, 2] и жестко связанного с ней инструмента

где B – магнитная индукция магнитного поля в зазоре; l – длина проводника обмотки катушки; i – сила тока.

В то же время движение катушки в магнитном поле создает в ее обмотке противоэлектродвижущую силу

где $x(t)$ – закон движения катушки.

Взаимодействие рабочего органа с обрабатываемой средой создает технологическую нагрузку на колебательную систему. Для описания технологической нагрузки используется нелинейная динамическая характеристика ${{f}_{l}} = {{f}_{l}}(x,\dot {x})$ рабочего процесса [6, 7], которая определяет зависимость силы взаимодействия инструмента с деталью от перемещения $x$ и скорости $\dot {x}$ инструмента.

Режимы холостого хода. Рассмотрим сначала динамические свойства системы при работе на холостом ходу, т.е. при отсутствии технологической нагрузки ${{f}_{l}} = 0$. Состояние электромеханической системы при установившихся гармонических колебаниях с учетом (1) и (2) описывается уравнениями

где m, с, b – масса подвижных частей, жесткость мембран и коэффициент вязкого сопротивления соответственно; R, L – сопротивление цепи питания и индуктивность катушки; $\tilde {U}$, $\tilde {I}$ – комплексные амплитуды напряжения питания катушки и тока в ее проводнике; $\tilde {a}$ – комплексная амплитуда колебаний инструмента; $\omega $ – частота колебаний; ${\text{j}} = \sqrt {--{\text{1}}} $.

Если сила тока задана, т.е. питание катушек производится от источника тока, и изменяется по гармоническому закону 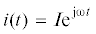, где I = const – амплитуда cилы тока, из уравнений (3) находим комплексные амплитуды колебаний инструмента и напряжения питания катушек

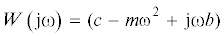где – динамическая жесткость механической части системы; 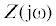= 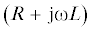– импеданс электрической цепи.

Из соотношений (4) после подстановки принятых обозначений получим выражения для комплексных амплитуд колебаний инструмента и напряжения питания катушек

Используя формулу Эйлера

где $\varphi $ – начальная фаза колебаний, из первого равенства (5) находим соотношения для амплитуды и начальной фазы колебаний рабочего органа

Выражения (6) и (7) эквивалентны соотношениям, получаемым при анализе вынужденных колебаний осциллятора при действии гармонической силы с амплитудой ${{F}_{0}} = BlI$.

Второе соотношение в (5) определяет напряжение питания. Второе слагаемое отражает влияние параметров механической части системы на импеданс электрической цепи. При питании от источника тока резонанс достигается при $\operatorname{Re} W\left( {{\text{j}}\omega } \right) = 0$, т.е. на собственной частоте ${{\omega }_{0}} = \sqrt {c{\text{/}}m} $ механической части системы. При этом достигают максимальных значений амплитуды, как колебаний инструмента, так и напряжения на выходе источника питания. Резонансные значения амплитуды колебаний инструмента и напряжения питания имеют вид

Отсюда видно, что в резонансном режиме колебания магнита создают добавочное активное электрическое сопротивление, которое тем сильнее, чем меньше коэффициент b вязкого сопротивления движению механической системы. Это объясняется возрастанием амплитуды колебаний при уменьшении b, а, следовательно, и противоэлектродвижущей силы. Заметим, что напряжение питания $U \to \infty $ при $\omega \to \infty $, что объясняется возрастанием индуктивного сопротивления катушки.

Питание электродинамического возбудителя колебаний, как правило, производится от источника напряжения. В этом случае сила тока в проводнике катушки зависит не только от параметров катушки. При движении в магнитном поле в проводнике катушки возникает противоэлектродвижущая сила $e = - Bl\dot {x}$. В этом случае состояние системы описывается уравнениями (2), в которых заданным является напряжение 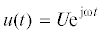. Решая систему уравнений (2) относительно неизвестных комплексных амплитуд $\tilde {a}$ и $\,\tilde {I}$ получим

Для более наглядной физической интерпретации полученных далее решений запишем эти уравнения в виде

где ${{W}_{\Sigma }}(j\omega ) = W(j\omega ) + j\omega {{\left( {Bl} \right)}^{2}}{\text{/}}Z(j\omega )$ – динамическая жесткость полной электромеханической системы. Приведем ее развернутое выражение где величина $k = {{{{{\left( {Bl} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {Bl} \right)}}^{2}}} {[{{R}^{2}} + {{{(\omega L)}}^{2}}]}}} \right. \kern-0em} {[{{R}^{2}} + {{{(\omega L)}}^{2}}]}}$ имеет смысл коэффициента приведения электрических параметров к их механическим аналогам.

Резонанс системы при ее питании от источника напряжения согласно (10) возникает при $\operatorname{Re} {{W}_{\Sigma }}\left( {{\text{j}}\omega } \right) = 0$, т.е. при частоте $\omega = {{\omega }_{r}}$, определяемой равенством

Поскольку коэффициент k зависит от частоты $\omega $, соотношение (11) является уравнением относительно искомой резонансной частоты ${{\omega }_{r}}$. В результате решения этого уравнения находим

Как следует из (12), при питании от источника напряжения резонансная частота системы оказывается более низкой, чем при питании от источника тока, за счет сложного сочетания параметров магнитоэлектрической и механической частей системы. В данном случае резонанс реализуется при ${{\left( {Bl} \right)}^{2}} < Lc$. При ${{\left( {Bl} \right)}^{2}} \to Lc$ резонансная частота ${{\omega }_{r}} \to 0$. Электродинамические возбудители с большими значениями ${{\left( {Bl} \right)}^{2}} \gg Lc$ используются в вибрационных стендах, позволяя получить практически постоянные амплитуды колебаний в достаточно широком диапазоне частот.

Из соотношений (9) с учетом равенств (10) и (11) найдем величины резонансных амплитуд колебаний инструмента и тока в цепи питания катушек

Рассмотрим поведение системы при двух характерных частотах. При частоте $\omega = 0$ из уравнений (8) с учетом принятых обозначений находим $I = U{\text{/}}R$, $a = BlU{\text{/}}Rc$, что вполне очевидно, так как система находится в состоянии статического равновесия. В практике эксплуатации вибрационных машин с электродинамическим возбудителем колебаний зачастую в качестве рабочей выбирают настройку на собственную частоту $\omega = {{\omega }_{0}}$ = $\sqrt {c{\text{/}}M} $ механической колебательной системы. В таком режиме амплитуда колебаний рабочего органа

Этот режим интересен тем, что амплитуда силы тока минимальна и при $b \to 0$ амплитуда силы тока $I \to 0$, т.е. механические колебания происходят, а ток в катушках отсутствует. Это происходит потому, что в этом режиме противоэлектродвижущая сила, возникающая в проводнике катушки, оказывается равной напряжению питания. По сути, в данном случае мы имеем дело с явлением антирезонанса в электрической цепи.

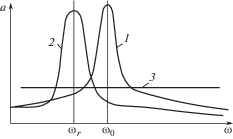
На рис. 2 показаны амплитудно-частотные характеристики колебаний рабочего инструмента при питании системы от источника тока (кривая 1) и источника напряжения при ${{\left( {Bl} \right)}^{2}} < Lc$ (кривая 2) и при ${{\left( {Bl} \right)}^{2}} > Lc$ (линия 3).

Нелинейная технологическая нагрузка. Перейдем к описанию работы машины с электродинамическим возбудителем колебаний при выполнении технологического процесса. Взаимодействие рабочего органа с обрабатываемым изделием или средой создает дополнительную технологическую нагрузку на рабочий орган машины. Как правило, нагрузку можно представить в виде действующей на рабочий орган силы ${{f}_{l}} = {{f}_{l}}(x,\dot {x})$, нелинейно зависящей от координаты $x$ и скорости $\dot {x}$ рабочего органа. Уравнение движения при питании от источника тока по аналогии с (3) принимает вид

Отыскивая приближенное гармоническое решение нелинейного уравнения (14), проведем гармоническую линеаризацию [6] функции ${{f}_{l}} = {{f}_{l}}(x,\dot {x})$

где ${{P}_{l}}(a)$ – постоянная составляющая технологической нагрузки; ${{c}_{l}}(a)$, ${{b}_{l}}(a)$ – коэффициенты гармонической линеаризации, вычисляемые по формулам где $T = 2\pi {\text{/}}\omega $ – период колебаний.

Поскольку вся система поджимается к обрабатываемой среде постоянной силой P (рис. 1), очевидно, что постоянная составляющая нелинейной нагрузки P_l = P, а уравнение колебаний (14) с учетом (15) принимает вид

Таким образом, получено линейное уравнение, коэффициенты которого зависят от неизвестной амплитуды. Решая уравнение (17), получаем выражение для комплексной амплитуды

Заметим, что по форме выражение (18) совпадает с выражением (5), полученным при описании работы на холостом ходу. Поэтому проведенные выше выкладки формально оказываются справедливыми при замене величин c и b на величины $\left( {c + {{с}_{l}}} \right)$ и $\left( {b + {{b}_{l}}} \right)$ соответственно. Существенное различие равенств (5) и (18) заключается в том, что последнее является алгебраическим уравнением относительно амплитуды a, от которой зависят коэффициенты ${{с}_{l}}$ и ${{b}_{l}}$.

В качестве примера рассмотрим работу системы, предназначенной, например, для внедрения инструмента в хрупкую среду. Примем, что рабочий процесс описывается характеристикой жесткопластического материала [7]

где D – сила, при которой происходит необратимая деформация или разрушение материала; $\eta \left( x \right)$ – функция Хевисайда; $\Delta $ – координата инструмента в момент начала его взаимодействия с обрабатываемой средой. Коэффициенты гармонической линеаризации функции (19) имеют вид [8]

Учитывая равенство ${{P}_{l}}\left( a \right) = P$, из первого соотношения в (20) находим ${\Delta \mathord{\left/ {\vphantom {\Delta a}} \right. \kern-0em} a}$ = = $\cos \left( {{{2\pi P} \mathord{\left/ {\vphantom {{2\pi P} D}} \right. \kern-0em} D}} \right)$ и после подстановки в (20) получаем и

Разность $a - \Delta $ определяет величину внедрения инструмента в обрабатываемую среду за один цикл колебаний. Очевидно, что средняя скорость процесса ${v} = {{\left( {a - \Delta } \right)\omega } \mathord{\left/ {\vphantom {{\left( {a - \Delta } \right)\omega } {2\pi }}} \right. \kern-0em} {2\pi }}$ и с помощью первого соотношения в (20) находим

В реальных процессах и машинах $P \ll D$. Поэтому, выражения (21) и (22) с высокой точностью можно представить в виде

Нелинейная динамика машины. Перейдем к построению динамических характеристик машины в рабочем режиме. Выше было показано, что все решения, полученные для режимов холостого хода, остаются справедливыми после замены величин c и b на величины $\left( {c + {{с}_{l}}} \right)$ и $\left( {b + {{b}_{l}}} \right)$. При питании возбудителя от источника тока по аналогии с (6) с учетом (23) находим

Соотношение (24) позволяет сразу найти связь резонансных частот и амплитуд с параметрами системы. Равенство нулю первого слагаемого в знаменателе (24) определяет значения резонансных частоты и амплитуды

Первое из равенств (25) является уравнением скелетной кривой амплитудно-частотной характеристики, второе – линии предельных амплитуд [6]. Решение уравнений (25) позволяет найти величины резонансных частот и амплитуд. Из (25) видно, что резонансы возникают в области частот ${{\omega }_{{rl}}} > {{\omega }_{0}}$ при условии

Из соотношений (25) следует, что резонансная частота в рабочем режиме ${{\omega }_{{rl}}} > {{\omega }_{0}}$, а резонансная амплитуда ${{a}_{{rl}}} \to \infty $ при $b \to 0$.

Уравнение (24) относительно неизвестной амплитуды колебаний рабочего органа приводится к следующему квадратному уравнению

Учитывая, что диссипация в системе существенно влияет на параметры колебаний только в окрестности резонанса, для получения ясной физической картины запишем решение уравнения, полагая b = 0

Из выражения (27) следует, что неравенство (26) является необходимым условием существования виброударного рабочего процесса. Покажем, что вид амплитудно-частотной характеристики существенно зависит от соотношения сил возбуждения BLI и подачи P. Учитывая условие a > 0, из (27) находим, что рабочий процесс реализуется во всем частотном диапазоне при условии

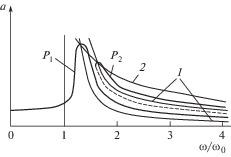
На рис. 3 показаны амплитудно-частотные характеристики при различных значениях силы P. Рассмотренному случаю отвечает кривая P₁. Резонансные частота и амплитуда определяются координатами точек пересечения скелетных кривых 1 и линии 2 предельных амплитуд. Ситуация радикально меняется, если увеличение силы P приводит к нарушению неравенства (28). В этом случае виброударные режимы возможны только в области $\omega > {{\omega }_{0}}$, и амплитудно-частотная характеристика имеет две ветви, разделенные скелетной кривой. На рис. 3 этому случаю отвечает кривая P₂. По мере увеличения силы P подачи резонансная частота все более смещается в сторону более высоких частот. Используя соотношения (25), можно показать, что по мере приближения параметров системы к границе неравенства (26) резонансная частота ${{\omega }_{{rl}}} \to \infty $.

Показанная штриховой линией нижняя ветвь резонансной кривой P₂ отвечает неустойчивым режимам. Вывод системы на устойчивые режимы с большой амплитудой можно осуществить либо внешним импульсом, либо затягиванием колебаний из области высоких частот, либо плавным увеличением силы P при заданной частоте $\omega \geqslant {{\omega }_{{rl}}}$. При этом следует иметь в виду опасность срыва колебаний при прохождении границы устойчивости.

Перейдем к построению и анализу амплитудно-частотных характеристик системы при питании от источника напряжения. По аналогии с (24), используя выражения (9), (10), (23), запишем уравнение относительно амплитуды колебаний инструмента

и линии предельных амплитуд

где ${{R}_{{rl}}} = \sqrt {({{R}^{2}} + \omega _{{rl}}^{2}{{L}^{2}})} $ – сопротивление цепи питания при частоте $\omega = {{\omega }_{{rl}}}$.

По физической сути соотношения (30) хорошо согласуются с равенствами (25). Из (30) следует, что скелетная кривая определена в частотной области $\omega > {{\omega }_{r}}$, а резонансные колебания можно реализовать при выполнении условия

Пренебрегая потерями энергии в механической (b = 0) и электрической (R = 0) частях системы, приведем уравнение (29) к квадратному

Решение уравнения имеет вид

Необходимое условие реализации виброударного режима имеет вид

При $\omega = {{\omega }_{{rl}}}$ неравенство (33), совпадающее с условием (31) реализации резонансных колебаний, ограничивает частотный диапазон существования виброударных процессов при заданной силе P

Заметим, что виброударный процесс в диапазоне $\omega < {{\omega }_{r}}$ возможен при

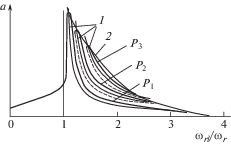
При выполнении (35) каждой частоте из диапазона (34) соответствует единственное значение амплитуды (32) колебаний. Отвечающая условию (35) амплитудно-частотная характеристика показана на рис. 4 (линия P₁).

При нарушении условия (35) виброударные режимы реализуются только в частотном диапазоне ${{\omega }_{r}} < \omega < {{\omega }_{m}}$, где амплитудно-частотная характеристика (32) имеет вид петли, ветви которой разделенные скелетной кривой (30). На рис. 4 показаны амплитудно-частотные характеристики при различных значениях силы P. Тонкими линиями показаны скелетные кривые 1 и линии 2 предельных амплитуд. Штриховыми линиями показаны ветви неустойчивых режимов. По мере увеличения силы P₃ > P₂ > P₁ частотный диапазон существования виброударного режима сужается и в пределе при P = P_m стягивается в точку, выделенную черным кружком. Графически в этой точке происходит касание скелетной кривой и линии предельных амплитуд, отвечающей предельному значению силы P.

В заключение отметим, что приведенные результаты позволяют провести полный расчет машины с электродинамическим возбудителем колебаний. Поскольку резонансные режимы являются наиболее эффективными [9] при работе вибрационной машины, понимание происходящих процессов позволяет найти лучшие пути реализации этих режимов.