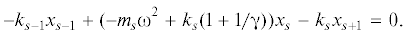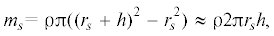Проблемы машиностроения и надежности машин, 2021, № 1, стр. 25-32
Динамические фракталы в биомеханике. виброрецепторы – тельца пачини
Л. Я. Банах *
Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия
* E-mail: banl@inbox.ru
Поступила в редакцию 02.06.2020
Принята к публикации 22.10.2020
Аннотация
В статье введено понятие динамически-фрактальных структур (динамического фрактала), заключающееся в изменении с одинаковым масштабом динамических, т.е. упруго-инерционных параметров, образующих ячеек. Показано, что убывающий по длине динамический фрактал, имеет свойство усиления поступающего сигнала вдоль структуры. Увеличивающийся по длине динамический фрактал, напротив, обладает хорошими виброизолирующими свойствами, интенсивность затухания в котором выше, чем в периодической структуре. Исследованы динамические свойства виброрецептора – тельца Пачини, являющегося детектором вибрации. Построена его механическая модель. Показано, что виброрецептор – это динамический фрактал с убывающими по длине параметрами и поэтому усиливает входящий сигнал, что позволяет улавливать даже слабые вибрационные воздействия на человека.
1. Постановка задачи. Широкий класс структур в природе и технике составляют самоподобные фрактальные структуры, в которых каждая последующая ячейка в определенном масштабе повторяет структуру предыдущей. В настоящее время широко известны фракталы Мандельброта [1], в которых происходит масштабирование геометрических параметров. Они хорошо описывают формообразование структур, успешно используются во многих вычислительных комплексах. Однако они не отражают динамических свойств механических систем. Поэтому представляет интерес изучение структур, состоящих из ячеек, подобных по динамическим, а не по геометрическим параметрам. Для этого, в отличие от геометрических фракталов Мандельброта следует ввести понятие динамического фрактала, описывающего структуры, в которых происходит масштабирование упруго-инерционных параметров, определяющих динамические свойства системы. К таким системам в механике можно отнести, например, стержни переменного сечения, валы с дисками переменного сечения, конические оболочки с ореберением, разветвленные структуры (например, дихотомические решетки).
Такие структуры обладают рядом специальных динамических свойств [2, 3]. Выявлено, что динамический фрактал, увеличивающийся по длине, имеет хорошие виброизолирующие свойства, при этом интенсивность затухания значительно выше, чем в эквивалентной периодической структуре. Динамический фрактал, уменьшающийся по длине, напротив, обладает способностью усиливать входящий сигнал вдоль длины. Эти характерные свойства динамически-фрактальных структур можно использовать в инженерных конструкциях.
Интенсивное снижение уровня колебаний в динамических фракталах целесообразно применять в системах виброизоляции. Достаточно распространенными такими системами виброизоляции являются решетчатые фундаментные конструкции с периодической структурой [4], характеризующиеся чередованием полос пропускания и непропускания гармонического сигнала. Однако, значительно более сильные виброизолирующие свойства имеют динамически-фрактальные решетки, интенсивность затухания колебаний в которых в γ раз выше, чем в периодической структуре [5] (γ – параметр масштабирования). Это позволяет также существенно сократить число рядов решетки.
Другое характерное свойство – усиление поступающего сигнала в убывающем по длине динамическом фрактале, что невозможно в периодической структуре. В инженерных конструкциях это качество используется в ультразвуковых колебательных системах для увеличения амплитуды колебаний, передаваемых от возбудителя колебаний к инструменту [6].
Наиболее сильным подтверждением работоспособности и целесообразности динамически-фрактальных структур является их существование в природе. Хорошо известны примеры успешного применения в инженерных конструкциях идей и технологий, заимствованных из Природы. С этой точки зрения очень важно исследовать природные динамические фракталы. Такой структурой является, в частности, виброрецептор – тельце Пачини, представляющий собой детектор гармонического сигнала при воздействии вибрации на человека. Его динамический анализ и является целью настоящей статьи.
В п. 2 изложены основные результаты и методы исследования колебаний динамически-фрактальных структур, необходимые при исследовании структуры виброрецептора. В п. 3 проводится анализ колебаний и распространения волн в математической модели виборецептора – тельца Пачини. Показано, что этот виброрецептор представляет собой убывающий динамический фрактал.
2. Динамический фрактал. Определение и основные свойства. Динамически-самоподобными (динамическим фракталом) назовем структуры, в которых упругие и инерционные параметры меняются с одинаковым масштабом γ для каждой ячейки структуры (или подсистемы) [2, 3]
где Ks – жесткость, Ms – инерционный параметр s-й ячейки.Необходимым (но не достаточным) следствием условий (1) является равенство парциальных частот образующих ячеек
(2)
$\nu _{s}^{2} = {{\left( {{{K}_{s}} + {{K}_{{s - 1}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{K}_{s}} + {{K}_{{s - 1}}}} \right)} {{{M}_{s}}}}} \right. \kern-0em} {{{M}_{s}}}} = \nu _{{s + 1}}^{2} = {{\left( {{{K}_{{s + 1}}} + {{K}_{s}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{K}_{{s + 1}}} + {{K}_{s}}} \right)} {{{M}_{{s + 1}}}}}} \right. \kern-0em} {{{M}_{{s + 1}}}}} = \operatorname{const} = {{\nu }^{2}}\quad (s = 1,\; \ldots ,\;n).$Условия (1) для динамического фрактала не совпадают с условиями геометрического подобия (scaling), использующегося в геометрических фракталах Мандельброта. Это совершенно другой вид структур, отличающийся от фракталов Мандельброта.
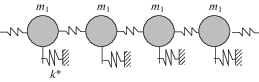
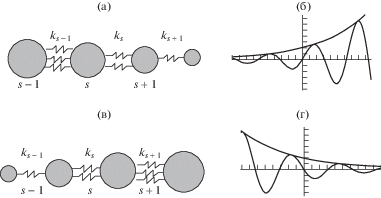
Проиллюстрируем основные свойства динамического фрактала на более простом примере фрактальной цепочки (рис. 1). Рассмотрим бесконечную одномерную цепочку, в которой s-я ячейка состоит из сосредоточенной массы ms и пружинки с жесткостью ks. Пусть упругие и инерционные параметры меняются с одинаковым масштабом γ от ячейки к ячейке (рис. 1а).
Рис. 1.
Динамически-фрактальные структуры: (a) – цепочка с уменьшающимися по длине параметрами (γ < 1); (б) – формы колебаний при ω0 < ω < ω* если $\gamma < 1$ $(\alpha > \mu )$; (в) – цепочка с увеличивающимися по длине параметрами (γ > 1); (г) – формы колебаний при ω0 < ω < ω*, если ${\gamma }\,\,{\text{ > }}\,{\kern 1pt} {\text{1}}$, $\gamma < 1$ $(\alpha < \mu )$.
Тогда жесткость и масса для элемента s + 1: ${{k}_{{s + 1}}} = {\gamma }{{k}_{s}}$, ${{m}_{{s + 1}}} = {\gamma }{{m}_{s}}$. Уравнение в конечных разностях s-й ячейки
Используя замену переменных
или(5)
${{\tilde {х}}_{s}} = C\exp (i\left( {\mu s - \omega t} \right)){\text{/}}{{\left( {\sqrt \gamma } \right)}^{s}} = C\exp (i(\mu + i\alpha )s - \omega t),\quad i\alpha = - \frac{1}{2}\ln \gamma ,$(6)
$ - {{k}_{1}}{{\tilde {x}}_{{s - 1}}}{\text{/}}\left( {\sqrt \gamma } \right) + \left( { - {{m}_{1}}{{\omega }^{2}} + \frac{{{{k}_{1}}(1 + \gamma )}}{\gamma }} \right){{\tilde {x}}_{s}} - {{k}_{1}}{{\tilde {x}}_{{s + 1}}}{\text{/}}\left( {\sqrt \gamma } \right) = 0.$Уравнение (6) описывает периодическую структуру (рис. 2), так как его коэффициенты не зависят от номера s. Жесткость между ячейками составляет ${{{{k}_{1}}} \mathord{\left/ {\vphantom {{{{k}_{1}}} {\sqrt {\gamma } }}} \right. \kern-0em} {\sqrt {\gamma } }}$, дополнительное закрепление масс равно $k* = \frac{{{{k}_{1}}(1 + {\gamma })}}{{\gamma }}$ – $\frac{{2{{k}_{1}}}}{{\sqrt {\gamma } }}$ = $\frac{{{{k}_{1}}{{{(1 - \sqrt {\gamma } )}}^{2}}}}{{\gamma }}$.
Дисперсионное уравнение периодической структуры
(7)
$ - {{m}_{1}}{{\omega }^{2}} + \frac{{{{k}_{1}}(1 + \gamma )}}{\gamma } - 2\frac{{{{k}_{1}}}}{{\sqrt \gamma }}\cos \mu = 0,\quad {{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {{{k}_{1}} = {{{{m}_{s}}} \mathord{\left/ {\vphantom {{{{m}_{s}}} {{{k}_{s}} = }}} \right. \kern-0em} {{{k}_{s}} = }}{{\nu }^{2}} = \operatorname{const} }}} \right. \kern-0em} {{{k}_{1}} = {{{{m}_{s}}} \mathord{\left/ {\vphantom {{{{m}_{s}}} {{{k}_{s}} = }}} \right. \kern-0em} {{{k}_{s}} = }}{{\nu }^{2}} = \operatorname{const} }}.$Такая структура [7, 8] представляет собой полосовой механический фильтр, полоса пропускания гармонического сигнала, как следует из (7)
Эта периодическая структура частотно эквивалентна исходному динамическому фракталу, так как линейное преобразование координат не меняет частотных свойств системы [9]. Однако, формы колебаний этих структур различны. Формы колебаний динамического фрактала, как следует из (4), (5), получаются из соответствующей волны периодической структуры рис. 2, путем изменения амплитуды колебаний каждого участка в ${1 \mathord{\left/ {\vphantom {1 {\sqrt {\gamma } }}} \right. \kern-0em} {\sqrt {\gamma } }}$ раз. На рис. 1б, 1г представлены высшие формы колебаний динамического фрактала при закрепленных концах. Из соотношения (4) следуют выводы: 1) при γ > 1 затухание гармонического сигнала вдоль структуры происходит во всем частотном диапазоне, а не только в полосе непропускания периодической структуры. Кроме того, из (5) следует, что снижение уровня колебаний в exp(α) интенсивнее по сравнению с эквивалентной периодической решеткой; 2) при γ < 1 происходит усиление входного сигнала при $\omega * < \omega < {{\omega }_{0}}$, а также и вне этой полосы при α > |μ|. Это важное свойство фрактальных структур, которое используется в дальнейшем.
3. Фрактальные структуры в биомеханике. Тельца Пачини. Тельца Пачини – это рецепторы подкожной ткани человека, которые являются детекторами вибрации [10–13] (рис. 3). Они состоят из достаточно близко расположенных замкнутых оболочек, вложенных одна в другую, пространство между которыми заполнено физиологической жидкостью, близкой по своим характеристикам к воде. Оболочки достаточно тонкие, их толщина не превосходит ≈1 мкм. Внутри корпускулы распложено ядро, к которому подходит нервное окончание. Количество оболочек N = 30, их радиусы связаны соотношением11
Рис. 3.
Виброрецептор – тельце Пачини: (а) – общий вид; (б) – механическая модель, продольное сечение; (в) – механическая модель, поперечное сечение.
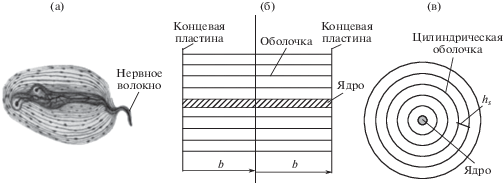
Концы оболочек закреплены на концевой пластине, примыкающей к ядру, которая предотвращает протекание жидкости между оболочками (рис. 3б, в).
Оболочки связаны между собой тонкими упругими радиальными элементами, которые распределены равномерно внутри оболочки и не мешают протеканию жидкости между оболочками. Они предотвращают контакт между оболочками, и в то же время передают перемещения на соседнюю оболочку.
Размер внешней оболочки: длина b = 700 мкм, радиус r1 = 255 мкм (табл. 1). Найдем теперь упруго-инерционные параметры и коэффициент демпфирования, обусловленный вязкостью жидкости. Оболочки достаточно тонкие, поэтому в механической модели (рис. 3б), их можно рассматривать как цилиндрические мембраны.
Таблица 1.
Изменение параметров мембраны в зависимости от номера s
| № оболочки | 1 | 2 | 3 | 4 | … | 10 | 11 | 12 | … |
|---|---|---|---|---|---|---|---|---|---|
| Радиус мембраны, мкм | 255 | 232 | 211 | 192 | 108 | 98.5 | 91 | ||
| Ks [Н/м3 × 10–5] | 0.470 | 0.420 | 0.380 | 0.330 | 0.130 | 0.110 | 0.097 |
При воздействии внешнего давления $P = A\cos (2\theta )\cos \left( {\pi \frac{x}{b}} \right)$, на s-ю мембрану, в ней возникают перемещения, пропорциональные Ks ([14], Приложение)
(9)
${{K}_{s}} = \frac{{E{{d}_{s}}}}{{r_{s}^{2}}}{{\left( {1 + \frac{{4{{b}^{2}}}}{{{{\pi }^{2}}r_{s}^{2}}}} \right)}^{{ - 2}}},\quad {{K}_{{s + 1}}} = \gamma {{K}_{s}},$Из табл. 1 видно, что условия масштабирования (8) выполнены как для радиусов мембран, так и для коэффициента Ks, характеризующего, по-существу, упругость мембраны. Действительно, с увеличением номера s эти параметры уменьшаются пропорционально коэффициенту подобия γ.
Внутренние радиальные связи испытывают деформации растяжения–сжатия. Если их моделировать в виде стержней, имеющих площадь поперечного сечения Fs и длину hs, где hs – расстояние между мембранами, то жесткость связей равна ${{k}_{s}} = E{{F}_{s}}{\text{/}}{{h}_{s}}$. Fs меняется пропорционально γ2, а hs – пропорционально γ, следовательно, ks + 1= γks. Имеющиеся экспериментальные данные [10] подтверждают этот вывод. Поскольку жесткость радиальных связей должна быть выше жесткости самой оболочки, будем рассматривать перемещение оболочек как перемещение твердого тела.
Жидкость между мембранами вязкая и несжимаемая, ее инерционные свойства можно не учитывать, так как движение жидкости ламинарное и число Рейнольдса мало. Статическое смещение внешней мембраны повышает давление внутри соседней, но не вызывает ее смещения в силу несжимаемости жидкости. Такие смещения возникают лишь при динамическом нагружении. Течение жидкости между мембранами можно анализировать на основе гидродинамической теории смазки [15], так как расстояние между цилиндрами hs значительно меньше его радиуса r. Воздействие жидкости можно рассматривать как вязкое демпфирование. Вследствие малости hs демпфирующие силы в вертикальной плоскости для s-й мембраны пропорциональны разности скоростей слоя жидкости, контактирующей с (s + 1)-й мембраной, где коэффициент пропорциональности βs зависит от вязкости и равен [10]
(10)
${{\beta }_{s}} = \frac{{12\mu {{b}^{2}}}}{{h_{s}^{3}{{\pi }^{2}}\left( {1 + \frac{{4{{b}^{2}}}}{{{{\pi }^{2}}a_{s}^{2}}}} \right)}},\quad {{\beta }_{{s + 1}}} = \gamma {{\beta }_{s}},\quad {{\beta }_{1}} = 1.34 \times {{10}^{4}}\;{\text{Н}}\;{\text{сек/}}{{{\text{м}}}^{2}}.$Масса s-й мембраны c присоединенной массой слоя жидкости составляет
вследствие малости толщины слоя по сравнению с радиусом мембраны, здесь ${\rho }$ – плотность среды. Поэтому ms меняется также пропорционально γ: ms + 1 = γms.Как следует из соотношений (8)–(11), упруго-инерционные параметры мембран, а также вязкость среды между ними меняются пропорционально коэффициенту γ. Следовательно, условия (1), (2) динамической фрактальности удовлетворены, и корпускула представляет собой динамический фрактал.
Динамическую модель тельца Пачини для анализа распространения волны вдоль корпускулы от внешней оболочки к ядру представим в виде системы твердых тел, имитирующих мембраны, связанные как с концевой пластиной, так и между собой упругими и демпфирующими связями (рис. 4).
Изменение толщины линий, обозначающих на рис. 4 упругие и демпфирующие элементы, имитирует уменьшение их величины вдоль длины структуры.
Следовательно, как показано в п. 2, корпускула имеет полосу частот, в которой происходит наибольшее усиление сигнала, поступающего на вход рецептора. Это свойство особенно важно для биологической системы, поскольку дает возможность распознать даже слабые сигналы при воздействии вибрации на человека. По данным [13] в организме человека имеется несколько различных видов виброрецепторов, каждый из которых предназначен для своего частотного диапазона, и в общей сложности, возможно, различать вибрации в пределах до 1000 Гц. Рассматриваемая нами система описывает один из таких виброрецепторов.
Динамическую модель рис. 3 можно рассматривать как метасистему [16, 17] и притом достаточно компактную, которая в зависимости от уменьшения или увеличения параметров по длине структуры может служить как усилителем входного сигнала, так и виброизолятором.
Результаты. Введено понятие динамической фрактальности (динамического фрактала), заключающееся в масштабировании упруго-инерционных параметров образующих подсистем.
Убывающий по длине динамический фрактал имеет свойства усиления поступающего сигнала вдоль его длины. Наибольший коэффициент усиления фрактала находится в полосе пропускания эквивалентной периодической структуры.
Увеличивающийся по длине динамический фрактал обладает хорошими виброизолирующими свойствами: в нем распространяются убывающие по длине волны, а интенсивность затухания амплитуд колебаний в γ раз превосходит демпфирование в эквивалентной периодической структуре.
Исследованы динамические свойства виброрецептора – тельца Пачини. Построена его механическая модель. Показано, что виброрецептор является убывающим динамическим фракталом и поэтому имеет полосы усиления входящего гармонического сигнала при воздействии вибрации на человека.
Приложение. Определение жесткости цилиндрической мембраны [16]
Уравнения равновесия мембраны
(П.1)
$\frac{{\partial {{N}_{x}}}}{{\partial x}} + \frac{{\partial {{N}_{{x{\theta }}}}}}{{r\partial {\theta }}} = 0,$(П.2)
$\frac{{\partial {{N}_{{x{\theta }}}}}}{{\partial x}} + \frac{{\partial {{N}_{{\theta }}}}}{{r\partial {\theta }}} = 0,$где Nx, Nθ – напряжения на единицу длины в направлениях x и θ, Nxθ – касательные напряжения в направлениях x и θ, P – давление.
Из (П.3), (П.4)
Из (П.5) и (П. 2)
(П.6)
${{N}_{{x{\theta }}}} = 2A\frac{b}{{\pi }}\cos (2{\theta })\cos \left( {{\pi }\frac{x}{b}} \right).$Из (П.6), (П.1)
(П.7)
${{N}_{{x{\theta }}}} = 2A\frac{b}{{\pi }}\cos (2{\theta })\cos \left( {{\pi }\frac{x}{b}} \right).$Произвольные постоянные равны нулю в силу принятых граничных условий: Nx = 0 при $x = \pm b$. Из этих уравнений найдем деформации
(П.8)
${{{\varepsilon }}_{x}} = \frac{{\partial u}}{{\partial x}} = \frac{1}{{Eh}}({{N}_{{\text{x}}}} - {\nu }{{N}_{{\theta }}}),$(П.9)
${{{\varepsilon }}_{{\theta }}} = \frac{{\partial \nu }}{{r\partial x}} - \frac{w}{r} = \frac{1}{{Ed}}({{N}_{{\theta }}} - {\nu }{{N}_{x}}),$(П.10)
${{{\gamma }}_{{x{\theta }}}} = \frac{{\partial u}}{{r\partial {\theta }}} + \frac{{\partial \nu }}{{\partial x}} = \frac{{2(1 + {\nu )}}}{{Ed}}{{N}_{x}}_{{\theta }},$Последнее соотношение используется в статье.
Список литературы
Mandelbrot. B. Fractal Geometry of Nature. New York, W. H. Freeman. 1982. 656 c.
Банах Л.Я. Распространение упругих волн в динамически-самоподобных структурах (динамический фрактал) //Акустический журнал. 2020. № 3. С. 265.
Banakh L.Ya., Barmina O.V. Dynamic Properties of self-Similar Structures in Mechanics // Journal of Machinery Manufacture and Reliability. 2013. V. 42. № 2. P. 89.
Артоболевский И.И., Бобровницкий Ю.И., Генкин М.Д. Введение в акустическую динамику машин. М.: Наука, 1979. 295 с.
Banakh L. The dynamic-selfsimilar lattice as the vibroisolation systems // Vibroengineering Procedia at the 49rd International Conference on Vibroengineering. 2019. P. 54.
Astashev V.K., Babitsky V.I. Ultrasonic Processes and Machines. Dynamics, Control and Applications. Springer, 2007. 330 p.
Рабинович М.И., Трубецков Д.И. Введение в теорию колебаний и волн. М.: Наука, 1984. 432 с.
Banakh L.Ya., Kempner M.L. Vibrations of mechanical systems with regular structure. Springer, Heidelberg, Dordrecht, London, New York, 2010. 262 p.
Bellman R. Introduction to matrix analysis. MCGRAW-Hill book Company. New York, Toronto, London, 1960. 328 p.
Lowenstein W.R., Skalak R. Mechanical Transmission in a pacinian corpuscle. An analysis and a theory // J. Physiol. 1966. V. 182. P. 346.
Миркин А.С., Тучков Б.С., Машанский В.Ф. Некоторые особенности ультраструктуры телец Пачини // Цитология. 1967. Т. 9. № 6. С. 633.
Машанский В.Ф., Миркин А.С., Винниченко Л.Н. Влияние вибрационного раздражения на ультраструктуру механорецептора – тельца Пачини // Цитология. 1969. Т. 11. № 12. С. 1572.
Кубарко А.И., Семенович А.А., Переверзев В.А. Нормальная физиология. Минск: Вышэйшая школа, 2013. 542 с.
Тимошенко С.П., Войнович-Кригер С. Пластины и оболочки. М.: Наука, 1966.
Повх И.Л. Техническая гидромеханика. Машиностроение, 1976. 502 с.
Бобровницкий Ю.И., Томилина Т.М. Поглощение звука и метаматериалы (обзор) // Акустический журнал. 2018. Т. 64. № 5. С. 517.
Bobrovnitskii Y.I., Tomilina T.M. Sound absorption and metamaterials: a review // Acoustical Physics. 2018. V. 64. № 5. C. 519.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин