Проблемы машиностроения и надежности машин, 2021, № 2, стр. 25-32
Исследование колебаний винтового стержня в условиях вихревого обтекания
Г. А. Щеглов *
Московский государственный технический университет имени Н.Э. Баумана
Москва, Россия
* E-mail: shcheglov_ga@bmstu.ru
Поступила в редакцию 04.02.2020
После доработки 29.11.2020
Принята к публикации 18.12.2020
Аннотация
С использованием разложения по собственным формам колебаний и метода вихревых элементов исследованы режимы малых колебаний стержня, ось которого представляет собой трехвитковую цилиндрическую спираль. Колебания возбуждаются пульсациями давления, которые возникают вследствие процессов интенсивного вихреобразования при обтекании стержня пространственным потоком несжимаемой среды. Показан полигармонический характер нестационарного нагружения и отклик колебательной системы, а также возможность возникновения внутренних резонансов в подобной системе. Результаты и методику моделирования можно использовать для оценки долговечности спиральных пучков труб теплообменных аппаратов.
На долговечность теплообменных аппаратов и парогенераторов энергетического оборудования существенно влияют параметры вибраций пучков труб в потоке теплоносителя [1]. Изучению колебаний стержней под действием нестационарных гидродинамических нагрузок посвящено значительное число работ, обзоры которых можно найти в монографиях [2–5]. Основными факторами, возбуждающими вибрации, являются пульсации давления вследствие образования вихрей Кармана и явления типа бафтинга, возникающие при взаимодействии стержня с вихревыми структурами образованными выше по потоку.
Наибольшее число исследований проведено для стержней, форма которых прямолинейна или близка к ней. В этом случае эффектами пространственного обтекания можно пренебречь и использовать математические модели, основанные на гипотезе плоских сечений, уменьшая размерность задачи. В меньшей степени изучены сильно искривленные пространственные стержни. Задача исследования гидроупругой динамики винтовых стержней, ось которых имеет форму цилиндрической или конической спирали является актуальной при проектировании спиральных теплообменных аппаратов и оценке их надежности с точки зрения вибраций труб и их фреттинг-износа [6, 7]. Как правило, в потоке теплоносителя находятся пучки из нескольких десятков труб, подкрепленные дистанцирующими решетками [8–10]. При этом шаг винтовой линии много меньше диаметра спирали. Исследование колебаний труб при таком режиме обтекания производится не для целой спирали, а для ее отрезков между дистанцирующими решетками поскольку при вихревом обтекании возникают не крупные вихри типа вихрей Кармана, а более мелкие турбулентные вихревые сгустки. Здесь эффективными оказываются сеточные методы вычислительной гидродинамики, использующие подходящие модели турбулентности [11].
Однако в некоторых типах парогенераторов используются теплообменные трубы, имеющие подъемный витой участок с шагом спирали порядка радиуса [12]. В подобных трубопроводах вихри Кармана, возникшие на наветренных витках спирали взаимодействуют с последующими витками. Пространственный характер обтекания не позволяет использовать гипотезу плоских сечений. Аэроупругая динамика таких стержней зависит от нелинейных взаимосвязей между процессами интенсивного вихреобразования и упругих перемещений. Пульсации нагрузки, действующей со стороны потока на подветренные витки, могут вызывать колебания наветренных витков, изменяя за счет появления дополнительной виброскорости обтекаемой поверхности условия их обтекания и, как следствие, параметры образования завихренности.
Для численного моделирования динамики крупных вихревых структур в пучках труб в инженерных приложениях эффективными оказываются лагранжевы вихревые методы в силу меньшей схемной вязкости и отсутствия подвижной сетки в области течения [13, 14]. Модификация метода вихревых элементов, использующая симметричные вортоны-отрезки, позволяет моделировать гидроупругие колебания конструкций при пространственном обтекании [15, 16]. В статье рассмотрено применение данной методики для исследования колебаний модельного винтового стержня в условиях вихревого обтекания. Вопросы связанные с теплообменом и течением жидкости в трубе не рассматриваются.
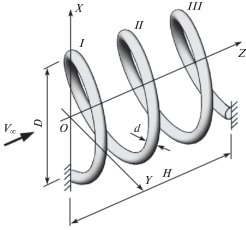
Постановка задачи и методика решения. Исследуется заделанный по краям винтовой стержень постоянного поперечного сечения, состоящий из трех витков. Неподвижная система координат OXYZ введена как показано на рис. 1. Стержень находится в безграничном потоке несжимаемой среды, имеющем постоянную скорость, вектор которой ${{{\mathbf{V}}}_{\infty }}$ сонаправлен с осью спирали (с осью OZ). Витки, по мере удаления от начала координат обозначены как передний (наветренный), средний, и задний. Торцевые поверхности на концах стержня считаются абсолютно жесткими и также обтекаются потоком. Влияние силы тяжести и других объемных сил не учитывается.
Общая математическая постановка задачи гидроупругости, включает уравнения малых колебаний стержня, уравнение неразрывности среды и уравнение сохранения импульса. Уравнения связаны граничным условием равенства скорости среды и скорости тела в точках обтекаемой поверхности (условием прилипания), а также зависимостью распределения давления среды по поверхности стержня от параметров его движения. Также вводится условие затухания возмущений скорости среды на бесконечном удалении от обтекаемого тела и условия заделки концов стержня. Начальными условиями являются равновесное положение стержня и поле скоростей среды, соответствующее потенциальному бесциркуляционному обтеканию стержня.
При расчете течения среды используется подход Прандтля: влияние вязкости считается пренебрежимо малым везде, кроме тонкого пристеночного слоя вблизи поверхности тела, где происходит образование завихренности ${\mathbf{\Omega }} = rot{\mathbf{V}}$. Такое допущение позволяет рассматривать уравнение сохранения импульса в виде уравнения Гельмгольца и осуществлять его решение бессеточным лагранжевым методом вихревых элементов с использованием ${{N}_{V}}$ симметричных вортонов-отрезков. По известным параметрам вихревых элементов (${{{\mathbf{r}}}_{i}}$ – радиус-вектор лагранжева маркера, ${{{\mathbf{h}}}_{i}}$ – направляющий вектор и ${{\Gamma }_{i}}$ – интенсивность) скорость среды восстанавливается по закону Био–Савара, а поле давления – с использованием аналога интеграла Коши–Лагранжа [17]. Это дает тождественное удовлетворение уравнения неразрывности и граничного условия на бесконечности. Эволюция параметров описывается системой обыкновенных дифференциальных уравнений [15]
(1)
$\frac{{d{{{\mathbf{r}}}_{i}}}}{{dt}} = {\mathbf{V}}({{{\mathbf{r}}}_{i}},t),\quad \frac{{d{{{\mathbf{h}}}_{i}}}}{{dt}} = \left( {\nabla {\mathbf{V}}({{{\mathbf{r}}}_{i}})} \right) \cdot {{{\mathbf{h}}}_{i}},\quad \frac{{d{{\Gamma }_{i}}}}{{dt}} = 0,\quad (i = 1...{{N}_{V}}).$Интегрирование уравнений (1) производится численным методом первого порядка с шагом $\Delta t$. Удовлетворение граничных условий на обтекаемой поверхности осуществляется введением потока завихренности [18]. По всей поверхности тела на каждом шаге интегрирования производится генерация вихревых элементов, что приводит к увеличению размерности ${{N}_{V}}$ системы (1). Начальные условия для новых уравнений задаются параметрами рожденных элементов: маркеры и векторы определяются сеткой вихревых рамок, а интенсивность элементов находится из условия равенства нормальных компонент скоростей тела и среды в контрольных точках на поверхности.
Уравнение динамики стержня приводится методом разложения по $q$ собственным формам колебаний к системе обыкновенных дифференциальных уравнений относительно вектора обобщенных координат ${\mathbf{s}}$
(2)
${\mathbf{\ddot {s}}} + n{{\omega }_{{{\text{diag}}}}}{\mathbf{\dot {s}}} + \omega _{{{\text{diag}}}}^{2}{\mathbf{s}} = \Phi ,$На i-м шаге алгоритма методом вихревых элементов проводится удовлетворение граничных условий, осуществляется генерация ВЭ и находится поле давлений среды на поверхности, вектор сосредоточенных гидродинамических нагрузок в узлах панелей ${{{\mathbf{F}}}_{G}}$ и вектор $\Phi = {{{\mathbf{A}}}^{T}}{{{\mathbf{F}}}_{G}}$. Считается, что обобщенные силы на шаге интегрирования $\Delta t$ остаются постоянными. Это дает возможность найти решение (2) аналитически и определить обобщенные координаты и скорости ${{s}_{k}}({{t}_{{i + 1}}})$ и ${{\dot {s}}_{k}}({{t}_{{i + 1}}})$ для ${{t}_{{i + 1}}} = {{t}_{i}} + \Delta t$ по известным значениям на предыдущем шаге ${{s}_{k}}({{t}_{i}})$ и ${{\dot {s}}_{k}}({{t}_{i}})$($k = 1 \ldots q$). Восстановленные по обобщенным координатам перемещения узлов панелей ${\mathbf{u}} = {\mathbf{As}}$ позволяют построить деформированную обтекаемую поверхность и найти скорости поверхности в контрольных точках. Далее проводится интегрирование уравнений (1) и осуществляется переход к следующему шагу. Расчет производится до достижения заданного конечного времени счета $T = \Delta t\,N$, где $N$ – число шагов интегрирования. Более подробное описание и результаты тестирования алгоритма можно найти в работе [16].
Результаты моделирования. В расчете при переходе к безразмерным величинам шаг витков спирали винтового стержня взят в качестве единицы длины $H = 1.0$; диаметр винтовой окружности при этом равен $D = 2.0$; поперечное сечение стержня – круговое кольцо диаметром $d = 0.2$ и толщиной $b = 0.001$. Единица массы выбрана из условия, что безразмерная плотность среды равна $\rho = 100.0$. Скорость невозмущенного потока среды имеет единичный модуль ${{V}_{\infty }} = 1.0$, т.е. частицы среды проходят расстояние, равное шагу спирали, что определяет единицу времени. Параметры материала стержня: модуль упругости $E = {{10}^{{10}}}$; плотность $\gamma = 6000$; коэффициент Пуассона $\nu = 0.3$. При этом соотношение погонных масс стержня и среды, занимающей эквивалентный объем, равно 1.2.
Использованная в расчетах сетка имела 240 ячеек вдоль винтовой линии и 8 ячеек в окружном направлении (общая размерность 1920 ячеек). Рассматривались первые десять тонов собственных колебаний ($q = 10$). Модальный анализ проведен в программе MSC Nastran с использованием решателя 103 и конечных элементов типа QUAD4. Собственные частоты стержня равны ${{\omega }_{1}} = 0.58$ Гц; ${{\omega }_{2}} = 0.73$ Гц; ${{\omega }_{3}} = 0.82$ Гц; ${{\omega }_{4}} = 1.00$ Гц; ${{\omega }_{5}} = 1.11$ Гц; ${{\omega }_{6}} = 1.42$ Гц; ${{\omega }_{7}} = 1.55$ Гц; ${{\omega }_{8}} = 1.63$ Гц; ${{\omega }_{9}} = 1.75$ Гц; ${{\omega }_{{10}}} = 2.16$ Гц.
Расчет методом вихревых элементов проводился с параметрами: радиус сглаживания поля скорости $\varepsilon = 0.08$; расстояние от поверхности до рождающегося вихревого элемента $\delta = 0.02$. Рассчитывался переходный режим длительностью $T = 30.0$, с шагом $\Delta t = 0.03$. Для уменьшения начального возмущения скорость среды за первые десять шагов увеличивалась от нуля до ${{V}_{\infty }}$. В области течения находилось от 30 до 60 тысяч вихревых элементов. Для сокращения размерности задачи вихревой след рассматривался только на расстоянии ${{L}_{f}} = 11.0$. Алгоритмы параллельных вычислений, реализованные с использованием технологий MPI и CUDA позволили повысить производительность вычислений более чем в 20 раз по сравнению с работой [15]. Расчет одного переходного режима на рабочей станции, оснащенной процессором Intel Core i9 (18 вычислительных ядер) и графическим ускорителем NVidia Tesla V100 занимал от 0.7–1.0 часа.
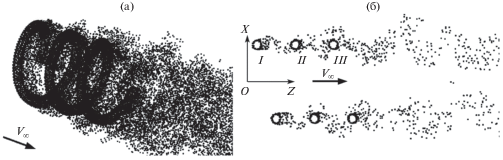
Пример вихревого следа за винтовым стержнем показан на рис. 2а, где точками отмечены маркеры вихревых элементов. На рис. 2б показаны вихревые структуры (визуализируемые маркерами) в поперечном сечении вихревого следа. Характерные сечения переднего среднего и заднего витков, центры которых лежат в плоскости OXZ обозначены как I, II, III. Видно, что вихри Кармана, формирующиеся за витком I, воздействуют на последующие витки II и III. Пространственный характер течения приводит к обтеканию витков под местными углами атаки вследствие чего гидродинамическая нагрузка, приведенная к центрам сечений имеет не только продольную и поперечную, но и боковую составляющую.
Рис. 2.
Вихревой след (точками обозначены маркеры вихревых элементов): (а) – общий вид, (б) – вид в сечении плоскостью OXZ.
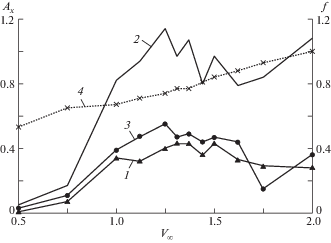
Полученная в расчетах зависимость частоты схода вихрей $f$ в сечении I от скорости набегающего потока, приведенная на рис. 3, показывает, что в диапазоне скоростей $0.50 \leqslant {{V}_{\infty }} \leqslant 2.00$ могут возникать резонансы по первым четырем собственным частотам. Первая собственная форма соответствует скручиванию витков спирали в фазе (вращение сечений стержня вокруг оси OZ с одновременным изменением радиуса спирали). Вторая и третья формы соответствуют смещениям витков спирали вдоль осей OX и OY соответственно. Четвертая собственная форма соответствует скручиванию переднего и заднего витков в противофазе к среднему витку.
Рис. 3.
Зависимость от скорости набегающего потока частоты схода вихрей и амплитуды поперечных колебаний сечений в направлении оси OX: 1 – сечение I; 2 – сечение II; 3 – сечение III; 4 – частота схода вихрей $f$, Гц.
Известно, что пульсации поперечной компоненты гидродинамической нагрузки при обтекании кругового профиля происходят с частотой схода вихрей, а пульсации продольной компоненты нагрузки – с удвоенной частотой. При обтекании винтового стержня за счет взаимосвязи между движением витков и режимом вихреобразования пульсации всех трех компонент главных векторов гидродинамической нагрузки, приведенных к центрам сечений I, II, III содержат две гармоники: частоту схода вихрей $f$ и удвоенную частоту. Для сечений II и III витков находящихся в спутном следе вихрей, образующихся за передним витком в спектре пульсаций заметны также гармоники $f{\text{/}}2$ и $3f$.
Гидродинамическое нагружение вызывает квазистатическое смещение витков и их колебаний относительно нового положения равновесия. Квазистатические (осредненные по времени) перемещения монотонно возрастают с увеличением скоростного напора. Перемещения центров сечений I, II, III, отнесенные к диаметру сечения стержня d, для характерных значений ${{V}_{\infty }}$ приведены в табл. 1. Как показано на рис. 4а. под действием продольной квазистатической нагрузки витки смещаются вдоль оси спирали, а также, в силу наличия местных углов атаки, происходит увеличение радиуса витков спирали. Средний виток, как наименее жесткий, деформируется сильнее всего.
Таблица 1.
Квазистатические перемещения сечений стержня (в долях d)
| V | ${{S}_{X}}$ | ${{S}_{Y}}$ | ${{S}_{Z}}$ | ||||||
|---|---|---|---|---|---|---|---|---|---|
| I | II | III | I | II | III | I | II | III | |
| 1.00 | –0.05 | 0.03 | 0.04 | 0.08 | 0.17 | 0.05 | 0.06 | 0.11 | 0.04 |
| 1.50 | –0.12 | 0.04 | 0.11 | 0.23 | 0.37 | 0.12 | 0.16 | 0.26 | 0.10 |
| 2.00 | –0.24 | 0.05 | 0.18 | 0.45 | 0.81 | 0.19 | 0.24 | 0.55 | 0.21 |
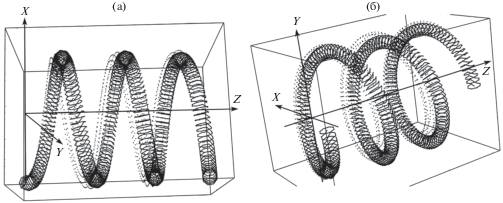
Рис. 4.
Перемещения стержня в потоке (точки – исходная форма, линии – деформированное состояние): (а) – квазистатическое отклонение от равновесия для скорости потока ${{V}_{\infty }} = 2.0\,$; (б) – перемещения при резонансе $f \approx {{\omega }_{2}}$ (${{V}_{\infty }} = 1.25$).
Амплитуды колебаний сечений стержня, отнесенные к диаметру сечения стержня d, даны в табл. 2. Максимальные амплитуды колебаний рассмотренных сечений достигаются в направлении оси OX. На рис. 3 дана зависимость амплитуды этих радиальных колебаний от скорости набегающего потока, показывающая наличие резонанса частоты схода вихрей со второй собственной частотой в диапазоне скоростей близких к ${{V}_{\infty }} = 1.25$. Перемещения стержня при резонансе показаны на рис. 4б. Спектры колебаний по всем трем компонентам перемещений центров сечений I, II, III содержат гармоники частоты схода вихрей $f$ и $2f$, а также первые четыре собственных частоты. Более высокие частоты, в том числе гармоника $3f$, по-видимому, демпфируются потоком.
Таблица 2.
Амплитуды вибраций сечений стержня (в долях d)
| V | ${{A}_{X}}$ | ${{A}_{Y}}$ | ${{A}_{Z}}$ | ||||||
|---|---|---|---|---|---|---|---|---|---|
| I | II | III | I | II | III | I | II | III | |
| 1.00 | 0.34 | 0.82 | 0.39 | 0.53 | 0.57 | 0.35 | 0.08 | 0.23 | 0.21 |
| 1.25 | 0.40 | 1.14 | 0.55 | 0.59 | 0.38 | 0.49 | 0.11 | 0.18 | 0.27 |
| 1.50 | 0.43 | 0.97 | 0.47 | 0.72 | 0.87 | 0.30 | 0.20 | 0.34 | 0.31 |
| 1.75 | 0.29 | 0.84 | 0.15 | 0.51 | 0.87 | 0.28 | 0.24 | 0.37 | 0.34 |
| 2.00 | 0.28 | 1.08 | 0.36 | 0.50 | 1.02 | 0.47 | 0.32 | 0.50 | 0.42 |
Поскольку у спирального стержня первые собственные частоты являются близкими, отличающимися не более чем на 20% при внешнем воздействии возможно возникновение внутренних резонансов между соседними тонами. Моделирование показало, что при скоростях потока $1.25 \leqslant {{V}_{\infty }} \leqslant 1.50$ колебания, возбуждаемые сходом вихрей сопровождаются внутренним резонансом между вторым и третьим тонами, что выражается в биениях между обобщенными координатами ${{s}_{2}}$ и ${{s}_{3}}$. Аналогично известному эффекту симпатических маятников, поперечные колебания витков в направлении оси OX (рис. 4б) периодически сменяются поперечными колебаниями витков в направлении оси OY. При скорости потока ${{V}_{\infty }} = 2.0\,$ также наблюдаются биения между обобщенными координатами ${{s}_{4}}$ и ${{s}_{5}}$, которые, однако, имеют малую амплитуду и не столь заметны при рассмотренных скоростях потока.
Выводы. Результаты моделирования показывают, что гидроупругие колебания сечений рассмотренного винтового стержня в целом подобны колебаниям сечений пучка труб. Однако в силу пространственного обтекания и наличия местных углов атаки в каждом сечении возникает дополнительная сила, действующая из плоскости сечения. Вибрация витков спирали возникает под действием полигармонической нагрузки в спектре которой проявляются не только частота схода вихрей с первого витка, но и ее удвоенная, утроенная и половинная гармоники. Отклик стержня также является полигармоническим. Наиболее интересным является возбуждение в системе внутренних резонансов, возникающие из-за близости собственных частот колебаний стержня. Результаты и методику моделирования можно использовать для оценки долговечности спиральных пучков труб теплообменных аппаратов.
Список литературы
Жукаускас А., Улинскас Р., Катинас В. Гидродинамика и вибрации обтекаемых пучков труб. Вильнюс: Мокслас, 1984. 312 с.
Светлицкий В.А. Механика трубопроводов и шлангов М.: Маш., 1982. 279 с.
Девнин С.И. Гидроупругость конструкций при отрывном обтекании. Л.: Судостроение, 1975. 192 с.
Blevins R.D. Flow-Induced Vibration. Sec. Ed. Malabar, FL: Krieger Publ., 1990. 254 p.
Robinson R.W., Hamilton J. A criterion for assessing wind induced crossflow vortex vibrations in wind sensitive structures. Health and Safety Executive – Offshore Technology Report OTH 92 379. London: Brown & Root Limited, 1992. 62 p.
Kven Umadhav, Sudhanshu Kumar, Chandrashekar Goud V. Performance analysis of different heat exchanger design using CFD simulation // Int. J. of Research in advanced engineering technologies. 2017. V. 6. Iss. 2. P. 158.
Ke Yan, Pei-qi Ge, Jun Hong. Experimental study of shell side flow-induced vibration of conical spiral tube bundle // J. of Hydrodynamics. 2013. V. 25. Iss. 5. P. 695.
Heqin Xu, Mallet M., Liszkai T. Turbulent Buffeting of Helical Coil Steam Generator Tubes // Proc. ASME 2014 Pressure Vessels and Piping Conference Vol. 4: Fluid-Structure Interaction. Anaheim, California, USA, July 20–24, 2014. No. PVP2014-28868, V004T04A075. 9 p.
Chen S.S., Jendrzejczyk J.A., Wambsganss M.W. Tube vibration in a half-scale sector model of a helical tube steam generator // J. of Sound and Vibration. 1983. № 91 (4). P. 539.
Marcum W.R., Harmon P.L. Characterizing fluid-structure interactions of a helical coil in cross flow // J. of Fluids and Structures. 2016. V. 65. P. 355.
Merzari E., Yuan H., Kraus A., Obabko A., Fischer P., Solberg J., Lee S., Lai J., Delgado M., Hassan Y. High-Fidelity Simulation of Flow-Induced Vibrations in Helical Steam Generators for Small Modular Reactors // Nuclear Technology. 2019. V. 205. Iss. 1–2. P. 33.
Васильев С.В., Кузьминов Ю.В. Парогенератор РУ БРЕСТ-ОД-300. Проектное направ-ление “ПРОРЫВ”: результаты реализации новой технологической платформы ядерной энергетики 3–4 апреля 2015. 18 с. http://www.innov-rosatom.ru/files/articles/634886229ac31981e4a37a00790a2e9b.pdf
Каплунов С.М., Вальес Н.Г., Самолысов А.В., Марчевская О.А. Определение критических параметров обтекания пучка труб методом численного эксперимента // Теплоэнергетика. 2015. № 8. С. 57.
Самолысов А.В. Повышение вибропрочности трубных пучков теплообменных аппаратов при гидроупругом возбуждении колебаний: дис. … канд. техн. наук: 01.02.06. М. 2016. 117 с.
Щеглов Г.А. Использование вортонов для расчета колебаний балки в пространственном потоке // Изв. РАН Проблемы машиностроения и надежности машин. 2009. № 4. С. 8.
Ермаков А.В., Щеглов Г.А. Моделирование методом вихревых элементов динамики цилиндрической оболочки в пространственном потоке жидкости // Изв. вузов. Машиностроение. 2014. № 3. С. 35.
Dynnikova G.Ya. The Integral Formula for Pressure Field in the Nonstationary Barotropic Flows of Viscous Fluid // J. of Mathematical Fluid Mechanics. 2014. V. 16. Iss. 1. P. 145.
Cottet G.-H., Koumoutsakos P. Vortex Methods: Theory and Practice. Cambridge: Cambridge University Press, 2000. 320 p.
Дополнительные материалы отсутствуют.
Инструменты
Проблемы машиностроения и надежности машин