1. На главную
  2. Электронные версии
  3. Проблемы машиностроения и надежности машин
  4. № 1, 2022

Проблемы машиностроения и надежности машин, 2022, № 1, стр. 39-46

Решение задач динамики манипуляционного механизма с шестью степенями свободы

С. В. Хейло 1, *, О. А. Гарин 2, А. Н. Терехова 1, В. Е. Прохорович 3, А. В. Духов 4

1 Российский государственный университет им. А.Н. Косыгина (Технологии. Дизайн. Искусство)
Москва, Россия

2 Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия

3 Национальный исследовательский университет ИТМО (Институт точной механики и оптики)
Санкт-Петербург, Россия

4 Институт машиноведения им. А.А. Благонравова РАН
Москва, Россия

* E-mail: sheilo@yandex.ru

Поступила в редакцию 29.06.2021
После доработки 12.08.2021
Принята к публикации 24.08.2021

Полный текст (PDF)

Аннотация

В статье рассмотрены механизмы параллельной структуры с шестью степенями свободы, c шестью линейными двигателями, установленными на основании таким образом, что оси двигателей параллельны осям неподвижной системы координат. Особенностью таких механизмов является то, что при одинаковом перемещении двух двигателей, оси которых параллельны одной оси, передаточное отношение от двигателей к выходному звену равно единице. Представлен кинематический анализ, а также определены силовые винты, передаваемые со стороны кинематических цепей на выходное звено с учетом моментов этих силовых винтов относительно осей подвижной системы координат. Показано решение прямой задачи динамики для некоторого положения механизма.

Ключевые слова: пространственные механизмы, динамический анализ, винтовое исчисление

Одним из эффективных средств решения многих технических задач, возникающих в технологических, измерительных, транспортных системах, являются механизмы параллельной структуры [1–6]. При исследовании таких устройств важное значение имеет кинематический и динамический анализ [7–9].

Одним из подходов к определению свойств механизмов параллельной структуры является винтовое исчисление, которое позволяет получить качественные характеристики, не прибегая к сложным математическим выкладкам [10–14].

Механизмы параллельной структуры обладают свойством кинематической и динамической связанности между приводами. Любое простое движение, например, по прямой линии, требует согласованного движения во всех кинематических цепях, при этом усилие в каждом приводе зависит от положения скорости и ускорения во всех других приводах механизма. Указанное свойство затрудняет управление этими устройствами, понижает их динамическую точность. Кроме того, что передаточное отношение между каждым приводом и выходным звеном также переменно и зависит от положения.

Для того чтобы устранить указанные недостатки были предложены различные технические решения. В частности, К. Конгом и К. Госленом был предложен механизм, обладающий свойством изоморфности [15]. В таком механизме имеет место постоянное передаточное отношение равное единице между любым приводом и выходным звеном. Этот механизм обладает тремя степенями свободы, и выходное звено может перемещаться по трем координатам только с постоянной ориентацией.

При синтезе механизмов с шестью степенями свободы проблема развязки приобретает особое значение [16, 17]. Ряд оригинальных решений был получен К. Миановски [18]. Он использовал подход, когда вращательные и поступательные двигатели установлены на основании с совмещением их осей. Таким образом, мы получаем две схемы механизмов с тремя степенями свободы в каждом.

Чтобы повысить функциональные возможности такого механизма И. Боневым с соавторами был предложен механизм, в котором имеет место шесть кинематических цепей расположенных попарно противоположно друг другу [19]. При одинаковых скоростях в приводах кинематических цепей имеет место поступательное движение выходного звена. Если скорости не равны, то движение вращательное.

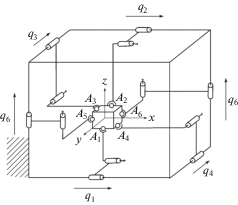
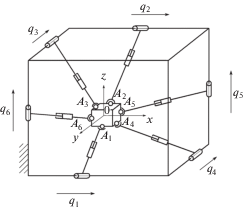
В настоящей статье рассматриваются новые механизмы (рис. 1, 2). Для этих механизмов были установлены кинематические свойства и решена задача о положении [20].

Рис. 1.

Механизм 6PRRS.

Рис. 2.

Механизм 6PRPS.

В работе ставится задача определения силовых винтов, действующих на выходное звено со стороны кинематических цепей. Этот анализ необходим для решения кинематических и динамических задач. Кроме того, решается задача определения моментов силовых винтов относительно главных центральных осей инерции выходного звена. Этот анализ необходим в тех случаях, когда имеет место вращательное движение выходного звена.

Центр неподвижной системы координат Oxyz поместим в точке пересечения диагоналей параллелепипеда, вдоль ребер которого расположены приводы. Центр связанной с выходным звеном подвижной системы координат Omξηζ совпадает с точкой пересечения главных центральных осей инерции выходного звена. Примем, что в начальном положении центры подвижной и неподвижной систем координат совпадают. Координаты центров сферических шарниров, расположенных на выходном звене: A1(0, a, –a); A2 (0, –a, a); A3(–a, 0, a); A4(a, 0, –a); A5(–a, a, 0); A6(a, –a, 0).

Усилия, создаваемые приводами, направлены параллельно осям неподвижной системы координат и передаются кинематическими цепями без изменения модуля и направления на выходное звено.

Каждый из моментов внешних сил, действующих на выходное звено, можно найти как произведение модуля усилия, передаваемого со стороны приводов и относительного момента единичного силового винта и орта оси мобильной системы координат, приведенных к общему центру.

Для нахождения относительных моментов решим задачу о положениях, используя метод Денавита–Хартенберга. Пусть некоторое текущее положение выходного звена задано углами поворота α, β, γ системы координат выходного звена Omξηζ относительно осей Ox, Oy, Oz системы координат основания соответственно и координатами точки Om(x; y; z) в системе Oxyz.

Координаты точек A1, A2, …, A6 – центров сферических пар на выходном звене выражены в подвижной системе координат и имеют вид

$A_{1}^{m} = \left( {\begin{array}{*{20}{c}} 0 \\ a \\ { - a} \\ 1 \end{array}} \right),\quad A_{2}^{m} = \left( {\begin{array}{*{20}{c}} 0 \\ { - a} \\ a \\ 1 \end{array}} \right),\quad A_{3}^{m} = \left( {\begin{array}{*{20}{c}} { - a} \\ 0 \\ a \\ 1 \end{array}} \right),\quad A_{4}^{m} = \left( {\begin{array}{*{20}{c}} a \\ 0 \\ { - a} \\ 1 \end{array}} \right),\quad A_{5}^{m} = \left( {\begin{array}{*{20}{c}} { - a} \\ a \\ 0 \\ 1 \end{array}} \right),\quad A_{6}^{m} = \left( {\begin{array}{*{20}{c}} a \\ { - a} \\ 0 \\ 1 \end{array}} \right).$

Координаты точек выходного звена в системе координат основания равны

$\begin{gathered} A_{1}^{b} = {{M}_{{bm}}} \cdot А_{1}^{m},\quad A_{2}^{b} = {{M}_{{bm}}} \cdot А_{2}^{m},\quad A_{3}^{b} = {{M}_{{bm}}} \cdot А_{3}^{m}, \\ A_{4}^{b} = {{M}_{{bm}}} \cdot А_{4}^{m},\quad A_{5}^{b} = {{M}_{{bm}}} \cdot А_{5}^{m},\quad A_{6}^{b} = {{M}_{{bm}}} \cdot А_{6}^{m}. \\ \end{gathered} $

Здесь ${{M}_{{bm}}} = \left( {\begin{array}{*{20}{c}} R&T \\ 0&1 \end{array}} \right)$ – матрица Денавита–Хартенберга; $R = {{R}_{\gamma }} \cdot {{R}_{\beta }} \cdot {{R}_{\alpha }}$ матрица поворотов, где

${{R}_{\alpha }} = \left( {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos \alpha }&{ - \sin \alpha } \\ 0&{\sin \alpha }&{\cos \alpha } \end{array}} \right),\quad {{R}_{\beta }} = \left( {\begin{array}{*{20}{c}} {\cos \beta }&0&{\sin \beta } \\ 0&1&0 \\ { - \sin \beta }&0&{\cos \beta } \end{array}} \right),\quad {{R}_{\gamma }} = \left( {\begin{array}{*{20}{c}} {\cos \gamma }&{ - \sin \gamma }&0 \\ {\sin \gamma }&{\cos \gamma }&0 \\ 0&0&1 \end{array}} \right)$

матрицы поворотов, описывающих вращение выходного звена относительно осей Ox, Oy, Oz соответственно; $T = \left( {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right)$ – матрица перемещения.

Далее следует определить плюккеровы координаты силовых винтов ${{{\mathbf{R}}}_{i}}({{{\mathbf{r}}}_{i}},{\mathbf{r}}_{i}^{0})$, передаваемых на выходное звено. Векторы силовых винтов первой и второй кинематических цепей действуют вдоль оси Ox, третьей и четвертой кинематических цепей вдоль оси Oy, векторы силовых винтов пятой и шестой кинематических цепей действуют вдоль оси Oz. Таким образом, координаты векторных частей силовых винтов можно представить как

${{{\mathbf{r}}}_{{\text{1}}}} = \left( {\begin{array}{*{20}{c}} 1 \\ 0 \\ 0 \end{array}} \right),\quad {{{\mathbf{r}}}_{{\text{2}}}} = \left( {\begin{array}{*{20}{c}} 1 \\ 0 \\ 0 \end{array}} \right),\quad {{{\mathbf{r}}}_{{\text{3}}}} = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \\ 0 \end{array}} \right),\quad {{{\mathbf{r}}}_{{\text{4}}}} = \left( {\begin{array}{*{20}{c}} 0 \\ 1 \\ 0 \end{array}} \right),\quad {{{\mathbf{r}}}_{{\text{5}}}} = \left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ 1 \end{array}} \right),\quad {{{\mathbf{r}}}_{{\text{6}}}} = \left( {\begin{array}{*{20}{c}} 0 \\ 0 \\ 1 \end{array}} \right).$

Плюккеровы координаты моментной части силовых винтов представляют собой векторное произведение радиус-вектора ${{{\mathbf{r}}}_{{{{A}_{i}}}}}$ точки Аi на соответствующий вектор силового винта ${\mathbf{r}}_{i}^{0}$, которые выражены в системе координат основания

${\mathbf{r}}_{i}^{0} = {{{\mathbf{r}}}_{{{{A}_{i}}}}} \cdot {{{\mathbf{r}}}_{i}}$.

Далее найдем плюккеровы координаты (ξ, ξ0), (η, η0), (ζ, ζ0) ортов осей подвижной системы координат в системе координат основания и относительные моменты единичных силовых винтов и ортов осей ξ, η, ζ. Каждая из кинематических цепей передает усилие Pi, задаваемое в i-м приводе, в точку крепления выходного звена Аi. Моменты сил Pi относительно осей подвижной системы координат найдем как относительные моменты вектора ri единичного силового винта Ri, задающего направление Pi, и ортов осей подвижной системы координат, приведя их к началу неподвижной системы отсчета

$\begin{gathered} {\text{mom}}({{{\mathbf{R}}}_{i}},{\mathbf{\xi }}) = {{{\mathbf{r}}}_{i}} \cdot {{{\mathbf{\xi }}}^{0}} + {\mathbf{r}}_{i}^{0} \cdot {\mathbf{\xi }};\quad {\text{mom}}({{{\mathbf{R}}}_{i}},{\mathbf{\eta }}) = {{{\mathbf{r}}}_{i}} \cdot {{{\mathbf{\eta }}}^{0}} + {\mathbf{r}}_{i}^{0} \cdot {\mathbf{\eta }}; \\ {\text{mom}}({{{\mathbf{R}}}_{i}},{\mathbf{\zeta }}) = {{{\mathbf{r}}}_{i}} \cdot {{{\mathbf{\zeta }}}^{0}} + {\mathbf{r}}_{i}^{0} \cdot {\mathbf{\zeta }};\quad (i = 1,2, \ldots ,6), \\ \end{gathered} $
где mom(Ri, ξ), mom(Ri, η), mom(Ri, ζ) – относительные моменты единичных силовых винтов Ri и ортов осей ξ, η, ζ.

Движение рассматриваемых механизмов описываются динамическими уравнениями Ньютона–Эйлера

${{J}_{\xi }} \cdot {{\ddot {\varphi }}_{\xi }} + {{\dot {\varphi }}_{\eta }} \cdot {{\dot {\varphi }}_{\zeta }}\left( {{{J}_{\zeta }} - {{J}_{\eta }}} \right) = M_{\xi }^{E},\quad {{J}_{\eta }} \cdot {{\ddot {\varphi }}_{\eta }} + {{\dot {\varphi }}_{\xi }} \cdot {{\dot {\varphi }}_{\zeta }}\left( {{{J}_{\zeta }} - {{J}_{\xi }}} \right) = M_{\eta }^{E},$
${{J}_{\zeta }} \cdot {{\ddot {\varphi }}_{\zeta }} + {{\dot {\varphi }}_{\xi }} \cdot {{\dot {\varphi }}_{\eta }}\left( {{{J}_{\eta }} - {{J}_{\xi }}} \right) = M_{\zeta }^{E},\quad m\ddot {x} = R_{x}^{E},\quad m\ddot {y} = R_{y}^{E},\quad m\ddot {z} = R_{z}^{E},$
где ${{J}_{\xi }}$, ${{J}_{\eta }}$, ${{J}_{\zeta }}$ – моменты инерции выходного звена относительно осей ξ, η, ζ соответственно; ${{\ddot {\varphi }}_{\xi }}$, ${{\ddot {\varphi }}_{\eta }}$, ${{\ddot {\varphi }}_{\zeta }}$ – проекции углового ускорения выходного звена на оси ξ, η, ζ соответственно; ${{\dot {\varphi }}_{\xi }}$, ${{\dot {\varphi }}_{\eta }}$, ${{\dot {\varphi }}_{\zeta }}$ – проекции угловой скорости выходного звена на оси ξ, η, ζ соответственно; $\ddot {x}$, $\ddot {y}$, $\ddot {z}$ – проекции линейного ускорения выходного звена на оси x, y, z соответственно; m – масса выходного звена; $M_{\xi }^{E}$, $M_{\eta }^{E}$, $R_{\zeta }^{E}$ – проекции главного момента внешних сил на оси ξ, η, ζ; $R_{x}^{E}$, $R_{y}^{E}$, $R_{z}^{E}$ – проекции главного вектора внешних сил на оси x, y, z.

Динамические уравнения Ньютона–Эйлера запишем в виде

$\begin{gathered} {{J}_{\xi }} \cdot {{{\ddot {\varphi }}}_{\xi }} = {{P}_{1}}\left( {{{{\mathbf{r}}}_{{\text{1}}}} \cdot {{\xi }^{{\text{0}}}} + {\mathbf{r}}_{{\text{1}}}^{{\text{0}}} \cdot \xi } \right) + {{P}_{2}}\left( {{{{\mathbf{r}}}_{{\text{2}}}} \cdot {{\xi }^{{\text{0}}}} + {\mathbf{r}}_{{\text{2}}}^{{\text{0}}} \cdot \xi } \right) + {{P}_{3}}\left( {{{{\mathbf{r}}}_{{\text{3}}}} \cdot {{\xi }^{{\text{0}}}} + {\mathbf{r}}_{{\text{3}}}^{{\text{0}}} \cdot {{\xi }}} \right) + \\ + \;{{P}_{4}}\left( {{{{\mathbf{r}}}_{{\text{4}}}} \cdot {{\xi }^{{\text{0}}}} + {\mathbf{r}}_{{\text{4}}}^{{\text{0}}} \cdot \xi } \right) + {{P}_{5}}\left( {{{{\mathbf{r}}}_{{\text{5}}}} \cdot {{\xi }^{{\text{0}}}} + {\mathbf{r}}_{{\text{5}}}^{{\text{0}}} \cdot \xi } \right) + {{P}_{6}}\left( {{{{\mathbf{r}}}_{{\text{6}}}} \cdot {{\xi }^{{\text{0}}}} + {\mathbf{r}}_{{\text{6}}}^{{\text{0}}} \cdot \xi } \right) - {{{\dot {\varphi }}}_{\eta }} \cdot {{{\dot {\varphi }}}_{\zeta }}\left( {{{J}_{\zeta }} - {{J}_{\eta }}} \right), \\ \end{gathered} $
$\begin{gathered} {{J}_{\eta }} \cdot {{{\ddot {\varphi }}}_{\eta }} = {{P}_{1}}\left( {{{{\mathbf{r}}}_{{\text{1}}}} \cdot {{\eta }^{{\text{0}}}} + {\mathbf{r}}_{{\text{1}}}^{{\text{0}}} \cdot \eta } \right) + {{P}_{2}}\left( {{{{\mathbf{r}}}_{{\text{2}}}} \cdot {{\eta }^{{\text{0}}}} + {\mathbf{r}}_{{\text{2}}}^{{\text{0}}} \cdot \eta } \right) + {{P}_{3}}\left( {{{{\mathbf{r}}}_{{\text{3}}}} \cdot {{\eta }^{{\text{0}}}} + {\mathbf{r}}_{{\text{3}}}^{{\text{0}}} \cdot \eta } \right) + \\ + \;{{P}_{4}}\left( {{{{\mathbf{r}}}_{{\text{4}}}} \cdot {{\eta }^{{\text{0}}}} + {\mathbf{r}}_{{\text{4}}}^{{\text{0}}} \cdot \eta } \right) + {{P}_{5}}\left( {{{{\mathbf{r}}}_{{\text{5}}}} \cdot {{\eta }^{{\text{0}}}} + {\mathbf{r}}_{{\text{5}}}^{{\text{0}}} \cdot \eta } \right) + {{P}_{6}}\left( {{{{\mathbf{r}}}_{{\text{6}}}} \cdot {{\eta }^{{\text{0}}}} + {\mathbf{r}}_{{\text{6}}}^{{\text{0}}} \cdot \eta } \right) - {{{\dot {\varphi }}}_{\xi }} \cdot {{{\dot {\varphi }}}_{\zeta }}\left( {{{J}_{\zeta }} - {{J}_{\xi }}} \right), \\ \end{gathered} $
$\begin{gathered} {{J}_{\zeta }} \cdot {{{\ddot {\varphi }}}_{\zeta }} = {{P}_{1}}\left( {{{{\mathbf{r}}}_{{\text{1}}}} \cdot {{\zeta }^{{\text{0}}}} + {\mathbf{r}}_{{\text{1}}}^{{\text{0}}} \cdot \xi } \right) + {{P}_{2}}\left( {{{{\mathbf{r}}}_{{\text{2}}}} \cdot {{\zeta }^{{\text{0}}}} + {\mathbf{r}}_{{\text{2}}}^{{\text{0}}} \cdot \zeta } \right) + {{P}_{3}}\left( {{{{\mathbf{r}}}_{{\text{3}}}} \cdot {{\zeta }^{{\text{0}}}} + {\mathbf{r}}_{{\text{3}}}^{{\text{0}}} \cdot \zeta } \right) + \\ + \;{{P}_{4}}\left( {{{{\mathbf{r}}}_{{\text{4}}}} \cdot {{\zeta }^{{\text{0}}}} + {\mathbf{r}}_{{\text{4}}}^{{\text{0}}} \cdot \zeta } \right) + {{P}_{5}}\left( {{{{\mathbf{r}}}_{{\text{5}}}} \cdot {{\zeta }^{{\text{0}}}} + {\mathbf{r}}_{{\text{5}}}^{{\text{0}}} \cdot \zeta } \right) + {{P}_{6}}\left( {{{{\mathbf{r}}}_{{\text{6}}}} \cdot {{\zeta }^{{\text{0}}}} + {\mathbf{r}}_{{\text{6}}}^{{\text{0}}} \cdot \zeta } \right) - {{{\dot {\varphi }}}_{\xi }} \cdot {{{\dot {\varphi }}}_{\eta }}\left( {{{J}_{\eta }} - {{J}_{\xi }}} \right), \\ \end{gathered} $
$m\ddot {x} = {{P}_{{1x}}} + {{P}_{{2x}}},\quad m\ddot {y} = {{P}_{{3y}}} + {{P}_{{4y}}},\quad m\ddot {z} = {{P}_{{5z}}} + {{P}_{{6z}}}.$

Относительные моменты являются коэффициентами, зависящими от положения и ориентации выходного звена.

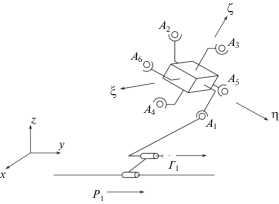
Используя представленный алгоритм, рассмотрим на конкретном примере решение прямой задачи динамики для рассматриваемых механизмов. На рис. 3 представлена схема первой кинематической цепи механизма. Пусть масса выходного звена m = 1 кг; линейные размеры выходного звена вдоль осей ξ, η, ζ равны 0.1 м, определяющие координаты точек A1, A2, …, A6; перемещение выходного звена задано значениями: α = = π/6 рад; β = π/6 рад; γ = π/6 рад, x = 0.1 м; y = 0.15 м; z = 0.2 м; усилия в приводах: P1 = P2 = 1 Н, P3 = P4 = 2 Н, P5 = P6 = 3 Н; проекции угловых скоростей: ${{\dot {\varphi }}_{\xi }} = 3$ рад/c, ${{\dot {\varphi }}_{\eta }} = 2$ рад/c, ${{\dot {\varphi }}_{\zeta }} = 1$ рад/с.

Рис. 3.

Схема первой кинематической цепи.

Координаты точек крепления приводов на выходном звене в системе координат выходного звена представим как

$\begin{gathered} A_{1}^{m} = \left( {\begin{array}{*{20}{c}} 0 \\ {0.1} \\ { - 0.1} \\ 1 \end{array}} \right),\quad A_{2}^{m} = \left( {\begin{array}{*{20}{c}} 0 \\ { - 0.1} \\ {0.1} \\ 1 \end{array}} \right),\quad A_{3}^{m} = \left( {\begin{array}{*{20}{c}} { - 0.1} \\ 0 \\ {0.1} \\ 1 \end{array}} \right),\quad A_{4}^{m} = \left( {\begin{array}{*{20}{c}} {0.1} \\ 0 \\ { - 0.1} \\ 1 \end{array}} \right), \\ A_{5}^{m} = \left( {\begin{array}{*{20}{c}} { - 0.1} \\ {0.1} \\ 0 \\ 1 \end{array}} \right),\quad A_{6}^{m} = \left( {\begin{array}{*{20}{c}} {0.1} \\ { - 0.1} \\ 0 \\ 1 \end{array}} \right). \\ \end{gathered} $

Координаты точек выходного звена в абсолютной системе координат имеют вид

$A_{1}^{b} = \left( {\begin{array}{*{20}{c}} {0.016} \\ {0.259} \\ {0.168} \end{array}} \right),\quad A_{2}^{b} = \left( {\begin{array}{*{20}{c}} {0.184} \\ {0.041} \\ {0.232} \end{array}} \right),\quad A_{3}^{b} = \left( {\begin{array}{*{20}{c}} {0.088} \\ {0.085} \\ {0.325} \end{array}} \right),$
$A_{4}^{b} = \left( {\begin{array}{*{20}{c}} {0.113} \\ {0.215} \\ {0.075} \end{array}} \right),\quad A_{5}^{b} = \left( {\begin{array}{*{20}{c}} {0.003} \\ {0.194} \\ {0.293} \end{array}} \right),\quad A_{6}^{b} = \left( {\begin{array}{*{20}{c}} {0.197} \\ {0.106} \\ {0.107} \end{array}} \right).$

Единичные векторы силовых винтов направлены параллельно осям координат, а моментные части найдены как векторные произведения

${\mathbf{r}}_{{\text{1}}}^{{\text{0}}} = \left( {\begin{array}{*{20}{c}} 0 \\ {0.168} \\ { - 0.25} \end{array}} \right),\quad {\mathbf{r}}_{{\text{2}}}^{{\text{0}}} = \left( {\begin{array}{*{20}{c}} 0 \\ {0.232} \\ { - 0.04} \end{array}} \right),\quad {\mathbf{r}}_{{\text{3}}}^{{\text{0}}} = \left( {\begin{array}{*{20}{c}} { - 0.32} \\ 0 \\ {0.068} \end{array}} \right),$
${\mathbf{r}}_{{\text{4}}}^{{\text{0}}} = \left( {\begin{array}{*{20}{c}} { - 0.075} \\ 0 \\ {0.113} \end{array}} \right),\quad {\mathbf{r}}_{{\text{5}}}^{{\text{0}}} = \left( {\begin{array}{*{20}{c}} {0.194} \\ { - 0.003} \\ 0 \end{array}} \right),\quad {\mathbf{r}}_{{\text{6}}}^{{\text{0}}} = \left( {\begin{array}{*{20}{c}} {0.106} \\ { - 0.19} \\ 0 \end{array}} \right).$

Плюккеровы координаты ортов осей системы координат выходного звена Omξηζ в неподвижной системе координат Oxyz можно представить как

$\begin{gathered} {{\xi }} = \left( {\begin{array}{*{20}{c}} {0.75} \\ {0.43} \\ { - 0.5} \end{array}} \right),\quad {{{{\xi }}}^{{\text{0}}}} = \left( {\begin{array}{*{20}{c}} { - 0.16} \\ {0.2} \\ { - 0.07} \end{array}} \right),\quad {{\eta }} = \left( {\begin{array}{*{20}{c}} { - 0.21} \\ { - 0.87} \\ {0.43} \end{array}} \right),\quad {{{{\eta }}}^{{\text{0}}}} = \left( {\begin{array}{*{20}{c}} { - 0.11} \\ { - 0.087} \\ {0.12} \end{array}} \right), \\ {{\zeta }} = \left( {\begin{array}{*{20}{c}} {0.625} \\ { - 0.217} \\ {0.75} \end{array}} \right),\quad {{{{\zeta }}}^{{\text{0}}}} = \left( {\begin{array}{*{20}{c}} {0.156} \\ {0.05} \\ { - 0.11} \end{array}} \right). \\ \end{gathered} $

Относительные моменты единичных силовых винтов и оси ξ

$\operatorname{mom} ({{{\mathbf{R}}}_{1}},{\mathbf{\xi }}) = 0.041;\quad \operatorname{mom} ({{{\mathbf{R}}}_{2}},{\mathbf{\xi }}) = --0.041;\quad \operatorname{mom} ({{{\mathbf{R}}}_{3}},{\mathbf{\xi }}) = --0.088;$
$\operatorname{mom} ({{{\mathbf{R}}}_{4}},{\mathbf{\xi }}) = 0.088;\quad \operatorname{mom} ({{{\mathbf{R}}}_{5}},{\mathbf{\xi }}) = 0.075;\quad \operatorname{mom} ({{{\mathbf{R}}}_{6}},{\mathbf{\xi }}) = --0.041.$

Относительные моменты единичных силовых винтов и оси η

$\operatorname{mom} ({{{\mathbf{R}}}_{1}},{\mathbf{\eta }}) = --0.075;\quad \operatorname{mom} ({{{\mathbf{R}}}_{2}},{\mathbf{\eta }}) = 0.075;\quad \operatorname{mom} ({{{\mathbf{R}}}_{3}},{\mathbf{\eta }}) = 0.022;$
$\operatorname{mom} ({{{\mathbf{R}}}_{4}},{\mathbf{\eta }}) = --0.022;\quad \operatorname{mom} ({{{\mathbf{R}}}_{5}},{\mathbf{\eta }}) = 0.075;\quad \operatorname{mom} ({{{\mathbf{R}}}_{6}},{\mathbf{\eta }}) = --0.075.$

Относительные моменты единичных силовых винтов и оси ζ

$\operatorname{mom} ({{{\mathbf{R}}}_{1}},{\mathbf{\zeta }}) = --0.075;\quad \operatorname{mom} ({{{\mathbf{R}}}_{2}},{\mathbf{\zeta }}) = 0.075;\quad \operatorname{mom} ({{{\mathbf{R}}}_{3}},{\mathbf{\zeta }}) = --0.088;$
$\operatorname{mom} ({{{\mathbf{R}}}_{4}},{\mathbf{\zeta }}) = 0.088;\quad \operatorname{mom} ({{{\mathbf{R}}}_{5}},{\mathbf{\zeta }}) = 0.0069;\quad \operatorname{mom} ({{{\mathbf{R}}}_{6}},{\mathbf{\zeta }}) = --0.0069.$

Модули линейного и углового ускорений и их проекций

$a = 7.483\;{\text{м/}}{{{\text{c}}}^{2}},\quad \ddot {x} = 2\;{\text{м/}}{{{\text{c}}}^{2}},\quad \ddot {y} = 4\;{\text{м/}}{{{\text{c}}}^{2}},\quad \ddot {z} = 6\;{\text{м/}}{{{\text{c}}}^{2}};$
$\ddot {\varphi } = 3.539\;{\text{рад/}}{{{\text{c}}}^{2}},\quad {{\ddot {\varphi }}_{\xi }} = 1.2\;{\text{рад/}}{{{\text{c}}}^{2}},\quad {{\ddot {\varphi }}_{\eta }} = 2.4\;{\text{рад/}}{{{\text{c}}}^{2}},\quad {{\ddot {\varphi }}_{\zeta }} = 2.308\;{\text{рад/}}{{{\text{c}}}^{2}}.$

Выводы. Таким образом, в настоящей статье представлены различные аспекты анализа механизмов параллельной структуры с линейными двигателями, устанавливаемыми на основании, причем оси линейных двигателей параллельны осям неподвижной системы координат. Это обусловлено тем, что оси силовых винтов, передаваемых со стороны кинематических цепей на выходное звено, параллельны осям линейных двигателей.

Для получения уравнения динамики, связанные с вращательными движениями выходного звена, необходимо дополнительно определить моменты силовых винтов, передаваемых на выходное звено. Для решения такой задачи эффективным подходом оказалось определение относительного момента между соответствующей осью подвижной системы координат, связанной с выходным звеном, и силовым винтом.

Представлено решение прямой задачи динамики, когда в произвольном положении известны абсолютные и обобщенные скорости, а также действующие в приводах силы. Найдены ускорения выходного звена.

Полученные зависимости позволяют исследовать динамические свойства механизмов и решать задачу управления.

Список литературы

  1. Ганиев Р.Ф. Проблемы механики машин и технологий. Перспективы развития Института машиноведения им. А.А. Благонравова РАН // Проблемы машиностроения и надежности машин. 2010. № 1. С. 3.

  2. Ганиев Р.Ф. О современном состоянии и перспективах развития ИМАШ РАН. Проблемы механики машин и прорывных технологий // М. Проблемы машиностроения и надежности машин 2014. № 3. С. 11.

  3. Ceccarelli M. Fundamentals of Mechanics of Robotic Manipulation. Kluwer Academic Publishers, 2004. 412 p.

  4. Glazunov V.A., Rashoyan G.V., Aleshin A.K., Shalyukhin K.A., Skvortsov S.A. Structural Synthesis of Spatial l-Coordinate Mechanisms wiith Additional Links for Technological Robots // Advances in Intelligent Systems and Computing. 2020. T. 902. C. 683.

  5. Велиев Е.И., Ганиев Р.Ф., Глазунов В.А., Филиппов Г.С. Перспективные малоинвазивные роботохирургические комплексы параллельной структуры // Доклады Российской академии наук. Физика, технические науки. 2020. Т. 495. С. 91.

  6. Glazunov V.A., Rashoyan G.V., Aleshin A.K., Shalyukhin K.A., Skvortsov S.A. Structural Synthesis of Spatial l-Coordinate Mechanisms with Additional Links for Technological Robots // Advances in Intelligent Systems and Computing. 2020. V. 902. P. 683.

  7. Glazunov V., Kheylo S. Dynamics and control of planar, translational, and spherical parallel manipulators. In: Dynamic balancing of mechanisms and synthesizing of parallel robots. Springer, 2016. P. 365.

  8. Glazunov V., Nosova N., Kheylo S., Tsarkov A. Design and Analysis of the 6-DOF Decoupled Parallel Kinematic Mechanism. In: Dynamic Decoupling of Robot Manipulators, Springer, 2018. P. 125.

  9. Antonov A., Aleshin A., Glazunov V., Rashoyan G., Skvortsov S., Shalyukhin K., Kovaleva N., Chernetsov R. Dynamics of a New Parallel Structure Mechanism with Motors Mounted on the Base outside the Working Area // Proceedings of 14th International Conference on Electomechanics and Robotics “Zavalishin’s Readings”, 2019. P. 183.

  10. Rashoyan G.V., Shalyukhin K.A., Gaponenko E.V. Development of structural schemes of parallel structure manipulators using screw calculus // IOP Conference Series: Materials Science and Engineering. 2018. V. 327 (4). 042090.

  11. Veliev E.I., Ganiev R.F., Glazunov V.A., Filippov G.S. Parallel and sequential structures of manipulators in robotic surgery // Doklady Physics. 2019. T. 64. № 3. C. 106.

  12. Глазунов В.А., Борисов В.А. Разработка механизмов параллельной структуры с четырьмя степенями свободы и четырьмя кинематическими цепями // Проблемы машиностроения и надежности машин. 2017. № 5. С. 3.

  13. Laryushkin P., Glazunov V., Erastova K. On the Maximization of Joint Velocities and Generalized Reactions in the Workspace and Singularity Analysis of Parallel Mechanisms // Robotica. 2019. V. 37. № 4. P. 675.

  14. Глазунов В.А. Структура пространственных механизмов. Группа винтов и структурные группы // Справочник. Инженерный журнал. Приложение № 3. 2010. № 4.

  15. Kong X., Gosselin C.M. Type synthesis of linear translational parallel manipulators // Advances in Robot Kinematics – Theory and Applications, Boston: Kluwer Academic Publishers. 2002. P. 411.

  16. Глазунов В.А., Данилин П.О., Левин С.В., Тывес Л.И., Шалюхин К.А. Разработка механизмов параллельной структуры с кинематической и динамической развязкой // Проблемы машиностроения и надежности машин. 2010. № 4. С. 23.

  17. Рашоян Г.В., Шалюхин К.А., Алешин А.К. Анализ кинематики механизма параллельной структуры со свойствами кинематической развязки // Вестник научно-технического развития. 2018. № 1 (125). С. 32.

  18. Mianovski K. Singularity analysis of parallel manipulator POLMAN 3×2 with six degrees of freedom // 12th IFToMM World Congress, Besançon (France), June 18–21, 2007. P. 126.

  19. Seward N., Bonev I.A. A new 6-DOF parallel robot with simple kinematic model, IEEE International Conference on Robotics and Automation (ICRA), Hong-Kong, China, 2, May 31–June 7, 2014. P. 4061.

  20. Kheylo S.V., Tsarkov A.V., Garin O.A. Kinematic analysis of novel 6-dof robot // Advances in Intelligent Systems and Computing. 2020. V. 1126. P. 442.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал