Проблемы машиностроения и надежности машин, 2022, № 6, стр. 81-87

Оптимизация конструкции прямоточной задвижки, применяемой в нефтепромысловом оборудовании

М. С. Рагимова^1, *, Г. И. Намазова¹

¹ Азербайджанский государственный университет нефти и промышленности
Баку, Азербайджан

Поступила в редакцию 06.04.2022
После доработки 26.07.2022
Принята к публикации 19.08.2022

EDN: SNHCNQ
DOI: 10.31857/S0235711922060104

Аннотация

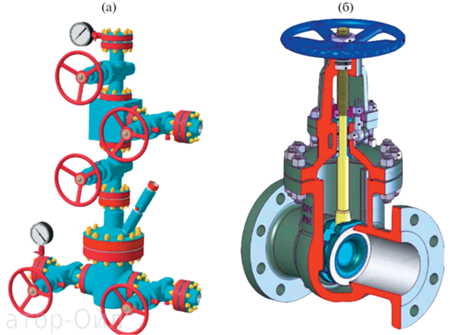
В статье проведен анализ причин негерметичности поверхностей клапанов фонтанной арматуры, рассмотрены условия обеспечения герметичности с учетом давления на поверхность, разработана оптимальная конструкции клапанов прямоточной задвижки, применяемой в фонтанной арматуре нефтепромыслового оборудования. Приведены и научно обоснованы значения основного геометрического параметра и выполнения всех условий, путем задания постоянных параметров конструкции. Для обоснования использованы методы математического анализа, геометрическое, линейное и нелинейное программирование, методы штрафных функций, методы аналитического расчета.

Ключевые слова: фонтанная арматура, тарельчатые конусные пружины, прямоточная задвижка, герметичность, конструкция

Размеры деталей фонтанной арматуры, таких как тарельчатые конусные пружины, прямоточная задвижка и т.д., определяются механическими свойствами материалов, из которых они изготовлены, и значениями нагрузок, действующих в эксплуатационных условиях. По мере увеличения коэффициента запаса прочности увеличивается и масса изделия (что является нежелательным фактором). Рабочее напряжение, действующее на части фонтанной арматуры, должно быть меньше допустимого напряжения, действующего на конструкции связывающих устройств для обеспечения герметичности, надежности и более высокой работоспособности.

Современные методы оптимизации дают возможность создавать конструкции, которые позволят коренным образом улучшить качественные и количественные показатели в фонтанной арматуре нефтепромыслового оборудования.

В настоящее время при проектировании фонтанной арматуры используют традиционные методы. Их основу составляет проверочный расчет. Такой подход в большинстве случаев не позволяет получить максимальный эффект при минимальных затратах. Для решения поставленной задачи будем использовать метод математического анализа, геометрическое, линейное и нелинейное программирование, методы штрафных функций, методы аналитического расчета.

На фонтанное оборудование, действуют силы нагрузки, изменяющиеся в зависимости от разных эксплуатационных условий. Расчеты в основном сводятся к подбору элементов арматуры, опираясь на показатель жесткости. Работоспособность нефтепромыслового оборудования и предел усталости элементов, можно определить действием малой напряженности. При испытании на статическое растяжение находим предел текучести, предел прочности, относительное растяжение, предел циклической прочности, сгиб, работа пластической деформации. В некоторых случаях, если равны пределы усталости элементов фонтанной арматуры, выбирается тот элемент, у которого предел пластической деформации больше.

Для оценки работоспособности фонтанной арматуры и ее элементов необходимо учесть устойчивость элементов конструкции на прочность, жесткость, износ, теплоту, коррозию.

Постановка задачи. Тарельчатые конусные пружины, которые нашли широкое применение в технике, используются для нивелирования, поглощения, действия очень больших сил при перемещениях и изготавливаются в виде пружинной шайбы методом штампования на конусе пружинного стального листа. Толщина пружин колеблется в пределах 1–20 мм; диаметр может быть 30–300 мм, d/D = 0.5–0.3; угол конусности $\theta $ = 2–6°.

Концы пружины полируются и точно сажаются на кольцевые опорные поверхности. От действия центральной силы конусная шайба сгибается, и концы приближаются друг к другу на (0.5–0.8)f; где f – высота усеченного конуса.

Решение задачи. В большинстве случаев пружины готовятся методом штампования или методом строгания. При этом увеличивается прочность пружины против его искривления под действием силы, хорошо работает в коррозионном условии.

Обозначим действующую силу F, высоту пружины h (в свободном положении). Тогда силу, действующую на пружину, можно найти по формуле

(1)

$\begin{gathered} F = \frac{{4E}}{{\left( {1 - {{\nu }^{2}}} \right)}}\frac{{t_{e}^{4}}}{{\alpha D_{e}^{2}}}\frac{\delta }{{{{t}_{e}}}}\left\{ {\left. {\beta \left( {\frac{h}{{{{t}_{e}}}} - \frac{\delta }{{{{t}_{e}}}}} \right)\left( {\frac{h}{{{{t}_{e}}}} - \frac{\delta }{{2{{t}_{e}}}}} \right) + 1} \right\}} \right.; \\ D = \frac{{{{D}_{i}}}}{{{{D}_{e}}}}; \\ \end{gathered} $

(2)

$\alpha = \frac{{18}}{\pi }\frac{{K(K - 1)}}{{K(K + 1) + 1}};$

(3)

$\beta = \frac{{3{{K}^{2}}}}{{K(K + 1) + 1}},$

где $\delta $ – деформация пружины; $\alpha $ – безразмерный коэффициент; β – безразмерный коэффициент: t_e – толщина пружины в основании; E – модуль упругости материала пружины; $\nu $ – коэффициент Пуассона, коэффициент жесткости; K – коэффициент упругости; R – наружный диаметр; D_e – внутренний диаметр; D_i – безразмерный диаметр.

Поперечное сечение пружин может быть меняющимся (конус) и постоянным. При больших давлениях с целью обеспечения герметичности в прямоточных задвижках седло прижимают к щиту с помощью тарельчатой пружины специальной конструкции [1–4].

Сила, создаваемая пружиной, выбирается так, чтобы контактное давление на поверхности седло–щит, обеспечило герметичность при заданном внутреннем давлении.

При повышении рабочего давления седло отступает назад к опоре, что защищает тарельчатую пружину от лишнего нагружения. По мере повышения давления, герметичность обеспечивается высоким контактным давленим, создаваемым из-за разницы площадей действующих поверхностей.

Рис. 1.

(a) – фонтанная арматура; (б) – задвижка клиновая.

Анализ результатов. Из-за того, что в тарельчатой пружине отношение d/D больше, чем у стандартных пружин, существующие методы расчета [1, 3, 5, 6] не дают правильных результатов. Поэтому, для расчета мы рассмотрели пружины в виде кругового кольца, чтобы уберечь от нагрузки в отличие от тарельчатых и стандартных пружин.

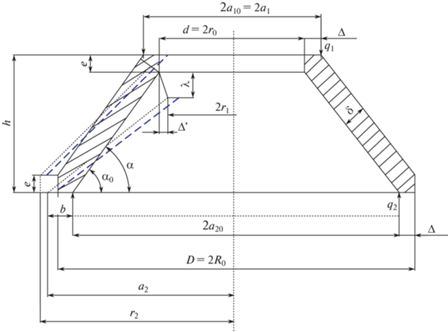
Для оптимизации конструкции из основных параметров была выбрана масса пружины (рис. 2).

Рис. 2.

Основные геометрические размеры пружины.

Массу пружины в зависимости от основных геометрических параметров можем выразить следующим образом:

(4)

$\begin{gathered} m = \rho \cdot V = \rho \left\{ {\pi R_{0}^{2}h - \pi \cdot r_{0}^{2}e - \frac{\pi }{3}(h - e)\left( {a_{{20}}^{2} + r_{0}^{2} + {{a}_{{20}}}{{r}_{0}}} \right) - } \right. \\ - \;\left. {\left[ {\pi R_{0}^{2}(h - e) - \frac{\pi }{3}\left( {h - e} \right)\left( {R_{0}^{2} + a_{1}^{2} + {{R}_{0}}{{a}_{1}}} \right)} \right]} \right\}. \\ \end{gathered} $

Запишем геометрические зависимости для положения пружины до деформации и после деформации

${{a}_{0}} = {{r}_{0}} + \Delta ;\quad {{a}_{{20}}} = {{R}_{0}} - \Delta ;\quad {{r}_{1}} = {{r}_{0}} - \Delta ;$

(5)

$\begin{gathered} {{a}_{2}} = {{a}_{{20}}} + b;\quad {{a}_{1}} = {{a}_{{10}}} - \Delta ;\quad {{r}_{2}} = {{R}_{0}} + b; \\ e = \frac{\delta }{{\cos {{\alpha }_{0}}}} - \Delta \operatorname{tg} {{\alpha }_{0}}, \\ \end{gathered} $

$\operatorname{tg} {{\alpha }_{0}} = \frac{{h - e}}{{{{a}_{{20}}} - {{r}_{0}}}} = \frac{{h - \Delta \left( {\frac{1}{{\cos {{\alpha }_{0}}}} - \operatorname{tg} {{\alpha }_{0}}} \right)}}{{{{a}_{{20}}} - {{r}_{0}}}}.$

Из последних двух формул находим а₀ по формуле

(6)

$\begin{gathered} {{a}_{0}} = \arg \operatorname{tg} \left[ {\frac{{2h({{a}_{{20}}} - {{r}_{0}} - \Delta }}{{2\left[ {{{{({{a}_{{20}}} - {{r}_{0}} - \Delta )}}^{2}} - {{\delta }^{2}}} \right]}} - } \right. \\ - \;\left. {\frac{{\sqrt {4{{h}^{2}}{{{({{a}_{{20}}} - {{r}_{0}} - \Delta )}}^{2}} - 4(h - \delta )\left[ {{{{({{a}_{{20}}} - {{r}_{0}} - \Delta )}}^{2}} - {{\delta }^{2}}} \right]} }}{{2\left[ {{{{({{a}_{{20}}} - {{r}_{0}} - \Delta )}}^{2}} - {{\delta }^{2}}} \right]}}} \right]. \\ \end{gathered} $

Конусный угол после деформации пружины можно найти как

(7)

$\sin \alpha = \frac{{h - e - \lambda }}{l};$

(8)

$\alpha = \arg \sin \frac{{h - e - \lambda }}{l};\quad b = l\cos \alpha - {{a}_{{20}}} - {{r}_{1}},$

где

(9)

$l = \sqrt {{{{({{a}_{{20}}} - {{r}_{0}})}}^{2}} + {{{(h - e)}}^{2}}} .$

Рассмотрим тарельчатую пружину как конус. Найдем ее геометрические параметры с и $J_{{}}^{*}$ [2]

(10)

$c = \operatorname{tg} \left( {\frac{{{{r}_{2}} - {{r}_{1}}}}{{\ln \frac{{{{r}_{2}}}}{{{{r}_{1}}}}}} - {{r}_{1}}} \right);$

(11)

$\begin{gathered} J* = \delta \frac{{{{{\operatorname{tg} }}^{2}}\alpha }}{{\cos \alpha }}\left[ {0.5\left( {r_{2}^{2} - r_{1}^{2}} \right) - 2{{r}_{1}}({{r}_{2}} - {{r}_{1}}) + r_{1}^{2}\ln \frac{{{{r}_{2}}}}{{{{r}_{1}}}}} \right] + \\ + \;\frac{\delta }{{12}}\cos \alpha \ln \frac{{{{r}_{2}}}}{{{{r}_{1}}}} - {{c}^{2}}\frac{\delta }{{\cos \alpha }}\ln \frac{{{{r}_{2}}}}{{{{r}_{1}}}}. \\ \end{gathered} $

Напряженность, возникающая в поперечном сечении кольца, можно найти как [3]

(12)

$\sigma = \frac{y}{r}\frac{{{{q}_{2}}a_{2}^{2} - {{q}_{1}}a_{1}^{2}}}{{J{\kern 1pt} *}}.$

Здесь, если принять

$r = {{r}_{1}},\quad y = e;\quad {{q}_{2}} = \frac{F}{{2\pi {{a}_{2}}}};\quad {{q}_{2}} = \frac{F}{{2\pi {{a}_{1}}}},$

получим

(13)

$\sigma = \frac{c}{{{{r}_{1}}}}\frac{{F\left( {{{a}_{2}} - {{a}_{1}}} \right)}}{{2\pi J{\kern 1pt} *}},$

где $F$ – сила, действующая на пружину.

Осевую деформацию пружины от воздействия силы $F$ найдем в виде

(14)

$\lambda = \frac{{\left( {{{q}_{2}}a_{2}^{2} - {{q}_{1}}a_{1}^{2}} \right)\left( {{{a}_{2}} - {{a}_{1}}} \right)}}{{EJ{\kern 1pt} *}} = \frac{{F{{{\left( {{{a}_{2}} - {{a}_{1}}} \right)}}^{2}}}}{{2\pi EJ{\kern 1pt} *}},$

где

(15)

$F = \frac{{2\pi EJ{\kern 1pt} *{\kern 1pt} \lambda }}{{{{{({{a}_{2}} - {{a}_{1}})}}^{2}}}}.$

Результат. Условия, обеспечивающие работоспособность тарельчатой пружины, можно записать в следующем виде.

Сила, созданная деформацией $\lambda $ кольца, должна быть в пределах

(16)

$F = \frac{{2\pi EJ{\kern 1pt} *{\kern 1pt} \lambda }}{{{{{({{a}_{2}} - {{a}_{1}})}}^{2}}}} \geqslant {{F}_{1}};$

(17)

$F = \frac{{2\pi EJ{\kern 1pt} *{\kern 1pt} \lambda }}{{{{{({{a}_{2}} - {{a}_{1}})}}^{2}}}} \leqslant {{F}_{2}}.$

Максимальное напряжение в поперечном сечении не должно быть больше допустимого, т.е.

(18)

$\sigma = \frac{{2E\lambda }}{{{{r}_{1}}({{a}_{2}} - {{a}_{1}})}} \leqslant \left[ \sigma \right].$

Значение деформации пружины не должно быть больше его 10–35-кратной максимальной деформации

(19)

$h - e - \frac{\lambda }{{0.35}} \geqslant 0.$

Следовательно, задача сводится к нахождению минимума целевой функции при выполнении условий

(20)

${{g}_{1}} = \frac{{2\pi EJ{\kern 1pt} *{\kern 1pt} \lambda }}{{{{{\left( {{{a}_{2}} - {{a}_{1}}} \right)}}^{2}}}} - {{F}_{1}} \geqslant 0;$

(21)

${{g}_{2}} = \frac{{2\pi EJ{\kern 1pt} *{\kern 1pt} \lambda }}{{{{{({{a}_{2}} - {{a}_{1}})}}^{2}}}} - {{F}_{2}} \leqslant 0;$

(22)

${{g}_{3}} = \left[ \sigma \right] - \frac{{2E\lambda }}{{{{r}_{1}}({{a}_{2}} - {{a}_{1}})}} \geqslant 0;$

(23)

${{g}_{4}} = h - e - \frac{\lambda }{{0.35}} \geqslant 0.$

Для решения задачи используем метод штрафной функции [3, 7, 8]. Для этого штрафную функцию составляем в виде $F({{x}_{i}})$ = $f({{x}_{i}})$ + $r\sum {\frac{1}{{f({{x}_{i}})}}} $.

Задавая первичные параметры, находим оптимальные значения переменных параметров D, δ, h.

В настоящее время, из эксплуатационного опыта серийно выпускаемых фонтанных арматур с переходным диаметром 65, 80 и 100 мм, расчитанных на допустимые давления 35, 70 и 105 МПа, известно, что работоспособность обеспечивается по определенным критериям: подбор элементов арматуры, предел усталости элементов, предел текучести, предел прочности и т.д.

Производство задвижек фонтанной арматуры в аспекте экономической эффективности заключается в создании оптимальной конструкции задвижки с учетом всех сторон эксплуатационного процесса. В результате оптимизации, основные параметры пружины, для которой проведен расчет, составляют

$\begin{gathered} D = 72.8\;{\text{мм}},\quad \delta = 1.48\;{\text{мм}},\quad h = 4.45\;{\text{мм}},\quad {{d}_{0}} = 59\;{\text{мм}}, \\ F = 9747\;{\text{H}},\quad \sigma = 14\,080\;{\text{MPa,}} \\ \end{gathered} $

что приводит к уменьшению веса существующей пружины на 12%.

Заключение. 1. Для оптимизации конструкции прямоточных задвижек составлена математическая модель, обеспечивающая выполнение условий прочности, жесткости и герметичности. Для решения используется метод штрафных функций, например, снижения веса металла, как наиболее точный и простой метод. 2. Для решения задачи оптимизации конструкций тарельчатый пружины, была выбрана минимальная масса пружины. 3. Установлено, что для большей эффективности работы задвижки в фонтанной арматуре тарельчатую пружину следует изготавливать из стали в виде переменного конусного кольца.

Список литературы

Рагимова М.С. Определение прочности деталей машин нефтепромыслового оборудования // Оборудование и технологии для нефтегазового комплекса. 2017. № 4. С. 13.
Рагимова М.С. Проектирование, конструирование и подготовка нефтепромыслового оборудования для магистральных трубопроводов // Оборудование и технологии для нефтегазового комплекса. 2015. № 6. С. 52.
Дунаев П.Ф., Леликов О.П. Конструирование узлов и деталей машин. Учеб. пособие для техн. спец. вузов. 6-е изд., М.: Высш. шк., 2000. 447 с., ил.
Рагимова М.С., Машадиева В.М., Намазова Г.И. Исследование прочности нефтепромыслового оборудования // Ухтинский государственный технический университет, XVIII Международной молодежной научной конференции СЕВЕРГЕОЭКОТЕХ-2017, Сборник трудов. Т. 1. Ухта 12–14 апреля 2017 г. С. 176.
Мордвинов А.А., Захаров А.А., Миклина О.А., Полубоярцев Е.Л. Устьевое оборудование фонтанных и нагнетательных скважин: Методические указания. Ухта: УГТУ, 2004. 31 с.
Kondakov L.A. et al. Sealing and sealing equipment: Handbook; M.: Machine building, 1994. 445 p.
New elastomeric material. New Elastomermaterial from Hitze and Kraftstoff in Motorraum // MTZ. 2008. V. 69 (2). P. 115.
Calculation of acoustic characteristics. Rechnergestütztes Verfahren zur akustischen Optimize rung van Dichtungen // MTZ. 2005. V. 66 (5). P. 386.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Проблемы машиностроения и надежности машин

Архивы выпусков Информация о журнале Отправить рукопись в журнал