Почвоведение, 2021, № 4, стр. 521-526
Моделирование истирания почвенных агрегатов в склоновых потоках
В. М. Гендугов a, Г. А. Ларионов a, С. Ф. Краснов a, Л. Ф. Литвин a, А. В. Горобец a, *
a МГУ им. М.В. Ломоносова
119991 Москва, Ленинские горы, 1, Россия
* E-mail: GorobetsAV@geogr.msu.ru
Поступила в редакцию 31.07.2020
После доработки 03.11.2020
Принята к публикации 06.11.2020
Аннотация
Эродирующая способность склонового водного потока – важнейший аргумент количественных оценок эрозии почв – определяется как разность между его транспортирующей способностью и суммарным содержанием в нем взвешенных и влекомых наносов. В связи с этим необходимо оценивать факторы и интенсивность истирания в потоке почвенных агрегатов, определяющие доли взвешенных и влекомых частиц. Попытки моделирования истирания речных наносов (Х. Штернберг) и почвенных агрегатов (Г.И. Швебс), предпринятые ранее, не полностью соответствуют условиям взаимодействия почв и склоновых потоков. Дальнейшее описание процесса истирания эмпирическими зависимостями не принесло принципиальных улучшений. Иная модель истирания частиц, опирающаяся на законы механики, позволяет описывать процессы истирания срываемых водным потоком почвенных агрегатов с разделением суммарного содержания наносов в потоке на влекомые и взвешенные. Верификация расчетов по этой модели экспериментальными данными, которые были получены нами ранее, оказалась удовлетворительной.
ВВЕДЕНИЕ
Наносы, перемещаемые потоком, оказывают большое влияние на интенсивность смыва почвы. Фостер с соавт. [8] полагали, что эродирующая способность определяется как разность транспортирующей способности потока и его мутности (как суммарного содержания наносов в потоке). Мирцхулава [5] считал, что если в ручейках на склонах не видно следов аккумуляции наносов, то наносы никак не влияют на смыв, и лишь когда уклон уменьшится настолько, что начинают наблюдаться аккумулятивные образования, стоит учитывать влияние наносов. В то же время имеются данные о влиянии на транспортирующую способность потока соотношения концентрации наносов в потоке в целом и в его придонном слое, что зависит от доли перемещаемых почвенных агрегатов [12].
В дальнейшем оказалось, что в зависимости от вида наносов (донные, взвешенные) их роль и механизм влияния на эрозионный процесс могут быть различными [3, 4]. Таким образом, не представляется возможным описать влияние наносов на эрозию почв единой зависимостью. Для оценки общей роли наносов в процессе эрозии необходимо располагать сведениями о количестве донных (влекомых) и взвешенных наносов на всем протяжении склоновых потоков. Впервые такие исследования провел Швебс [6], используя циркуляционный лоток, скорость в котором была постоянной, что ограничивает ценность его исследований. Изучалось истирание в потоке на протяжении до 2–3 км, тогда как склонов такой длины в естественных условиях практически не имеется. Было отмечено, что при прохождении первой сотни метров наблюдается взрывной характер разрушения почвенных агрегатов. Причем Швебс [6] предложил зависимость очень сложного вида, с неопределенностью оценки почвенных характеристик.
В работах по моделированию истирания почвенных агрегатов и речных наносов при их переносе водными потоками используются различные методы. Ванг с соавт. [13] применили чисто эмпирический подход для оценки варьирования размеров и формы почвенных агрегатов при их истирании в потоке в зависимости от пройденного ими расстояния. Другие исследователи при изучении процесса истирания модельных наносов (мергелистые и известковые породы) в потоке, применяли произвольно вводимые уравнения и дискретную стохастическую модель измельчения [7], или модель, основанную на физическом описании процессов истирания и фрагментации с помощью статистических распределений [9].
Таким образом, сорванные почвенные агрегаты при движении в потоке разрушаются до исходных пылеватых и глинистых частиц, поэтому появляется потребность в модели, описывающей этот процесс.
Цель работы – разработка модели истирания почвенных частиц (агрегатов), которая опирается на законы механики и позволяет описывать процессы истирания срываемых водным потоком агрегатов с разделением суммарного содержания наносов в потоке на влекомые и взвешенные.
ЭМПИРИЧЕСКИЕ МЕТОДЫ И РЕШЕНИЯ
Для получения количественных данных о разрушении почвенных агрегатов в склоновом потоке, которые послужили бы в дальнейшем для верификации соответствующей модели, провели две серии опытов [1, 2]. В экспериментах использовали гидравлический лоток длиной 10 м. Дно лотка для имитации шероховатости ложа склонового потока на пашне было выстлано окатанным гравием и залито сверху смесью суглинка с клеем ПВА. Эксперименты проводили следующим образом. Водопрочные почвенные агрегаты отбирали методом мокрого рассеивания почвы. Затем почвенные агрегаты высушивали до воздушно-сухого состояния. Водопрочные воздушно-сухие агрегаты диаметром 2 и 4 мм в количестве 10 шт. взвешивали и капиллярно увлажняли на листе фильтровальной бумаги в течение 10–12 ч. Каждую такую порцию агрегатов вносили в поток в головной части лотка и улавливали на сито с ячейками размером 0.25 мм в его нижнем конце. Почвенные агрегаты смывали с сита в чашку и вновь добавляли в поток в головной части лотка. Это повторялось до тех пор, пока длина пробега агрегатов не достигала заданной величины (10, 20, 50, 100 и 200 м). Сохранившиеся частицы агрегатов высушивали на бумажном фильтре и взвешивали. Разность между начальным и конечным весом образца рассматривали как потери агрегатов на истирание и разрушение до размеров менее 0.25 мм. Опыты для каждой серии проводили в 3–6-кратной повторности.
В первой серии опытов исследовали влияние крупности агрегатов и инокуляции в почву микроорганизмов (дрожжевых культур) на истирание [2]. Установлено, что истирание почвенных агрегатов не описывается известным уравнением Штернберга [11], которое дает удовлетворительные результаты лишь для обломков горных пород в руслах рек. Коэффициент истирания в этом уравнении является константой для обломков породы различной крупности и зависит только от механических свойств породы. Для почвенных агрегатов этот коэффициент оказался переменной величиной и уменьшался с длиной пробега. Оценка этого явления была получена при помощи ряда эмпирических зависимостей [2].
Другая серия экспериментов была посвящена исследованию влияния скорости и глубины потока на истирание агрегатов в зависимости от длины пробега агрегатов [1]. Визуальные наблюдения показали, что почвенные агрегаты движутся в потоке скачками (путем сальтации) и разрушение их происходит в момент касания дна потока. В соответствии с законами механики сила удара агрегатов о ложе потока пропорциональна квадрату скорости перемещения агрегата, которая, как показали замеры, практически совпадает со средней скоростью потока. Исходя из этой посылки, было предложено эмпирическое уравнение для описания разрушения почвенных агрегатов в процессе их движения по склону в ручейковой сети. В целом предложенное уравнение удовлетворительно описывает процесс истирания почвенных агрегатов в широком диапазоне гидравлических условий. Коэффициент корреляции между экспериментальными и расчетными данными, полученными для агрегатов крупностью 2 и 4 мм при глубине потока 10 и 15 мм и уклонах 2°, 3° и 5°, составил 0.92, что следует признать хорошим показателем, так как вариабельность скорости истирания агрегатов высока (табл. 1).
Таблица 1.
Разрушение и истирание почвенных агрегатов в зависимости от пройденного ими пути, глубины и скорости потока
| Диаметр агрегата, мм |
Уклон, градусы |
Глубина потока, мм |
Остаток навески (%) после пробега пути длиной (м) | ||||
|---|---|---|---|---|---|---|---|
| 10 | 20 | 50 | 100 | 200 | |||
| 2 | 2 | 10 | 75.7 | 68.2 | 37.6 | 18.9 | 6.23 |
| 2 | 2 | 15 | 83.8 | 76.7 | 28.7 | 16.7 | 12.3 |
| 2 | 5 | 5 | – | 87.7 | 72.5 | 48.9 | 27.1 |
| 2 | 5 | 10 | 58.3 | 34.8 | 27.2 | 4.85 | 5.30 |
| 2 | 5 | 15 | 82.3 | 73.6 | 32.4 | 4.15 | 0 |
| 4 | 2 | 5 | 74.9 | 69.3 | 57.7 | 37.1 | 21.7 |
| 4 | 2 | 10 | 74.6 | 72.6 | 42.8 | 22.7 | 9.20 |
| 4 | 2 | 15 | 74.9 | 36.2 | 30.2 | 22.6 | 12.4 |
| 4 | 3 | 5 | 79.8 | 54.3 | 49.5 | 30.0 | 10.7 |
| 4 | 3 | 10 | 77.8 | 57.5 | 42.5 | 25.2 | 8.60 |
| 4 | 3 | 15 | 78.2 | 62.7 | 42.5 | 40.6 | 17.3 |
| 4 | 5 | 5 | 69.4 | 59.8 | 46.4 | 15.0 | 5.15 |
| 4 | 5 | 10 | 72.6 | 77.4 | 49.1 | 28.0 | 6.10 |
| 4 | 5 | 15 | 68.8 | 52.7 | 23.2 | 9.10 | 6.96 |
Однако данные по истиранию агрегатов при глубине потока 5 мм, т.е. при относительной глубине 1–2 ед. (H/d, где d – диаметр агрегата и H – глубина потока) резко отличаются от результатов, полученных при больших глубинах. Из этого следует, что предложенное уравнение описывает лишь частные случаи истирания агрегатов, а именно при глубине потоков, превосходящей в несколько раз диаметр агрегатов. Таким образом, задача разработки универсальной модели истирания почвенных агрегатов в склоновых потоках не была решена, несмотря на ее большую актуальность, как одного из этапов в разработке физически обоснованной модели эрозии почвы. В связи с этим были продолжены теоретические исследования с целью поиска общего решения проблемы на основе представлений о механизме разрушения агрегатов в потоке, полученных при проведении экспериментальных работ.
ТЕОРЕТИЧЕСКОЕ РЕШЕНИЕ ПРОБЛЕМЫ
Первые теоретические исследования процесса истирания обломков горной породы были проведены Штернбергом [11], который вывел дифференциальное уравнение из представления о том, что потеря веса частицы (P) пропорциональна ее весу в воде и изменению длины пути в потоке (х), то есть
Решением уравнения Штернберга при C = const является функция:
где Р0 и Р – соответственно начальный и конечный вес частицы, C – коэффициент, зависящий от твердости породы, скорости течения и перемещения частицы в потоке, и других физических свойств частицы и породы, слагающей дно потока, по которому она перемещается, х – расстояние, на которое переместилась частица.Если записать вес частицы через объем шара с эффективным диаметром D, то получим формулу
Шоклич [10] в результате обработки экспериментальных данных, предложил следующее выражение для коэффициента С уравнения Штернберга:
где v – скорость движения частиц в потоке, м/с; С1 – коэффициент, величина которого определяется твердостью горной породы; D – диаметр частиц, мм.Однако следует заметить, что помимо диаметра (D) в уравнение (4) входит также неизвестная скорость движения частицы (v). Кроме того, из работы Ларионова с соавт. [2] следует, что показатель степени в формуле (2) зависит от х в некоторой степени n (n = 0.64).
Результаты опытов подводят к мысли о необходимости пересмотра теории Штернберга [11] и построении новой модели истирания частицы, опирающиеся на законы механики. Напомним их формулировки. Изменение массы частицы (m) в единицу времени равно скорости ее потери (m'), то есть
И второй закон Ньютона – изменение количества движения (mv) в единицу времени равно действию внешних сил (F)
Очевидно, что выбор m' и F определяет закон истирания. В этой связи рассмотрим некоторые варианты задания m' и F.
Вариант 1.
а) Предположим, что скорость истирания частицы пропорциональна ее весу в воде, а коэффициент истирания пропорционален скорости движения частицы (v), то есть
где g – ускорение силы тяжести, ρч – плотность частицы, ρ – плотность воды, μ – коэффициент потери массы, r – радиус частицы.б) Примем также, что внешняя сила есть сумма из сил лобового давления и сухого трения, то есть
(8)
$F = {{C}_{x}}\pi {{r}^{2}}\rho {{(u - v)}^{2}} - Kg({{\rho }_{{\text{ч}}}} - \rho )\frac{4}{3}\pi {{r}^{3}},$(10)
$m\frac{{dv}}{{dt}} = {{C}_{x}}\pi {{r}^{2}}\rho {{(u - v)}^{2}} - Kg\left( {1 - \frac{\rho }{{{{\rho }_{{\text{ч}}}}}}} \right)m.$Из уравнения (10) легко определить наибольший радиус частицы (r*), которая не будет перемещаться потоком (v = 0):
(11)
$r* = \frac{{\frac{3}{4}{{C}_{x}}\frac{\rho }{{{{\rho }_{{\text{ч}}}}}}{{u}^{2}}}}{{Kg\left( {1 - \frac{\rho }{{{{\rho }_{{\text{ч}}}}}}} \right)}}.$Иначе говоря, начальный радиус частицы r0, способной перемещаться потоком, должен отвечать условию r0 < r*.
Рассмотрим уравнение (9). Разделим обе части на v и, учитывая равенство dx = vdt, получим:
Умножая обе части уравнения (12) на g, получаем уравнение Штернберга (1):
с зависимостью истирания от относительной плотности частицы.
Вариант 2. Будем полагать, что скорость истирания частицы пропорциональна весу частицы в воде, с коэффициентом, пропорциональным квадрату скорости:
Внешняя сила есть сумма силы сопротивления в форме (8), пропорциональной разности скоростей потока и частицы:
(13)
$F = {{C}_{x}}\pi {{r}^{2}}\rho {{(u - v)}^{2}} - Kg\left( {1 - \frac{\rho }{{{{\rho }_{{\text{ч}}}}}}} \right)m.$С учетом допущений о виде m и F уравнения (5) и (6) принимают вид:
(14)
$\frac{{dm}}{{dt}} = - \mu \left( {1 - \frac{\rho }{{{{\rho }_{{\text{ч}}}}}}} \right)m{{v}^{2}},$(15)
$m\frac{{dv}}{{dt}} = {{C}_{x}}\pi {{r}^{2}}\rho {{(u - v)}^{2}} - Kg\left( {1 - \frac{\rho }{{{{\rho }_{{\text{ч}}}}}}} \right)m.$Заметим, что, как правило, процесс истирания и, как следствие, изменение радиуса частицы происходит сравнительно медленно. Поэтому скорость движения частицы также меняется медленно. Это обстоятельство позволяет пренебречь инерционным членом уравнения (15) и определить скорость из уравнения:
Отсюда получаем:
Запишем теперь уравнение (14) в виде:
Разделим обе части последнего уравнения на v и с учетом равенства vdt = dx и (16) получим
(17)
$\frac{{dr}}{{dx}} = - \frac{\mu }{3}\left( {1 - \frac{\rho }{{{{\rho }_{{\text{ч}}}}}}} \right)u\left( {1 - \sqrt {\frac{r}{{r{\kern 1pt} *}}} } \right)r.$Разделим обе части (17) на r* и, вводя новую переменную, y = $\sqrt {\frac{r}{{r{\text{*}}}}} ,$ приведем уравнение (17) к виду удобному для интегрирования:
Решим (18) относительно y: y = $\frac{{A{{e}^{{ - {\lambda }x}}}}}{{1 + A{{e}^{{ - {\lambda }x}}}}},$ где A = $\frac{{{{y}_{{\text{0}}}}}}{{1 - {{y}_{{\text{0}}}}}},$ и, учитывая введенное обозначение, получим окончательное решение:
(19)
$\begin{gathered} r = r{\kern 1pt} *{{\left( {\frac{{A{{e}^{{ - \lambda x}}}}}{{1 + A{{e}^{{ - \lambda x}}}}}} \right)}^{2}} = \\ = \,\,r{\kern 1pt} *{{\left( {\frac{{\sqrt {\frac{{{{r}_{0}}}}{{r{\kern 1pt} *}}} }}{{1 - \sqrt {\frac{{{{r}_{0}}}}{{r{\kern 1pt} *}}} }}{{e}^{{ - \lambda x}}}{{{\left( {1 + \frac{{\sqrt {\frac{{{{r}_{0}}}}{{r{\kern 1pt} *}}} }}{{1 - \sqrt {\frac{{{{r}_{0}}}}{{r{\kern 1pt} *}}} }}{{e}^{{ - \lambda x}}}} \right)}}^{{ - 1}}}} \right)}^{2}}. \\ \end{gathered} $Последнее уравнение удовлетворительно описывает все экспериментальные результаты, полученные нами ранее [1].
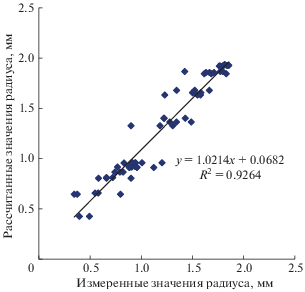
Сопоставление рассчитанных значений радиуса агрегатов по уравнению (19) с экспериментальными данными при различной длине (10, 20, 50, 100 и 200 м) их пробега в потоке показало значимую корреляцию (R2 = 0.926, P = 0.95), что свидетельствует о существенно большей предикативности теоретического уравнения по сравнению с эмпирическим (рис. 1). Расчеты показали, что коэффициент угла наклона (1.0214) значимо (P = 0.95) не отличается от 1, оценка стандартной ошибки углового коэффициента регрессии – 0.036. Оценка свободного члена регрессии (0.0682) значимо (P = = 0.95) не отличается от 0. Кроме того, теоретическое уравнение истирания почвенных агрегатов в отличие от эмпирического оказалось применимым и к потокам малой глубины.
Рис. 1.
Сопоставление рассчитанных по формуле (19) значений радиуса агрегатов с измеренными после пробега пути длиной 10, 20, 50, 100 и 200 м.
ВЫВОДЫ
1. Теоретический анализ процесса истирания почвенных частиц в потоке дал два решения. Первое решение привело к известному уравнению Штернберга и показало, что коэффициент истирания зависит от относительной плотности частицы.
2. Второе решение, в основу которого положена зависимость истирания от квадрата скорости частицы, привело к уравнению совершенно иного вида. При помощи этого уравнения удалось описать все экспериментальные данные, которые были получены нами ранее.
3. Последнее уравнение может быть использовано для описания истирания срываемых в процессе эрозии почвенных агрегатов и деления суммарного содержания наносов в потоке на влекомые и взвешенные, что необходимо знать для расчета смыва почвы по продольному профилю склона.
Список литературы
Ларионов Г.А. Истирание почвенных агрегатов в склоновых потоках // Эрозия почв и русловые процессы. 2008. Вып. 16. С. 74–83.
Ларионов Г.А., Бушуева О.Г., Добровольская Н.Г., Кирюхина З.П., Литвин Л.Ф., Максимова И.А. Разрушение почвенных агрегатов в склоновых потоках // Почвоведение. 2007. № 10. С. 1263–1269.
Ларионов Г.А., Добровольская Н.Г., Кирюхина З.П., Литвин Л.Ф. Влияние твердости донных наносов ложа потока на его эрозионную способность // Почвоведение. 2005. № 4. С. 494–498.
Ларионов Г.А., Добровольская Н.Г., Кирюхина З.П., Литвин Л.Ф. Влияние взвешенных наносов на эродирумость почв // Почвоведение. 2008. № 7. С. 871–876.
Мирцхулава Ц.Е. Инженерные методы расчета и прогноза водной эрозии. М.: Колос, 1970. 240 с.
Швебс Г.И. Формирование водной эрозии стока наносов и их оценка (на примере Украины и Молдавии). Л.: Гидрометеоиздат, 1974. 184 с.
Domokos G., Jerolmack D.J., Sipos A.Á., Török Á. How River Rocks Round: Resolving the Shape-Size Paradox // PLOS One. 2014. V. 9. № 2. P. e88657. https://doi.org/10.1371/journal.pone.0088657
Foster G.R., Lane L.J., Nearing M.A., Finkner S.C., Flanagan D.C. Erosion component // USDA – Water Erosion Prediction Project: Hillslope Profile Model Documentation. NSERL Report No. 2. USDA-ARS National Soil Erosion Research Laboratory. West Lafayette, Ind. 1989. P. 10.1–10.12.
Le Bouteiller C., Naaim-Bouvet F., Mathys N., Lavé J. A new framework for modeling sediment fining during transport with fragmentation and abrasion // J. Geophys. Res. Earth Surf. 2011. V. 116. F03002. https://doi.org/10.1029/2010JF001926
Schoklitsch A. Handbuch des Wasserbaues [Handbook of Hydraulic Structures]. Zweiter Band. Wien: Springer–Verlag, 1962. 1071 s.
Sternberg H. Untersuchungen über Längen- und Querprofil geschiebeführender Flüsse // Zeitschrift für Bauwesen. 1875. Jg. XXV. H. XI/XII. S. 483–506.
Tödten H. A mathematical model to describe surface erosion caused by overland flow // Quantitative slope models. Zeitschrift für Geomorphology. 1976. V. 25. P. 89–105.
Wang J., Li Z., Cai C., Ma R. Particle size and shape variation of Ultisol aggregates affected by abrasion under different transport distances in overland flow // Catena. 2014. V. 123. № 4. P. 153–162. https://doi.org/10.1016/j.catena.2014.07.020
Дополнительные материалы отсутствуют.
Инструменты
Почвоведение


