Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2019, № 4, стр. 100-107

Асимптотические формулы в теории дифракционного и переходного излучения на проводящей сфере

В. В. Сыщенко^1, *, Э. А. Ларикова¹

¹ Белгородский государственный национальный исследовательский университет
308015 Белгород, Россия

Поступила в редакцию 26.06.2018
После доработки 20.07.2018
Принята к публикации 14.07.2018

DOI: 10.1134/S0207352819040188

Аннотация

Дано описание дифракционного и переходного излучения равномерно движущейся нерелятивистской заряженной частицы на идеально проводящей сфере, основанное на известном из электростатики методе изображений. Построены асимптотические формулы, описывающие характеристики излучения в области низких и высоких частот. Показано, что в высокочастотном пределе возможно распространение данного подхода на случай релятивистской налетающей частицы.

Ключевые слова: дифракционное излучение, переходное излучение, проводящая сфера, метод изображений, фиктивный заряд.

ВВЕДЕНИЕ

Равномерно движущаяся частица может порождать излучение электромагнитных волн либо в однородной среде (если выполняется условие черенковского излучения), либо при взаимодействии с неоднородностями среды. В последнем случае принято разделять переходное излучение, возникающее при пересечении движущейся частицей двух сред, и дифракционное излучение, отвечающее случаю движения частицы вблизи пространственно локализованной неоднородности среды (мишени) без пересечения ее границы.

С микроскопической точки зрения, излучение порождается нестационарными токами, индуцированными в мишени полем пролетающей частицы. В альтернативном случае (макроскопическом подходе) излучение обусловлено условиями, налагаемыми на решения уравнений Максвелла на границе мишени. Оказывается, что удовлетворить граничным условиям можно, лишь прибавив к полю, создаваемому в двух средах пролетающей частицей, решение свободных уравнений Максвелла, которое и представляет собой поле излучения [1]. Поэтому задача о переходном излучении на мишени сколько-нибудь сложной геометрии (в отличие от задачи о переходного излучения на плоскопараллельной пластинке) сопряжена со значительными вычислительными трудностями.

Излучение, возникающее на сферических мишенях (проводящих либо диэлектрических), рассматривалось во многих работах [2–5]. Однако результаты этих работ либо касались лишь некоторых частных случаев (таких как пролет частицы через центр сферы), либо решение представлялось в громоздкой форме бесконечного ряда, затрудняющей его анализ и интерпретацию. В настоящей статье развивается предложенный в работе [6] подход к описанию дифракционного излучения и переходного излучения нерелятивистской частицы на проводящей сфере, основанный на известном в электростатике методе изображений [7]. Исследуются различные предельные случаи, допускающие построение простых асимптотических формул, а также возможность распространения данного подхода на случай релятивистской налетающей частицы. Следует отметить, что именно метод изображений был использован в пионерской работе [8], предсказавшей явление переходного излучения на проводящей плоскости. В задаче о переходном излучении на проводящей сфере метод изображений был впервые предложен в заметке [9], однако использованное автором дипольное приближение не приводит к правильному результату.

МЕТОДИКА

Одним из способов удовлетворить граничным условиям на границе вакуума и идеального проводника является известный в электростатике метод изображений [7]. В этом методе влияние проводящей поверхности на распределение электрического поля в пространстве имитируется вводом, наряду с реальным точечным зарядом, одного или нескольких фиктивных зарядов (“изображений” реального заряда). В частности, распределение электрического поля точечного заряда в присутствии заземленной сферы будет таким же (вне сферы), как поле двух точечных зарядов, реального и фиктивного (расположенного внутри сферы, рис. 1). При этом реальный заряд ${{e}_{0}}$ и фиктивный заряд $e = {{ - {{e}_{0}}R} \mathord{\left/ {\vphantom {{ - {{e}_{0}}R} {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}$ должны располагаться на одной прямой с центром сферы радиуса R, где ${{r}_{0}}$ – расстояние от реального заряда до центра сферы, а расстояние от фиктивного заряда до центра сферы составляет $r = {{{{R}^{2}}} \mathord{\left/ {\vphantom {{{{R}^{2}}} {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}{\kern 1pt} .$

Рис. 1.

Положения реального заряда e₀ и его “изображения” e относительно заземленной проводящей сферы радиуса R. Если $b < R$ частица e₀ пересекает сферу, $b > R$ частица не пересекает сферу.

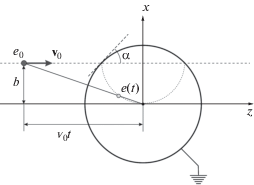
Рассмотрим ситуацию, когда реальный заряд движется прямолинейно и равномерно со скоростью ${{{\mathbf{v}}}_{0}}$ под некоторым прицельным параметром b мимо центра сферы. Очевидно, что в этом случае движение фиктивного заряда будет ускоренным, что и приведет к возникновению излучения. Величина и координаты фиктивного заряда будут определяться следующими соотношениями:

(1)

$\begin{gathered} e(t) = - {{e}_{0}}\frac{R}{{\sqrt {{{b}^{2}} + v_{0}^{2}{{t}^{2}}} }},\quad x(t) = \frac{{{{R}^{2}}b}}{{{{b}^{2}} + v_{0}^{2}{{t}^{2}}}}, \\ z(t) = \frac{{{{R}^{2}}{{v}_{0}}t}}{{{{b}^{2}} + v_{0}^{2}{{t}^{2}}}}. \\ \end{gathered} $

Очевидно, компоненты скорости фиктивного заряда будут равны:

(2)

$\begin{gathered} {{\text{v}}_{x}}(t) = \frac{{dx}}{{dt}} = - \frac{{2{{R}^{2}}b\text{v}_{0}^{2}t}}{{{{{({{b}^{2}} + \text{v}_{0}^{2}{{t}^{2}})}}^{2}}}}, \\ {{\text{v}}_{z}}(t) = \frac{{dz}}{{dt}} = \frac{{{{R}^{2}}{{\text{v}}_{0}}\left( {{{b}^{2}} - \text{v}_{0}^{2}{{t}^{2}}} \right)}}{{{{{\left( {{{b}^{2}} + \text{v}_{0}^{2}{{t}^{2}}} \right)}}^{2}}}}. \\ \end{gathered} $

Спектрально-угловая плотность излучения произвольно движущегося заряда описывается известной формулой [10]:

(3)

$\frac{{dE}}{{d{\omega }d{\Omega }}} = \frac{1}{{4{{{\pi }}^{2}}c}}{{\left| {{\mathbf{k}} \cdot {\mathbf{I}}} \right|}^{2}} = \frac{1}{{4{{{\pi }}^{2}}с }}\left\{ {{{k}^{2}}{{{\left| {\mathbf{I}} \right|}}^{2}} - {{{\left| {{\mathbf{k}} \cdot {\mathbf{I}}} \right|}}^{2}}} \right\},$

где ω – частота излученной волны, k – ее волновой вектор, $\left| {\mathbf{k}} \right| = {{\omega } \mathord{\left/ {\vphantom {{\omega } c}} \right. \kern-0em} c},$ c – скорость света в вакууме,

(4)

${\mathbf{I}} = \int\limits_{ - \infty }^\infty {e(t){\mathbf{v}}(t)\exp [i({\omega }t - {\mathbf{kr}}(t))]dt} $

(легко проверить, что формулы (3), (4), обычно используемые для постоянного заряда e, остаются справедливыми и для переменной величины заряда e(t), как в нашем случае).

В случае $b > R,$ когда траектория реального заряда не пересекает сферу, возникающее излучение носит название дифракционного. Подставляя в (4) выражения для координат и компонент скорости фиктивного заряда, получим:

(5)

$\begin{gathered} {{I}_{x}} = 2{{e}_{0}}b{{R}^{3}}v_{0}^{2}\int\limits_{ - \infty }^\infty {\frac{t}{{{{{\left( {{{b}^{2}} + v_{0}^{2}{{t}^{2}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}} \times \\ \times \,\,\exp \left\{ {i\left[ {{\omega }t - \frac{{{{k}_{x}}{{R}^{2}}b}}{{{{b}^{2}} + v_{0}^{2}{{t}^{2}}}} - \frac{{{{k}_{z}}{{R}^{2}}{{v}_{0}}t}}{{{{b}^{2}} + v_{0}^{2}{{t}^{2}}}}} \right]} \right\}dt, \\ \end{gathered} $

(6)

$\begin{gathered} {{I}_{z}} = - {{e}_{0}}{{R}^{3}}{{\text{v}}_{0}}\int\limits_{ - \infty }^\infty {\frac{{{{b}^{2}} - \text{v}_{0}^{2}{{t}^{2}}}}{{{{{\left( {{{b}^{2}} + \text{v}_{0}^{2}{{t}^{2}}} \right)}}^{{5/2}}}}}} \times \\ \times \,\,\exp \left\{ {i\left[ {{\omega }t - \frac{{{{k}_{x}}{{R}^{2}}b}}{{{{b}^{2}} + \text{v}_{0}^{2}{{t}^{2}}}} - \frac{{{{k}_{z}}{{R}^{2}}{{\text{v}}_{0}}t}}{{{{b}^{2}} + \text{v}_{0}^{2}{{t}^{2}}}}} \right]} \right\}dt. \\ \end{gathered} $

В случае $b < R,$ когда реальный заряд пересекает сферу, возникающее излучение называется переходным. В этом случае формулы для компонент I будут выглядеть несколько сложнее, чем (5) и (6), поскольку они должны учитывать “исчезновение” реального заряда и его изображения в момент времени $ - {{t}_{0}}$ в точке входа заряда в сферу и их “рождение” в момент времени ${{t}_{0}} = {{{{{({{R}^{2}} - {{b}^{2}})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \mathord{\left/ {\vphantom {{{{{({{R}^{2}} - {{b}^{2}})}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} {{{\text{v}}_{0}}}}} \right. \kern-0em} {{{\text{v}}_{0}}}}$ в точке выхода заряда из сферы:

(7)

${{I}_{{x,z}}} = I_{{x,z}}^{{({\text{real}}{\text{.in}})}} + I_{{x,z}}^{{({\text{image}}{\text{.in}})}} + I_{{x,z}}^{{({\text{real}}{\text{.out}})}} + I_{{x,z}}^{{({\text{image}}{\text{.out}})}},$

где

(8)

${{I}_{z}}^{{({\text{real}}{\text{.in}})}} = - i{{e}_{0}}{{\text{v}}_{0}}\frac{{\exp \left[ { - i{{k}_{x}}b - i\left( {{\omega } - {{k}_{z}}{{\text{v}}_{0}}} \right){{t}_{0}}} \right]}}{{{\omega } - {{k}_{z}}{{\text{v}}_{0}}}},$

(9)

$\begin{gathered} I_{x}^{{\left( {{\text{image}}{\text{.in}}} \right)}} = 2{{e}_{0}}b{{R}^{3}}\text{v}_{0}^{2}\int\limits_{ - \infty }^{ - {{t}_{0}}} {\frac{{tdt}}{{{{{\left( {{{b}^{2}} + \text{v}_{0}^{2}{{t}^{2}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}} \times \\ \times \,\,\exp \left\{ {i\left[ {{\omega }t - \frac{{{{k}_{x}}{{R}^{2}}b}}{{{{b}^{2}} + \text{v}_{0}^{2}{{t}^{2}}}} - \frac{{{{k}_{z}}{{R}^{2}}{{\text{v}}_{0}}t}}{{{{b}^{2}} + \text{v}_{0}^{2}{{t}^{2}}}}} \right]} \right\}, \\ \end{gathered} $

(10)

$\begin{gathered} I_{z}^{{\left( {{\text{image}}{\text{.in}}} \right)}} = - {{e}_{0}}{{R}^{3}}{{\text{v}}_{0}}\int\limits_{ - \infty }^{ - {{t}_{0}}} {\frac{{\left( {{{b}^{2}} - \text{v}_{0}^{2}{{t}^{2}}} \right)dt}}{{{{{\left( {{{b}^{2}} + \text{v}_{0}^{2}{{t}^{2}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}} \times \\ \times \,\,\exp \left\{ {i\left[ {{\omega }t - \frac{{{{k}_{x}}{{R}^{2}}b}}{{{{b}^{2}} + \text{v}_{0}^{2}{{t}^{2}}}} - \frac{{{{k}_{z}}{{R}^{2}}{{\text{v}}_{0}}t}}{{{{b}^{2}} + \text{v}_{0}^{2}{{t}^{2}}}}} \right]} \right\}, \\ \end{gathered} $

(11)

$I_{z}^{{({\text{real}}{\text{.out)}}}} = i{{e}_{0}}{{\text{v}}_{0}}\frac{{\exp \left[ { - i{{k}_{x}}b + i\left( {{\omega } - {{k}_{z}}{{\text{v}}_{0}}} \right){{t}_{0}}} \right]}}{{{\omega } - {{k}_{z}}{{\text{v}}_{0}}}},$

(12)

$\begin{gathered} I_{x}^{{\left( {{\text{image}}{\text{.out}}} \right)}} = 2{{e}_{0}}b{{R}^{3}}\text{v}_{0}^{2}\int\limits_{{{t}_{0}}}^\infty {\frac{{tdt}}{{{{{\left( {{{b}^{2}} + v_{0}^{2}{{t}^{2}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}} \times \\ \times \,\,\exp \left\{ {i\left[ {{\omega }t - \frac{{{{k}_{x}}{{R}^{2}}b}}{{{{b}^{2}} + \text{v}_{0}^{2}{{t}^{2}}}} - \frac{{{{k}_{z}}{{R}^{2}}{{\text{v}}_{0}}t}}{{{{b}^{2}} + \text{v}_{0}^{2}{{t}^{2}}}}} \right]} \right\}, \\ \end{gathered} $

(13)

$\begin{gathered} I_{z}^{{\left( {{\text{image}}{\text{.out}}} \right)}} = - {{e}_{0}}{{R}^{3}}{{\text{v}}_{0}}\int\limits_{{{t}_{0}}}^\infty {\frac{{\left( {{{b}^{2}} - \text{v}_{0}^{2}{{t}^{2}}} \right)dt}}{{{{{\left( {{{b}^{2}} + \text{v}_{0}^{2}{{t}^{2}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}} \times \\ \times \,\,\exp \left\{ {i\left[ {{\omega }t - \frac{{{{k}_{x}}{{R}^{2}}b}}{{{{b}^{2}} + \text{v}_{0}^{2}{{t}^{2}}}} - \frac{{{{k}_{z}}{{R}^{2}}{{\text{v}}_{0}}t}}{{{{b}^{2}} + \text{v}_{0}^{2}{{t}^{2}}}}} \right]} \right\}. \\ \end{gathered} $

Численное интегрирование приводит к результату для спектрально-угловой плотности излучения вида:

(14)

$\frac{{d{\rm E}}}{{d{\omega }d{\Omega }}} = \frac{{e_{0}^{2}}}{{4{{{\pi }}^{2}}c}}{\Phi }({\theta ,\varphi ,\omega }),$

где функция Φ(θ, φ, ω) представлена для некоторых частных случаев в виде диаграммы направленности на рис. 2. Спектральная плотность излучения, т.е. результат интегрирования (14) по телесному углу, представлена на рис. 3.

Рис. 2.

Величина Φ(θ, φ, ω) (14), описывающая угловое распределение переходного излучения частицы, движущейся со скоростью v₀ = 0.1c сквозь сферу под прицельным параметром b = 0.8R (a), b = 0.7R (б) и b = 0.6R (в) при Rω/v₀ = 200.

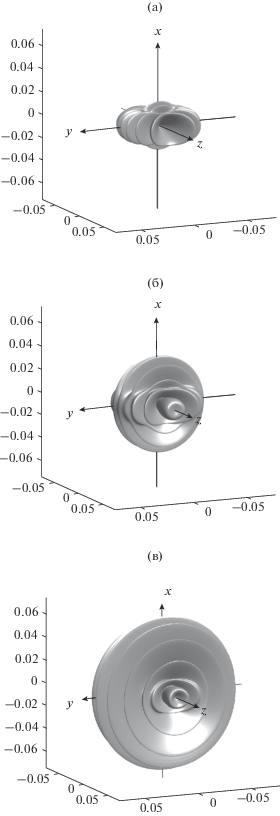
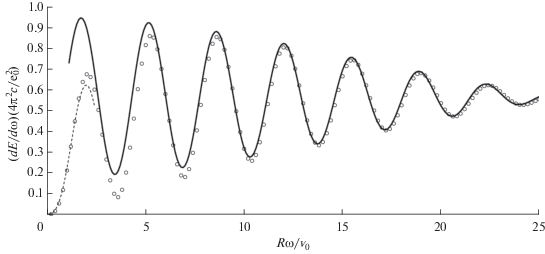
Рис. 3.

Спектр переходного излучения частицы, движущейся со скоростью v₀ = 0.1c сквозь сферу под прицельным параметром b = 0.4R, рассчитанный численно (кружки), по аналитическим формулам (23) (пунктирая линия) и (29) (сплошная линия), проинтегрированным по углам.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Несмотря на то, что интегрирование в формулах для компонент I (5), (6), (9), (10), (12), (13) легко может быть выполнено численно, представляет интерес получение приближенных асимптотических формул для спектрально-угловой плотности излучения, позволяющих в ряде случаев дать наглядную интерпретацию полученным результатам.

Рассмотрим сначала случай низких частот. Рассмотрим сначала дифракционное излучение, описываемое формулами (5), (6). Существенное упрощение этих формул может быть достигнуто, если пренебречь третьим слагаемым в показателе экспоненты по сравнению с первым, что справедливо для любых частот в нерелятивистском случае $\left( {{{v}_{0}} \ll c} \right),$ а также и вторым слагаемым в показателе экспоненты, что справедливо для низких частот излучения:

(15)

${\omega } \ll {{cb} \mathord{\left/ {\vphantom {{cb} {{{R}^{2}}}}} \right. \kern-0em} {{{R}^{2}}}}.$

Действительно, первое слагаемое в показателе экспоненты (ωt) стремится к нулю $\left( {t \to 0} \right),$ в то время как второе слагаемое стремится к отличной от нуля константе. Эта константа должна быть много меньше единицы всюду, особенно где $\left| {{\omega }t} \right| \ll 1.$ Поэтому самое сильное ограничение будет возникать при условии $t = 0,$ откуда и вытекает требование (15), или в терминах длины волны ${\lambda } = {{2{\pi }с } \mathord{\left/ {\vphantom {{2{\pi }с } {\omega }}} \right. \kern-0em} {\omega }}$ и ${{{\lambda } \gg 2{\pi }R} \mathord{\left/ {\vphantom {{{\lambda } \gg 2{\pi }R} b}} \right. \kern-0em} b}.$

Таким образом, справедливость данного приближения будет ограничена областью малых частот или больших длин волн ${\lambda } \gg R.$ С учетом сделанных приближений и четности подынтегральных функций величина $I_{x}^{{({\text{image}})}}$ становится чисто мнимой, а $I_{z}^{{({\text{image}})}}$ – чисто вещественной. Интегралы, остающиеся в (5), (6) после сделанных упрощений, вычисляются аналитически, в результате чего находим:

(16)

${{I}_{x}} = \frac{4}{3}{{e}_{0}}{{R}^{3}}\frac{{{{{\omega }}^{2}}}}{{\text{v}_{0}^{2}}}i{{K}_{1}}\left( {\frac{{\omega }}{{{{\text{v}}_{0}}}}b} \right),$

(17)

${{I}_{z}} = - \frac{4}{3}{{e}_{0}}{{R}^{3}}\frac{{{{{\omega }}^{2}}}}{{\text{v}_{0}^{2}}}{{K}_{0}}\left( {\frac{{\omega }}{{{{\text{v}}_{0}}}}b} \right) - \frac{2}{3}{{e}_{0}}{{R}^{3}}\frac{{\omega }}{{{{\text{v}}_{0}}b}}{{K}_{1}}\left( {\frac{{\omega }}{{{{\text{v}}_{0}}}}b} \right),$

где ${{K}_{0}}(x)$ и ${{K}_{1}}(x)$ – модифицированные функции Бесселя третьего рода (функции Макдональда). Спектрально-угловая плотность дифракционного излучения в этом случае описывается формулой

(18)

$\begin{array}{*{20}{c}} {\frac{{dE}}{{d{\omega }d{\Omega }}} = \frac{4}{{9{{{\pi }}^{2}}}}\frac{{e_{0}^{2}{{R}^{6}}{{{\omega }}^{6}}}}{{{{c}^{3}}\text{v}_{0}^{4}}}\left\{ {\left( {1 - {{{\sin }}^{2}}{\theta }{{{\cos }}^{2}}{\varphi }} \right)K_{1}^{2}\left( {\frac{{\omega }}{{{{\text{v}}_{0}}}}b} \right) + } \right.} \\ {\left. { + {{{\sin }}^{2}}{\theta }{{{\left( {\frac{{{{\text{v}}_{0}}}}{{2{\omega }b}}} \right)}}^{2}}{{{\left[ {{{K}_{1}}\left( {\frac{{\omega }}{{{{\text{v}}_{0}}}}b} \right) + 2\frac{{\omega }}{{{{\text{v}}_{0}}}}b{{K}_{0}}\left( {\frac{{\omega }}{{{{\text{v}}_{0}}}}b} \right)} \right]}}^{2}}} \right\}.} \end{array}$

Обратимся теперь к случаю переходного излучения. Обсуждение возможности упрощений, аналогичных случаю дифракционного излучения, удобно начать с вклада реального заряда, вычисляемого точно. Полный вклад реального заряда в излучение будет описываться суммой величин (8) и (11):

(19)

$\begin{array}{*{20}{c}} \begin{gathered} I_{z}^{{({\text{real}})}} = I_{z}^{{({\text{real}}{\text{.in}})}} + I_{z}^{{({\text{real}}{\text{.out}})}} = \\ = - 2{{e}_{0}}{{\text{v}}_{0}}\frac{{\sin \left[ {\left( {{\omega } - {{k}_{z}}{{\text{v}}_{0}}} \right){{t}_{0}}} \right]}}{{{\omega } - {{k}_{z}}{{\text{v}}_{0}}}}\exp \left( { - i{{k}_{x}}b} \right) = \\ \end{gathered} \\ { = - 2{{e}_{0}}{{\text{v}}_{0}}\frac{{\sin \left[ {{\omega }\left( {1 - \frac{{{{\text{v}}_{0}}}}{c}\cos {\theta }} \right){{t}_{0}}} \right]}}{{{\omega }\left( {1 - \frac{{{{\text{v}}_{0}}}}{c}\cos {\theta }} \right)}}\exp \left( { - i{{k}_{x}}b} \right).} \end{array}$

На первый взгляд, нерелятивистское приближение позволяет пренебречь членом $ - ({{{{\text{v}}_{0}}} \mathord{\left/ {\vphantom {{{{\text{v}}_{0}}} c}} \right. \kern-0em} c})\cos {\theta }$ по сравнению с единицей, как в числителе, так и в знаменателе. Однако в реальности такое упрощение будет справедливо лишь для достаточно низких частот. Действительно, при изменении полярного угла θ от 0 до π аргумент синуса в числителе изменится на величину порядка ${{2{\omega }R} \mathord{\left/ {\vphantom {{2{\omega }R} c}} \right. \kern-0em} c}.$ Таким образом, слагаемое $ - ({{{{\text{v}}_{0}}} \mathord{\left/ {\vphantom {{{{\text{v}}_{0}}} c}} \right. \kern-0em} c})\cos {\theta }$ окажет пренебрежимо малое влияние на угловое распределение излучения только в случае

(20)

${{{\omega }R} \mathord{\left/ {\vphantom {{{\omega }R} {c \ll 1}}} \right. \kern-0em} {c \ll 1}},$

что совпадает по порядку величины с ограничением (15), полученным для дифракционного излучения из других соображений. В противоположном случае высоких частот, когда

(21)

${{{\omega }R} \mathord{\left/ {\vphantom {{{\omega }R} {c \geqslant 1}}} \right. \kern-0em} {c \geqslant 1}},$

в угловом распределении переходного излучения будет наблюдаться сильная угловая зависимость, минимумы и максимумы которой связаны с интерференцией излучения, возникающего в двух точках пересечения частицей сферы. Случай высоких частот будет рассмотрен ниже.

При выполнении условия (20) в показателях экспонент в (9), (10), (12), (13) возможны те же упрощения, что и в формулах (5), (6), описывающих дифракционное излучение. С учетом этого, интегралы (9), (10), (12), (13) могут быть приближенно оценены в двух случаях: скользящего столкновения частицы со сферой ($b \to R$) и пролета частицы вблизи центра сферы $\left( {b \ll R} \right).$

В первом случае интегралы в (9), (10), (12), (13) удобно представить в виде разностей интегралов в полубесконечных пределах (суммы которых будут равны (16) и (17) соответственно) и в пределах от $ - {{t}_{0}}$ до 0 или от 0 до ${{t}_{0}}$ соответственно. При этом подынтегральные выражения последних могут быть разложены по малому параметру $\left( {{{\text{v}{}_{0}{{t}_{0}}} \mathord{\left/ {\vphantom {{\text{v}{}_{0}{{t}_{0}}} {b \ll 1}}} \right. \kern-0em} {b \ll 1}}} \right).$ Выполняя интегрирование и подставляя результат в (3), получим формулу спектрально-угловой плотности переходного излучения для случая скользящего столкновения:

(22)

$\begin{gathered} \frac{{dE}}{{d{\omega }d{\Omega }}} = \frac{{e_{0}^{2}{{{\omega }}^{2}}}}{{4{{{\pi }}^{2}}{{c}^{3}}}}\left\{ {\left( {1 - {{{\sin }}^{2}}{\theta }{{{\cos }}^{2}}{\varphi }} \right)} \right. \times \\ \times \,\,{{\left[ {\frac{4}{3}{{R}^{3}}\frac{{{{{\omega }}^{2}}}}{{\text{v}_{0}^{2}}}K_{1}^{{}}\left( {\frac{{\omega }}{{{{\text{v}}_{0}}}}b} \right) - A\sin {\omega }{{t}_{0}} + B\cos {\omega }{{t}_{0}}} \right]}^{2}} + \\ + {{\sin }^{2}}{\theta }\left[ { - 2\frac{{{{\text{v}}_{0}}}}{{\omega }}\sin {\omega }{{t}_{0}} - \frac{4}{3}{{R}^{3}}\frac{{{{{\omega }}^{2}}}}{{\text{v}_{0}^{2}}}{{K}_{0}}\left( {\frac{{\omega }}{{{{\text{v}}_{0}}}}b} \right) - } \right. \\ \left. {{{{\left. { - \frac{2}{3}{{R}^{3}}\frac{{\omega }}{{{{\text{v}}_{0}}b}}{{K}_{1}}\left( {\frac{{\omega }}{{{{\text{v}}_{0}}}}b} \right) + D\sin {\omega }{{t}_{0}} - C\cos {\omega }{{t}_{0}}} \right]}}^{2}}} \right\}, \\ \end{gathered} $

где

$A = \frac{{4{{R}^{3}}}}{{{{b}^{2}}}}\frac{{\text{v}_{0}^{2}}}{{{{{\omega }}^{2}}{{b}^{2}}}}\left[ {1 - \frac{{15}}{2}\left( {\frac{{{{R}^{2}}}}{{{{b}^{2}}}} - 1} \right) + 15\frac{{\text{v}_{0}^{2}}}{{{{{\omega }}^{2}}{{b}^{2}}}}} \right],$

$B = \frac{{4{{R}^{3}}}}{{{{b}^{2}}}}\frac{{{{\text{v}}_{0}}}}{{{\omega }b}}\sqrt {\frac{{{{R}^{2}}}}{{{{b}^{2}}}} - 1} \left[ {1 - \frac{5}{2}\left( {\frac{{{{R}^{2}}}}{{{{b}^{2}}}} - 1} \right) + 15\frac{{\text{v}_{0}^{2}}}{{{{{\omega }}^{2}}{{b}^{2}}}}} \right],$

$С = \frac{{14{{R}^{3}}}}{{{{b}^{2}}}}\frac{{\text{v}_{0}^{2}}}{{{{{\omega }}^{2}}{{b}^{2}}}}\sqrt {\frac{{{{R}^{2}}}}{{{{b}^{2}}}} - 1} ,$

$D = \frac{{2{{R}^{3}}}}{{{{b}^{2}}}}\frac{{{{\text{v}}_{0}}}}{{{\omega }b}}\left[ {1 - \frac{7}{2}\left( {\frac{{{{R}^{2}}}}{{{{b}^{2}}}} - 1} \right) + 7\frac{{\text{v}_{0}^{2}}}{{{{{\omega }}^{2}}{{b}^{2}}}}} \right].$

В противоположном случае пролета частицы вблизи центра сферы $(b \ll R)$ роль малого параметра в подынтегральных выражениях (9), (10), (12), (13) будет играть величина ${b \mathord{\left/ {\vphantom {b {\text{v}{}_{0}{{t}_{0}}}}} \right. \kern-0em} {\text{v}{}_{0}{{t}_{0}}}} \ll 1.$ В этом случае вычисления интегралов и подстановка результатов в (3) приводит к следующей формуле для спектрально-угловой плотности излучения:

(23)

где

$P = \frac{{2{{R}^{3}}b{\omega }}}{{3\text{v}_{0}^{3}t_{0}^{2}}}\left[ {1 - \frac{{3{{b}^{2}}}}{{4\text{v}_{0}^{2}t_{0}^{2}}} + \frac{{{{b}^{2}}{{{\omega }}^{2}}}}{{8\text{v}_{0}^{2}}}} \right],$

$Q = \frac{{2{{R}^{3}}b{{{\omega }}^{2}}}}{{3\text{v}_{0}^{3}{{t}_{0}}}}\left[ {1 - \frac{2}{{t_{0}^{2}{{{\omega }}^{2}}}} + \frac{{3{{b}^{2}}}}{{\text{v}_{0}^{2}{{{\omega }}^{2}}t_{0}^{4}}} - \frac{{{{b}^{2}}}}{{4\text{v}_{0}^{2}t_{0}^{2}}} + \frac{{{{b}^{2}}{{{\omega }}^{2}}}}{{8\text{v}_{0}^{2}}}} \right],$

$S = \frac{{2{{R}^{3}}b{{{\omega }}^{3}}}}{{3\text{v}_{0}^{3}}}\left[ {1 + \frac{{{{b}^{2}}{{{\omega }}^{2}}}}{{8\text{v}_{0}^{2}}}} \right],$

$F = \frac{{{{R}^{3}}}}{{\text{v}_{0}^{2}t_{0}^{2}}}\left[ {1 - \frac{{7{{b}^{2}}}}{{4\text{v}_{0}^{2}t_{0}^{2}}} + \frac{{7{{b}^{2}}{{{\omega }}^{2}}}}{{24\text{v}_{0}^{2}}}} \right],$

$G = \frac{{{{R}^{3}}{\omega }}}{{\text{v}_{0}^{2}{{t}_{0}}}}\left[ {1 - \frac{{7{{b}^{2}}}}{{12\text{v}_{0}^{2}t_{0}^{2}}} + \frac{{7{{b}^{2}}{{{\omega }}^{2}}}}{{24\text{v}_{0}^{2}}}} \right],$

$H = {{R}^{3}}\frac{{{{{\omega }}^{2}}}}{{\text{v}_{0}^{2}}}\left( {1 + \frac{{7{{b}^{2}}{{{\omega }}^{2}}}}{{24\text{v}_{0}^{2}}}} \right),$

интегральный косинус определяется как

$\operatorname{ci} ({\omega }x) = - \int\limits_x^\infty {\frac{{\cos ({\omega }t)}}{t}dt} .$

Обратимся теперь к области высоких частот, когда

(24)

${{R{\omega }} \mathord{\left/ {\vphantom {{R{\omega }} {{{\text{v}}_{0}}}}} \right. \kern-0em} {{{\text{v}}_{0}}}} \gg 1.$

В этом случае также возможно упрощение общих формул, благодаря тому, что характерный поперечный размер кулоновского поля движущейся частицы ${{{{\text{v}}_{0}}} \mathord{\left/ {\vphantom {{{{\text{v}}_{0}}} {\omega }}} \right. \kern-0em} {\omega }}$ [7] оказывается мал, по сравнению радиусом сферы. Это означает, что в окрестности точки пересечения со сферой можно пренебречь кривизной проводника и описывать возникающее излучение как п на двух наклонных плоскостях. (Исключение составляет лишь область прицельных параметров, очень близких к радиусу сферы, $R - b \leqslant {{{{\text{v}}_{0}}} \mathord{\left/ {\vphantom {{{{\text{v}}_{0}}} {\omega }}} \right. \kern-0em} {\omega }},$ в которой пренебрежение краевыми эффектами не будет оправданным.) В случае взаимодействия частицы с проводящей плоскостью применение метода изображений существенно упрощается: величина фиктивного заряда будет равна с точностью до знака величине реального, $e = - {{e}_{0}},$ а его траектория будет зеркальным отражением траектории реального заряда в этой плоскости. С учетом этого, общая формула (4) даст нам следующее приближенные выражения для вклада в излучение фиктивного заряда в точке входа реальной частицы в сферу вместо (9), (10):

(25)

$I_{x}^{{({\text{image}}{\text{.in}})}} = i{{e}_{0}}{{\text{v}}_{x}}( - {{t}_{0}})\frac{{\exp \left[ { - i{{k}_{x}}b - i\left( {{\omega } - {{k}_{z}}{{\text{v}}_{0}}} \right){{t}_{0}}} \right]}}{{{\omega } - {{k}_{x}}{{\text{v}}_{x}}( - {{t}_{0}}) - {{k}_{z}}{{\text{v}}_{z}}( - {{t}_{0}})}},$

(26)

$I_{z}^{{({\text{image}}{\text{.in}})}} = i{{e}_{0}}{{\text{v}}_{z}}( - {{t}_{0}})\frac{{\exp \left[ { - i{{k}_{x}}b - i\left( {{\omega } - {{k}_{z}}{{\text{v}}_{0}}} \right){{t}_{0}}} \right]}}{{\omega - {{k}_{x}}{{\text{v}}_{x}}( - {{t}_{0}}) - {{k}_{z}}{{\text{v}}_{z}}( - {{t}_{0}})}},$

где ${{\text{v}}_{x}}( - {{t}_{0}})$и ${{\text{v}}_{z}}( - {{t}_{0}})$ – компоненты скорости фиктивного заряда в момент входа реального заряда в сферу, определяемые формулами (2) при $t = - {{t}_{0}}$. Формулы (25) и (26) допускают простую интерпретацию. Поскольку траектория фиктивного заряда оканчивается в той же точке и в тот же момент времени, в которое реальный заряд входит в сферу, фазовый множитель в (25) и (26) совпадает с таковым в (8). Отличия же (25) и (26) от вклада реального заряда (8) обусловлены изменением знака заряда и поворотом скорости фиктивного заряда v относительно скорости реального заряда ${{\text{v}}_{0}}$ на угол 2α (где α – угол между скоростью налетающей частицы v₀ и касательной к сфере в точке входа частицы в сферу, рис. 1), так что ${{\text{v}}_{x}}( - {{t}_{0}}) = {{\text{v}}_{0}}\sin 2{\alpha ,}$ ${{\text{v}}_{z}}( - {{t}_{0}}) = {{\text{v}}_{0}}\cos 2{\alpha }{\text{.}}$ Таким образом, вместо величины ${\mathbf{k}}{{{\mathbf{v}}}_{0}} = {{k}_{z}}{{\text{v}}_{0}},$ фигурирующей в (8), в (25) и (26) присутствует величина

${\mathbf{kv}}( - {{t}_{0}}) = {{k}_{x}}{{\text{v}}_{0}}\sin 2{\alpha } + {{k}_{z}}{{\text{v}}_{0}}\cos 2{\alpha }{\text{.}}$

Аналогичным образом, вклад фиктивного заряда в точке выхода реальной частицы из сферы в момент времени ${{t}_{0}}$ будут описываться вместо (12), (13), приближенными формулами:

(27)

$I_{x}^{{({\text{image}}{\text{.out}})}} = - i{{e}_{0}}{{\text{v}}_{x}}({{t}_{0}})\frac{{\exp \left[ { - i{{k}_{x}}b + i\left( {{\omega } - {{k}_{z}}{{\text{v}}_{0}}} \right){{t}_{0}}} \right]}}{{{\omega } - {{k}_{x}}{{\text{v}}_{x}}({{t}_{0}}) - {{k}_{z}}{{\text{v}}_{z}}({{t}_{0}})}},$

(28)

$I_{z}^{{({\text{image}}{\text{.out}})}} = - i{{e}_{0}}{{\text{v}}_{z}}({{t}_{0}})\frac{{\exp \left[ { - i{{k}_{x}}b + i\left( {{\omega } - {{k}_{z}}{{\text{v}}_{0}}} \right){{t}_{0}}} \right]}}{{{\omega } - {{k}_{x}}{{\text{v}}_{x}}({{t}_{0}}) - {{k}_{z}}{{\text{v}}_{z}}({{t}_{0}})}},$

причем ${{\text{v}}_{x}}({{t}_{0}}) = - {{\text{v}}_{x}}( - {{t}_{0}}),$ ${{\text{v}}_{z}}({{t}_{0}}) = {{\text{v}}_{z}}( - {{t}_{0}}).$

Полученные результаты позволяют понять причудливый характер углового распределения переходного излучения в области высоких частот. Угловое распределение излучения, порождаемое независимо каждым из четырех векторов ${{{\mathbf{I}}}^{{({\text{real}}{\text{.in}})}}},$ ${{{\mathbf{I}}}^{{({\text{real}}{\text{.out}})}}},$ ${{{\mathbf{I}}}^{{({\text{real}}{\text{.in}})}}},$ ${{{\mathbf{I}}}^{{({\text{real}}{\text{.out}})}}},$ описывающих парциальные вклады в излучение реального и фиктивного зарядов на входе реального заряда в сферу и на выходе из нее, имело бы одинаковую форму, но разную ориентацию: ось симметрии каждого из них параллельна скорости данного заряда в точке столкновения со сферой. При этом фазовые множители на входе и на выходе отличаются, что приводит к интерференции, которая будет конструктивной, либо деструктивной в зависимости от угла излучения θ между k и ${{{\mathbf{v}}}_{0}}.$

Обратим внимание на то обстоятельство, что при $b < {R \mathord{\left/ {\vphantom {R {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}$ продольная (z-ая) компонента скорости фиктивного заряда (как ${{\text{v}}_{z}}( - {{t}_{0}}),$так и ${{\text{v}}_{z}}({{t}_{0}})$) отрицательна, что с учетом противоположного знака фиктивного заряда относительно ${{e}_{0}}$ приводит к взаимному усилению величин ${{I}_{z}}$ для реального и фиктивного зарядов. В результате этого излучение будет сосредоточено преимущественно в плоскости, перпендикулярной оси z (рис. 3в). В случае же $b > {R \mathord{\left/ {\vphantom {R {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}$ знак компонент скорости фиктивного заряда ${{v}_{z}}( - {{t}_{0}})$ и ${{v}_{z}}({{t}_{0}})$ изменится на противоположный, что приведет к взаимному ослаблению величин ${{I}_{z}}$ для реального и фиктивного зарядов. В результате излучение будет в этом случае сосредоточено преимущественно в плоскости перпендикулярной оси x (рис. 3a).

Подстановка величин (19) и (25)–(28) в (7) приводит к следующей формуле для спектрально-угловой плотности переходного излучения на сфере в пределе высоких частот:

(29)

$\begin{gathered} \frac{{d{\rm E}}}{{d{\omega }d{\Omega }}} = \frac{{e_{0}^{2}\text{v}_{0}^{2}}}{{{{{\pi }}^{2}}{{c}^{3}}}}\left\{ {M\sin \left[ {{\omega }\left( {1 - \frac{{{{\text{v}}_{0}}}}{c}\cos {\theta }} \right){{t}_{0}}} \right] + } \right. \\ + \,\,\left. {N\cos \left[ {{\omega }\left( {1 - \frac{{{{\text{v}}_{0}}}}{c}\cos {\theta }} \right){{t}_{0}}} \right]} \right\}, \\ \end{gathered} $

где

$\begin{gathered} M = \left( {\frac{{ - 1}}{{1 - \frac{{{{\text{v}}_{0}}}}{c}\cos {\theta }}} + } \right. \\ {{\left. { + \,\,\frac{{\cos 2{\alpha }\left( {1 - \frac{{{{\text{v}}_{0}}}}{c}\cos {\theta }\cos 2{\alpha }} \right)}}{{{{{\left( {1 - \frac{{{{\text{v}}_{0}}}}{c}\cos {\theta }\cos 2{\alpha }} \right)}}^{2}} - {{{\left( {\frac{{{{\text{v}}_{0}}}}{c}\sin {\theta }\cos {\varphi }\sin {2\alpha }} \right)}}^{2}}}}} \right)}^{2}} + \\ \end{gathered} $

$ + \,\,{{\left( {\frac{{\frac{{{{\text{v}}_{0}}}}{c}\sin {\theta }\cos {\varphi }{{{\sin }}^{2}}2{\alpha }}}{{{{{\left( {1 - \frac{{{{\text{v}}_{0}}}}{c}\cos {\theta }\cos 2{\alpha }} \right)}}^{2}} - {{{\left( {\frac{{{{\text{v}}_{0}}}}{c}\sin {\theta }\cos {\varphi }\sin {2\alpha }} \right)}}^{2}}}}} \right)}^{2}} - $

$\begin{gathered} - \,\,\left( {\frac{{ - \cos {\theta }}}{{1 - \frac{{{{\text{v}}_{0}}}}{c}\cos {\theta }}} + } \right. \\ \left. { + \,\,\frac{{\cos {\theta }\cos 2{\alpha }\left( {1 - \frac{{{{\text{v}}_{0}}}}{c}\cos {\theta }\cos 2{\alpha }} \right)}}{{{{{\left( {1 - \frac{{{{\text{v}}_{0}}}}{c}\cos {\theta }\cos 2{\alpha }} \right)}}^{2}} - {{{\left( {\frac{{{{\text{v}}_{0}}}}{c}\sin {\theta }\cos {\varphi }\sin {2\alpha }} \right)}}^{2}}}}} \right) + \\ \end{gathered} $

${{\left. { + \,\,\frac{{\frac{{{{\text{v}}_{0}}}}{c}{{{\sin }}^{2}}{\theta }{{{\cos }}^{2}}{\varphi }{{{\sin }}^{2}}2{\alpha }}}{{{{{\left( {1 - \frac{{{{\text{v}}_{0}}}}{c}\cos {\theta }\cos 2{\alpha }} \right)}}^{2}} - {{{\left( {\frac{{{{\text{v}}_{0}}}}{c}\sin {\theta }\cos {\varphi }\sin {2\alpha }} \right)}}^{2}}}}} \right)}^{2}},$

$N{\kern 1pt} = {{\left( {\frac{{\frac{{{{\text{v}}_{0}}}}{c}\sin {\theta }\cos {\varphi }\sin 2{\alpha }\cos 2{\alpha }}}{{{{{\left( {1 - \frac{{{{\text{v}}_{0}}}}{c}\cos {\kern 1pt} {\theta }\cos {\kern 1pt} 2{\alpha }} \right)}}^{2}} - {{{\left( {\frac{{{{\text{v}}_{0}}}}{c}\sin {\kern 1pt} {\theta }{\kern 1pt} \cos {\varphi }{\kern 1pt} \sin {\kern 1pt} {2\alpha }} \right)}}^{2}}}}} \right)}^{2}} + $

$ + \,\,{{\left( {\frac{{\sin 2{\alpha }\left( {1 - \frac{{{{\text{v}}_{0}}}}{c}\cos {\theta }\cos 2{\alpha }} \right)}}{{{{{\left( {1 - \frac{{{{\text{v}}_{0}}}}{c}\cos {\kern 1pt} {\theta }{\kern 1pt} \cos 2{\alpha }} \right)}}^{2}} - {{{\left( {\frac{{{{\text{v}}_{0}}}}{c}\sin {\theta }\cos {\kern 1pt} {\varphi }\sin {\kern 1pt} {2\alpha }} \right)}}^{2}}}}} \right)}^{2}} - $

$ - \,\,{{\left( {\frac{{\sin {\theta }\cos {\varphi }\sin 2{\alpha }}}{{{{{\left( {1 - \frac{{{{\text{v}}_{0}}}}{c}\cos {\theta }\cos 2{\alpha }} \right)}}^{2}} - {{{\left( {\frac{{{{\text{v}}_{0}}}}{c}\sin {\theta }\cos {\varphi }\sin {2\alpha }} \right)}}^{2}}}}} \right)}^{2}}.$

ЗАКЛЮЧЕНИЕ

Дано описание дифракционного и переходного излучений, возникающих при взаимодействии равномерно движущейся заряженной частицы с идеально проводящей сферой, основанное на известном из электростатики методе изображений. Построены асимптотические формулы, описывающие характеристики излучения как в области низких, так и в области высоких частот.

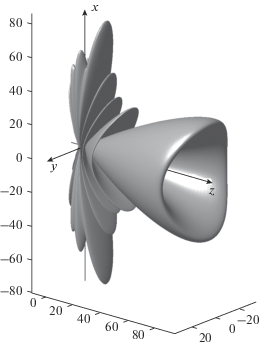
Применимость метода изображений на сфере, когда введение фиктивного заряда позволяет имитировать граничные условия для электрического поля на поверхности проводника, ограничена нерелятивистской областью, в которой кулоновские поля реального и фиктивного зарядов не претерпевают лоренцевского сжатия. Однако это ограничение снимается в важном случае высоких частот излучения, при которых малый поперечный размер соответствующей фурье-компоненты кулоновского поля частицы позволяет пренебречь локальной кривизной поверхности проводника и описывать процесс как переходное излучение на наклонной плоскости. В этом случае полученные результаты будут справедливы и для релятивистской налетающей частицы (рис. 4).

Рис. 4.

Величина Φ(θ, φ, ω) (14), описывающая угловое распределение переходного излучения частицы, движущейся со скоростью v₀ = 0.99c сквозь сферу под прицельным параметром $b = {R \mathord{\left/ {\vphantom {R {\sqrt 2 }}} \right. \kern-0em} {\sqrt 2 }}$ при Rω/v₀ = 25.

Другое ограничение применимости полученных результатом связано со справедливостью приближения идеального проводника, при котором распределение индуцированных в сфере зарядов успевает мгновенно подстраиваться под изменение поля пролетающей частицы таким образом, чтобы лежащее в основе метода изображений граничное условие на поверхности проводника (обращение в нуль тангенциальной компоненты электрического поля) выполнялось в каждый момент времени. Это требование будет заведомо выполнено для частот, меньших обратного времени релаксации в металле. Например, для меди эта величина составляет 5 × 10¹³ с^–1 [11].

Таким образом, полученные результаты будут справедливы (как минимум) вплоть до частот терагерцевого и дальнего инфракрасного диапазонов. В работе [12 ] отмечается, что приближение идеального проводника в задаче о переходном излучении будет выполнено и для более высоких частот (до видимой части спектра включительно). Однако применимость наших результатов в видимой области нуждается в дальнейшем исследовании, учитывающем возможность плазмонных резонансов в металле.

БЛАГОДАРНОСТИ

Авторы благодарны Е.А. Памятных за обсуждение последнего круга вопросов.

Список литературы

Тер-Микаелян М.Л. Влияние среды на электромагнитные процессы при высоких энергиях. Ереван: Изд-во АН Арм. ССР, 1969. 457 с.
Garcia de Abajo F.J. // Phys. Rev. E. 2000. V. 61. P. 5743. doi 10.1103/PhysRevE.61.5743
Shulga N.F., Dobrovolsky S.N., Syshchenko V.V. // Russian Physics J. 2001. V. 44. № 3. P. 317.
Lekomtsev K.V., Strikhanov M.N., Tishchenko A.A. // J. Physics: Conference Series. 2010. V. 236. P. 012023. doi 10.1088/1742-6596/236/1/012023
Astapenko V.A., Sakhno S.V., Krotov Yu.A. // J. Physics: Conference Series. 2016. V. 732. P. 012025. doi 10.1088/1742-6596/732/1/012025
Shul’ga N.F., Syshchenko V.V., Larikova E.A. // Nucl. Instrum. Methods. B. 2017. V. 402. P. 167. doi 10.1016/j.nimb.2017.03.013
Джексон Дж. Классическая электродинамика. М.: Мир, 1965. 702 с.
Ginzburg V.L., Frank I.M. // J. Phys. USSR. 1945. V. 9. P. 353.
Аскарьян Г.А. // ЖЭТФ. 1955. Т. 29. С. 388. Ахиезер А.И., Шульга Н.Ф. Электродинамика высоких энергий в веществе. М.: Наука, 1993. 344 с.
Памятных Е.А., Туров Е.А. Основы электродинамики материальных сред в переменных и неоднородных полях. М.: Наука, Физматлит, 2000. 240 с.
Гинзбург В.Л., Цытович В.Н. Переходное излучение и переходное рассеяния. М.: Наука, 1984. 360 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал