Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2019, № 9, стр. 103-112

ВВЕДЕНИЕ

Как было показано экспериментально [1] и путем численного моделирования [2], при уменьшении размера наночастицы (нанокристалла или нанокапли) со свободной поверхностью параметры фазового перехода кристалл–жидкость (ФП К–Ж) в ней изменяются. При уменьшении числа атомов (N) в наночастице уменьшаются как температура плавления (T_m), так и температура начала кристаллизации (T_N < T_m), уменьшается скачок удельной (на атом) энтропии (Δs) и удельная скрытая теплота ФП К–Ж (Δh = T_mΔs). Причем если экстраполировать эти размерные зависимости на малые значения N, то при некотором значении числа атомов (N₀) обе эти функции становятся равными нулю: Δs(N₀) = 0 и Δh(N₀) = 0, а зависимости T_m(N) и T_N(N) пересекаются: T_m(N₀) = T_N(N₀) > 0 K. Как было показано в работе [3], в наночастице, состоящей из N₀ атомов исчезает скачок удельного объема ФП К–Ж: Δv(N₀) = 0, и достигается равенство удельных (на единицу площади) поверхностных энергий твердой и жидкой фаз: Δσ = σ(s) – σ(l) = 0. Таким образом, при N ≤ N₀ различие фаз исчезает и ФП К–Ж здесь уже невозможен, так как для такого кластера термодинамическое понятие фазы уже не применимо. Для металлов была получена оценка: N₀ = = 300 [2]; 50–300 [3].

Но данное утверждение об исчезновении ФП К–Ж при N ≤ N₀ было сделано нами в [3] на основании экстраполяции размерных зависимостей, которая неоднозначна и не объясняет физических причин исчезновения ФП К–Ж. В связи с этим до сих пор в ряде работ на основании определенных критериев теоретически изучают ФП К–Ж в наночастицах аргона из 13-ти и даже меньшего числа атомов.

Поэтому целью данной работы является изучение исчезновения ФП К–Ж при уменьшении числа атомов на основании статистической модели простого однокомпонентного вещества, ограниченного определенной поверхностью.

Создание аналитической модели поверхности – это очень сложная и до сих пор не решенная задача. Сложность заключается в том, что на поверхности имеется большой градиент плотности, в результате чего атомы на поверхности находятся в динамическом равновесии с обеими фазами, которые и образуют поверхность. Более того, если считать вещество в поверхностном слое как иную фазу (отличную от “объемной”), то возникают вопросы, каcающиеся как толщины поверхностного слоя, так и изменения термодинамических свойств вещества в этом слое при переходе от одной фазы в другую.

Чтобы обойти эти проблемы, Дж.В. Гиббс вместо реальной межфазной границы ввел разделяющую поверхность (dividing surface) [4–6], к которой относятся поверхностные характеристики. Если реальная поверхность представляет собой переходную зону и имеет некоторую толщину, то разделяющая поверхность – это чисто геометрическая поверхность, которая толщины не имеет. Такую виртуальную поверхность называют поверхностью Гиббса, при этом все рассчитанные для такой модели поверхностные характеристики относятся к гладкой геометрической поверхности, не имеющей толщины. Мы будем полагать, что наша модель ограничена поверхностью Гиббса, а для изучения образования S-петли на изотерме уравнения состояния, которая описывает ФП К–Ж, используем трехфазную модель простого однокомпонентного вещества, формализм которой представлен в работах [7–9].

ТРЕХФАЗНАЯ МОДЕЛЬ ПРОСТОГО ВЕЩЕСТВА

Предположим, что рассматриваемая система образует решеточную структуру из N + N_v сферических ячеек одинакового объема, из которых N_v ячеек вакантны, а N ячеек заняты тождественными сферически симметричными атомами, масса каждого из которых равна m. Из N атомов только часть атомов (N – N_d) локализована в ячейках, а другая часть (N_d) – делокализована, т.е. они могут перемещаться по всему объему. Причем со временем локализованный атом, возбудившись, может стать делокализованным, и наоборот.

Пусть атомы взаимодействуют посредством потенциала Ми-Леннард-Джонса [6, 7]:

где D и r_o – глубина и координата минимума потенциала, b > a > 1 – параметры.

Если в решетке содержится N_v вакансий, однородно распределенных по объему, то первое координационное число (т.е. число ближайших соседних атомов) равно:

где $k_{n}^{{\text{o}}}$ – число ближайших к данному атому ячеек (как занятых, так и вакантных), т.е. это первое координационное число при N_v = 0, ϕ_v – вероятность образования вакансии в решетке простого вещества [7, 10]: где k_B – постоянная Больцмана, E_v – энергия создания вакантного узла в решетке.

Объем системы равен сумме объемов, приходящихся на одну (занятую либо вакантную) ячейку (v_a), форму которой считаем сферической:

где c = c_o(1 – ϕ_v)^1/3 – расстояние между центрами ближайших ячеек, k_p – коэффициент упаковки структуры из (N + N_v) сферических ячеек, c_o – расстояние между центрами ближайших ячеек в исходной (не срелаксировавшей в активированное вакансиями состояние) безвакансионной (при N_v = 0) системе.

Учитывая, что центр делокализованного атома может перемещаться по всему объему системы, а центр локализованного атома только в пределах ячейки, в которой он локализован, для удельной (на атом) свободной энергии Гельмгольца макроскопической системы (где N → ∞ и V → ∞ при N/V = const) было получено выражение [7–9]:

Здесь f_i – это удельная свободная энергия трансляционного движения делокализованных атомов:

где введены обозначения

Здесь $\hbar $ – постоянная Планка, e = 2.718 – основание натурального логарифма, x_d – доля делокализованных атомов, т.е. это вероятность атома иметь кинетическую энергию выше, чем E_d – энергии делокализации атома [7, 11]:

Второе слагаемое в выражении (6) – удельная свободная энергия статического взаимодействия всех атомов между собой, которая при использовании приближения “взаимодействия только ближайших соседей” имеет вид:

где R = r_o/c – относительная линейная плотность системы,

Третье слагаемое в (6) –удельная свободная энергия колебательного движения локализованных атомов по модели кристалла Эйнштейна (Θ_E – температура Эйнштейна):

Функция f_d – удельная свободная энергия динамического взаимодействия делокализованных атомов из-за их смещения от центров ячеек при миграции по объему. В приближении “взаимодействия только ближайших соседей” для этой функции в работах [7, 8, 12] было получено выражение:

где введены обозначения:

Последнее слагаемое в (6) f_k – это удельная свободная энергия “перестановочного движения” атомов, которая возникает из-за применения формулы Стирлинга, и которое исчезает в “термодинамическом пределе”, т.е. при N → ∞, V→ ∞ и v = V/N = const [7]:

Входящие в (2)–(12) функции E_v, E_d и Θ_E были определены для макросистемы простого вещества в работах [7–11, 13]. Энергия создания вакансии в структуре имеет вид [7, 10]:

где введены обозначения

Индекс “o” у функций c_o и Θ_Eo означает, что функции рассчитаны для исходной (не срелаксировавшей в активированное вакансиями состояние) безвакансионной виртуальной решетки (т.е. при ϕ_v = 0).

Для энергии делокализации атома было получено выражение [7, 9, 11]:

где введены обозначения

Здесь Θ – температуры Дебая, которая связана с температурой Эйнштейна соотношением: Θ = = (4/3)Θ_E [12, 14]. Для функции Θ было получено выражение [7, 13]:

где введены следующие обозначения:

Было показано, что данные определения функций E_v, E_d и Θ_E позволяют получить результаты, хорошо согласующиеся с экспериментальными оценками. Кроме этого, использование входящих в (6) функций E_v, E_d и Θ_E в виде (15)–(20) приводит к выполнимости как третьего начала термодинамики в “сильной” формулировке Планка, так и к согласованности термического и калорического уравнений состояния для макросистемы. Было показано, что данный формализм полностью учитывает “коллективную энтропию” (communal entropy) [7, 12, 15, 16]. “Коллективная энтропия” определяет собой ту поправку, которую необходимо было включать в “твердоподобные” или в “газоподобные” теории жидкого состояния из-за некорректного учета в них как разницы в областях доступности у локализованных и делокализованных атомов, так и для корректного учета числа возможных перестановок в системе. В соответствии с (14) “параметр коллективной энтропии” равен [7]: σ_com = exp[x_d(v, T)]. Отсюда при х_d = 1 (т.е. для газа при высоких T) получаем: σ_com = e, а при х_d = 0 (т.е. для кристалла при низких T) имеем: σ_com = 1.

РАСЧЕТ ИЗОТЕРМ УРАВНЕНИЯ СОСТОЯНИЯ ДЛЯ МАКРОСИСТЕМЫ

Для расчетов был взят аргон (m(Ar) = = 39.95 a. е. м.), имеющий в твердой фазе гранецентрированную кубическую (ГЦК) структуру: $k_{n}^{{\text{o}}}$ = 12, k_p = 0.7405. Тогда структурные параметры решеточной модели будут равны:

Параметры межатомного потенциала Ми-Леннард-Джонса (1) для Ar были определены самосогласованным образом в [7] из экспериментальных данных для твердой фазы:

Тогда входящие в формализм термодинамические константы модели будут равны:

Здесь N_A – число Авогадро, γ = (∂ ln Θ/∂ ln v)_T – первый параметр Грюнайзена. Значение 1 у функций A_w, Θ_E и γ указывает на то, что они определены при аргументе равном: R = r_o/c = 1.

Расчет термического уравнения состояния проводился численным дифференцированием изотермической зависимости функции f_H/D по аргументу v/v_o = (c_o/r_o)³:

Здесь v = V/N = (π/6k_p)$c_{{\text{o}}}^{3}$ – удельный (на атом) объем системы при расстоянии между центрами ближайших атомов равном c_o.

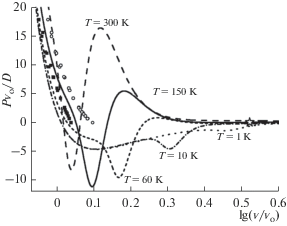
Расчет зависимости функции Pv_o/D от аргумента v/v_o показал, что при средних температурах изотермы имеют две S-петли, соответствующие по физическому смыслу ФП К–Ж и Ж–Г, как это показано на рис. 1 и 2. Однако рассчитанные параметры ФП К–Ж заметно отличаются от экспериментальных параметров плавления аргона из работ [15, 17–19]. На рис. 1 бинодали ФП К–Ж показаны кубиками для кристалла, и кружками для жидкой фазы.

Расчеты показали, что при высоких температурах S-петля ФП Ж–Г стягивается в критическую точку (на рис. 2 она показана кружком), имеющую следующие параметры:

Эти значения существенно отличаются от экспериментальных параметров критической точки аргона, которые равны (звездочка на рис. 1 и 2) [20]:

Хотя имеются и другие данные из справочника [21]:

Экспериментальное значение первого координационного числа в критической точке аргона равно: k_{n cr} = 4.8–5.6 [22], 3.6 ± 0.1 = 3.5–3.7 [23], 3.7 ± 0.5 = 3.2–4.2 [24]. Отсюда, согласно (3), вероятность образования вакантного узла в ГЦК-виртуальной решетке аргона в критической точке должна быть равной: ϕ_v = 1 – $({{{{k}_{n}}} \mathord{\left/ {\vphantom {{{{k}_{n}}} {k_{n}^{{\text{o}}}}}} \right. \kern-0em} {k_{n}^{{\text{o}}}}})$ = 1 – (k_n/12), т.е.: ϕ_vcr = 0.6 – 0.533 [22], 0.7 ± 0.0083 [23], 0.6917 ± 0.0417 [24]. Это достаточно близко к полученным нами величинам ϕ_vcr и k_{n cr}.

При низких температурах две S-петли ФП К–Ж и Ж–Г сливаются в одну большую S-петлю, соответствующую ФП кристалл–газ. На рис. 1 видно, что на изотермах T = 10 и 1 K S-петли ФП Ж–Г уже нет.

Таким образом, модель позволяет с единых позиций получить качественную картину для всех трех фаз простого вещества. При этом в модели не содержится никаких “внешних критериев” для запуска ФП К–Ж и никаких подгоночных постоянных. Но количественные результаты еще далеки от экспериментальных данных. Вместе с тем стоит напомнить, что уравнение Ван-дер-Ваальса тоже плохо описывает линию ФП Ж–Г даже для инертных газов. Экспериментальная кривая ФП Ж–Г в приведенных координатах лежит между результатами приведенных уравнений Ван-дер-Ваальса и Бертло [25]. Однако этот факт не препятствует широкому использованию уравнения Ван-дер-Ваальса для изучения качественных вопросов ФП Ж–Г. Поэтому представленный здесь формализм трехфазной модели можно использовать для изучения качественных вопросов ФП К–Ж. В данном случае на основе этой модели будет изучен вопрос изменения S-петли ФП К–Ж при уменьшении размера наносистемы.

МОДЕЛЬ НАНОКРИСТАЛЛА С ВАКАНСИЯМИ

Обобщим формализм из (2)–(20) на случай нанокристалла из N + N_v = N/(1 – ϕ_v) одинаковых ячеек, из которых N_v вакантных ячеек однородно распределено по объему нанокристалла. Как и в работах [7, 26–28] положим, что нанокристалл со свободной поверхностью имеет вид прямоугольного параллелепипеда с квадратным основанием, ограненный гранями типа (100) с геометрической поверхностью Гиббса. Ячейки образуют кристаллическую структуру с коэффициентом упаковки k_p. Величина f = N_ps/N_po = ${{N_{{ps}}^{{\text{o}}}} \mathord{\left/ {\vphantom {{N_{{ps}}^{{\text{o}}}} {N_{{po}}^{{\text{o}}}}}} \right. \kern-0em} {N_{{po}}^{{\text{o}}}}}$ – представляет собой параметр формы, который определяется отношением числа $N_{{ps}}^{{\text{o}}}$ атомов (или N_ps = $N_{{ps}}^{{\text{o}}}$/(1 – – ϕ_v)^1/3 ячеек) на боковом ребре к числу $N_{{po}}^{{\text{o}}}$ атомов (или N_po = $N_{{po}}^{{\text{o}}}$/(1 – ϕ_v)^1/3 ячеек) на ребре квадратного основания. Для стержневидной формы f > 1, для куба f = 1, для пластинчатой формы f < 1.

Число ячеек и атомов в нанокристалле определенной формы (т.е. при данном f ) равно:

где α = π/(6k_p) – параметр структуры.

Ограничение системы поверхностью приводит к обрыву связей на границе. Поэтому если использовано приближение “взаимодействия только ближайших соседей”, то вместо первого координационного числа (k_n) необходимо брать 〈k_n〉 – среднее (по всей наносистеме) значение первого координационного числа, которое будет зависеть как от размера, так и от формы наносистемы. При этом структуру системы полагаем неизменной: k_p = const. Данную модель нанокристалла в виде прямоугольного параллелепипеда (Rectangular Parallelepiped), форму которого можно варьировать с помощью параметра формы f, назовем RP-моделью с вакансиями, или RP(vac)-моделью.

В рамках RP(vac)-модели зависимость среднего по наносистеме значения первого координационного числа от аргументов α, N, ϕ_v и f имеет вид [7, 26–28]:

где $k_{n}^{{\text{o}}}$(∞) – первое координационное число (т.е. число ближайших к данному атому занятых или вакантных ячеек) для макрокристалла,

Функция формы Z_s(f) достигает минимума равного единице при f = 1, т.е. для формы куба. Для пластинчатых (f < 1) или стержневидных (f > 1) форм значение функции формы больше единицы: Z_s(f ≠ 1) > 1. Поэтому функция k_n(f)* = = k_n(f )/k_n(∞) при любом значении N + N_v имеет максимум при f = 1, т.е. для наиболее энергетически устойчивой – кубической формы прямоугольного параллелепипеда.

Кубическая форма может реализовываться только при определенном числе ячеек, из которого можно построить куб: (N + N_v)_cub = = INT[${{(N_{{po}}^{{\text{o}}})}^{3}}$/[α(1 – ϕ_v)]], где $N_{{po}}^{{\text{o}}}$ = 2, 3, 4,…, функция INT[x] округляет величину x до целого значения, ибо число атомов это величина целочисленная. При “некубичном” значении числа ячеек: N + N_v ≠ (N + N_v)_cub параллелепипед может иметь либо пластинчатую, либо стержневидную форму, причем выполняется: k_n((N + N_v)_cub ± 1)* < < k_n$(N + {{N}_{{v}}})_{{{\text{cub}}}}^{*}.$

Изоморфная (т.е. рассчитанная при f = const) зависимость k_n(N + N_v) монотонно уменьшается при N + N_v → N_min = INT[8/[α(1 – ϕ_v)]], но общая зависимость k_n(N + N_v) имеет осциллирующий вид с максимумами в точках k_n(N + N_v)_cub, соответствующих нанокристаллам с кубической формой, и с минимумами при таких значениях N + N_v ≠ ≠ (N + N_v)_cub, из которых можно построить только стержень. А так как многие свойства нанокристалла определяются именно значением k_n(N), то зависимость этих свойств от N также будет иметь осциллирующий вид.

Таким образом, использование функции (22) в формализме (2)–(20) при k_p = const позволяет получить зависимость свободной энергии Гельмгольца как от размера (числа атомов N), так и от формы нанокристалла при данных значениях температуры и удельного объема (v = V/N), для нанокристалла со свободной геометрической поверхностью Гиббса.

ДЕЛОКАЛИЗАЦИЯ АТОМОВ НА СВОБОДНОЙ ПОВЕРХНОСТИ ГИББСА

Здесь возникает вопрос о делокализации атомов на свободной поверхности Гиббса. С одной стороны атомы на поверхности можно считать делокализованными, так как они могут переходить в окружающее пространство и возвращаться (ибо наложено условие постоянства числа атомов в системе), находясь в динамическом равновесии с ним. Но, с другой стороны, так как поверхность не имеет толщины, то поверхностные атомы находятся в таких же термодинамических условиях, что и атомы внутри кристалла, и поэтому они должны делокализовываться по тому же способу, как и атомы в объеме нанокристалла.

Для изучения этого вопроса рассчитаем изотерму T = 150 K уравнения состояния аргона при уменьшении числа атомов в наносистеме. Расчеты показали, что S-петли ФП К–Ж и Ж–Г уменьшаются, но не исчезают даже при минимально возможном для RP(vac)-модели значении: $N_{{po}}^{{\text{o}}}$ = 2, т.е. при N = INT[${{(N_{{po}}^{{\text{o}}})}^{3}}$/α] = 11. Из этого результата следует вывод, что атомы на поверхности Гиббса делокализуются по иному способу, чем атомы в объеме нанокристалла. Здесь для ГЦК структуры имеем: α = π/(6k_p) = 0.707.

В RP(vac)-модели локализованный атом колеблется в ячейке, образованной ближайшими соседями. При этом для описания колебаний локализованных атомов используется модель Эйнштейна, т.е. колебательное движение локализованного атома рассматривается как колебания трех независимых гармонических осциллятора с одинаковой частотой. Но для атома, колеблющегося на поверхности Гиббса некоторые направления являются свободными для ухода из ячейки. Поэтому движения в этих направлениях следует моделировать не как движения гармонического осциллятора, а как движение делокализованного атома.

В рамках RP(vac)-модели число ячеек (как занятых, так и свободных), лежащих на поверхности равно [7, 29]:

Здесь N_ss = N_foN_fs и N_so = $N_{{fo}}^{2}$ – число ячеек на поверхности боковой грани и грани основания (без учета ячеек на ребрах и вершинах); N_fs = N_ps – 2 и N_fo = N_po – 2 – число ячеек на боковом ребре и на ребре основания (без учета ячеек в вершинах) параллелепипеда. Тогда для RP(vac)-модели получим:

При этом число занятых ячеек (т.е. атомов) на поверхности Гиббса будет равно:

Из них локализованными по “объемному способу”, который описывается формулой (9), будет следующее число атомов:

где x_dv – доля делокализованых атомов в объеме, которая рассчитывается по формулам (9) и (17), а функция ϕ_v рассчитывается по формулам (3), (15) и (16) при использовании значения x_dv, определенного для объема.

На поверхности боковой грани и грани основания из колебаний локализованного атома нужно исключить один гармонический осциллятор из трех, так как в этом, перпендикулярном грани, направлении делокализация будет происходить уже по-иному, отличному от “объемного”, способу. Для атома на боковом ребре и на ребре основания по аналогичным причинам нужно исключить два гармонических осциллятора, ибо гармонические колебания в ячейке совершает только тот осциллятор, который колеблется вдоль ребра. По этим же причинам следует считать, что атом в вершине делокализуется по отличному от “объемного” способа. Поэтому среди локализованных на поверхности Гиббса атомов некоторую часть (N_ds) следует считать делокализующимися по отличному от “объемного” способа. В рамках RP(vac)-модели для N_ds можно получить:

Пусть x_ds – это вероятность делокализации атома на поверхности Гиббса способом, отличным от того, каким атом делокализуется в объеме. Тогда для доли общего числа делокализованных атомов в наносистеме получим:

где доля атомов, делокализованных на поверхности Гиббса по отличному от “объемного” способа, равна:

Из (27) видно, что для идеального (x_dv = 0 и ϕ_v = 0) нанокристалла функция η_ds(N) плавно убывает от η_ds = 1 при N = 11 и Z_s(f = 1) = 1 (или $N_{{po}}^{{\text{o}}}$ = 2 и f = 1) до нуля при N → ∞.

Пусть делокализация атома со свободной поверхности Гиббса связана с переходом атома в газовую фазу и возвратом атома обратно. Тогда для величины энергии делокализации атома в формуле (9) можно принять: E_ds = m〈v〉²/2, где 〈v〉 – некоторая, характерная для газовой среды, скорость атома. Если брать 〈v〉 как наиболее вероятную скорость (〈v〉 = (2k_BT/m)^1/2), или как среднеквадратичную скорость атомов в газе (〈v〉 = = (3k_BT/m)^1/2) [6, 12], то можно получить: E_ds/(k_BT) = 1 (если 〈v〉 наиболее вероятная скорость атомов) – 1.5 (если 〈v〉 среднеквадратичная скорость атомов). Поэтому в соответствии с (9), величина x_ds будет равна постоянной величине: x_ds = 0.392 (если 〈v〉 среднеквадратичная скорость атомов), x_ds = 0.572 (если 〈v〉 наиболее вероятная скорость атомов). В соответствии с этим, для простоты можно принять: x_ds = 0.5. Это допущение означает, что атом на поверхности Гиббса с равной вероятностью можно считать, как локализованным, так и делокализованным. Отметим, что для нанокристалла лежащего на подложке величина N_ds будет меньше, чем значение из (25), которое получено для свободного (безопорного (free-standing)) нанокристалла.

РАСЧЕТ ИЗОТЕРМ УРАВНЕНИЯ СОСТОЯНИЯ ДЛЯ НАНОСИСТЕМЫ

Используя формализм RP(vac)-модели из (21)–(23) и полученные для поверхности Гиббса выражения (25)–(27), трехфазная модель простого вещества была обобщена на случай наносистемы. При подстановке в “формализм” (2)–(20) формул (23) и (26) было получено аналитическое выражение для зависимости f_H (T, v; N, f). Нормированное уравнение состояния было получено путем численного дифференцирования изотермической зависимости функции f_H/D по нормированному объему

Расчет изотермо-изоморфных (т.е. при постоянных значениях T и f) зависимостей уравнения состояния для ГЦК-Ar показал, что при уменьшении числа атомов S-петли ФП К–Ж и Ж–Г на изотерме уменьшаются. На рис. 3 показаны изотермо-изоморфные (T = 150 K, f = 1) зависимости нормированного давления от нормированного объема при следующих значениях числа атомов в системе: $N_{{po}}^{{\text{o}}}$ = 10⁸, т.е. N = 1.4 × 10²⁴ = Macro – сплошная линия; $N_{{po}}^{{\text{o}}}$ = 20, т.е. N = INT[($N_{{po}}^{{\text{o}}}$)³/ 0.707] = 11 315 – пунктирная линия; $N_{{po}}^{{\text{o}}}$ = 8, т.е. N = 724 – линия с коротким пунктиром; $N_{{po}}^{{\text{o}}}$ = 6, т.е. N = 305 – точечная линия; $N_{{po}}^{{\text{o}}}$ = 2, т.е. N = 11 – штрих-пунктирная линия.

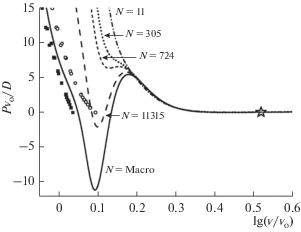
Как видно из рис. 3 для изотермы T = 150 K, при определенном значении числа атомов (N₀) S-петля ФП К–Ж исчезает. Расчеты показали, что S-петля ФП К–Ж для кубического (f = 1) нанокристалла исчезает при $N_{{po}}^{{\text{o}}}$ = 7, т.е. N₀ = 485 для изотермы T = 150 K, и при $N_{{po}}^{{\text{o}}}$ = 3, т.е. N₀ = 38 для изотермы T = 60 K.

Величина N₀ увеличивается как с ростом температуры на изотерме, так и при отклонении формы наносистемы от наиболее энергетически оптимальной формы (для RP(vac)-модели – это куб). В кластере из N < N₀ атомов ФП К–Ж уже нет. Такой кластер при изотермическом увеличении удельного объема v = V/N плавно переходит в жидкую фазу. Заметим, что для изомерно-изоморфного нанокристалла (т.е. с такими же значениями N и f) находящегося на подложке величина N₀ будет меньше, чем значение N₀ для свободного (безопорного (free-standing)) нанокристалла при тех же T-v-условиях. Это обусловлено тем, что для нанокристалла на подложке величина x_d будет меньше, чем для нанокристалла со свободной поверхностью.

Отметим, что при уменьшении числа атомов S-петля для ФП Ж–Г также уменьшается. Параметры критической точки для ФП Ж–Г с уменьшением числа атомов изменяются: критические температура и давление уменьшаются, а критический удельный объем возрастает. Это согласуется как с экспериментальными, так и с теоретическими результатами по смещению параметров критической точки различных веществ в нанопорах [30, 31]. Но применять модель наносистемы в виде прямоугольного параллелепипеда со свободной поверхностью Гиббса для изучения количественных сдвигов ФП Ж–Г с уменьшением N не вполне корректно. Поэтому эти оценки для ФП Ж–Г можно рассматривать только как качественные.

ЗАКЛЮЧЕНИЕ

На основе предложенных ранее трехфазной модели простого вещества и RP(vac)-модели нанокристалла получено выражение для свободной энергии Гельмгольца для нанокристалла, в котором имеются как вакансии в решетке, так и делокализованные (диффундирующие) атомы.

Предложена модель поверхности Гиббса, на которой часть ячеек вакантна, а часть атомов находится в делокализованном состоянии, причем, из делокализованных атомов часть делокализована по “объемному” способу, а часть – по “поверхностному” способу.

Расчеты уравнения состояния, проведенные для макросистемы аргона показали, что при средних температурах на изотермах уравнения состояния есть две S-петли, соответствующие ФП К–Ж и Ж–Г. При высоких температурах S-петля ФП Ж–Г стягивается в критическую точку. При низких температурах две S-петли ФП К–Ж и Ж–Г сливаются в одну большую S-петлю, соответствующую ФП кристалл–газ.

Показано, что при уменьшении числа атомов N в наносистеме S-петли ФП К–Ж и ФП Ж–Г на изотерме уравнения состояния уменьшаются, а при определенном значении числа атомов (N₀) S‑петля ФП К–Ж исчезает. Величина N₀ увеличивается как с ростом температуры на изотерме, так и при отклонении формы наносистемы от наиболее энергетически оптимальной формы (для RP(vac)-модели – это куб). В кластере из N < N₀ атомов ФП К–Ж уже нет. Такой кластер при изотермическом увеличении удельного объема плавно переходит в жидкую фазу. Этот вывод согласуется с результатами работы [32], где на основе электронно-статистической модели было показано, что межфазная энергия кристаллических граней на границе с собственным расплавом для 4d- и 5d-металлов нелинейно уменьшается при уменьшении размера нанокристалла, а при определенном размере исчезает.

Таким образом, показано, что теоретически предсказанное в работах [3, 33] исчезновение ФП К–Ж обусловлено ростом доли делокализованных атомов при уменьшении размера наносистемы.

В заключение отметим, что при уменьшении числа атомов в системе возрастают флуктуации различных термодинамических параметров. Исходя из этого факта и полученного здесь результата (что при N → N₀ уменьшается энергетический барьер между жидкой и твердой фазами), можно указать на ряд эффектов, которые могут реализоваться в наносистемах. Например,

1) начиная с определенного размера N_F > N₀ может наблюдаться осцилляция ФП К–Ж;.

2) как следствие данной осцилляции ФП К–Ж также может наблюдаться осцилляция формы (габитуса) нанокристалла;

3) может наблюдаться осцилляция кристаллической структуры нанокристалла, включая появление таких структур, которые в макрокристалле не наблюдаются;

4) если дать наносистеме электрический заряд или поместить ее во внешнее электрическое поле, то как показано в [34], указанные осцилляции ФП К–Ж могут генерировать электромагнитные волны.

БЛАГОДАРНОСТИ

Работа выполнена при финансовой поддержке РФФИ (грант № 18-29-11013_мк) и Программы Президиума РАН (программа № I.13).

Автор выражает благодарность Э.Н. Ахмедову, С.П. Крамынину, Н.Ш. Газановой, З.М. Сурхаевой и М.М. Гаджиевой за плодотворные дискуссии и помощь в работе.