Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2020, № 1, стр. 106-111

ВВЕДЕНИЕ

Послойный анализ современных полупроводниковых гетероструктур с использованием метода вторичной ионной масс-спектрометрии (ВИМС) требует сверхнизкой энергии первичных ионов для уменьшения эффекта ионного вбивания и перемешивания. В современных масс-спектрометрах уже достигнута энергия ионов порядка 200–250 эВ, ниже которой измерения из-за малого коэффициента распыления проводить нецелесообразно. Тем не менее, измеренные профили элементов значительно отличаются от оригинальных, поэтому требуется специальная процедура восстановления реального распределения интересующего элемента, или обратная свертка. В данном случае речь идет о таких структурах, как квантово-размерные ямы, дельта-легированные слои, сверхрешетки и так далее. В общем случае экспериментальный профиль I(z) можно записать математически как свертку исходного распределения С(z) и так называемой функции разрешения по глубине g(z'). Ее можно найти, решив интегральное уравнение

если известно исходное распределение С(z). На практике для экспериментального определения функции разрешения по глубине используют выращенные методом молекулярно-пучковой эпитаксии так называемые дельта-слои – слои с моноатомным слоем определенного состава. Для описания распределения элемента в таком слое используют дельта-функцию Дирака и ее свойства (интеграл гладкой функции с дельта-функцией вблизи точки x₀ равен значению этой функции в точке x₀), позволяющие решить интегральное уравнение (1) и найти функцию разрешения по глубине. Применение полученной таким образом функции разрешения по глубине ограничено случаем стационарного режима распыления с постоянным коэффициентом и отсутствием матричного эффекта для вторичных ионов.

В настоящее время наибольшее распространение получила функция разрешения по глубине, предложенная Хофманом [1] (так называемая модель MRI (Mixing–Roughness–Information depth)), и модель аппаратной функции Доусета [2]. В обеих моделях функция разрешения по глубине сконструирована из трех функций, описывающих три разных процесса: растущая экспоненциальная функция описывает глубину выхода вторичных частиц (Information depth); функция Гаусса используется для описания шероховатости поверхности травления (Roughness), и спадающая экспоненциальная функция описывает ионное перемешивание (Mixing). Сама функция разрешения по глубине является сверткой этих трех функций с дельта-функцией Дирака. Поскольку в интеграл свертки входит функция ошибки (интеграл от функции Гаусса) [1, 2], функция разрешения по глубине является табулированной, а не аналитической функцией, но это не мешает использовать ее для численных расчетов и сравнения с экспериментальным профилем дельта-функции. Совпадение экспериментального профиля легированного дельта-слоя и свертки функции разрешения по глубине позволяет определять три параметра – λ_μ, λ_ω, σ_ρ [1, 2] – для трех указанных выше функций. Эти параметры могут затем быть использованы для процедуры обратной свертки, примененной к другим экспериментальным распределениям того же элемента и в такой же матрице, измеренным в тех же условиях. Простота и функциональность предложенной функции разрешения по глубине привела к заслуженной популярности модели MRI. Тем не менее, эта модель имеет ряд недостатков, для устранения которых была предложена усовершенствованная модель функции разрешения по глубине, которая условно названа RMR (Roughness–Mixing–Recoil implantation) [3–6].

МОДЕЛЬ RMR

В первую очередь следует остановиться на такой характеристике процесса распыления, как глубина выхода вторичных частиц. Действительно, глубина выхода вторичных ионов – это экспоненциально спадающая функция. Подавляющее число вторичных атомов (ионов) покидает первые два–три моноатомных слоя. Однако если рассмотреть подробнее реальные образцы, которые имеются в лабораториях, то первое, что следует отметить, это отсутствие структур, в которых анализируемый элемент сосредоточен действительно только в одном моноатомном слое. Шероховатость подложек, используемых при росте гетероструктур методом молекулярно-пучковой эпитаксии, составляет обычно 3–5 Å, что предполагает наличие на поверхности большого количества атомных ступенек, на которые в процессе роста будут адсорбироваться атомы из газовой фазы. Поскольку любой дельта-слой имеет две границы, можно предположить, что в реальном “дельта-слое” анализируемый элемент распределен как минимум в трех моноатомных слоях. Следует напомнить, что ВИМС-анализ обычно осуществляют на площади от 100 × 100 до 300 × × 300 мкм², т.е. эмиссия вторичных ионов усредняется по очень большой (в сравнении с атомарным размером) площади. Если же рассмотреть образцы, приготовленные другими методами, то шероховатость поверхности как следствие граница раздела значительно больше, чем в случае образцов, выращенных методом молекулярно-пучковой эпитаксии. Таким образом, глубину выхода вторичных ионов и “толщину” минимального слоя невозможно разделить на практике. Поэтому в модели RMR исключена экспоненциальная функция, описывающая выход ионов (information depth), из предлагаемой функции разрешения по глубине. Отметим, что в более поздних работах и Хофман, и Доусет пришли к схожим заключениям [7, 8]. Шероховатость поверхности травления описывали так же, как и авторы указанных выше моделей, используя функцию Гаусса с параметром шероховатости, который можно определить в ходе простого исследования поверхности травления методом атомно-силовой микроскопии.

Принципиальное отличие модели от MRI и модели Доусета заключается в описании процесса атомного перемешивания в анализируемом дельта-слое, вызванного первичным ионом. Спадающая экспоненциальная функция, которая используется и в модели MRI, и в модели Доусета, на самом деле описывает только часть смещенных атомов, а именно имплантацию атомов отдачи, происходящую при столкновении первичного иона с атомами дельта-слоя с малым прицельным параметром (столкновение, близкое к лобовому). Однако помимо таких столкновений есть еще и множество столкновений между первичным ионом и атомами дельта-слоя с большими прицельными параметрами, а также между атомами отдачи ближайших моноатомных слоев и атомов дельта-слоя [3]. Передаваемая в таких столкновениях энергия невелика, и вызванные столкновениями смещения атомов дельта-слоя тоже невелики – в пределах нескольких межатомных расстояний. Однако такое перемешивание интенсивно и изотропно и начинается задолго до приближения анализируемого дельта-слоя к поверхности травления. Последнее означает, что атомы дельта-слоя при таких столкновениях смещаются во все стороны, в том числе и к поверхности травления, причем примерно с одинаковой вероятностью. Все это позволило описать такое перемешивание с использованием диффузионного приближения [9] и функции Гаусса.

Таким образом, окончательно функция разрешения по глубине в представленной модели есть свертка двух функций Гаусса и одной экспоненциально спадающей функции с дельта-функцией [3]:

т.е. функция с тремя параметрами λ_k, σ_m, σ_r, характеризующими имплантацию атомов отдачи, изотропное каскадное перемешивание и шероховатость поверхности, вызванную ионным облучением соответственно.

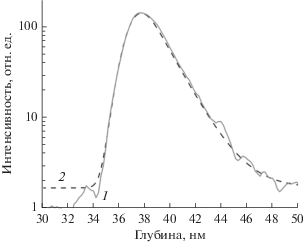
На рис. 1 приведено экспериментальное распределение алюминия в дельта-слое Al_xGa_1 – xAs, аппроксимированное в рамках модели RMR. Послойный анализ проводили при распылении ионами цезия с энергией 1.5 кэВ и угле падения первичных ионов примерно 62.2° относительно нормали к поверхности. Для аппроксимации использовали следующие значения параметров модели: λ_k = 1.6, σ_m = 0.685, σ_r = 0. Обнуление шероховатости поверхности вполне обосновано, если принять во внимание близость дельта-слоя к поверхности. Разрешение по глубине определяется спадающим фронтом профиля, равным примерно ~3 нм и определяемым как глубина, на которой интенсивность сигнала падает от 0.84I_max до 0.16I_max (где I_max – максимальная интенсивность сигнала в дельта-слое). Важно отметить, что аппроксимация функцией Гаусса очень хорошо описывает растущий фронт дельта-слоя, что подтверждает ненужность растущей экспоненты, описывающей глубину выхода вторичных ионов в альтернативных моделях.

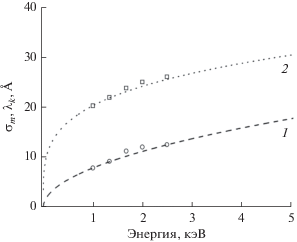
Ранее экспериментально [4] и теоретически [3] показано, что параметр, характеризующий имплантацию атомов отдачи λ_k, растет с энергией как ~k₁$E_{0}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}$, тогда как параметр изотропного каскадного перемешивания σ_m как ~k₂$E_{0}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}$. На рис. 2 приведены экспериментальные данные и их аппроксимация зависимостями параметров имплантации атомов отдачи и каскадного перемешивания от энергии первичного пучка ионов ${\text{O}}_{2}^{ + }$. Константы k₁ и k₂ использованы как подгоночные параметры. На практике такие зависимости приводят к тому, что каскадное перемешивание значительно слабее “размывает” исходный профиль при сверхнизких энергиях (менее 1 кэВ), чем имплантация атомов отдачи. В результате экспериментальный профиль дельта-слоя выглядит асимметричным. С ростом энергии первичных ионов разница между этими двумя эффектами уменьшается, и при энергии выше 25 кэВ параметры каскадного перемешивания и имплантации атомов отдачи сравниваются. Однако при такой энергии первичных ионов анализировать сверхтонкие слои уже невозможно, т.е. эффект может быть заметен лишь при анализе достаточно толстых (более 50 нм) слоев. Заметим, что в модели MRI и модели Доусета смещение атомов в результате ионного перемешивания в процессе распылении в сторону поверхности не рассматривается вовсе.

Свертка функции Гаусса и экспоненциальной функции выражается через сумму и произведение экспонент и функции ошибки [5], которая является табулированной функцией, что ограничивает ее применение на практике. После Хофмана с соавторами [7] было использовано приближенное соотношение для разрешения по глубине ΔZ, выраженное через квадратуру параметров функций:

Такое приближение позволяет по экспериментальному профилю дельта-слоя находить экспериментально параметр λ_k, а при наличии нескольких дельта слоев и оставшиеся параметры функции разрешения по глубине [4–6].

Одним из важнейших преимуществ модели RMR является возможность двухэтапного восстановления исходного распределения по экспериментальному профилю. В [10] была кратко описана процедура такого восстановления. Сначала после изменения порядка интегрирования в тройном интеграле появляется возможность частично решить интегральное уравнение (1) относительно имплантации атомов отдачи, выраженной через экспоненциально спадающую функцию:

где N(z) – ядро интеграла свертки, являющееся, в свою очередь, сверткой исходного распределения и двух гауссианов, описывающих каскадное перемешивание и шероховатость поверхности: Свертка двух функций Гаусса – это тоже функция Гаусса с параметром, равным через квадратуру сумме параметров, указанных двух процессов. Таким образом, для восстановления исходного профиля распределения в качестве второго шага остается провести обратную свертку с функцией Гаусса, что реализовано практически во всех коммерческих математических пакетах (MathLab, MathCad, LabView), что значительно упрощает решение проблемы восстановления исходного профиля. “Прямая реализация” обратной свертки для несимметричной функции, каковой является экспериментальный профиль дельта-слоя, приводит к необходимости использования метода регуляризации Тихонова. Однако остается еще одна проблема, к обсуждению которой в литературе время от времени возвращаются разные авторы, но окончательного общепринятого решения пока нет. Речь идет о смещении гипотетического дельта-слоя в процессе послойного анализа в сравнении с его исходной глубиной.

СМЕЩЕНИЕ ДЕЛЬТА-СЛОЯ В ПРОЦЕССЕ ПОСЛОЙНОГО АНАЛИЗА

На самом деле существуют, как минимум, две разные физические причины смещения дельта-слоя в экспериментальном профиле в сравнении с исходным распределением. Доусет с соавторами в ряде работ [11, 12] рассмотрел смещение экспериментального положения дельта-слоя вследствие изменения скорости распыления мишени сразу после начала процесса: в первые секунды ионного травления скорость распыления мишени выше, далее в процессе распыления первых 50 нм она падает до некоторого стационарного значения. Сдвиг к поверхности возникает, если использовать экспериментальную скорость травления, полученную после измерения глубины кратера травления (стандартный метод пересчета времени травления в глубину в методе ВИМС). Особенно велика разность скоростей распыления в случае низкоэнергетического травления ионами кислорода, когда она может быть десятикратной [12]. Во всех известных работах для разных комбинаций первичный ион–мишень [13, 14] экспериментально подтверждено уменьшение скорости травления. А это означает смещение дельта-слоя к поверхности в экспериментальном профиле по сравнению с исходным (при использовании постоянного коэффициента травления в ходе пересчета глубины).

Изменение (уменьшение) скорости после начала травления и вызванный этим сдвиг к поверхности дельта-слоя легко объяснимы с точки зрения каскадной модели распыления. Первичный ион генерирует большое количество точечных дефектов (вакансий), т.е., по сути, верхний слой образца толщиной примерно в два проекционных пробега первичных ионов “разрыхляется”, а значит, плотность материала уменьшается. А выход распыления, как известно, прямо пропорционален плотности облучаемой мишени. Кроме того, верхние два–три моноатомных слоя твердого тела должны быть более “плотными”, чем объемный материал, из-за обрыва связей между поверхностными атомами и замыкания этих связей на соседние атомы твердого тела (реконструкция поверхности). То есть скорость распыления этих первых двух–трех моноатомных слоев должна быть чуть больше, чем более глубоких слоев. Конечно же, в случае распыления кислородом кремния (аналогично в случае других химически активных ионов) добавляется эффект образования в первые моменты распыления материала с меньшим коэффициентом распыления (SiO). Таким образом, можно заключить, что при послойном анализе действительно имеет место смещение гипотетического дельта-слоя к поверхности из-за уменьшения скорости распыления после начала ионного травления из некоего “начального” положения в “стационарное”. Контроль изменения скорости травления возможен, но очень трудоемок и не годится для рутинных измерений.

Однако в ряде работ предполагают другую причину смещения дельта-слоя. Хофман с соавторами, а также их последователи утверждают [15–17], что в процессе послойного анализа дельта-слой смещается относительно исходного положения к поверхности из-за ионного перемешивания. Это перемешивание описывают экспоненциально спадающей функцией (имплантацией атомов отдачи в настоящей интерпретации). К сожалению, ни сам Хофман, ни его последователи не дали никакого физического объяснения этого эффекта. Публикуют только результаты математического моделирования, демонстрирующие такое смещение. Доусет с соавторами, проводя аналогичные численные расчеты, не говорит о смещении дельта-слоя к поверхности из-за ионного перемешивания, хотя в обеих моделях используются одинаковые функции, формирующие функцию разрешения по глубине.

Для начала укажем, что функция разрешения по глубине, сконструированная из двух функций Гаусса и одной спадающей экспоненциальной функции (2), предсказывает ровно противоположное, а именно, что в процессе послойного анализа “центр масс” анализируемого дельта-слоя должен смещаться от поверхности. Это смещение равно примерно параметру экспоненты, описывающей в представленной модели имплантацию атомов отдачи. То есть при первом интегрировании уравнения (1), как это предложено выше и рассмотрено подробнее в [10], экспериментальный профиль дельта-слоя после процедуры обратной свертки смещается к поверхности по шкале глубин (например, рис. 5a , 5б в [10]). Прежде чем делать окончательные выводы о наличии смещения и его направлении, рассмотрим физические процессы, сопровождающие распыление.

В действующей теории распыления, основанной на линейных каскадах, рассматривается передача энергии от первичного иона к атомам твердого тела в серии парных упругих взаимодействий. Как известно из теории атомных столкновений, такое рассмотрение должно включать не только закон сохранения энергии, но и закон сохранения импульса. К сожалению, задача поиска распределения импульсов всех участвующих в каскаде столкновений частиц до сих пор не решена теоретически. Однако можно сделать некоторые выводы из простых логических рассуждений. До момента взаимодействия первичного иона с поверхностью суммарный импульс системы ион–атомы твердого тела (P) равен импульсу иона p_i. После того как первичный ион потеряет всю свою энергию и прекратит движение в твердом теле, его импульс станет равен нулю. Тогда из закона сохранения импульса следует, что суммарный импульс всех атомов отдачи, участвовавших в столкновениях, должен быть равен импульсу первичного иона. То есть закон сохранения импульса можно записать как:

Здесь p_aj – импульс j-го атома отдачи, все переменные в уравнении – векторы.

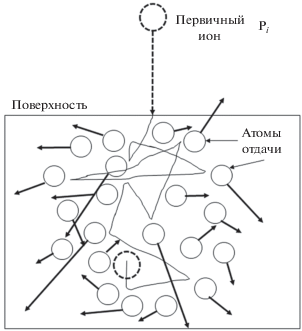
На рис. 3 приведено схематическое распределение атомов отдачи по их импульсам. Стрелкой обозначено направление переданного импульса, а длина вектора соответствует его величине. Для обсуждаемой проблемы в первую очередь важно направление этого импульса. Из уравнения (6) следует, что он направлен от поверхности вглубь мишени. То есть, суммарное число смещений атомов дельта-слоя от поверхности должно быть больше, как и абсолютная величина этого смещения. В принципе, это следует из формы экспериментального профиля дельта-слоя: для любых элементов в любых мишенях и при любых условиях экспериментов растущий фронт всегда значительно меньше, нежели спадающий (рис. 1). Это говорит о смещении большего числа атомов и с большей энергией (импульсом) именно от поверхности травления.

Таким образом, в процессе послойного анализа дельта-слоя необходимо принимать во внимание смещение этого слоя к поверхности вследствие изменения (уменьшения) скорости ионного травления в самом начале процесса, а также его смещение от поверхности из-за перераспределения импульса между атомами отдачи в каскаде столкновений. Положение дельта-слоя можно точно определить в просвечивающем электронном микроскопе. Изменение скорости травления также измеряется экспериментально [11, 12].