1. На главную
  2. Электронные версии
  3. Поверхность. Рентгеновские, синхротронные и нейтронные исследования
  4. № 1, 2020

Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2020, № 1, стр. 9-15

Взаимодействие ультрахолодных нейтронов с осциллирующим в пространстве нейтронным интерференционным фильтром

М. А. Захаров a, *, А. И. Франк a, **, Г. В. Кулин a, С. В. Горюнов a

a Объединенный институт ядерных исследований
141980 Дубна, Россия

* E-mail: zakharovmax@jinr.ru
** E-mail: frank@nf.jinr.ru

Поступила в редакцию 28.01.2019
После доработки 22.06.2019
Принята к публикации 05.07.2019

Полный текст (PDF)

Аннотация

Исследована задача о взаимодействии ультрахолодных нейтронов с осциллирующим в пространстве нейтронным интерференционным фильтром (интерферометром Фабри–Перо). В задаче исследуется эволюция волнового пакета путем численного решения нестационарного уравнения Шрёдингера методом расщепления оператора эволюции. Осциллирующий в пространстве фильтр действует в качестве квантового модулятора потока ультрахолодных нейтронов. Получены результирующие спектры прошедших и отраженных состояний в зависимости от параметров движения интерферометра.

Ключевые слова: физика ультрахолодных нейтронов, нейтронная оптика, нестационарные квантовые эффекты, фундаментальные исследования, нейтронный фильтр Фабри–Перо, нестационарное уравнение Шрёдингера, численные методы.

ВВЕДЕНИЕ

Изучение нестационарных квантовых явлений является одним из фундаментальных направлений исследований в нейтронной оптике. К числу подобных явлений можно отнести взаимодействие нейтронов с потенциалом, положение и величина которого зависит от времени [1–4]. Если такая зависимость является периодической, то результирующий спектр оказывается расщепленным.

Можно ожидать, что подобная ситуация будет возникать при прохождении квазимонохроматического пучка нейтронов через осциллирующую в пространстве резонансную структуру, нейтронный интерференционный фильтр, обладающую узкой линией пропускания. Такие устройства (аналоги оптического интерферометра Фабри–Перо) в течение долгого времени используются в практике нейтронного эксперимента [5–10].

В простейшем случае нейтронный интерференционный фильтр представляет собой комбинацию трех пленок, характеризующихся различающимися значениями плотности вещества длины рассеяния и, соответственно, эффективного потенциала:

(1)
${{U}_{{{\text{ef}}}}} = \frac{{2\pi {{\hbar }^{2}}}}{m}\rho b,$
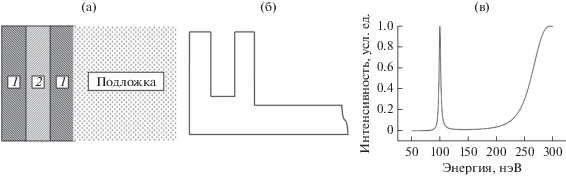
где m – масса нейтрона, ρ – число ядер в единице объема и b – длина когерентного рассеяния. Потенциальная структура такого фильтра представляет собой два барьера и яму между ними (рис. 1). При не слишком малой ширине ямы d в ней возможно образование уровней квазисвязанных состояний, положение которых с некоторым приближением определяется соотношением
(2)
${{k}_{{2, \bot }}}d\sim p\pi ,\,\,\,\,p = 1,{\text{ }}2,{\text{ }}3,$
где ${{k}_{{2, \bot }}}$ – нормальная компонента волнового числа в веществе средней пленки, образующей потенциальную яму. Такая потенциальная структура имеет ярко выраженный резонансный характер пропускания нейтронов, что хорошо подтверждается экспериментом. Аналитическое решение для амплитуд отражения и пропускания такого объекта дано в [11], а проблеме туннелирования частиц через двугорбый барьер посвящены работы [12–14]. Вопросам времени взаимодействия c резонансными структурами посвящена недавняя работа [15].

Рис. 1.

Схема нейтронного интерференционного фильтра. а – структура фильтра, б – потенциал фильтра, в – функция пропускания фильтра.

Если фильтр с узкой линией пропускания осциллирует в пространстве по гармоническому закону, то в его системе координат осциллирует также и скорость падающих на него нейтронов. Можно ожидать, что если на фильтр падает волна с энергией, соответствующей его линии пропускания в состоянии покоя, то пропускание осциллирующего фильтра будет периодически меняться, дважды за период, достигая максимума в моменты остановки фильтра. Наоборот, в фазах движения, соответствующих максимальному значению скорости, пропускание фильтра будет минимальным. Таким образом, поток частиц, прошедших через фильтр, оказывается промодулированным во времени, а энергетический спектр прошедшего состояния должен стать линейчатым. Расстояние между соответствующими линиями (параметр расщепления спектра), должно определяться частотой осцилляции фильтра f:

(3)
$\Delta E = \hbar \Omega ,\,\,\,\,\Omega = {\text{2}}\pi {\kern 1pt} f.$

Очевидно, что приведенные выше соображения основаны на очень упрощенной картине, и реальная ситуация может заметно отличаться от ожидаемой. Прежде всего, любая резонансная структура характеризуется определенным временем жизни состояния ${{\tau }_{{{\text{St}}}}} \approx {\hbar \mathord{\left/ {\vphantom {\hbar {\delta E}}} \right. \kern-0em} {\delta E}},$ где $\delta E$ – ширина линии пропускания. Конечное значение времени жизни состояния ${{\tau }_{{{\text{St}}}}}$ непосредственно связано со временем его формирования и величиной задержки в пропускании. Типичное значение последнего для нейтронного интерференционного фильтра составляет порядка 10–7 с, что было измерено в прямом эксперименте [16]. Очевидно, что при больших частотах осцилляции $f \approx \tau _{{{\text{St}}}}^{{ - 1}},$ это должно существенно сказываться на характере пропускания. Вторым фактором, усложняющим задачу, является то обстоятельство, что при пространственной осцилляции объекта последний движется с переменным ускорением. В силу универсального эффекта ускоренного вещества [17, 18], ускоренное движение объекта неизбежно приводит к изменению частоты, прошедшей через него волны, и, стало быть, энергии частицы. К каким следствиям это приводит в случае прохождения нейтронов через осциллирующий фильтр предсказать трудно.

В настоящей работе предпринята первая попытка численного исследования квантовой задачи о прохождения волнового пакета через осциллирующую в пространстве резонансную структуру.

МЕТОД РАСЧЕТА

Задаче о взаимодействии волны с движущейся потенциальной структурой отвечает нестационарное уравнение Шрёдингера:

(4)
$\begin{gathered} i\hbar \frac{\partial }{{\partial t}}\Psi \left( {x,t} \right) = \left( { - \frac{{{{\hbar }^{2}}}}{{2m}}{{\nabla }^{2}} + u\left( {x,t} \right)} \right)\Psi \left( {x,t} \right), \\ \Psi \left( {x,0} \right) = {{\Psi }_{0}}. \\ \end{gathered} $

Потенциал u(x, t) ограничен конечной пространственной областью и задается выражением:

(5)
$u(x,t) = V\left[ {x - A\sin \left( {\Omega t + \varphi } \right)} \right],$
где $V(x)$ − движущаяся (как целое) заданная потенциальная структура.

Решение уравнения (4) находилось путем численных вычислений, основанных на методе расщепления оператора эволюции [19]. Волновую функцию в некоторый момент времени t можно представить в виде результата действия оператора эволюции $\hat {U}\left( {t,t{\kern 1pt} '} \right)$ на волновую функцию в предшествующий момент времени $t{\kern 1pt} '$ [20].

При этом временной отрезок $\left[ {0,T} \right],$ в течение которого необходимо проследить эволюцию волнового пакета ${{\Psi }_{0}},$ разбивается на малые части. Полагая для простоты такое разбиение равномерным, задаем последовательность точек на временной шкале в виде ${{t}_{n}} = n\tau ,$ $n = 0,\,\,1,\,\,2,\,\,...,\,\,N;$ $N\tau = T.$ Тогда решение в момент времени ${{t}_{{n\, + \,1}}}$ определяется решением в момент времени ${{t}_{n}}{\text{:}}$

(6)
$\Psi \left( {{{t}_{{т\, + \,1}}}} \right) = \hat {U}\left( {{{t}_{{n\, + \,1}}},\,\,{{t}_{n}}} \right)\Psi \left( {{{t}_{n}}} \right).$

Согласно работам [21–25], оператор $\hat {U}\left( {{{t}_{{n\, + \,1}}},{{t}_{n}}} \right)$ можно представить в виде:

(7)
$\hat {U}\left( {{{t}_{{n\, + \,1}}},{{t}_{n}}} \right) = \hat {V}\left( {x,{{t}_{{n\, + \,1}}}} \right)\hat {T}\hat {V}\left( {x,{{t}_{n}}} \right),$

где

(8)
$\begin{gathered} \hat {T} = \exp \left( { - i\tau \frac{{{{\hbar }^{2}}}}{{2{{m}_{n}}}}\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}} \right), \\ \hat {V}\left( {x,t} \right) = \exp \left( { - i\frac{\tau }{2}u\left( {x,t} \right)} \right). \\ \end{gathered} $

Решение уравнения Шрёдингера выглядит тогда следующим образом:

(9)
$\begin{gathered} \Psi \left( {x,{{t}_{0}} + \tau } \right) = {{e}^{{ - i\frac{\tau }{2}u\left( {x,\,{{t}_{0}} + \tau } \right)}}} \times \\ \times \,\,\left( {{{e}^{{ - i\tau \frac{{{{\hbar }^{2}}}}{{2{{m}_{n}}}}\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}}}}\left[ {{{e}^{{ - i\frac{\tau }{2}u\left( {x,\,{{t}_{0}}} \right)}}}\Psi \left( {x,{{t}_{0}}} \right)} \right]} \right) + O({{\tau }^{3}}). \\ \end{gathered} $

Действие дифференциального оператора $\hat {T}$ на функцию B(x, t) можно выполнить в Фурье-представлении, следуя формуле:

(10)
$\hat {T}B\left( {x,t} \right) = {{F}^{{ - 1}}}\left( {{{{\hat {T}}}^{F}}\left[ {FB\left( {x,t} \right)} \right]} \right),$
где F – дискретное преобразование Фурье, ${{\hat {T}}^{F}}$ – оператор $\hat {T}$ в Фурье представлении:
(11)
${{\hat {T}}^{F}} = F\hat {T} = {{e}^{{i\frac{{{{\hbar }^{2}}}}{{2{{m}_{n}}}}{{k}^{2}}\tau }}}.$
Действие ${{\hat {T}}^{F}}$ на функцию $\left[ {FB\left( {x,t} \right)} \right] = {{B}^{F}}\left( {k,t} \right)$ сводится просто к умножению на эту функцию.

Таким образом, численное решение описанной задачи сводится к расчету действия оператора эволюции на волновую функцию по формуле

(12)
$\begin{gathered} \Psi \left( {x,{{t}_{0}} + \tau } \right) = {{e}^{{ - i\frac{{u\left( {x,\,{{t}_{0}}\, + \,\tau } \right)}}{\hbar }\frac{\tau }{2}}}}{{F}^{{ - 1}}} \times \\ \times \,\,{{e}^{{i\frac{{{{\hbar }^{2}}}}{{2{{m}_{n}}}}{{k}^{2}}\tau }}}F{{e}^{{ - i\frac{{u\left( {x,\,{{t}_{0}}} \right)}}{\hbar }\frac{\tau }{2}}}}\Psi \left( {x,{{t}_{0}}} \right). \\ \end{gathered} $

Вычисления производятся последовательно для каждого шага по времени. В численных расчетах использовался алгоритм быстрого преобразования Фурье (БПФ) [26].

РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ РАСЧЕТОВ И ИХ ОБСУЖДЕНИЕ

Потенциальная структура, используемая в численных расчетах, состояла из трех слоев шириной 30, 23, 30 нм и потенциалами 200, 2.05 и 200 нэВ соответственно.

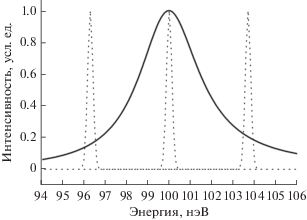
Параметры движения фильтра подбирались таким образом, чтобы в движущейся системе координат, связанной с фильтром, изменение энергии падающей волны вдвое превышало полуширину его линии пропускания, как это показано на рис. 2. Этому условию соответствует максимальная скорость фильтра ${{V}_{{\max }}} = A\Omega \approx {\text{8}}$ см/с. Таким образом должна была достигаться глубокая модуляция прошедшего потока.

Рис. 2.

Линия пропускания фильтра – сплошная кривая. Спектры нейтронов, падающих на фильтр, измеренные в системе координат фильтра в трех фазах движения − пунктирные кривые.

Расчеты проводились для частот 100, 500, 900 кГц, при амплитудах колебаний 128, 25.6, 14.2 нм соответственно. Максимальная скорость движения фильтра ${{V}_{{\max }}}$ во всех случаях была одинаковой.

Начальная волновая функция представлялась в виде гауссова волнового пакета:

(13)
${{\Psi }_{0}}(x,k) = \frac{{\sqrt {{{\delta }_{k}}} }}{{\sqrt[4]{\pi }}}\exp \left( { - i{{k}_{0}}x} \right)\exp \left( { - \frac{{{{{\left( {x - {{x}_{0}}} \right)}}^{2}}}}{{2\delta _{x}^{2}}}} \right),$

где δx и δk – ширины волнового пакета в координатном пространстве и в пространстве волновых чисел соответственно, k0 – начальное волновое число, соответствующее центру волнового пакета.

Энергия, соответствующая центру волнового пакета, падающего на фильтр, была равна E = = 100 нэВ и совпадала с центром линии резонансного пропускания стационарного фильтра. Ширина волнового пакета на полувысоте δЕ принималась в расчетах равной 0.125 нэВ при частоте осцилляции 100 кГц и 0.25 нэВ для частот 500, 900 кГц.

Точность вычислений непосредственно связана с величиной шага дискретизации как по координате, так и по и времени. Шаг по координате принимался равным δх = 0.3 нм, а шаг дискретизации по времени был равен δt ~ 0.1 нс. Для получения физически значимых результатов время прохождения волнового пакета через область, занимаемую фильтром, по крайней мере, в несколько раз должно превосходить период осцилляции. С другой стороны, при заданной величине шага пространственной дискретизации область определения по координате не может быть выбрана произвольно большой, поскольку ее величина непосредственно влияет на время вычисления. Исходя из этого, область определения волновой функции была выбрана в пределах от 0 до 600 мкм при расчетах с частотой осцилляции 100 кГц и от 0 до 300 мкм при частотах осцилляции 500 и 900 кГц.

Центр рассматриваемой области совпадает с центром покоящегося фильтра. Начальный волновой пакет располагался слева от фильтра и двигался в положительном направлении.

Результатами расчетов являлись: квадрат модуля волновой функции после взаимодействия с фильтром (рис. 3), спектры прошедшего и отраженного состояния (рис. 4), зависимость от времени квадрата модуля волновой функции в точке на выходе из фильтра (рис. 5).

Рис. 3.

Квадрат модуля волновой функции после взаимодействия с фильтром при разных частотах f, кГц: а – 100, б – 500, в – 900.

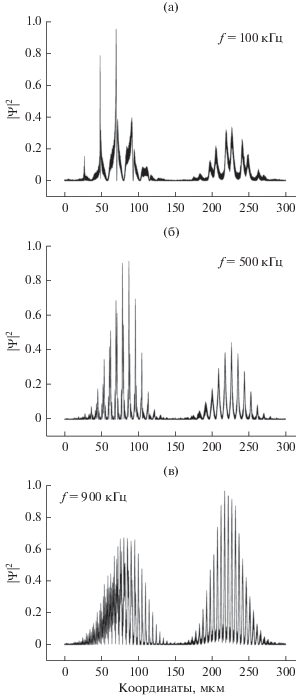
Рис. 4.

Энергетические спектры отраженного (а) и прошедшего (б) состояний для нескольких частот осцилляции f, кГц.

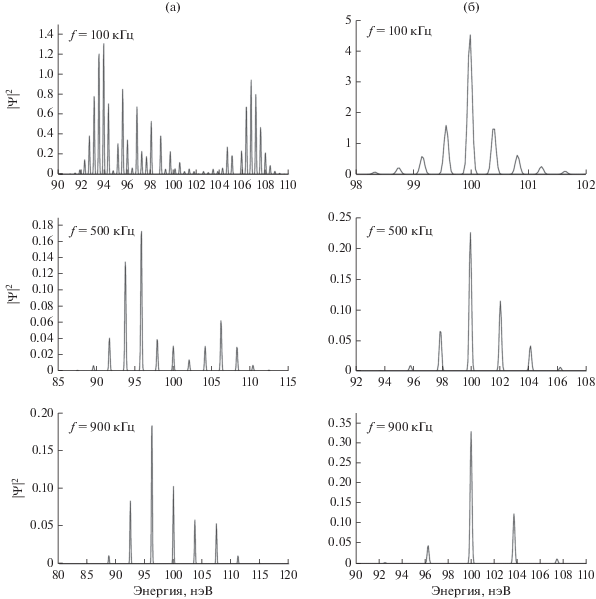
Рис. 5.

Зависимость квадрата модуля волновой функции от времени на внешней поверхности фильтра для нескольких частот f, кГц. Сплошная линия 1 – квантовый расчет, сплошная линия с точками 2 – полуклассический расчет.

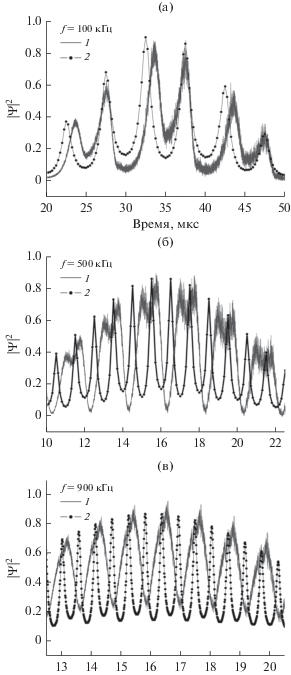
На последнем из этих рисунков приведены также результаты расчетов, основанные на полуклассических представлениях, в которых квадрат модуля волновой функции прошедшей волны на выходе из фильтра задается сверткой падающего спектра в системе координат фильтра и функции пропускания фильтра.

Основные результаты расчетов представлены ниже.

1. Прошедшее состояние действительно промодулировано по амплитуде (рис. 3).

2. Как и ожидалось, энергетические спектры прошедшего и отраженного состояний имеют линейчатую структуру, причем расстояние между линиями равно (как и следует) значению $\Delta E = \hbar \Omega .$

3. При малых частотах в спектре отраженного состояния имеется широкий провал в области максимума пропускания фильтра (рис. 4). Исходя из классических представлений, наличие такого провала и следовало ожидать, поскольку при этих энергиях амплитуда отраженной волны мала. Неожиданным являлась заметная асимметрия этого провала (с минимумом около 102 нэВ, при максимуме пропускания в 100 нэВ). Это можно интерпретировать как свидетельство смещения максимума пропускания фильтра в область более высоких энергий. При увеличении частоты этот провал уменьшается и впоследствии полностью исчезает. Однако спектр отраженного состояния остается асимметричным.

4. Спектр прошедшего состояния также асимметричен, а интенсивности линий, соответствующих увеличению энергии $\Delta E = + n\hbar \Omega ,$ заметно превышают интенсивности линий, соответствующих уменьшению энергии $\Delta E = - n\hbar \Omega $ (здесь n – номер порядка). Эта асимметрия возрастает с частотой.

5. Обращает на себя внимание вырождение спектра прошедшего состояния с ростом частоты. Интенсивность нулевого порядка при этом растет за счет интенсивности высоких порядков. Такая картина не очень хорошо соответствует картине с глубокой модуляцией интенсивности, демонстрируемой на графиках рис. 3. Чтобы прояснить ситуацию нами были проделаны тестовые расчеты, в которых генерировался значительно изрезанный волновой пакет, зрительно соответствующий картине рис. 3, а затем вычислялся его энергетический спектр. Подчеркнем, что при таком подходе полностью игнорировалась фазовая структура волнового пакета. Полученные спектры, соответствующие различным частотам модуляции, как и ожидалось, оставались симметричными, а относительная интенсивность амплитуды первых порядков практически не зависела от частоты.

6. При низких частотах осцилляции фильтра частота модуляции прошедшего состояния равна удвоенной частоте осцилляции. Это вполне соответствует классическим представлениям, поскольку за время периода колебания скорость фильтра дважды обращается в нуль. Однако положение максимумов оказалось сдвинутым по времени относительно положений, вычисленных в полуклассическом подходе. При этом с увеличением частоты осцилляции пики, соответствующие двум направлениям скорости, сближаются, а начиная с некоторой частоты, сливаются в один, что хорошо видно на рис. 5. Частота модуляции совпадает при этом с частотой осцилляции.

В целом, общая картина отраженного и прошедшего состояний заметно отличается от того, что можно было ожидать, исходя из априорных предсказаний, основанных на полуклассических соображениях.

ВОЗМОЖНОСТЬ ЭКСПЕРИМЕНТАЛЬНОЙ РЕАЛИЗАЦИИ

Представляется, что эксперимент, воспроизводящий условия рассмотренной выше задачи, вполне может быть осуществлен. Его принципиальная схема приведена на рис. 6. Трехслойный интерференционный фильтр нанесен на пьезоэлектрическую пластину, (пьезо-движитель, с определенной резонансной частотой). Возможность приведения пленки вещества в колебательное движение с помощью такого пьезо-движителя экспериментально подтверждена в работе [3].

Рис. 6.

Схема эксперимента: 1 – монохроматор, 2 – нейтронный интерференционный фильтр, 3 – конвертирующий слой, 4 – пьезодрайвер.

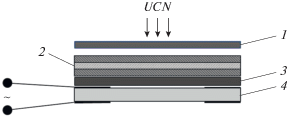
В предлагаемом опыте между пьезоэлектрической пластиной и фильтром будет иметься тонкий слой конвертора с большим сечением реакции (nγ), содержащий, например, изотоп 10B. При захвате нейтрона это ядро излучает помимо α-частицы также и γ-квант с энергией 480 кэВ, который может быть зарегистрирован сцинтилляционным детектором, не показанном на рисунке. С помощью такого устройства можно будет измерить временнýю зависимость нейтронов, прошедших через осциллирующий фильтр, аналогичную той, что представлена на рис. 5.

Используя структуры, нанесенные на пьезо-пластины с различающими собственными частотами, можно будет измерить такую зависимость для нескольких частот осцилляции.

ЗАКЛЮЧЕНИЕ

Приведены результаты исследования задачи о взаимодействии ультрахолодных нейтронов с осциллирующим в пространстве нейтронным интерференционным фильтром – интерферометром Фабри–Перо. Численное решение нестационарного уравнения Шрёдингера находилось методом расщепления оператора эволюции. Получены результирующие спектры прошедших и отраженных состояний в зависимости от параметров движения интерферометра.

Результаты расчетов в основном соответствуют ожиданиям. Прошедшее состояние промодулировано по амплитуде, а спектр состояния имеет дискретный вид. Вместе с тем существенные детали полученной картины заметно отличаются от предсказаний, основанных на полуклассических представлениях. Возможно, наиболее значимым из обнаруженных эффектов, является смещение максимумов пропускания системы при увеличении частоты с последующим слиянием соседних пиков. В результате видимая частота модуляции интенсивности уменьшается вдвое. Такое поведение картины прошедшего состояния не может быть объяснено на основе простых соображений о временнóй модуляции интенсивности, обусловленной переменной скоростью интерферометра. Вероятно, существенную роль тут играет конечное время формирования состояния в резонансной системе, каковой является интерферометр Фабри–Перо и совершенно не учитываемые в полуклассическом подходе эффекты, связанные с ускорением интерферометра.

Предложен принципиальный подход к нестационарному квантовому эксперименту нового типа. Его осуществление позволит проверить справедливость полученных теоретических предсказаний.

Подчеркнем, что полученные результаты основаны на предположении о справедливости представлений об эффективном потенциале (1). Вместе с тем в случае среды, движущейся с большим ускорением, справедливость такого предположения совершенно не очевидно [17]. Более того, имеются соображения [28] о критическом ускорении, ограничивающем область применимости модели потенциала (1). В предлагаемом эксперименте с ультрахолодными нейтронами такое ускорение может быть достигнуто.

Работы по теоретическому исследованию явления будут продолжены, так как начата подготовка к экспериментальной проверке полученных результатов.

Список литературы

  1. Gerasimov A.S., Kazarnovskii M.V. // J. Exp. Theor. Phys. 1976. V. 44. P. 892.

  2. Haavig D., Reifenberger R. // Phys. Rev. B. 1982. V. 25. P. 6408.

  3. Felber J., Gähler R., Rausch C., Golub R. // Phys. Rev. A. 1996. V. 53. P. 319.

  4. Pimpale A., Holloway S., Smith R.J. // J. Phys. A: Math. Gen. 1999. V. 24. P. 3533.

  5. Покотиловский Ю.Н., Новопольцев М.И. Препринт P3-81-821, Объединенный Институт Ядерных Исследований, Дубна, 1981.

  6. Bondarenko I.V., Bodnarchuk V.I., Balashov S.N., Geltenbort P., Klein A.G., Kozlov A.V., Korneev D.A., Masalovich S.V., Nosov V.G., Frank A.I., Hoghoj P., Cimmin oA. // Phys. At. Nucl. 1999. V. 62. P. 721.

  7. Frank A.I., Balashov S.V., Bodnarchuk V.I., Bondarenko I.V., Cimmino A., Geltenbort P., Hoghoj P., Klein A.G., Korneev D.A., Kozlov A.V., Masalovich S.V. // Proc. SPIE. 1999. V. 3767. P. 360.

  8. Kulin G.V., Strepetov A.N., Frank A.I., Geltenbort P., Goryunov S.V., Jentschel M., Kustov D.V. // Phys. Lett. A. 2014. V. 378. P. 2553.

  9. Kulin G.V., Frank A.I., Goryunov S.V., Kustov D.V., Geltenbort P., Jentschel M., Strepetov A.N., Bushuev V.A. // Nucl. Instrum. Methods Phys. Res., Sect. A. 2015. V. 792. P. 38.

  10. Kulin G.V., Frank A.I., Goryunov S.V., Geltenbort P., Jentschel M., Bushuev V.A., Lauss B., Schmidt-Wellenburg P., Panzarella A., Fuchs Y. // Phys. Rev. A. 2016. V. 93. P. 033606.

  11. Xiao Z., Du S., Zhang C. Revisiting 1-Dimensional Double-Barrier Tunneling in Quantum Mechanics. https://arxiv.org/pdf/1210.0970.pdf

  12. Olkhovsky V.S., Recami E., Zaichenko A.K. // Europhys. Lett. 2005. V. 70. P. 712.

  13. Frank A.I., Balashov S.N., Bondarenko I.V., Geltenbort P., Hoghoj P., Kozlov A.V., Masalovich S.V., Toperverg B.P. Preprint E3-2004-216, JINR Communication, Dubna, 2004.

  14. Maaza M., Hamidi D. // Phys. Rep. 2012. V. 514. P. 177.

  15. Bushuev V.A., Frank A.I. // Phys.-Usp. 2018. V. 61. P. 952.

  16. Frank A.I., Bondarenko I.V., Vasil’ev V.V, Anderson I., Ehlers G., Hoghoj P. // JETP Letters. 2002. V. 75. P. 705.

  17. Frank A.I., Geltenbort P., Jentschel M., Kustov D.V., Kulin G.V., Nosov V.G., Strepetov A.N. // Phys. At. Nucl. 2008. V. 71. P. 1656.

  18. Frank A.I. // Phys. Part. Nucl. 2016. V. 47. P. 647.

  19. Hardin R.H., Tappert F.D. // SIAM Rev. 1973. V. 15. P. 423.

  20. Мессиа А. Квантовая механика. Москва: Наука, 1979. 367 с.

  21. Magnus W. // Communications on Applied Mathematics. 1954. V. 7. P. 649.

  22. Hardin R.H., Tappert F.D. // SIAM Rev. 1973. V. 15. P. 423.

  23. Fisher R.A., Bischel W.K. // Appl. Phys. Lett. 1973. V. 23. P. 661.

  24. Agrawal G., Govind P. Nonlinear. Fiber Optics. San Diego: Academic Press, 2001.

  25. Weiss G.H., Maradudin A.A. // J. Math. Phys. 1962. V. 3. P. 771.

  26. Cooley J.W., Tukey J.W. // Mathematics of Computation 1965. V. 19. P. 297.

  27. Frank A.I., Kustov D.V., Kulin G.V., Goryunov S.V., Roshchupkin D.V., Irzhak D.V. // J. Phys.: Conf. Ser. 2016. V. 746. P. 012054.

  28. Frank A.I. // JETP Letters. 2014. V. 100. P. 613.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал