1. На главную
  2. Электронные версии
  3. Поверхность. Рентгеновские, синхротронные и нейтронные исследования
  4. № 11, 2020

Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2020, № 11, стр. 109-112

Особенности прохождения квантовых частиц через пористые структуры

Г. М. Филиппов a, *, А. С. Сабиров b, **, В. А. Александров b, А. В. Степанов c, ***

a Чувашский государственный педагогический университет имени И.Я. Яковлева
428000 Чебоксары, Россия

b Чувашский государственный университет имени И.Н. Ульянова
428015 Чебоксары, Россия

c Чувашская государственная сельскохозяйственная академия
428003 Чебоксары, Россия

* E-mail: filippov38-gm@yandex.ru
** E-mail: sas731@yandex.ru
*** E-mail: for.antonstep@gmail.com

Поступила в редакцию 11.01.2020
После доработки 19.02.2020
Принята к публикации 20.02.2020

Полный текст (PDF)

Аннотация

Исследуется прохождение волновых пакетов квантовых частиц через пористые структуры в тонких полупрозрачных пленках. Используется численное решение нестационарного уравнения Шредингера в двумерном (для щелей) и трехмерном (круглые отверстия) случаях. Проводится сравнение коэффициента прохождения квантовых частиц со случаем движения классических частиц с тем же распределение плотности. Исследуется вихревое движение плотности потока, имеющее гидродинамическую аналогию. Рассматривается вариант “квантовой каустики” при рассеянии волнового пакета частицы на препятствии.

Ключевые слова: волновой пакет, уравнение Шредингера, вихри вероятностей, численное решение, пористые пленки, коэффициент прохождения.

ВВЕДЕНИЕ

В настоящей работе продолжается рассмотрение проникновения потока квантовых частиц через пористую структуру на основе законов квантовой механики (начатое ранее в работе [1]). Специальное внимание уделяется возможности образования вихрей [2–5] в потоке вероятности при прохождении частицы как через отдельную пору в мишени, так и возможное влияние интерференционных явлений при прохождении частицы через систему упорядоченных пор. Возможность вихреобразования следует из представления ротора плотности тока ${\mathbf{j}}$ в виде векторного произведения:

${\text{rot}}{\kern 1pt} {\mathbf{j}} = \frac{{2\hbar }}{m}\left[ {\nabla {{\psi }_{1}} \times \nabla {{\psi }_{2}}} \right],$
в котором ${{\psi }_{1}}$ и ${{\psi }_{2}}$ − соответственно вещественная и мнимая части волновой функции, $m$ и $\hbar $ − масса частицы и постоянная Планка.

МЕТОД РАСЧЕТА

Рассмотрим движение квантово-механической частицы вдоль оси $z$ перпендикулярно тонкой пленке, в которой имеются одна или несколько круглых пор радиуса $R$. Наряду с этим, рассматривался случай падения волнового пакета на щель в тонкой пленке. Пленка моделировалась как пространственный слой толщины $a$, в котором задано поле, обладающее постоянным потенциалом величины ${{U}_{0}}$. Плоскость $xOy$ проходит через середину слоя, причем центры пор симметрично расположены на оси $y$. Начальное состояние частицы задается в виде широкого в поперечном направлении пакета, описываемого волновой функцией (ВФ) вида:

$\Psi = \exp (i{{p}_{x}}x)\exp \left[ { - \frac{{{{{\left( {x - {{x}_{0}}} \right)}}^{2}}}}{{2\sigma _{x}^{2}}} - \frac{{{{y}^{2}}}}{{2\sigma _{y}^{2}}} - \frac{{{{z}^{2}}}}{{2\sigma _{z}^{2}}}} \right],$
где ${{x}_{0}}$ − координата центра пакета, ${{\sigma }_{x}}$, ${{\sigma }_{y}}$, ${{\sigma }_{z}}$ − определяют средне-квадратичные ширины пакета по каждому направлению. Далее используются атомные единицы.

Эволюция волнового пакета определялась методом численного решения трехмерного нестационарного уравнения Шредингера (УШ). Важное значение имеет применение таких методов, которые давали бы достаточно точное решение УШ при больших значениях времени. Отметим, что обычные итерационные методы, такие как метод Кранка–Николсона, накапливают существенную погрешность в расчетах эволюции волновой функции. В последнее время получили развитие новые подходы к численному решению УШ при больших временах [6, 7]. Сравнение эффективности различных методов дано в работе [8]. В данной работе для численного решения УШ использовался метод расщепления оператора эволюции. Этот метод предполагает пошаговое выполнение оператора эволюции и основан на разложении Штранга [9] для операторной экспоненты:

(1)
$\begin{gathered} {\text{exp(}}{\kern 1pt} - {\kern 1pt} \tau (\hat {A} + \hat {B}){\text{)}} = {\text{exp(}}{{ - \tau \hat {A}} \mathord{\left/ {\vphantom {{ - \tau \hat {A}} 2}} \right. \kern-0em} 2}{\text{)}} \times \\ \times \,\,{\text{exp(}}{\kern 1pt} - {\kern 1pt} \tau \hat {B}{\text{)exp(}}{\kern 1pt} {{ - \tau \hat {A}} \mathord{\left/ {\vphantom {{ - \tau \hat {A}} 2}} \right. \kern-0em} 2}{\text{)}} + \hat {o}({{\tau }^{3}}). \\ \end{gathered} $
Представление (1) имеет погрешность порядка ${{\tau }^{3}}$. Существуют аналогичные формулы более высокого порядка точности [10], однако в этом случае возрастает трудоемкость вычислений. В работах [11, 12] анализируются погрешности подобных разложений операторной экспоненты.

С учетом (1), разделив кинетическую и потенциальную энергии в гамильтониане, эволюцию ВФ для достаточно малого шага по времени $\tau $ можно представить в виде:

$\begin{gathered} \psi {\text{(}}{\mathbf{r}},t + \tau {\text{)}} = {\text{exp}}\left( {{{ - i\tau \hat {H}} \mathord{\left/ {\vphantom {{ - i\tau \hat {H}} \hbar }} \right. \kern-0em} \hbar }} \right)\psi {\text{(}}{\mathbf{r}},t{\text{)}} = \\ = {\text{exp}}\left( {\frac{{i\hbar \tau }}{{4m}}{{\Delta }_{{\mathbf{r}}}}} \right){\text{exp}}\left( {\frac{{ - i\tau }}{\hbar }V{\text{(}}{\mathbf{r}}{\text{)}}} \right) \times \\ \times \,\,{\text{exp}}\left( {\frac{{i\hbar \tau }}{{4m}}{{\Delta }_{{\mathbf{r}}}}} \right)\psi {\text{(}}{\mathbf{r}},t{\text{)}} + o{\text{(}}{{\tau }^{3}}{\text{)}}{\text{.}} \\ \end{gathered} $
Вычисление действия операторных экспонент, входящих в это выражение, удобно проводить путем перехода в импульсное представление ВФ:
$\psi {\text{(}}{\mathbf{r}},t{\text{)}} = \int\limits_{ - \infty }^\infty {{{d}^{3}}k\tilde {\psi }{\text{(}}{\mathbf{k}},t{\text{)}}} \exp (i{\mathbf{kr}}).$
Тогда имеем:
$\begin{gathered} {\text{exp}}\left( {\frac{{i\hbar \tau }}{{4m}}{{\Delta }_{{\mathbf{r}}}}} \right)\psi {\text{(}}{\mathbf{r}},t{\text{)}} = \\ = {\text{exp}}\left( {\frac{{i\hbar \tau }}{{4m}}{{\Delta }_{{\mathbf{r}}}}} \right)\int\limits_{ - \infty }^\infty {{{d}^{3}}k\tilde {\psi }{\text{(}}{\mathbf{k}},t{\text{)}}} \exp (i{\mathbf{kr}}) = \\ = \int\limits_{ - \infty }^\infty {{{d}^{3}}k\tilde {\psi }{\text{(}}{\mathbf{k}},t{\text{)}}} {\kern 1pt} {\text{exp}}\left( { - {{i\hbar \tau {{k}^{2}}} \mathord{\left/ {\vphantom {{i\hbar \tau {{k}^{2}}} {4m}}} \right. \kern-0em} {4m}}} \right)\exp (i{\mathbf{kr}}). \\ \end{gathered} $
Для перехода в импульсное представление и возвращения обратно в координатное использовалось дискретное преобразование Фурье (ДПФ) с применением алгоритмов быстрого преобразования Фурье (БПФ). При этом эволюция волновой функции рассматривалась на трехмерной прямоугольной области, достаточно большой, чтобы взаимодействие волнового пакета со структурами пленки происходило далеко от границ области решения УШ. Для подавления нефизического отражения на границе области использовался метод поглощающих границ, который состоит в добавлении мнимого дополнительного потенциала в некотором δ-слое вблизи границы сетки.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Мы уделяем внимание отличию закономерностей потока вероятности от потока идеальной жидкости в гидродинамике. В процессе работы нами производилось предварительное исследование возможности возникновения специфического квантового трения и соответствующей вязкости в потоке вероятности.

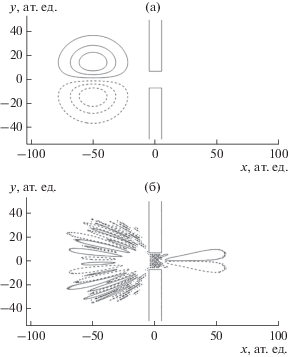
На рис. 1 и 2 рассмотрен случай прохождения двумерного (цилиндрического) пакета частицы через щель. Плотность распределения вероятности квантовой частицы показана на рис. 1. На рис. 2 приведены результаты расчета проекции ротора ${{\left( {{\text{rot}}{\kern 1pt} {\mathbf{j}}} \right)}_{z}}$ плотности потока вероятности на ось $z$, направленную перпендикулярно к плоскости рисунка $xOy$. Сплошные линии соответствуют положительной, а штриховые − отрицательной проекции. Отметим, что при движении гауссового пакета наблюдаются вихри плотности вероятности. После прохождения через щель (рис. 2б) возникает интерференционная картина с перемежающимися областями положительной и отрицательной проекции ${{\left( {{\text{rot}}{\kern 1pt} {\mathbf{j}}} \right)}_{z}}$. Аналогичное явление имеет место при движении вязкой жидкости в трубе. Проведенные расчеты для двухмерного случая в упрощенном виде демонстрируют наличие вихрей при квантово-механической эволюции плотности вероятности. Аналогичные вихревые явления существуют и в трехмерном случае.

Рис. 1.

Эволюция волнового пакета, падающего на плоскую щель в непрозрачной пленке: а − плотность вероятности для налетающего гауссового волнового пакета перед падением на пористую мишень; б − поведение волнового пакета непосредственно после прохождения через щель. Расчет выполнен при значениях параметров: ${{\sigma }_{x}} = {{\sigma }_{y}} = {{\sigma }_{z}} = 20$,$a = 10$; ${{p}_{x}} = 2$; ${{U}_{0}} = 100$.

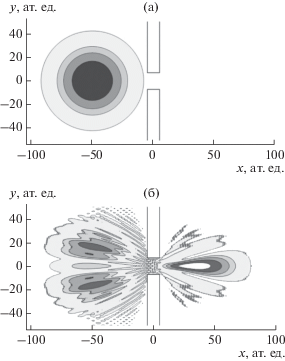
Рис. 2.

Распределение проекции ротора плотности тока ${{\left( {{\text{rot}}{\kern 1pt} {\mathbf{j}}} \right)}_{z}}$на ось $z$ для случая, представленного на рис. 1а, 1б.

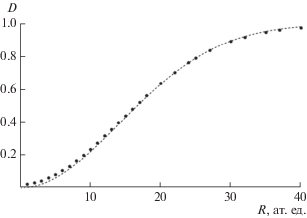
Проводилось сравнение коэффициентов прохождения (рис. 3) через круглую пору в тонкой пленке потоков классических и квантовых частиц. Несмотря на сложный характер эволюции волновой функции, расчеты показывают хорошее согласие интегральных коэффициентов прохождения в обоих рассмотренных случаях.

Рис. 3.

Зависимость коэффициента прохождения $D$ потока частиц через круглую пору в непрозрачной пленке от ее радиуса. Точки – квантовый расчет, пунктир – классический.

Упорядочение потоков вероятности, представленное на рис. 1, невозможно объяснить с точки зрения классической механики.

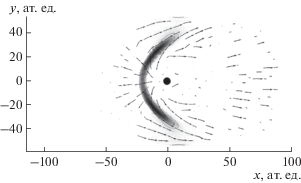
Нами также проводился расчет рассеяния волнового пакета в двумерном аналоге отталкивающего кулоновского поля. На рис. 4 показаны распределение плотности вероятности и линии тока в момент взаимодействия. Несмотря на отсутствие понятия каустической поверхности в квантовом случае, отчетливо наблюдается характерное сгущение плотности вероятности, которое можно трактовать как квантовый аналог классической каустической поверхности. Более правильно называть данный объект каустической областью, поскольку он не обладает пониженной пространственной размерностью.

Рис. 4.

Распределение плотности вероятности падающего гауссового волнового пакета в процессе рассеяния на модельном потенциале.

ЗАКЛЮЧЕНИЕ

Коэффициент прохождения волнового пакета через круглую пору в рассмотренных случаях согласуется с коэффициентом, рассчитанным “классически”, несмотря на то, что распределения потоков в классическом и квантовом расчетах кардинально различаются во многих деталях.

В специальных “резонансных” случаях остается возможным значительное различие в интегральных вероятностях прохождения квантовых и эквивалентных классических потоков частиц через пористые структуры. Особенно это касается тех случаев, в которых пористая пленка обладает определенной проницаемостью в неперфорированных участках ее поверхности (как для классических, так и для квантовых частиц).

При решении задач об огибании препятствий потоками квантовых частиц полезно вводить понятие о квантовой каустической области, поведение ВФ в которой должно определять некоторые важные физические характеристики, такие как, например, силу, действующую со стороны квантовой волны на препятствие.

Список литературы

  1. Филиппов Г.М., Александров В.А., Лысова И.В., Степанов А.В. // Известия РАН. Cерия физическая. 2018. Т. 82. № 2. С. 210. https://doi.org/10.7868/S0367676518020151

  2. Madelung E.Z. // Phys. 1927. V. 40. P. 322.

  3. Dirac P.A.M. // Proc. R. Soc. London Ser. A. 1931. V. 133. P. 60.

  4. Ovchinnikov S.Y., Macek J.H., Schultz D.R. // Phys. Rev. A. 2014. V. 90. P. 062713. https://doi.org/10.1103/PhysRevA.90.062713

  5. Ларионов Н.В., Овчинников С.Ю., Смирновский А.А., Шмидт А.А. // ЖТФ. 2018. Т. 88. № 11. С. 1621. https://doi.org/10.21883/JTF.2018.11.46621.177-18

  6. Kosloff R. // Annu. Rev. Phys. Chem. 1994. V. 45. P. 145. https://doi.org/10.1146/annurev.pc.45.100194.001045

  7. Kosloff R. // J. Phys. Chem. 1988. V. 92. P. 2087.

  8. Thanh N. Truong, John J. Tanner, Piotr Bala, J. Andrew McCammon, Donald J. Kouri et al. // J. Chem. Phys. 1992. V. 96. № 3. P. 2077. https://doi.org/10.1063/1.462870

  9. Strang G. SIAM // J. Numer. Anal. 1968. V. 5. P. 506. MR 0235754. https://doi.org/10.1137/0705041

  10. Bandrauk A.D., Shen H. // Chem. Phys. Letters. 1991. V. 176. № 5. P. 428.

  11. Bandrauk A.D., Shen H. // Can. J. Chem. 1992. V. 70. P. 555.

  12. Sheng Q. // IMA Journal of Numerical Analysis. 1993. V. 14. P. 27. https://doi.org/10.1093/imanum/14.1.27

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал