Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2020, № 12, стр. 95-104

ВВЕДЕНИЕ

Источники заряженных частиц, работающие в режиме полевой электронной эмиссии (ПЭЭ), продолжают оставаться неисчерпаемой темой для теоретических и практических исследований [1]. Разработка новых приборов и устройств, в основе которых заложено явление ПЭЭ, стимулируется как достоинствами таких катодов, так и их недостатками [2, 3]. К преимуществам обычно принято относить мгновенный токовый отклик системы на изменение управляющего напряжения и крутизну вольтамперной характеристики (ВАХ). Выделяется среди положительных особенностей сравнительно малая ширина энергетического спектра [4]. К основному недостатку относится чувствительность рабочей поверхности к давлению газа, адсорбция атомов которого способна сильно изменить эмиссионные свойства образца.

Одним из способов борьбы с нежелательной эволюцией поверхности эмиссионного катода является поиск новых материалов, способных снизить требования к уровню вакуума в межэлектродном пространстве. Такого рода меры не проходят бесследно. Энергетические спектры электронов могут расширяться и становиться мультимодальными [5]. ВАХ может приобрести характер гистерезиса [6]. И подобные результаты уже невозможно согласовать с первоначальной теорией ПЭЭ.

Можно вспомнить о том, что первичным анализом данных является их визуальное восприятие. Так выдвигаются гипотезы о характере связи между наблюдаемыми величинами: в нашем случае ими являются напряжение $V$ и сила тока $I.$ В математической статистике за эту область исследований отвечает регрессионный анализ. Здесь предметом изучения будут как предполагаемая зависимость $I = I\left( V \right),$ так и погрешности измерений. Особенно удачной можно признать ситуацию, когда для выдвижения гипотезы о виде функции $I = I\left( V \right)$ существуют теоретические предпосылки. Такого рода регрессионные модели и будут рассмотрены ниже.

Тем не менее, визуальный вывод о характере связи между изучаемыми характеристиками является зачастую субъективным. Поэтому целью настоящей работы является не только анализ существующих подходов к описанию токового отклика на изменение напряжения и их качественные признаки. Важно уметь провести количественное сравнение моделей с помощью математических критериев и вынести аргументированное заключение о преимуществе одной из них. В свою очередь адекватно выбранный способ описания отклика сигнала ПЭЭ может оказать влияние на качество прогноза поведения ВАХ за пределами рассмотренных режимов работы катодных узлов.

ОБЩАЯ МОДЕЛЬ

Будем придерживаться следующей общей постановки задачи для однофакторной модели. Имеется набор измерений $\left\{ {{{x}_{i}},{{{\tilde {y}}}_{i}}} \right\},$ где $i = \overline {1,N} .$ Значения фактора ${\mathbf{x}} = \left\{ {{{x}_{1}},...,{{x}_{N}}} \right\}$ полагаются определенными точно, при этом отклики ${\mathbf{\tilde {y}}} = \left\{ {{{{\tilde {y}}}_{1}},...,{{{\tilde {y}}}_{N}}} \right\}$ содержат погрешности, что можно отразить в виде:

Здесь $f{\text{*}}$ – оцениваемая неизвестная функция отклика, ${\mathbf{q}}* = \left( {q_{1}^{*},...,q_{p}^{*}} \right)$ – набор неизвестных параметров, ${{\varepsilon }_{i}}$ – ошибки измерений или, другими словами, “шум”.

Для параметров ${\mathbf{q}}{\text{*}}$ необходимо получить оптимальную оценку ${\mathbf{\hat {q}}},$ исходя из того, что так называемая функция регрессии $f\left( {x;{\mathbf{q}}} \right),$ которую должен предложить исследователь, является также оценкой истинной зависимости $f{\text{*}}\left( {{{x}_{i}};{\mathbf{q}}} \right).$ В результате пишут

где $Q \subseteq {{R}^{p}}$ – область определения параметров, $J\left( {{\mathbf{x}},{\mathbf{\tilde {y}}};{\mathbf{q}}} \right)$ – некоторый функционал качества, ${{\hat {e}}_{i}}$ – остатки регрессионной модели [7].

В общем случае функция $f\left( {x;{\mathbf{q}}} \right)$ может быть нелинейной как по отклику, так и по параметрам. Пусть удается с помощью некоторого взаимно-однозначного соответствия

получить вместо (1) новые наблюдения в виде: где область $\Theta \subseteq {{R}^{p}}$ является отображением $Q$ с помощью (2). При рассмотрении (3) можно предполагать, что структура функционала качества не меняется. Тогда преобразованную модель отклика $Y\left( X \right)$ будем называть линеаризованной по параметрам (в литературе можно встретить термины “квазилинейная”, “внутренне линейная” и т.п.). Обратим внимание на то, что остатки ${{\hat {e}}_{i}}$ в (3) изменились по причине проведенного преобразования.

МОДЕЛЬ ФАУЛЕРА–НОРДГЕЙМА

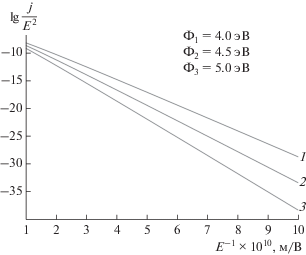
На основе туннельного эффекта [8] в 1928-м году Фаулером и Нордгеймом была построена теория полевой электронной эмиссии [9]. Основным результатом исследования стала связь плотности эмиссионного тока $j$ с напряженностью внешнего электростатического поля $E{\text{:}}$

Параметры формулы (4) получаются постоянными величинами при использовании математической модели треугольного потенциального барьера, который преодолевают заряды:

$e$ – элементарный заряд, $\Phi $ – работа выхода, $m$ – масса электрона, $\hbar $ – приведенная постоянная Планка. Можно обратить внимание, что если по оси абсцисс отложить величину обратной напряженности, а по оси ординат – логарифм отношения плотности тока к квадрату напряженности, то получится линейная зависимость, наклон которой определяется значением работы выхода (рис. 1). Данное преобразование в литературе закреплено термином “координаты Фаулера–Нордгейма”. В итоге методика измерения $\Phi $ по наклону ВАХ стала одной из общепринятых [10].

В основе теории Фаулера–Нордгейма лежал ряд предположений и допущений. Также при выводе (4) не обошлось без математических упрощений. В частности, теория справедлива для металлических эмиттеров; распределение электронов по энергиям было использовано для предельного случая нулевой абсолютной температуры; образец считался полубесконечным с плоской границей, что позволило рассматривать задачу как одномерную; вероятность прохождения потенциального барьера была вычислена в квазиклассическом приближении [11]. Позднее Нордгейм ввел поправку на характер взаимодействия электрона с поверхностью катода согласно методу сил изображения [12]:

где ${{\varepsilon }_{0}}$ – электрическая постоянная, а $t\left( \tau \right)$ и $\upsilon \left( \tau \right)$ – связанные с эллиптическими интегралами функции Нордгейма. При теоретических расчетах используются протабулированные значения данных функций или их аппроксимации. Одна из удачных аппроксимаций функций Нордгейма представлена в работе [13]:

Простейшей системой, реализующей механизм ПЭЭ, является классический полевой диод. Между катодом и анодом создается напряжение $V.$ При этом фиксируется полный эмиссионный ток $I.$ Данные характеристики являются интегральными. Для плоского случая справедливо:

где $d$ – расстояние между катодом и анодом, $S$ – площадь эмиссии. Чтобы получить электрическое поле нужной напряженности, полевые катоды изготавливают с формой поверхности малого радиуса кривизны (∼100 нм [3]), в виде острий или лезвий. Тогда в пространственном случае может быть использована запись вида: где $\beta $ – геометрический фактор поля (напр. [14]), $\Omega $ – поверхность катода. В любом случае связь между дифференциальными характеристиками $E$ и $j$ позволяет рассчитывать на то, что закон Фаулера–Нордгейма справедлив и в интегральной форме: где $A$ и $B$ в нулевом приближении также можно считать постоянными величинами для конкретного образца. Этот тезис подтверждается экспериментальными данными. В (5) дополнительно введены калибровочные значения напряжения ${{V}_{0}}$ и силы тока ${{I}_{0}}$ для придания параметрам $A$ и $B$ безразмерного вида. Стоит также отметить, что в координатах Фаулера–Нордгейма, где напряженность заменяется напряжением, а плотность тока – его силой, на наклон интегральной ВАХ начинают влиять геометрические характеристики поверхности катода (кривизна, угол раствора, шероховатость), совокупное воздействие которых чаще всего описывается фактором поля $\beta .$

Параметры $A$ и $B,$ как правило, необходимо определить из данных натурного эксперимента. В рамках нелинейной задачи регрессионного анализа можно записать:

Такую двухпараметрическую модель [15] будем обозначать как FN. Выбор первой регрессионной модели – (5) – является очевидным, поскольку основан не на субъективном восприятии данных исследователем, а продиктован теорией Фаулера–Нордгейма. При этом остатки ${{\hat {e}}_{i}}$ будут сформированы не только величинами погрешностей, но и неучтенными факторами, например, влиянием температуры.

Явление ПЭЭ является не единственным для применения модели FN. Действительно, можно вспомнить, что термоэлектронная эмиссия описывается законом Ричардсона–Дешмана [8], который имеет схожий с (4) вид:

$k$ – постоянная Больцмана; $\bar {R}$ – усредненный коэффициент отражения электронов от границы раздела эмиттера с внешней средой. Роль основного управляющего фактора в данном случае выполняет температура. Значения работы выхода $\Phi ,$ определенные с помощью формул (4) и (6), оказываются различными из-за сильных отличий в условиях проведения экспериментов [10].

Вернемся к функции регрессии. Легко убедиться, что

Таким образом, погрешность в измерениях напряжения можно представить, как ошибку измерения силы тока, причем, пропорциональную величине сигнала. Иными словами, значения факторов в модели FN можно считать точными: ${{\varepsilon }_{V}} = 0.$

Осуществим переход к координатам Фаулера–Нордгейма, что является примером применения преобразования (2):

Тогда предоставляется возможность иметь дело с простой линейной регрессией:

Здесь $\Theta = \left\{ {\left( {A{\kern 1pt} ',B{\kern 1pt} '} \right){\kern 1pt} :A{\kern 1pt} ' \in \left( { - \infty , + \infty } \right),B{\kern 1pt} ' < 0} \right\}.$

Заметим, что

То есть, если для погрешности ${{\varepsilon }_{I}}$ использовать прогрессивную модель, в которой соотношение интенсивности сигнала и шума остается постоянным, то

где ${{\varepsilon }_{i}} \equiv {{\varepsilon }_{{I,i}}} = f\left( {{{x}_{i}},{\mathbf{q}}} \right)\varepsilon {\kern 1pt} '\delta ,$ а величина $\delta $ выделена отдельно для характеристики уровня помех.

МОДЕЛЬ ХЕ–КАТЛЕРА–МИСКОВСКИ

При изучении эмиссионных свойств новых материалов и разных конфигураций систем, работающих на основе ПЭЭ, периодически наблюдались отклонения от закона Фаулера–Нордгейма. Недостаток тока часто объяснялся наличием пространственного заряда в межэлектродном зазоре, который препятствует рассматриваемому процессу переноса [16]. Избыток тока тоже можно объяснить. Например, он может быть вызван ростом площади эмиссии или подключением новых вспомогательных механизмов образования носителей заряда таких, как термический разогрев или элементарные акты взрывной эмиссии.

В работе [17] Хе, Катлер и Мисковски при рассмотрении неплоской геометрии металлического катода предложили зависимость плотности тока $j$ от напряжения $V,$ обобщающую FN. Представим ее в интегральных характеристиках следующим образом:

Дополнительный параметр $C$ призван сделать соответствие теории с экспериментом более удачным. Как и ранее, набор $\left( {A,B,C} \right)$ зависит от свойств и параметров конкретной эмиссионной системы.

В терминах регрессионного анализа для безразмерных величин новой модели HCM запишем:

Здесь мы не ограничиваем область определения параметра $С,$ поскольку формальные предпосылки для этого отсутствуют.

По аналогии с FN можно убедиться, что погрешности измерения напряжения по-прежнему можно не учитывать, рассматривая их как составляющую шума в отклике. Действительно,

Снова произведем логарифмическое преобразование (7). В случае HCM

Здесь $\Theta = \left\{ {\left( {A{\kern 1pt} ',B{\kern 1pt} ',C{\kern 1pt} '} \right){\kern 1pt} :A{\kern 1pt} ' \in \left( { - \infty , + \infty } \right),} \right.$ B ' < 0, C ' ∈ $\left. { \in \left( { - \infty , + \infty } \right)} \right\}.$ Результаты моделирования сигнала приведены пунктирной линией на рис. 2. Здесь полагается, что $A* = 2.0,$ $B* = 4.0,$ ${{I}_{0}} = 1.0$ А, ${{V}_{0}} = 1.0$ В. Значения третьего параметра приведены на самом рисунке. Случай $С* = 0$ отвечает модели FN. При выбранной системе масштабирования отклонения от линейности в координатах Фаулера–Нордгейма приходятся на область малых значений напряжения.

Видно, что линеаризованная модель HCM является стандартным обобщением простой линейной регрессии, которое осуществляется с помощью добавки квадратичного члена или более общего перехода к полиномиальному случаю [7]. Обратим также внимание на то, что в координатах Фаулера–Нордгейма для HCM полностью справедливо представление (9).

ОБОБЩЕННАЯ МОДЕЛЬ ФАУЛЕРА–НОРДГЕЙМА

Отклонения от теории Фаулера–Нордгейма наблюдались не только при анализе экспериментальных данных, но и в теоретических выкладках. Так при рассмотрении вопроса оптимизации многоострийного полевого источника авторы [18] пришли к выводу о пропорциональности силы тока с одного острия третьей (а не второй) степени напряженности электрического поля. Аналогичный вывод можно проследить и в работах [19, 20] для катодов с поверхностью в виде полости двуполостного гиперболоида вращения и половины вытянутого эллипсоида вращения. В работе [21] при исследовании значений тока в ходе туннелирования, носящего резонансный характер, было получено значение показателя степени напряжения, равное 5/3. Автор же [22] возвращает внимание читателей к тому факту, что в формулу (4') входят функции, зависящие от напряженности $E,$ и это не стоит игнорировать. В указанной работе анализ ВАХ предлагается проводить в модифицированных координатах Фаулера–Нордгейма для большего согласования теории с экспериментом.

На основе вышеизложенного можно ввести в рассмотрение модель токового отклика FNgen следующего характера:

где уже параметр η будет отвечать за отклонение ВАХ от модели (5).

Для нелинейной регрессионной модели FNgen запишем:

Удостоверимся, что и в данном случае погрешность фактора $x$, а значит и напряжения $V,$ можно представить как ошибку измерения силы тока, пропорциональную величине сигнала:

Логарифмическое преобразование (7) для линеаризации FNgen дает (см. также [23]):

Здесь $\Theta = \left\{ {\left( {A{\kern 1pt} ',B{\kern 1pt} ',\eta {\kern 1pt} '} \right){\kern 1pt} :A{\kern 1pt} ' \in \left( { - \infty , + \infty } \right),\,\,B{\kern 1pt} ' < 0,} \right.$ η' ∈ $\left. { \in \left( { - \infty ,2} \right)} \right\}.$ Результаты моделирования сигнала приведены пунктирной линией на рис. 3. Для параметров $A{\text{*,}}$ $B{\text{*}}$ и калибровочных значений напряжения и силы тока использованы те же значения, что и ранее. Значения параметра $\eta {\text{*}}$ приведены на самом рисунке. Случай $\eta * = 0$ отвечает модели FN. Здесь при выбранной системе масштабирования отклонения от линейности приходятся на область высоких значений напряжения.

В случае модели FNgen обобщение простой регрессии осуществляется с помощью добавки логарифма, что не выглядит очевидным шагом для выбора системы функций ${{g}_{j}}\left( X \right).$ Однако такой подход (как и прежде) продиктован имеющимися теоретическими предпосылками. Снова укажем на тот факт, что в координатах Фаулера–Нордгейма для FNgen сохраняется представление (9).

КОМПЬЮТЕРНЫЙ ЭКСПЕРИМЕНТ И РЕЗУЛЬТАТЫ

Современные автоматизированные системы сбора информации позволяют получать достаточно большое количество опытных данных для их дальнейшей обработки, в том числе и статистической. Однако натурный эксперимент всегда сопряжен с материальными затратами, связанными с его проведением. Поэтому для тестирования различных подходов к решению поставленных задач, анализа помехоустойчивости реализованных алгоритмов, прогнозирования результата при значениях параметров, выходящих за рамки возможностей конкретной экспериментальной установки, и т.п. удобно проводить компьютерные эксперименты на основе исследуемых математических моделей [24].

В нашем случае отклик сигнала ПЭЭ моделировался на основе одного из трех законов: (5), (11) или (13), т.е. полагалось, что $f* \equiv f.$ При этом задавался вектор параметров $q = q*,$ значения компонент которого уже приводились ранее. Случайный шум $\varepsilon $ генерировался в соответствии с предположением (10):

где $\varepsilon {\kern 1pt} '$ – стандартная нормально распределенная случайная величина, $\delta $ – задаваемый уровень шума (интенсивность погрешности). Поскольку значения силы тока не могут быть отрицательными, то выборка $\varepsilon {\kern 1pt} ',$ строго говоря, должна принадлежать усеченному распределению [25]. Положив $\delta = 0,$ всегда можно проверить сходимость используемых алгоритмов получения оценки $\hat {q}$ к точному результату $q{\text{*}}.$

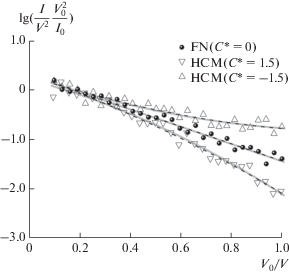
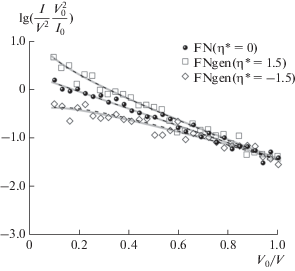
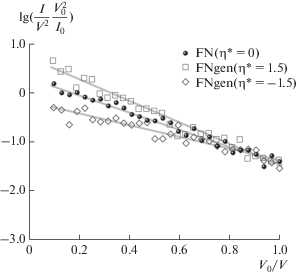
На рис. 2–5 представлены результаты моделирования $N = 30$ откликов ${{\tilde {Y}}_{i}}$ с погрешностями измерения согласно схеме (15) на уровне 20% от величины сигнала. Моделирование $\varepsilon {\text{'}}$ осуществлялось методом отбора [25] с использованием генератора псевдослучайных величин Mersenne Twister [26], который показал хорошие результаты при прохождении системы разнообразных тестов для проверки качества [27]. Значения напряжения ${{V}_{i}}$ были выбраны таким образом, чтобы факторы ${{X}_{i}}$ оказались равноотстоящими. Этот момент обсуждался ранее в [24]. Методом наименьших квадратов построены аппроксимации линеаризованных откликов в рамках рассматриваемых регрессионных моделей:

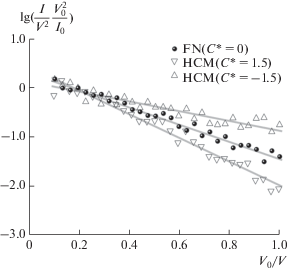
где компоненты матрицы ${\mathbf{{\rm M}}}$ и вектора ${\mathbf{b}}$ вычисляются по формулам: На рис. 2–5 функции (16) представлены сплошными серыми линиями.

Данные, представленные на рис. 4 и 5, позволяют говорить о том, что при существенном (как в данном случае) уровне шума отклонение ВАХ в координатах Фаулера–Нордгейма от линейного вида может остаться незамеченным. Это стоит обсудить ниже. Как меру влияния функции регрессии на результат обработки данных выберем скорректированный или приведенный коэффициент детерминации [7], который позволит сравнить модели с разным количеством параметров:

Ранее упоминалось, что регрессионные модели HCM и FNgen предложены в таком виде, что при значении ${{q}_{{\text{3}}}} = 0$ (или ${{\vartheta }_{{\text{3}}}} = 0$) классический закон (5) становится их частным случаем. В рамках обработки результатов натурного эксперимента целесообразным видится один из двух подходов [28]. Можно осуществить проверку с заданной доверительной вероятностью значимости третьего параметра. Если нет оснований считать величину ${{\vartheta }_{{\text{3}}}}$ значимой, то следует вернуться к общепринятой модели FN. Альтернативно можно построить доверительные интервалы для компонент вектора $\vartheta .$ Если на заданном уровне значимости в такой интервал для ${{\vartheta }_{{\text{3}}}}$ попал ноль, то это также является поводом не проводить усложнение регрессионной модели. Будем придерживаться второго способа. Для доверительных интервалов справедливо:

где ${{t}_{{1\, - \,{{\alpha } \mathord{\left/ {\vphantom {{\alpha } 2}} \right. \kern-0em} 2}}}}\left( k \right)$ –$\left( {1 - {\alpha \mathord{\left/ {\vphantom {\alpha 2}} \right. \kern-0em} 2}} \right)$ – квантиль t-распределения Стьюдента с $k$ степенями свободы, ${{\tilde {m}}_{{jj}}}$ – диагональные элементы матрицы ${{{\mathbf{{\rm M}}}}^{{ - 1}}}$ [28].

В табл. 1 приведены данные по применению линеаризованных моделей (8) и (12) к сигналу, сформированному на основе (11). Показатель $R_{{{\text{adj}}}}^{2}$ для модели (8) оказался достаточно высок, чтобы выдвинуть гипотезу о линейности отклика в координатах Фаулера–Нордгейма (рис. 4). Однако для обоих значений $C{\text{*}}$ применение трехпараметрической функции регрессии HCM привело к увеличению $R_{{{\text{adj}}}}^{2}.$ Следовательно, скорректированный коэффициент детерминации помогает идентифицировать, что $C* \ne 0.$ Это подтверждается построенными на уровне значимости α = = 0.05 доверительными интервалами. Отметим, что для случая $C* = 1.5$ в доверительные интервалы не попали моделируемые значения $\vartheta {\text{*}}.$ Это результат нельзя признать хорошим, но в [24] отмечалась возможность получить не слишком удачные данные при моделировании. Поскольку в натурном эксперименте может встретиться похожая ситуация, авторы решили не исключать из рассмотрения данный случай. Кроме того, рис. 2 демонстрирует тот факт, что даже с “неудачно” оцененными параметрами функция $\hat {Y}\left( X \right)$ очень близка по поведению к “чистому” cигналу $Y\left( X \right).$

В табл. 2 сведены результаты использования линеаризованных моделей (8) и (14) к отклику, полученному из (13). Статистика $R_{{{\text{adj}}}}^{2}$ для модели (8) и здесь принимает значения, позволяющие говорить о линейности (рис. 5). Тем не менее, применение трехпараметрической функции регрессии FNgen снова привело к увеличению $R_{{{\text{adj}}}}^{2}.$ И гипотеза о том, что $C* \ne 0,$ снова оправдана построенными доверительными интервалами. Здесь для случая $\eta * = - 0.5$ коэффициент $A{\kern 1pt} '$ оказался незначим, что влечет за собой$A = 1.0.$ Эта ситуация не считается критической, поскольку для анализа ВАХ более важным является наклон кривой. На рис. 3 показано хорошее соответствие восстановленной функции $\hat {Y}\left( X \right)$ и первоначальной зависимости $Y\left( X \right).$

Табл. 3 содержит данные по восстановлению зависимости, моделируемой с помощью (5), линеаризованными моделями (8), (12) и (14). Применение избыточных в данном случае трехпараметрических моделей HCM и FNgen привело к уменьшению скорректированного коэффициента детерминации. В дополнение, доверительные интервалы для параметра ${{\vartheta }_{{\text{3}}}}$ включают в себя нулевые значения. Таким образом, удалось идентифицировать, что мы имеем дело с изначально двухпараметрической моделью сигнала.

В заключении отметим, что, в согласии с предыдущим исследованием [24], остатки ${{\hat {e}}_{i}}$ всех регрессионных моделей (11 выборок, на основе которых составлены табл. 1–3) были подвергнуты тесту Шипиро–Уилка на принадлежность нормальному закону распределения. С доверительной вероятностью 95% оснований отвергать такие гипотезы не нашлось.

ЗАКЛЮЧЕНИЕ

В работе были рассмотрены три регрессионных модели для сигнала полевой электронной эмиссии: FN, HCM и FNgen, каждая из которых имеет свое теоретическое обоснование, предложенное различными авторами. При выбранной системе масштабирующих множителей трехпараметрические функции позволяют учесть отклонения ВАХ в координатах Фаулера–Нордгейма от прямой линии как в области высоких значений напряжения, так и в области низких. В ходе численного эксперимента было рассмотрено пять выборок, остатки ${{\hat {e}}_{i}}$ которых можно признать нормально распределенными случайными величинами на основе критерия Шапиро–Уилка. Это послужило основой для построения точечной и интервальной оценок параметров для функций регрессии. Установлено, что для каждого конкретного набора данных может понадобиться своя модель. В частности, высокие значения скорректированного коэффициента детерминации $R_{{{\text{adj}}}}^{2},$ который использовался для демонстрации меры зависимости отклика от фактора, не являются поводом для того, чтобы не рассматривать более сложный вариант регрессии. И статистика $R_{{{\text{adj}}}}^{2},$ и доверительные интервалы, несмотря на некоторые недочеты, позволили корректно идентифицировать значимость или ее отсутствие для третьего параметра в моделях HCM и FNgen.