Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2020, № 12, стр. 3-11
Классификация фрактальных и нефрактальных объектов в пространстве двух измерений
П. М. Пустовойт a, b, *, Е. Г. Яшина a, b, К. А. Пшеничный a, b, С. В. Григорьев a, b
a Физический факультет, Санкт-Петербургский государственный университет
198504 Санкт-Петербург, Россия
b Петербургский институт ядерной физики им. Б.П. Константинова Национального исследовательского центра “Курчатовский институт”
188300 Гатчина, Россия
* E-mail: polinapus@mail.ru
Поступила в редакцию 15.03.2020
После доработки 12.04.2020
Принята к публикации 14.04.2020
Аннотация
Для изучения фрактальных свойств двумерных объектов от микрометрового до сантиметровых масштабов используется метод численного фурье-анализа, моделирующий эксперимент по малоугловому рассеянию света. В эксперименте изучены различные двумерные геометрические регулярные фракталы такие, как ковер Серпинского, треугольник Серпинского, снежинка Коха и снежинка Вишека. Двумерные фракталы по аналогии с трехмерными можно разделить на “плоскостные” и “приграничные” с фрактальными размерностями, лежащими в пределах от 1 до 2 и от 2 до 3 соответственно. Для объекта с гладкой границей – круга, модельная кривая малоуглового рассеяния спадает по степеннóму закону q–3, где q – переданный импульс.
1. ВВЕДЕНИЕ
Многие физические объекты и явления живой природы обладают свойствами самоподобия или, иначе, фрактальными свойствами [1–4]. Например, русла рек, горные массивы, ландшафты [5], разряд молнии [6], протекание жидкости в пористой структуре [7] и многие другие природные процессы и объекты демонстрируют фрактальные свойства. Более того, структура легких и кровеносная система человека, корневая система и ветвление дерева и многих других растений подпадают под эту категорию, демонстрируя тем самым, что биологические системы в процессе роста нередко формируют фракталы [8, 9]. Фрактальные объекты изучаются уже несколько десятилетий, и существуют хорошо разработанные методы определения фрактальной размерности объектов, как основной характеристики их фрактальных свойств. Одним из основных методов является метод Минковского [10], в котором для определения фрактальной размерности необходимо “замостить” поверхность фрактала, например, совокупностью шаров радиуса ε. Фрактальную размерность системы можно определить, как:
(1)
$D = \mathop {\lim }\limits_{\varepsilon \to 0} \frac{{{\text{ln}}\left( {N\left( {\varepsilon } \right)} \right)}}{{{\text{ln}}\left( {\varepsilon } \right)}},$Для изучения фрактальных объектов нанометрового масштаба широко используется метод малоуглового рассеяния нейтронов или рентгеновского излучения [11–13], основанный на измерении зависимости интенсивности рассеянного излучения от переданного импульса и описываемый выражением:
где I – интенсивность рассеянного излучения, q – переданный импульс, Δ – показатель степени. Связь показателя степени Δ с фрактальной размерностью D довольно проста.Для описания рассеяния на образцах с гладкой поверхностью и однородной плотностью вещества в частице используется закон Порода, который утверждает, что интенсивность рассеяния является степенной зависимостью от переданного импульса: I(Q) ∝ q−Δ , где Δ = 4 (при значениях переданного импульса q > 1/R, где R – характерный масштаб рассеивающей частицы). В свою очередь отклонение показателя Δ от 4 свидетельствует о фрактальной структуре частицы [11–14]. По величине Δ судят о фрактальности исследуемой системы.
Известно, что для объемных или массовых фракталов (классических однородных фракталов в трехмерном пространстве), показатель Δ совпадает с фрактальной размерностью DV, при этом 1 ≤ DV ≤ 3. Для рассеяния на трехмерных объектах равномерно плотных внутри, но имеющих фрактальную поверхность, Δ = 6 – DS, при этом 3 < Δ ≤ 4, а DS – это фрактальная размерность поверхности, которая меняется в пределах 2 ≤ DS < 3 [11–13]. Фрактальные и нефрактальные объекты в трехмерном пространстве были классифицированы по значению их фрактальной размерности, опираясь на эксперименты с использованием метода малоуглового рассеяния нейтронов и рентгеновского излучения (табл. 1). Корреляционная функция такого фрактального объекта (вероятность найти ненулевую плотность на расстоянии r от выбранной начальной точки, усредненная по всем точкам частицы) имеет вид степенной функции расстояния r, $\gamma (r) \sim {{\left( {\frac{r}{\xi }} \right)}^{{{{D}_{{v}}}\, - \,3}}},$ где γ(r) – корреляционная функция объекта, ξ – размер частицы. Кубическая зависимость интенсивности рассеяния нейтронов q−3, являющаяся пограничным случаем перехода от объемного к поверхностному фракталу, приводит к корреляционной функции, асимптотика которой внутри частицы (при r/ξ < 1) пропорциональна ln(r/ξ). В свою очередь, логарифмическая зависимость соответствует особому типу самоподобия в образце с аддитивным законом масштабирования, а не мультипликативным, как в случае объемного фрактала [14, 15].
Таблица 1.
Классификация фрактальных и нефрактальных объектов в трехмерном пространстве на основе измерения размерности методом малоуглового рассеяния нейтронов или рентгеновского излучения
| Класс объектов | Показатель степени Δ | Размерность объекта |
|---|---|---|
| Объект с гладкой границей | Δ = 4 | D = 3 |
| Массовый (объемный) фрактал | 1 < Δ < 3 | DV = Δ |
| Поверхностный фрактал | 3 < Δ < 4 | DS = 6–Δ |
| Логарифмический фрактал | Δ = 3 | D = Δ |
Методом малоуглового рассеяния нейтронов или рентгеновского излучения изучают объекты в диапазоне размеров от одного ангстрема до одного микрометра. Для изучения более крупных фрактальных объектов, от микрона и больше, можно также применить метод малоуглового рассеяния, используя в этом случае более длинноволновое–оптическое–излучение [16–19].
Следует отметить, что рассеяние света на трехмерном объекте зачастую сопровождается сильным поглощением излучения. Этот режим рассеяния света следует назвать режимом пропускания. Тогда, основной вклад в дифракционную картину дает рассеяние от границ проекции этого объекта на плоскость, перпендикулярную оптической оси. Таким образом, при рассеянии света мы, фактически, имеем дело с двумерными проекциями трехмерных объектов. В то время как о фрактальных объектах в трехмерном пространстве многое известно, двумерные фрактальные объекты остаются практически не изученными с использованием методики рассеяния.
Рассеяние света на двумерных объектах-“масках” давно стало предметом учебников [19, 20]. Для получения качественного изображения рассеянного излучения на детекторе используют собирающую падающий свет линзу, а детектор устанавливают в ее фокусе. Такая схема позволяет получить на детекторе картину рассеяния как квадрат модуля фурье-образа от рассеивающего объекта [19]. Простейшая схема эксперимента для изучения фрактальных объектов, предложенная в статье [18], состоит из лазера как источника излучения, собирающей линзы и детектора, расположенного в фокальной плоскости линзы. Интересно отметить, что фрактальные характеристики двумерных объектов активно используют при обработке изображений [16]. А в работе [21] методом низко когерентной интерференции света были проведены исследования фрактальных свойств структуры биологических клеток. С помощью света можно также изучать более сложные фрактальные объекты – мультифракталы, используя вейвлет-анализ вместо фурье-анализа [22, 23].
Так как эксперименты по малоугловому рассеянию света, характеризующиеся сильным поглощением в веществе, можно интерпретировать как рассеяние через маску, т.е. сводя задачу к рассеянию на двумерных объектах, то такой эксперимент можно заменить численным моделированием с использованием фурье-анализа двумерных образов практически любых размеров.
В работе [24] были изучены двумерные регулярные геометрические фракталы, такие как ковер Серпинского, треугольник Серпинского, снежинка Коха и снежинка Вишека. В качестве модельной картины рассеяния рассчитывался квадрат модуля фурье-образа двумерного объекта. Полученные фрактальные размерности регулярных геометрических фракталов, расположенных на плоскости, удовлетворительно согласуются с теоретическими фрактальными размерностями.
В настоящей работе мы предлагаем классификацию двумерных фрактальных и нефрактальных объектов, которые возникают в задачах малоуглового рассеяния света, характеризующихся сильным поглощением. Мы численно моделируем рассеяние в двумерном пространстве на геометрических регулярных фракталах таких, как ковер Серпинского, треугольник Серпинского, снежинка Коха и снежинка Вишека и показываем, что численное моделирование является достоверным методом определения их фрактальной размерности. Показано, что фрактальные объекты в двумерном пространстве по аналогии с объектами в пространстве трех измерений можно разделить на “плоскостные” и “приграничные” с показателем степени, лежащим в пределах от 1 до 2 и от 2 до 3, соответственно, а для объекта с гладкой границей – круга, кривая форм-фактора, аналогичная кривой малоуглового рассеяния, спадает по степенному закону (qR)–3, где q – переданный импульс (при значениях переданного импульса q > 1/R, где R – радиус круга). Эта классификация может быть использована для характеристики любых двумерных фрактальных изображений.
В разделе 2 описан метод численного фурье-анализа от двумерных образов, моделирующий эксперимент по малоугловому рассеянию света в режиме пропускания. В разделе 3 представлен способ определения степенной зависимости интенсивности рассеяния от переданного импульса для различных объектов фрактальной и нефрактальной природы в пространстве двух измерений. В разделе 4 представлена классификация фрактальных объектов, ее обсуждение и выводы.
2. МЕТОД ЧИСЛЕННОГО ФУРЬЕ-АНАЛИЗА ДВУМЕРНЫХ ОБЪЕКТОВ
Поскольку картина интенсивности малоуглового рассеяния представляет собой квадрат модуля фурье-образа объекта исследования, то эксперимент по малоугловому рассеянию света можно смоделировать, используя схему, представленную на рис. 1.
Рис. 1.
Схема численного моделирования эксперимента по малоугловому рассеянию света на двумерных объектах.
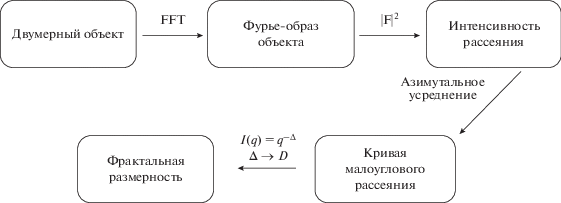
Схема такого численного эксперимента состоит из четырех шагов. Объект исследования представляет собой образ внутри квадрата с размерами 1 × 1 см2, описывающегося бинарной двумерной матрицей. Первым шагом является фурье-преобразование такого объекта (FFT – Fast Fourier Transform). Полученный фурье-образ объекта также будет двумерной матрицей, где каждый элемент матрицы характеризуется амплитудой и фазой. Второй шаг – формирование двумерной карты интенсивности, как квадрата модуля Фурье-образа объекта (|F|2, где F – фурье-образ объекта). В эксперименте по малоугловому рассеянию света наблюдается аналогичная этой карта интенсивности. На этом шаге теряется фаза интерференционной картины рассеяния. Третий шаг алгоритма – азимутальное усреднение интенсивности рассеяния вокруг центра карты, которое формирует кривую форм-фактора объекта, аналогичную кривой малоуглового рассеяния в реальном эксперименте, т.е. зависимости интенсивности от угла рассеяния. Последний шаг – определение показателя степени Δ из кривого форм-фактора, как отношение логарифмов интенсивности и переданного импульса q:
Фрактальная размерность связана с показателем степени Δ определенным образом, хотя и по-разному, для различных типов фракталов в двумерном пространстве (для фракталов в трехмерном пространстве, см. табл. 1). На программной платформе Qt была написана программа fractal для обработки изображений [26], которая выполняет первые три шага этого алгоритма.
Для наглядной демонстрации работы программы fractal по численному преобразованию фурье-объектов в двумерном пространстве рассмотрим пример простейшего нефрактального объекта двумерного пространства – круга с радиусом R = 0.165 см в квадрате со стороной 1 см. Известно, что фурье-образ круга представляет собой систему колец на двумерной карте, а интенсивность рассеяния имеет вид:
где j1 – функция Бесселя первого порядка, R – радиус круга, q – переданный импульс.На рис. 2. представлены объект исследования – круг, и модельная картина интенсивности рассеяния – квадрат модуля фурье-образа круга. Некоторые отклонения от привычной для нас картины фурье-образа круга как концентрических колец происходит в области больших значений фурье-координаты q из-за краевых эффектов на границе образа. При фурье-преобразовании происходит свертка самого объекта – круга и границы изображения – квадрата. Следует отметить, что двубитный, состоящий из единиц и нулей, черно-белый образ круга превратился при этом в цветной образ (оттенки серого) в двумерном пространстве Фурье, где цвет означает различную степень интенсивности образа. Образ оказывается наиболее интенсивным в точке с координатами (0, 0), и именно эту точку берут за центр окружности при азимутальном усреднении интенсивности рассеяния. Исследования в этой области показывают, что возможно однозначное восстановление двумерной черно-белой (не бинарной) картины из полученной в эксперименте двумерной карты интенсивности рассеяния с помощью методики последовательного восстановления фазы фурье-образа при многократном процессе аппроксимации квадрата амплитуды, при условии, что объект занимает меньше 25% всего изображения [25, 27].
Рис. 2.
(а) Объект исследования – круг; (б) модельная картина интенсивности – квадрат модуля фурье-образа круга, полученная с помощью программы fractal [26], (вставка) увеличенная картина интенсивности для малых q с концентрическими кольцами.
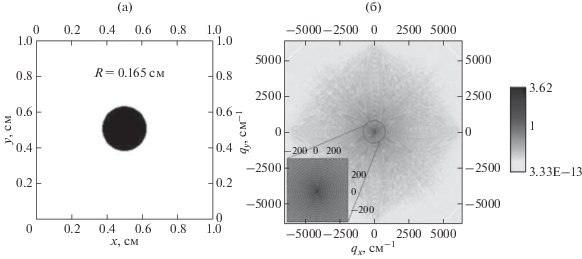
Моделирование процесса рассеяния происходит следующим образом: объект исследования расположен внутри квадрата с размерами 1 × 1 см2 и N × N единичных элементов (пикселей), где для сокращения времени обработки изображений N должно быть равно двойке в некоторой целой степени 2n, n = 1,2,3…. Программа fractal использует быстрое фурье-преобразование. Квадрат модуля фурье-образа объекта хорошо моделирует картину интенсивности рассеяния в малоугловом приближении. Эта картина представляет собой зависимость интенсивности рассеяния от компонент вектора, соответствующего волновым векторам qx, qy, выраженных в обратных единицах длины реального пространства. Максимальное значение координаты q в пространстве Фурье вычисляется как πN/X, где Х – общий размер изображения в единицах длины, N – размер изображения в пикселях, а X/N, соответственно, размер одного пикселя в единицах длины. Оси qx, qy делятся на N равных интервалов и минимальный размер в q-пространстве равен π/X.
Кривую форм-фактора объекта, аналогичную кривой малоуглового рассеяния получали, азимутально усредняя интенсивность по кольцу с радиусом |q| = (πNi/X) и шириной в 1 пиксель, используя программу fractal. График зависимости интенсивности от импульса |q| для круга в двойном логарифмическом масштабе представлен на рис. 3. Здесь квадратами показаны значения интенсивности рассеяния, полученной в численном эксперименте, а сплошная кривая представляет собой теоретическую зависимость (уравнение (4)) для круга с радиусом R = 0.165 см.
Рис. 3.
Зависимость квадрата модуля фурье-образа (интенсивности) для круга от переданного импульса в двойном логарифмическом масштабе: квадраты – численный расчет, осциллирующая сплошная линия соответствует уравнению (4), линейная зависимость – q–3.
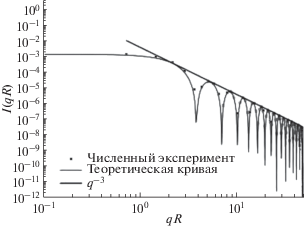
Из рис. 3. видно, что значения, полученные в результате моделирования, практически ложатся на теоретическую кривую, при этом интенсивность максимумов спадает по мере роста q по степенному закону q–3. Такое же поведения наблюдается и для других двумерных однородных нефрактальных объектов (квадрат, треугольник). Хорошее совпадение численного расчета с теоретической кривой говорит о корректной работе программы fractal. Для того, чтобы значения интенсивности, полученные в численном эксперименте, хорошо описывали кривую рассеяния нужно, чтобы несколько точек попадали на одну осцилляцию. Количество точек, приходящихся на одну осцилляцию, характеризуется отношением размера квадрата, в который помещен круг, т.е. размера самого изображения, к радиусу круга, при условии, что количество пикселей N, на которые разбита картина, остается постоянным. Так, количество точек, приходящихся на одну осцилляцию функции Бесселя, будет равно (X/R × 3/8), где Х – размер изображения, а R – радиус круга.
Несмотря на то, что необходимо несколько точек, приходящихся на одну осцилляцию, чтобы прописать все особенности кривой, следует отметить, что для определения фрактальной размерности, т.е. наклона огибающей, такое условие необязательно.
3. ИССЛЕДОВАНИЕ ФРАКТАЛЬНЫХ СВОЙСТВ ОБЪЕКТОВ В ДВУМЕРНОМ ПРОСТРАНСТВЕ МЕТОДОМ ЧИСЛЕННОГО ФУРЬЕ-АНАЛИЗА
Мы исследовали фрактальную размерность ковра Серпинского, принцип построения которого представлен на рис. 4. На первом шаге из центра квадрата со стороной 1 см вырезается другой квадрат со стороной 1/3 от начальной длины. В получившемся объекте можно выделить 8 квадратов со стороной 1/3 см, из центра которых на втором шаге вырезается еще по квадрату со стороной 1/9 см, и т.д. Для исследования был построен ковер Серпинского пятой генерации.
Поскольку все реальные фракталы имеют ограничения по размерам, как со стороны больших масштабов, так и со стороны малых, то необходимо контролировать соответствие размеров фрактального объекта размеру всего квадрата и минимальному размеру его разбиения на элементы. Минимальное значение переданного импульса равно 3.14 см–1, что соответствует в реальном пространстве размеру всего квадрата с размерами 1 × 1 см2. Поскольку максимальный линейный размер фрактала совпадает с размерами квадрата, то информацию о фрактальных свойствах объекта несут все точки зависимости из диапазона малых переданных импульсов. Максимальное значение переданного импульса равно 1600 см–1, что соответствует в реальном пространстве размеру единичного элемента разбиения квадрата с размерами 0.002 × 0.002 см2. При этом минимальный размер элемента, из которого состоит фрактал пятой генерации, равен 0.004 × 0.004 см2 (1/35), что превосходит минимальный размер разбиения в два раза! Поэтому следует учитывать, что фрактальные свойства объекта в пространстве переданных импульсов ограничены со стороны больших импульсов величиной 785 см–1 (равной π × 1/0.004 см–1).
Зависимость I(q) аппроксимировали прямой в двойном логарифмическом масштабе в соответствии с выражением (3), при этом наклон прямой должен равняться значению фрактальной размерности со знаком минус.
Как видно из рис. 5, зависимость I(q) можно описать прямой с наклоном –1.91 ± 0.03 в диапазоне переданных импульсов от 5 до 785 см–1, т.е. там, где объект обладает фрактальными свойствами. Полученное значение корректно описывает в пределах погрешности фрактальные характеристики ковра Серпинского, фрактальная размерность которого, посчитанная теоретически, равна с точностью до последней цифры 1.89. При этом в диапазоне переданных импульсов от 785 до 1600 см–1 зависимость I(q) описывается прямой линией с наклоном –2.97 ± 0.09. Как показано выше на примере круга, это соответствует рассеянию на минимальном элементе фрактала, т.е. на однородном нефрактальном объекте в двумерно пространстве, обладающим резкой границей.
Рис. 5.
Зависимость усредненной интенсивности от переданного импульса в двойном логарифмическом масштабе для ковра Серпинского пятой генерации (полые квадраты); усредненные по полосам данные (заполненные квадраты).
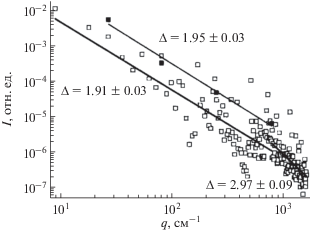
В большинстве случаев для регулярных фракталов на кривые рассеяния возникают осцилляции интенсивности, обусловленные регулярностью структуры. В этом случае аппроксимация прямой линией дает некорректное значение фрактальной размерности из-за того, что точки неравномерно расположены по оси абсцисс. В этом случае можно разбить весь диапазон q пространства, соответствующий фрактальному объекту, на полосы равной ширины в логарифмическом масштабе и усреднить все точки в каждой полосе, т.е. посчитать среднее арифметическое для каждой из полос. Как показано в работе [18], количество таких полос должно быть на одну меньше, чем номер генерации фрактала. Полученную таким образом зависимость I(q) следует аппроксимировать прямой, наклон которой будет равен фрактальной размерности исследуемого объекта (черные квадраты на рис. 5). Для пятой генерации ковра Серпинского данные разбиваются на четыре полосы и получаемый наклон равен 1.95 ± 0.03, что также близок к теоретической размерности в пределах погрешности.
Для верификации метода была получена зависимость фрактальной размерности от количества полос усреднения для шестой генерации ковра Серпинского (рис. 6).
Рис. 6.
Зависимость фрактальной размерности от числа полос усреднения для шестой генерации ковра Серпинского.
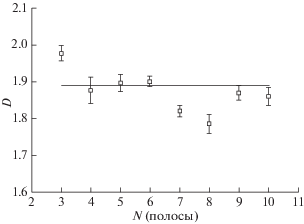
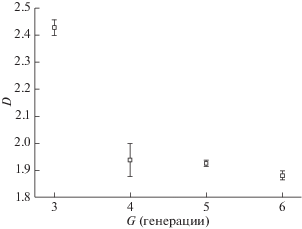
Видно, что при количестве полос усреднения от 4 до 6 фрактальная размерность соответствует теоретической (сплошная линия на графике) в пределах погрешности, однако наилучшее соответствие имеет фрактальная размерность, полученная при пяти полосах усреднения, что на одну меньше, чем номер генерации фрактала. Также была прослежена зависимость фрактальной размерности от номера генерации фрактала (рис. 7).
Из графика на рис. 7 видно, что при увеличении номера генерации фрактальная размерность стремится к теоретической фрактальной размерности, а ковер Серпинского третьей генерации, по существу не является фрактальным объектом.
Используя методику, описанную выше, были также измерены фрактальные размерности и других геометрических двумерных фракталов: треугольника Серпинского, снежинки Коха и снежинки Вишека (рис. 8).
Полученные в численном эксперименте фрактальные размерности представлены в табл. 2 .
Таблица 2.
Фрактальные размерности регулярных геометрических фракталов, определяемые численным методом с помощью фурье-анализа
| Фрактальная размерность вычисленная, D | Фрактальная размерность теоретическая | |
|---|---|---|
| Ковер Серпинского | 1.91 ± 0.03 | 1.89 |
| Треугольник Серпинского | 1.57 ± 0.012 | 1.585 |
| Снежинка Коха | 1.35 ± 0.016 | 1.262 |
| Снежинка Вишека | 1.32 ± 0.024 | 1.465 |
В пределах погрешности полученные фрактальные размерности ковра Серпинского и треугольника Серпинского равны фрактальным размерностям, вычисленным теоретически. Некоторое несоответствие результатов численного эксперимента теоретическим значениям для снежинки Вишека и снежинки Коха связано с недостаточным числом генераций фрактального объекта, использованного в численном эксперименте. Видно, что все фрактальные размерности лежат в диапазоне от 1 до 2.
4. ОПРЕДЕЛЕНИЕ “ПРИГРАНИЧНОГО” ФРАКТАЛА: СНЕЖИНКА КОХА
По аналогии с поверхностным фракталом, часто наблюдаемом методом малоуглового рассеяния в трехмерном пространстве [11–13], можно определить так называемый “приграничный” фрактал в двумерном пространстве, когда с одной стороны фрактальной границы пустота, а с другой однородная среда, т.е. объект закрашен. Для такого “приграничного” фрактала можно предположить по аналогии с поверхностным фракталом в трехмерном пространстве, что фрактальная размерность его будет равна 2d – Δ, где d = 2 – размерность пространства, Δ – наклон прямой, аппроксимирующей данные, лежащий в интервале от 2 до 3.
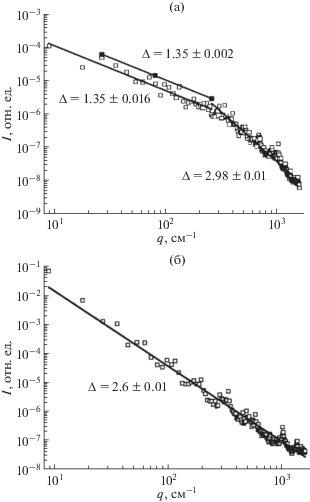
Для иллюстрации этого утверждения рассмотрим снежинку Коха, как простой, “плоскостной” фрактал, представляющий собой только линию границы. В качестве “приграничного” фрактала рассмотрим ту же снежинку, но с совершенно заполненной внутренней частью. Их вид представлен на рис. 9.
Для “плоскостного” фрактала снежинки Коха наклон кривой равен фрактальной размерности 1.35 ± 0.016, тогда как для “приграничного” фрактала снежинки Коха наклон кривой равен 2.6 ± ± 0.01 (рис. 10), что в пределах погрешности соответствует фрактальной размерности кривой Коха, рассчитанной по формуле 2d – Δ. Таким образом, можно сказать, что среди объектов двумерного пространства действительно существует аналог поверхностного фрактала в трехмерном пространстве.
5. ЗАКЛЮЧЕНИЕ
Все полученные результаты для двумерных фрактальных объектов можно обобщить в виде таблицы (табл. 3).
Таблица 3.
Классификация фрактальных и нефрактальных объектов в двумерном пространстве
| Класс объектов | Показатель степени Δ | Размерность объекта |
|---|---|---|
| 2D-объект с гладкой границей | Δ = 3 | D = 2 |
| “Плоскостной” (plane) фрактал | 1 < Δ < 2 | DP = Δ |
| “Приграничный” (boundary) фрактал | 2 < Δ < 3 | DB = 4 – Δ |
Для объекта с гладкой границей – круга – показатель степени равен трем, для обычного, назовем его “плоскостным”, фрактала в двумерном пространстве показатель степени или фрактальная размерность лежит в интервале от 1 до 2. Фрактальная размерность “приграничного” фрактала будет равна (2d – Δ), а показатель степени лежит в интервале от 2 до 3.
Таким образом, в данной работе, используя метод численного фурье-анализа, нами дополнена классификация фрактальных объектов в двумерном пространстве.
Список литературы
Peitgen H.O., Richter P.H. The Beauty of Fractals. Berlin: Springer, 1986. 199 p.
Mandelbrot B. The Fractal Geometry of Nature. N.Y.: Freeman, 1983.
Зельдович Я.Б., Соколов Д.Д. // Успехи физических наук. 1985. Т. 146. № 3. P. 493.
Морозов А.Д. Введение в теорию фракталов. Москва–Ижевск: Институт компьютерных исследований, 2002. 160 с.
Федер Е. Фракталы. М.: Мир, 1991. 262 с.
Балханов В.К., Башкуев Ю.Б. // Журн. технической физики. 2012. Т. 82. № 12. С. 126.
Васин С.И., Харитонова Т.В., Филиппов А.Н. // Коллоидный журн. 2011. Т. 73. № 2. С. 155.
Симонян Г.С., Симонян А.Г. // Международный журн. прикладных и фундаментальных исследований. 2016. № 3. С. 268.
Симонян Г.С., Симонян А.Г. // Успехи современного естествознания. 2015. № 11. С. 93.
Кроновер P.M. Фракталы и хаос в динамических системах. Основы теории. М.: Постмаркет, 2000.
Bale H.D., Schmidt P.W. Phys. Rev. Lett. 1984. V. 53. P. 596.
Teixeira J. // J. Applied Crystallography. 1988. № 21. P. 781.https://doi.org/10.1107/S0021889888000263
Po-zen Wong, Alan J. Bray, Phys. Rev. Lett. 1988. V. 60. № 13. P. 786.
Яшина Е.Г., Григорьев. С.В. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2017. № 9. С. 5. https://doi.org/10.7868/S0207352817090013
Iashina E.G., Velichko E. V., Filatov M. V. et al. // Phys. Rev. E. 2017. V. 96. № 1. https://doi.org/10.1103/PhysRevE.96.012411
Zwiggelaar R., Bull C.R. // Optical Engineering. 1995. V. 34. № 5. P. 1325.
Zimnyakov D.A., Tuchin V.V. // Applied Optics. 1996. V. 35. № 22. P. 4325.https://doi.org/10.1364/AO.35.004325
Allain C., Cloitre M. // Phys. Rev. B. 1986. V. 33. № 5. P. 3566. https://doi.org/10.1007/978-1-4757-1402-9_16
Гудмен Дж. Введение в Фурье-оптику. М.: Мир, 1970. С. 116.
Матвеев А.Н. Оптика. М.: Высшая школа, 1985. 353 с.
Wax A., Yang Ch., Backman V. et al. // Biophysical J. 2002. V. 82. № 4. P. 2256. https://doi.org/10.1016/S0006-3495(02)75571-9
Freysz E., Pouligny B., Argoul F., Arneodo A. // Phys. Rev. Let. 1990. V. 64. № 7. P. 745. https://doi.org/10.1103/PhysRevLett.64.745
Muzy J.F., Pouligny B. // Physical Review A. 1992. V. 45. № 12. P. 8961. https://doi.org/10.1103/PhysRevA.45.8961
Зинчик А.А., Музыченко Я.Б., Смирнов А.В., Стафеев С.К. // Научно-технический вестник СПбГУ ИТМО. 2009. № 2(60). С. 17.
Fienup J.R. // Optics Letters. 1978. V. 3. № 1. P. 27.
https://github.com/tre3k/fractal.
Fienup J.R. // Applied Optics. 1982. V. 21. № 15. P. 2758.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования