Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2021, № 12, стр. 31-34
Электрическая поляризация в малых магнитных частицах
Т. С. Шапошникова a, *, Р. Ф. Мамин a, **
a Казанский физико-технический институт
им. Е.К. Завойского ФИЦ Казанский научный центр РАН
420029 Казань, Россия
* E-mail: t_shap@kfti.knc.ru
** E-mail: mamin@kfti.knc.ru
Поступила в редакцию 25.04.2021
После доработки 22.05.2021
Принята к публикации 24.05.2021
Аннотация
В рамках феноменологического подхода получено неоднородное вихревое распределение намагниченности и связанной с ней неоднородной электрической поляризации в малых магнитных частицах. Микроскопический механизм такой связи намагниченности с поляризацией обусловлен взаимодействием Дзялошинского–Мории. Конкретный вид выражений для намагниченности и поляризации определяется геометрической формой нанообластей. Фазовые переходы в малых сферических частицах ферромагнетиков исследовались в рамках феноменологической теории Гинзбурга–Ландау. Используя выражение свободной энергии для намагниченности в сферических наночастицах, мы получили неоднородное распределение намагниченности в виде трехмерных магнитных вихрей. Для больших радиусов сферы возможен фазовый переход в вихревое состояние, в то время как для радиуса, который меньше определенного критического значения, наночастица может находиться в однородном состоянии. Рассчитана неоднородная электрическая поляризация. В нашем случае электрическая поляризация имеет вид двумерных ежей. Определена область существования таких неоднородных состояний.
ВВЕДЕНИЕ
Магнетизм частиц субмикронного размера в последние годы привлекает большое внимание в связи с возможностью их практического применения [1, 2]. “Однодоменные” частицы являются потенциальными кандидатами для использования в качестве элементов памяти в накопителях данных на жестких дисках высокой плотности. Однако при увеличении размера частиц их магнитное состояние изменяется на вихревое или многодоменное [3–5]. Обсуждение магнитных фазовых переходов (ФП) в малых частицах стало особенно распространенным [5]. Существуют материалы с различными типами структурного, магнитного, зарядового и орбитального упорядочения, например, манганиты, высокотемпературные купратные сверхпроводники и мультиферроики. Разделение фаз в этих материалах часто сопровождается неоднородным распределением заряда [6–9].
Мультиферроики также представляют большой научный и практический интерес, поскольку эти материалы являются как ферромагнитными, так и сегнетоэлектрическими в одной фазе [10]. Это обусловлено существованием магнитоэлектрического эффекта, который наблюдается в мультиферроиках [11]. Антиферромагнетизм и сегнетоэлектричество чаще всего сосуществуют в мультиферроиках, но сегнетоэлектрические ферромагнетики являются довольно редкими материалами. Появление вызванной магнитным полем электрической поляризации можно объяснить, ссылаясь на три наиболее популярных микроскопических механизма: механизма, связанного с антисимметричным взаимодействием Дзялошинского–Мории (ДМ) [12, 13], механизма магнитострикции [9] и механизма спин-зависимой гибридизации металл–лиганд. Взаимодействие ДМ вызывает неколлинеарное упорядочение спинов. Неоднородное магнитное упорядочение, в свою очередь, может привести к поляризации [8, 14].
В данной работе рассматривается взаимосвязь магнетизма и сегнетоэлектричества в субмикронных частицах сегнетоэлектрического ферромагнетика вблизи магнитного фазового перехода. Целью работы является определение пространственного распределения неоднородной намагниченности, обусловленной размерными эффектами, пространственного распределения неоднородной поляризации, возникающей вследствие пространственной неоднородности намагниченности. Также будет определена область существования таких состояний. Все расчеты проводились в рамках феноменологического подхода.
МЕТОДИКА
Рассмотрим трехмерную сферическую частицу мультиферроика, помещенную в параэлектрическую среду. В сферических координатах гармоническая часть свободной энергии Ландау–Гинзбурга–Девоншира [14] вблизи фазового перехода второго порядка имеет вид
(1)
$\begin{gathered} F = \int {{{r}^{2}}\sin \left( \theta \right)drd\theta d\varphi } \times \\ \times \,\,\left( {\frac{A}{2}{{m}^{2}} + \frac{g}{2}\left\{ {{{{\left( {\frac{{\partial {{m}_{r}}}}{{\partial r}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{m}_{\theta }}}}{{\partial r}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{m}_{\varphi }}}}{{\partial r}}} \right)}}^{2}} + } \right.} \right. \\ + \,\,\frac{1}{{{{r}^{2}}}}\left[ {{{{\left( {\frac{{\partial {{m}_{r}}}}{{\partial \theta }} - {{m}_{\theta }}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{m}_{\theta }}}}{{\partial \theta }} - {{m}_{r}}} \right)}}^{2}} + {{{\left( {\frac{{\partial {{m}_{\varphi }}}}{{\partial \theta }}} \right)}}^{2}}} \right] + \\ + \,\,\frac{1}{{{{r}^{2}}{{{\left( {\sin \left( \theta \right)} \right)}}^{2}}}}\left[ {{{{\left( {\frac{{\partial {{m}_{r}}}}{{\partial \varphi }} - {{m}_{\varphi }}\sin \left( \theta \right)} \right)}}^{2}} + } \right. \\ + \,\,{{\left( {\frac{{\partial {{m}_{\theta }}}}{{\partial \varphi }} - {{m}_{\varphi }}\cos \left( \theta \right)} \right)}^{2}} + \\ \left. {\left. {\left. { + \,\,{{{\left( {{{m}_{r}}\sin \left( \theta \right) + {{m}_{{\theta ~}}}\cos \left( \theta \right) + \frac{{\partial {{m}_{\varphi }}}}{{\partial \varphi }}} \right)}}^{2}}} \right]} \right\}} \right), \\ \end{gathered} $Эффективное магнитное поле ${{H}^{{{\text{eff}}}}}\left( {{\mathbf{r}},~t} \right)$ определяется как вариация изменения свободной энергии F по магнитному моменту m:
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Для определения пространственного распределения вектора магнитного момента M и вектора электрической поляризации P рассмотрим вариацию $\delta F$ по $\delta {{m}_{\varphi }}.$ Если эта вариация равна нулю, то намагниченность является решением уравнения:
(3)
$\begin{gathered} A{{m}_{\varphi }} + \frac{g}{{{{r}^{2}}{{{\left( {\sin \left( \theta \right)} \right)}}^{2}}}}{{m}_{\varphi }} - \frac{g}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}\left( {{{r}^{2}}\frac{{\partial {{m}_{\varphi }}}}{{\partial r}}} \right) - \\ - \,\,\frac{g}{{{{r}^{2}}\sin \left( \theta \right)}}\frac{\partial }{{\partial \theta }}\left( {\sin \left( \theta \right)\frac{{\partial {{m}_{\varphi }}}}{{\partial \theta }}} \right) = 0. \\ \end{gathered} $(4)
${{m}_{r}} = 0,\,\,\,\,{{m}_{\theta }} = 0\,\,\,{\text{и}}\,\,\,{{m}_{\varphi }}\left( {r,\varphi } \right) = C{{j}_{1}}\left( {{{p_{1}^{1}r} \mathord{\left/ {\vphantom {{p_{1}^{1}r} R}} \right. \kern-0em} R}} \right)\sin \left( \theta \right),$На рис. 1а показано распределение намагниченности в объеме сферической частицы. Векторы локальной намагниченности показаны толстыми стрелками. Вблизи фазового перехода второго порядка в ферромагнитное состояние для частиц субмикронного размера можно использовать приближение, когда значение локальной намагниченности зависит от расстояния до центра частицы. Одним из решений уравнения (3) является вихрь (4).
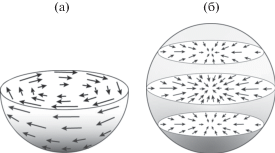
Рис. 1.
Распределение намагниченности сразу после парамагнитно-ферромагнитного фазового перехода в объеме сферы для ${{m}_{r}} = {{m}_{\theta }} = 0$ и ${{m}_{\varphi }} = {{m}_{\varphi }}\left( {r,~\varphi } \right)$ (выражение (4)), 3D-вихрь. Показана половина сферической частицы (а). Локальная электрическая поляризация (выражение (6)), рассчитанная для трех значений h: –0.707 R; 0; 0.707R, где R – радиус частицы (б).
Для кубических кристаллов допустимой формой магнитно-индуцированной электрической поляризации [14] является
Это выражение получено для случая, когда электрическая поляризация возникает из-за взаимодействия Дзялошинского–Мории [12, 13]. Для 3D-вихревого состояния в объеме сферы при ${{m}_{r}} = {{m}_{\theta }} = 0,$ и ${{m}_{\varphi }} = {{m}_{\varphi }}\left( {r,\varphi } \right)$ (3) поляризация имеет вид 3D-ежа [5] с ${{P}_{\varphi }} = 0$ и(6)
$\begin{gathered} P\left( {r,\theta } \right) \sim - \frac{{j_{1}^{2}\left( {{{p_{1}^{1}r} \mathord{\left/ {\vphantom {{p_{1}^{1}r} R}} \right. \kern-0em} R}} \right)\sin \left( \theta \right)}}{r} \times \\ \times \,\,\left( {\sin \left( \theta \right){{e}_{r}} + \cos \left( \theta \right){{e}_{\theta }}} \right). \\ \end{gathered} $Рассмотрим второй случай, когда ${{m}_{r}} = {{m}_{\varphi }} = 0,$ и ${{m}_{\theta }} = {{m}_{\theta }}\left( {r,\varphi } \right).$ При этом решение уравнения, подобного уравнению (3), будет иметь следующий вид:
(7)
${{m}_{\theta }}\left( {r,\varphi } \right) = C{{j}_{1}}\left( {{{p_{1}^{1}r} \mathord{\left/ {\vphantom {{p_{1}^{1}r} R}} \right. \kern-0em} R}} \right)\sin \left( \theta \right).$Рис. 2.
Распределение намагниченности сразу после парамагнитно-ферромагнитного фазового перехода в объеме сферы для ${{m}_{r}} = {{m}_{\varphi }} = 0$ и ${{m}_{\theta }} = {{m}_{\theta }}\left( {r,~\varphi } \right)$ (выражение (7)). Показана половина сферической частицы (а). Локальная электрическая поляризация, рассчитанная для трех значений h: –0.707R; 0; 0.707R, где R – радиус частицы (б).

Распределение вихревой намагниченности, рассмотренное в этой статье, приводит к распределению поляризации, для которого полная поляризация частицы равна нулю. Но по нашим предварительным оценкам, при таком распределении намагниченности полная поляризация может отличаться от нуля во внешнем магнитном поле.
ОБЛАСТЬ СУЩЕСТВОВАНИЯ
Мелкие ферромагнитные частицы могут также представлять собой “однодоменные”, однородно намагниченные образования. Критерий их “однодоменности” получается из сравнения магнитной энергии равномерно намагниченной частицы с энергией, которая возникает при наличии значительной неоднородности в распределении намагниченности в объеме частицы. Первая энергия имеет порядок $A{{M}^{2}}V,$ а вторая – порядок ${{g{{M}^{2}}V} \mathord{\left/ {\vphantom {{g{{M}^{2}}V} {{{l}^{2}}}}} \right. \kern-0em} {{{l}^{2}}}}$ (здесь $M$ – суммарная намагниченность частицы, $V$ – ее объем, $A$ и $g$ – параметры выражения для свободной энергии (1)). Тогда размер однодоменных частиц имеет значение, по порядку величины равное ${{R}_{c}} \sim {{\left( {{g \mathord{\left/ {\vphantom {g A}} \right. \kern-0em} A}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ [15]. Существует постоянное магнитное поле ${{h}_{s}}$ (hs = $ = - {{\left[ {{{\mu }_{0}}\left( {\mu + 2} \right)} \right]}^{{ - 1}}}M$), которое создается внутри равномерно намагниченной частицы в нулевом внешнем магнитном поле для однородной намагниченности шара, и стабильность состояния с однородной намагниченностью теряется при $A = - {{\left[ {{{\mu }_{0}}\left( {\mu {\text{\;}} + 2} \right)} \right]}^{{ - 1}}}.$ В этом выражении $\mu $ – магнитная проницаемость мультиферроика, а ${{\mu }_{0}}$ – магнитная постоянная. Выражение A = $ = - {{\left[ {{{\mu }_{0}}\left( {\mu + 2} \right)} \right]}^{{ - 1}}}$ определяет критическую температуру TCS = TC – ΔTS (здесь ΔTS $ = {{\left[ {A{\kern 1pt} '{{\mu }_{0}}\left( {\mu + 2} \right)} \right]}^{{ - 1}}}$), выше которой однородное состояние становится неустойчивым по отношению к возникновению неоднородного состояния, так как энергия неоднородного состояния становится меньше, чем у однородного. Поэтому для критического радиуса мы имеем $~R = {{R}_{{\text{c}}}} = p_{1}^{1}{{\left( {g{{\mu }_{0}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\left( {\mu + 2} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ при этом ${{R}_{{\text{c}}}}$ имеет порядок 100 нм [2]. Обсуждаемое вихревое состояние существует в диапазоне температур ниже TCV и выше TCS и соответствует минимуму свободной энергии системы, поэтому это состояние является стабильным. Верхняя граничная температура TCV существования неоднородного вихревого состояния определяется выражением $A = - g{{\left( {{{p_{n}^{1}} \mathord{\left/ {\vphantom {{p_{n}^{1}} R}} \right. \kern-0em} R}} \right)}^{2}}$ для n = 1. Таким образом, она равна TCV = TC – ΔTV, где $\Delta {{T}_{{\text{V}}}} = 4.41g{{\left[ {A{\kern 1pt} '{{R}^{2}}} \right]}^{{ - 1}}}.$ Так как величина ${g \mathord{\left/ {\vphantom {g {A{\kern 1pt} '}}} \right. \kern-0em} {A{\kern 1pt} '}}$ достаточно мала (${g \mathord{\left/ {\vphantom {g {A{\kern 1pt} '}}} \right. \kern-0em} {A{\kern 1pt} '}}$ ≈ ≈ 5 × 10–16 м2 · K), то TCV ~ TC (ΔTV≈ 0.05 K для R ≈ ≈ 100 нм). Поэтому температурный интервал области существования вихревого состояния составляет порядка ΔTS. По нашим оценкам, ΔTS составляет несколько десятков градусов K. Выше TC однородное парамагнитное состояние является основным состоянием, а ниже TCS однородное магнитное состояние является основным состоянием.
ЗАКЛЮЧЕНИЕ
Исследован фазовый переход в трехмерных сферических частицах кубического мультиферроика в рамках феноменологической теории. Получены выражения для намагниченности этих частиц в двух состояниях в нулевом внешнем магнитном поле с учетом вариаций амплитуды намагниченности. При использовании выражения свободной энергии для намагниченности в сферических наночастицах, получено неоднородное распределение намагниченности в виде трехмерных магнитных вихрей. Локальная электрическая поляризация рассчитана для двух различных распределений намагниченности. Показано, что конкретный вид выражений для намагниченности и поляризации определяется геометрической формой нанообластей.
Список литературы
Hehn M., Ounadjela K., Bucher J.-P., Rousseaux F., Decanini D., Bartenlian B., Chapper C. // Science. 1996. V. 272. № 5269. P. 1782.https://doi.org/10.1126/science.272.5269.1782
Cowburn R.P., Koltsov D.K., Adeyeye A.O., Welland M.E., Tricker D.M. // Phys. Rev. Lett. 1999. V. 83. № 21. P. 1042.https://doi.org/10.1103/PhysRevLett.83.1042
Stapper C.H., Jr. // J. Appl. Phys. 1969. V. 40. № 2. P. 798.https://doi.org/10.1063/1.1657466
Coey J. Magnetism and Magnetic Materials. Cambridge: Cambridge University Press, 2010. 617 p.https://doi.org/10.1017/CBO9780511845000
Usov N.A., Nesmeyanov M.S. // Scientific Reports. 2020. V. 10. № 1. P. 10173.https://doi.org/10.1038/s41598-020-67173-5
Levanyuk A.P., Blinc R. // Phys. Rev. Lett. 2013. V. 111. № 9. P. 097601.https://doi.org/10.1103/PhysRevLett.111.097601
Rößler U.K., Bogdanov A.N., Pfleiderer C. // Nature. 2006. V. 442. № 7104. P. 797.https://doi.org/10.1038/nature05056
Cheong S.-W., Mostovoy M. // Nature Materials. 2007. V. 6. № 1. P. 13.https://doi.org/10.1038/nmat1804
Sergienko I.A., Dagotto E. // Phys. Rev. B. 2006. V. 73. № 9. P. 094434.https://doi.org/10.1103/PhysRevB.73.094434
Hill N.A. // J. Phys. Chem. B. 2000. V. 104. № 29. P. 6694.https://doi.org/10.1021/jp000114x
Khanh N.D., Abe N., Sagayama H., Nakao A., Hanashima T., Kiyanagi R., Tokunaga Y., Arima T. // Phys. Rev. B. 2016. V. 93. № 7. P. 075117.https://doi.org/10.1103/PhysRevB.93.075117
Дзялошинский И.Е. // ЖЭТФ. 1959. Т. 37. № 3. С. 881.
Moriya T. // Phys. Rev. 1960. V. 120. № 1. P. 91.https://doi.org/10.1103/PhysRev.120.91
Mostovoy M. // Phys. Rev. Lett. 2006. V. 96. № 6. P. 067601.https://doi.org/10.1103/PhysRevLett.96.067601
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, 1982. 620 с.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования


