Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2021, № 3, стр. 105-112
Каналирование заряженных частиц около поверхности проводников и проводящих кристаллов
В. И. Высоцкий a, *, М. В. Высоцкий a, Н. В. Максюта a
a Киевский национальный университет им. Т. Шевченко
01033 Киев, Украина
* E-mail: vivysotskii@gmail.com
Поступила в редакцию 14.07.2020
После доработки 17.08.2020
Принята к публикации 20.08.2020
Аннотация
Рассмотрены особенности ориентационного движения и каналирования заряженных частиц, движущихся в околоповерхностной потенциальной яме, структура которой сформирована поверхностной плоскостью кристалла и действием векторного потенциала электрического тока, протекающего сквозь кристалл или вдоль проводника, возле которого находится непроводящий кристалл. Ширина потенциальной ямы, формирующей режим околоповерхностного каналирования, зависит от толщины кристалла и плотности электрического тока и может изменяться в интервале от нескольких миллиметров до единиц микрометров при изменении плотности тока в интервале 1–1000 А/см2. Процесс околоповерхностного каналирования в поле плоского проводника с током обеспечивает аномально слабое торможение частиц и может быть использован для транспортировки пучков частиц вдоль проводников с током на большое расстояние. Аналогичный режим аксиального каналирования характеризуется полным подавлением рассеяния и торможения пучка ионов при их движении в свободном пространстве вдоль поверхности цилиндрического проводника с током.
ВВЕДЕНИЕ
Традиционная схема каналирования заряженных частиц соответствует их движению вдоль определенных кристаллографических направлений в объеме кристалла [1–4]. Этот режим ориентационного движения характеризуется сильным электростатическим взаимодействием движущихся частиц с ядрами и электронами атомов, локализованными около конкретных осей и плоскостей. Конкретный расчет такого взаимодействия осуществляется за счет использования скалярного потенциала атомов и ионов, усредненного вдоль этих кристаллографических направлений.
Такие особенности взаимодействия способствуют эффективному управлению траекторией частиц за счет влияния сильного внутрикристаллического поля, включая возможность отклонения пучка при внутреннем отражении от кристаллографических плоскостей слабо изогнутого кристалла [5], но одновременно ведут к быстрому деканалированию и невозможности использования каналирования для транспортировки частиц на большое расстояние. Очень малая длина деканалирования, не превышающая единиц или десятков микрон, также приводит к малой эффективности генерации квазихарактеристического излучения, механизм которой непосредственно связан с межуровневыми радиационными переходами частицы при ее движении в режиме каналирования. Еще один недостаток внутриобъемного каналирования связан с неизбежной деградацией кристаллической решетки при прохождении сквозь кристалл интенсивных пучков частиц или при длительном пропускании малоинтенсивных пучков.
В работе рассмотрено влияние суммарного действия стандартного скалярного потенциала кристалла и дополнительного векторного потенциала на ориентационное движение частиц. Одним из эффективных и управляемых источников такого векторного потенциала является электрический ток, протекающий по проводящему кристаллу или по проводнику, около которого находится рассматриваемый диэлектрический кристалл. Проведенный анализ особенностей ориентационного движения заряженных частиц с импульсом р = ерр в вакууме непосредственно около внешней поверхности проводящего кристалла или при нахождении диэлектрического кристалла около проводника с током J = ezJпоказывает возможность реализации каналирования заряженных частиц в свободном пространстве около поверхности кристалла.
ОСОБЕННОСТИ КАНАЛИРОВАНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ ПРИ НАЛИЧИИ ВЕКТОРНОГО ПОТЕНЦИАЛА ОКОЛО КРИСТАЛЛА
Состояние и движение заряженных частиц при наличии как скалярного потенциала кристалла V(r) = qφ(r), так и векторного потенциала ${\mathbf{A}}({\mathbf{r}}) = {{{\mathbf{e}}}_{z}}{{A}_{z}}({\mathbf{r}})$ (в том числе внешнего источника), но без учета влияния спина частиц, описывается уравнением Клейна–Гордона:
(1)
${{\left( {\varepsilon - q\varphi ({\mathbf{r}})} \right)}^{2}}\Psi ({\mathbf{r}}) = \left( {{{{\left( {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p} }} - \frac{q}{c}{\mathbf{A}}({\mathbf{r}},t)} \right)}}^{2}}{{c}^{2}} + m_{{}}^{2}{{c}^{4}}} \right){\kern 1pt} \Psi ({\mathbf{r}}).$Рассмотрим случай, когда источником векторного потенциала является электрический ток J = = ezJ, протекающий непосредственно по исследуемому проводящему кристаллу (металлу или полупроводнику) или по плоскому проводнику, около поверхности которого находится непроводящий кристалл. После использования замены
(2)
$\Psi ({\mathbf{r}}) = \tilde {\Psi }({{{\mathbf{r}}}_{ \bot }})\exp \left( {i\frac{{{{p}_{z}}z}}{\hbar }} \right)$(3)
$\left[ { - {{{{\hbar }^{2}}{{\Delta }_{ \bot }}} \mathord{\left/ {\vphantom {{{{\hbar }^{2}}{{\Delta }_{ \bot }}} {2\gamma m}}} \right. \kern-0em} {2\gamma m}} + U\left( r \right)} \right]\tilde {\Psi }({{{\mathbf{r}}}_{ \bot }}) = {{E}_{{{\text{eff}}}}}\tilde {\Psi }({{{\mathbf{r}}}_{ \bot }});$(4)
$\begin{gathered} U\left( r \right) = {{U}_{A}}\left( r \right) + {{U}_{V}}\left( r \right),\,\,\,\,{{E}_{{{\text{eff}}}}} = {{E + {{E}^{2}}} \mathord{\left/ {\vphantom {{E + {{E}^{2}}} {2\gamma m{{c}^{2}},}}} \right. \kern-0em} {2\gamma m{{c}^{2}},}} \\ {{U}_{A}}\left( r \right) = - q{\mathbf{A}}{{{\mathbf{e}}}_{p}}\sqrt {1 - {{{{1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }}}^{2}}} + {{{{q}^{2}}{{А}^{2}}} \mathord{\left/ {\vphantom {{{{q}^{2}}{{А}^{2}}} {2\gamma m{{c}^{2}}}}} \right. \kern-0em} {2\gamma m{{c}^{2}}}}, \\ {{U}_{V}}\left( r \right) = V(r) - {{{{{(V(r))}}^{2}}} \mathord{\left/ {\vphantom {{{{{(V(r))}}^{2}}} {2\gamma m{{c}^{2}},}}} \right. \kern-0em} {2\gamma m{{c}^{2}},}} \\ \end{gathered} $Для плоского проводника в форме пластины шириной L и толщиной $2a \ll L,$ центральная плоскость которой расположена при x = 0, векторный потенциал электрического тока с плотностью ${\mathbf{j}} = {{{\mathbf{e}}}_{z}}j$ = ${{{{{\mathbf{e}}}_{z}}J} \mathord{\left/ {\vphantom {{{{{\mathbf{e}}}_{z}}J} {2aL}}} \right. \kern-0em} {2aL}}$ определяется выражением:
(5)
$\begin{gathered} {\mathbf{A}}(x) = {{{\mathbf{e}}}_{z}}A(x), \\ A = \left\{ \begin{gathered} {{ - \pi {{x}^{2}}j} \mathord{\left/ {\vphantom {{ - \pi {{x}^{2}}j} c}} \right. \kern-0em} c},\,\,\,\,\left| x \right| \leqslant a \hfill \\ - \left( {{{\pi {{a}^{2}}j} \mathord{\left/ {\vphantom {{\pi {{a}^{2}}j} c}} \right. \kern-0em} c}} \right)\left\{ {({{2\left| x \right|} \mathord{\left/ {\vphantom {{2\left| x \right|} a}} \right. \kern-0em} a}) - 1} \right\},\,\,\,\,\left| x \right| \geqslant a. \hfill \\ \end{gathered} \right. \\ \end{gathered} $(6)
$\begin{gathered} {{U}_{A}}\left( x \right) = - q({{{\mathbf{e}}}_{z}}{{{\mathbf{e}}}_{p}})A\sqrt {1 - {{{{1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0em} \gamma }}}^{2}}} + {{{{q}^{2}}{{А}^{2}}} \mathord{\left/ {\vphantom {{{{q}^{2}}{{А}^{2}}} {2\gamma m{{c}^{2}}}}} \right. \kern-0em} {2\gamma m{{c}^{2}}}} = \\ = \left\{ \begin{gathered} \frac{{\pi q{{x}^{2}}j\sqrt {{{\gamma }^{2}} - 1} }}{{c\gamma }} + {{\left( {\frac{{\pi q{{x}^{2}}j}}{c}} \right)}^{2}}\frac{1}{{2\gamma m{{c}^{2}}}},\,\,\,\,\left| x \right| \leqslant a; \hfill \\ \frac{{\pi q{{a}^{2}}j\left\{ {({{2\left| x \right|} \mathord{\left/ {\vphantom {{2\left| x \right|} a}} \right. \kern-0em} a}) - 1} \right\}\sqrt {{{\gamma }^{2}} - 1} }}{{c\gamma }} + {{\left( {\frac{{\pi q{{a}^{2}}j}}{c}\left[ {\frac{{2\left| x \right|}}{a} - 1} \right]} \right)}^{2}}\frac{1}{{2\gamma m{{c}^{2}}}},\,\,\,\,\left| x \right| \geqslant a. \hfill \\ \end{gathered} \right. \\ \end{gathered} $(7)
$j < \frac{{2m{{c}^{2}}\sqrt {{{\gamma }^{2}} - 1} }}{{\pi q{{a}^{2}}\left\{ {({{2\left| x \right|} \mathord{\left/ {\vphantom {{2\left| x \right|} a}} \right. \kern-0em} a}) - 1} \right\}}}$В типичной ситуации усредненная потенциальная энергия заряженной частицы с $q = e$ в пределах кристаллографической плоскости, где находятся все ядра и только небольшая часть атомных электронов, соответствует потенциальному барьеру высотой ${{V}_{0}}$ в случае положительно заряженных частиц (в частности, позитронов и протонов), движущихся под малым углом около этих плоскостей. Возрастающая потенциальная энергия UA(х) (6) при $\left| x \right| \geqslant a,$ формируемая векторным потенциалом тока, приводит к появлению потенциальной ямы, расположенной за пределами кристалла (около его поверхности).
Следует отметить, что в легких кристаллах некоторых типов с ионной связью имеет место инверсия структуры потенциала, и некоторые кристаллические плоскости представляют потенциальный барьер для каналируемых электронов и, соответственно, яму для протонов и позитронов. Такая ситуация имеет место, например, в кристалле LiH, в котором плоскости $(1\bar {1}1)$ и (111) из-за перехода электрона от атома лития к атому водорода при образовании ионной связи имеют суммарный отрицательный заряд и, соответственно, представляют потенциальный барьер для электронов [5, 6]. При использовании таких кристаллов эффект околоповерхностного каналирования будет реализовываться для отрицательно заряженных частиц с $q = - e$ при том же условии $q({{{\mathbf{e}}}_{z}}{{{\mathbf{e}}}_{p}}) > 0,$ что и в случае движения частиц против направления электрического тока.
Наличие отмеченных выше особенностей позволяет реализовать систему околоповерхностного (за пределами кристалла) каналирования заряженных частиц в потенциальной яме, примыкающей к внешней поверхности кристалла. Структура этой ямы близка к несимметричному треугольнику, а ее эффективная ширина, определяемая из условия равенства максимальной потенциальной энергии на обеих стенках ямы, определяется формулой:
(8)
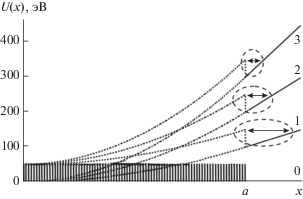
$\Delta x \approx \frac{{c{{V}_{0}}}}{{2\pi \left| q \right|aj\sqrt {{{1 - 1} \mathord{\left/ {\vphantom {{1 - 1} {{{\gamma }^{2}}}}} \right. \kern-0em} {{{\gamma }^{2}}}}} }},$Общая структура потенциальной энергии релятивистских позитронов в объеме и около поверхности проводящих кристаллов типа Ge толщиной 2a = 2 см при типичной высоте V0 ≈ 50 эВ усредненного потенциала плоскости и разной плотности тока (j = 1, 2, 3 А/cм2) представлена на рис. 1. Структура приповерхностной потенциальной ямы выделена замкнутой штриховой линией. Видно, что эта несимметричная яма по своей структуре схожа с треугольной ямой с вертикальной внутренней стенкой, близкой к прямолинейной внешней стенке. Можно отметить, что, хотя типичные потенциальные ямы для внутриобъемного каналирования в кристаллах (как плоскостного, так и аксиального, в том числе каналирования внутри нанотрубок) имеют, как правило, симметричный вид, нет никаких ограничений на каналирование частиц в такой приповерхностной несимметричной яме.
Рис. 1.
Зависимость потенциальной энергии U(x) положительно заряженной частицы в объеме и около поверхности (при x > a) проводящего кристалла толщиной 2a = 2 см при протекании тока с плотностью j = 0, 1, 2 и 3 А/cм2 (значения указаны возле каждой кривой). Расчеты проведены при использовании типичного усредненного потенциала кристаллической плоскости V0 = 50 эВ. Стрелками показана ширина приповерхностной потенциальной ямы.
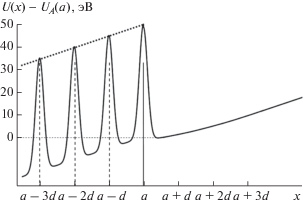
На рис. 2 представлена более детальная структура внутренней “стенки” этой потенциальной ямы, примыкающей к плоскости на поверхности кристалла. Видно, что при возрастании плотности тока увеличивается суммарная потенциальная энергия частицы и формируется изменяющаяся по ширине потенциальная яма в области пространства за крайней плоскостью кристалла. Из результатов расчета следует, что в указанном интервале параметров электрического тока ширина околоповерхностной потенциальной ямы соответствует нескольким миллиметрам и уменьшается в соответствии с формулой (8) при возрастании плотности тока. Эта закономерность сохраняется и при использовании более высокой плотности тока – при увеличении плотности тока до j = 103 А/см2 ширина ямы уменьшается до Δх ≈ ≈ 2.7 мкм. Общая потенциальная энергия заряженной частицы (в частности, энергия, которая соответствует дну потенциальной ямы) резко возрастает от нескольких сотен эВ до десятков и сотен кэВ. Для медленных частиц (в частности, протонов) ширина плоскостной потенциальной ямы при тех же параметрах кристалла и тока возрастает пропорционально величине ${{({{1 - 1} \mathord{\left/ {\vphantom {{1 - 1} {{{\gamma }^{2}}}}} \right. \kern-0em} {{{\gamma }^{2}}}})}^{{ - 1}}}.$
Рис. 2.
Структура потенциальной энергии частицы около плоской поверхности проводящего кристалла с током или кристалла, расположенного около поверхности плоского проводника.
Легко убедиться, что учет спина движущихся частиц не влияет на характер рассматриваемого режима околоповерхностного каналирования. Это следует из простых оценок. При протекании тока через рассматриваемый проводящий кристалл (или через плоский проводник, находящийся непосредственно возле диэлектрического кристалла шириной L и толщиной 2a $ \ll $ L) около его поверхности формируется магнитное поле. Его напряженность при условии 2a $ \ll $ L вычисляется с помощью интегральной теоремы Гаусса и равна величине
При изменении плотности тока в интервале j = 1–1000 А/см2 напряженность магнитного поля изменяется в интервале 0.6–600 Э. Энергия взаимодействия спинового магнитного момента позитрона с таким полем очень мала:(10)
${{W}_{{\mu H}}} = - ({\mathbf{\mu H}}) \approx {{10}^{{ - 10}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 6}}}\,\,{\text{эВ}}$Аналогичным образом можно рассмотреть особенности околоповерхностного каналирования заряженных частиц возле цилиндрического проводника с током. В случае однородного проводника в форме цилиндра с радиусом R векторный потенциал электрического тока J описывается выражением:
(11)
${\mathbf{A}} = {{{\mathbf{e}}}_{z}}A = \left\{ \begin{gathered} {{ - {{{\mathbf{e}}}_{z}}J{{r}^{2}}} \mathord{\left/ {\vphantom {{ - {{{\mathbf{e}}}_{z}}J{{r}^{2}}} {c{{R}^{2}}}}} \right. \kern-0em} {c{{R}^{2}}}},\,\,\,\,r \leqslant R \hfill \\ - {{{\mathbf{e}}}_{z}}\left( {{J \mathord{\left/ {\vphantom {J c}} \right. \kern-0em} c}} \right)\left\{ {1 + \ln ({{{{r}^{2}}} \mathord{\left/ {\vphantom {{{{r}^{2}}} {{{R}^{2}}}}} \right. \kern-0em} {{{R}^{2}}}})} \right\},\,\,\,\,r \geqslant R. \hfill \\ \end{gathered} \right.$(12)
${{U}_{A}}\left( r \right) = \left\{ \begin{gathered} ({{{\mathbf{e}}}_{z}}{{{\mathbf{e}}}_{p}})\frac{{qJ{{{({r \mathord{\left/ {\vphantom {r R}} \right. \kern-0em} R})}}^{2}}\sqrt {{{\gamma }^{2}} - 1} }}{{\gamma c}} + \frac{{{{q}^{2}}{{J}^{2}}{{{({r \mathord{\left/ {\vphantom {r R}} \right. \kern-0em} R})}}^{4}}}}{{2\gamma m{{с}^{4}}}},\,\,\,\,r \leqslant R; \hfill \\ ({{{\mathbf{e}}}_{z}}{{{\mathbf{e}}}_{p}})\frac{{qJ\sqrt {{{\gamma }^{2}} - 1} }}{{\gamma c}}\left\{ {1 + 2\ln \frac{r}{R}} \right\} + \frac{{{{q}^{2}}{{J}^{2}}}}{{2\gamma m{{с}^{4}}}}{{\left\{ {1 + 2\ln \frac{r}{R}} \right\}}^{2}},\,\,\,\,r \geqslant R. \hfill \\ \end{gathered} \right.$На рис. 3 и 4 представлены результаты расчета структуры потенциальной энергии релятивистских позитронов (рис. 3) и нерелятивистских протонов (рис. 4), движущихся около поверхности цилиндрических проводников с током. Видно, что при выполнении необходимого условия (ezep)q > 0 за пределами проводника с током существует возрастающий потенциальный барьер (внешняя “стенка” потенциальной ямы). Из данных, представленных на рис. 3, следует, что высота потенциального барьера для каналируемых электронов и позитронов очень резко возрастает с увеличением тока в проводнике, достигая 300–400 кэВ при протекании тока несколько килоампер. Также видно, что глубина потенциальной ямы существенно возрастает при увеличении продольной скорости частиц. Это наглядно видно из данных, представленных на рис. 4. Высота потенциального барьера, формируемого векторным потенциалом тока, для движущихся протонов оказывается во много раз меньше, чем для легких и более быстрых частиц.
Рис. 3.
Изменение структуры аксиального отражающего барьера, формируемого током J в цилиндрическом проводнике с радиусом R для движущихся около проводника электронов и позитронов с энергией 100 кэВ (a, в) и 100 МэВ (б, г). Величина тока J = 1, 2, 3, 1000, 2000, 3000 А указана около соответствующей кривой.
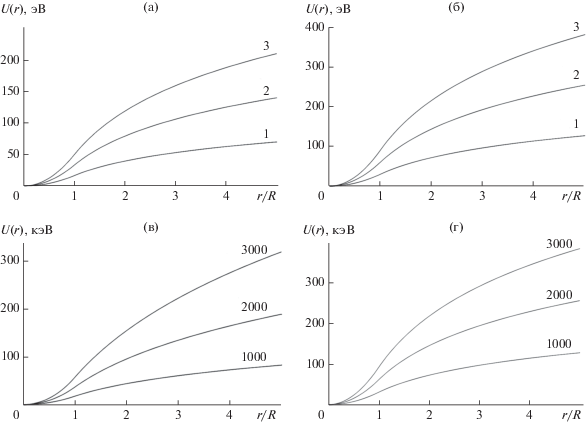
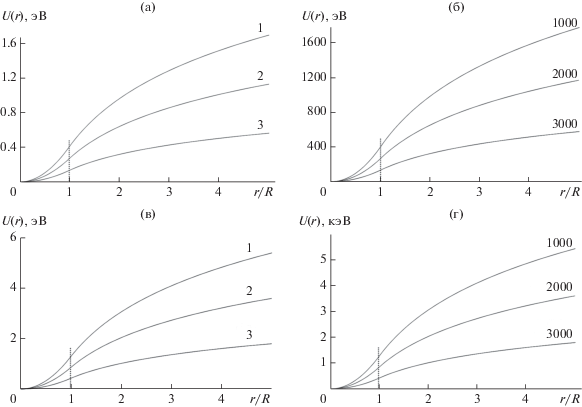
Рис. 4.
Изменение характеристик аксиального отражающего барьера, формируемого током J в цилиндрическом проводнике с радиусом R для протонов с энергией 10 кэВ (a, б) и 100 кэВ (в, г), движущихся вдоль проводника. Величина тока J = 1, 2, 3, 1000, 2000, 3000 А указана около соответствующей кривой.
Следует отметить, что эффективная внутренняя “стенка” аксиальной потенциальной ямы может быть реализована как при использовании проводников с полированной поверхностью, так и за счет специфики аксиального движения частиц обоих знаков (но, естественно, при их движении в противоположных направлениях) и без требования существования реального потенциального барьера на поверхности проводника. Этот эффект, как и в случае любого аксиального движения, обусловлен большой центробежной энергией
(13)
$T(r) = {{{{L}^{2}}} \mathord{\left/ {\vphantom {{{{L}^{2}}} {2\gamma m{{r}^{2}}}}} \right. \kern-0em} {2\gamma m{{r}^{2}}}} = {{{{\hbar }^{2}}l(l + 1)} \mathord{\left/ {\vphantom {{{{\hbar }^{2}}l(l + 1)} {2\gamma m{{r}^{2}}}}} \right. \kern-0em} {2\gamma m{{r}^{2}}}},$Такая система качественно похожа на режим аксиального каналирования в объеме пустотелых углеродных нанотрубок, но имеет то несомненное преимущество, что роль отражающей поверхности такой нанотрубки выполняет поле векторного потенциала постоянного тока, протекающего по тонкому цилиндрическому проводнику.
ЗАКЛЮЧЕНИЕ
Рассмотренные особенности формирования одномерной или двумерной аксиальной потенциальной ямы около поверхности проводника с током позволяют прогнозировать возможность эффективного и бездиссипативного каналирования быстрых и медленных заряженных частиц около поверхности (вне объема) как ориентированных токопроводящих кристаллов, так и “обычных” цилиндрических проводников.
Параметры потенциальных ям (их глубина и ширина) существенно зависят от энергии продольного движения частиц и от величины тока, протекающего по этим проводникам. При относительно слабом токе несколько ампер (для цилиндрического проводника) и при плотности тока 1–3 А/см2 (для плоского проводника) глубина потенциальной ямы сопоставима с глубиной аналогичной ямы кристаллической плоскости при “стандартном” каналировании или значительно превышает ее. При возрастании тока высота удаленного от проводника потенциального барьера (одна из “стенок” потенциальной ямы) быстро возрастает и при токе несколько килоампер может достигать для релятивистских частиц несколько сотен кэВ.
Ширина ямы зависит от сечения и формы проводника, а также от величины и плотности тока и энергии частицы. При увеличении силы тока яма сужается и ее центр приближается к поверхности проводника. Основное преимущество такого “внеобъемного” каналирования связано с очень существенным ослаблением процессов рассеяния и торможения частиц, а в случае аксиального каналирования частиц любого знака – с практически полным устранением этих диссипативных процессов. Наличие такой потенциальной ямы, “привязанной” к поверхности проводника, но отделенной от нее, позволяет реализовать простой и принципиально новый механизм управляемой транспортировки частиц вдоль проводников с током на большое расстояние, не требующий громоздких и сложных систем фокусирующих магнитов и других методов управления пучками частиц. Большая высота внешней “стенки” потенциальной ямы, создаваемой векторным потенциалом тока, позволяет эффективно удерживать пучок в режиме управляемого каналирования при изгибах и поворотах проводника. При периодической модуляции тока в проводящем кристалле в такой системе возможна реализация ондулятора [6] с переменными параметрами, в системе которого возможна реализация источников квазикогерентного спонтанного и вынужденного рентгеновского излучения с использованием пучков релятивистских электронов.
Кроме того, в такой периодически модулированной системе возможно формирование когерентных коррелированных состояний пучка медленных протонов [7–17], что ведет к синхронизации и резкому возрастанию флуктуаций их поперечной энергии в радиальном направлении. Амплитуда этих флуктуаций может намного превышать энергию их поступательного движения [10–16].
Еще одна особенность каналирования в поле тока около проводящих кристаллов связана с большой эффективностью удержания частиц при изгибе поверхности кристалла. Такую задачу в случае внутрикристаллического каналирования рассматривали во многих работах (например, в обзоре особенностей каналирования быстрых частиц в изогнутых кристаллах [18]), и соответствующую методику расчета можно использовать для данной задачи.
При локальном изгибе радиусом $R$ одной из стенок потенциальной ямы (поверхности проводящего кристалла) и, соответственно, аналогичном изгибе другой (полевой) стенки уравнение движения быстрой частицы в локальной системе с координатой $x{\kern 1pt} ',$ перпендикулярной поверхности стенки, и координатой z вдоль этой стенки, имеет вид [18]:
(14)
$p{v}\frac{{{{d}^{2}}x{\kern 1pt} '}}{{d{{z}^{2}}}} + \frac{d}{{dx{\kern 1pt} '}}(U(x{\kern 1pt} ') + {{x{\kern 1pt} '{\kern 1pt} p{v}} \mathord{\left/ {\vphantom {{x{\kern 1pt} '{\kern 1pt} p{v}} R}} \right. \kern-0em} R}) = 0.$(15)
${{R}_{{\min }}} = {{p{v}} \mathord{\left/ {\vphantom {{p{v}} {\left| {\frac{{dU(x{\kern 1pt} ')}}{{dx{\kern 1pt} '}}} \right|}}} \right. \kern-0em} {\left| {\frac{{dU(x{\kern 1pt} ')}}{{dx{\kern 1pt} '}}} \right|}} = {{\sqrt {{{\gamma }^{2}} - 1} {\kern 1pt} {\kern 1pt} m{v}c} \mathord{\left/ {\vphantom {{\sqrt {{{\gamma }^{2}} - 1} {\kern 1pt} {\kern 1pt} m{v}c} {\left| {\frac{{dU(x{\kern 1pt} ')}}{{dx{\kern 1pt} '}}} \right|}}} \right. \kern-0em} {\left| {\frac{{dU(x{\kern 1pt} ')}}{{dx{\kern 1pt} '}}} \right|}}.$При изгибе поверхности кристалла в направлении, противоположном внешней (полевой) стенке, величина U(x') соответствует потенциальной энергии этой внешней стенки, которая характеризуется градиентом $\left| {\frac{{dU(x{\kern 1pt} ')}}{{dx{\kern 1pt} '}}} \right| \approx {{{{V}_{0}}} \mathord{\left/ {\vphantom {{{{V}_{0}}} {x{\kern 1pt} '}}} \right. \kern-0em} {x{\kern 1pt} '}}.$ Как следует из формулы (8), ширина приповерхностной потенциальной ямы для быстрых позитронов при плотности тока j = 100 А/cм2 и толщине кристалла 2a = 2 см равна Δx ≈ x' ≈ 2.7 × 10–3 см. В этом случае минимальный радиус изгиба поверхности кристалла, при котором быстрые позитроны удерживаются в режиме каналирования, соответствует величине ${{R}_{{\min }}} \approx 30\sqrt {{{\gamma }^{2}} - 1} $ см. При увеличении плотности тока и толщины кристалла величина Rmin уменьшается пропорционально 1/a j, а при увеличении массы частиц (в случае протонов) возрастает пропорционально их массе. Комбинация этих параметров позволяет реализовать режим устойчивого каналирования при достаточно малом радиусе изгиба. Аналогичные соотношения для Rmin могут быть получены при изгибе цилиндрического проводника с током.
Рассмотренный метод управляемой транспортировки пучков на большое расстояние технологически реализовать намного проще, чем, например, использование для такой же цели коротких углеродных нанотрубок [19–21]. Другие потенциально возможные методы использования “приповерхностного” каналирования (включая задачи, обсуждаемые в [22]) будут рассмотрены позже.
Список литературы
Линдхард Й. // УФН. 1960. Т. 99. Вып. 2. С. 249.
Gemmel D.S. // Rev. Mod. Phys. 1974. V. 46. № 1. P. 129.
Оцуки Е.Х. Взаимодействие заряженных частиц с твердыми телами. М.: Мир, 1985. 280 с.
Барышевский В.Г. Каналирование, излучение и реакции в кристаллах при высоких энергиях. Минск: Изд-во БГУ, 1982. 253 с.
Бирюков В.М., Котов В.И., Чесноков Ю.А. // УФН. 1994. Т. 164. Вып. 10. С. 1017.
Смоляков Н.В. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2017. № 12. С. 76.
Schrödinger E. // Ber. Kgl. Akad. Wiss. 1930. V. 24. P. 296.
Robertson H.P. // Phys. Rev. A. 1930. V. 35. P. 667.
Додонов В.В., Манько В.И. // Тр. ФИАН. 1987. Т. 183. С. 71.
Додонов В.В., Климов А.В., Манько В.И. // Тр. ФИАН. 1991. Т. 200. С. 56.
Vysotskii V.I., Vysotskyy M.V. // Eur. Phys. J. A. 2013. V. 49. Iss. 8. P. 99.
Vysotskii V.I., Adamenko S.V., Vysotskyy M.V. // Ann. Nucl. En. 2013. V. 62. P. 618.
Высоцкий В.И., Высоцкий М.В. // ЖЭТФ. 2014. Т. 118. Вып. 4. С. 534.
Высоцкий В.И., Высоцкий М.В. // ЖЭТФ. 2015. Т. 120. Вып. 2. С. 246.
Высоцкий В.И., Высоцкий М.В., Bartalucсi S. // ЖЭТФ. 2018. Т. 154. С. 560.
Высоцкий В.И., Высоцкий М.В. // ЖЭТФ. 2019. Т. 155. Вып. 6. С. 1009.
Bartalucci S., Vysotskii V.I., Vysotsky M.V. // Phys. Rev. Accel. Beams. 2019. V. 22. № 5. P. 054503.
Бирюков В.М., Котов В.И., Чесноков Ю.А. // УФН. 1994. Т. 164. Вып. 10. С. 1017.
Геворкян Л.Г., Испирян К.А., Испирян Р.К. // Письма в ЖЭТФ. 1997. Т. 66. С. 304.
Miskovic Z.L. // Rad. Eff. Def. Solids. 2007. V. 162. № 3–4. P. 185.
Матюхин С.И., Фроленков К.Ю. // Письма в ЖТФ. 2007. Т. 33. Вып. 2. С. 23.
Высоцкий В.И., Высоцкий М.В., Корнилова А.А. // ЖЭТФ. 2020. Т. 158. Вып. 4. С. 645.
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования


