Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2022, № 1, стр. 107-112
Механизм деформационного старения материалов с высокими барьерами Пайерлса: ОЦК-металлы, полупроводники и другие
Б. В. Петухов *
Институт кристаллографии им. А.В. Шубникова ФНИЦ “Кристаллография и фотоника” РАН
119333 Москва, Россия
* E-mail: petukhov@ns.crys.ras.ru
Поступила в редакцию 25.05.2021
После доработки 11.06.2021
Принята к публикации 25.06.2021
- EDN: XYQMRT
- DOI: 10.31857/S1028096022010149
Аннотация
Развивается модель динамического взаимодействия дислокаций с примесной подсистемой кристаллов с высоким потенциальным рельефом кристаллической решетки (барьерами Пайерлса). К числу таких материалов относятся металлы с объемно центрированной кубической структурой, полупроводники, керамики и многие другие. Показано, что модификация примесных миграционных барьеров вблизи дислокационного ядра существенно влияет на сегрегацию примесей на движущейся дислокации. Получено аналитическое описание начальной стадии кинетики сегрегации, приводящей к аномалиям дислокационной динамики и предела текучести материалов. Построенная теория динамического взаимодействия дислокаций с примесной подсистемой кристалла учитывает обратное влияние примесей, увлекаемых движущимися дислокациями, на динамику самих дислокаций. Следствиями самосогласованного характера процесса являются: возникновение неустойчивости движения дислокаций в определенном интервале скоростей и иммобилизация дислокаций при напряжениях, значения которых ниже некоторого порога.
ВВЕДЕНИЕ
Влияние примесей на динамику дислокаций существенно модифицирует механические свойства кристаллических материалов и является предметом всестороннего изучения (как экспериментального, так и теоретического) [1–4]. При определенных условиях примеси диффундируют к дислокациям и осаждаются на них, приводя к так называемому “старению”. При сравнимых подвижностях дислокаций и примесей нередко возникает нестабильность пластического течения, проявляющаяся в виде скачков на деформационных кривых (эффект Портевена–Ле Шателье [5–7]).
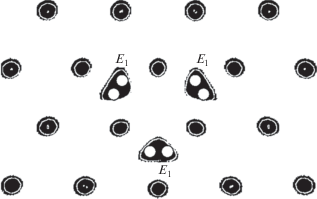
К настоящему времени динамическое взаимодействие примесей с дислокациями хорошо изучено для материалов с ГЦК-структурой кристаллической решетки [8–13], в которых собственный потенциальный рельеф кристаллической решетки (барьеры Пайерлса) низок в сравнении с локальными чужеродными включениями (стопорами). Значительно менее изучена ситуация для кристаллов с ОЦК-структурой, полупроводников, керамик и других материалов, в которых движение дислокаций контролируется высокими барьерами Пайерлса. Закономерности динамического старения дислокаций, зависящие от механизма их движения, различны для двух указанных типов материалов [14]. Нередко считается, что в ОЦК-металлах, в которых пластическая деформация осуществляется винтовыми дислокациями, их взаимодействием с примесями можно пренебречь. Основанием этому служит то обстоятельство, что винтовые дислокации не создают дальнодействующего поля гидростатического давления, взаимодействующего с центрами дилатации. Однако при этом не учитываются многие другие типы взаимодействий, имеющие место на межатомной шкале в дислокационных ядрах, например, химической природы. Атомистические расчеты выявляют наличие достаточно большой энергии связи примесей с винтовыми дислокациями. Так, например, в работе [15] методом функционала плотности рассчитывалось взаимодействие примесей водорода с винтовой дислокацией в W в различных позициях, и для наиболее благоприятной позиции получена довольно значительная энергия связи, равная 256 ± 32 МэВ. Шесть таких эквивалентных позиций, обозначаемых E1, изображены на рис. 1.
Рис. 1.
Расположение узлов E1 с максимальной энергией связи примесных атомов с винтовой дислокацией в α-Fe.
Ключевым вопросом теории динамического деформационного старения материалов является кинетика сегрегации примесей на дислокационных линиях. Однако этот вопрос в имеющихся работах освещается недостаточно последовательно и нередко кинетический закон просто постулируется [13]. Для лучшего понимания явления было бы полезно не постулировать, а вывести кинетический закон из лежащих в основе физических механизмов, хотя бы в рамках упрощенной модели. Развитие соответствующей теории и является целью настоящей работы.
МОДЕЛЬ КОРОТКОДЕЙСТВУЮЩИХ ПРИМЕСЕЙ
В изучаемом здесь случае достаточно быстрого движения дислокации оказываются существенными малые масштабы (порядка одного или двух ближайших к ядру) периодов кристаллической решетки. Скачкообразное изменение положения дислокации приводит к перераспределению примесной атмосферы на каждом шаге, кинетика которого зависит от устройства потенциального рельефа, для миграции примесей в окрестности дислокационного ядра. Схематически простейший одномерный вид такого рельефа изображен на рис. 2. Под рассматриваемыми состояниями примесного содержания в ядре и вокруг ядра, как это для наглядности иллюстрируется на рис. 1 тремя состояниями, в действительности могут пониматься любые совокупности эквивалентных ячеек, заполняемые примесями, как, например, на рис. 1.
Рис. 2.
Схема миграционного рельефа примесей вблизи ядра дислокации. Выделены состояния непосредственно в ядре (d), соседние предыдущее (–) и последующее (+) с указанием времен переходов примесей между этими состояниями и объемом кристалла.
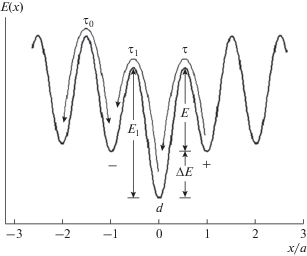
Вдали от дислокации миграционный рельеф периодичен, и время τ0 смещения примеси на период решетки имеет невозмущенное значение. В окрестности ядра потенциальный рельеф искажен взаимодействием, так что имеется глубокий минимум, отвечающий наиболее энергетически выгодному расположению примеси относительно дислокации, отмеченный на рис. 2 буквой d. Притяжение к этому положению понижает барьер E для перехода примеси в него и уменьшает время соответствующего термоактивируемого скачка τ = ${{\tau }_{*}}$ exp(E/kT) (${{\tau }_{*}}$ – предэкспоненциальный фактор, считающийся постоянным) по сравнению со временем обратного перехода τ1 или временем миграции вдали от ядра τ0, так что τ $ \ll $ τ0, τ1. Существование пониженного барьера E для перехода примесей в ядро дислокации по сравнению с барьерами переходов E0 в объеме кристалла приводит к необходимости выделения процессов перераспределения примесей вокруг ядра в особый класс и требует отдельного рассмотрения, как это отмечалось в [16]. Похожий подход применялся в работе [17], в которой принималось во внимание только перераспределение примесных атомов водорода между ближайшими междоузлиями при перемещении дислокации в α-Fe.
Так как считается, что дислокации движутся с достаточно большой скоростью V, время ta = a/V, проводимое в одной долине кристаллического рельефа, в рассматриваемой упрощенной модели предполагается недостаточным для включения в игру примесей из более удаленных узлов кристаллической решетки. Здесь a – период решетки, V – средняя скорость дислокации. Изучим эволюцию примесного содержания в ядре дислокации, характеризуемого концентрацией cd в расчете на один период решетки вдоль дислокационной линии. Введем также обозначение c для концентрации примесей в примыкающих состояниях и c0 для средней концентрация примесей в объеме кристалла. Особый интерес для дальнейшего рассмотрения представляет поведение на начальной стадии, для которого приведем аналитическое описание.
Запишем уравнение для перераспределения примесных концентраций в течение времени ta, когда дислокация покоится в одной из долин кристаллического рельефа в ожидании скачка в следующую долину:
(1)
$\frac{{d{{c}_{d}}}}{{dt}} = {{c({\text{1}} - {{c}_{d}})} \mathord{\left/ {\vphantom {{c({\text{1}} - {{c}_{d}})} {\tau .}}} \right. \kern-0em} {\tau .}}$(2)
${{c}_{d}}(t)\, = \,\frac{{({{c}_{{d0}}} + {{c}_{{c0}}}){\kern 1pt} (1 - {{c}_{0}}){\kern 1pt} \exp [(1 - {{c}_{{d{\text{0}}}}} - {{c}_{{c0}}}){t \mathord{\left/ {\vphantom {t \tau }} \right. \kern-0em} \tau }] - {{c}_{{c0}}}}}{{(1 - {{c}_{0}}){\kern 1pt} \exp [(1 - {{c}_{{d{\text{0}}}}} - {{c}_{{c0}}}){t \mathord{\left/ {\vphantom {t \tau }} \right. \kern-0em} \tau }] - {{c}_{{c0}}}}}{\kern 1pt} .$УВЛЕЧЕНИЕ ПРИМЕСЕЙ ПРИ СТАЦИОНАРНОМ ДВИЖЕНИИ ДИСЛОКАЦИИ
При скачке дислокации через барьер она попадает в новое состояние с невозмущенной концентрацией c0, а набранные ею примеси cd(ta) сбрасываются. Примеси, оставленные в покинутой дислокацией долине кристаллического рельефа, стремятся релаксировать к новому положению дислокации. При этом величины примесного содержания, достигнутые на предыдущем шаге к моменту скачка дислокации ta, будут играть роль начальных условий для релаксации концентраций на новом этапе $c_{{c0}}^{{(2)}}$ = $c_{d}^{{(1)}}({{t}_{a}}),$ согласно уравнению (2).
Эволюция кинетических зависимостей cd(t) для нескольких последовательных шагов, начиная от “свежей” дислокации, проиллюстрирована на рис. 3. Устанавливающееся при большом количестве переходов дислокации амплитудное значение примесного содержания в ядре $c_{{da}}^{{\text{s}}}$ может быть найдено из уравнения (2) при t = ta и сравнивающихся последовательных значениях cd(ta),
(3)
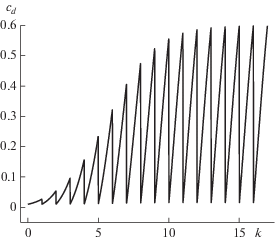
$c_{{da}}^{{\text{s}}} = \frac{{(c_{{da}}^{{\text{s}}} + {{c}_{0}})(1 - {{c}_{0}})\exp \left[ {{{(1 - c_{{da}}^{{\text{s}}} - {{c}_{0}}){{t}_{a}}} \mathord{\left/ {\vphantom {{(1 - c_{{da}}^{{\text{s}}} - {{c}_{0}}){{t}_{a}}} \tau }} \right. \kern-0em} \tau }} \right] - c_{{da}}^{{\text{s}}}}}{{(1 - {{c}_{0}})\exp \left[ {{{(1 - c_{{da}}^{{\text{s}}} - {{c}_{0}}){{t}_{a}}} \mathord{\left/ {\vphantom {{(1 - c_{{da}}^{{\text{s}}} - {{c}_{0}}){{t}_{a}}} \tau }} \right. \kern-0em} \tau }} \right] - c_{{da}}^{{\text{s}}}}}.$Рис. 3.
Эволюция содержания примесей в дислокационном ядре для серии 16 переходов на период решетки первоначально “свежей” дислокации при c0 = 0.01.
Выражение (3) позволяет рассчитывать зависимость примесного содержания на дислокации от скорости ее движения V, температуры T и других параметров. Возможен также другой вариант кинетики дислокационного старения, а именно, при заданной движущей дислокацию силе (или, эквивалентно, напряжении). В этом случае следует выразить скорость движения дислокации через барьеры в зависимости от движущей силы, например, с помощью термоактивационного закона V = V0 exp{–[Ed0 – γσeff]/kT]}, где Ed0 – энергия активации движения дислокации в отсутствие нагрузки, γ – активационный объем, σeff – эффективное напряжение. В случае, когда среднее расстояние между примесями a/cd меньше величины порядка размера кинка dk ~ a(G/σP)1/2 [18, 19] (G – модуль сдвига, σP – напряжение Пайерлса), можно использовать усредненное описание взаимодействия между примесями и дислокациями и характеризовать его некоторым тормозящим напряжением σi, пропорциональным избыточной примесной концентрации: σi = β(cd – c0). При этом входящее в энергию активации эффективное напряжение имеет вид: σef= σ – β(cd – c0), где σ – внешнее прикладываемое напряжение.
Так как σeff зависит от времени, следует вычислять среднюю скорость от 0 до ta:
(4)
$\begin{gathered} {{V}_{{{\text{av}}}}} = \frac{1}{{{{t}_{a}}}}{{V}_{0}}\int\limits_0^{{{t}_{a}}} {dt\exp \left\{ { - \frac{{{{E}_{0}} - \gamma [\sigma - \beta {{c}_{d}}(t) + \beta {{c}_{0}}]}}{{kT}}} \right\}} = \\ = {{V}_{0}}{\text{exp}}\left\{ { - \frac{{{{E}_{0}} - \gamma (\sigma + \beta {{c}_{0}})}}{{kT}}} \right\}\frac{\tau }{{{{t}_{a}}}}J(c_{{da}}^{{\text{s}}}), \\ \end{gathered} $Уравнение, связывающее $c_{{da}}^{{\text{s}}}$ с напряжением и температурой, следующее из соотношения (4), есть exp{–(Ed0 – γσ)/kT} = a/(V0τ) или
(5)
$({\gamma \mathord{\left/ {\vphantom {\gamma {{{E}_{{d0}}}}}} \right. \kern-0em} {{{E}_{{d0}}}}}){\kern 1pt} \sigma \, = \,1 - {E \mathord{\left/ {\vphantom {E {{{E}_{{d0}}}}}} \right. \kern-0em} {{{E}_{{d0}}}}} - \left( {{{kT} \mathord{\left/ {\vphantom {{kT} {{{E}_{{d0}}}}}} \right. \kern-0em} {{{E}_{{d0}}}}}} \right){\text{ln}}[J(c_{{da}}^{{\text{s}}}){{{{V}_{0}}{{\tau }_{*}}} \mathord{\left/ {\vphantom {{{{V}_{0}}{{\tau }_{*}}} a}} \right. \kern-0em} a}].$(6)
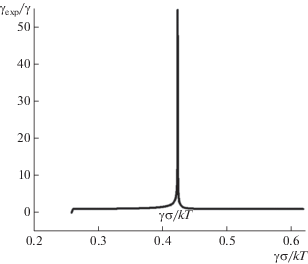
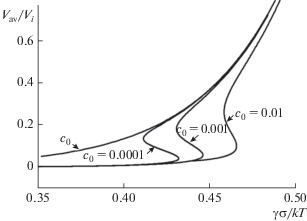
${{V}_{{{\text{av}}}}} = \frac{a}{\tau }\frac{{1 - c_{{da}}^{{\text{s}}} - {{c}_{0}}}}{{\ln \left\{ {{{\left( {1 - c_{{da}}^{{\text{s}}}} \right)c_{{da}}^{{\text{s}}}} \mathord{\left/ {\vphantom {{\left( {1 - c_{{da}}^{{\text{s}}}} \right)c_{{da}}^{{\text{s}}}} {[(1 - {{c}_{0}}){{c}_{0}}]}}} \right. \kern-0em} {[(1 - {{c}_{0}}){{c}_{0}}]}}} \right\}}}.$Рис. 4.
Зависимость скорости дислокаций, нормированной на Vi = a/τ, от напряжения для трех значений средней концентрации примесей. Значения параметров: E/E0 = 0.5, γβ/kT = 3, ai = Vd0${a \mathord{\left/ {\vphantom {a {{{\tau }_{*}}}}} \right. \kern-0em} {{{\tau }_{*}}}}$ = 1.
С помощью уравнений (5), (6) можно находить и другие представляющие интерес величины, например, так называемую “скоростную чувствительность” dσ/dV :
(7)
$\begin{gathered} \frac{{d\sigma }}{{dV}} = - \frac{{kT}}{\gamma }\frac{{dJ}}{{dc_{{da}}^{{\text{s}}}}}\frac{{dc_{{da}}^{{\text{s}}}}}{{dV}} = \\ = {{ - \frac{{kT}}{\gamma }\frac{{dJ}}{{dc_{{da}}^{{\text{s}}}}}} \mathord{\left/ {\vphantom {{ - \frac{{kT}}{\gamma }\frac{{dJ}}{{dc_{{da}}^{{\text{s}}}}}} {\left\{ {\frac{{({{dJ} \mathord{\left/ {\vphantom {{dJ} {dc_{{da}}^{{\text{s}}}\left( {1 - c_{{da}}^{{\text{s}}}{{c}_{0}}} \right) - J}}} \right. \kern-0em} {dc_{{da}}^{{\text{s}}}\left( {1 - c_{{da}}^{{\text{s}}}{{c}_{0}}} \right) - J}}}}{{\ln \left\{ {(1 - c_{{da}}^{{\text{s}}})c_{{da}}^{{\text{s}}}[(1 - {{c}_{0}}){{c}_{0}}]} \right\}}}} \right.}}} \right. \kern-0em} {\left\{ {\frac{{({{dJ} \mathord{\left/ {\vphantom {{dJ} {dc_{{da}}^{{\text{s}}}\left( {1 - c_{{da}}^{{\text{s}}}{{c}_{0}}} \right) - J}}} \right. \kern-0em} {dc_{{da}}^{{\text{s}}}\left( {1 - c_{{da}}^{{\text{s}}}{{c}_{0}}} \right) - J}}}}{{\ln \left\{ {(1 - c_{{da}}^{{\text{s}}})c_{{da}}^{{\text{s}}}[(1 - {{c}_{0}}){{c}_{0}}]} \right\}}}} \right.}} - \\ \left. { - \,\,\frac{{J\left( {1 - c_{{da}}^{{\text{s}}}{{c}_{0}}} \right)\left( {{{1 - 2c_{{da}}^{{\text{s}}}} \mathord{\left/ {\vphantom {{1 - 2c_{{da}}^{{\text{s}}}} {\left[ {(1 - c_{{da}}^{{\text{s}}}c_{{da}}^{{\text{s}}})} \right]}}} \right. \kern-0em} {\left[ {(1 - c_{{da}}^{{\text{s}}}c_{{da}}^{{\text{s}}})} \right]}}} \right)}}{{{{{\ln }}^{2}}\left\{ {{{(1 - c_{{da}}^{{\text{s}}}){\kern 1pt} c_{{da}}^{{\text{s}}}} \mathord{\left/ {\vphantom {{(1 - c_{{da}}^{{\text{s}}}){\kern 1pt} c_{{da}}^{{\text{s}}}} {[(1 - {{c}_{0}}){{c}_{0}}]}}} \right. \kern-0em} {[(1 - {{c}_{0}}){{c}_{0}}]}}} \right\}}}} \right\}. \\ \end{gathered} $МАКРОПЛАСТИЧНОСТЬ
Будем находить скорость пластического течения $\dot {\varepsilon }$ с помощью закона Орована $\dot {\varepsilon }$ = ρbV, в котором плотность дислокаций ρ приближенно считается постоянной. Здесь b – величина вектора Бюргерса дислокации. Выражая скорость дислокации через $\dot {\varepsilon },$ находим зависимость напряжения от скорости деформации и “экспериментальный активационный объем”:
(8)
${{\gamma }_{{{\text{exp}}}}} = \frac{{kT}}{{{{d\sigma } \mathord{\left/ {\vphantom {{d\sigma } {d\ln \dot {\varepsilon }}}} \right. \kern-0em} {d\ln \dot {\varepsilon }}}}} = - \gamma \frac{J}{{{{dJ} \mathord{\left/ {\vphantom {{dJ} {dc_{{da}}^{{\text{s}}}}}} \right. \kern-0em} {dc_{{da}}^{{\text{s}}}}}{{dc_{{da}}^{{\text{s}}}} \mathord{\left/ {\vphantom {{dc_{{da}}^{{\text{s}}}} {d\ln V}}} \right. \kern-0em} {d\ln V}}}}.$ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Наличие примесей в ядре вследствие зацепления примесей за кристаллическую решетку тормозит движение дислокации, приводя к упрочнению материала. Специфика динамического старения дислокаций проявляется при достаточно быстром их движении и обусловлена показанным в настоящей работе наличием особой начальной стадии в кинетике перераспределения примесей вокруг дислокационного ядра. Предсказываемый рост содержания примесей обусловливает различного типа аномалии, которые неоднократно наблюдались в экспериментальных работах во многих материалах: в металлах с ОЦК-структурой Mo, V и др., в разупорядоченных твердых растворах полупроводников, при призматическом скольжении в металлах с ГПУ-структурой Ti, Zr, Be и интерметаллидах (обзор в [2, 3]). Достаточно большое увеличение содержания примесей в ядрах способно понизить подвижность дислокаций ниже наблюдаемого предела, приводя фактически к иммобилизации дислокаций [20] или к охрупчиванию материала [15, 17].
ЗАКЛЮЧЕНИЕ
Основными результатами исследования являются следующие:
1. Сформулирована модель динамического старения быстро движущихся дислокаций в примесных материалах с высоким кристаллическим рельефом, когда континуальное описание примесных атмосфер неприменимо.
2. Показано наличие стадии динамического старения дислокаций с образованием существенно неравновесного содержания примесей вблизи ядра дислокации.
3. Рассчитаны кинетические закономерности динамического старения дислокаций, обосновано отличающиеся от произвольно постулируемых в классической теории.
4. Показано, что существование стадии первоначального быстрого роста примесного содержания в дислокационном ядре является механизмом аномальной отрицательной скоростной чувствительности пластического течения материалов и наличия пиков в зависимости эффективного активационного объема от напряжения.
Список литературы
Фридель Ж. Дислокации. М.: Мир, 1967. 643 с.
Messerschmidt U. Dislocation Dynamics During Plastic Deformation. / Eds Hull R. et al. Berlin, Heidelberg: Springer Series in Material Science, 2010.
Caillard D., Martin J.L. Thermally Activated Mechanisms in Crystal Plastisity / Amsterdam etc: Pergamon, 2003.
Петухов Б.В. Динамика дислокаций в кристаллическом рельефе. Дислокационные кинки и пластичность кристаллических материалов. Saarbrücken: Lambert Academic Publishing, 2016. 385 p.
Portevin A., Le Chatelier F. // Trans. Am. Soc. St. Tr. 1924. V. 5. P. 457.
Лебедкин М.А. Самоорганизация и коллективные эффекты при неустойчивой пластической деформации кристаллов. Дис. д-ра физ.-мат. наук: Ин-т физики твердого тела РАН. Черноголовка, 2002. 248 с.
Rizzi E., Hähner P. // Int. J. Plasticity. 2004. V. 20. P. 121. https://doi.org/10.1016/S0749-6419(03)00035-4
McCormick PG. // Acta Metall. 1972. V. 20. № 3. P. 351. https://doi.org/10.1016/0001-6160(72)90028-4
Van den Beukel A. // Phys. Status Solidi. A. 1975. V. 30. № 1. P. 197. https://doi.org/10.1002/pssa.2210300120
Ananthakrishna G. // Physics Reports. 2007. V. 440. № 4–6. P. 113. https://doi.org/10.1016/j.physrep.2006.10.003
Sills R.B., Cai. W. // Phil. Mag. A. 2016. V. 96. № 10. P. 895. https://doi.org/10.1080/14786435.2016.1142677
William A. Curtin, David L. Olmsted, Louis G. Hector, Jr. // Nature Materials. 2006. V. 5. P. 875. https://doi.org/10.1038/nmat1765
Louat N. // Scr. Metall. 1981. V. 15. № 11. P. 1167. https://doi.org/10.1016/0036-9748(81)90290-8
Park S.C., Beckerman L.P., Reed-Hill R.E. // Metallurg. Trans. A. 1983. V. 14. P. 463. https://doi.org/10.1007/BF02644223
Itakura M., Kaburaki H., Yamaguchi M., Okita T. // Acta. Mater. 2013 V. 61. P. 6857. https://doi.org/10.1016/j.actamat.2013.07.064
Petukhov B.V. // J. Physics: Conference Series. 2010. V. 240. P. 012012. https://doi.org/10.1088/1742-6596/240/1/012012
Gong P., Katzarov I.H., Nutter J., Paxton A.T., Rainforth W.M. // Sci. Reps. 2020. V. 10. Art. 10209. https://doi.org/10.1038/s41598-020-66965-z
Петухов Б.В. // Физ. мет. и металловед. 1983. Т. 56. № 6. С. 1177.
Petukhov B.V. // Mater. Sci. Eng. A. 1997. V. 234–236. P. 177. https://doi.org/10.1016/S0921-5093(97)00188-3
Bondarenko I.E., Eremenko V.G., Nikitenko V.I., Yakimov E.B. // Phys. Status Solidi. A. 1980. V. 69. № 2. P. 341. https://doi.org/10.1002/pssa.2210600202
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования