Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2022, № 2, стр. 109-112

Моделирование электронных термов двухатомных молекул

В. П. Кощеев^a, *, Ю. Н. Штанов^b, **

^a НИУ МАИ, филиал “Стрела”
140180 Жуковский, Московская область, Россия

^b Тюменский индустриальный университет, филиал ТИУ в г. Сургуте
628404 Сургут, Россия

^* E-mail: koshcheev1@yandex.ru
^** E-mail: yuran1987@mail.ru

Поступила в редакцию 08.02.2020
После доработки 17.05.2021
Принята к публикации 25.05.2021

EDN: XPDDSD
DOI: 10.31857/S1028096022020066

Полный текст (PDF)

Аннотация

В первом порядке теории возмущений вычислена поправка к электронным термам (потенциальной энергии взаимодействия между атомами) в двухатомной молекуле с учетом принципа Паули. Рассмотрено условие применимости поправки в первом порядке теории возмущений к энергии системы в невозмущенном состоянии. Вычислены электронные термы для двухатомной молекулы (димера) ${\text{HF}}$ и ${\text{HNe}}$ в первом порядке теории возмущений. Для двухатомной молекулы ${\text{HF}}$ наблюдается удовлетворительное согласие с результатами эксперимента.

Ключевые слова: потенциальная энергия взаимодействия, принцип Паули, приближение Мольер.

ВВЕДЕНИЕ

Новый подход к вычислению потенциальной энергии взаимодействия двух атомов [1, 2] удовлетворительно описывает результаты эксперимента для атомов благородных газов, если атомный форм-фактор изолированного атома выбран в приближении Мольер.

В настоящей публикации будут построены электронные термы для двухатомной молекулы (димера) ${\text{HF}}$ и в первом порядке теории возмущений.

МОДЕЛЬ

Двухатомную молекулу будем описывать с помощью стационарного уравнения Шредингера:

(1)

$H{{\psi }} = E{{\psi }}{\text{.}}$

Гамильтониан уравнения (1) представим в виде

(2)

$\begin{gathered} H = {{H}^{0}} + U;\, \\ \,U = \frac{{{{Z}_{1}}{{Z}_{2}}{{e}^{2}}}}{{\left| {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{2}}} \right|}} + \sum\limits_{{{j}_{1}}\,\, = \,\,1}^{{{Z}_{1}}} {\sum\limits_{{{j}_{2}}\,\, = \,\,1}^{{{Z}_{2}}} {\frac{{{{e}^{2}}}}{{\left| {{{{\mathbf{r}}}_{1}} + {{{\mathbf{r}}}_{{1{{j}_{1}}}}} - {{{\mathbf{r}}}_{2}} - {{{\mathbf{r}}}_{{2{{j}_{2}}}}}} \right|}}} } - \\ - \,\,\sum\limits_{{{j}_{1}}\,\, = \,\,1}^{{{Z}_{1}}} {\frac{{{{Z}_{2}}{{e}^{2}}}}{{\left| {{{{\mathbf{r}}}_{1}} + {{{\mathbf{r}}}_{{1{{j}_{1}}}}} - {{{\mathbf{r}}}_{2}}} \right|}}} - \sum\limits_{{{j}_{2}}\,\, = \,\,1}^{{{Z}_{2}}} {\frac{{{{Z}_{1}}{{e}^{2}}}}{{\left| {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{2}} - {{{\mathbf{r}}}_{{2{{j}_{2}}}}}} \right|}}} , \\ \end{gathered} $

где $U$ – потенциальная энергия взаимодействия двух атомов; ${{{\mathbf{r}}}_{1}}$ и ${{{\mathbf{r}}}_{2}}$ – координаты первого и второго атомного ядра; ${{{\mathbf{r}}}_{1}} + {{{\mathbf{r}}}_{{1{{j}_{1}}}}}$ и ${{{\mathbf{r}}}_{2}} + {{{\mathbf{r}}}_{{2{{j}_{2}}}}}$ – координаты ${{j}_{1}}$ и ${{j}_{2}}$ электронов первого и второго атома, соответственно.

Решение уравнения (1) с гамильтонианом (2) будем искать с помощью теории возмущений:

${{\psi }} = {{{{\psi }}}^{0}} + {{{{\psi }}}^{1}} + \ldots ,\,\,\,\,E = {{E}^{0}} + {{E}^{1}} + ....$

Электронные термы двухатомной молекулы будем искать в первом порядке теории возмущений:

(3)

${{E}^{1}}\left( r \right) = \left\langle {\left. {{{{{\psi }}}^{0}}} \right|\left. U \right|{{{{\psi }}}^{0}}} \right\rangle ,$

где $r = \left| {{{{\mathbf{r}}}_{1}} - {{{\mathbf{r}}}_{2}}} \right|;$ угловые скобки $\left\langle {...} \right\rangle $ были введены Дираком [3].

Гамильтониан представим ${{H}^{0}}$ как

${{H}^{0}} = H_{1}^{0} + H_{2}^{0},$

где $H_{i}^{0}$ – гамильтониан i-го атома; i = 1, 2.

Решение уравнения Шредингера

${{H}^{0}}{{{{\psi }}}^{0}} = {{E}^{0}}{{{{\psi }}}^{0}},$

будем искать с помощью следующих уравнений:

${{{{\psi }}}^{0}} = {{\psi }}_{1}^{0}{{\psi }}_{2}^{0},\,\,\,\,{{E}^{0}} = E_{1}^{0} + E_{2}^{0},$

где уравнение Шредингера для i-го изолированного атома имеет вид:

(4)

$H_{i}^{0}{{\psi }}_{i}^{0} = E_{i}^{0}{{\psi }}_{i}^{0},$

здесь ${{\psi }}_{i}^{0} = {{\psi }}_{i}^{0}\left( {{{{\mathbf{r}}}_{{i1}}},{{{\mathbf{r}}}_{{i2}}},...,{{{\mathbf{r}}}_{{i{{Z}_{i}}}}}} \right).$

Известно [4], что с помощью вариационного принципа из стационарного уравнения Шредингера (4) можно построить уравнение Хартри–Фока, если волновые функции атомных электронов записать в виде детерминанта Слэтера. Водородоподобные волновые функции, которые аппроксимируют решение уравнения Хартри–Фока для изолированного атома, представлены в [5]:

(5)

${{\psi }}_{i}^{0} = {{{{\theta }}}_{{i1}}}\left( {{{{\mathbf{r}}}_{{i1}}}} \right){{{{\theta }}}_{{i2}}}\left( {{{{\mathbf{r}}}_{{i2}}}} \right) \ldots {{{{\theta }}}_{{i{{Z}_{i}}}}}\left( {{{{\mathbf{r}}}_{{i{{Z}_{i}}}}}} \right),$

где ${{{{\theta }}}_{{ij}}} = {{{{\theta }}}_{{ij}}}\left( {{{{\mathbf{r}}}_{{ij}}}} \right)$ – водородоподобные волновые функции, которые образуют ортонормированную систему.

С помощью формул (2) и (5) вычислим (3) следуя [1]:

(6)

$\begin{gathered} {{E}^{1}}\left( r \right) = \int {{{E}^{1}}\left( k \right)\exp \left( {i{\mathbf{kr}}} \right)} \frac{{{{{\text{d}}}^{3}}{\mathbf{k}}}}{{{{{\left( {2{{\pi }}} \right)}}^{3}}}}, \\ {{E}^{1}}\left( k \right) = \frac{{4{{\pi }}{{Z}_{1}}{{Z}_{2}}{{e}^{2}}}}{{{{k}^{2}}}}\left[ {1 - \frac{{{{F}_{1}}\left( k \right)}}{{{{Z}_{1}}}}} \right]\left[ {1 - \frac{{{{F}_{2}}\left( k \right)}}{{{{Z}_{2}}}}} \right]. \\ \end{gathered} $

Формула (6) не учитывает действие принципа Паули между электронами первого и второго атомов. В [1] по аналогии с (например, [6]), было предложено учитывать принцип Паули с помощью сомножителя:

(7)

$P\left( k \right) = \left[ {1 - \frac{{{{F}_{1}}\left( k \right)}}{{{{Z}_{1}}}}} \right]\left[ {1 - \frac{{{{F}_{2}}\left( k \right)}}{{{{Z}_{2}}}}} \right].$

Величина ${{{{F}_{i}}\left( k \right)} \mathord{\left/ {\vphantom {{{{F}_{i}}\left( k \right)} {{{Z}_{i}}}}} \right. \kern-0em} {{{Z}_{i}}}}$ – является Фурье-компонентой плоскости распределения атомных электронов, которая нормирована на единицу. В результате получим выражение для электронного терма (потенциальной энергии взаимодействия двух атомов $U(r) = E_{p}^{1}(r) + ...$) с учетом принципа Паули в следующем виде:

(8)

$E_{p}^{1}\left( r \right) = \int {{{E}^{1}}\left( k \right)P\left( k \right)} \exp \left( {i{\mathbf{kr}}} \right)\frac{{{{{\text{d}}}^{3}}{\mathbf{k}}}}{{{{{\left( {2{{\pi }}} \right)}}^{3}}}}.$

Условие применимости поправки в первом порядке теории возмущений к энергии системы в невозмущенном состоянии имеет следующий вид:

$\left| {E_{p}^{1}\left( r \right)} \right| < < \left| {{{E}^{0}}} \right|,$

где ${{E}^{0}} = E_{1}^{0} + E_{2}^{0},$ энергии $E_{i}^{0}$ также представлены в [5] вместе с водородоподобными волновыми функциями, которые аппроксимируют решение уравнения Хартри–Фока для изолированного атома.

РЕЗУЛЬТАТЫ РАСЧЕТОВ И ИХ ОБСУЖДЕНИЕ

Было выполнено моделирование потенциальной энергии взаимодействия двух атомов, когда форм-фактор первого атома был выбран в приближении Мольер:

(9)

$\begin{gathered} U\left( r \right) \approx \int {\frac{{4{{\pi }}{{Z}_{1}}{{Z}_{2}}{{e}^{2}}}}{{{{k}^{2}}}}{{{\left[ {1 - \frac{{{{F}_{1}}\left( k \right)}}{{{{Z}_{1}}}}} \right]}}^{2}}{{{\left[ {1 - \frac{{{{F}_{2}}\left( k \right)}}{{{{Z}_{2}}}}} \right]}}^{2}}} \times \\ \times \,\,\exp \left( {i{\mathbf{kr}}} \right)\frac{{{{{\text{d}}}^{3}}{\mathbf{k}}}}{{{{{\left( {2{{\pi }}} \right)}}^{3}}}}, \\ \end{gathered} $

(10)

${{F}_{1}}\left( k \right) = {{Z}_{1}}\sum\limits_{i\,\, = \,\,1}^3 {\frac{{{{{{\alpha }}}_{i}}{{{\left( {{{{{{{\beta }}}_{i}}} \mathord{\left/ {\vphantom {{{{{{\beta }}}_{i}}} {{{a}_{1}}}}} \right. \kern-0em} {{{a}_{1}}}}} \right)}}^{2}}}}{{{{k}^{2}} + {{{\left( {{{{{{{\beta }}}_{i}}} \mathord{\left/ {\vphantom {{{{{{\beta }}}_{i}}} {{{a}_{1}}}}} \right. \kern-0em} {{{a}_{1}}}}} \right)}}^{2}}}}} ,$

где ${{{{\alpha }}}_{i}},\,\,{{{{\beta }}}_{i}}$ – коэффициенты приближения Мольер [7]; ${{a}_{1}} \approx {\text{0}}{\text{.88534}}{{a}_{0}}Z_{1}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}}};$ ${{a}_{0}} = 0.529\,{\AA}.$

Атомный форм-фактор ${{F}_{2}}\left( k \right)$ вычислялся с помощью волновой функции атома водорода в $1s$-состоянии:

(11)

${{F}_{2}}\left( k \right) = \frac{{16}}{{{{{\left( {4 + a_{2}^{2}{{k}^{2}}} \right)}}^{2}}}},$

где ${{a}_{2}} = {{{{a}_{0}}} \mathord{\left/ {\vphantom {{{{a}_{0}}} {{{Z}_{2}}}}} \right. \kern-0em} {{{Z}_{2}}}} \approx 0.529\,{\AA}$ – длина экранирования атома водорода.

Выражения (9) вычислим с помощью формул (10) и (11):

(12)

$\begin{gathered} U\left( r \right) \approx \frac{{18{{e}^{2}}}}{r}\left[ {{\text{exp}}\left( { - \frac{{14.0968r}}{{{{a}_{0}}}}} \right)\left( {0.0973 - 0.0352\frac{r}{{{{a}_{0}}}}} \right) + } \right. \\ + \,\,{\text{exp}}\left( { - \frac{{2.8194r}}{{{{a}_{0}}}}} \right)\left( { - 0.03236 - 0.0001451\frac{r}{{{{a}_{0}}}}} \right) + \\ + \,\,\exp \left( { - \frac{{0.7048r}}{{{{a}_{0}}}}} \right)\left( {0.0182 - 0.00199\frac{r}{{{{a}_{0}}}}} \right) + \\ {\text{ + }}\,\,{\text{exp}}\left( { - \frac{{2r}}{{{{a}_{0}}}}} \right)\left( {0.416838 - 0.62409\frac{r}{{{{a}_{0}}}} + 0.0846\frac{{{{r}^{2}}}}{{a_{0}^{2}}} - } \right. \\ - \,\,\left. {\left. {0.002121\frac{{{{r}^{3}}}}{{a_{0}^{3}}}} \right)} \right]. \\ \end{gathered} $

Численные расчеты выполнены с использованием программы [8]. На рис. 1 представлены графики потенциальной энергии взаимодействия атомов в молекулах ${\text{HF}}$ и ${\text{HNe}}{\text{.}}$ Так как атомный форм-фактор для атомов фтора и неона был выбран в приближении Мольер, то результаты расчета потенциальной энергии взаимодействия атомов в молекулах ${\text{HF}}$ и ${\text{HNe}}$ незначительно отличаются друг от друга. Видно, что дальний потенциальный минимум (рис. 1в), который соответствует области действия сил Ван-дер-Ваальса, в 10⁴–10⁵ раз менее глубок, чем ближний потенциальный минимум (рис. 1а). На рис. 2 можно видеть удовлетворительное согласие графика потенциальной энергии взаимодействия атомов в молекуле ${\text{HF}}$ в сравнении с данными эксперимента, которые представлены в [9]. В работе [2] было продемонстрировано удовлетворительное согласие с экспериментом графика потенциальной энергии взаимодействия двух атомов неона в области действия сил Ван-дер-Ваальса. Форм-факторы атомов неона в [2] были взяты в приближении Мольер. Согласие результатов расчета с экспериментом можно улучшить, если форм-факторы атомов фтора и неона построить с помощью водородоподобных волновых функций [5], которые аппроксимируют решение уравнения Хартри–Фока для изолированного атома. Видно, что для образования молекулы ${\text{HNe}}$ при сближении атомов водорода и неона требуется преодолеть потенциальный барьер высотой порядка $0.04$ электронвольта (как это видно на рис. 1б). При низких температурах возможно образование димеров ${\text{HF}}$ и ${\text{HNe}}$ в области действия сил Ван-дер-Ваальса. Глубина потенциальной ямы составляет ${{10}^{{ - 4}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 5}}}$ электронвольт, а расстояние между атомами порядка 5–6 Å (как это видно на рис. 1в).

Рис. 1.

Потенциальная энергия взаимодействия атомов в молекулах ${\text{HF}}$ (сплошная линия) и ${\text{HNe}}$ (пунктирная линия) в различных масштабах: а – ${r \mathord{\left/ {\vphantom {r {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}} \in \left[ {0;3} \right],$ б – ${r \mathord{\left/ {\vphantom {r {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}} \in \left[ {3;8} \right],$ в – ${{{r \mathord{\left/ {\vphantom {r a}} \right. \kern-0em} a}}_{0}} \in \left[ {8;15} \right].$

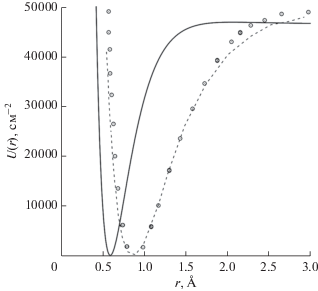
Рис. 2.

Потенциальная энергия взаимодействия $U(r),$ которая вычислена по формуле (12) (сплошная линия), в сравнении с результатом эксперимента, представленном в работе [9] (кружки), и потенциалом Морзе [9] (пунктирная линия) для молекулы HF.

ЗАКЛЮЧЕНИЕ

Процесс взаимодействие атомов на близких и далеких расстояниях подробно обсуждался в [10]. Было отмечено, что на далеких расстояниях между атомами действуют слабые силы ван-дер-ваальсовского притяжения, а на близких расстояниях атомы образуют устойчивые соединения. Тем не менее, в [10] не обсуждался вопрос о наличии потенциального барьера между этими двумя потенциальными ямами, который появляется в нашем подходе. Сравнение результатов расчета для димеров благородных газов в [2] показало удовлетворительное согласие с экспериментом на больших расстояниях между атомами, а в настоящей работе было продемонстрировано удовлетворительное согласие с экспериментом на близких расстояниях между атомами водорода и фтора. Согласие результатов расчета с экспериментом может быть улучшено как с помощью вычисления следующих членов разложения в ряд теории возмущений, так и с помощью вычисления атомного форм-фактора с водородоподобными волновыми функциями [5], которые аппроксимируют решение уравнения Хартри–Фока для изолированного атома.

Список литературы

Кощеев В.П., Штанов Ю.Н. // Письма в ЖТФ. 2018. Т. 44. В. 13. С. 28. https://doi.org/10.21883/PJTF.2018.13.46324.17133
Кощеев В.П., Штанов Ю.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2020. № 8. С. 97. https://doi.org/10.31857/S1028096020080105
Дирак П.А.М. Принципы квантовой механики. М.: Наука, 1979. 479 с.
Фок В.А. Начала квантовой механики. М.: ЛКИ, 2007. 374 с.
Clementi E., Roetti C. // Atomic Data and Nuclear Data Tables. 1974. V. 14. P. 177.
Лифшиц Е.М., Питаевский Л.П. Физическая кинетика. М.: Физматлит, 2007. 536 с.
Molière G. // Zeitschrift Naturforsch. T l. A. 1947. V. 2. P. 133.
А.с. 2020617054 (РФ). Программа для моделирования потенциальной энергии взаимодействия атомов с водородоподобными волновыми функциями. / Штанов Ю.Н., Кощеев В.П. // Б.И. 2020. С. 1.
Fan Q. et al. // The European Physical Journal D. 2014. V. 68. № 1. P. 5. https://doi.org/10.1140/epjd/e2013-40437-2
Ландау Л.Д., Лифшиц Е.М. Квантовая механика. М.: Физматлит, 1974. 752 с.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Поверхность. Рентгеновские, синхротронные и нейтронные исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал