Поверхность. Рентгеновские, синхротронные и нейтронные исследования, 2022, № 4, стр. 106-112
Вершина конуса затенения при рассеянии атомных частиц низких и средних энергий
А. Н. Пустовит *
Институт проблем технологии микроэлектроники и особочистых материалов РАН
142432 Черноголовка, Московская область, Россия
* E-mail: pustan@iptm.ru
Поступила в редакцию 14.02.2021
После доработки 20.05.2021
Принята к публикации 25.05.2021
- EDN: BULIUE
- DOI: 10.31857/S1028096022010162
Аннотация
Предложен метод расчета вершины конуса затенения при рассеянии атомных частиц низких и средних энергий. Вычислены зависимости наибольших расстояний сближения частиц от прицельного параметра. Предложена эмпирическая формула для расчета зависимости больших углов отклонения в системе центра масс от прицельного параметра. Вычислена вершина конуса затенения, и исследованы влияния параметров частиц и потенциала взаимодействия на ее форму. Рассчитана энергия блокировки для проникновения атомных частиц в твердое тело. Рассмотрена связь между блокирующей энергией и пороговой энергией распыления. Проведена оценка критерия применимости классической механики в реализованных расчетах. Установлено, что выполненные в работе вычисления с использованием классической механики правомерны.
ВВЕДЕНИЕ
Изучение процессов взаимодействия атомных частиц низких и средних энергий имеет фундаментальный и практический интерес. Примером областей применения этих взаимодействий является спектроскопия рассеянных ионов [1–3] и распыление материала [4], где важным фактором является рассеяние первичных ионов атомами мишени, начиная от пороговых энергий и выше. В случае параллельного пучка ионов (порядковый номер Z1, масса m1), взаимодействующего с атомами мишени (Z2, m2), траектории ионов в лабораторной системе координат отклоняются отталкивающим потенциалом взаимодействия (ПВ) U(r) между ними, и за атомом образуется область, куда ионы попасть не могут. Граница между областями возможного и невозможного проникновения иона имеет форму конуса и называется конусом затенения (КЗ). Для практических применений представляют интерес зависимости формы КЗ и угла рассеяния иона от его начальной энергии Е, соотношения масс частиц и порядковых номеров.
При взаимодействии частиц обычно рассматривают парные столкновения и привлекают теорию рассеяния. Для вычисления угла отклонения χ в системе центра масс используют известное интегральное уравнение рассеяния [5, 6]:
(1)
$\chi = \pi - 2\int\limits_{{{\rho }_{{ms}}}}^\infty {\frac{{\rho dr}}{{{{r}^{2}}\sqrt {1 - {{{\left( {{\rho \mathord{\left/ {\vphantom {\rho r}} \right. \kern-0em} r}} \right)}}^{2}} - {{U(r)} \mathord{\left/ {\vphantom {{U(r)} {{{E}_{0}}}}} \right. \kern-0em} {{{E}_{0}}}}} }}} ,$(2)
$1 - {{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{{\rho }_{{ms}}}}}} \right. \kern-0em} {{{\rho }_{{ms}}}}}} \right)}^{2}} - {{U\left( {{{\rho }_{{ms}}}} \right)} \mathord{\left/ {\vphantom {{U\left( {{{\rho }_{{ms}}}} \right)} {{{E}_{0}}}}} \right. \kern-0em} {{{E}_{0}}}} = 0.$Дополнительный знак s в нижнем индексе ρms связан с экранировкой ПВ и будет определен ниже.
Обычно, при проведении дальнейших вычислений используют малоугловое рассеяние (импульсное приближение) и потенциал Мольера [7, 8]. При расчете зависимости радиуса Rsh КЗ от расстояния l за атомом используется уравнение для кулоновского ПВ [2, 7]:
(3)
${{R}_{{{\text{sh}}}}} = {{\left( {{{{{Z}_{1}}{{Z}_{2}}{{q}^{2}}l} \mathord{\left/ {\vphantom {{{{Z}_{1}}{{Z}_{2}}{{q}^{2}}l} E}} \right. \kern-0em} E}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$При расчете радиуса Мольера $\left( {R_{{{\text{sh}}}}^{{{\text{Moliere}}}}} \right)$ для экранированного ПВ Мольера и малоуглового рассеяния используют эмпирическое выражение [7, 8]:
(4)
$\begin{gathered} \frac{{R_{{{\text{sh}}}}^{{{\text{Moliere}}}}}}{{{{R}_{{{\text{sh}}}}}}} = \\ = \left\{ \begin{gathered} 1.0 - 0.12k + 0.01{{k}^{2}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0 \leqslant k \leqslant 4.5, \hfill \\ 0.924 - 0.182\ln k + 0.0008k\,\,\,\,4.5 \leqslant k \leqslant 100, \hfill \\ \end{gathered} \right. \\ \end{gathered} $По уравнениям (3) и (4) можно сделать следующие замечания. Во-первых, поскольку отсчет l начинается с атома, то центр вершины КЗ расположен на атоме для всех указанных ПВ. Это не соответствует истинному положению дел, так как в отталкивающем ПВ всегда существует некоторое расстояние между ионом и атомом (даже при лобовом столкновении). Во-вторых, поскольку малоугловое рассеяние может быть использовано для χ $ \ll $ 1, предложенный подход справедлив только для расчета боковой поверхности КЗ (для θ1 $ \ll $ π/2, где θ1 – угол отклонения иона в лабораторной системе координат).
Первая цель данной работы состояла в вычислении вершины КЗ, определяемой рассеянием на большие углы θ1 ≥ π/2, и определении параметров, влияющих на ее форму.
Второе направление исследований связано с расширением области использования представления КЗ, в частности, к процессу распыления. В работе [4] при вычислении пороговой энергии распыления Eth было найдено, что первичный ион при нормальном падении на поверхность сначала проникает внутрь мишени на глубину ~d, затем рассеивается на угол ~π и уже при движении из глубины мишени выбивает внешний атом. Полученная в [4] формула для Eth хорошо описывает экспериментальные данные, но механизм разворота на угол ~π не ясен. По-видимому, это связано с блокировкой дальнейшего проникновения иона внутрь мишени.
Вторая цель данной работы состояла в исследовании возможной блокировки поверхности и ее связи с пороговой энергией распыления.
РАСЧЕТ ФОРМЫ ВЕРШИНЫ КОНУСА ЗАТЕНЕНИЯ
Все расчеты проводили с использованием отталкивающего степенного ПВ Линдхарда–Нильсена–Шарфа (ЛНШ) [9]:
(5)
$U(r) = {{Z}_{1}}{{Z}_{2}}{{q}^{2}}\frac{{{{k}_{s}}}}{{sa}}{{\left( {\frac{a}{r}} \right)}^{s}},$Выбор этого ПВ обусловлен тем, что, во-первых, в диапазоне значений 0 ≤ a/r ≤ 5 (1 ≤ s ≤ 4) многие ПВ совпадают [10]. Во-вторых, используя потенциал (5), можно описать экспериментальные результаты зависимости пороговых энергий распыления от отношения масс сталкивающихся частиц [4]. В-третьих, при анализе эффекта экранирования в (5) необходимо изменить только одну величину s в отличие от многих других ПВ. В-четвертых, гораздо проще проводить аналитические расчеты с использованием степенного ПВ.
Далее все расчеты будут проведены для значений s в диапазоне от 1 до 4 и без учета возможных химических реакций при столкновении. Учет неупругих столкновений Q выполним с помощью замены Е на Е – Q [11]. Применительно к процессам распыления Q ~ U0, где U0 – энергия сублимации атомов мишени, и составляет несколько эВ [4].
На рис. 1 приведена схема рассеяния падающего перпендикулярно на поверхность образца (ось Х) иона (m1, Z1) на угол θ1 в лабораторной системе координат в результате взаимодействия с покоящимся в начале координат поверхностным атомом (m2, Z2). Отрезок ОD равен наибольшему расстоянию сближения ρms, а отрезок ОС его минимальной величине bs при лобовом столкновении. Кривая ACDB образована концами ρms при изменении прицельного параметра ρ.
Рис. 1.
Схема рассеяния на угол θ1 в лабораторной системе координат налетающего иона (m1, Z1) на покоящемся в начале координат атоме (m2, Z2).
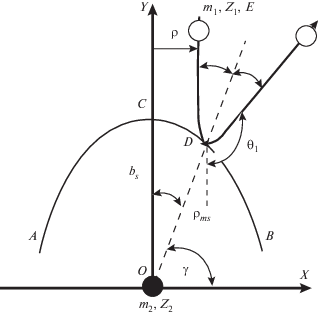
В зависимости от значения ρ существуют две области, определяющие форму КЗ. Для углов θ1 ≥ ≥ π/2 все конечные траектории рассеянных ионов лежат в верхней полуплоскости (рис. 1, выше оси Х). В этой области форму КЗ определяют наибольшие расстояния сближения сталкивающихся частиц ρms, и совокупность проекций ρms на оси координат описывает вершину КЗ. Во второй области для углов θ1 < π/2 все конечные траектории рассеянных ионов лежат в нижней полуплоскости (рис. 1, ниже оси Х). Форму КЗ в этом случае описывают траектории ионов после достижения наибольшего расстояния сближения сталкивающихся частиц ρms, образуя его боковую поверхность. Расчеты формы КЗ для этой области и потенциала Мольер выполнены в работах [7, 8].
Для всех ионов, имеющих угол отклонения θ1 = π/2, конечные траектории при рассеянии располагаются параллельно оси Х. Концы ρms для этих траекторий образуют границу между двумя областями на кривой конуса затенения.
Из рис. 1 видно, что γ = θ1/2. Поэтому координаты точки D находятся по уравнениям:
(6)
$X = {{\rho }_{{ms}}}\cos \left( {{{{{\theta }_{1}}} \mathord{\left/ {\vphantom {{{{\theta }_{1}}} {\text{2}}}} \right. \kern-0em} {\text{2}}}} \right),\,\,\,\,Y = {{\rho }_{{ms}}}\sin \left( {{{{{\theta }_{1}}} \mathord{\left/ {\vphantom {{{{\theta }_{1}}} {\text{2}}}} \right. \kern-0em} {\text{2}}}} \right).$Функциональная зависимость Y = f(Х) описывает кривую ACDB.
Согласно уравнению (6) при θ1 = π/2 из-за симметрии следует, что |Хb| = Yb. Это равенство является условием для нахождения границы между двумя областями и поэтому отмечено нижними индексами.
При вычислениях удобно использовать наибольшее расстояние сближения частиц при лобовом столкновении bs. Эта величина находится из равенства U(r) = Е0 и равна:
(7)
${{b}_{s}} = {{\left( {{{{{Z}_{1}}{{Z}_{2}}{{q}^{2}}{{k}_{s}}} \mathord{\left/ {\vphantom {{{{Z}_{1}}{{Z}_{2}}{{q}^{2}}{{k}_{s}}} {sa{{E}_{0}}}}} \right. \kern-0em} {sa{{E}_{0}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0em} s}}}}a.$Используя (5) и (7), запишем уравнение (2) в виде:
(8)
$1 - {{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{{\rho }_{{ms}}}}}} \right. \kern-0em} {{{\rho }_{{ms}}}}}} \right)}^{2}} - {{\left( {{{{{b}_{s}}} \mathord{\left/ {\vphantom {{{{b}_{s}}} {{{\rho }_{{ms}}}}}} \right. \kern-0em} {{{\rho }_{{ms}}}}}} \right)}^{s}} = 0.$Равенство (8) представляет собой уравнение, в котором начальные параметры взаимодействия сталкивающихся частиц (кроме ρ) присутствуют через величину bs. Для целых значений s в диапазоне 1–4 уравнение (8) имеет точные решения соответственно:
(9)
${{\rho }_{{m1}}} = {{b}_{1}}\left[ {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right) + \sqrt {\left( {{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right) + {{{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{{b}_{s}}}}} \right. \kern-0em} {{{b}_{s}}}}} \right)}}^{2}}} } \right],$(10)
${{\rho }_{{m2}}} = {{b}_{2}}{{\left[ {1 + {{{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{{b}_{2}}}}} \right. \kern-0em} {{{b}_{2}}}}} \right)}}^{2}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$(11)
$\begin{gathered} {{\rho }_{{m3}}} = {{b}_{3}}\left[ {\sqrt[3]{{\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right) + \sqrt {\left( {{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right) - \left( {{1 \mathord{\left/ {\vphantom {1 {27}}} \right. \kern-0em} {27}}} \right){{{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{{b}_{3}}}}} \right. \kern-0em} {{{b}_{3}}}}} \right)}}^{6}}} }} + } \right. \\ \left. { + \,\,\sqrt[3]{{\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right) - \sqrt {\left( {{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right) - \left( {{1 \mathord{\left/ {\vphantom {1 {27}}} \right. \kern-0em} {27}}} \right){{{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{{b}_{3}}}}} \right. \kern-0em} {{{b}_{3}}}}} \right)}}^{6}}} }}} \right], \\ \end{gathered} $(12)
${{{{\rho }}}_{{m4}}} = {{b}_{4}}\sqrt {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right){{{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{{b}_{4}}}}} \right. \kern-0em} {{{b}_{4}}}}} \right)}}^{2}} + \sqrt {1 + \left( {{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right){{{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{{b}_{4}}}}} \right. \kern-0em} {{{b}_{4}}}}} \right)}}^{4}}} } .$Чтобы найти зависимость ρms от ρ для промежуточных значений s представим (8) в виде:
(13)
${{{{{{b}_{s}}} \mathord{\left/ {\vphantom {{{{b}_{s}}} \rho }} \right. \kern-0em} \rho }}_{{ms}}} = {{\left[ {1 - {{{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{{\rho }_{{ms}}}}}} \right. \kern-0em} {{{\rho }_{{ms}}}}}} \right)}}^{2}}} \right]}^{{{1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0em} s}}}}.$Поскольку всегда ρ/ρms < 1, то разлагая правую часть уравнения (13) в ряд и учитывая два первых члена в разложении, получаем квадратное уравнение относительно ρms. Решением полученного уравнения является:
(14)
${{\rho }_{{ms}}} = {{b}_{s}}\left[ {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right) + \sqrt {\left( {{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}} \right) + \left( {{1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0em} s}} \right){{{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{{b}_{s}}}}} \right. \kern-0em} {{{b}_{s}}}}} \right)}}^{2}}} } \right].$Для s = 1 уравнения (9) и (14) полностью совпадают. При других целых значениях s между результатами, полученными по уравнениям (10)–(12) и (14) наблюдаются отличия, возрастающие с увеличением ρ/bs и составляющие 3–5% при ρ/bs = 1. Такая точность достаточна для проведения дальнейших расчетов.
Углы отклонения иона (θ1, χ) связаны уравнением [13]:
(15)
$\cos {\kern 1pt} {{\theta }_{1}}\, = \,{{{{\left( {{{m}_{1}} + {{m}_{2}}{\kern 1pt} \sin {\kern 1pt} \chi } \right)} \mathord{\left/ {\vphantom {{\left( {{{m}_{1}} + {{m}_{2}}{\kern 1pt} \sin {\kern 1pt} \chi } \right)} {\left( {m_{1}^{2} + m_{2}^{2} + 2{{m}_{1}}{{m}_{2}}{\kern 1pt} \cos {\kern 1pt} \chi } \right)}}} \right. \kern-0em} {\left( {m_{1}^{2} + m_{2}^{2} + 2{{m}_{1}}{{m}_{2}}{\kern 1pt} \cos {\kern 1pt} \chi } \right)}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$Для установления зависимости угла χ от ρ/bs необходимо решить уравнение (1). Один из способов получения этой зависимости состоит в аналитическом решении. Для ПВ (5) и s, равных 1 и 2, это возможно сделать [5, 6]. С учетом формулы (7) решения имеют следующий вид:
(16)
${{\chi }_{{\text{1}}}} = \pi - 2{\text{arctg}}\left( {{{4\rho } \mathord{\left/ {\vphantom {{4\rho } {{{b}_{1}}}}} \right. \kern-0em} {{{b}_{1}}}}} \right),$(17)
${{\chi }_{{\text{2}}}} = \pi \left\{ {{\text{1}} - \left( {{\rho \mathord{\left/ {\vphantom {\rho {{{b}_{{\text{2}}}}}}} \right. \kern-0em} {{{b}_{{\text{2}}}}}}} \right){{{\left[ {1 + {{{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{{b}_{2}}}}} \right. \kern-0em} {{{b}_{2}}}}} \right)}}^{2}}} \right]}}^{{ - \left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)}}}} \right\}.$Для s, равных 3 и 4, точных решений нет. Приближенные вычисления для углов χ > π/2, выполненные в соответствии с рекомендациями [6] дают приемлемые результаты в очень узкой области около ρ/bs ~ 0. Поэтому для получения аналитической функциональной зависимости χ от ρ/bs, позволяющей проводить расчеты в более широкой области изменений величины s, был использован следующий подход. На первом этапе было использовано численное решение уравнения (1) с помощью программы Mathсad-2000 [14] для целых s в диапазоне 1–4. При выполнении этих расчетов для ρms применяли формулы (9)–(12). Второй этап состоял в нахождении эмпирической аппроксимации точных и численных результатов в диапазоне изменений ρ/bs от 0 до 1. Конечный результат хорошо совпадает с формулой:
(18)
${{\chi }_{{{\text{emp}}}}} = {\pi \mathord{\left/ {\vphantom {\pi {\left[ {{\text{1}} + ({\pi \mathord{\left/ {\vphantom {\pi {{{s}^{{{1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0em} s}}}}}}} \right. \kern-0em} {{{s}^{{{1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0em} s}}}}}}){{{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{{b}_{s}}}}} \right. \kern-0em} {{{b}_{s}}}}} \right)}}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0em} 5}}}}} \right]}}} \right. \kern-0em} {\left[ {{\text{1}} + ({\pi \mathord{\left/ {\vphantom {\pi {{{s}^{{{1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0em} s}}}}}}} \right. \kern-0em} {{{s}^{{{1 \mathord{\left/ {\vphantom {1 s}} \right. \kern-0em} s}}}}}}){{{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{{b}_{s}}}}} \right. \kern-0em} {{{b}_{s}}}}} \right)}}^{{{7 \mathord{\left/ {\vphantom {7 5}} \right. \kern-0em} 5}}}}} \right]}}.$При s = 2 аналитические, численные и эмпирические результаты полностью совпадают, в то время как между точными и численными результатами для s = 1 существует разница. Для значений s > 2 существуют различия между численными и эмпирическими расчетами, которые увеличиваются с увеличением ρ/bs. При значении χ ~ 90 градусов (ρ/bs = 0.6) эти различия не превышает ~5%, а при углах ~60 градусов (ρ/bs = 0.8) ~ 10%.
Уравнения (6), (14), (15) и (18) образуют замкнутую параметрическую систему уравнений для расчета Х и Y в лабораторной системе координат. При фиксированных значениях степенного показателя, масс, порядковых номеров и энергии сталкивающихся частиц единственной изменяемой величиной является прицельный параметр ρ (или ρ/bs).
РЕЗУЛЬТАТЫ РАСЧЕТОВ ВЕРШИНЫ КОНУСА ЗАТЕНЕНИЯ И ИХ ОБСУЖДЕНИЕ
На рис. 2 приведены результаты расчетов зависимостей Y от X. Рис. 2а, 2б соответствуют системе 4He+–59Co с энергиями ионов 2000 и 4000 эВ соответственно. Результаты расчетов для системы 40Ar+–59Co приведены на рис. 2в с энергией ионов 2000 эВ. Сплошные кривые на рис. 2 были построены с использованием значений s равных 1, 1.5, 2 для ионов 4He+ и 2, 3, 4 для ионов 40Ar+ соответственно. Для оценки точности вычислений на рис. 2 представлены графики (пунктирные линии), полученные для s = 2 при использовании уравнений (10) и (17) вместо (14) и (18) соответственно. В табл. 1 сравниваются некоторые расчетные параметры для рассмотренных систем с целью исследования динамики их изменений. Черные точки на графиках соответствуют границе между двумя областями |Хb| = Yb. Рассеянные в этих точках ионы летят параллельно оси Х, а внутренняя область между ними представляет вершину КЗ. Ширина пика ∆X, приведенная в табл. 1, равна расстоянию между черными точками на рис. 2. Для рассматриваемых систем в табл. 1 представлены расчетные значения параметра bs/a.
Рис. 2.
Зависимости Y от X для систем: а – 4He+–59Co с энергией ионов гелия 2000 эВ, б – 4He+–59Co с энергией ионов гелия 4000 эВ, в – 40Ar+–59Co с энергией ионов аргона 2000 эВ. Черные точки на графиках соответствуют границе между вершиной конуса затенения и его боковой поверхностью. Сплошные линии – расчет по приближенным формулам. Пунктирные линии – расчет по точным формулам для s = 2.
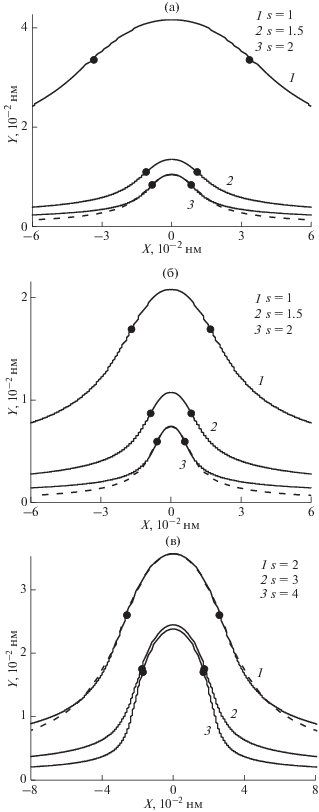
Таблица 1.
Некоторые параметры рассмотренных систем и полученных графиков
| Ион-мишень, (энергия) | а, 10–2 нм |
s | bs, 10–2 нм |
bs/a | ∆X, 10–2 нм |
|---|---|---|---|---|---|
| 4He+–59Co (2000 эВ) |
1.44 | 1 | 14.16 | 2.89 | 6.7 |
| 1.5 | 1.35 | 0.94 | 2.2 | ||
| 2 | 1.05 | 0.73 | 1.68 | ||
| 4He+–59Co (4000 эВ) |
1.44 | 1 | 2.08 | 1.44 | 3.38 |
| 1.5 | 1.07 | 0.74 | 1.71 | ||
| 2 | 0.74 | 0.51 | 1.19 | ||
| 40Ar+–59Co (2000 эВ) |
1.18 | 2 | 3.57 | 3.03 | 5.2 |
| 3 | 2.45 | 2.08 | 3.5 | ||
| 4 | 2.38 | 2.02 | 3.4 |
Все графики, показанные на рис. 2, расположены выше оси Х, при этом их формы напоминают колокола. Формы вершин КЗ хорошо совпадают в расчетах с использованием точных и приближенных уравнений на всех графиках. Полученные результаты свидетельствуют о том, что совпадение наблюдается не только при рассеянии на углы θ1 ≥ π/2, но и до углов θ1 ~ 50–60 град. Этот факт свидетельствует о допустимости приближений, используемых при получении уравнений (14) и (18).
Центры КЗ расположены на расстоянии bs от атома. Если s фиксировано, то bs является наименьшим возможным значением ρms и зависит от параметров частиц. Его абсолютные значения приведены в табл. 1. С увеличением s величина bs непропорционально уменьшается, а коэффициент падения уменьшается с увеличением энергии ионов (в ~4 и 2.8 раза для 4He+ с энергиями 2000 и 4000 эВ соответственно). Для более тяжелых ионов величина bs увеличивается (для 4He+ и 40Ar+ при s = 2 в ~3.4 раза) и также непропорционально уменьшается с увеличением s, но с меньшим коэффициентом (~1.5). Ширина пика ∆X всегда больше расстояния наибольшего сближения bs: для 4He+ в 1.6 и для 40Ar+ в 1.4 раза. Что касается изменений ∆X, то они аналогичны вариациям bs с аналогичными коэффициентами. Следует отметить, что обе эти величины в приведенных выше примерах в 2–3 раза превышают атомные тепловые колебания поверхностных атомов, оценки которых (≤10–2 нм) приведены в работе [15].
Полученные данные показывают, что форма вершины КЗ зависит от степени экранировки, порядкового номера и соотношения масс, сталкивающихся частиц. С усилением экранировки кривые становятся более узкими. Для тяжелых ионов графики расположены более близко друг к другу.
Представленные выше расчеты и выводы важны при изучении отражений атомных частиц низких и средних энергий на большие углы (например, для метода Impact Collision Ion Scattering Spectroscopy [3, 15]).
ЭНЕРГИЯ БЛОКИРОВКИ ПОВЕРХНОСТИ
Далее рассмотрим блокировку поверхности мишени и ее связь с пороговыми энергиями распыления.
Предположим, что мишень является аморфным телом, состоящим из атомов (Z2, m2), со средним межатомным расстоянием d. Нормально к поверхности мишени падает параллельный пучок ионов (Z1, m1) с энергией Е в несколько кВ. Постепенно при уменьшении энергии Е величина bs возрастает, а вершина КЗ увеличивается в размерах. При этом для фиксированного значения прицельного параметра ρ величина второго слагаемого под квадратным корнем в формуле (14) уменьшается. При условии
(19)
$\left( {{4 \mathord{\left/ {\vphantom {4 s}} \right. \kern-0em} s}} \right){{{{\rho }^{2}}} \mathord{\left/ {\vphantom {{{{\rho }^{2}}} {b_{s}^{2}}}} \right. \kern-0em} {b_{s}^{2}}} \ll 1.$Для того, чтобы найти блокирующую энергию Еbl поступим следующим образом. Наибольшее значение прицельного параметра ρ для рассматриваемого случая может составлять d/2. Величина блокирующей энергии может быть сопоставима с неупругими потерями иона, поэтому в данном случае необходим их учет, который выполнен с помощью замены Еbl на Еbl – U0, где U0 – энергия сублимации атомов мишени. С учетом этих замечаний из (7) и (19) получаем выражение для вычисления блокирующей энергией:
(20)
$\begin{gathered} {{E}_{{{\text{bl}}}}} - {{U}_{0}} \ll \left( {1 + {{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} \right) \times \\ \times \,\,({{{{Z}_{1}}{{Z}_{2}}{{q}^{2}}{{k}_{s}}{{s}^{{{{\left( {s - 2} \right)} \mathord{\left/ {\vphantom {{\left( {s - 2} \right)} 2}} \right. \kern-0em} 2}}}}} \mathord{\left/ {\vphantom {{{{Z}_{1}}{{Z}_{2}}{{q}^{2}}{{k}_{s}}{{s}^{{{{\left( {s - 2} \right)} \mathord{\left/ {\vphantom {{\left( {s - 2} \right)} 2}} \right. \kern-0em} 2}}}}} a}} \right. \kern-0em} a}){{\left( {{a \mathord{\left/ {\vphantom {a d}} \right. \kern-0em} d}} \right)}^{s}} = {{E}_{{{\text{cr}}}}}, \\ \end{gathered} $Между изменениями величин Z, m и d в формуле (20) нет корреляции. С ростом Zi от 1 (для 2Н) до 92 (238U) коэффициент mi/Zi непрерывно возрастает от ~2 до ~2.59. Вариации d носят циклический характер и изменяются от минимального (для С ~ 0.154 нм) до максимального (для Cs ~ ~ 0.5235 нм) значений [16]. Энергия сублимации атомов мишени изменяется также в широких пределах от ~0.6 до ~9 эВ [17]. По этой причине все дальнейшие расчеты были выполнены при значениях d = 0.3 нм, U0 = 5 эВ и mi/Zi = 2 для всех элементов мишени. Расчеты были выполнены для ионов с большим отличием в порядковых номерах и массах: гелия 4Не+ и ртути 200Hg+. Кроме того, значения s возрастали с увеличением Z1 и m1 иона и были равны 1.15 и 4 для 4Не+ и 200Hg+ соответственно. Расчетный диапазон изменений m2/m1 составил для ионов гелия от 1 до 60 а ртути от 0.01 до 2.
С учетом этих замечаний на рис. 3 представлен график зависимости критической энергии Ecr от отношения масс (сплошные линии (1) для 200Hg+ и (2) для 4Не+). Для выполнения неравенства (20) с точностью 5% при расчете энергии блокировки Еbl (пунктирные линии) от отношения масс m2/m1 для 200Hg+ (1) и 4Не+ (2) считали, что Еbl – U0 = = Ecr/20.
Рис. 3.
Зависимости критической Ecr (сплошные линии) и блокирующей Еbl (пунктирные линии) для ионов 200Hg+ (1) и 4He+ (2) от соотношения масс систем мишень–ион (m2/m1).
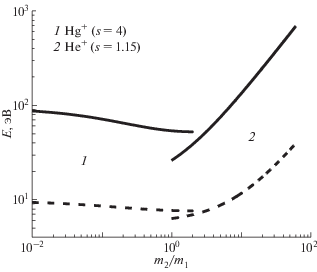
С увеличением m2/m1 представленные кривые показывают рост величин Ecr и Еbl для 4Нe+ и падение для 200Hg+. Наибольшее возрастание критической и блокирующей энергий наблюдается для ионов гелия. Суммарная форма кривых (1) и (2) для Еbl или Ecr напоминает зависимость пороговой энергии распыления Eth от отношения масс m2/m1 [4], отличаясь от нее количественно.
При небольшом увеличении энергии ионов Е > Еbl между соседними атомами на поверхности мишени образуется щель. Часть падающих ионов, имеющих соответствующий прицельный параметр ρ, может пройти через эту щель, попасть внутрь мишени и взаимодействовать со следующим слоем атомов твердого тела, расположенном на расстоянии d от поверхности. Но затратив часть своей энергии при взаимодействии с поверхностным атомом и имея энергию Е ≤ Еbl, ион будет блокироваться этим внутренним слоем и рассеиваться в сторону поверхности. Если этот ион обладает достаточной энергией для выбивания атома из верхнего слоя (равной энергии сублимации атома мишени U0), то начинается процесс распыления.
Такой же механизм, предполагающий, что первичный ион при нормальном падении на поверхность сначала проникает внутрь мишени на глубину ~d, затем рассеивается на угол ~π и уже при движении из глубины мишени выбивает внешний атом, был использован в [4] при вычислении пороговой энергии распыления Eth. При этом глубина выхода распыленных частиц h (отсчет от поверхности вглубь мишени) предполагалась равной нулю. Полученная в [4] формула для Eth хорошо описывает экспериментальные данные, но механизм разворота на угол ~π, по-видимому, связан с результатами данной работы. Такой же вариант распыления был рассмотрен в работе [18] и признан доминирующим в области низких энергий. Следует отметить, что Eth больше Еbl в несколько раз и связано это с необходимостью дополнительных затрат энергии на движение иона внутри твердого тела и неупругие взаимодействия.
В заключение оценим критерий применимости классической механики в проведенных расчетах. Известно, что если длины волн де Бройля частиц малы по сравнению с характерными размерами L, определяющими условия данной конкретной задачи, то свойства системы близки к классическим [19]. В нашем случае L = d = 0.3 нм, а длина волны иона λ с массой m и энергией E определяется уравнением λ = 2πћ/(mE)1/2 [19]. Для ионов Hе+ (m = m1 =4) наименьшая энергия Ebl, найденная из рис. 3, составляет ~6 эВ. Расчет с использованием уравнения дает значение λ ~ ~ 5.9 × 10–3 нм, что в ~50 раз меньше используемого в работе значения d. Все расчеты, выполненные для других ионов в разделах выше, дают меньшие значения λ. Кроме того, для всех значений bs, представленных в табл. 1, выполняется условие bs > λ с учетом зависимости длины волны иона главным образом от его энергии. Таким образом, можно сделать вывод, что выполненные в работе расчеты с использованием классической механики правомерны.
ЗАКЛЮЧЕНИЕ
Вершина конуса затенения является основой для дальнейшего построения его боковой поверхности и может влиять на результаты расчетов и обработки экспериментальных данных. Предложенный метод расчета позволил вычислить и систематически исследовать формирование вершины КЗ при рассеянии атомных частиц. По-видимому, энергетическая область этого метода расчета может быть расширена до нескольких МэВ, несмотря на то, что рассмотрение ограничено низкими и средними энергиями. Что касается применения результатов этой работы, то они достаточно широки (технология и диагностика твердых тел, связанных с ионными пучками) и коррелируют с нано- и субнано-размерами. Некоторые приложения будут рассмотрены в дальнейших исследованиях.
Список литературы
Ackerman P.A.J. Surface Analysis by Low-Energy Ion Scattering: Two-Dimensional Detection and Ouantification. Eindhoven: Technische Universiteit Eindhoven, 1990. 107 p. https://doi.org/10.6100/IR338284
Rabalais J.W. Principles and Applications of Ion Scattering Spectrometry. Surface Chemical and Structural Analysis. John Wiley & Sons. Inc., Hoboken, New Jersey. 2003. 306 p. ISBN 0-471-20277-0. https://us.nicebooks.com/search/isbn?isbn=0-471-20277-0
Aono M. Katayama M. // Compendium of Surface and Interface Analysis. Ed. by The Surface Science Society of Japan. Springer Nature Singapore Pte Ltd., 2018. P. 275. https://doi.org/10.1007/978-981-10-6156-1_45
Пустовит А.Н. // Поверхность. Рентген., синхротр. и нейтрон. исслед. 2017. № 10. С. 77. DOI: 10.7868 /S20735281700122
Landau L.D., Lifshits E.V. Mechanics. V. 1. 3rd Ed., Butterworth-Heinemann, 1982. 224 p. ISBN 9780750628969. https://us.nicebooks.com/search/ isbn?isbn=9780750628969
Lehmann Chr. Interaction of Radiation with Solids and Elementary Defect Production. North-Holland, Elsevier North-Holland, 1977. 359 p. ISBN 10: 0720404169 ISBN 13: 9780720404166. https://us.nicebooks.com/ search/isbn?isbn=0720404169
Oen O.S. // Surf. Sci. V. 131. 1983. P. L407. https://doi.org/10.1016/0039-6028(83)90269-8
Hird D. // Can. J Phys. V. 69. 1991. P. 70. https://doi.org/10.1139/p91-011
Lindhard J., Nielsen V., Scharff M. // Mat.-Fys. Medd. K. Dan. Vidensk. Selsk. V. 36. № 10. 1968. P. 1.
Torrens I.M. Interatomic Potentials. Academic Press, N.Y. 1972. 247 p. ISBN 9780126958508, 0126958505. https://us.nicebooks.com/search/isbn?isbn= 9780126958508
Pustovit A.N. // Bull. Russ. Acad. Sci. Phys. V. 74. 2010. P. 165. https://doi.org/10.3103/S1062873810020140
Oura K., Lifshits V.G., Saranin A.A., Zotov A.V., Katayama M. Surface Science: An Introduction. Springer-Verlag, 2003. 452 p. ISBN 3-540-00545-5. https://us.nicebooks.com/search/isbn?isbn=3-540-00545-5
Shkarofsky I.P., Johnston T.W., Bachynski M.P. The Particle Kinetics of Plasmas. Addison-Wesley Publ., Reading: Massachusetts, 1966. 518 p. ISBN 10: 0201070197. ISBN 13: 9780201070194. https://us.nicebooks.com/search/isbn?isbn=0201070197
Horhager M., Partoll H. MathCad: Einfuhrung, Anwendung, Referenz. Addison-Wesley, 1998. 477 p. ISBN 3-8273-1343-0. https://us.nicebooks.com/ search/isbn?isbn=3-8273-1343-0
Aono M., Soudo R. // Jpn. J. Appl. Phys. V. 24. 1985. P. 1249. https://iopscience.iop.org/article/10.1143/ JJAP.24.1249
Kittel Ch. Introduction To Solid State Physics. 8Th Ed. John Wiley & Sons, 2005. 704 p. ISBN 0-471-41526-X, https://us.nicebooks.com/search/isbn?isbn=0-471-41526-X
Габович М.Д., Плешивцев Н.В., Семашко Н.Н. Пучки ионов и атомов для управляемого термоядерного синтеза и технологических целей. М.: Энергоатомиздат, 1986. 249 с.
Behrisch R., G. Maderlechner G., Scherzer B.M.U., Robinson M.T. // Appl. Phys. V. 18. 1979. P. 391. https://doi.org/10.1007/BF00899693
Landau L.D., E Lifshits E.V. Quantum Mechanics: Non-Relativistic Theory. V. 3, 3rd Ed. Butterworth-Heinemann, 1981. 689 p. ISBN 10:0750635398. ISBN 13:978-0750635394. https://us.nicebooks.com/search/ isbn?isbn=978-0750635394
Дополнительные материалы отсутствуют.
Инструменты
Поверхность. Рентгеновские, синхротронные и нейтронные исследования


