Приборы и техника эксперимента, 2019, № 1, стр. 103-109

ВВЕДЕНИЕ

Использование магнетронов с дисковым катодом для напыления покрытий с малой неравномерностью толщины затруднено из-за неоднородности потока распыленных атомов [1]. Как было показано в [2], такие покрытия могут быть получены при напылении на смещенную, расположенную параллельно плоскости распыляемого катода магнетрона, вращающуюся подложку. Этот способ размещения является частным случаем позиционирования смещенной относительно магнетрона наклонной вращающейся подложки [3, 4]. При этом как для частного, так и для общего случая актуальны вопросы наличия положения подложки, оптимального по критерию массопереноса распыленного материала, а также оценки преимуществ, которые дает наклон подложки.

Для оценки эффективности процесса напыления удобно использовать коэффициент массопереноса:

где ∆m_s, мг – полная масса распыленного с катода магнетрона материала; ∆m_d, мг – масса осажденного на подложку материала.

Этот параметр можно увеличить кратно количеству подложек, которые возможно одновременно разместить вокруг магнетрона. Коэффициент массопереноса определяет себестоимость процесса напыления. Наличие оптимума по коэффициенту массопереноса позволило бы минимизировать размеры вакуумной камеры и, следовательно, снизить необходимую производительность откачной системы, а также расход рабочего газа.

Данная работа посвящена исследованию наличия оптимального положения подложки при напылении, разработке алгоритма его расчета, выявлению общих закономерностей при оптимальном позиционировании и сравнению описанных выше способов размещения вращающейся подложки при напылении.

ОБОРУДОВАНИЕ И МЕТОДИКА ЭКСПЕРИМЕНТА

Схема взаимного размещения магнетрона и подложки, а также фотография использованного оборудования представлены на рис. 1.

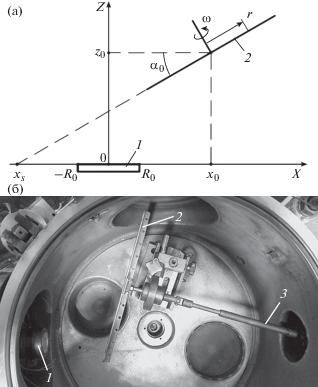
Вращение подложки в вакуумной камере осуществлялось с использованием магнитной муфты, установленной на фланце вакуумной камеры. Телескопическая конструкция вала привода вращения 3 обеспечивала возможность изменения длины в осевом направлении при изменении положения подложкодержателя 2, а карданная передача – возможность наклона подложки. Для позиционирования подложки использовался шаблон.

Эксперименты по напылению проводились на установке с цилиндрической вакуумной камерой диаметром 380 мм и высотой 240 мм и с турбомолекулярной откачной системой. Рабочий газ – Ar. Образцы взвешивались на аналитических весах CAS CAUW 220D с точностью измерения 10^–5 г.

Для нанесения покрытий использовался планарный магнетрон с дисковым катодом радиусом R₀ = 12.5 мм и встроенным изолированным кольцевым анодом. Напуск газа осуществлялся непосредственно в зону распыления. Магнитная система была выполнена из постоянных NdFeB-магнитов (N42). Центральный цилиндрический магнит имел размеры ∅10 × 10 мм, периферийный кольцевой магнит – ∅25 × ∅18 × 5 мм. Магниты устанавливались на дисковый магнитопровод из стали Ст3 с размерами ∅25 × 10 мм и цилиндрическим вырезом ∅18 × 5 мм. Максимальная толщина распыляемого Cu-катода составляла 3 мм. Распыление проводилось в режиме стабилизации мощности разряда, чем обеспечивалось постоянство скорости напыления [5]. Режим магнетронного напыления: давление аргона P_Ar = 3 ⋅ 10^–3 Торр, напряжение U_d = 440 В, ток I_d = 0.072 А.

Коэффициент энергетической эффективности [5] рассчитывался по формуле

где W_d, Вт – мощность разряда; T, мин – время напыления. Для использованного магнетрона для Cu экспериментально определенное значение K_W составило 0.159 мг/(Вт · мин).

Толщина покрытия измерялась на установке рентген-флуоресцентного анализа “Clever B23” [6]. Пересчетные зависимости для перевода интенсивности характеристической линии меди в толщину покрытия были определены путем сравнения с данными, полученными весовым методом измерения толщины (по результатам взвешивания марок до и после напыления).

Толщина покрытия H, мм, на расстоянии r, мм, от центра подложки рассчитывалась как

Здесь где x₀, мм, z₀, мм, α₀, градус – параметры позиционирования подложки (см. рис. 1а); r, мм – расстояние от оси вращения подложки до точки осаждения; F₁(ξ) – аппроксимирующая функция для экспериментально измеренной, нормированной на единицу в максимуме зависимости потока распыленных атомов от угла вылета ξ (угловое распределение); A, B, C, D, K₁ – параметры аппроксимации для Cu; F₂(ρ) – аппроксимирующая функция для экспериментально измеренной, нормированной на единицу в максимуме зависимости глубины эрозии от расстояния до центра распыляемого катода магнетрона ρ, мм (профиль зоны эрозии); σ₁, σ₂, n₁, n₂, K₂ – параметры аппроксимации; ρ₀, мг/мм³ – плотность материала катода; ρ_max, мм – экспериментально измеренное расстояние от центра катода до максимума зоны эрозии; θ, градус – угол осаждения частиц на подложке; d, мм – расстояние от точки распыления (на катоде магнетрона) до точки осаждения (на подложке); γ, градус – параметр позиционирования точки осаждения на подложке. Подробный вывод формулы (3) представлен в приложении “Аналитическая модель напыления покрытий на вращающуюся подложку” к настоящей публикации.

Параметры аппроксимации экспериментально измеренных профиля зоны эрозии и углового распределения рассчитывались методом обобщенного регрессионного анализа с использованием функции “Genfit” в среде Mathcad. Были получены следующие значения: 1) для углового распределения при распылении Сu: A = 1.131, B = = 1.079, C = 0.428, D = 7.818, K₁ = 0.151; 2) для профиля зоны эрозии: σ₁ = 2.49, n₁ = 1.62, σ₂ = 1.73, n₂ = 1.62, ρ_max = 6.63 мм, K₂ = 0.09 мм.

МЕТОДИКА РАСЧЕТА ПАРАМЕТРОВ ОПТИМАЛЬНОГО ПОЗИЦИОНИРОВАНИЯ ПОДЛОЖКИ

Оптимальное позиционирование подложки определяется выбором таких значений x₀, z₀ и α₀, при которых неравномерность толщины покрытия соответствует заданной величине и обеспечивается максимальный массоперенос материала с катода на подложку. Под коэффициентом неравномерности покрытия по толщине K_u, %, здесь понимается величина

где H_max, H_min, мм – соответственно максимальная и минимальная толщина покрытия.

Коэффициент массопереноса K_d, %, распыленного материала на подложку с учетом выражения (1) можно записать в виде:

где R_S, мм – радиус напыляемой подложки.

Для определения взаимосвязи параметров позиционирования подложки с неравномерностью напыляемого покрытия по толщине использовался следующий алгоритм расчета. Задавались радиус подложки R_S и массив исходных значений параметров позиционирования: x₀ (диапазон изменения 0–150 мм с шагом 2.5 мм), z₀ (40–200 мм с шагом 5 мм), α₀ (0°–30° c шагом 0.1°). Для каждой тройки параметров {x₀, z₀, α₀} рассчитывались неравномерность покрытия по толщине и коэффициент массопереноса. Для каждого заданного z₀ строились линии уровня для коэффициента неравномерности толщины покрытия и коэффициента массопереноса при варьировании значений α₀ и x₀. Характерный вид линий при z₀ = 110 мм и R_S = 100 мм представлен на рис. 2.

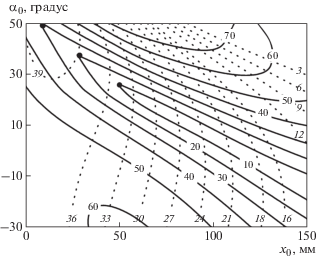
Согласно рис. 2, для фиксированного значения z₀ при заданной неравномерности покрытия по толщине существует единственная пара значений {x₀, α₀} (соответствуют точке перегиба линии уровня K_u на рис. 2), при которых обеспечивается максимальный массоперенос распыленного материала на подложку. Результаты расчета профиля покрытия при таком позиционировании представлены на рис. 3.

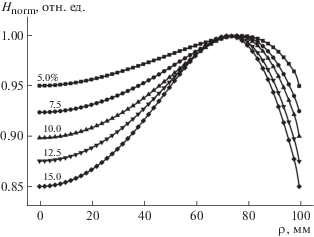
Расчет показал, что при таком размещении подложки профиль покрытия имеет максимум, смещенный относительно центра подложки, а толщины покрытия на оси вращения подложки и на ее краю – одинаковы. Было сделано предположение, что это является необходимым (но не достаточным) условием для оптимального позиционирования подложки.

Исходя из этого предположения, был разработан усовершенствованный алгоритм расчета, обеспечивший значительное сокращение времени счета (с нескольких суток до нескольких часов на использованном оборудовании). Для расчета формировалось множество пар исходных значений {x₀, z₀}, где x₀ ∈ [0, R_S] и z₀ ∈ [0.5R_S, 1.5R_S]. Шаг по x₀ и z₀ соответственно составлял: Δx₀ = 2.5 мм, Δz₀ = 1 мм. Для каждого элемента этого множества методом последовательных приближений проводился поиск значения угла наклона подложки α₀, при котором толщины покрытия в центре и на краю подложки были равны.

Таким образом, было сформировано новое множество параметров позиционирования {x₀, z₀, α₀}. Для каждого элемента этого массива проводился расчет коэффициентов K_u и K_d. Далее, для каждого z₀ определялись координаты {x₀, α₀}, для которых K_u соответствовало заданному значению. Для этих координат рассчитывался коэффициент массопереноса K_d. Характерный вид зависимостей K_d(z₀), x₀(z₀) и α₀(z₀) при выполнении условия равенства толщины покрытия в центре и на краю подложки с радиусом R_S = 100 мм при заданных значениях K_u = {5, 7.5, 10, 12.5, 15%} представлен на рис. 4.

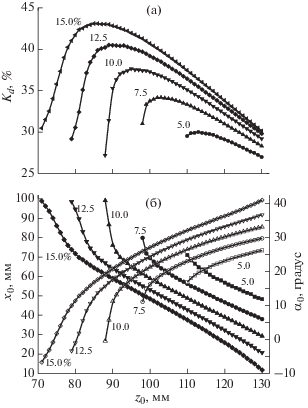
Для каждого K_u из полученных результатов выбиралась точка, соответствующая максимальному значению K_d (соответствует максимуму на рис. 4а). Полученные значения {x₀, z₀, α₀} и являются параметрами оптимального позиционирования. На рис. 5 представлены результаты расчета оптимальных параметров для подложек с радиусом R_S = {20, 40, 60, 80, 100, 120, 140, 160 мм} и неравномерностей толщины покрытия K_u = {5, 7.5, 10, 12.5, 15%}.

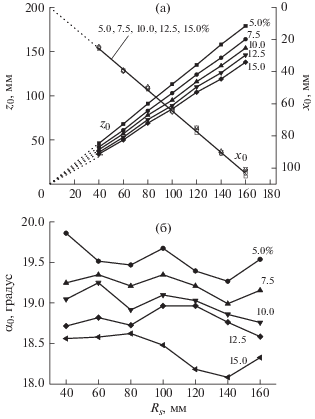
Из рис. 5 следует, что зависимости оптимальных параметров позиционирования x₀ и z₀ от R_S при заданном значении неоднородности покрытия по толщине носят линейный характер и проходят через начало координат (центр катода магнетрона), а α₀ не зависит от R_S и является постоянной величиной при заданной неоднородности. Эти закономерности могут быть использованы для дальнейшего усовершенствования расчетного кода.

На рис. 6 представлена зависимость коэффициента массопереноса K_d от неравномерности покрытия по толщине K_u при оптимальном положении подложки.

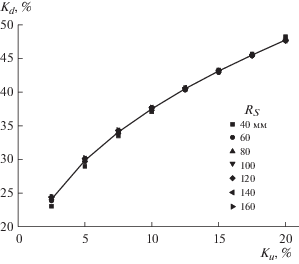
Отметим, что K_d(K_u) не зависит от радиуса подложки R_S.

ЭКСПЕРИМЕНТАЛЬНАЯ ПРОВЕРКА ТОЧНОСТИ РАСЧЕТА ОПТИМАЛЬНОГО ПОЛОЖЕНИЯ И СООТВЕТСТВУЮЩЕГО ЕМУ ПРОФИЛЯ ПОКРЫТИЯ НА СМЕЩЕННОЙ ВРАЩАЮЩЕЙСЯ ПОДЛОЖКЕ

Проверка точности расчета напыления на вращающуюся подложку была проведена для подложки радиусом R_S = 100 мм при ее оптимальном позиционировании (x₀ = 66 мм, z₀ = 112 мм, α₀ = 19.1°) путем сравнения с экспериментально измеренным профилем толщины осажденной пленки. При этом заданное значение неравномерности покрытия по толщине составляло K_u = 5%. Результаты расчета и измерения профиля покрытия, полученного при напылении, представлены на рис. 7.

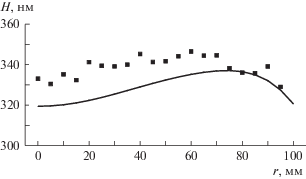
Отклонение результатов расчета от экспериментально измеренных значений не превышает 6%. С учетом неизбежных неточностей в позиционировании и при экспериментальном измерении параметров магнетронного распыления (K_W, F₁(ξ), F₂(ρ)), а также учитывая, что точность измерения толщины методом рентген-флуоресцентного анализа [7] для Cu на использованном оборудовании составляет ≈10 нм, полученная точность расчета является очень хорошим результатом.

СРАВНИТЕЛЬНЫЙ АНАЛИЗ ЭФФЕКТИВНОСТИ НАПЫЛЕНИЯ ПРИ НАЛИЧИИ И ОТСУТСТВИИ НАКЛОНА ПОДЛОЖКИ

На основе разработанного алгоритма расчета был проведен сравнительный анализ зависимости коэффициента массопереноса K_d от радиуса подложки R_S для K_u = 5% при оптимальном позиционировании c наклоном и без наклона (α₀ = 0°) подложки. Результаты представлены на рис. 8.

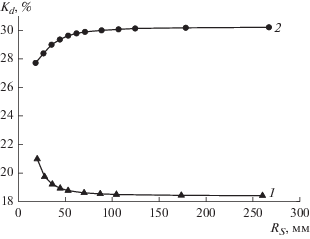
При больших диаметрах подложки (больше 50 мм для использованного магнетрона) коэффициент массопереноса при оптимальном размещении подложки практически не зависит от ее радиуса и является постоянной величиной. Наклон подложки позволяет значительно увеличить массоперенос (на ≈64% для использованного магнетрона) и, помимо этого, уменьшить размеры вакуумной камеры за счет меньшего оптимального смещения x₀ подложки.

ЗАКЛЮЧЕНИЕ

Полученные формулы для расчета профиля покрытия включают в себя параметры универсальных аппроксимаций профиля зоны эрозии и углового распределения потока распыленных атомов при магнетронном распылении, т.е. могут быть использованы для широкого круга планарных магнетронных распылительных устройств с дисковым катодом и любого распыляемого материала без каких-либо доработок. Отличительной особенностью предложенной методики расчета профиля покрытия является возможность учета особенностей используемого для напыления устройства и вакуумных условий путем измерения требуемых для расчетов параметров (K_W, F₁(ξ), F₂(θ)) непосредственно на используемом оборудовании в режиме напыления покрытия. Ввод в аппроксимацию углового распределения экспериментально измеряемого коэффициента K₁ позволяет учесть рассеяние и термализацию распыленных частиц на рабочем газе при транспортировке до подложки. При этом достигается достаточная для проведения инженерных расчетов точность.

На основе анализа результатов расчетов выявлено, что для наклонной вращающейся подложки при заданном значении неравномерности покрытия по толщине существует единственный набор оптимальных параметров позиционирования, при которых потери распыленного материала минимальны. Значение этих оптимальных параметров зависит от конструкции магнетрона, распыляемого материала, размера подложки и требуемой неравномерности толщины покрытия. Выявлено, что равенство толщины покрытия в центре и на краю подложки является необходимым (но не достаточным) условием оптимального позиционирования вращающейся подложки. На основе этого разработан алгоритм расчета параметров оптимального позиционирования.

Сравнительный анализ показал, что наклон подложки обеспечивает существенное увеличение эффективности переноса материала с катода на подложку (более 60% для использованного магнетрона) при прочих равных условиях. Наилучшие результаты по увеличению эффективности напыления могут быть получены, если размер подложки значительно превышает размеры используемого магнетрона. Выявлены закономерности между оптимальными параметрами позиционирования и размером подложки.

Представленная методика расчета оптимального положения подложки может быть использована для уменьшения потерь распыленного материала при напылении однородных по толщине покрытий на крупногабаритные подложки, а также при комплексной разработке оптимизированного оборудования для напыления.