Приборы и техника эксперимента, 2019, № 4, стр. 28-36

1. ВВЕДЕНИЕ

Разрешающая способность измерительных систем как временная, так и пространственная является одной из важнейших характеристик установок для проведения экспериментальных исследований и во многом зависит от технических характеристик применяемого оборудования. Задача повышения разрешающей способности аппаратуры сопряжена с целым рядом научно-технических проблем и требует значительных материальных затрат и финансовых вложений. Разработка математических методов, позволяющих повысить эффективную разрешающую способность измерительных систем вплоть до физических ограничений путем реконструкции и оптимизации полученных экспериментальных данных, является приоритетной альтернативной задачей, не требующей больших затрат.

С точки зрения математики задача реконструкции импульсного отклика измерительных систем из их интегрального отклика, представляющего собой свертку импульсного отклика и функции наложения произвольного вида, относится к классу некорректно поставленных задач [1]. Однако в целом ряде случаев, таких, например, как представленная в [2] реконструкция отклика времяпролетных спектрометров типа ТРОНС (троицкий нейтронный спектрометр) ИЯИ РАН [3] и многих других, задача реконструкции и оптимизации измерений может быть успешно решена.

Возможность реконструкции зависит от многих условий, таких как вид функции наложения и точность ее определения, объем экспериментальных данных и уровень помех в них и др., что требует разработки различных методов, эффективных в том или ином случае.

В данной работе анализируются достоинства и недостатки метода пошаговых сдвигов и его модификаций, предложенных в [2] для математической реконструкции и оптимизации отклика нейтронных спектрометров, связанные с видом функции наложения и наличием помех в экспериментальных данных. Предлагается метод комбинированных сдвигов, позволяющий преодолеть указанные ограничения метода пошаговых сдвигов. Проводится сравнительный анализ методов, рассматривается возможность их применения для восстановления смазанных при сдвиге и размытых по Гауссу многомерных изображений или объектов в них, включая цветные изображения. Приводятся примеры реконструкции экспериментальных данных и изображений.

2. ПОСТАНОВКА ЗАДАЧИ РЕКОНСТРУКЦИИ

Интегральный отклик $H(x)$ измерительной системы при наложении импульсных откликов $h(x)$ по закону $S(x)$ в одномерном случае можно представить в виде свертки функций $S(x)$ и $h(x)$:

В случае дискретных измерений функции $S(x)$ и $h(x)$ можно представить соответственно в виде: $S = \sum\nolimits_k {{{s}_{k}}{{\delta }_{k}}} $ и $h = \sum\nolimits_m {{{h}_{m}}{{\delta }_{m}}} $, где ${{\delta }_{i}}$ – символ Кронекера, отличающийся от 0 и равный 1 только на i-м интервале разбиения оси $x$. При этом интегральному отклику $H(x)$, согласно (1), будет соответствовать суммарный:

С точки зрения математики задача реконструкции импульсного отклика $h(x)$ из интегрального $H(x)$ при известной функции наложения $S(x)$ относится к классу некорректно поставленных задач [1], но в целом ряде случаев может быть решена. Универсального метода решения задачи реконструкции в данной постановке не существует. Возможность реконструкции зависит от вида функции наложения и точности ее определения, от объема экспериментальных данных, уровня помех в них и многих других причин, что требует разработки различных методов, эффективных в том или ином случае.

3. МЕТОД ПОШАГОВЫХ СДВИГОВ

Метод пошаговых сдвигов, предложенный в [2], основан на линейности уравнения (1) относительно функции наложения $S(x)$ и в дискретном случае (2) реализуется посредством итерационных уравнений:

где ${{a}_{n}} = s_{{n + 1}}^{n}{\text{/}}{{s}_{0}}$, ${{S}^{0}} = S$, ${{H}^{0}} = H$, ${{S}^{n}} = \sum\nolimits_k {s_{k}^{n}{{\delta }_{k}}} $ и Hⁿ = $\sum\nolimits_k {\sum\nolimits_m {s_{k}^{n}h_{m}^{n}{{\delta }_{{k + m}}}} } $ – функции наложения и отклика на $n$-м шаге итерации; $S_{l}^{n} = \sum\nolimits_k {s_{k}^{n}{{\delta }_{{k + l}}}} $ и $H_{l}^{n} = \sum\nolimits_k {\sum\nolimits_m {s_{k}^{n}h_{m}^{n}{{\delta }_{{k + m + l}}}} } $ – те же функции, сдвинутые вправо на l интервалов дискретизации.

Алгоритм (3) заключается в последовательном обнулении коэффициентов $s_{1}^{n} = s_{2}^{n} = \cdots = s_{n}^{n} = 0$ в функции наложения ${{S}^{n}}$, поэтому на $n$-м шаге итерации:

т.е. на интервале $[0,n]$: ${{S}^{n}} = {{s}_{0}}{{\delta }_{0}}$, а H_n = ${{s}_{0}}\sum\nolimits_m {{{h}_{m}}{{\delta }_{m}}} $ = = s₀h, что означает решение задачи реконструкции импульсного отклика измерительной системы на этом интервале.

На рис. 1 представлен пример реконструкции импульсного отклика системы $h$ из исходного $H$ при функции наложения $S$ методом пошаговых сдвигов [2].

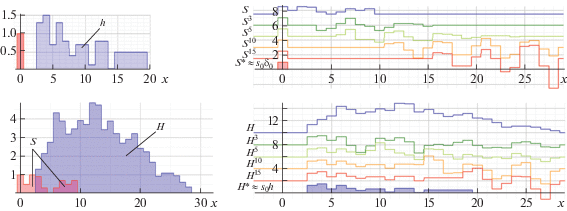
На диаграммах показаны функции наложения и отклика на начальном, 3-м, 5-м, 10-м, 15-м и конечном шагах итерации. В данном примере погрешность реконструкции на исследуемом интервале $err = H{\text{*}} - {{s}_{0}}h$ не превысила $2.5 \cdot {{10}^{{ - 15}}}$.

Достоинством метода пошаговых сдвигов является возможность реконструкции необходимого количества элементов импульсного отклика, что важно при реконструкции откликов неограниченной длины. На диаграммах рис. 1 видно, что на $n$-м шаге итерации происходит последовательная реконструкция $n$ элементов импульсного отклика, начиная с первого, отличного от нуля члена суммарного отклика.

Если функция $S = {{s}_{0}}{{\delta }_{0}} + {{s}_{l}}{{\delta }_{l}}$ описывает наложение двух откликов, то, опуская в (3) шаги итерации, на которых при ${{s}_{k}} = 0$ функции $S$ и $H$ не меняются, получим модифицированные итерационные уравнения:

где $a = {{s}_{l}}{\text{/}}{{s}_{0}}$, $n = 1,{\text{ }}2,{\text{ }} \ldots $, ${{S}^{0}} = S$, ${{S}^{1}} = {{S}^{0}} - aS_{l}^{0}$, ${{H}^{0}} = H$, ${{H}^{1}} = {{H}^{0}} - aH_{l}^{0}$.

Модифицированный метод значительно сокращает число итераций, необходимых для реконструкции. Так, если $N$ – число итераций, необходимых для реконструкции методом пошаговых сдвигов, то число итераций $N{\text{*}}$ модифицированным методом составит: N* = ${\text{lo}}{{{\text{g}}}_{2}}(N{\text{/}}l)$.

Модифицированный метод удобно использовать для моделирования отклика измерительной системы на инициирующий импульс меньшей длительности, что означает возможность повышения эффективной разрешающей способности измерительной аппаратуры вплоть до физических ограничений.

Теоретически метод пошаговых сдвигов дает возможность реконструкции импульсного отклика системы при любом виде функции наложения $S = \sum {{{s}_{k}}{{\delta }_{k}}} $, но на практике, если какой-нибудь из коэффициентов ${{s}_{k}} > {{s}_{0}}$, то множители ${{a}_{n}}$ в (3) или ${{a}^{{{{2}^{n}}}}}$ в (5) будут быстро возрастать, что приведет к резкому росту погрешности численных вычислений, к расходимости итерационной последовательности и, в итоге, к ошибкам реконструкции. На рис. 2 показано возрастание ошибок реконструкции при уменьшении коэффициента ${{s}_{0}}$ от 0.1 до 0.01 в функции наложения на рис. 1.

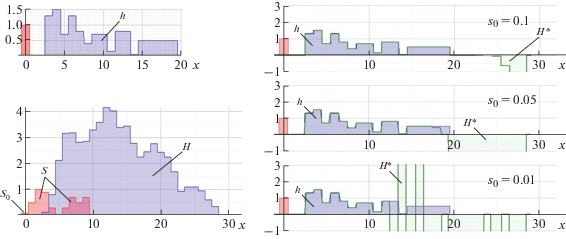
Действительно, если $S = {{s}_{0}}{{\delta }_{0}} + {{s}_{l}}{{\delta }_{l}}$, где ${{s}_{l}}{\text{/}}{{s}_{0}}$ = = a > 1, то даже при ${{s}_{l}}$ больше ${{s}_{0}}$ всего на один процент, т.е. при $a = 1.01$, коэффициент ${{a}^{{{{2}^{n}}}}}$ уже на двадцатом шаге итерации будет равен ${{a}^{{{{2}^{{20}}}}}} \approx {{a}^{{{{{10}}^{6}}}}}$ ≈ ≈ 1.94 · 10⁴⁵³¹. При допустимом максимальном значении числа при вычислениях ${{N}_{{\max }}}$ оказывается возможным реконструировать ${{M}_{{\max }}}$ членов импульсного отклика:

Формулу (6) можно использовать для оценки ${{M}_{{\max }}}$ в случае произвольной функции наложения. Так, на рис. 2: ${{s}_{{\max }}} = {{s}_{2}} = 1$ и при s₀, равных 0.01, 0.05, 0.1, значения М_max соответственно составят ~13, ~19–20, 26, что хорошо согласуется с формулой (6), расчет М_max по которой дает: ~13, ~19.98, ~26.

При двух наложениях $S = {{s}_{0}}{{\delta }_{0}} + {{s}_{l}}{{\delta }_{l}}$, где ${{s}_{l}}{\text{/}}{{s}_{0}} > 1$, реконструкцию можно осуществить относительно члена ${{s}_{l}}{{\delta }_{l}}$, сдвигая итерационную последовательность не вправо, а влево. При этом ${{s}_{0}}{\text{/}}{{s}_{l}} = a < 1$, и множитель ${{a}^{{{{2}^{n}}}}}$ в итерационном уравнении (5) будет быстро уменьшаться. Так, при $a = 0.99$ уже на девятом шаге итерации погрешность реконструкции составит $0.6$%, а на десятом – $3.4 \cdot {{10}^{{ - 3}}}$%.

Однако если максимальный член функции наложения не является крайним, то одновременно обнулить коэффициенты справа и слева от него методом пошаговых сдвигов ни в одну из сторон не удается. В частности, подобная проблема характерна для функций наложения в виде функции Гаусса, что часто встречается на практике. Так, например, импульс, инициирующий поток нейтронов на времяпролетном нейтронном спектрометре ИБР-2М, описывается функцией Гаусса [4].

Кроме того, реконструкция методом пошаговых сдвигов, даже при небольшом уровне помех (${{H}_{{noise}}}$) в экспериментальных данных ($H$), оказывается невозможной, так как итерационная последовательность, как показано на рис. 3, начинает быстро расходиться.

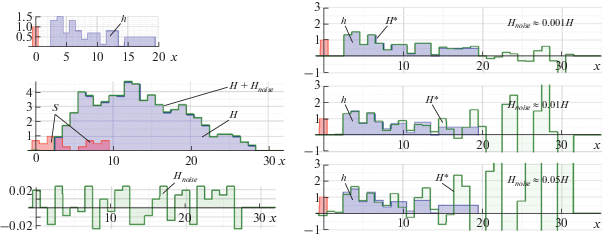
Эти недостатки напрямую связаны с принципиальной проблемой метода пошаговых сдвигов в случае статистических измерений, так как реконструкция импульсного отклика относительно крайнего члена, не являющегося максимальным, означает восстановление отклика относительно члена с меньшей статистикой. Предлагаемый для устранения указанных недостатков метод основан на методе пошаговых сдвигов, но использует комбинацию нескольких сдвигов.

4. МЕТОД КОМБИНИРОВАННЫХ СДВИГОВ

Рассмотрим функцию $S{\text{*}}$, являющуюся линейной комбинацией смещенных функций наложения $S = {{s}_{0}}{{\delta }_{0}} + {{s}_{1}}{{\delta }_{1}} + {{s}_{2}}{{\delta }_{2}}$ с коэффициентами ${{\mu }_{i}}$, где ${{s}_{{\max }}} = {{s}_{1}}$:

Здесь ${{S}_{i}} = {{s}_{0}}{{\delta }_{i}} + {{s}_{1}}{{\delta }_{{i + 1}}} + {{s}_{2}}{{\delta }_{{i + 2}}}$ – смещенная на $i$ дискретных интервалов функция $S$, а коэффициенты ${{\mu }_{i}}$ выбираются так, чтобы в новой функции $S{\text{*}}$ коэффициенты $s_{0}^{*},s_{2}^{*} = 0$ и $s_{1}^{*} = 1$. Представляя функцию ${{S}^{*}} = s_{{ - 1}}^{*}{{\delta }_{{ - 1}}} + {{\delta }_{1}} + s_{3}^{*}{{\delta }_{3}}$ в виде вектора $[\begin{array}{*{20}{c}} {s_{{ - 1}}^{*}}&0&1&0&{s_{3}^{*}} \end{array}]$, уравнение (7) можно записать в матричном виде:

Так как в данном примере значения $s_{{ - 1}}^{*},{\text{ }}s_{3}^{*}$ не важны, для нахождения неизвестных коэффициентов ${{\mu }_{i}}$ достаточно решить сокращенное матричное уравнение:

Согласно наложенным условиям, определитель квадратной матрицы сдвигов ${\mathbf{\Sigma }}$ не равен 0: $\det ({\mathbf{\Sigma }}) \ne 0$, поэтому матрица сдвигов имеет обратную, ${{{\mathbf{\Sigma }}}^{{ - 1}}}$, и уравнение (9) всегда имеет решение:

Таким образом, с помощью линейной комбинации (7) сдвинутых функций наложения $S$ с коэффициентами (10) можно получить новую функцию наложения $S{\text{*}}$, в которой коэффициенты справа и слева от выбранного члена равны нулю.

Аналогично, используя линейную комбинацию функций $S$, сдвинутых вправо и влево на $L$ шагов с коэффициентами $[{{\mu }_{{ - L}}}, \ldots ,{{\mu }_{0}}, \ldots ,{{\mu }_{L}}]$, можно получить функцию наложения S* = ${{\mu }_{{ - L}}}{{S}_{{ - L}}} + \cdots + {{\mu }_{0}}{{S}_{0}}$ + + ··· + μ_LS_L, в которой справа и слева от выбранного члена с индексом ${{k}_{m}}$ стоят $L$ нулевых элементов.

В этом случае, если $L > M$, где $M$ – число членов импульсного отклика системы h = $\sum\nolimits_{m = 0}^M {{{h}_{m}}{{\delta }_{m}}} $, то соответствующий $S{\text{*}}$ отклик

на интервале $[{{k}_{m}},{\text{ }}L + {{k}_{m}}]$ совпадет с $h$: $H{\text{*}} \approx h$. Этот способ реконструкции будем называть методом комбинированных сдвигов.

При реконструкции импульсного отклика $h$ в уравнении (11) вектор ${\mathbf{e}}$ размерности $2L + 1$ имеет лишь один ненулевой элемент: ${{e}_{{L + 1}}} = 1$, а матрица ${{\Sigma }^{{ - 1}}}$ является обратной к квадратной матрице сдвигов $\Sigma $ размерности $2L + 1$. На главной диагонали матрицы сдвигов $\Sigma = \{ {{\Sigma }_{{ij}}}\} $ расположен коэффициент выбранного члена дискретной функции наложения ${{s}_{{{{k}_{m}}}}}$, а на диагоналяx под и над главной диагональю – коэффициенты членов слева и справа от него, в то время как оставшиеся элементы – нулевые, т.е. ${{\Sigma }_{{ij}}} = {{s}_{{{{k}_{m}} + j - i}}}$, $i,j = 0,\; \ldots ,\;2L$.

Коэффициенты сдвига ${\mathbf{\mu }}$ большой размерности удобно искать с помощью прямых или итерационных методов решения линейного уравнения $\mu \cdot \Sigma = {\mathbf{e}}$, где для лучшей сходимости методов выбранным членом в матрице сдвигов должен быть член с максимальным коэффициентом функции наложения: ${{s}_{{{{k}_{m}}}}} = {{s}_{{\max }}}$.

Метод комбинированных сдвигов дает возможность реконструкции отклика относительно выбранного члена при любых функциях наложения $S$, если размерности $K$ и $M$ функции наложения $S$ и импульсного отклика $h$ конечны. При этом исходный отклик $H$ должен быть полностью определен, т.е. его размерность должна быть не меньше, чем $K + M$.

Метод комбинированных сдвигов легко справляется с задачей реконструкции импульсного отклика системы при функции наложения $S$ на рис. 2 со сколь угодно малыми коэффициентами ${{s}_{0}}$, при которых метод пошаговых сдвигов приводил к расходимости итерационной последовательности. Пример такой реконструкции методом комбинированных сдвигов представлен на рис. 4. При ${{s}_{0}} = 0.01$ погрешность реконструкции $err = H{\text{*}} - h$ составляет $3.0 \cdot {{10}^{{ - 12}}}$, а при ${{s}_{0}} = 0.001$ – не превышает $3.0 \cdot {{10}^{{ - 8}}}$.

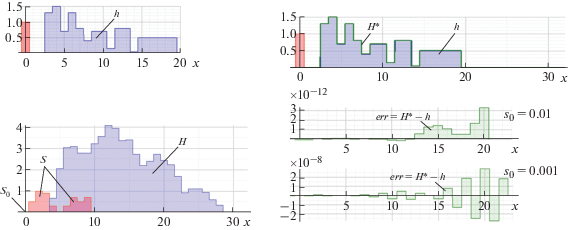
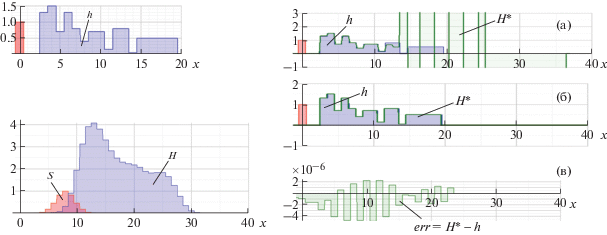
Также легко метод комбинированных сдвигов справляется с реконструкцией импульсного отклика при наложениях в виде функции Гаусса. Пример такой реконструкции методами пошаговых и комбинированных сдвигов представлен соответственно на рис. 5а и 5б. Погрешность реконструкции методом комбинированных сдвигов (рис. 5в) не превышает $4.0 \cdot {{10}^{{ - 12}}}$, в то время как применение метода пошаговых сдвигов приводит к расхождению итерационной последовательности.

Возможность выбора члена, относительно которого осуществляется реконструкция, является важным достоинством метода комбинированных сдвигов при обработке статистических данных, так как означает, что реконструкция проводится относительно члена с наибольшей набранной статистикой. Это преимущество определяет и возможность реконструкции отклика при наличии помех в экспериментальных данных.

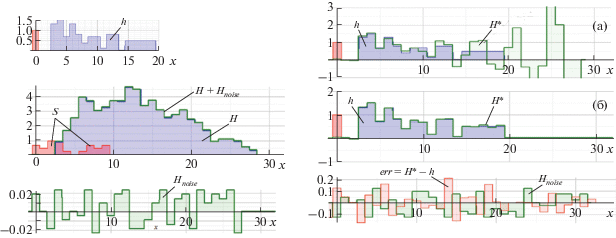
На рис. 6 представлены результаты реконструкции импульсного отклика $h$ методом пошаговых (рис. 6а) и комбинированных (рис. 6б) сдвигов при наличии случайных помех (${{H}_{{noise}}}$) порядка 1.0% от максимального значения исходного отклика H. В то время как в методе пошаговых сдвигов итерационная последовательность расходится (см. рис. 6а), погрешность реконструкции $err = H{\text{*}} - h$ методом комбинированных сдвигов (см. рис. 6б) такого же порядка, как уровень помех ${{H}_{{noise}}}$.

Метод комбинированных сдвигов дает возможность оптимизации экспериментальных данных путем моделирования отклика измерительной системы при любой выбранной функции наложения. При этом достаточно, чтобы вектор ${\mathbf{s}}$ в уравнении (11) описывал желаемую функцию наложения. На практике оптимизация может оказаться единственной альтернативой в случае невозможности реконструкции импульсного отклика системы.

Таким образом, метод комбинированных сдвигов позволяет реконструировать импульсный отклик системы относительно выбранного члена с наибольшей статистикой, смоделировать экспериментальные данные от функции наложения оптимального вида или импульсного отклика меньшей дискретизации, что означает повышение разрешающей способности измерительных систем. При этом применение метода комбинированных сдвигов ограничено условием конечности интервалов функции наложения и импульсного отклика. Также метод комбинированных сдвигов требует выполнения большого объема вычислений при операциях с матрицами большой размерности.

5. ВОССТАНОВЛЕНИЕ ИЗОБРАЖЕНИЙ

В многомерном случае интегральный отклик измерительной системы $H({\mathbf{x}})$, где ${\mathbf{x}} = ({{x}_{1}},{\text{ }}{{x}_{2}},\; \ldots )$, при наложении многомерного изображения $I({\mathbf{x}})$ по закону $S({\mathbf{x}})$ можно представить в виде свертки:

В дискретном случае функции $S({\mathbf{x}})$ и $I({\mathbf{x}})$ описываются соответственно выражениями: S = = $\sum\nolimits_{{{k}_{1}},{{k}_{2}}, \ldots } {{{s}_{{{{k}_{1}}{{k}_{2}} \ldots }}}{{\delta }_{{{{k}_{1}}{{k}_{2}} \ldots }}}} $ и $I = \sum\nolimits_{{{m}_{1}},{{m}_{2}}, \ldots } {{{I}_{{{{m}_{1}}{{m}_{2}} \ldots }}}{{\delta }_{{{{m}_{1}}{{m}_{2}} \ldots }}}} $, где ${{\delta }_{{{{i}_{1}}{{i}_{2}} \ldots }}}$ – многомерный символ Кронекера, отличающийся от 0 и равный 1 только в объеме, ограниченном i₁-м, i₂-м, … интервалами разбиения осей ${{x}_{1}},{{x}_{2}},\; \ldots $ соответственно. При этом интегральному отклику $H({\mathbf{x}})$ будет соответствовать суммарный:

Рассмотренные методы пошаговых и комбинированных сдвигов можно применять для реконструкции многомерных изображений при определенных функциях наложения, которые позволяют свести уравнения (12) и (13) к одномерному случаю или к комбинации одномерных.

Наиболее простым является случай параллельного смещения с наложением, т.е. “смазывания” изображения $I({\mathbf{x}})$ вдоль одной из осей. Так, если, не теряя общности, считать, что смещение происходит вдоль оси $x = {{x}_{1}}$, то выражения (12), (13) сразу преобразуются к одномерному случаю (1), (2):

В этом случае методы пошаговых (3), (5) и комбинированных (11) сдвигов применимы для реконструкции изображений $I({\mathbf{x}})$. Изображения могут быть и цветными, при этом каждый из цветовых слоев восстанавливается аналогично.

На рис. 7 представлены диаграммы последовательного восстановления цветного двумерного изображения $I$ размером 79 $ \times $ 100 пикселей из смазанного по оси x изображения $H$ при функции наложения $S$ методом пошаговых сдвигов на 0-м, 10-м, 20-м, 40-м и 100-м шагах итерации (3). При этом ошибки восстановления $err = H{\text{*}} - I$ не превысили 5 ⋅ 10^–15.

Аналогичным образом можно восстановить смазанный, например быстро двигающийся, объект на изображении. Если направление смещения изображения не совпадает с осями изображения, то наиболее простым способом восстановления является приведение задачи к виду (14), (15) путем поворота координатных осей до совмещения оси смещения с одной из координатных осей. При этом, однако, необходимо учитывать возрастание ошибок дискретизации при повороте осей.

Важным случаем смазанных изображений является равномерно смазанное изображение, которое образуется, например, при регистрации быстро двигающихся объектов. Значительно сократить число необходимых итераций при восстановлении изображений таких объектов позволяет модифицированный метод (5). Так, например, равномерно смазанное изображение с функцией наложения $S = {{\delta }_{{0 - 20}}}$ на рис. 8 можно восстановить модифицированным методом всего за 4 итерации вместо 100 итераций, необходимых в предыдущем случае. При этом, смещая $S$ на один интервал и вычитая ${{S}_{1}}$ из исходной функции, получим: ${{S}^{1}} = S - {{S}_{1}} = {{\delta }_{0}} - {{\delta }_{{21}}}$, к которой применим модифицированный метод (5), позволяющий резко сократить число итераций, необходимых для реконструкции.

Если функция наложения допускает разделение переменных в виде: $S({\mathbf{x}})\, = \,{{S}_{1}}({{x}_{1}}){{S}_{2}}({{x}_{2}}){\kern 1pt} \cdots {\kern 1pt} {{S}_{n}}({{x}_{n}})$, то многомерные уравнения (12), (13) можно свести к комбинации одномерных (1), (2) и решить задачу восстановления изображений рассмотренными одномерными методами. Действительно, в случае разделения переменных уравнение свертки можно представить в виде

и восстановить изображение, последовательно реконструируя функции ${{I}_{1}}({\mathbf{x}}),{{I}_{2}}({\mathbf{x}}), \ldots ,{{I}_{n}}({\mathbf{x}})\, = \,I({\mathbf{x}})$ рассмотренными ранее одномерными методами пошаговых или комбинированных сдвигов:

Порядок реконструируемых функций может быть произвольным. Так, например, в двумерном случае существует два пути восстановления изображения через реконструкцию ${{I}_{x}}(x,y)$ или ${{I}_{y}}(x,y)$:

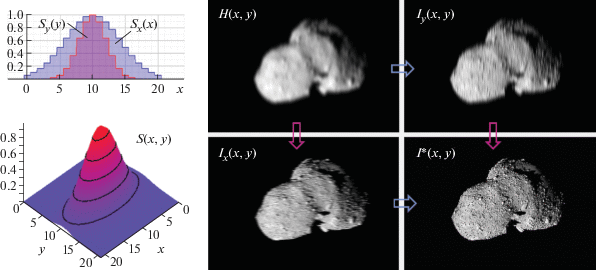
На рис. 9 представлен пример восстановления размытого изображения при функции наложения в виде двумерной функции Гаусса, которая допускает разделение переменных: S(x, y) = ${\text{exp}}\left[ { - {\kern 1pt} \frac{1}{2}\left( {\frac{{{{x}^{2}}}}{{\sigma _{x}^{2}}}\, + \,\frac{{{{y}^{2}}}}{{\sigma _{y}^{2}}}} \right)} \right]\, = \,{\text{exp}}\left( { - {\kern 1pt} \frac{{{{x}^{2}}}}{{2\sigma _{x}^{2}}}} \right){\text{exp}}\left( { - \frac{{{{y}^{2}}}}{{2\sigma _{y}^{2}}}} \right)$. Стрелками показаны два возможных пути восстановления изображения $I(x,y)$ из исходного размытого $H(x,y)$: через реконструкцию размытых по x или по y изображений ${{I}_{x}}(x,y)$ и ${{I}_{y}}(x,y)$ соответственно. Ошибка реконструкции err = $I{\text{*}}(x,y) - I(x,y)$ не превысила 1.5%, а разница между изображениями, восстановленными разными путями, err = = $I_{{xy}}^{*}(x,y) - I_{{yx}}^{*}(x,y)$ составила 2 ⋅ 10^–4%.

Функция Гаусса имеет важное практическое значение при восстановлении изображений, поскольку описывает случайные отклонения регистрируемых объектов или регистрирующей аппаратуры от начального зафиксированного положения.

6. ЗАКЛЮЧЕНИЕ

Предлагаемые математические методы реконструкции позволяют путем обработки экспериментальных данных устранить искажения в них, вызванные наложениями, например, из-за различных нестабильностей работы оборудования, и оптимизировать измерения, что означает возможность повышения разрешающей способности измерительной аппаратуры вплоть до физических ограничений. Математические методы реконструкции являются альтернативой техническим методам, сопряженным с трудноразрешимыми научно-техническими проблемами и требующим больших материальных затрат.

Универсального метода решения задачи реконструкции экспериментальных данных, наложенных друг на друга, не существует. Возможность реконструкции зависит от вида функции наложения, точности ее определения, от объема экспериментальных данных, уровня помех в них и многих других причин, что требует разработки различных методов, эффективных в том или ином случае. Методы пошаговых и комбинированных сдвигов взаимно дополняют друг друга.

Важным достоинством методов является возможность восстановления многомерных данных, в частности, смазанных при параллельном смещении или размытых по Гауссу изображений или объектов в них.

Благодаря простоте и эффективности предлагаемые методы могут применяться в различных областях: при обработке данных в экспериментальной физике, в области цифровой обработки сигналов и изображений, при разработке методов деконволюции в математике.