Приборы и техника эксперимента, 2020, № 5, стр. 48-59
ПРЯМАЯ РЕКОНСТРУКЦИЯ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ ПРИ ПЛОХОЙ ОБУСЛОВЛЕННОСТИ ЗАДАЧ И НАЛИЧИИ ИСКАЖЕНИЙ
А. В. Новиков-Бородин *
Институт ядерных исследований РАН
117312 Москва, просп. 60-летия Октября, 7а, Россия
* E-mail: novikov.borodin@gmail.com
Поступила в редакцию 17.02.2020
После доработки 26.04.2020
Принята к публикации 01.05.2020
Аннотация
Исследуются возможности реконструкции дискретных экспериментальных данных с помощью прямой инверсии – деконволюции. Предлагаются методы оптимизации, сглаживания, компенсации и разложения, позволяющие во многих случаях при плохой обусловленности задач и наличии искажений провести реконструкцию с минимальными потерями информации. Методы заключаются в формировании с помощью линейных преобразований из переопределенных систем уравнений, соответствующих уравнениям свертки, хорошо обусловленных систем с компенсацией случайных искажений. Проведен сравнительный анализ предлагаемых методов, рассмотрены их возможности и погрешности реконструкции. Представлены примеры реконструкции.
1. ВВЕДЕНИЕ
Реальные измерительные системы имеют конечное быстродействие, в цифровых системах его ограничивает, прежде всего, конечная частота дискретизации сигнала. Искаженный экспериментальный сигнал выражается в виде свертки неискаженного сигнала и импульсной характеристики измерительной системы, описывающей характер искажения сигнала. Для восстановления неискаженного сигнала из экспериментальных данных требуется обратное преобразование – деконволюция. Это преобразование относится к классу некорректно поставленных задач [1–3], общего решения которых без потери информации не существует. Эффективность реконструкции зависит от множества факторов, таких как вид импульсной характеристики, объем обрабатываемых данных, уровень шумов в них и др., что делает разработку различных методов реконструкции, эффективных в том или ином случае, актуальным направлением исследований.
В случае дискретных измерений уравнения свертки сводятся к системам линейных алгебраических уравнений, и решить задачу деконволюции можно множеством различных способов, начиная от методов прямой матричной инверсии до методов интегральных преобразований и техники регуляризации [4–7]. Основные проблемы заключаются в плохой обусловленности систем и наличии шумов в данных, что приводит к неустойчивости решений и большим погрешностям.
Системы, соответствующие уравнениям свертки, принципиально переопределены, т.е. число уравнений в них превышает число неизвестных. Это дает возможность сформировать из них множество квадратных систем, в которых число уравнений равно числу неизвестных, и выбрать из них системы, наиболее подходящие для решения конкретных задач.
В предлагаемых методах оптимизации, сглаживания, компенсации и разложения используются линейные преобразования, что позволяет избежать потерь информации при формировании систем и осуществить реконструкцию сигналов методами прямой матричной инверсии с минимальными потерями информации во многих сложных случаях плохой обусловленности задач и при наличии случайных шумов в данных.
2. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Искажения в экспериментальных данных H(x), возникающие при свертке неискаженного сигнала h(x) и импульсной характеристики S(x), без дополнительных случайных шумов описываются с помощью уравнения:
(1)
$\begin{gathered} H(x) = (S * h)(x) = \\ \, = \int {S(\xi )h(x - \xi )d\xi = \int {S(x - \xi )h(\xi )d\xi } } . \\ \end{gathered} $Импульсная характеристика S(x) описывает различные искажения, например, обусловленные движением исследуемого объекта, смещениями или колебаниями измерительной аппаратуры, а также вносимые самой измерительной аппаратурой или средой между объектом и аппаратурой (см. примеры в работах [8–10]).
В дальнейшем под реконструкцией будем понимать процесс нахождения функции h(x) из функции H(x), а под моделированием – процесс определения функции S(x) для конструирования из известной функции h(x) заданной функции H(x). В такой постановке обе задачи являются инверсными задачами деконволюции, где при реконструкции в качестве ядра преобразования (1) выступает функция S(x), а при моделировании – функция h(x).
В случае дискретных вычислений функции S(x) и h(x) можно представить в виде: $S = \sum {{{s}_{i}}{{\delta }_{i}}} $ и $h = \sum {{{h}_{i}}{{\delta }_{i}}} $, где δi – аналог символа Кронекера, отличающийся от 0 и равный 1 только на i-м интервале разбиения оси x, и выразить функцию H = (S*h) как:
(2)
$\begin{gathered} H = \sum\limits_n {{{H}_{n}}{{\delta }_{n}}} = \sum\limits_j {\sum\limits_i {{{s}_{i}}{{h}_{j}}{{\delta }_{{i + j}}}} } = \\ \, = \sum\limits_j {{{h}_{j}}\sum\limits_i {{{s}_{i}}{{\delta }_{{i + j}}}} } = \sum\limits_i {{{s}_{i}}\sum\limits_j {{{h}_{j}}{{\delta }_{{i + j}}}} } . \\ \end{gathered} $Дискретный сигнал h определим как отклик H измерительной системы при S = δ0: H = h при S = δ0, т.е. при времени измерений, равному интервалу дискретизации.
Обозначая через ${{S}_{{[j]}}} = \sum\nolimits_i {{{s}_{i}}{{\delta }_{{i + j}}}} $ и ${{h}_{{[i]}}}\, = \,\sum\nolimits_j {{{h}_{j}}{{\delta }_{{i + j}}}} $ функции S и h, смещенные соответственно на j и i интервалов разбиения вправо по оси x, из (2) получим
Представив функции H, S и h в виде векторов-строк H = {Hi}, S = {si} и h = {hi}, а наборы смещенных функций S[j] и h[j] – в виде матриц MS = {si–j} и Mh = {hi-j} с соответствующей векторам H, S и h размерностью (в общем случае бесконечной), уравнения (3) можно записать в матричном виде:
(4)
$\begin{gathered} {\mathbf{H}} = {\mathbf{h}} \cdot {{{\mathbf{M}}}_{S}} = {\mathbf{h}} \cdot \left[ {\begin{array}{*{20}{c}} {{{s}_{0}}}&{{{s}_{1}}}&{{{s}_{2}}}& \cdots \\ 0&{{{s}_{0}}}&{{{s}_{1}}}& \cdots \\ 0&0&{{{s}_{0}}}& \ddots \\ \vdots & \vdots & \ddots & \ddots \end{array}} \right], \\ {\mathbf{H}} = {\mathbf{S}} \cdot {{{\mathbf{M}}}_{h}} = {\mathbf{S}} \cdot \left[ {\begin{array}{*{20}{c}} {{{h}_{0}}}&{{{h}_{1}}}&{{{h}_{2}}}& \cdots \\ 0&{{{h}_{0}}}&{{{h}_{1}}}& \cdots \\ 0&0&{{{h}_{0}}}& \ddots \\ \vdots & \vdots & \ddots & \ddots \end{array}} \right]. \\ \end{gathered} $Матрицы MS и Mh, строки которых представляют собой сдвинутые вектора S и h, будем называть матрицами сдвигов, а вектора S и h – производящими для них. Выражения (4), соответствующие уравнению свертки (1), будем называть сверточными системами.
Если известны первые m элементов функции H, то, образуя из коэффициентов функции S матрицу сдвигов ${{{\mathbf{M}}}_{0}} = \{ {{s}_{{i - j}}}\} _{{i,j = 0}}^{{m - 1}}$ размерности m × m, можно из (4) сформировать квадратную систему из m линейных алгебраических уравнений:
(5)
$\begin{gathered} {{{\mathbf{H}}}_{0}} = [\begin{array}{*{20}{c}} {{{H}_{0}},}&{{{H}_{1}},}& \cdots &{{{H}_{{m - 1}}}} \end{array}] = \\ \, = [\begin{array}{*{20}{c}} {{{h}_{0}},}&{{{h}_{1}},}& \cdots &{{{h}_{{m - 1}}}} \end{array}] \cdot \left[ {\begin{array}{*{20}{c}} {{{s}_{0}}}&{{{s}_{1}}}&{{{s}_{2}}}& \cdots \\ 0&{{{s}_{0}}}&{{{s}_{1}}}& \cdots \\ \vdots & \ddots & \ddots & \ddots \\ 0& \cdots &0&{{{s}_{0}}} \end{array}} \right] = {\mathbf{h}} \cdot {{{\mathbf{M}}}_{0}}, \\ \end{gathered} $Систему (5) будем называть неоптимизированной для сверточных систем (4). Она имеет единственное решение, если определитель матрицы M0 не равен 0. Для матрицы M0 определитель det(M0) = = $s_{0}^{m}$, что эквивалентно условию s0 ≠ 0, которое для реальных физических измерений всегда имеет место, так как характеризует начало измерений. Для многих реальных измерений коэффициенты si функции S характеризуют интервал или интенсивность сигналов при наложении и определены положительно.
При плохой обусловленности неоптимизированной системы (5), даже небольшие помехи в данных или ошибки в вычислениях, например, при округлении действительных чисел, могут привести к значительным погрешностям решения и даже к его расходимости. Например, элементы функции h можно реконструировать из системы (5), последовательно решая уравнения s0h0 = H0, s1h0 + s0h1 = = H1, …, что соответствует обратному ходу метода Гаусса–Жордана:
(6)
${{h}_{i}} = \frac{{{{H}_{i}}}}{{{{s}_{0}}}} - \sum\limits_{j = 0}^{i - 1} {{{h}_{i}}\frac{{{{s}_{{i - j}}}}}{{{{s}_{0}}}}} ,\quad {{h}_{0}} = \frac{{{{H}_{0}}}}{{{{s}_{0}}}},\quad i = {\text{1, 2}} \ldots \,.$При этом, если значение коэффициента s0 мало по сравнению с максимальным коэффициентом smax функции S (что, как правило, характерно для большинства практических измерений), то в результате многократного деления на s0 погрешность вычислений экспоненциально возрастает и решение быстро расходится (см. примеры, приведенные на рис. 1 и 2).
Рис. 1.
Реконструкция hrec функции h с погрешностью ${{\eta }_{{rec}}}$ = hrec – h из данных H = (S * h) (а) для неоптимизированной (б) и оптимизированной (в) систем с плохой (cond(M0) = 2.78 ⋅ 1020) и лучшей (cond(Mr) = 621) обусловленностью соответственно.
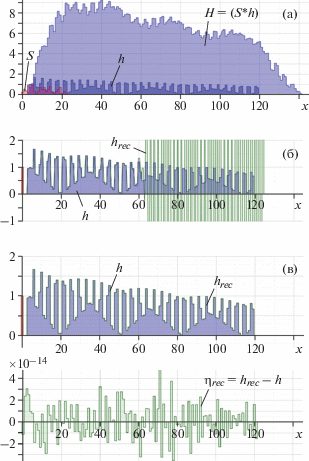
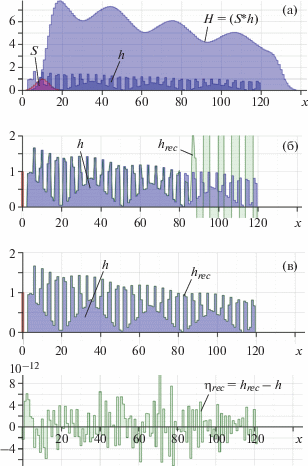
Рис. 2.
Реконструкция hrec функции h с погрешностью ${{\eta }_{{rec}}}$ = hrec – h из размытых по Гауссу данных H = = (S * h) (S(x) = exp[–(x – a)2/(2σ2)]) (а) для неоптимизированной (б) и оптимизированной (в) систем.
Тем не менее, решить задачу реконструкции можно, если из сверточных систем (4) сформировать более оптимальные для решения конкретных задач системы уравнений. Ниже предлагаются критерии и рассматриваются методы формирования из сверточных систем (4) систем линейных алгебраических уравнений, позволяющих осуществить реконструкцию данных при плохой обусловленности неоптимизированной системы (5) и при наличии шумов в данных S и H.
3. РЕКОНСТРУКЦИЯ ПРИ ПЛОХОЙ ОБУСЛОВЛЕННОСТИ
На практике время наблюдений ограничено, и дискретные экспериментальные данные имеют конечную размерность, т.е. функции S, h и H = (S * h) имеют конечное количество актуальных элементов. Если размерность вектора S = [s0, s1,⋯, sk – 1] равна k, а вектора h = [h0, h1, ⋯, hm – 1] – m, то, согласно (2), размерность вектора H = [H0, H1, ⋯, Hn – 1] будет равна n = m + k – 1. Если k = 1, то H = = s0h и реконструкции не требуется, а при k > 1 имеем n > m, и из сверточной системы (4) с матрицей сдвигов MS размерности m × n и с производящим вектором S получим систему, которую будем называть исходной сверточной системой:
(7)
$\begin{gathered} {\mathbf{H}} = \left[ {\begin{array}{*{20}{c}} {{{h}_{0}},}&{{{h}_{1}},}& \cdots &{{{h}_{{m - 1}}}} \end{array}} \right] \times \\ \, \times \left[ {\begin{array}{*{20}{c}} {{{s}_{0}}}&{{{s}_{1}}}&{{{s}_{2}}}& \cdots &{{{s}_{{n - 2}}}}&{{{s}_{{n - 1}}}} \\ 0&{{{s}_{0}}}&{{{s}_{1}}}& \cdots & \cdots &{{{s}_{{n - 2}}}} \\ \vdots & \ddots & \ddots & \ddots & \ddots & \vdots \\ 0& \cdots &0&{{{s}_{0}}}& \cdots &{{{s}_{{n - m}}}} \end{array}} \right] = {\mathbf{h}} \cdot {{{\mathbf{M}}}_{S}}. \\ \end{gathered} $При n > m матрица сдвигов MS является прямоугольной и система (7) переопределена, т.е. количество уравнений n в ней больше, чем количество неизвестных m, под которыми понимаются элементы вектора h. Из переопределенной системы (7) можно сформировать множество квадратных систем из m линейных алгебраических уравнений с m неизвестными путем умножения обеих частей сверточных уравнений (7) на матрицу перемещений R = {rij} размерности n × m, в каждом j-м столбце которой находится лишь один ненулевой элемент rij = 1:
(8)
${{{\mathbf{H}}}_{R}} = {\mathbf{H}} \cdot {\mathbf{R}} = {\mathbf{h}} \cdot ({{{\mathbf{M}}}_{S}} \cdot {\mathbf{R}}) = {\mathbf{h}} \cdot {{{\mathbf{M}}}_{R}}.$При решении системы (8) относительная погрешность реконструкции вектора h не превысит (см., например, [11, 12]):
(9)
$\frac{{\left\| {\Delta {\mathbf{h}}} \right\|}}{{\left\| {\mathbf{h}} \right\|}} \leqslant \left\| {{{{\mathbf{M}}}_{R}}} \right\| \cdot \,{\text{||}}{{{\mathbf{M}}}_{R}}^{{ - 1}}{\text{||}} \cdot \frac{{\left\| {\Delta {{{\mathbf{H}}}_{R}}} \right\|}}{{\left\| {{{{\mathbf{H}}}_{R}}} \right\|}}\, = \,cond({{{\mathbf{M}}}_{R}}) \cdot \frac{{\left\| {\Delta {{{\mathbf{H}}}_{R}}} \right\|}}{{\left\| {{{{\mathbf{H}}}_{R}}} \right\|}},$Оптимальной будем считать такую систему (8), в которой число обусловленности матрицы MR будет минимально, а неравенство (9) будет критерием оптимальности при формировании квадратных систем (8) из переопределенной системы (7).
Всего существует n!/(n – m)! вариантов формирования квадратных систем (8) из (7) (порядок чередования столбцов матрицы имеет значение с точки зрения обусловленности системы), что при больших значениях n делает задачу поиска оптимальной системы простым перебором вариантов практически неразрешимой. Например, если размер данных H равен n = 1000, а данных h – m = 900, то существует 4.31 ⋅ 102409 вариантов формирования систем (8). На практике количество вариантов может быть еще больше. Так, в работе [8] n = = 140 000 и m = 139 900, что соответствует n!/(n – m)! = = 5.01 ⋅ 10659 501 вариантам формирования систем.
Поэтому для формирования оптимальной системы (8) из сверточных систем (7) будем использовать упрощенную процедуру, которую назовем методом оптимизации. Согласно этой процедуре, не меняя порядок столбцов и отбрасывая в уравнениях (7) “лишние” столбцы и элементы слева и справа в матрице MS и в векторе H, сформируем квадратную систему:
(10)
$\begin{gathered} {{{\mathbf{H}}}_{r}} = [\begin{array}{*{20}{c}} {{{H}_{r}},}&{{{H}_{{r + 1}}},}& \cdots &{{{H}_{{m + r - 1}}}} \end{array}] = \\ \, = {\mathbf{h}} \cdot \left[ {\begin{array}{*{20}{c}} {{{s}_{r}}}&{{{s}_{{r + 1}}}}&{{{s}_{{r + 2}}}}& \cdots &{{{s}_{{r + m - 1}}}} \\ \vdots &{{{s}_{r}}}&{{{s}_{{r + 1}}}}& \cdots &{{{s}_{{r + m - 2}}}} \\ {{{s}_{0}}}& \ddots & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots &{{{s}_{r}}}&{{{s}_{{r + 1}}}} \\ 0& \cdots &{{{s}_{0}}}& \cdots &{{{s}_{r}}} \end{array}} \right] = {\mathbf{h}} \cdot {{{\mathbf{M}}}_{r}}, \\ \end{gathered} $При поиске матрицы Mr с наименьшим числом обусловленности можно варьировать не только параметр отсечки r в диапазоне от 0 до (n – m*), но и размерность матрицы m*, где m* > m, в пределах от m до (n – r), так как в силу условий (7) элементы вектора h размерности m* с индексами m* > m будут равны нулю.
На рис. 1 представлен пример реконструкции hrec функции h из данных H = (S * h) (рис. 1а) для неоптимизированной (рис. 1б) и оптимизированной (рис. 1в) систем. Значения числа обусловленности оптимизируемой матрицы Mr при изменении параметров r и m* приведены в табл. 1. Вид функции h был выбран по аналогии с данными спектров (см., например, [8] и рис. 5 разд. 5) с явно выраженными спектральными пиками. Вид импульсной характеристики S с начальным и максимальным элементами, равными s0 = 0.25 < < smax = 1.0, был выбран таким, чтобы соответствующая данному случаю неоптимизированная система (5) была плохо обусловленной, что легко достигается изменением значения элемента s0 (см. комментарии к (6)).
Таблица 1.
Число обусловленности оптимизируемой матрицы Mr в зависимости от ее размерности m* и параметра отсечки r
| m* | r | ||||
|---|---|---|---|---|---|
| 7 | 8 | 9 | 10 | 11 | |
| m | 5.32 · 104 | 2.75 · 103 | 1.94 · 103 | 708 | 1.12 · 104 |
| m+1 | 2.25 · 105 | 1.67 · 103 | 2.06 · 104 | 598 | 3.08 · 103 |
| m+2 | 4.48 · 104 | 2.91 · 103 | 467 | 621 | 2.04 · 103 |
| m+3 | 5.22 · 104 | 1.78 · 103 | 2.51 · 104 | 628 | 1.69 · 103 |
| m+4 | 3.55 · 104 | 2.83 · 103 | 516 | 761 | 1.66 · 103 |
| m+5 | 5.45 · 104 | 1.85 · 103 | 1.52 · 104 | 614 | 1.67 · 103 |
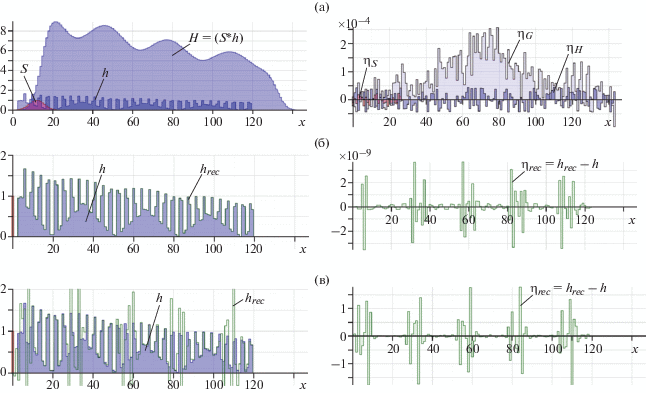
Рис. 3.
Реконструкция hrec функции h с погрешностью ${{\eta }_{{rec}}}$ = hrec – h из данных H = (S * h) при наличии общих искажений ${{\eta }_{G}}$ от случайных шумов ${{\eta }_{H}}$ и ${{\eta }_{S}}$ в функциях H и S (а) для неоптимизированной (б) и оптимизированной (в) систем методами линейного сглаживания (г), сглаживания по Гауссу (д) и методом компенсации (е).
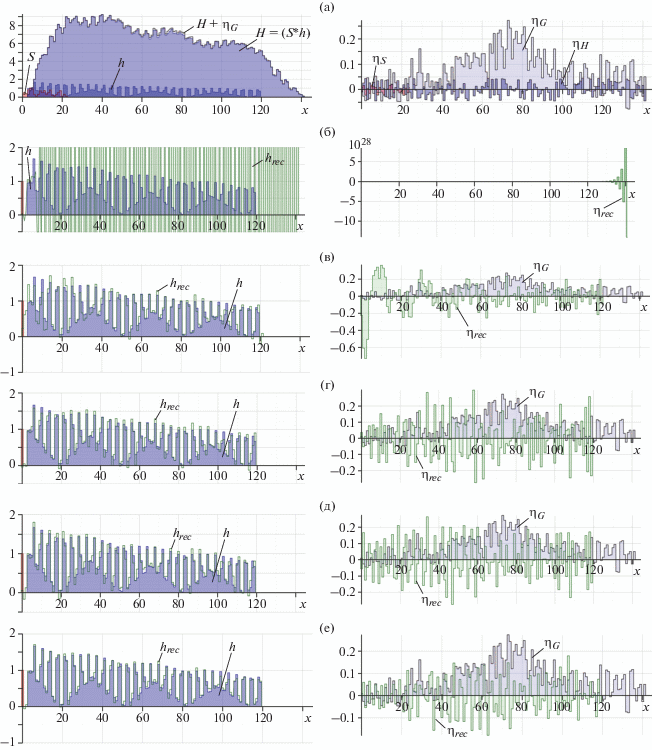
Рис. 4.
Частичная реконструкция отклика hP от опорного импульса P во второй серии измерений (Изм. 2) из экспериментальных данных H = (S * h) (а) времяпролетного нейтронного спектрометра РАДЭКС ИЯИ РАН за три последовательные итерации (б) методом сдвигов.
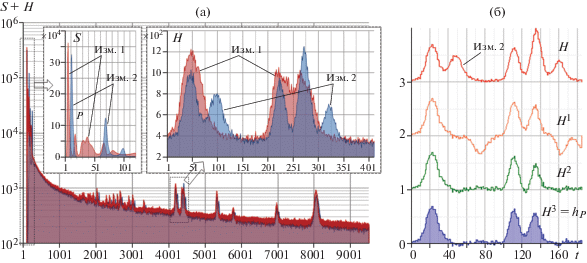
Рис. 5.
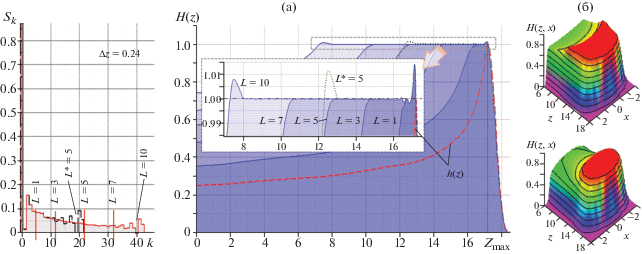
а – одномерное формирование полей дозного облучения $H(z) = \sum\nolimits_k {{{S}_{k}}h(z + k\Delta z)} $ в форме полочек длиной L [см] на Комплексе протонной терапии КПТ ИЯИ РАН путем наложения опорных кривых Брэгга h(z + k∆z), смещенных с коэффициентами Sk; б – результаты двумерного моделирования полей H(z, x) при облучении цилиндрической мишени пассивным и модифицированным методами.
До оптимизации число обусловленности матрицы M0 при r = 0 и m* = m = 120 было равно cond(M0) = 2.78 ⋅ 1020, и решение неоптимизированной системы расходилось (см. рис. 1б). После оптимизации число обусловленности матрицы Mr при r = 10 и m* = m + 2 уменьшилось почти на 18 порядков: cond(Mr) = 621, что позволило провести реконструкцию с погрешностью менее чем ||${{{\mathbf{\eta }}}_{{rec}}}$|| = ||hrec – h|| < 4.79 ⋅ 10–14 (см. рис. 1в).
Из приведенных в табл. 1 данных видно, что при оптимизации по методу (10) существует ярко выраженный минимум числа обусловленности матрицы Mr при параметрах отсечки r = 9 и 10. Было выбрано значение r = 10, так как при нем число обусловленности матрицы Mr слабо зависит от m*, что свидетельствует о большей устойчивости решения оптимизированной системы (10).
Если при оптимизации ограничиться варьированием только параметра отсечки r при неизменной размерности матриц и векторов m* = m, то погрешность реконструкции может возрасти. Так, в примере на рис. 1 при оптимизации только по параметру отсечки погрешность реконструкции была бы примерно на порядок больше: ||${{{\mathbf{\eta }}}_{{rec}}}$|| < 1.38 ⋅ 10–13.
Метод оптимизации (10) эффективен для импульсных характеристик S различного вида. На рис. 2 представлен еще один пример реконструкции hrec функции h из данных H = (S * h) (рис. 2а), размытых по Гауссу (при S(x) = exp(–(x–a)2/(2σ2)), где a и σ – параметры размытия), для неоптимизированной (рис. 2б) и оптимизированной (рис. 2в) систем. Подобные искажения соответствуют нормальному распределению случайной величины и часто встречаются на практике.
Как и в примере на рис. 1, соответствующая данному случаю неоптимизированная система (5) была плохо обусловлена (cond(M0) = 1.07 ⋅ 1020), и ее решение расходилось (см. рис. 2б). После оптимизации число обусловленности матрицы Mr при r = 8 и m* = m + 11 уменьшилось примерно на 16 порядков: cond(Mr) = 52243, что позволило реконструировать функцию h с погрешностью ||${{{\mathbf{\eta }}}_{{rec}}}$|| < < 1.05 ⋅ 10–11 (см. рис. 2в).
Предложенный метод матричной оптимизации (10) с критерием (9) дает хорошие результаты при плохой обусловленности неоптимизированных систем, но недостаточно эффективен при дополнительном наличии шумов в данных H и S (рис. 3в), что требует разработки альтернативных “помехоустойчивых” методов реконструкции.
4. РЕКОНСТРУКЦИЯ ПРИ НАЛИЧИИ СЛУЧАЙНЫХ ШУМОВ
На практике при реконструкции почти всегда приходится иметь дело с неточностями в данных H и S, что может быть связано с погрешностью измерений, ошибками округлений, наличием помех и др. Подобные неопределенности в данных, отличные от искажений сигналов при свертке (1), будем называть шумами. К шумам можно отнести и ошибки вычислений, возникающие при решении систем уравнений, которые рассматривались в предыдущем разделе. Уровень шумов, рассматриваемых в данном разделе, включает в себя и другие неопределенности и может быть значительно выше.
При добавлении шумов ${{\eta }_{H}}$ и ${{\eta }_{S}}$ в функции H и S сверточные уравнения (1) и (2) преобразуются к виду: $\dddot H = H + {{\eta }_{H}} = ((S + {{\eta }_{S}}) * h) = (\dddot S * h)$, и вместо исходной сверточной системы (7) получим исходную систему с зашумленными данными:
(11)
${\mathbf{\dddot H}} = {\mathbf{H}} + {{{\mathbf{\eta }}}_{H}} = {\mathbf{h}} \cdot {{{\mathbf{M}}}_{{S + {{\eta }_{S}}}}} = {\mathbf{h}} \cdot {{{\mathbf{\dddot M}}}_{S}}.$Общий уровень шумов в системе (11) составит: ${{{\mathbf{\eta }}}_{G}} = {{{\mathbf{\eta }}}_{H}} - {\mathbf{h}} \cdot ({{{\mathbf{\dddot M}}}_{S}} - {{{\mathbf{M}}}_{S}})$, а ее решение ${\mathbf{\dddot h}}$, вообще говоря, будет отличаться от решения h системы (7). Причем при плохой обусловленности неоптимизированной системы, даже при небольшом уровне помех, это отличие может быть катастрофическим.
Если шумы ${{\eta }_{H}}$ и ${{\eta }_{S}}$ в функциях $\dddot H$ и $\dddot S$ носят случайный характер, то их среднее значение равно нулю, и для линейной комбинации элементов зашумленных функций (например, для функции $\dddot H$) с произвольными коэффициентами αi будем иметь:
(12)
$\begin{gathered} \left\langle {\sum\limits_i {{{\alpha }_{i}}{{{\dddot H}}_{i}}} } \right\rangle = \left\langle {\sum\limits_i {{{\alpha }_{i}}({{H}_{i}} + \eta _{i}^{H})} } \right\rangle = \\ \, = \sum\limits_i {{{\alpha }_{i}}{{H}_{i}}} + \sum\limits_i {{{\alpha }_{i}}\langle \eta _{i}^{H}\rangle } \cong \sum\limits_i {{{\alpha }_{i}}{{H}_{i}}} . \\ \end{gathered} $.То есть линейная комбинация элементов зашумленных функций $\dddot H$ и $\dddot S$ примерно равна линейной комбинации элементов функций H и S без шума. Случайные искажения компенсируют друг друга, но компенсация носит вероятностный характер, что не гарантирует точного равенства в (12) при суммировании конечного числа элементов, но приводит к уменьшению относительного уровня случайных шумов в линейных комбинациях зашумленных элементов.
При определенном выборе коэффициентов αi алгоритм компенсации (12) представляет собой процедуру сглаживания функции H сплайном G = = $\sum\nolimits_i {{{\alpha }_{i}}{{\delta }_{i}}} $. При этом элементы сглаженной функции будут равны ${{\tilde {H}}_{i}} = \sum\nolimits_j {\alpha {}_{j}{{H}_{{i + j}}}} $. Представляя функции H и G в виде векторов H и G, сглаженный вектор ${\mathbf{\tilde {H}}}$ можно выразить с помощью матричного уравнения:
(13)
$\begin{gathered} {\mathbf{\tilde {H}}} = [\begin{array}{*{20}{c}} {{{{\tilde {H}}}_{0}},}&{{{{\tilde {H}}}_{1}},}& \cdots \end{array}] = \\ \, = [\begin{array}{*{20}{c}} {{{H}_{0}},}&{{{H}_{1}},}& \cdots \end{array}] \cdot \left[ {\begin{array}{*{20}{c}} {{{\alpha }_{0}}}&0& \cdots &0 \\ {{{\alpha }_{1}}}&{{{\alpha }_{0}}}& \ddots & \vdots \\ \vdots &{{{\alpha }_{1}}}& \ddots &0 \\ {{{\alpha }_{i}}}& \vdots & \ddots &{{{\alpha }_{0}}} \\ \vdots &{{{\alpha }_{i}}}& \ddots &{{{\alpha }_{1}}} \\ {}& \vdots & \ddots & \vdots \end{array}} \right] = {\mathbf{H}} \cdot {\mathbf{M}}_{G}^{T}, \\ \end{gathered} $Задавая элементы вектора G = {αi}, можно осуществить различные способы сглаживания. Например, при αi = 1/k, где i = 0, …, k – 1, реализуется линейное скользящее сглаживание по k элементам, а при αi = c · exp[–(i – a)2/(2σ2)], где a и σ – параметры сглаживания, а с – нормировочный коэффициент, реализуется сглаживание по Гауссу.
В дальнейшем при сглаживании в (13) будут учитываться только актуальные значения вектора H, что непринципиально для переопределенных систем и удобно для дальнейшего анализа, так как позволяет избежать сложностей при сглаживании крайних элементов. При этом размерность $\tilde {n}$ сглаженного вектора ${\mathbf{\tilde {H}}}$ будет меньше размерности n сглаживаемого вектора H: $\tilde {n} = n - k + 1$, где k – количество элементов в сплайне при сглаживании.
Если в исходной системе (7) (H = h ⋅ MS) осуществить сглаживание вектора H, то решение системы ${\mathbf{\tilde {H}}} = {\mathbf{H}} \cdot {\mathbf{M}}_{G}^{T} = {\mathbf{h}} \cdot {{{\mathbf{M}}}_{S}}$ в общем случае будет отличаться от решения системы (7). Также будет отличаться и решение уравнения ${\mathbf{H}} = {\mathbf{h}} \cdot {{{\mathbf{\tilde {M}}}}_{S}}$, где производящим вектором матрицы сдвигов ${{{\mathbf{\tilde {M}}}}_{S}}$ является сглаженный вектор ${\mathbf{\tilde {S}}} = {\mathbf{S}} \cdot {\mathbf{M}}_{G}^{T}$. Однако, если в системе (7) одновременно сглаживать с помощью одинаковой функции G оба вектора H и S, то оказывается, что решение ${\mathbf{\tilde {h}}}$ системы
со сглаженными данными: ${\mathbf{\tilde {H}}}\, = \,{\mathbf{H}}\, \cdot \,{\mathbf{M}}_{G}^{T}$ и ${\mathbf{\tilde {S}}}\, = \,{\mathbf{S}}\, \cdot \,{\mathbf{M}}_{G}^{T}$ – будет равно решению h исходной системы (7): ${\mathbf{\tilde {h}}}$ = h, т.е. потерь информации при таком двойном сглаживании не происходит.Докажем это утверждение. Умножим левую и правую части сверточной системы (7) H = h ⋅ MS на матрицу сглаживания ${\mathbf{M}}_{G}^{T}$: H · ${\mathbf{M}}_{G}^{T}$= (h ⋅ MS) · ${\mathbf{M}}_{G}^{T}$. Согласно (13), такое умножение означает линейную комбинацию столбцов, преобразующих систему (7) в равноценную систему: ${\mathbf{\tilde {H}}} = {\mathbf{H}} \cdot {\mathbf{M}}_{G}^{T}$ = = $({\mathbf{h}} \cdot {{{\mathbf{M}}}_{S}}) \cdot {\mathbf{M}}_{G}^{T} = {\mathbf{h}} \cdot ({{{\mathbf{M}}}_{S}} \cdot {\mathbf{M}}_{G}^{T})$, решение которой ${\mathbf{\tilde {h}}}$ совпадает с решением исходной системы (7): ${\mathbf{\tilde {h}}}$ = h. Поскольку матрица MS является матрицей сдвигов, ее i-я строка представляет собой смещенный производящий вектор S[i], и при умножении матрицы MS на матрицу ${\mathbf{M}}_{G}^{T}$ каждая строка матрицы MS · ${\mathbf{M}}_{G}^{T}$, согласно (13), преобразуется в сглаженный смещенный вектор ${{{\mathbf{\tilde {S}}}}_{{{\text{[}}i{\text{]}}}}} = {{{\mathbf{S}}}_{{{\text{[}}i{\text{]}}}}} \cdot {\mathbf{M}}_{G}^{T}$. Это означает, что сглаженный вектор ${\mathbf{\tilde {S}}}$ будет производящим для матрицы сдвигов $({{{\mathbf{M}}}_{S}} \cdot {\mathbf{M}}_{G}^{T}) = {{{\mathbf{\tilde {M}}}}_{S}}$, откуда и приходим к выражению (14). С учетом равноценности систем (7) и (14) утверждение полностью доказано.
Если осуществить сглаживание функций $\dddot H$ и $\dddot S$ в зашумленной системе (11) $({\mathbf{\dddot H}} = {\mathbf{h}} \cdot {{{\mathbf{\dddot M}}}_{S}})$, то придем к сглаженной зашумленной системе:
(15)
${\mathbf{\tilde {\dddot H}}} = {\mathbf{\dddot H}} \cdot {\mathbf{M}}_{G}^{T} = {\mathbf{h}} \cdot {{{\mathbf{\dddot M}}}_{S}} \cdot {\mathbf{M}}_{G}^{T} = {\mathbf{h}} \cdot {{{\mathbf{\tilde {\dddot M}}}}_{S}},$Способ формирования системы (15) из зашумленной системы (11), позволяющий реализовать алгоритм компенсации (12), будем называть методом сглаживания.
Поскольку матрица сглаживания ${\mathbf{M}}_{G}^{T}$ входит в обе части линейных систем уравнений (14) и (15), нормировка функции сглаживания G становится необязательной. Более того, меняется само понятие “сглаживания”, так как в общем случае коэффициенты αi могут быть произвольными, но такими, чтобы ранг матриц ${{{\mathbf{\tilde {M}}}}_{S}}$ и ${{{\mathbf{\tilde {\dddot M}}}}_{S}}$ был равен рангу матрицы MS. При соответствующем выборе размерности матрицы сглаживания ${\mathbf{M}}_{G}^{T}$ системы (14) и (15) можно сразу привести к квадратному виду.
Обобщенный подход к сглаживанию приводит к важному частному случаю метода сглаживания (15), который будем называть методом компенсации. В этом методе в качестве сглаживающих коэффициентов αi выступают коэффициенты si импульсной характеристики S: αi = si, и вектор сглаживания G = S будет производящим для матрицы ${\mathbf{M}}_{G}^{T} = {\mathbf{M}}_{S}^{T}$. В этом случае система (15) автоматически преобразуется к квадратному виду:
(16)
${\mathbf{\tilde {\dddot H}}} = {\mathbf{\dddot H}} \cdot {\mathbf{M}}_{S}^{T} = {\mathbf{h}} \cdot ({{{\mathbf{\dddot M}}}_{S}} \cdot {\mathbf{M}}_{S}^{T}) = {\mathbf{h}} \cdot {{{\mathbf{\tilde {\dddot M}}}}_{S}}.$На рис. 3 представлены результаты реконструкции hrec функции h из данных H = (S*h) при наличии общих искажений ${{\eta }_{G}}$ от случайных шумов ${{\eta }_{H}}$ и ${{\eta }_{S}}$ в функциях H и S (рис. 3а) для неоптимизированной (рис. 3б) и оптимизированной (рис. 3в) систем методами линейного сглаживания (рис. 3г), сглаживания по Гауссу (рис. 3д) и методом компенсации (рис. 3е). Здесь к функциям S и H из примера на рис. 1 были добавлены случайные шумы с амплитудами ||${{{\mathbf{\eta }}}_{S}}$/smax|| ≤ 5% и ||${{{\mathbf{\eta }}}_{H}}$/Hmax|| ≤ 1% соответственно. При этом общий уровень искажений, приведенных к функции h, составил $\left\| {{{{\mathbf{\eta }}}_{G}}{\text{/}}{{h}_{{\max }}}} \right\|$ ~ 16.4%. При наличии шумов решение неоптимизированной системы (рис. 3б) расходится еще быстрее, чем на рис. 1б, а погрешность реконструкции методом оптимизации, где алгоритм компенсации не используется, достигает 43.9% (рис. 3в). С использованием линейного сглаживания по двенадцати точкам (рис. 3г) удалось достичь уровня погрешности ||${{{\mathbf{\eta }}}_{{rec}}}$/hmax|| ≤ 17.9%, подбором параметров сглаживания по Гауссу (рис. 3д) – 16.5%, а при применении метода компенсации наложений (рис. 3е) погрешность не превысила 10.7%, что оказалось даже меньше начальной неопределенности в данных (16.4%).
Алгоритм компенсации (12) в силу вероятностного характера эффективно работает при большом количестве сглаживаемых элементов. Так, в приведенном на рис. 3 примере эффект от линейного сглаживания начинал заметно проявляться лишь при сглаживании по десяти точкам и стабильно проявлял себя при числе сглаживаемых точек, примерно равном количеству элементов импульсной характеристики (в примере количество элементов равно 25). Подбор оптимальных параметров сглаживания по Гауссу тоже оказался непростой задачей.
Наиболее простым в реализации и не требующим процедуры подбора параметров сглаживания оказался метод компенсации (16), который также показал лучшие результаты реконструкции, но вопрос его оптимальности при любых импульсных характеристиках, в особенности зашумленных, остается открытым. Так, например, если в зашумленной исходной системе (11) импульсная характеристика S равна функции Гаусса, то при решении этой системы методом сглаживания (15) наименьших погрешностей реконструкции удается достичь, когда функция сглаживания совпадает с импульсной характеристикой: G = S, что как раз и характерно для метода компенсации (16). Точнее, метод сглаживания при G = S дает чуть лучшие результаты, поскольку в нем используется точная импульсная характеристика S, а в методе компенсации – зашумленная $G = \dddot S$.
Использование прямых методов матричной инверсии для решения сформированных систем (15) и (16) не является обязательным. Если позволяют условия задачи, вполне можно использовать методы интегральных преобразований или методы регуляризации, но формат статьи не позволяет включить в нее детальный анализ условий, критериев и эффективности такого применения.
5. ЧАСТИЧНАЯ РЕКОНСТРУКЦИЯ ДАННЫХ
При современном уровне развития цифровой техники интервал дискретизации данных зачастую оказывается значительно меньше, чем постоянные времени изучаемых динамических процессов или разрешение измерительной аппаратуры. В этом случае бывает достаточно реконструировать не точный неискаженный отклик h, что может оказаться неразрешимой задачей, а отклик измерительной системы hP на некоторый опорный импульс $P = \sum\nolimits_i {{{p}_{i}}{{\delta }_{i}}} $. При этом системы уравнений, сформированные для реконструкции отклика hP, могут оказаться гораздо более простыми и лучше обусловленными.
В силу линейности свертки (1) отклик hP(x) измерительной системы на импульс P(x) является сверткой: hP(x) = (h ∗ P)(x). Выражая отсюда h(x) = = (hP ∗ P–1)(x), где (P ∗ P–1)(x) = δ(x), и подставляя это выражение в (1), с учетом свойства ассоциативности свертки (см., например, [13]) получим:
(17)
$\begin{gathered} H(x) = (h * S)(x) = \\ \, = (({{h}_{P}} * {{P}^{{ - 1}}}) * S)(x) = ({{h}_{P}} * ({{P}^{{ - 1}}} * S))(x). \\ \end{gathered} $Уравнение (17) представляет собой уравнение свертки функции hP(x) с ядром (P–1 ∗ S)(x) и принципиально ничем не отличается от уравнения (1), поэтому все методы решения уравнения (1) пригодны и для решения уравнения (17) при условии, что преобразование P–1(x) существует. Свертку (1) можно считать частным случаем (17) при P(x) = δ(x) (при этом P–1(x) = δ(x)).
В случае дискретных вычислений функцию hP(x) = (h∗P)(x) можно представить как
(18)
${{{\mathbf{h}}}_{P}} = [\begin{array}{*{20}{c}} {{{h}_{0}},}&{{{h}_{1}},}& \cdots \end{array}] \cdot \left[ {\begin{array}{*{20}{c}} {{{p}_{0}}}&{{{p}_{1}}}&{{{p}_{2}}}& \cdots \\ 0&{{{p}_{0}}}&{{{p}_{1}}}& \cdots \\ 0&0&{{{p}_{0}}}& \ddots \\ \vdots & \vdots & \ddots & \ddots \end{array}} \right] = {\mathbf{h}} \cdot {{{\mathbf{M}}}_{P}},$(19)
${\mathbf{H}} = ({{{\mathbf{h}}}_{P}} \cdot {\mathbf{M}}_{P}^{{ - {\text{1}}}}) \cdot {{{\mathbf{M}}}_{S}} = {{{\mathbf{h}}}_{P}} \cdot ({\mathbf{M}}_{P}^{{ - {\text{1}}}} \cdot {{{\mathbf{M}}}_{S}}).$Уравнения (19) являются дискретной формой представления уравнения свертки (17), так же как уравнения (4) являются дискретной формой представления уравнения свертки (1). Поэтому матрица (${\mathbf{M}}_{P}^{{ - 1}}$ ⋅ MS) является матрицей сдвига (это можно показать и прямыми вычислениями элементов), и реконструкция функции hP из (19) принципиально ничем не отличается от реконструкции функции h из (4). То есть все рассмотренные ранее методы оптимизации, сглаживания и компенсации пригодны и для сверточных систем (19).
Метод формирования систем (19) из систем (4) будем называть методом частичной реконструкции, так как с его помощью реконструируется не неискаженный отклик h измерительной системы, а ее отклик hP = (h∗P) на выбранный опорный импульс P. Фактически этот метод заключается в разложении импульсной характеристики S по опорному импульсу P, поэтому метод частичной реконструкции будем также называть методом разложения.
Метод разложения легко реализуется, если импульсная характеристика представляет собой линейную комбинацию сдвинутых импульсов P: $S = \sum\nolimits_k {{{s}_{k}}{{\delta }_{k}}} $ = $\sum\nolimits_{i,j} {{{с}_{i}}{{P}_{{[j]}}}} $, ${{P}_{{[j]}}} = \sum\nolimits_i {{{p}_{i}}{{\delta }_{i}}_{{ + j}}} $. Тогда производящий вектор C = [с0, с1, …] матрицы сдвигов (${\mathbf{M}}_{P}^{{ - 1}}$ ⋅ MS) из (19) будет состоять только из коэффициентов сi, равных амплитудам сдвинутых импульсов P[j], и не будет содержать коэффициенты pi, отражающие форму опорного импульса P. Реальный импульс P может иметь различную форму обычно с передним и задним фронтами. В этом случае коэффициенты p0 и s0 будут малы, что приведет к плохой обусловленности неоптимизированной системы (5), формируемой из (4), но не отразится на обусловленности неоптимизированной системы, формируемой из (19). Влияние шумов, обычно присутствующих в реальных импульсах P, может быть учтено подбором коэффициентов сi, что предопределяет помехоустойчивость систем, формируемых из (19).
Примером применения метода разложения (19) может служить проведенная в работе [8] частичная реконструкция экспериментальных данных времяпролетного нейтронного спектрометра РАДЭКС ИЯИ РАН, представленная на рис. 4. Частичная реконструкция отклика hP от опорного импульса P во второй серии измерений (Изм. 2) из экспериментальных данных H = (S * h) (рис. 4а) была осуществлена за три последовательные итерации методом сдвигов (рис. 4б), специально разработанным и позволяющим обрабатывать данные большой размерности без использования матриц и операций с ними. Импульсная характеристика представляла собой сумму импульса P и смещенного на j интервалов разбиения второго импульса P[j] с амплитудой с ≈ 0.5: S ≈ P + сP[j]. Так как амплитуда второго импульса была меньше амплитуды опорного, обусловленность неоптимизированной системы, соответствующей (19), была достаточно хорошей для реконструкции данных методом прямой инверсии (использовался метод сдвигов). При этом полная реконструкция данных h спектрометра из сверточных уравнений (4), которые включали в себя 140 000 цифровых каналов с разрешением 150 нс/канал и высоким уровнем шумов, была практически невозможной и избыточной с точки зрения необходимого разрешения измерений.
Метод разложения (19) можно использовать для работы не только с дискретными, но и с непрерывными функциями. Пример такого использования описан в работе [14], где решалась задача формирования поля дозного облучения на Комплексе протонной терапии КПТ ИЯИ РАН, что необходимо для проведения лечения онкологических новообразований. На рис. 5а приведен пример формирования одномерных полей дозного облучения $H(z) = \sum\nolimits_k {{{S}_{k}}h(z + k\Delta z)} $ в форме полочек длиной L [см] путем наложения смещенных опорных кривых Брэгга h(z + k∆z) с коэффициентами Sk. Коэффициенты Sk вектора S определялись путем решения системы уравнений H = S ⋅ Mh, где вектор H формировался из требуемых значений поля Hk = H(zk) в точках zk = zmax –k∆z, zmax – координата пика Брэгга, а элементы mij матрицы сдвигов Mh были равны mij = h[z + (i – j)∆z]. На рис. 5б также представлены результаты двумерного моделирования полей H(z, x) для облучения цилиндрической мишени пассивным и модифицированным методами (см. детали в [14]).
Метод частичной реконструкции можно отнести к приближенным методам, но он позволяет провести реконструкцию данных до возможного или достаточного с точки зрения проведения конкретных измерений уровня, даже тогда, когда полная реконструкция невозможна. Частичная реконструкция не может быть полностью алгоритмизирована для решения любых задач, так как индивидуальна для каждой задачи и подразумевает предварительный анализ конкретных условий эксперимента, выбор определенного опорного импульса, параметров реконструкции и др.
6. ОСОБЕННОСТИ ПРИМЕНЕНИЯ МЕТОДОВ РЕКОНСТРУКЦИИ
Предложенные методы реконструкции экспериментальных данных с помощью оптимизации, сглаживания, компенсации и разложения не являются универсальными. Эффективность применения методов зависит от конкретной задачи: вида импульсной характеристики, размера данных, уровней шумов в них и пр.
При отсутствии шумов в данных наилучшие результаты показывает метод оптимизации. Однако в некоторых достаточно редких случаях, при незначительном отличии параметров оптимизации (параметра отсечки r или размерности m*) от оптимальных, при реконструкции появляются ошибки, похожие на резонансные, что резко увеличивает погрешность реконструкции. При добавлении к данным даже небольших по уровню шумов ситуация усугубляется.
Появление резонансных ошибок иллюстрирует рис. 6, где представлены результаты реконструкции данных H = (S*h) (рис. 6а) при гауссовой импульсной характеристике S и при отличии параметра отсечки от оптимального: r = ropt + 1. Резонансные ошибки на 3–4 порядка превышают общий уровень погрешности при реконструкции. Без шумов в данных (рис. 6б) они составляют ||${{{\mathbf{\eta }}}_{{rec}}}$/hmax|| ~ 10–8–10–7%, а при наличии в данных даже сравнительно небольших шумов (||${{{\mathbf{\eta }}}_{G}}$/hmax|| ~ ~ 0.015%) уровень ошибок резко возрастает и достигает фатальных значений ||${{{\mathbf{\eta }}}_{{rec}}}$/hmax|| ~ 108.8% (рис. 6в). Отметим, что при оптимальном значении параметра отсечки (r = ropt) резонансные искажения отсутствуют и при наличии шумов погрешность реконструкции не превышает ||${{{\mathbf{\eta }}}_{{rec}}}$/hmax|| ~ 1.80%. Появление резонансных ошибок может быть связано с нестабильностью решения и нерегулярной зависимостью числа обусловленности при изменении параметров оптимизации, что можно видеть из данных табл. 1.
Рис. 6.
Резонансные ошибки ${{\eta }_{{rec}}}$ = hrec – h: а – при реконструкции hrec функции h из размытых по Гауссу данных H = (S*h) при отличии параметра отсечки от оптимального (r = ropt + 1); б – без шумов в функциях H и S; в – при наличии искажений ${{\eta }_{G}}$ от шумов ${{\eta }_{H}}$ и ${{\eta }_{S}}$ в них.
Резонансные ошибки, аналогичные представленным на рис. 6, могут возникать и при применении метода сглаживания (15) при изменении количества точек сглаживающего сплайна. Такие ошибки, как правило, возникают, когда число точек сглаживания намного отличается от количества элементов в импульсной характеристике, т.е. вдали от области стабильной реконструкции. Вероятно, в данном случае возникновение резонансных ошибок связано с увеличением неопределенностей в данных и с вероятностным характером алгоритма компенсации (12). Детальный анализ причин возникновения резонансных ошибок требует серьезных дополнительных исследований.
К недостаткам методов сглаживания (15) можно отнести необходимость подбора функции сглаживания G и ее параметров, что является довольно трудоемкой задачей. В этом смысле метод компенсации (16) более удобен в использовании, так как не требует выбора функции сглаживания, которая по умолчанию совпадает с импульсной характеристикой: G = S. Кроме того, обычно метод компенсации показывает меньшие погрешности реконструкции, чем другие методы сглаживания (15). Показательным является упоминавшийся ранее пример использования метода сглаживания для решения системы (15), в которой импульсная характеристика была равна функции Гаусса: G = S. Наименьших погрешностей реконструкции удалось достичь при совпадении функции сглаживания с импульсной характеристикой G = S, что как раз и характерно для метода компенсации (16). Тем не менее, вопрос оптимальности метода компенсации при любых импульсных характеристиках не очевиден и остается открытым. Отметим, что резонансных ошибок реконструкции при применении метода компенсации при различных импульсных характеристиках не наблюдалось. Возможно, это связано с тем, что в этом методе количество элементов сглаживания по умолчанию совпадает с количеством элементов в импульсной характеристике и находится в области стабильной реконструкции.
Метод разложения относится к приближенным, так как при его применении осуществляется лишь частичная реконструкция данных, но зачастую на практике этого может оказаться вполне достаточно для достижения необходимой точности измерений. Простота реализации этого метода и возможность проведения частичной реконструкции данных даже тогда, когда полная реконструкция другими методами невозможна, во многих практических случаях делает его незаменимым. Однако метод частичной реконструкции не может быть полностью алгоритмизирован для решения любых задач, так как подразумевает анализ конкретных условий эксперимента, выбор определенных параметров реконструкции, таких как вид опорного импульса, подбор коэффициентов при наличии помех и др.
Предложенные методы оптимизации, сглаживания, компенсации и частичной реконструкции не являются универсальными, но взаимно дополняют друг друга при обработке экспериментальных данных различных физических экспериментов.
7. ЗАКЛЮЧЕНИЕ
Методы оптимизации, сглаживания, компенсации и разложения, представленные в данной работе, позволяют решить задачу реконструкции экспериментальных данных в наиболее сложных, но также и наиболее часто встречающихся на практике случаях плохой обусловленности задач и при наличии случайных искажений в данных.
Методы состоят в формировании из сверточных систем уравнений с помощью линейных преобразований систем уравнений с хорошей обусловленностью и устойчивостью к влиянию помех, что позволяет реконструировать экспериментальные данные методами прямой матричной инверсии с минимальными потерями информации. Использование прямых методов матричной инверсии для решения сформированных систем не является обязательным. Когда позволяют условия задачи, можно применять методы интегральных преобразований и методы регуляризации, причем эффективность их применения для решения сформированных систем также значительно возрастает.
Предлагаемые методы взаимно дополняют друг друга в различных случаях реконструкции данных физических экспериментов. При отсутствии или при низком уровне шумов в данных наименьшую погрешность дает метод матричной оптимизации. Методы сглаживания и компенсации наложений более эффективны при сравнительно высоком уровне шумов в данных, причем наилучшие результаты показывает метод компенсации наложений, но вопрос его оптимальности при любых импульсных характеристиках не очевиден и остается открытым. Метод частичной реконструкции относится к приближенным методам, но он позволяет провести корректировку данных до возможного уровня даже тогда, когда полная реконструкция невозможна, что во многих практических случаях делает его незаменимым.
Предложенные методы математической обработки данных могут быть использованы не только в экспериментальной физике, но и в других областях цифровой обработки сигналов и изображений, а также могут быть полезны при разработке методов деконволюции в математике. Подобные методы дополняют, а зачастую являются доступной альтернативой конструктивно-техническим методам повышения качества измерений, сопряженным с трудноразрешимыми научно-техническими проблемами и требующим больших материальных затрат.
Список литературы
Digital Signal Processing. Handbook / Ed. V.K. Madisetti, D.B. Williams. Chapmann& Hall, 1999.
Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979.
Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1972.
Оппенгейм А., Шафер Р. Цифровая обработка сигналов. М.: Техносфера, 2006.
Jackson L.B. Signals, Systems, and Transforms. MA, Reading: Addison-Wesley, 1991.
Smith S.W. The Scientist and Engineer’s Guide to Digital signal processing. 2nd ed. CA, San Diego: California Technical Publishing, 1999.
Gonzalez R. Digital Image Processing. 3rd ed. Pearson Hall, 2008.
Новиков-Бородин А.В. // ПТЭ. 2018. № 6. С. 174. https://doi.org/10.1134/S0032816218050269
Новиков-Бородин А.В. // ПТЭ. 2019. № 4. С. 28. https://doi.org/10.1134/S0032816219040268
Novikov-Borodin A.V. // EPJ Web of Conferences. 2020. V. 226. P. 03014. https://doi.org/10.1051/epjconf/202022603014
Ильин В.А., Ким Г.Д. Линейная алгебра и аналитическая геометрия. М.: Изд-во МГУ, 1998.
Голуб Дж., Ван Лоун Ч. Матричные вычисления / Пер. с англ. М.: Мир, 1999.
Владимиров В.С. Уравнения математической физики. М.: Наука, 1981.
Новиков-Бородин А.В. Препринт ИЯИ № 1440/2019. М., 2019.
Дополнительные материалы отсутствуют.
Инструменты
Приборы и техника эксперимента


