1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 83, № 2, 2019

Прикладная математика и механика, 2019, T. 83, № 2, стр. 314-322

КОНТАКТНАЯ ЗАДАЧА ПРИ ОБЪЕМНОМ ПРИЛОЖЕНИИ СИЛ МЕЖМОЛЕКУЛЯРНОГО ВЗАИМОДЕЙСТВИЯ: УПРОЩЕННЫЙ МЕТОД РЕШЕНИЯ (ДВУХУРОВНЕВАЯ МОДЕЛЬ)

И. А. Солдатенков *

Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

* E-mail: iasoldat@hotmail.com

Поступила в редакцию 04.08.2018
После доработки 29.11.2018
Принята к публикации 25.12.2018

Полный текст (PDF)

Аннотация

Рассматривается постановка контактной задачи при наличии объемно приложенных сил межмолекулярного взаимодействия контактирующих тел. Предлагается метод оценки контактного зазора, позволяющий существенно упростить расчет контактного взаимодействия в рамках самосогласованного подхода. С использованием полученной оценки контактного зазора выполнен расчет подповерхностных напряжений в упругом полупространстве, контактирующим со сферическим индентором.

Ключевые слова: контактная задача, упругость, межмолекулярное взаимодействие

При решении контактных задач с учетом межмолекулярного взаимодействия (адгезии) широко используются упрощающие допущения. Например, используется классическое решение Герца (модели JKR [1] и DMT [2]), применяются кусочно-постоянные аппроксимации потенциала Леннард–Джонса и адгезионного давления [3, 4].

Строгая постановка контактной задачи, учитывающая межмолекулярное взаимодействие, предполагает существование некоторого зазора $r$ между контактирующими телами, величина которого зависит от деформации тел и должна обеспечивать равенство деформационных и межмолекулярных сил на контакте (самосогласованный подход по Дерягину [5]). При таком подходе возможны постановки задачи с поверхностным (традиционная постановка [6–8]) и объемным (уточненная постановка [9–12]) приложением сил межмолекулярного взаимодействия.

Контактная задача в рамках самосогласованного подхода сводится к нелинейному интегральному уравнению относительно контактного зазора r, решение которого может быть получено только в приближенном виде, например, с помощью метода последовательных приближений [5, 8]. Задача существенно упрощается при заранее известном контактном зазоре, например, когда форма индентора обеспечивает постоянство зазора по области контакта [13].

В данной работе в рамках самосогласованного подхода рассматривается контакт гладкого индентора с упругим полупространством при условии, что характерный размер a области контакта (крупномасштабный уровень 1) значительно превышает зазор r (мелкомасштабный уровень 2). Предлагается упрощенный метод расчета такого контакта на основе гипотезы, согласно которой зазор r на уровне 2 определяется контактным давлением, которое находится из решения классической контактной задачи на уровне 1. Выполнена проверка выдвинутой гипотезы. Полученная таким образом оценка контактного зазора используется для расчета объемно приложенных в полупространстве сил межмолекулярного взаимодействия и соответствующего напряженно-деформированного состояния.

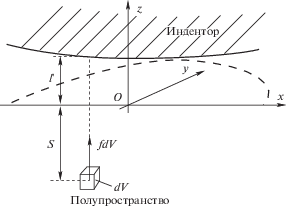
1. Постановка задачи и основные уравнения. Рассмотрим контактное взаимодействие абсолютно жесткого тела (индентора) с упругим полупространством в рамках самосогласованного подхода (фиг. 1). Наличие сил межмолекулярного взаимодействия приводит к существованию некоторого контактного зазора r, обеспечивающего баланс сил межмолекулярного и упругого взаимодействия контактирующих тел [5].

Фиг. 1

Межмолекулярное взаимодействие индентора и полупространства определяется парными взаимодействиями молекул (гипотеза Гамакера). Соответствующая сила F зависит от свойств пары молекул и расстояния l между ними. Существуют разные формы такой зависимости, среди которых наиболее известен закон Леннард–Джонса [14]:

$F(l) = \frac{{{{a}_{1}}}}{{{{l}^{m}}}} - \frac{{{{a}_{2}}}}{{{{l}^{n}}}},$
где ${{a}_{1}}$, ${{a}_{2}}$, $m$, $n$ – параметры взаимодействия, причем обычно полагают $m = 7$, $n = 13$.

При определенных допущениях [7, 10, 15] суммирование парных взаимодействий молекул позволяет рассчитать объемную силу $f$ в полупространстве, обусловленную межмолекулярным взаимодействием, а также силу $p$ воздействия индентора на полупространство, приходящуюся на единицу площади его границы:

(1.1)
$p(x,y) = \Phi (r(x,y)),\quad \Phi (r) \equiv - \int\limits_0^\infty f (r + s)ds$

Здесь величина $d = r + s$ определяет расстояние от индентора до точки приложения силы $f$ (фиг. 1), сила $f$ направлена вдоль оси $z$, а определение (1.1) величины $p$ позволяет интерпретировать ее как контактное давление [5–7, 12].

В случае закона Леннард–Джонса функции $f(d)$ и $\Phi (r)$ имеют вид [12] (аналогичные формулы см. также [7, 10, 11])

(1.2)
$f(d) = \frac{{{{b}_{1}}}}{{{{d}^{{m - 3}}}}} - \frac{{{{b}_{2}}}}{{{{d}^{{n - 3}}}}} \equiv \frac{{{{b}_{1}}}}{{d_{e}^{{m - 3}}}}\left[ {{{{\left( {\frac{{{{d}_{e}}}}{d}} \right)}}^{{m - 3}}} - {{{\left( {\frac{{{{d}_{e}}}}{d}} \right)}}^{{n - 3}}}} \right],\quad {{d}_{e}} = {{\left( {\frac{{{{b}_{1}}}}{{{{b}_{2}}}}} \right)}^{{1/(m - n)}}}$
(1.3)
$ - \Phi (r) = \frac{{{{A}_{1}}}}{{{{r}^{{m - 4}}}}} - \frac{{{{A}_{2}}}}{{{{r}^{{n - 4}}}}} \equiv \frac{{{{A}_{1}}}}{{r_{e}^{{m - 4}}}}\left[ {{{{\left( {\frac{{{{r}_{e}}}}{r}} \right)}}^{{m - 4}}} - {{{\left( {\frac{{{{r}_{e}}}}{r}} \right)}}^{{n - 4}}}} \right],\quad {{r}_{e}} = {{\left( {\frac{{{{A}_{1}}}}{{{{A}_{2}}}}} \right)}^{{1/(m - n)}}},$
причем
${{b}_{1}} = \frac{{2\pi N{{N}_{s}}{{a}_{1}}}}{{(m - 1)(m - 3)}},\quad {{b}_{2}} = \frac{{2\pi N{{N}_{s}}{{a}_{2}}}}{{(n - 1)(n - 3)}},\quad {{A}_{1}} = \frac{{{{b}_{1}}}}{{m - 4}},\quad {{A}_{2}} = \frac{{{{b}_{2}}}}{{n - 4}},$
$N$ и ${{N}_{s}}$ – концентрации молекул полупространства и индентора, соответственно. Согласно формуле (1.2), объемные силы $f$ быстро затухают и сконцентрированы в подповерхностном слое нанометровой толщины ~${{d}_{e}}$ в пределах области контакта.

Традиционная постановка контактной задачи при наличии межмолекулярного взаимодействия подразумевает, что определяемое по формуле (1.1) контактное давление прикладывается к границе полупространства, в результате чего оно деформируется [5–8]. Ниже рассматривается уточненная постановка, в которой естественным образом предполагается, что деформация полупространства порождается объемными силами $f$, распределенными по его глубине, тогда как граница полупространства свободна от нагрузок [9–12].

Рассматриваемое контактное взаимодействие индентора с полупространством описывается следующими уравнениями, в которых зазор $r(x,y)$ выступает в качестве искомой функции [12, 13]:

(1.4)
$r(x,y) - r(0,0) + w(x,y) - w(0,0) = g(x,y)--{\text{у с л о в и е к о н т а к т а }}$
(1.5)
$P = \iint\limits_{\text{D}} \Phi (r(x,y))dxdy--{\text{у с л о в и е р а в н о в е с и я }}$
(1.6)
$\begin{gathered} w(x,y) = \iint\limits_{\text{D}} {\Gamma (\sqrt {{{{(\xi - x)}}^{2}} + {{{(\eta - y)}}^{2}}} ;\;r(\xi ,\eta ))}d\xi d\eta \\ --\;{\text{д е ф о р м а ц и о н н о е с о о т н о ш е н и е }} \\ \end{gathered} $

Здесь $w(x,y)$ – нормальное (по оси $z$) перемещение границы полупространства, P – нормальная нагрузка на индентор, D – область контакта, $g(x,y)$ – форма индентора, $g(0,0)$ = 0

(1.7)
$\begin{gathered} \Gamma (\rho ;r) = \frac{{1 + \nu }}{{2\pi E}}[(3 - 2\nu ){{\Lambda }_{1}}(\rho ,r) + {{\Lambda }_{2}}(\rho ,r)] \\ {{\Lambda }_{{\left\{ {\begin{array}{*{20}{c}} 1 \\ 2 \end{array}} \right\}}}}(\rho ,r) = \mathop \smallint \limits_0^\infty \left\{ {\begin{array}{*{20}{c}} {f(r + s)} \\ {sf{\kern 1pt} '(r + s)} \end{array}} \right\}\frac{{ds}}{{\sqrt {{{\rho }^{2}} + {{s}^{2}}} }} \\ \end{gathered} $
$E$ и $\nu $ – модуль Юнга и коэффициент Пуассона материала полупространства. Величина $\Gamma (\rho ;r)$ представляет собой функцию влияния (Грина), определяющую нормальное перемещение границы полупространства от локального воздействия индентора, при этом зазор $r$ выступает в качестве характеристики этого воздействия.

Заметим, что при наличии контактного зазора, обусловленного межмолекулярным взаимодействием, область контакта D определяется однозначно только для индентора ограниченного (в плоскости $z$) размера [8, 13]. В случае произвольного индентора его взаимодействие с полупространством может распространяться на всю границу полупространства и область контакта D можно определить только условно, например, как область с положительными значениями контактного давления p, определяемого по формуле (1.1). Если характерный размер a такой области значительно превышает зазор r, то такое определение области контакта D будет достаточно корректным ввиду быстрого затухания межмолекулярного взаимодействия вне области D.

Далее будет дана априорная оценка зазора $r$ в предположении его малости по сравнению с характерным размером $a$ области контакта:

(1.8)
$r(x,y) \ll a$

Условие (1.8) позволяет для задачи (1.4)–(1.6) выделить крупномасштабный уровень 1 и мелкомасштабный уровень 2, характеризуемые размерами $a$ и $r$, соответственно. На масштабном уровне 1 взаимодействие индентора с полупространством будем рассматривать в терминах классической контактной задачи, пренебрегая зазором $r$. Соответствующие контактное давление ${{p}_{c}}(x,y) \geqslant 0$ и область контакта ${{{\text{D}}}_{с }}$ считаются известными.

Существование контактного зазора будем учитывать на масштабном уровне 2, при этом найденное на уровне 1 распределение ${{p}_{c}}(x,y)$ используется в качестве контактного давления $p(x,y)$, связанного с зазором $r(x,y)$ первым равенством (1.1). Другими словами, допустим, что $p(x,y) = {{p}_{c}}(x,y)$ и определим соответствующий зазор ${{r}_{c}}(x,y)$ из уравнения

(1.9)
${{p}_{c}}(x,y) = \Phi ({{r}_{c}}(x,y)),\quad x,y \in {{{\text{D}}}_{c}}$

По определению (1.3) функция $\Phi (X)$ – монотонная при $X > 0$, поэтому при положительных значениях ${{p}_{c}}$ уравнение (1.9) однозначно разрешимо относительно ${{r}_{c}}$.

Величина ${{r}_{c}}(x,y)$ представляет собой искомую оценку контактного зазора. Наличие такой оценки позволяет избежать прямого решения задачи (1.4)–(1.6), которое представляется весьма проблематичным ввиду присутствия нелинейного интегрального оператора (1.6).

В описанном выше методе оценки контактного зазора центральным является допущение $p(x,y) = {{p}_{c}}(x,y)$ (далее, гипотеза С). В следующем разделе будет выполнена

2. Проверка гипотезы С. Обозначим через ${{g}_{c}}(x,y)$ левую часть условия контакта (1.4) при подстановке в нее величины ${{r}_{c}}(x,y)$ в качестве контактного зазора:

(2.1)
${{g}_{c}}(x,y) = {{r}_{c}}(x,y) - {{r}_{c}}(0,0) + {{w}_{c}}(x,y) - {{w}_{c}}(0,0),\quad x,y \in {{{\text{D}}}_{c}},$
причем, в силу соотношения (1.6)

(2.2)
${{w}_{c}}(x,y) = \iint\limits_{{{{\text{D}}}_{с }}} {\Gamma (\sqrt {{{{(\xi - x)}}^{2}} + {{{(\eta - y)}}^{2}}} ;\;{{r}_{c}}(\xi ,\eta ))}d\xi d\eta $

Функцию ${{g}_{c}}(x,y)$ можно интерпретировать как некоторую эффективную форму индентора, обеспечивающую выполнение условия контакта (1.4) при использовании в качестве контактного зазора оценки ${{r}_{c}}(x,y)$. Если бы функция ${{r}_{c}}(x,y)$ представляла собой точное решение задачи (1.4)–(1.6), то эффективная форма ${{g}_{c}}(x,y)$ совпадала бы с заданной формой $g(x,y)$ индентора. Расхождение этих форм характеризует степень согласованности задачи при использовании оценки ${{r}_{c}}(x,y)$ в качестве контактного зазора и может служить мерой правомерности гипотезы С.

Отметим, что условие равновесия (1.5) для зазора ${{r}_{c}}(x,y)$ выполняется точно в силу равенства (1.9) и определения контактного давления ${{p}_{c}}(x,y)$ как решения классической контактной задачи для индентора, нагруженного силой $P$.

Далее будет рассматриваться осесимметричный случай сферического индентора радиуса $R$:

(2.3)
$g(x,y) \equiv g(\rho ) = \frac{1}{{2R}}{{\rho }^{2}},\quad \rho = \sqrt {{{x}^{2}} + {{y}^{2}}} ,$
для которого близость эффективной формы ${{g}_{c}}(x,y) \equiv {{g}_{c}}(\rho )$ к заданной форме $g(\rho )$ и, следовательно, правомерность гипотезы С можно охарактеризовать показателем

(2.4)
$\varepsilon = \frac{1}{{{{S}_{g}}}}\int\limits_0^a {\left| {g(\rho ) - {{g}_{c}}(\rho )} \right|d\rho ,\quad } {{S}_{g}} = \int\limits_0^a {\left| {g(\rho )} \right|d\rho } $

Для сферического индентора [16]:

(2.5)
${{p}_{c}}(x,y) \equiv {{p}_{c}}(\rho ) = \frac{{2E}}{{\pi (1 - {{\nu }^{2}})R}}\sqrt {{{a}^{2}} - {{\rho }^{2}}} ,\quad a = {{\left( {\frac{{3(1 - {{\nu }^{2}})RP}}{{4E}}} \right)}^{{1/3}}}$
область контакта ${{{\text{D}}}_{c}}$ представляет собой круг радиуса $a$. Соответствующий зазор ${{r}_{c}}(x,y)$ ≡ ${{r}_{c}}(\rho )$ находится из уравнения (1.9): ${{p}_{c}}(\rho )$ = $\Phi ({{r}_{c}}(\rho ))$, $\rho \in [0,a]$.

В случае круговой области ${{{\text{D}}}_{c}}$, используя полярную систему координат $\rho $, $\varphi $, выражение (2.2) можно представить в виде

(2.6)
${{w}_{c}}(x,y) \equiv {{w}_{c}}(\rho ) = \int\limits_0^a {ldl} \int\limits_0^{2\pi } {d\varphi \Gamma (L(\rho ,l,\varphi );{{r}_{c}}(l))} ,\quad L(\rho ,l,\varphi ) = \sqrt {{{\rho }^{2}} + {{l}^{2}} - 2\rho l\cos \varphi } $

В свою очередь, учитывая представления (1.2) и (1.7) для функций $f(d)$ и $\Gamma (\rho ;r)$ и выполняя интегрирование по $\varphi $, выражение (2.6) можно преобразовать и установить, что

(2.7)
${{w}_{c}}(\rho ) = \frac{{2(1 + \nu )}}{{\pi E}}\left\{ {{{b}_{1}}\int\limits_0^a {\left[ {4r{{N}_{5}} - (1 + 2\nu ){{N}_{4}}} \right]ldl} - {{b}_{2}}\int\limits_0^a {\left[ {10r{{N}_{{11}}} - (7 + 2\nu ){{N}_{{10}}}} \right]ldl} } \right\},$
где
(2.8)
${{N}_{m}} = \int\limits_0^\infty {\frac{{{\mathbf{K}}\left( k \right)ds}}{{{{{({{r}_{c}}(l) + s)}}^{m}}\sqrt {{{{(\rho + l)}}^{2}} + {{s}^{2}}} }}} ,\quad k = \sqrt {\frac{{4\rho l}}{{{{{(\rho + l)}}^{2}} + {{s}^{2}}}}} ,$
${\mathbf{K}}(k)$ – полный эллиптический интеграл 1-го рода. Интегралы (2.7) и (2.8) могут быть определены с помощью известных численных методов.

На основе выражений (2.1), (2.4) и (2.7) были проведены расчеты эффективной формы ${{g}_{c}}(\rho )$ и соответствующего показателя $\varepsilon $ при следующих значениях параметров задачи:

$E = {{10}^{8}}\;{\text{П а }},\quad \nu = 0.3,\quad R = 1\;{\text{м к м }},P,{\text{ н Н }} = 5{\text{ }}(1),{\text{ }}10{\text{ }}(2),{\text{ }}20{\text{ }}(3),{\text{ }}50{\text{ }}(4)$

Выбранным вариантам нагружения отвечают значения

$a,{\text{ н м }} \approx 32.436{\text{ }}(1),{\text{ }}40.866{\text{ }}(2),{\text{ }}51.489{\text{ }}(3),{\text{ }}69.881{\text{ }}(4)$
${{r}_{c}}(0),\;{\text{н м }} \approx 0.94935{\text{ }}(1),{\text{ }}0.94018{\text{ }}(2),{\text{ }}0.92996{\text{ }}(3),{\text{ }}0.91486{\text{ }}(4),$
которые удовлетворяют условию (1.8). Параметры ${{b}_{{{\kern 1pt} 1,2}}}$ межмолекулярного взаимодействия при расчетах принимались такими, что в формуле (1.3) ${{r}_{e}} = 1$ нм, ${{A}_{1}} = {{(6\pi )}^{{ - 1}}}{{A}_{H}}$; ${{A}_{H}} = {{10}^{{ - 19}}}$ Дж – постоянная Гамакера [5, 13].

Расчетные значения показателя $\varepsilon $ составили: 0.0557 (1), 0.04026 (2), 0.02894 (3), 0.01881 (4). Как видно, особенно малые значения показатель $\varepsilon $ имеет при больших нагрузках $P$ и, следовательно, больших размерах $a$ области контакта (варианты 3 и 4), когда условие (1.8) выполняется в полной мере.

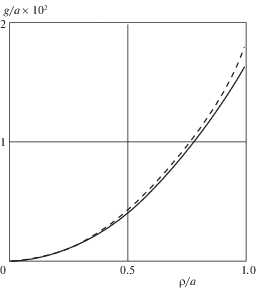
Полученные значения $\varepsilon $ свидетельствуют о незначительном отличии эффективной формы индентора от заданной. Это иллюстрируется фиг. 2, на которой для варианта 1 нагружения изображены функции ${{g}_{c}}(\rho )$ (штриховая линия) и $g(\rho )$ (сплошная линия).

Фиг. 2

Таким образом, выполненный анализ позволяет сделать заключение о допустимости использования гипотезы С для оценки контактного зазора при условии (1.8).

3. Расчет подповерхностных напряжений. Как указывалось выше, при рассматриваемой постановке задачи деформация полупространства обуславливается распределение объемных сил $f(r(x,y) + s)$ по его глубине $s$. Вклад каждой силы $fdV$ (фиг. 1) в напряженно-деформированное состояние (НДС) полупространства может быть определен с помощью решения Миндлина о внутренней сосредоточенной силе [17]. Суммирование этих вкладов по всему распределению объемных сил позволяет рассчитать НДС полупространства [13, 18].

Далее будет рассматриваться осесимметричный случай сферического индентора (2.3) и использоваться цилиндрическая система координат $\rho $, $\varphi $, $z$, ось $z$ которой направлена внутрь полупространства [16, 17]. Соответствующие ненулевые компоненты перемещений и тензора напряжений будут обозначаться через $u$, $w$, ${{\sigma }_{\rho }}$, ${{\sigma }_{\varphi }}$, ${{\sigma }_{z}}$, ${{\tau }_{{\rho z}}}$. Указанная выше процедура расчета НДС полупространства в таком случае приводит к следующим результатам:

(3.1)
$\begin{gathered} u(\rho ,z) = c\int\limits_0^a {ldl} \int\limits_0^{2\pi } {{{E}_{{10}}}(\rho ,z,l,\varphi )d\varphi } ,\quad w(\rho ,z) = c\int\limits_0^a {ldl} \int\limits_0^{2\pi } {{{E}_{{20}}}(\rho ,z,l,\varphi )d\varphi } \\ {{u}_{{\left\{ {\begin{array}{*{20}{c}} {,\rho } \\ {,z{\mkern 1mu} } \end{array}} \right\}}}}(\rho ,z) = c\int\limits_0^a {ldl} \int\limits_0^{2\pi } {{{E}_{{\left\{ {\begin{array}{*{20}{c}} {11} \\ {12} \end{array}} \right\}}}}(\rho ,z,l,\varphi )d\varphi } ,\quad {{w}_{{\left\{ {\begin{array}{*{20}{c}} {,\rho } \\ {,z{\mkern 1mu} } \end{array}} \right\}}}}(\rho ,z) = c\int\limits_0^a {ldl} \int\limits_0^{2\pi } {{{E}_{{\left\{ {\begin{array}{*{20}{c}} {21} \\ {22} \end{array}} \right\}}}}(\rho ,z,l,\varphi )d\varphi } , \\ \end{gathered} $
где запятая перед индексом $\rho $ или $z$ обозначает соответствующую частную производную,

${{E}_{{10}}} = {{\rho }_{{\text{*}}}}U,\quad {{E}_{{20}}} = W,\quad {{E}_{{11}}} = U + \frac{{\rho _{{\text{*}}}^{2}}}{L}{{U}_{{,L}}},\quad {{E}_{{12}}} = {{\rho }_{{\text{*}}}}{{U}_{{,z}}}$
(3.2)
${{E}_{{21}}} = \frac{{{{\rho }_{{\text{*}}}}}}{L}{{W}_{{,L}}},\quad {{E}_{{22}}} = {{W}_{{,z}}};\quad {{\rho }_{{\text{*}}}} = \rho - l\cos \varphi $
$\left\{ {\begin{array}{*{20}{c}} {U(L,z,l)} \\ {W(L,z,l)} \end{array}} \right\} = - \int\limits_0^\infty {f(r(l) + s){{{\hat {M}}}_{{\left\{ {\begin{array}{*{20}{c}} 1 \\ 2 \end{array}} \right\}}}}(L,z;s)ds} ,\quad c = \frac{{1 + \nu }}{{8\pi (1 - \nu )E}}$

Функции ${{\hat {M}}_{{1,2}}}$ определяют поле перемещений $u$, $w$ в полупространстве при действии в нем сосредоточенной силы ${{F}_{z}}$, приложенной в точке $\rho = 0$, $z = s$ и направленной по оси $z$ (задача Миндлина [17]), так что

$u(\rho ,z) = c\rho {{\hat {M}}_{1}}(\rho ,z;s){{F}_{z}},\quad w(\rho ,z) = c{{\hat {M}}_{2}}(\rho ,z;s){{F}_{z}}$

Производные ${{U}_{{,L}}}$, ${{U}_{{,z}}}$, ${{W}_{{,L}}}$, ${{W}_{{,z}}}$ находятся путем внесения операции дифференцирования под знак интеграла (3.2) – правомерность такого действия может быть установлена для $z > 0$.

Поле перемещений (3.1) позволяет на основе закона Гука определить компоненты тензора напряжений для рассматриваемого осесимметричного случая [19]:

(3.3)
${{\sigma }_{\rho }} = \lambda \theta + 2\mu {{u}_{{,\rho }}},\quad {{\sigma }_{\varphi }} = \lambda \theta + 2\mu \frac{u}{\rho },\quad {{\sigma }_{z}} = \lambda \theta + 2\mu {{w}_{{,z}}},\quad {{\tau }_{{\rho z}}} = \mu ({{u}_{{,z}}} + {{w}_{{,\rho }}}),$
причем

$\theta = {{u}_{{,\rho }}} + u{\text{/}}\rho + {{w}_{{,z}}},\quad \lambda = {{[(1 + \nu )(1 - 2\nu )]}^{{ - 1}}}\nu E,\quad \mu = {{[2(1 + \nu )]}^{{ - 1}}}E$

Располагая компонентами тензора напряжений, можно определить интенсивность касательных напряжений и удельную потенциальную энергию деформаций

(3.4)
$\begin{gathered} {{\tau }_{i}} = \frac{1}{{\sqrt 6 }}{{[{{({{\sigma }_{1}} - {{\sigma }_{2}})}^{2}} + {{({{\sigma }_{2}} - {{\sigma }_{3}})}^{2}} + {{({{\sigma }_{1}} - {{\sigma }_{3}})}^{2}}]}^{{1/2}}} \\ \Pi = \frac{1}{{2E}}[\sigma _{1}^{2} + \sigma _{2}^{2} + \sigma _{3}^{2} - 2\nu ({{\sigma }_{1}}{{\sigma }_{2}} + {{\sigma }_{2}}{{\sigma }_{3}} + {{\sigma }_{1}}{{\sigma }_{3}})], \\ \end{gathered} $
которые используются в некоторых критериях пластического течения и разрушения материалов [20]. Здесь ${{\sigma }_{1}}$, ${{\sigma }_{2}}$, ${{\sigma }_{3}}$ – главные напряжения, которые выражаются известным образом через компоненты ${{\sigma }_{\rho }}$, ${{\sigma }_{\varphi }}$, ${{\sigma }_{z}}$, ${{\tau }_{{\rho z}}}$ [19]. Например, при $\rho = 0$: ${{\sigma }_{1}} = {{\sigma }_{2}} = {{\sigma }_{\rho }}$, ${{\sigma }_{3}} = {{\sigma }_{z}}$.

На основе формул (3.1)–(3.4) были выполнены расчеты величин ${{\tau }_{i}}$ и $\Pi $, при этом в качестве контактного зазора использовалась полученная выше оценка ${{r}_{c}}(\rho )$. Расчеты проводились при указанных в разделе 2 значениях параметров задачи.

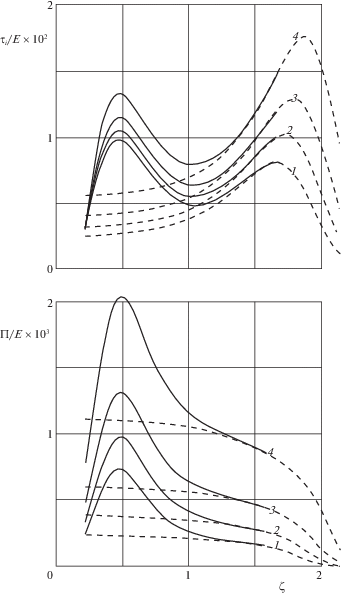
На фиг. 3 показаны распределения величин ${{\tau }_{i}}$ и $\Pi $ по глубине $z > 0$ полупространства при $\rho = 0$. Для того чтобы иметь возможность изобразить на одном графике особенности рассматриваемых величин при малых и больших значениях $z{\text{/}}{{r}_{e}}$, здесь используется переменная $\zeta = {{[\ln (1 + z{\text{/}}{{r}_{e}})]}^{{1/2}}}$. Кривые 1, 2, 3, 4 соответствуют выбранным в разд. 2 вариантам нагружения. Решению (2.5) классической контактной задачи отвечают напряжения, распределения которых по глубине полупространства описываются известными формулами [16, 21]. Величины ${{\tau }_{i}}$ и $\Pi $, рассчитанные на основе этих формул, представлены на фиг. 3 штриховыми кривыми.

Фиг. 3

Выполненные расчеты свидетельствуют о существенном различии напряженных состояний в тонком (толщина ~${{r}_{e}}$) подповерхностном слое полупространства при классической постановке контактной задачи (фиг. 3, штриховые кривые) и при самосогласованном подходе с объемным приложением межмолекулярных сил (сплошные кривые). Это согласуется с ранее полученными результатами [11, 13].

Важная особенность распределений по глубине полупространства величин ${{\tau }_{i}}$ и $\Pi $, связанных с разрушением материала – наличие у них при самосогласованном подходе дополнительных локальных максимумов, отсутствующих при классической постановке. Как показывают расчеты, значения этих максимумов существенно зависят от контактной нагрузки $P$. Таким образом, использование самосогласованного подхода позволяет прогнозировать существование дополнительных очагов разрушения в полупространстве.

4. Выводы.

1. Предложен и обоснован метод оценки контактного зазора, использующий концепцию двух масштабных уровней и позволяющий существенно упростить расчет контактного взаимодействия в рамках самосогласованного подхода.

2. С использованием полученной оценки контактного зазора выполнен расчет подповерхностных напряжений в упругом полупространстве, контактирующим со сферическим индентором при различных нагрузках.

3. Показано, что использование самосогласованного подхода с объемным приложением межмолекулярных сил позволяет прогнозировать существование дополнительных очагов подповерхностного разрушения материала.

Работа выполнена по теме государственного задания (№ госрегистрации АААА-А17-117021310379-5) и при частичной финансовой поддержке Российского фонда фундаментальных исследований (17-58-52030, 18-08-00558).

Список литературы

  1. Johnson K.L., Kendall K., Roberts A.D. Surface energy and the contact of elastic solids // Proc. Roy. Soc. London. Ser. A. 1971. V. 324. № 1558. P. 301–313.

  2. Derjaguin B.V., Muller V.M., Toporov Yu.P. Effect of contact deformations on the adhesion of particles // J. Colloid Interface Sci. 1975. V. 53. № 2. P. 314–326.

  3. Горячева И.Г., Маховская Ю.Ю. Адгезионное взаимодействие упругих тел // ПММ. 2001. Т. 65. Вып. 2. С. 279–279.

  4. Goryacheva I.G., Makhovskaya Yu.Yu. Adhesion effects in contact interaction of solids // CR Mecanique. 2008. V. 336. № 1–2. P. 118–125.

  5. Muller V.M., Yushchenko V.S., Derjaguin B.V. On the influence of molecular forces on the deformation of an elastic sphere and its sticking to a rigid plane // J. Coll. Interface Sci. 1980. V. 77. № 1. P. 91–101.

  6. Attard P., Parker J.L. Deformation and adhesion of elastic bodies in contact // Phys. Rev. A. 1992. V. 46. № 12. P. 7959–7971.

  7. Greenwood J.A. Adhesion of small spheres // Phil. Mag. 2009. V. 89. № 11. P. 945–965.

  8. Солдатенков И.А. Применение метода последовательных приближений к расчету упругого контакта при наличии молекулярной адгезии // ПММ. 2012. Т. 76. Вып. 5. С. 734–743.

  9. Sauer R.A., Li S. A contact mechanics model for quasi-continua // Int. J. Numer. Meth. Engng. 2007. V. 71. № 8. P. 931–962.

  10. Sauer R.A., Wriggers P. Formulation and analysis of a three-dimensional finite element implementation for adhesive contact at the nanoscale // Computer Methods Appl. Mech. Engng. 2009. V. 198. № 49–52. P. 3871–3883.

  11. He L.H. Stress and deformation in soft elastic bodies due to intermolecular forces // J. Mech. Phys. Solids. 2013. V. 61. № 6. P. 1377–1390.

  12. Солдатенков И.А. Контактная задача при объемном приложении сил межмолекулярного взаимодействия (уточненная постановка) // ПММ. 2013. Т. 77. Вып. 6. С. 877–893.

  13. Солдатенков И.А. Контактная задача при объемном приложении сил межмолекулярного взаимодействия: особенности подповерхностных напряжений // ПММ. 2016. Т. 80. Вып. 6. С. 733–745.

  14. Kaplan I.G. Intermolecular interactions: physical picture, computational methods and model potentials. Chichester: Wiley, 2006.

  15. Israelachvili J.N. Intermolecular and Surface Forces. 3-rd ed. London: Academic, 2011.

  16. Johnson K.L. Contact Mechanics. Cambridge: Univ. Press, 1982.

  17. Mindlin R.D. Force at a point in the interior of a semi-infinite solid // Phys. 1936. V. 7. № 5. P. 195–202.

  18. Солдатенков И.А. Контактная задача при объемном приложении сил межмолекулярного взаимодействия: функция влияния для неоднородного упругого полупространства // ПММ. 2018. Т. 82. Вып. 3. С. 358–371.

  19. Hahn H.G. Elastizitätstheorie. Grundlagen der linearen Theorie und Anwendungen auf eindimensionale, ebene und räumliche Probleme. Stuttgart: Teubner, 1985.

  20. Collins J.A. Failure of Materials in Mechanical Design. Analysis, Prediction, Prevention. N.Y.: The Ohio State University, John Wiley & Sons, 1981.

  21. Terazawa K. On the elastic equilibrium of a semi-infinite solid under given boundary conditions, with some applications // J. Coll. Sci. Imp. Univ. Tokyo. 1916. V. 37. Art. 7. P. 1–64.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал