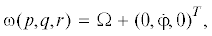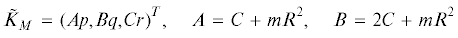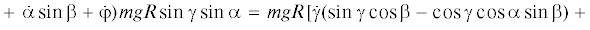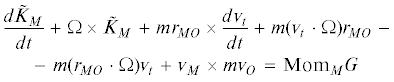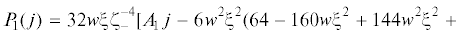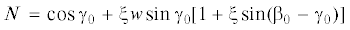Прикладная математика и механика, 2019, T. 83, № 2, стр. 234-248

Неголономной модели качения круглого диска по абсолютно твердой опоре без скольжения посвящено немало работ. Не претендуя на полноту библиографии, отметим, что в самом начале [1–3] решалась задача о составлении уравнений движения, затем – задача об интегрировании полученных уравнений [3–7], позднее изучались [8–17] характерные частные движения диска, их устойчивость. Кроме неголономной модели, рассматривались и другие силовые модели взаимодействия диска с опорной поверхностью [18, 19]. В последние 10–15 лет особый интерес вызвала [20–25] задача о финальном движении тяжелого диска (по сути, затухающей прецессии при наличии диссипации) на горизонтальной плоскости, когда диск заканчивает движение плашмя с характерным усиливающимся звуком (“диск Эйлера”). За некоторым исключением (например, [26, 27] и др.) практически во всех работах рассматривалась задача о качении диска по плоскости, горизонтальной или наклонной. Ниже рассматривается задача о качении диска без проскальзывания по поверхности вращения отрицательной кривизны. Такая специфическая постановка вызвана наблюдением одной механической системы (см., например, https://www.youtube.com/watch?v=rfNpjrPTYzU&fs=1&hl=en_US&rel=0).

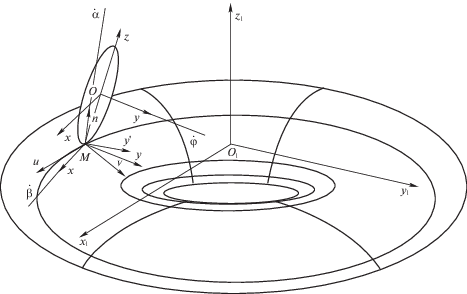
1. Кинематика движения. Тяжелый тонкий однородный диск массы $m$ и радиуса $R$ катится, опираясь на неподвижную поверхность $S$, представляющую собой поверхность вращения вокруг вертикальной оси ${{O}_{1}}{{z}_{1}}$, $Mu\text{v}n\quad$ – ее сопутствующий триэдр: ось $Mu$ направлена по касательной к параллели, ось $Mn$ ортогональна поверхности (фиг. 1).

В начальном положении диск расположен так, что ось $Mn$ совпадает с диаметром диска, а плоскость диска совпадает с плоскостью . Сначала диск поворачиваем вокруг оси $Mn$ на угол $\quad\alpha $, оси триэдра $Mu\text{v}n$ занимают положение $Mxy{\text{'}}n$. Затем наклоняем диск вокруг оси $Mx$ на угол $\beta $, оси $Mxy{\text{'}}n$ займут положение $Mxyz$. Центральные оси $Oxyz$ параллельны соответствующим осям $Mxyz$.

Матрица перехода от осей $Mu\text{v}n\quad$ к осям $Mxyz$ имеет, следовательно, вид

Проекции угловой скорости осей $Mxyz$ относительно триэдра $Mu\text{v}n\quad$ на сами оси $Mxyz$ соответственно равны $\dot {\beta }$, $\dot {\alpha }\sin \beta $, $\dot {\alpha }\cos \beta $.

Введем цилиндрические координаты ($r$, $\quad\psi $, ${{z}_{1}}$), где $r$ – полярный радиус в плоскости ${{O}_{1}}{{x}_{1}}{{y}_{1}}$, $\psi $ – угол поворота меридианной плоскости $\quad{{O}_{1}}r{{z}_{1}}$ вокруг оси ${{O}_{1}}{{z}_{1}}$. Пусть $r = f({{z}_{1}})$ – уравнение меридиана опорной поверхности $S$. Условимся в дальнейшем называть точку $M$ опорной поверхности, в которой ее касается движущийся диск, полюсом. Для краткости обозначений будем считать, что $r$, $\psi $, $\quad{{z}_{1}}$ – координаты полюса $M$. В осях $Mu\text{v}n\quad$ скорость этой точки имеет компоненты

Введем угол $\gamma \in (0,\quad\pi {\text{/}}2)$, который составляет ось $Mn$ с осью ${{O}_{1}}{{z}_{1}}$. Имеем

Напомним, что кривизна нормального сечения поверхности по данному направлению имеет знак плюс, если направление вектора кривизны сечения совпадает с нормалью к поверхности. В противном случае нормальная кривизна отрицательна. При этом направление нормали $n$ к поверхности определяется выбором внутренних (гауссовых) координат поверхности так, что трехгранник $Mu\text{v}n$ правоориентированный.

Для нормального сечения, проведенного через касательную 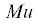, кривизна по теореме Менье [28] равна

Гауссова кривизна опорной поверхности отрицательна:

Относительно осей 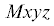вектор скорости полюса $M$ имеет компоненты

Угловая скорость вращения триэдра $Mu\text{v}n$ относительно системы отсчета ${{O}_{1}}{{x}_{1}}{{y}_{1}}{{z}_{1}}$ имеет в осях $Mu\text{v}n$ компоненты

Для угловой скорости вращения осей $Mxyz$ относительно системы отсчета ${{O}_{1}}{{x}_{1}}{{y}_{1}}{{z}_{1}}$ в проекциях на оси $Mxyz$ получим

В осях $Mxyz$ абсолютная угловая скорость диска имеет вид

а скорость центра диска равна где ${{\text{v}}_{t}}$ – мгновенная скорость точки диска, касающейся опорной поверхности. В неголономной модели ${{\text{v}}_{t}} = 0$, в то время как скорость движения полюса $M$ по опорной поверхности ненулевая. Напротив, если диск пробуксовывает, оставаясь на месте, то ${{\text{v}}_{t}} \ne 0$, а скорость полюса $M$ равна нулю.

Для вектора силы тяжести в осях $Mxyz\quad$ имеем выражение

Следовательно, момент силы тяжести диска относительно точки $M$ равен

Обозначим

вектор кинетического момента диска, подсчитанный для точки контакта $M$ в осях $Mxyz\quad$ при условии ${{\text{v}}_{t}} = 0$. Кинетический момент абсолютного движения диска равен (${{r}_{{MO}}}$ – радиус-вектор из точки $M$ в центр $O$ диска).

2. Уравнения движения. Запишем уравнение изменения кинетического момента материальной системы в ее абсолютном движении. Когда момент подсчитан относительно произвольного полюса $P$, это уравнение имеет вид [29] (производная $d{\text{/}}dt$ отнесена к неподвижной системе координат)

где $\quad{{\text{v}}_{P}}$ – скорость полюса в абсолютном пространстве, ${{\text{v}}_{O}}$ – скорость центра масс $O$ системы, а справа записан момент относительно точки $P$ результирующей внешних сил, приложенных к системе. Если система представляет собой твердое тело, опирающееся на твердую поверхность, то в общем случае в правую часть равенства (2.1) входит момент реакции опорной поверхности.

Неголономная модель. Уравнения неголономных связей выражают постоянное в процессе движения отсутствие скольжения диска по опорной поверхности, т.е. скорость точки диска, которой он в рассматриваемое мгновение касается поверхности, равна нулю

В осях $Mxyz$ точка имеет координаты $l = {{(0,0,R)}^{T}}$. Следовательно, по формуле Эйлера (${{\text{v}}_{M}}$ – скорость начала координат триэдра 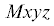) получим

Переходя к координатной записи, заключаем, что имеется всего два уравнения связей

которые можно записать еще и так:

При помощи уравнений связей компоненты переносной угловой скорости преобразуются к виду

Следуя известному подходу [30–32], выбираем в качестве подвижного полюса $P$ точку $M$ и перепишем уравнение (2.1) в виде (производная $d{\text{/}}dt$ отнесена к подвижной системе координат $Mxyz$)

С учетом равенства $B = A + C$ в проекциях на оси $Mxyz\quad$ это векторное уравнение запишем в виде

Так как неголономная система имеет три степени свободы, динамические уравнения (2.3) вместе с кинематическими (1.3) и уравненями связей (2.2) составляют замкнутую систему дифференциальных уравнений движения системы.

Неголономная система консервативна.

Если умножим первое из динамических уравнений (2.3) на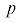, второе – на $q$, третье – на $r$ и сложим, то слева получим

а справа получится выражение

Следовательно, имеем интеграл энергии

Выражение в квадратных скобках представляет собой высоту центра $O\quad$ диска над плоскостью $\quad{{O}_{1}}{{x}_{1}}{{y}_{1}}$:

Голономная модель. Скорость точки диска, которой он в данное мгновение касается поверхности в безотрывном движении, может быть отлична от нуля, и из уравнений (1.4) и (2.1) при выборе $P \equiv M$ вытекает, что

К этому уравнению следует добавить уравнение движения центра масс

где ${{R}_{n}}$ – нормальная компонента реакции, ${{R}_{t}}$ – тангенциальная компонента реакции (сила трения), равная $ - {{k}_{f}}\left| N \right|{{\text{v}}_{t}}{\text{/}}\left| {{{\text{v}}_{t}}} \right|$ при ${{\text{v}}_{t}} \ne 0$, $N = {{R}_{n}} \cdot n$. Параметр ${{k}_{f}}$ – эмпирический коэффициент сухого трения, обычно $0 < {{k}_{f}} < 1$. Если ${{\text{v}}_{t}} = 0$, то $\left| {{{R}_{t}}} \right| \leqslant {{k}_{f}}N$.

Производная $d{\text{/}}dt$ в формулах (2.4) и (2.5) отнесена к подвижной системе координат $Mxyz$.

Голономная система имеет пять степеней свободы, если не происходит отрыв диска от опорной поверхности. Кинематические (1.3) и динамические (2.4) и (2.5) уравнения вместе с заданным конечным уравнением опорной поверхности представляют собой замкнутую совокупность относительно неизвестных $\varphi $, $\alpha $, $\beta $, $p$, $q$, $r$, ${{w}_{1}}$, ${{w}_{2}}$, $\quad{{z}_{1}}$ задачи.

3. Приведение уравнений к безразмерному виду. Положим

где $\tau $ – новое безразмерное время. Дифференцирование по $\tau $ обозначаем штрихом. Тильду над буквами далее опускаем.

Диск однородный, поэтому $A = 1.25$, $B = 1.5$, $C = 0.25$.

Запишем в безразмерной форме динамические уравнения (2.3) и интеграл энергии

а также уравнения связей и уравнения для компонент абсолютной угловой скорости диска где $\xi = R{{f}^{{ - 1}}}$ и $\eta = Rk$ – безразмерные функции от ${{z}_{1}}$. Кроме того, имеем уравнение для безразмерной аппликаты точки контакта

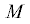
Приведенные к безразмерному виду уравнения (2.4) и (2.5) не приводим. Они получаются аналогично с теми же масштабирующими коэффициентами.

4. Приведение уравнений к виду, удобному для численного интегрирования. Разрешаем кинематические уравнения относительно $\alpha {\text{'}}$, $\quad\beta {\text{'}}$, $\varphi {\text{'}}\quad$ и подставляем выражение для $\varphi {\text{'}}\quad$ в динамические уравнения, уравнения связей и в уравнение для $z_{1}^{{\text{'}}}$. Получим дифференциальную систему девятого порядка в нормальной форме с девятью неизвестными функциями $\alpha $, $\beta $, $\varphi $, $p$, $q$, $r$, $\psi $, $\gamma $, ${{z}_{1}}$. Углы $\varphi $ и $\psi $ будут циклическими координатами в том смысле, что правые части системы их не содержат. Одна из двух координат $\gamma $ и ${{z}_{1}}$ избыточная, так как эти координаты связаны конечным соотношением (второе равенство (1.1)).

Из уравнений (3.3) находим

Формулы теряют смысл при $Z = 0$, т.е. когда

Условие (4.2) имеет ясный геометрический смысл. По формуле Эйлера [28] правая его часть – нормальная кривизна опорной поверхности в направлении $Mx$ (фиг. 1), а левая часть – проекция вектора кривизны окружности диска на нормаль к поверхности. Движение диска возможно, только когда левая часть больше правой. Так как ${{k}_{2}} < 0$, то при любом значении угла $\alpha \quad$это неравенство выполняется, если

Дополнительно примем, что $R < f\cos \beta $. Тогда неравенство (4.3) справедливо при любом значении угла $\gamma \in (0,\pi {\text{/}}2)$, а безразмерная величина $\xi = R\quad{{f}^{{ - 1}}} < 1$.

5. Стационарные качения диска по параллели опорной поверхности. Рассмотрим вопрос о существовании стационарных движений в неголономной модели диска, когда

Уравнения связей (3.2) дают

Кинематические уравнения (3.3) дают значения для $p$, $q$, :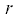

И наконец, динамические уравнения (3.1) дают единственное соотношение

Так как $B > C$ и $0 < \xi < 1$, правая часть полученного равенства положительна только при условии $\chi < 0$, которое необходимо для существования стационарных движений – качений диска по произвольной параллели.

Пусть левая часть уравнения (5.1) имеет значение $w > 0$. Выясним, существует ли решение этого уравнения относительно неизвестной величины $\chi $. После замены

уравнение принимает вид

Ряд Штурма [33] содержит пять многочленов, начиная с ${{P}_{4}}(j)$, и строится по правилу: многочлен ${{P}_{3}}(j) = d{{P}_{4}}(j){\text{/}}dj$, многочлен ${{P}_{{n - 2}}}(j)$ равняется остатку от деления многочлена ${{P}_{n}}(j)$ на многочлен ${{P}_{{n - 1}}}(j)$ (n = 4, 3, 2). Следовательно,

Последний многочлен ${{P}_{0}}(j)$ является отрицательной постоянной в силу неравенства $0 < \xi < 1$.

Обращая внимание на старшие по степени $j$ члены, замечаем, что при любом знаке постоянной ${{A}_{1}}$ число смены знака в ряду Штурма при $j = - \left| L \right|$ на две единицы больше, чем число смены знака при $j = \left| L \right|\quad$ ($\left| L \right| \gg 1$). По теореме Штурма это означает, что уравнение (5.2) имеет ровно два действительных корня разных знаков (в силу отрицательности свободного члена).

Таким образом, доказано, что для произвольной параллели (угол ${{\gamma }_{0}}$ определен) существует единственное значение угла ${{\beta }_{0}} < {{\gamma }_{0}}$, соответствующее заданному произвольному значению $w\quad$ квадрата угловой скорости собственного вращения диска.

Однако не при любых значениях $w$ и ${{\beta }_{0}}$, ${{\gamma }_{0}}$ стационарное движение диска реализуется на практике. Так как контактная связь неудерживающая, необходимо, чтобы нормальная составляющая реакции опоры постоянно в процессе качения диска удовлетворяла условию

Далее. В неголономной модели реакция опорной поверхности определяется однозначно из уравнений движения и наложенных связей как функция переменных задачи и их производных по времени. Вопрос о физическом происхождении этой силы обычно не затрагивается. Если, однако, предположить, что сила реакции – следствие твердости (непроницаемости) опоры и сопротивления скольжению движущегося по опорной поверхности тела, то требуется проверка дополнительных условий, обеспечивающих движение тела. Например, если тангенциальная компонента силы реакции является силой сухого трения, то в процессе безотрывного движения тела необходимо, кроме условия (5.3), постоянное выполнение еще одного условия

(предполагаем, что коэффициент сухого трения лежит в интервале (0, 1), как это обычно принято в инженерной практике).

Условия (5.3) и/или (5.4) могут нарушаться, и тогда соответствующее движение неголономной системы не имеет механического смысла, поскольку нет физических сил, обеспечивающих контакт тел и отсутствие относительного скольжения, как это предписано в неголономной модели.

Поясним сказанное подробнее на примере рассматриваемой задачи.

Из уравнения (2.5) стационарного движения центра диска после преобразования уравнения к безразмерной форме и учета условия непроскальзывания $\psi {\text{'}} = \varphi {\text{'}}\xi $ легко определяются следующие стационарные значения нормальной и тангенциальной (силы трения) компонент реакции, приложенной к катящемуся диску в точке контакта с опорной поверхностью:

На произвольном стационарном движении диска условие (5.3) выполняется всегда, так как $0 < \xi < 1$, $w > 0$, а неравенство (5.4) может не выполняться.

Например, неравенство

не выполняется при ${{\gamma }_{0}} < \pi {\text{/}}4$ и достаточно большом значении $w$, которое согласно равенству (5.1) достигается, когда угол ${{\gamma }_{0}} - {{\beta }_{0}}$ имеет близкое к $\pi {\text{/}}2$ значение. Неравенство не выполняется, когда ${{\gamma }_{0}} > \pi {\text{/}}4$, но $w \ll 1$.

6. Условия устойчивости стационарных качений диска по параллели опорной поверхности. Составим систему уравнений линейного приближения

для стационарного движения диска. Здесь $x\quad$ – вектор возмущений. Характеристическое уравнение имеет вид типичный для консервативной механической системы со связями.

Так как корень $\lambda = 0$ кратности два, будем искать частные решения алгебраической системы

в виде ${{C}_{i}}\quad$ и ${{F}_{i}}$ – неизвестные постоянные, $\tau \quad$ – безразмерное время. Прямые вычисления показывают, что система имеет два линейно независимых частных решения ${{C}_{3}}$ и ${{С }_{5}}$ – произвольные постоянные.

Так как найденные решения не являются растущими по $\tau $, то справедливо следующее утверждение: если квадратное уравнение ${{y}^{2}} + ly + d = 0$ имеет простые отрицательные корни, то стационарное качение диска вдоль параллели опорной поверхности вращения устойчиво в первом приближении.

Необходимые условия устойчивости стационарного движения, следовательно, имеют вид

Рассмотрим примеры численного расчета по формулам (6.1).

Пример 1. Пусть опорная поверхность $S$ – внутренняя сторона однополостного гиперболоида вращения с расположенной вертикально осью симметрии

Начало неподвижной системы координат ${{O}_{1}}{{x}_{1}}{{y}_{1}}{{z}_{1}}$ расположим в центре верхней горловины (фиг. 1). Диаметр параллели ${{z}_{1}} \approx - 2.2$ см равен 135 см. Возьмем в качестве диска монету 2 евро, диаметр которой $2R = 2.575$ см, и пустим ее по этой высокой параллели с угловой скоростью $\dot {\psi } = 2.4$ рад/с.

Согласно формулам (1.1) и (5.1), соответствующее стационарное движение диска определяется однозначно: диск катится по параллели ${{z}_{1}} = - 2.2$ см опорной поверхности с заданной угловой скоростью при сохранении постоянным угла 27.5° между пересекающимися положительными полуосями $Oz$ и ${{O}_{1}}{{z}_{1}}$ (фиг. 1). Коэффициенты характеристического уравнения 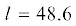и 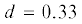удовлетворяют условиям (6.1), причем $\quad{{\Delta }_{{62}}}$ = 0.08.

Пустим монету по низкой параллели ${{z}_{1}} = - 30$ см с угловой скоростью $\dot {\psi }$ = 21.4 рад/с. Условия устойчивости (6.1) выполняются, так как $l = 18.24$, $d = 17.02$, причем $\quad{{\Delta }_{{62}}}$ = = 0.28. Кроме того,

Пример 2. Пусть опорная поверхность – псевдосфера. Уравнение кривой (трактрисы), вращением которой вокруг ее асимптоты, расположенной вертикально, образована псевдосфера, записывается в виде

($s = f({{z}_{1}})$ в обозначениях разд. 1).

Примем, что радиус верхней горловины $a = 67.5$ см, глубина параллели ${{z}_{1}} = - 2.3$ см. Пусть начальная угловая скорость диска $\dot {\psi } = 2.4$ рад/с, тогда углы ${{\beta }_{0}} = - 4.8^\circ $ и $\quad{{\gamma }_{0}} = 25.8^\circ $. Стационарное качение диска определено однозначно и для него 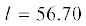, $d = 1.09$, ${{\Delta }_{{62}}} = - 0.01$. Все три неравенства (6.1) выполнены.

Таким образом, рассмотренные в примерах стационарные качения диска устойчивы в первом приближении по отношению к переменным $p$, $q$, $r$, $\alpha $, $\beta $, $\quad\gamma $.

7. Учет трения качения и трения верчения. За последние 10–12 лет в общественных местах ряда стран появились развлекательные простые механические устройства для сбора денег, в основном, на благотворительные цели. Каждое такое устройство представляет собой стол в форме чаши, установленный на ножке-подставке. Внутренняя поверхность чаши изготовлена в форме двояковыпуклой круглой воронки с отверстием внизу по центру (фиг. 2). Столы имеют разные размеры и глубину. На самой высокой параллели установлены один или несколько “запускающих механизмов” в виде горки со спускающейся к ее основанию канавкой, по которой с вершины горки посетитель пускает без начальной скорости монету (или жетон в виде тонкого круглого диска). Встречаются и другие принципиально мало отличающиеся конструкции таких механизмов. Монета начинает скатываться почти по параллели, на которую она запущена, постепенно переходя на более низкие (и следовательно, более короткие) параллели, ускоряя свое вращение вокруг вертикальной оси симметрии стола. В итоге монета проваливается через отверстие в монетоприемник. Одновременно можно запустить несколько монет, причем в противоположных направлениях. Скатываясь вниз, монеты не сталкиваются друг с другом, так как угол наклона каждой монеты к оси симметрии стола принимает строго определенное значение, определяемое текущей мгновенной скоростью качения и текущим расстоянием центра монеты до оси симметрии.

Рассмотренная выше неголономная модель не может объяснить описанное движение монеты, пока не принята в расчет диссипация механической энергии. Внутренняя поверхность стола выполнена из мягкого пластика или имеет специальное, обычно тефлоновое покрытие. Контакт твердого диска с такой поверхностью не является точечным, а представляет собой малое пятно контакта, размеры которого, в частности, зависят от величины прижимающей диск силы. В этом пятне развиваются пары сил трения качения и верчения, которые тормозят движение диска.

Было описано [25] экспериментальное исследование величин моментов указанных диссипативных сил для диска, катающегося по горизонтальной плоскости, с целью выявления аналитических зависимостей для этих моментов. В результате статистической обработки полученных экспериментальных данных оказалось, что хорошее соответствие результатам экспериментов дают следующие формулы:

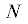где ${{m}_{1}}$ – выражение момента сил трения качения в зависимости от и скорости прецессии $\sigma $, ${{m}_{2}}$ – момент сил трения верчения, размерные коэффициенты ${{k}_{r}}$ и ${{k}_{p}}$ зависят от свойств материалов трущихся поверхностей, $N > 0$ – нормальная компонента силы реакции (сила давления), приложенная к диску со стороны опоры, ${{\omega }_{n}}$ – проекция мгновенной угловой скорости диска на вертикаль. При этом момент сил трения качения направлен по прямой пересечения вертикальной плоскости симметрии диска с опорной плоскостью, момент сил трения верчения – по вертикали.

В рассматриваемой системе момент ${{m}_{1}}$ направлен по оси $My{\text{'}}$, момент ${{m}_{2}}$ – по нормали $n$ к поверхности $S$ (фиг. 1)

После перехода к безразмерным величинам динамические уравнения рассматриваемой системы принимают вид

В выражениях для безразмерных диссипативных моментов ${{m}_{1}}$ и ${{m}_{2}}$ коэффициенты трения качения и верчения получены делением размерных коэффициентов на соответственно ${{R}^{2}}{{g}^{{ - 1}}}$ и $R$, а безразмерная сила давления $N$ получена делением размерной силы давления на $mg$.

Для вычисления силы $N$ найдем абсолютное ускорение центра $O$ диска в осях $Mu\text{v}n$

Вместо компонент вектора $\omega {\text{'}} = {{(p{\text{'}},q{\text{'}},r{\text{'}})}^{T}}$ следует подставить их выражения, полученные из системы (7.1), вместо $\varphi {\text{'}}$ – первое выражение (4.1).

С другой стороны, согласно закону о движении центра масс для вектора ${{a}_{O}}$ в осях $Mu\text{v}n$ имеем выражение

(${{R}_{t}} = {{({{R}_{{tu}}},{{R}_{{t\text{v}}}},0)}^{T}}$ – тангенциальная компонента силы реакции). Следовательно,

Выражения для ${{R}_{{tu}}}\quad$ и ${{R}_{{t\text{v}}}}$ не приводим.

Формула (7.2) замыкает систему кинематических (3.2), (4.1) и динамических (7.1) уравнений движения диска при наличии диссипации.

Пример 3. Рассмотрим условия примера 1, учитывая, что масса монеты 2 евро равна 8.5 г. Пусть

и монета скатывается без скольжения при нулевой начальной скорости с горки высотой $H = 20$ см над параллелью ${{z}_{1}} = - 2.2$ см так, что выполняются следующие начальные условия для осуществления стационарного качения монеты (диска) по указанной параллели:

Величина ${{\beta }_{0}}$ конструктивно задается наклоном к оси ${{O}_{1}}{{z}_{1}}$ боковых стенок канавки, по которой скатывается монета, и определяется в соответствии с угловой скоростью

с которой монета выкатывается на параллель, из формулы (5.1), где значения $\xi $ и ${{\gamma }_{0}}$ известны для рассматриваемой параллели.

Система дифференциальных уравнений качения диска оказалась “жесткой” [34], для ее интегрирования применен неявный метод Рунге–Кутты высокого порядка точности с автоматическим выбором величины шага.

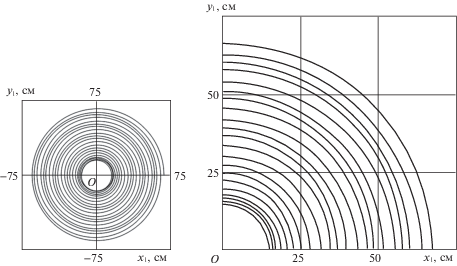
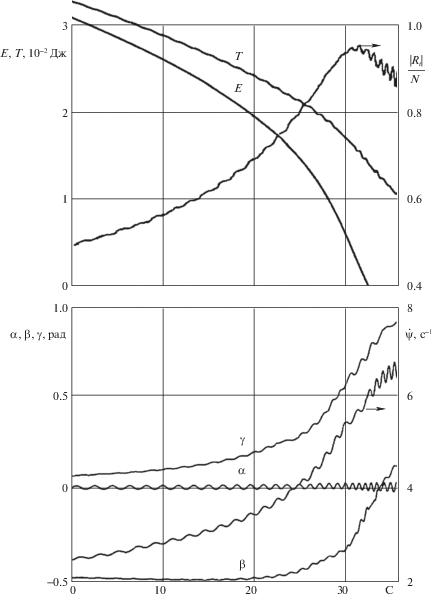
Далее приведены некоторые результаты численного интегрирования рассматриваемой задачи. За 35 с монета сделала 20 оборотов вокруг оси симметрии стола, приблизилась к ней на полметра и опустилась вниз на 10 см.

На фиг. 3 слева изображена спиралеобразная траектория проекции точки контакта 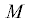на плоскость ${{O}_{1}}{{x}_{1}}{{y}_{1}}$, справа представлен увеличенный фрагмент траектории.

В верхней части фиг. 4 показано, что условие (5.4) реализации неголономных связей силой сухого трения в процессе движения выполнено, а также представлены графики убывания кинетической $T$ и полной механической $E$ энергий диска в процессе движения. В нижней части даны графики изменения углов ориентации диска и показано изменение угловой скорости вращения точки $M$ вокруг оси симметрии ${{O}_{1}}{{z}_{1}}$ стола.

Параметры системы (радиус диска, размеры стола, стартовая скорость, числовые значения коэффициентов трения качения и верчения) менялись. Результаты расчетов получились похожими.

Уравнение поверхности стола-воронки, трибологические свойства материала, из которого сделана его поверхность, другие параметры неизвестны (know-how фирм-изготовителей). Тем не менее, опираясь на неголономную модель движения, удалось так подобрать параметры системы, что результаты численного моделирования качения диска оказались близкими к наблюдаемым в действительности.

8. Выводы. Рассмотренная механическая система является многопараметрической, весьма чувствительной к изменению параметров. Числовые варианты расчетов предложенной неголономной модели с диссипацией показали, по крайней мере на качественном уровне, хорошее соответствие наблюдаемым натурным экспериментам. Классическая неголономная модель остается полезным инструментом для изучения механических свойств некоторых систем.