Прикладная математика и механика, 2019, T. 83, № 3, стр. 428-438

Введение. Растворенные вещества в жидкостях и взвешенные частицы в газах под действием гравитации или глобального вращения Земли распределяются неравномерно и образуют устойчивую стратификацию. В соответствии с типом уравнения состояния сплошной среды в поле плотности определяются температурой, концентрацией примеси, а также профилями давления. Неравновесная среда с молекулярным потоком стратифицирующих компонентов покоится только в том случае, если градиенты плотности параллельны направлению силы тяжести. Прерывание молекулярного потока на непроницаемых границах произвольной формы создает течения, индуцированные диффузией. Теоретические исследования стратифицированных течений начались в начале 1940-х годов [1], а немного позже стали моделироваться в лабораторных условиях [2].

Интерес к изучению градиентных потоков сохраняется благодаря их распространенности в окружающей среде. В нормальных условиях возмущения концентрируются в тонких слоях на непроницаемых поверхностях и достигают штормовых значений, формирующих большие температурные градиенты в атмосфере на крутых склонах поверхности [3] и вблизи ледников [4]. В последние годы особое внимание уделяется изучению влияния течений, индуцированных диффузией, на динамику и структуру процессов в водоемах, озерах, морях [5] и океанах с учетом влияния силы Кориолиса [6]. В некоторых исследованиях [7] особое внимание уделялось анализу уравнения состояния морской среды и наличию дополнительного стратифицирующего компонента с собственным коэффициентом диффузии (“дифференциальная диффузия”).

Наряду с аналитическими исследованиями стационарных течений [1, 2, 5, 8] в конце прошлого века начали развиваться нестационарные модели процесса формирования течений, индуцированных диффузией на различных препятствиях (наклонная и горизонтальная пластина, цилиндр и сфера). Также проводились лабораторные опыты с использованием высокочувствительных теневых приборов, которые показали наличие пучков диссипативных нестационарных гравитационных волн на полюсах препятствий, кроме ранее наблюдаемых больших вихрей [9].

Вдоль склоновых течений формируется интегральная сила, которая отсутствует на симметричных препятствиях (сфера, цилиндр или горизонтальная пластина и др.), но принимает конечное значение на наклонной пластине и других телах, несимметричных относительно направления силы тяжести. Результирующие градиенты давления достаточно велики и способны вызывать самодвижение свободных тел нейтральной плавучести (“diffusion fish” [10]), что играет важную роль в динамике морской среды. Был выполнен расчет стационарных течений на плоском фиксированном клине [11–13]. Практический интерес представляет изучение механизмов формирования сил, приводящих к самодвижению тел разной формы.

С началом движения тела разномасштабные элементы течений, индуцированных диффузией, не исчезают, а наоборот, превращаются в гораздо более сложные и тонкие структуры, такие как квазистационарные высокоградиентные прослойки, разделяющие разные типы возмущений, вихревой след и внутренние волны [9, 14]. Структура течения существенно зависит от параметров задачи, таких как форма тела, величина стратификации, скорость внешнего потока.

Вихри и волны в неоднородных средах существуют одновременно и активно взаимодействуют друг с другом вместе с тонкой структурой потока, что влияет на процессы переноса вещества, разделения компонентов потока и увеличения локальной концентрации примесей. Пренебрежение небольшими изменениями плотности и навязывание условия постоянной плотности, т.о. приближение однородной несжимаемой жидкости, приводят к вырождению системы основных уравнений, обусловленной слиянием некоторых элементов течений тонкой структуры разной природы [15].

Была предложена [14] методика построения точных решений основной системы уравнений механики неоднородных жидкостей в линейном приближении. В случае вязкой экспоненциально стратифицированной жидкости были рассчитаны поля двумерных присоединенных внутренних волн, вызванные равномерным движением пластины вдоль подстилающей плоскости. Точное решение задачи, удовлетворяющей физически обоснованным граничным условиям, было получено в квадратурах и визуализировано численно. Полученные закономерности потока четко демонстрируют две группы внутренних волн, структура которых существенно зависит от угла наклона поверхности к горизонту и неволновых особенностей вблизи краев препятствия.

В то же время теоретические исследования течений, индуцированных диффузией, проводились для объектов бесконечной или полубесконечной геометрии, таким образом краевые эффекты не учитывались. Поскольку реальные тела имеют конечные размеры, исследования структуры потока вблизи крайних точек тела представляют наибольший интерес, что побуждает к построению численных моделей течений, индуцированных диффузией, и закономерностей внутренних волн вокруг тел конечных размеров.

1. Система определяющих уравнений. В двумерном приближении рассматривается эволюция структуры изначально линейно стратифицированной жидкости, плотность которой $\rho = {{\rho }_{0}}(1 - z{\text{/}}\Lambda )$ определяется распределением солености ${{S}_{0}}(z)$ и характеризуется масштабом плавучести Λ = ${{\left| {{{\partial \ln \rho } \mathord{\left/ {\vphantom {{\partial \ln \rho } {\partial z}}} \right. \kern-0em} {\partial z}}} \right|}^{{ - 1}}}$, частотой N = $\sqrt {g{\text{/}}\Lambda } $ и периодом T_b = $2\pi {\text{/}}N$.

Математическое моделирование поставленной задачи основано на системе уравнений для многокомпонентной неоднородной несжимаемой жидкости в приближении Буссинеска [15] с учетом эффектов плавучести и диффузии стратифицирующей примеси. При исследовании медленных, по сравнению со скоростью звука, течений жидкости, характеризующейся высокой теплопроводностью, в расчетах можно учесть только изменения плотности, связанные с концентрацией стратифицирующего компонента, пренебрегая изменениями температуры. Таким образом, определяющая система уравнений записывается в виде

Здесь S = S₀(z) + s – общая соленость, включая степень солевого сжатия, s – возмущение солености, v – вектор скорости, P – давление, за исключением гидростатического, ν – коэффициент кинематической вязкости, ${{\kappa }_{s}}$ – коэффициент диффузии соли, $\nabla $ и ∆ – операторы Гамильтона и Лапласа, g – ускорение свободного падения. Член с вертикальной составляющей скорости потока ${{{v}}_{z}}$ в последнем уравнении (1.1) представляет собой конвективный перенос солености, нарушающий исходную стратификацию.

На поверхности клина задано условие прилипания для компонент скорости и непротекания для солености, а также невозмущенный свободный поток на бесконечности:

где U – скорость внешнего потока, n – внешняя нормаль к поверхности клина Σ. Начальным условием для вынужденного потока стратифицированной среды является установившееся течение, вызванное прерыванием диффузионного потока стратифицирующей примеси на непроницаемой поверхности неподвижного тела. Детальное исследование структуры и динамики течений, индуцированных диффузией на неподвижных препятствиях, проводилось экспериментально и численно [9, 12, 13].

Система уравнений (1.1) с начальными и граничными условиями (1.2) характеризуется рядом характерных масштабов, включая масштаб времени $t = {{T}_{b}}$ и $\delta _{U}^{L} = {L \mathord{\left/ {\vphantom {L U}} \right. \kern-0em} U}$, скорости ($U_{N}^{\nu } = \sqrt {\nu N} $, $U_{N}^{{{{\kappa }_{s}}}} = \sqrt {{{\kappa }_{s}}N} $, U) и шкалы длины (шкала плавучести, Λ, горизонтальные и вертикальные размеры препятствия, L и h, длина поверхностных гравитационных волн ${{\lambda }_{s}} = 2\pi {{U}^{2}}{\text{/}}g$, а также внутренних $\lambda = U{{T}_{b}}$ и вязких ${{\Lambda }_{\nu }}$ = $\sqrt[3]{{g\nu }}{\text{/}}N$ = = $\sqrt[3]{{\Lambda {{{(\delta _{N}^{\nu })}}^{2}}}}$ волн, вязкий $\delta _{N}^{\nu } = \sqrt {\nu {\text{/}}N} $ и диффузионный $\delta _{N}^{{{{\kappa }_{s}}}}$ = $\sqrt {{{\kappa }_{s}}{\text{/}}N} $ микромасштабы). Разнообразие линейных масштабов и широкий диапазон их значений (4–6 порядков) указывают на сложность внутренней структуры изучаемых процессов, которая возникает из-за неоднородности молекулярного потока стратифицирующей примеси.

Крупные динамические масштабы, которые представляют собой длину внутренней волны λ и масштаб вязкой волны ${{\Lambda }_{\nu }}$, характеризуют структуру присоединенных внутренних волновых полей [16, 17]. Тонкая структура течения характеризуется универсальными микромасштабами $\delta _{N}^{\nu }$ и $\delta _{N}^{{{{\kappa }_{s}}}}$, определяемыми диссипативными коэффициентами и частотой плавучести [18]. Другая пара параметров, таких как масштабы Прандтля $\delta _{U}^{\nu } = {\nu \mathord{\left/ {\vphantom {\nu U}} \right. \kern-0em} U}$ и Пекле $\delta _{U}^{{{{\kappa }_{s}}}} = {{{{\kappa }_{s}}} \mathord{\left/ {\vphantom {{{{\kappa }_{s}}} U}} \right. \kern-0em} U}$, определяются диссипативными коэффициентами и скоростью движения тела [15].

Значительные различия значений линейных масштабов указывают на сложность внутренней структуры стратифицированного течения, которое включает в себя набор регулярно возмущенных компонентов, характеризующих волны или вихри, и сингулярно возмущенных, описывающих компоненты тонкой структуры потока [9]. Все компоненты полного решения, как регулярно, так и сингулярно возмущенные, существуют одновременно в неоднородных средах, активно взаимодействуя друг с другом и проявляя себя в широком диапазоне определяющих параметров. Крупные масштабы длины предписывают выбор размера для областей наблюдения или расчета, которые должны содержать все изученные структурные компоненты течения, такие как опережающие возмущения, след вниз по течению, внутренние волны, вихри, в то время как микромасштабы определяют разрешение сетки и шаг по времени. При малых скоростях движения тела масштаб Стокса является критическим, в то время как при высоких скоростях доминирующей становится шкала Прандтля.

В нелинейной постановке задача (1.1), (1.2) обеспечивает одновременное изучение всех элементов течения в рамках одного описания в естественных физических переменных без дополнительных констант и соотношений. В связи с многомасштабностью изучаемого явления и нелинейностью определяющих уравнений, один из основных инструментов анализа таких эволюционных процессов – численное моделирование.

3. Численное моделирование. Решение задачи (1.1), (1.2) строится численно в полной нелинейной постановке с использованием метода конечных объемов в вычислительном пакете OpenFOAM (www.openfoam.com) с открытым исходным кодом. Пакет, который был первоначально разработан для численного расчета трехмерных задач механики сплошных сред, также может эффективно моделировать двумерные задачи, что технически выполняется путем выбора только одной вычислительной ячейки в третьем измерении и задания специальных “пустых” граничных условий, на передней и задней границах расчетной области.

Стандартная численная модель открытого пакета OpenFOAM была дополнена оригинальными программными модулями, учитывающими эффекты стратификации и диффузии [19]. К исходной модели icoFoam, реализующей второе и третье уравнения (1.1), были добавлены новые переменные (ρ, s), дополнительные первое и четвертое уравнения (1.1) и новые физические параметры (N, Λ, ${{\kappa }_{s}}$, g). Граничное условие возмущения солености (последнее условие (1.6)) было реализовано с помощью расширенной утилиты funkySetBoundaryField, которая позволяет определять аналитические выражения для физических переменных. Для вычисления дополнительных физических переменных использовались утилиты vorticity, forceCoeffs, funkySetFields и др.

Для интерполяции конвективных членов использовалась ограниченная TVD-схема, которая обеспечивает минимальную численную диффузию и отсутствие осцилляций решения. Для дискретизации производной по времени использовалась неявная асимметричная трехточечная схема второго порядка с разностями назад, которая обеспечивает хорошее разрешение физического процесса по времени. На ортогональных участках сетки нормальные градиенты скорости, необходимые при вычислении диффузионных членов по теореме Гаусса, находились на поверхности ячейки из значений скорости в центроидах соседних ячеек по схеме второго порядка. На неортогональных участках использовалась итерационная процедура коррекции погрешности, вызванной неортогональностью сетки.

Для решения полученной системы линейных алгебраических уравнений использовались разные итерационные методы, такие как метод сопряженных градиентов с пред-обусловливателем PCG, применяемым к симметричным матрицам, и метод бисопряженных градиентов с предобусловливателем PBiCG для асимметричных матриц. В качестве предобусловливателя для симметричных и асимметричных матриц были выбраны процедуры DIC и DILU соответственно, основанные на упрощенных процедурах неполной факторизации Холецкого. Для связи уравнений сохранения импульса и массы использовался устойчивый хорошо сходящийся алгоритм PISO (Pressure-Implicit Split-Operator), который работает наиболее эффективно для нестационарных задач.

Дискретизация расчетной области выполнялась с использованием открытой интегрируемой платформы SALOME, которая позволяет создавать, редактировать, импортировать и экспортировать модели CAD (Computer Aided Design), а также строить сетку для них, используя различные алгоритмы и связывая физические параметры изучаемой проблемы с геометрией. Для построения вычислительной сетки также использовались стандартные утилиты OpenFOAM, такие как “blockMesh”, “topoSet” и “refineMesh”. Основной класс OpenFOAM “polyMesh”, который обрабатывает сетку, создается с использованием минимального количества информации, необходимой для определения элементов и параметров разбиения, таких как вершины, ребра, грани, ячейки, блоки, внешние границы и т.д. Выбрав подходящий тип расчетной сетки, то есть структурированный или неструктурированный, ортогональный или неортогональный, согласующийся с границами области или нет, каждый из которых обычно имеет свои преимущества и недостатки, можно обеспечить успешный поиск решения изучаемой проблемы. Поэтому методы построения сетки выбирались индивидуально для конкретной задачи на основе значений характерных масштабов длины и геометрической сложности рассматриваемой задачи.

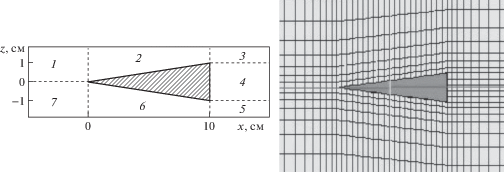
Расчетная область представляет собой прямоугольник, разделенный на семь блоков. Обтекаемое тело расположено в центральной части расчетной области, которая представляет собой горизонтальный клин длиной L и высотой основания h (левая часть рис. 1). Процедура пространственной дискретизации задачи была параметризована, что позволяет значительно сократить продолжительность перестройки сетки при изменении параметров задачи. Простота геометрии клина позволяет построить блочно-структурированную шестигранную вычислительную сетку с узлами, совпадающими на границах раздела блоков. Тестовые расчеты с различными разрешениями сетки подтверждают необходимость разрешения наименьших микромасштабов задачи, поскольку относительно грубая сетка с общим числом ячеек ${{N}_{c}}\sim {{10}^{6}}$ дает нестабильное решение. Таким образом, численное моделирование даже двумерных задач непрерывно стратифицированных течений около непроницаемых препятствий требует высокопроизводительных вычислений. Алгоритм дискретизации расчетной области включает в себя сгущение сетки по направлению к препятствию (правая часть рис. 1). Вблизи тела соотношение сторон ячейки сетки приблизительно равно единице, что положительно влияет на сходимость решения.

Необходимость высокого пространственного разрешения поставленной задачи приводит к довольно большому количеству расчетных узлов, что делает нерациональным выполнение вычислений на однопроцессорном персональном компьютере. Разбиение расчетной области для расчетов в параллельном режиме выполняется простым геометрическим разложением, в котором домен разбивается на части в определенных направлениях с равным количеством вычислительных ячеек в каждом блоке. Такой подход позволяет установить высокое пространственное разрешение расчетной области и исследовать проблему в широком диапазоне основных параметров за вполне приемлемое время. Параллельные расчеты поставленной задачи проводились в web-лаборатории UniHUB (www.unihub.ru).

В расчетах использовались следующие значения параметров задачи:

Расчетный шаг по времени, ∆t, определяется условием Куранта $Co$ = $\left| {\mathbf{v}} \right|\Delta t{\text{/}}\Delta r$ ≤ 1, где $\Delta r$ – минимальный размер ячеек сетки, а v – локальная скорость потока.

4. Результаты расчетов. Изначальная комплексная структура среды, образованная течениями, индуцированными диффузией на неподвижном клине, резко изменяется с началом вынужденного движения даже при низкой скорости (рис. 2). В непрерывно стратифицированной жидкости формируются опережающие возмущения, розетки нестационарных и поля присоединенных внутренних волн, а также протяженный след за экстремальными точками.

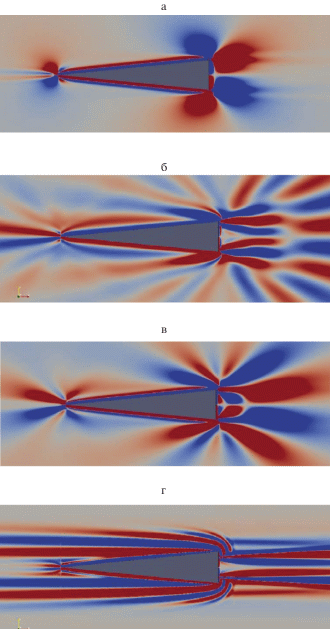
Когда скорость внешнего потока сравнима по порядку величины с характерной скоростью течений, индуцированных диффузией, $U_{N}^{{{{\kappa }_{s}}}} = \sqrt {{{\kappa }_{s}}N} $, структура поля в течение долгого времени сохраняет элементы исходного поля (рис. 2а). В этом случае пучки знакопеременных полос остаются прикрепленными к острым углам препятствий, которые сносятся вниз по течению с увеличением скорости внешнего потока. Длина присоединенных внутренних волн увеличивается. Источниками внутренних волн являются углы клина, генерирующие интенсивное вертикальное смещение жидкости. Отклонение слоев жидкости от исходного положения нейтральной плавучести создает, следовательно, их периодические колебания. Неровности гребней и впадин внутренних волновых форм отражают сложную картину интерференции растущих нестационарных и присоединенных внутренних волн.

Число наблюдаемых нестационарных волн, которые не проникают вслед за телом, увеличивается со временем. Резкие границы раздела, очерчивающие верхнюю и нижнюю границы следа плотности, четко выражены далеко за пределами тела. На рис. 2б и 2в при $1 < t{\text{/}}{{T}_{b}} < 3$ хорошо наблюдаются нестационарные внутренние волны вокруг угловых точек клина.

Структура пограничного потока вблизи сторон клин также сильно зависит от скорости внешнего потока (рис. 3). С увеличением скорости тела вносимые возмущения становятся все более выраженными и перекрывают картину потока, создаваемую слабыми медленными начальными течениями, индуцированными диффузией.

Наблюдение последовательности рассчитанных картин течения показывает, что обтекание клина нестационарное. Вихри, которые периодически образуются на передней кромке, движутся вдоль сторон тела вниз по течению. Помимо вихрей вблизи тела наблюдаются высокоградиентные тонкоструктурные прослойки и длинные внутренние волны. При этом внутренняя волновая картина стационарная относительно тела.

При увеличении скорости внешнего потока пропорционально увеличивается длина присоединенной внутренней волны в соответствии с линейной теорией: $\lambda = U{{T}_{b}}$. Фазовая поверхность, разделяющая волновые возмущения противоположных знаков, изогнута в сторону движения клина. Четко определенные периодические структуры формируются за экстремальными точками углов клина (рис. 3а и 3б). Рядом с передней острой вершиной клина образуются мелкомасштабные возмущения, формирующие множество тонких структур в потоке вблизи границы тела (рис. 3в). При скоростях $U > {{10}^{{ - 2}}}$ м/с вихревые возмущения формируются в следе за клином (рис. 3г и 3д).

Структура расчетных полей градиента солености при обтекании клина качественно согласуется с теневой визуализацией полей градиента коэффициента преломления, выполненных в лабораторном резервуаре “цветным теневым методом” с горизонтальной щелью и решеткой для тел других геометрических форм [9].

Заключение. Расчеты стратифицированных течений около горизонтального клина нейтральной плавучести показали высокую работоспособность предложенной численной модели.

Поле изучаемого течения, индуцированного диффузией, в стратифицированной жидкости даже около неподвижного тела характеризуется сложной внутренней структурой, на краях проявляются диссипативно гравитационные волны. Острые края обтекаемого препятствия создают расширяющиеся горизонтальные высокоградиентные прослойки, которые четко наблюдаются в лабораторных экспериментах с помощью теневой визуализации с высоким разрешением.

Вокруг медленно движущегося тела по краям образуется группа присоединенных волн с противоположными фазами относительно горизонта нейтральной плавучести. Затем основные компоненты течения становятся вихрями, которые образуются на острых краях клина и сносятся вслед вниз по течению. С дальнейшим увеличением скорости обтекания тела картина потока становится более сложной и нестационарной.

Обтекание клина стратифицированной жидкостью представляет собой сложный, многомасштабный и нестационарный физический процесс, который требует дополнительного подробного экспериментального и теоретического изучения с учетом эффектов диффузии, теплопроводности и сжимаемости среды.