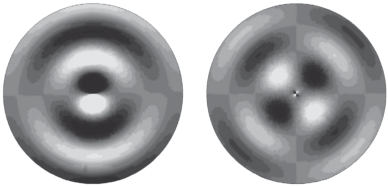Прикладная математика и механика, 2019, T. 83, № 3, стр. 384-392

Класс задач, связанных с определением акустического излучения при движении тела в жидкости, актуальных при разработке насосного оборудования, гребных винтов и т.п. [1, 2], характеризуется значительным различием пространственно-временных масштабов акустических и гидродинамических процессов. В большинстве практически значимых случаев это приводит к чрезмерно высоким вычислительным затратам, необходимым для прямого численного интегрирования (DNS) уравнений Навье–Стокса и массопереноса в целях прямого расчета искомого звукового давления. Вычисления обычно проводят в “гибридной постановке” путем разделения задачи на гидродинамическую и акустическую. При этом в пределах ближнего акустического поля решаются базовые уравнения гидродинамики (Эйлера или Навье–Стокса) с помощью выбранного численного подхода. Для нахождения излучения в дальнем поле используются интегральные методы Кирхгофа или Фоукс Вильямса–Хоукингса (FW–H), основанные на решении волнового уравнения [3, 4].

Альтернативный подход, который позволяет исследовать гидродинамический шум при отсутствии ограничений на геометрию потока жидкости, основан на методе конечных элементов (МКЭ). Задача при этом также разбивается на гидродинамическую и акустическую. Решение акустической задачи ищется по МКЭ на сетке с размерами, пропорциональными пространственным периодам возмущений. Можно ознакомиться с основами подхода конечно-элементного (КЭ) описания аналогии Лайтхилла [5], внедренного, в частности, в ПО MSC ACTRAN [6], и примерами его применения в конкретных приложениях акустического проектирования (см. например [7]).

Имеется детальное описание аналогичного алгоритма КЭ-представления аналогии Лайтхилла для тетраэдрических сеток [8]. Авторами был предложен способ решения, при котором акустическое излучение рассчитывается в спектральной области как результат рассеяния турбулентного псевдозвукового поля обтекаемым телом. Показано, что в такой постановке можно успешно обойти сложности, связанные с интерполяцией, точностью учета и заданием типа источников в узлах сетки. Показано, что подход, при котором решение гидродинамической задачи переносится в акустическую задачу в виде распределения квадрупольных источников звука (напряжений Лайтхилла), позволяет подавить влияние границ гидродинамических моделей и нефизичных источников, возникающих в RANS-LES интерфейсах. Таким образом, метод позволяет решить важный класс задач о шумоизлучении локальных неоднородностей с использованием компактных численных гидродинамических моделей.

Ниже приводятся результаты обобщения МКЭ на случай призматической КЭ-сетки.

1. Обобщение метода на случай призматической КЭ сетки акустической модели. Рассматривалась следующая акустическая задача излучения и рассеяния на теле псевдозвукового поля турбулентных источников (напряжений Лайтхилла) с соответствующими граничными условиями на поверхности тела Г и на бесконечности [8]:

где тильдой обозначено преобразование Фурье по времени (далее этот символ опущен), P – искомое давление, k – волновое число, ω – циклическая частота, c – скорость звука, u_n (u_m) – компоненты вектора скорости жидкости, ρ – ее плотность, R – расстояние от источника, N – нормаль к поверхности обтекаемого тела, U – нормальное перемещение точек тела, m и n – индексы от 1 до 3 (символы суммирования по n и m здесь и далее опущены).

Из формализма МКЭ следует возможность представления

где j – номер узла КЭ-сетки, φ_j – функция формы, ξ, η, ζ – параметрические координаты точки внутри КЭ.

Первое уравнение системы (1.1) может быть проинтегрировано в области, занятой жидкостью, с использованием весовых функций φ_j. Тогда, при учете теоремы Остроградского–Гаусса и граничных условий, можно получить следующую систему s уравнений:

где Ω – область, занятая жидкостью.

Система (1.3) описывает взаимодействия сжимаемой жидкости и упругих тел, а s-й элемент вектора правой части имеет физический смысл точечного источника объемного ускорения. Совокупность таких источников формирует волны “псевдозвукового” давления, движущиеся в среде со скоростью потока и являющиеся акустически короткозамкнутыми. Для обеспечения физичности решения короткозамкнутые турбулентные псевдозвуковые источники необходимо заменить набором точечных квадруполей, расположенных в узлах сетки гидродинамической численной модели. Учитывая условия прилипания и непротекания на поверхности тела и интегрируя по частям правую часть равенства (1.3), можно записать следующее выражение для s-й компоненты вектора правой части матричной системы уравнений, описывающих акустическую задачу:

где g – номер конечного элемента численной акустической модели, $\varphi _{s}^{{(g)}}$ – функция формы g КЭ и s-го узла сетки, b – номер узла сетки гидродинамической модели (ГМ), K_bnm – интенсивность квадрупольных источников, получаемых из решения гидродинамической задачи, V_b – часть объема Ω, приходящаяся на b узел сетки.

Единичный квадруполь с направленностью mn, который действует в точке пространства с координатами x_b, y_b, z_b внутри g-го элемента акустической сетки, определяется выражением (1.5):  f_sb – элемент матрицы, интерпретирующей единичный квадрупольный источник из узла сетки ГМ в точечные монопольные источники в узлах g-го элемента сетки акустической конечно-элементной модели (АКМ). Суммарная интенсивность таких точечных монопольных источников и их дипольные моменты будут нулевыми, что обеспечит корректность решения акустической задачи. Такая интерпретация осуществима при наличии минимум 10 узлов у элемента АКМ, т.е. в АКМ могут быть использованы квадратичные КЭ с промежуточными узлами на ребрах (тетраэдр – 10 степеней свободы, пирамида – 13, призма – 15 и гексаэдр – 20).

В данной работе в алгоритме для решения акустической задачи используются призматические КЭ, позволяющие эффективно моделировать акустику вытянутых тел или тел вращения. Аналогичные зависимости могут быть получены и для других типов элементов. Использование призматических квадратичных 15-узловых изопараметрических КЭ в сетке АКМ подразумевает, что координаты точки внутри элементов сетки определяются аналогично представлению (1.2):

где x_s, y_s, z_s – координаты 15 узлов АКМ, ξ и η – “треугольные” параметрические координаты, изменяющиеся в пределах элемента на интервале от нуля до единицы, а ζ – параметрическая координата в диапазоне от –1 до 1.

Вид функций формы φ_s известен (см., например, [9]). Введя дополнительную переменную χ = 1 – ξ – η, можно получить выражение

где многоточием обозначены два элемента, которые получаются из предыдущего элемента круговой перестановкой ξ, η, χ.

Вторые производные функций формы φ_s в выражении (1.5) можно вычислить с помощью матричной зависимости (вторые производные по параметрическим координатам определяются с использованием формулы (1.7)):

где многоточием в строках матриц A, B и C обозначены два элемента, которые получаются из предыдущего элемента строки круговой перестановкой x, y, z.

Для расчета по формулам (1.8) и (1.9) необходимо знать значения параметрических координат ξ, η, ζ внутри g-элемента АКМ, которые описывают положение квадрупольного источника в b-узле сетки ГМ с координатами x_b, y_b, z_b. В пренебрежении кривизной ребер призматических элементов АКМ нахождение параметрических координат сводится к решению нелинейной системы:

где $x_{s}^{{(g)}}$, $y_{s}^{{(g)}}$, $z_{s}^{{(g)}}$ – координаты угловых точек призматического g-элемента; многоточием в столбцах матриц L^± обозначены два элемента, которые получаются из верхнего элемента столбца круговой перестановкой символов x, y, z.

Учитывая соотношение χ + ξ + ζ = 1, систему уравнений (1.10) можно свести к кубическому уравнению относительно неизвестной величины ζ в следующем виде:

Его решение может быть найдено при учете условия, что единственное физичное решение должно лежать на отрезке [–1, 1]. В противном случае точка с координатами x_b, y_b, z_b лежит вне пределов рассматриваемого элемента.

После определения величины ζ, оставшиеся три неизвестных уравнения (1.10) можно вычислить следующим образом:

Таким образом, для каждого b-узла ГМ можно с помощью соотношений (1.11) и (1.12) определить параметрические координаты, описывающие положение данного узла в одном из g-элементов АКМ. Затем с помощью выражений (1.4), (1.6)–(1.9) и поля скоростей, полученного в гидродинамическом расчете, можно сформировать акустические источники для решения задачи рассеяния псевдозвукового поля на обтекаемом теле.

2. Описание ГМ, используемых для валидации метода. Для валидации метода были выполнены тестовые расчеты обтекания неподвижных жестких тел: цилиндра и сферы. Решение гидродинамической задачи осуществлялось с помощью ANSYS CFX (лицензия № 00280108), акустической – с использованием ПО “АСТРА” (программа разработки Института прикладной физики РАН, свидетельство о государственной регистрации № 2014617046 от 10.07.2014).

Для валидации решения в двумерной постановке проведен расчет обтекания цилиндра диаметром d_c = 5 мм жидкостью со скоростью 1 м/c (число Рейнольдса Re = = 5000). Использована ГМ цилиндрической области диаметром 100 мм для слоя жидкости толщиной b = 2 мм в плоскости, перпендикулярной оси цилиндра. Течение рассчитывалось при условии несжимаемости жидкости с использованием RANS подхода (SST модели турбулентности) на сетке, сгущенной вблизи поверхности цилиндра и в области вихревого следа. На рис. 1 слева представлен один из временных кадров, полученных в процессе решения гидродинамической задачи – мгновенное распределение модуля скорости около цилиндра и в окрестности дорожки Кармана.

Для реализации аналогичного расчета в трехмерной постановке для обтекания сферы была создана ГМ, описывающая течение жидкости в сферическом объеме диаметром 100 мм вокруг неподвижной жесткой сферы диаметром d_sph = 5 мм. В этом случае течение рассчитывалось с использованием LES-WALE модели турбулентности. Общее количество ячеек сетки ГМ, сгущенной вблизи сферы и в области вихревого следа, составило 8 × 10⁶. На рис. 1 справа приведен один из кадров временной реализации для мгновенного распределения модуля скорости, на котором хорошо видны рассчитанные вихревые структуры.

Представленные результаты решения гидродинамических задач носят вспомогательный характер и требуются лишь для получения исходных данных в интересах валидации описанного КЭМ расчета шумоизлучения.

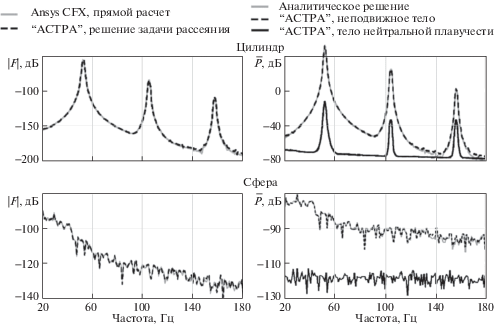
3. Результаты валидации метода для задачи обтекания цилиндра. В качестве исходных данных были использованы следующие результаты расчета ГМ: вычисленная с помощью ANSYS CFX переменная сила F, действующая на тело со стороны потока, и среднеквадратичная величина звукового давления $\bar {P}$ в дальней акустической зоне (на расстоянии от оси цилиндра R $ \gg $k ^–1). Величина $\bar {P}$ для d_ck $ \ll $ 1 связана с F соотношением

Описанные величины приведены в верхней части рис. 2 (серые сплошные кривые, величина звукового давления $\bar {P}$ приведена для R = 50 м). Уровни величины |F| приведены в дБ относительно 1 ньютона, $\bar {P}$ – в дБ относительно 20 микропаскалей. Видно, что при использовании указанной модели турбулентности течение оказывает гармоническое воздействие на обтекаемое тело. Спектр действующей на тело переменной силы представлен в виде набора дискретных составляющих. Первая гармоника на частоте 53 Гц ориентирована в направлении, перпендикулярном направлению потока жидкости, вторая гармоника имеет на порядки меньшую амплитуду и направлена вдоль потока.

Для расчета указанных величин с использованием представленного алгоритма была построена АКМ диаметром 100 м и толщиной слоя, как у ГМ. Центральная часть модели, совпадающая по размерам с ГМ, была разбита призматическими КЭ (один элемент на толщину модели, как и в ГМ), периферийная – гексаэдрами. На внешней границе АКМ размещены импедансные КЭ, имитирующие граничные условия излучения Зоммерфельда. В соответствии с методом в эту модель из ГМ был внесен тензор напряжений Лайтхилла.

Результаты расчета |F| и $\bar {P}$ с помощью АКМ представлены на рис. 2 (штриховые кривые). Видно, что величины, вычисленные в ПО “АСТРА”, совпали с результатами, полученными из расчета ANSYS CFX (серые сплошные кривые). Небольшие расхождения наблюдаются лишь для уровней на 120 дБ ниже максимального, что связано с конечной точностью выводимых из ANSYS CFX величин. Дополнительно на рис. 2 (сплошная черная линия) приведен спектр среднеквадратичного уровня звукового давления, рассчитанный в ПО “АСТРА” при R = 50 м по описанному в работе алгоритму для цилиндра нейтральной плавучести. Как можно видеть из графиков, по сравнению с неподвижным цилиндром интенсивность излучения на дискретных составляющих снизилась на порядки, что полностью соответствует физическим предпосылкам.

В качестве примера на рис. 3 представлены полученные в ПО “АСТРА” картины пространственных распределений звукового давления на частоте 53 Гц. Видно, что шумоизлучение, вызванное обтеканием жесткого неподвижного тела, при d_ck $ \ll $ 1 имеет ярко выраженный дипольный вид (левая часть рис. 3). Напротив, в случае тела нейтральной плавучести излучение звука носит квадрупольный характер (правая часть), что, соответственно, и объясняет падение уровня излучения.

4. Результаты валидации метода для задачи обтекания сферы. Для выполнения расчетов шумоизлучения обтекаемой сферы, по аналогии с предыдущим примером, была создана трехмерная АКМ. Диаметр сферической расчетной области равен 4 м. Центральная часть АКМ, совпадающая по размерам с ГМ, разбита призматическими КЭ, периферийная – гексаэдрическими. На внешней сферической границе расчетной области расположены специальные элементы, реализующие граничные условия поглощения звуковых волн и позволяющие восстановить дальнее акустическое поле. Вычисление искомых сил и звуковых давлений осуществлялось на основе рассчитанного в ANSYS CFX поля напряжений Лайтхилла. Широкополосность и частотная изрезанность спектров искомых величин при отсутствии дискретных составляющих вызвана использованием LES-WALE модели турбулентности в отличие от использованного в двумерной постановке RANS подхода.

Алгоритм валидации полученных результатов аналогичен представленному для цилиндра. Соответствующие результаты для |F| и $\bar {P}$ приведены на рис. 2 в нижнем ряду. Аналитический расчет звукового давления, соответствующего F, выполнялся с использованием следующей зависимости:

Видно, что величины, вычисленные в ПО “АСТРА” (черные штриховые кривые), совпали с результатами, полученными из расчета ANSYS CFX (серые сплошные кривые).

Дополнительно на рис. 2 приведен уровень излучения для сферы нейтральной плавучести (черная сплошная линия). Излучение приобретает мультипольный характер, а его уровень значительно снижается, как и в случае цилиндра.

Практическое отсутствие акустического излучения тел малых волновых размеров (условия d_ck $ \ll $ 1 и d_sphk $ \ll $ 1) нейтральной плавучести в потоке – известный факт и объясняется тем, что такие тела не являются для жидкости неоднородностью, на которой возникает равнодействующая инерционная сила, препятствующая перетеканию жидкости. Как следствие, при взаимодействии с потоком эти тела не способны создать рассеянное дипольное акустическое поле.

Заключение. Проведена валидация численного метода определения акустического излучения тел, обтекаемых жидкостью, выполненная на основе решения классических задач, имеющих аналитическое решение для акустического поля, в двумерной и трехмерной конфигурациях. Метод дает хорошую точность результатов на квадратичных сетках со сгущением элементов в окрестности обтекаемых неоднородностей.

Сравнение интенсивности переизлучения звука жесткими телами и телами нейтральной плавучести наглядно демонстрирует общепринятое представление о том, что гидродинамический шум, вызванный обтеканием неподвижных тел медленным потоком жидкости, имеет дипольную природу. Предложенный метод достаточно точен, чтобы дать количественное соотношение эффективности дипольного переизлучения телом гидродинамического шума и мультипольного излучения звука вихрями турбулентного потока, которое в обоих примерах снижается на несколько порядков.

Предложенный способ расчета упрощает решение практических задач для тел сложной геометрии при обеспечении высокой точности вычислений. Он удобен с точки зрения оптимизации аппаратных средств в силу возможности его реализации на персональных компьютерах со средней производительностью.

Работа выполнена в рамках Государственного задания № 0035–2014–0010.