Прикладная математика и механика, 2019, T. 83, № 3, стр. 495-508

О ВЛИЯНИИ ВИХРЕВОГО СЛОЯ И ТОЧЕЧНЫХ ВИХРЕЙ ПРИ ПРИБЛИЖЕННОМ РЕШЕНИИ ГРАНИЧНОГО ИНТЕГРАЛЬНОГО УРАВНЕНИЯ В ДВУМЕРНЫХ ВИХРЕВЫХ МЕТОДАХ ВЫЧИСЛИТЕЛЬНОЙ ГИДРОДИНАМИКИ

К. С. Кузьмина^1, 2, *, И. К. Марчевский^1, 2, **

¹ Московский государственный технический университет имени Н.Э. Баумана
Москва, Россия

² Институт системного программирования имени В.П. Иванникова РАН
Москва, Россия

^* E-mail: kuz-ksen-serg@yandex.ru
^** E-mail: iliamarchevsky@mail.ru

Поступила в редакцию 04.03.2019
После доработки 15.03.2019
Принята к публикации 19.03.2019

DOI: 10.1134/S003282351903010X

Полный текст (PDF)

Аннотация

Рассмотрено граничное интегральное уравнение относительно интенсивности вихревого слоя, возникающее при использовании вихревых методов моделирования двумерных течений. Для его приближенного решения применен метод Галёркина с кусочно-постоянным и кусочно-линейным представлением решения на участках границы профиля. Коэффициенты возникающей системы линейных уравнений выражают влияние вихревого слоя, расположенного на одних участках границы профиля, на другие участки; компоненты вектора правой части выражают влияние точечных вихрей, моделирующих вихревой след в области течения. При аппроксимации границы профиля ломаной, состоящей из прямолинейных участков-панелей, получены точные аналитические выражения для коэффициентов матрицы и правой части системы; при учете криволинейности панелей профиля предложена методика их приближенного вычисления и получены все необходимые расчетные формулы.

Ключевые слова: вихревые методы, граничное интегральное уравнение, вычислительная гидродинамика

Введение. Вихревые методы относятся к классу лагранжевых методов вычислительной гидродинамики. Их история восходит к фундаментальным работам Н.Е. Жуковского и Л. Розенхеда [1, 2]; к настоящему времени разработано множество модификаций вихревых методов, как чисто лагранжевых, так и гибридных – лагранжево-эйлеровых. Обзоры современного на тот момент состояния вихревых методов были даны Сарпкайей [3] и Леонардом [4], однако на сегодняшний день они носят скорее историческую ценность. Представление о современном состоянии вихревых методов можно получить из монографий [5–10], краткого обзора [11], а также многочисленных статей по соответствующей тематике.

Следует отметить, что в большинстве работ по вихревым методам основное внимание уделено проблеме моделирования эволюции завихренности в области течения, а вопросы удовлетворения граничных условий часто затрагиваются весьма поверхностно, за исключением работ И.К. Лифанова и его последователей, в основном относящихся к задачам моделирования трехмерных течений. В данной работе ограничимся рассмотрением плоских течений и приведем результаты, относящиеся к вопросу удовлетворения на профиле граничного условия прилипания, которое может быть сведено к граничному интегральному уравнению относительно интенсивности вихревого слоя.

1. Сведение задачи к решению граничного интегрального уравнения. Среда считается однородной, вязкой и несжимаемой. Без ограничения общности будем рассматривать внешнее обтекание профиля; все приведенные далее результаты без существенных изменений можно перенести на случай обтекания системы профилей и моделирования внутренних течений.

В соответствии с обобщенным разложением Гельмгольца [12, 13] поле скоростей среды в любой точке области течения $S$ можно вычислить по формуле

(1.1)

$\begin{gathered} \alpha ({\mathbf{r}}){\mathbf{V}}({\mathbf{r}}) = {{{\mathbf{V}}}_{\infty }} + \int\limits_S {\frac{{{\mathbf{\Omega }}({\mathbf{\xi }}) \times ({\mathbf{r}} - {\mathbf{\xi }})}}{{2\pi {{{\left| {{\mathbf{r}} - {\mathbf{\xi }}} \right|}}^{2}}}}d{{S}_{\xi }}} + \oint\limits_K {\frac{{{\mathbf{\gamma }}({\mathbf{\xi }}) \times ({\mathbf{r}} - {\mathbf{\xi }})}}{{2\pi {{{\left| {{\mathbf{r}} - {\mathbf{\xi }}} \right|}}^{2}}}}d{{l}_{\xi }}} + \\ + \;\oint\limits_K {\frac{{({\mathbf{n}}({\mathbf{\xi }}) \times {\mathbf{V}}({\mathbf{\xi }})) \times ({\mathbf{r}} - {\mathbf{\xi }})}}{{2\pi {{{\left| {{\mathbf{r}} - {\mathbf{\xi }}} \right|}}^{2}}}}d{{l}_{\xi }}} + \oint\limits_K {\frac{{({\mathbf{n}}({\mathbf{\xi }}) \cdot {\mathbf{V}}({\mathbf{\xi }}))({\mathbf{r}} - {\mathbf{\xi }})}}{{2\pi {{{\left| {{\mathbf{r}} - {\mathbf{\xi }}} \right|}}^{2}}}}d{{l}_{\xi }}} \\ \end{gathered} $

Здесь $\alpha ({\mathbf{r}})$ – коэффициент, равный единице для точек, находящихся внутри области течения S, нулю для точек, находящихся внутри контура профиля K, и внешнему углу, отнесенному к $2\pi $, для точек контура K. Величина $\Omega ({\mathbf{r}})$ = $\Omega ({\mathbf{r}}){\mathbf{k}}$ означает распределение завихренности в области течения, ${\mathbf{\gamma }}({\mathbf{r}})$ = $\gamma ({\mathbf{r}}){\mathbf{k}}$ – искомую интенсивность вихревого слоя на профиле, ${\mathbf{k}}$ – орт нормали к плоскости течения, ${\mathbf{n}}({\mathbf{\xi }})$ – орт нормали к границе профиля, направленный в сторону среды, ${\mathbf{V}}({\mathbf{\xi }})$ в контурных интегралах в правой части равенства (1.1) – скорость течения на границе. Эта скорость в силу выполнения условия прилипания равна скорости движения границы профиля ${{{\mathbf{V}}}_{K}}({\mathbf{r}})$, что позволяет трактовать два последних слагаемых как влияние присоединенного вихревого слоя и слоя источников соответственно с интенсивностями

${{{\mathbf{\gamma }}}^{{\operatorname{att} }}}({\mathbf{\xi }}) = {\mathbf{n}}({\mathbf{\xi }}) \times {{{\mathbf{V}}}_{K}}({\mathbf{\xi }}),\quad {{q}^{{\operatorname{att} }}}({\mathbf{\xi }}) = {\mathbf{n}}({\mathbf{\xi }}) \cdot {{{\mathbf{V}}}_{K}}({\mathbf{\xi }}),\quad {\mathbf{\xi }} \in K$

Далее примем, что скорости движения точек границы профиля ${{{\mathbf{V}}}_{K}}({\mathbf{r}})$ известны. Рассматривая уравнение (1.1) на границе профиля K и переходя к предельным значениям контурных интегралов, которые в этом случае становятся сингулярными, получаем граничное интегральное уравнение (ГИУ)

(1.2)

$\begin{gathered} \oint\limits_K {\frac{{{\mathbf{k}} \times ({\mathbf{r}} - {\mathbf{\xi }})}}{{2\pi {{{\left| {{\mathbf{r}} - {\mathbf{\xi }}} \right|}}^{2}}}}} \gamma ({\mathbf{\xi }})d{{l}_{\xi }} - \alpha ({\mathbf{r}})({\mathbf{k}} \times {\mathbf{n}}({\mathbf{r}}))\gamma ({\mathbf{r}}) = {\mathbf{f}}({\mathbf{r}}),\quad {\mathbf{r}} \in K \\ {\mathbf{f}}({\mathbf{r}}) = \alpha ({\mathbf{r}}){{{\mathbf{V}}}_{K}}({\mathbf{r}}) - {{{\mathbf{V}}}_{\infty }} - \int\limits_S {\frac{{{\mathbf{\Omega }}({\mathbf{\xi }}) \times ({\mathbf{r}} - {\mathbf{\xi }})}}{{2\pi {{{\left| {{\mathbf{r}} - {\mathbf{\xi }}} \right|}}^{2}}}}d{{S}_{\xi }}} - \oint\limits_K {\frac{{{{{\mathbf{\gamma }}}^{{{\text{att}}}}}({\mathbf{\xi }}) \times ({\mathbf{r}} - {\mathbf{\xi }})}}{{2\pi {{{\left| {{\mathbf{r}} - {\mathbf{\xi }}} \right|}}^{2}}}}d{{l}_{\xi }}} - \oint\limits_K {\frac{{{{q}^{{{\text{att}}}}}({\mathbf{\xi }})({\mathbf{r}} - {\mathbf{\xi }})}}{{2\pi {{{\left| {{\mathbf{r}} - {\mathbf{\xi }}} \right|}}^{2}}}}d{{l}_{\xi }}} \\ \end{gathered} $

ГИУ (1.2) – векторное уравнение относительно скалярной неизвестной величины $\gamma ({\mathbf{r}})$, ${\mathbf{r}} \in K$; показано [12], что для его решения достаточно рассмотреть любое из двух скалярных ГИУ, получаемых из ГИУ (1.2) путем проецирования на направление нормали к границе профиля:

(1.3)

$\oint\limits_K {{{Q}_{n}}({\mathbf{r}},{\mathbf{\xi }})} \gamma ({\mathbf{\xi }})d{{l}_{\xi }} = {{f}_{n}}({\mathbf{r}})$

или на направление касательной к границе профиля:

(1.4)

$\oint\limits_K {{{Q}_{\tau }}({\mathbf{r}},{\mathbf{\xi }})} \gamma ({\mathbf{\xi }})d{{l}_{\xi }} - \alpha ({\mathbf{r}})\gamma ({\mathbf{r}}) = {{f}_{\tau }}({\mathbf{r}})$

Здесь и далее

$\begin{gathered} {{Q}_{n}}({\mathbf{r}},{\mathbf{\xi }}) = - \frac{{{\mathbf{\tau }}({\mathbf{r}}) \cdot ({\mathbf{r}} - {\mathbf{\xi }})}}{{2\pi {{{\left| {{\mathbf{r}} - {\mathbf{\xi }}} \right|}}^{2}}}},\quad {{Q}_{\tau }}({\mathbf{r}},{\mathbf{\xi }}) = \frac{{{\mathbf{n}}({\mathbf{r}}) \cdot ({\mathbf{r}} - {\mathbf{\xi }})}}{{2\pi {{{\left| {{\mathbf{r}} - {\mathbf{\xi }}} \right|}}^{2}}}} \\ {{f}_{n}}({\mathbf{r}}) = {\mathbf{f}}({\mathbf{r}}) \cdot {\mathbf{n}}({\mathbf{r}}),\quad {{f}_{\tau }}({\mathbf{r}}) = {\mathbf{f}}({\mathbf{r}}) \cdot {\mathbf{\tau }}({\mathbf{r}}) \\ \end{gathered} $

– ядра и правые части соответствующих уравнений, ${\mathbf{\tau }}({\mathbf{r}})$ – орт касательной к границе профиля в соответствующей точке, направление которого выбирается таким образом, что ${\mathbf{n}}({\mathbf{r}})$ × ${\mathbf{\tau }}({\mathbf{r}})$ = k.

При рассмотрении внешних течений оба ГИУ (1.3) и (1.4) имеют бесконечное множество решений; для выделения единственного решения, имеющего физический смысл, обычно задается величина интеграла вдоль границы контура K:

(1.5)

$\oint\limits_K {\gamma (\xi )d{{l}_{\xi }}} = \Gamma ,$

где величина $\Gamma $ – циркуляция поля скоростей среды вдоль границы профиля.

Следует отметить, что при моделировании внутренних течений свойства ГИУ (1.3) не изменяются, тогда как ГИУ (1.4) в этом случае имеет единственное решение, и необходимости в постановке дополнительного условия в виде равенства (1.5) не возникает, так как его выполнение обеспечивается автоматически.

ГИУ (1.3) является сингулярным, его ядро неинтегрируемо в обычном смысле, а интеграл в нем понимается в смысле главного значения по Коши, в то время как ядро ГИУ (1.4) – функция, ограниченная при $\left| {{\mathbf{r}} - {\mathbf{\xi }}} \right| \to 0$, если граница обтекаемого профиля – гладкая кривая, и абсолютно интегрируемая, если K – кусочно-гладкая кривая. При этом $\alpha (\vec {r}) = 1{\text{/}}2$, $\vec {r} \in K$, за исключением угловых точек профиля.

2. Подход Галеркина. Для приближенного численного решения ГИУ (1.3) или (1.4) совместно с дополнительным условием (1.5) возможно применение процедуры Галеркина, в соответствии с которой искомое решение выражается линейной комбинацией функций, называемых базисными, а неизвестные коэффициенты находятся из условий ортогональности невязки системе проекционных функций. Такая процедура останется корректной также и в случае кусочно-гладких профилей с угловыми точками, поскольку искомая функция $\gamma ({\mathbf{r}})$, хотя и может стать неограниченной в окрестности угловых точек, останется интегрируемой с квадратом [14].

Отметим, что традиционную расчетную схему известного метода дискретных вихрей [14] можно получить как результат применения описанной процедуры к ГИУ (1.3), выбрав в качестве базисных и проекционных семейства дельта-функций Дирака. Здесь будем рассматривать ГИУ (1.4), поскольку расчетные схемы вихревых методов на его основе обеспечивают бóльшую точность [15], однако изложенные подходы могут быть применены и к численному решению ГИУ (1.3).

Границу профиля K заменим совокупностью N участков-панелей ${{K}_{i}}$, $i = 1, \ldots ,N$. Введем набор базисных функций $\phi _{i}^{q}({\mathbf{r}})$ ($i = 1, \ldots ,N$, $q = 0, \ldots ,m$) и примем, что функция $\phi _{i}^{q}({\mathbf{r}})$ отлична от нуля только на i-й панели. Приближенное решение ГИУ будем искать в виде линейной комбинации базисных функций

(2.1)

$\gamma ({\mathbf{r}}) = \sum\limits_{i = 1}^N \,\sum\limits_{q = 0}^m \,\gamma _{i}^{q}\phi _{i}^{q}({\mathbf{r}})$

Неизвестные $\gamma _{i}^{q}$ найдем из условия ортогональности невязки уравнения (1.4) после подстановки в него представления (2.1) набору проекционных функций, которые выберем совпадающими с базисными:

(2.2)

$\begin{gathered} \sum\limits_{j = 1}^N \,\sum\limits_{q = 0}^m \,\gamma _{j}^{q}\int\limits_{{{K}_{i}}} {\phi _{i}^{p}(r)d{{l}_{r}}} \int\limits_{{{K}_{j}}} {{{Q}_{\tau }}(r,\xi )\phi _{j}^{q}(\xi )d{{l}_{\xi }}} - \frac{1}{2}\sum\limits_{q = 0}^m \,\gamma _{i}^{q}\int\limits_{{{K}_{i}}} {\phi _{i}^{q}(r)\phi _{i}^{p}(r)d{{l}_{r}}} = \int\limits_{{{K}_{i}}} {{{f}_{\tau }}(r)\phi _{i}^{p}(r)d{{l}_{r}}} , \\ i = 1, \ldots ,N,\quad p = 0, \ldots ,m \\ \end{gathered} $

Завихренность $\Omega ({\mathbf{r}})$ в области течения в вихревых методах представляется заданной в виде набора точечных вихрей с циркуляциями ${{\Gamma }_{w}}$, расположенных в точках ${{{\mathbf{\rho }}}_{w}}$ ($w = 1, \ldots ,{{N}_{{v}}}$):

$\Omega ({\mathbf{r}}) = \sum\limits_{w = 1}^{{{N}_{{v}}}} \,{{\Gamma }_{w}}\delta ({\mathbf{r}} - {{{\mathbf{\rho }}}_{w}}),$

где $\delta ({\mathbf{r}} - {{{\mathbf{\rho }}}_{w}})$ – двумерная дельта-функция Дирака.

Интенсивности присоединенных слоев вихрей и источников ${{\gamma }^{{\operatorname{att} }}}({\mathbf{r}})$ и ${{q}^{{\operatorname{att} }}}({\mathbf{r}})$ будем считать представлеными в виде разложения по базисным функциям:

${{\gamma }^{{\operatorname{att} }}}({\mathbf{r}}) = \sum\limits_{i = 1}^N \,\sum\limits_{q = 0}^m \,({{\gamma }^{{{\text{att}}}}})_{i}^{q}\phi _{i}^{q}({\mathbf{r}}),\quad {{q}^{{\operatorname{att} }}}({\mathbf{r}}) = \sum\limits_{i = 1}^N \,\sum\limits_{q = 0}^m \,({{q}^{{\operatorname{att} }}})_{i}^{q}\phi _{i}^{q}({\mathbf{r}})$

Вводя обозначение ${\mathbf{G}}({\mathbf{r}}) = \frac{1}{{2\pi }}\frac{{\mathbf{r}}}{{{{r}^{2}}}}$ для градиента функции Грина – фундаментального решения двумерного уравнения Лапласа, систему ураванений (2.2) можно записать в виде

$\sum\limits_{j = 1}^N \,\sum\limits_{q = 0}^m \,\gamma _{j}^{q}\int\limits_{{{K}_{i}}} {\phi _{i}^{p}({\mathbf{r}})d{{l}_{r}}} \int\limits_{{{K}_{j}}} {{\mathbf{n}}({\mathbf{r}}) \cdot {\mathbf{G}}({\mathbf{r}} - {\mathbf{\xi }})\phi _{j}^{q}({\mathbf{\xi }})d{{l}_{\xi }}} - \frac{1}{2}\,\sum\limits_{q = 0}^m \,\gamma _{i}^{q}\int\limits_{{{K}_{i}}} {\phi _{i}^{q}({\mathbf{r}})\phi _{i}^{p}({\mathbf{r}})ds} = $

$ = \int\limits_{{{K}_{i}}} {{\mathbf{\tau }}({\mathbf{r}})} \cdot \left( {\frac{{{{{\mathbf{V}}}_{K}}({\mathbf{r}})}}{2} - {{{\mathbf{V}}}_{\infty }}} \right)\phi _{i}^{p}({\mathbf{r}})d{{l}_{r}} - \sum\limits_{w = 1}^{{{N}_{{v}}}} \,{{\Gamma }_{w}}\int\limits_{{{K}_{i}}} {{\mathbf{n}}({\mathbf{r}}) \cdot G({\mathbf{r}} - {{{\mathbf{\rho }}}_{w}})\phi _{i}^{p}({\mathbf{r}})d{{l}_{r}}} - $

$ - \;\sum\limits_{j = 1}^N \,\sum\limits_{q = 0}^m \,({{\gamma }^{{\operatorname{att} }}})_{j}^{q}\int\limits_{{{K}_{i}}} {\phi _{i}^{p}({\mathbf{r}})d{{l}_{r}}} \int\limits_{{{K}_{j}}} {{\mathbf{n}}({\mathbf{r}}) \cdot {\mathbf{G}}({\mathbf{r}} - {\mathbf{\xi }})\phi _{j}^{q}({\mathbf{\xi }})d{{l}_{\xi }}} - $

(2.3)

$ - \;\sum\limits_{j = 1}^N \,\sum\limits_{q = 0}^m \,({{q}^{{\operatorname{att} }}})_{j}^{q}\int\limits_{{{K}_{i}}} {\phi _{i}^{p}({\mathbf{r}})d{{l}_{r}}} \int\limits_{{{K}_{j}}} {{\mathbf{\tau }}({\mathbf{r}}) \cdot {\mathbf{G}}({\mathbf{r}} - {\mathbf{\xi }})\phi _{j}^{q}({\mathbf{\xi }})d{{l}_{\xi }}} $

$i = 1, \ldots ,N,\quad p = 0, \ldots ,m$

Дополнительное условие для выделения единственного решения (1.5) принимает вид

(2.4)

$\sum\limits_{i = 1}^N \,\sum\limits_{p = 0}^m \,\gamma _{i}^{p}\int\limits_{{{K}_{i}}} {\phi _{i}^{p}({\mathbf{r}})d{{l}_{r}}} = \Gamma $

В качестве базисных и проекционных далее будем рассматривать систему финитных полиномиальных функций, считая, что функция $\phi _{i}^{p}({\mathbf{r}}){\kern 1pt} $ отлична от нуля только на панели ${{K}_{i}}$ и задана на ней полиномом степени p.

Система линейных алгебраических уравнений (2.3), (2.4) переопределенная, для ее регуляризации можно применить подход, аналогичный описанному И.К. Лифановым [14], состоящий во введении дополнительной регуляризирующей переменной.

Считая, что $m = 1$, т.е. рассматривая кусочно-постоянные и кусочно-линейные базисные функции $\phi _{i}^{0}({\mathbf{r}}){\kern 1pt} $ и $\phi _{i}^{1}({\mathbf{r}})$, результирующую систему можно записать в блочной форме:

(2.5)

$\left( {\begin{array}{*{20}{c}} {{{A}^{{00}}} + {{D}^{{00}}}}&{{{A}^{{01}}} + {{D}^{{01}}}}&{{{I}_{N}}} \\ {{{A}^{{10}}} + {{D}^{{10}}}}&{{{A}^{{11}}} + {{D}^{{11}}}}&{{{O}_{N}}} \\ {{{L}^{0}}}&{{{L}^{1}}}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{{\gamma }^{0}}} \\ {{{\gamma }^{1}}} \\ R \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{b}^{0}}} \\ {{{b}^{1}}} \\ \Gamma \end{array}} \right),$

где ${{A}^{{pq}}}$ – квадратные матрицы размером $N \times N$, ${{D}^{{pq}}}$ – диагональные матрицы размером $N \times N$ ($p,q = 0,1$), ${{L}^{0}}$ и ${{L}^{1}}$ – $N$-мерные вектор-строки; ${{I}_{N}}$ – столбец из единиц; ${{O}_{N}}$ – столбец из нулей, ${{\gamma }^{0}}$ и ${{\gamma }^{1}}$ – $N$-мерные векторы, составленные из искомых коэффициентов, ${{b}^{0}}$ и ${{b}^{1}}$ – $N$-мерные векторы, образующие правую часть системы:

$A_{{ij}}^{{pq}} = \int\limits_{{{K}_{i}}} {\left( {\int\limits_{{{K}_{j}}} {({\mathbf{G}}({\mathbf{r}} - {\mathbf{\xi }})} \cdot {\mathbf{n}}({\mathbf{r}}))\varphi _{j}^{q}({\mathbf{\xi }})d{{l}_{\xi }}} \right)} \varphi _{i}^{p}({\mathbf{r}})d{{l}_{r}}$

$D_{{ii}}^{{pq}} = - \frac{1}{2}\int\limits_{{{K}_{i}}} {\varphi _{i}^{p}({\mathbf{r}})\varphi _{i}^{q}({\mathbf{r}})d{{l}_{r}}} ,\quad L_{i}^{p} = \int\limits_{{{K}_{i}}} {\varphi _{i}^{p}({\mathbf{r}})d{{l}_{r}}} $

$b_{i}^{p} = ({{b}_{V}})_{i}^{p} - \sum\limits_{w = 1}^{{{N}_{{v}}}} {{{\Gamma }_{w}}({{z}_{w}})_{i}^{p}} - \sum\limits_{j = 1}^N {\sum\limits_{q = 0}^m {A_{{ij}}^{{pq}}({{\gamma }^{{\operatorname{att} }}})_{j}^{q}} } - \sum\limits_{j = 1}^N {\sum\limits_{q = 0}^m {S_{{ij}}^{{pq}}({{q}^{{\operatorname{att} }}})_{j}^{q}} } $

$p,q = 0,1,\quad i,j = 1, \ldots ,N$

В выражении для компонент вектора правой части введены следующие обозначения для коэффициентов:

(2.6)

$\begin{gathered} ({{b}_{V}})_{i}^{p} = \int\limits_{{{K}_{i}}} {\left( {\frac{{{{{\mathbf{V}}}_{K}}({\mathbf{r}})}}{2} - {{{\mathbf{V}}}_{\infty }}} \right)} \cdot {\mathbf{\tau }}({\mathbf{r}})\varphi _{i}^{p}({\mathbf{r}})d{{l}_{r}},\quad ({{z}_{w}})_{i}^{p} = \int\limits_{{{K}_{i}}} {({\mathbf{G}}({\mathbf{r}} - {{{\mathbf{\rho }}}_{w}}) \cdot {\mathbf{n}}({\mathbf{r}}))} \varphi _{i}^{p}({\mathbf{r}})d{{l}_{r}} \\ S_{{ij}}^{{pq}} = \int\limits_{{{K}_{i}}} {\left( {\int\limits_{{{K}_{j}}} {({\mathbf{G}}({\mathbf{r}} - {\mathbf{\xi }}) \cdot {\mathbf{\tau }}({\mathbf{r}}))\varphi _{j}^{q}({\mathbf{\xi }})d{{l}_{\xi }}} } \right)} \varphi _{i}^{p}({\mathbf{r}})d{{l}_{r}},\quad p,q = 0,1,\quad i,j = 1, \ldots ,N \\ \end{gathered} $

Отметим, что по аналогии с системой (2.5) можно получить систему, соответствующую расчетной схеме с кусочно-постоянными базисными функциями $\phi _{i}^{0}({\mathbf{r}}){\kern 1pt} $ [16].

Вычисление интегралов, входящих в выражения для коэффициентов системы (2.5), является нетривиальной задачей. Далее рассмотрим случай аппроксимации профиля прямолинейными панелями, а также общий случай криволинейной границы профиля.

3. Случай прямолинейных панелей. Наиболее простым подходом, позволяющим точно вычислить интегралы, входящие в коэффициенты системы (2.5), представляется замена исходной границы профиля прямолинейными панелями ${{K}_{i}}$. Базисные функции имеют вид

(3.1)

$\phi _{i}^{0}({\mathbf{r}}) = \left( \begin{gathered} 1,\quad {\mathbf{r}} \in {{K}_{i}} \hfill \\ 0,\quad {\mathbf{r}} \notin {{K}_{i}} \hfill \\ \end{gathered} \right.\quad \phi _{i}^{1}({\mathbf{r}}) = \left( \begin{gathered} \frac{{({\mathbf{r}} - {{{\mathbf{c}}}_{i}}) \cdot {{{\mathbf{\tau }}}_{i}}}}{{{{L}_{i}}}},\quad {\mathbf{r}} \in {{K}_{i}} \hfill \\ 0,\quad {\mathbf{r}} \notin {{K}_{i}} \hfill \\ \end{gathered} \right.$

где ${{{\mathbf{c}}}_{i}}$ – радиус-вектор центра $i$-й панели, ${{{\mathbf{\tau }}}_{i}}$ – направляющий вектор (орт касательной), ${{L}_{i}}$ – длина $i$-й панели. Тогда элементы диагональных матриц ${{D}^{{pq}}}$ и вектор-строк ${{L}^{p}}$ таковы:

$D_{{ii}}^{{00}} = - \frac{{{{L}_{i}}}}{2},\quad D_{{ii}}^{{11}} = - \frac{{{{L}_{i}}}}{{24}},\quad D_{{ii}}^{{01}} = D_{{ii}}^{{10}} = 0,\quad L_{i}^{0} = {{L}_{i}},\quad L_{i}^{1} = 0,\quad i = 1, \ldots ,N$

Поскольку орты касательных и внешних нормалей остаются постоянными на панелях, выражения для всех коэффициентов системы (2.5) с учетом свойства ${\mathbf{G}}({\mathbf{r}} - {\mathbf{\xi }})$ = = $ - {\mathbf{G}}({\mathbf{\xi }} - {\mathbf{r}})$ сводятся к вычислению шести интегралов:

${\mathbf{I}}_{j}^{0}({\mathbf{r}}) = \int\limits_{{{K}_{j}}} {{\mathbf{G}}({\mathbf{r}} - {\mathbf{\xi }})d{{l}_{\xi }}} ,\quad {\mathbf{I}}_{j}^{1}({\mathbf{r}}) = \int\limits_{{{K}_{j}}} {{\mathbf{G}}({\mathbf{r}} - {\mathbf{\xi }})\phi _{j}^{1}({\mathbf{\xi }})d{{l}_{\xi }}} $

${\mathbf{I}}_{{ij}}^{{00}} = \int\limits_{{{K}_{i}}} {d{{l}_{r}}} \int\limits_{{{K}_{j}}} {{\mathbf{G}}({\mathbf{r}} - {\mathbf{\xi }})d{{l}_{\xi }}} ,\quad {\mathbf{I}}_{{ij}}^{{01}} = \int\limits_{{{K}_{i}}} {d{{l}_{r}}} \int\limits_{{{K}_{j}}} {{\mathbf{G}}({\mathbf{r}} - {\mathbf{\xi }})\phi _{j}^{1}({\mathbf{\xi }})d{{l}_{\xi }}} $

${\mathbf{I}}_{{ij}}^{{10}} = \int\limits_{{{K}_{i}}} {d{{l}_{r}}} \int\limits_{{{K}_{j}}} {{\mathbf{G}}({\mathbf{r}} - {\mathbf{\xi }})\phi _{i}^{1}({\mathbf{r}})d{{l}_{\xi }}} ,\quad {\mathbf{I}}_{{ij}}^{{11}} = \int\limits_{{{K}_{i}}} {d{{l}_{r}}} \int\limits_{{{K}_{j}}} {{\mathbf{G}}({\mathbf{r}} - {\mathbf{\xi }})\phi _{i}^{1}({\mathbf{r}})\phi _{j}^{1}({\mathbf{\xi }})d{{l}_{\xi }}} $

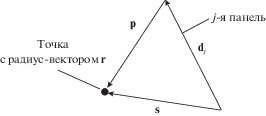
Вычисление интегралов ${\mathbf{I}}_{j}^{0}({\mathbf{r}})$ и ${\mathbf{I}}_{j}^{1}({\mathbf{r}})$. На рис. 1 изображены j-я панель и точка ${\mathbf{r}}$, а также введены вспомогательные векторы: вектор ${{{\mathbf{d}}}_{j}}$ совпадает с j-й панелью; векторы ${\mathbf{s}}$ и ${\mathbf{p}}$ соединяют начало и конец j-й панели с точкой ${\mathbf{r}}$ соответственно.

Рис. 1.

Точка ${\mathbf{r}}$, j-я панель и вспомогательные векторы.

С помощью данных векторов можно записать

${\mathbf{I}}_{j}^{0}({\mathbf{r}}) = \alpha {{{\mathbf{u}}}_{0}} \times {\mathbf{k}} + \lambda {{{\mathbf{u}}}_{0}},\quad {\mathbf{I}}_{j}^{1}({\mathbf{r}}) = \alpha {{{\mathbf{u}}}_{1}} \times {\mathbf{k}} + \lambda {{{\mathbf{u}}}_{1}} - \frac{1}{{2\pi }}{{{\mathbf{\tau }}}_{j}}$

Здесь введены обозначения

${{{\mathbf{u}}}_{0}} = {\mathbf{\omega }}({{{\mathbf{\tau }}}_{j}},{{{\mathbf{\tau }}}_{j}},{{{\mathbf{\tau }}}_{j}}) = {{{\mathbf{\tau }}}_{j}},\quad {{{\mathbf{u}}}_{1}} = \frac{1}{{2\left| {{{{\mathbf{d}}}_{j}}} \right|}}{\mathbf{\omega }}({\mathbf{p}} + {\mathbf{s}},{{{\mathbf{\tau }}}_{j}},{{{\mathbf{\tau }}}_{j}}),\quad \alpha = \frac{1}{{2\pi }}\angle ({\mathbf{p}},{\mathbf{s}}),\quad \lambda = \frac{1}{{2\pi }}\ln \frac{{\left| {\mathbf{s}} \right|}}{{\left| {\mathbf{p}} \right|}},$

где

${\mathbf{\omega }}({\mathbf{a}},{\mathbf{b}},{\mathbf{c}}) = ({\mathbf{a}} \cdot {\mathbf{b}}){\mathbf{c}} + ({\mathbf{a}} \times {\mathbf{b}}) \times {\mathbf{c}},\quad \angle ({\mathbf{p}},{\mathbf{s}}) = \operatorname{Arg} {\text{(}}{\mathbf{p}} \cdot {\mathbf{s}} + i({\mathbf{psk}}){\text{)}},$

функция $\operatorname{Arg} (z)$ означает главное значение аргумента комплексного числа $z$.

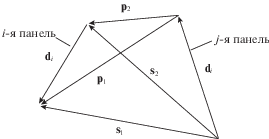
Вычисление интегралов ${\mathbf{I}}_{{ij}}^{{00}}$, ${\mathbf{I}}_{{ij}}^{{01}}$, ${\mathbf{I}}_{{ij}}^{{10}}$ и ${\mathbf{I}}_{{ij}}^{{11}}$. На рис. 2 изображены $i$-я и $j$-я панели и вспомогательные векторы, введенные по аналогии со сказанным выше: векторы ${{{\mathbf{d}}}_{i}}$ и ${{{\mathbf{d}}}_{j}}$ совпадают с $i$-й и $j$-й панелями, векторы ${{{\mathbf{s}}}_{1}}$ и ${{{\mathbf{s}}}_{2}}$ соединяют начало $j$-й панели с концом и началом $i$-й панели соответственно; векторы ${{{\mathbf{p}}}_{1}}$ и ${{{\mathbf{p}}}_{2}}$ соединяют конец $j$-й панели с концом и началом $i$-й панели соответственно.

Рис. 2.

Вспомогательные векторы для $i$-й и $j$-й панелей.

Введенные векторы позволяют записать следующие формулы:

${\mathbf{I}}_{{ij}}^{{00}} = ({{\alpha }_{1}}{{{\mathbf{v}}}_{1}} + {{\alpha }_{2}}{{{\mathbf{v}}}_{2}} + {{\alpha }_{3}}{{{\mathbf{v}}}_{3}}) \times {\mathbf{k}} + ({{\lambda }_{1}}{{{\mathbf{v}}}_{1}} + {{\lambda }_{2}}{{{\mathbf{v}}}_{2}} + {{\lambda }_{3}}{{{\mathbf{v}}}_{3}})$

${\mathbf{I}}_{{ij}}^{{01}} = (({{\alpha }_{1}} + {{\alpha }_{3}}){{{\mathbf{v}}}_{4}} + ({{\alpha }_{2}} + {{\alpha }_{3}}){{{\mathbf{v}}}_{5}}) \times {\mathbf{k}} + (({{\lambda }_{1}} + {{\lambda }_{3}}){{{\mathbf{v}}}_{4}} + ({{\lambda }_{2}} + {{\lambda }_{3}}){{{\mathbf{v}}}_{5}}) - \frac{1}{{4\pi }}\left| {{{{\mathbf{d}}}_{i}}} \right|{{{\mathbf{\tau }}}_{j}}$

${\mathbf{I}}_{{ij}}^{{10}} = (({{\alpha }_{1}} + {{\alpha }_{3}}){{{\mathbf{v}}}_{6}} + {{\alpha }_{3}}{{{\mathbf{v}}}_{7}}) \times {\mathbf{k}} + (({{\lambda }_{1}} + {{\lambda }_{3}}){{{\mathbf{v}}}_{6}} + {{\lambda }_{3}}{{{\mathbf{v}}}_{7}}) + \frac{1}{{4\pi }}\left| {{{{\mathbf{d}}}_{j}}} \right|{{{\mathbf{\tau }}}_{i}}$

${\mathbf{I}}_{{ij}}^{{11}} = (({{\alpha }_{1}} + {{\alpha }_{3}}){{{\mathbf{v}}}_{8}} + ({{\alpha }_{2}} + {{\alpha }_{3}}){{{\mathbf{v}}}_{9}} + {{\alpha }_{3}}{{{\mathbf{v}}}_{{10}}}) \times {\mathbf{k}} + (({{\lambda }_{1}} + {{\lambda }_{3}}){{{\mathbf{v}}}_{8}} + ({{\lambda }_{2}} + {{\lambda }_{3}}){{{\mathbf{v}}}_{9}} + {{\lambda }_{3}}{{{\mathbf{v}}}_{{10}}}) + $

$ + \;\frac{1}{{24\pi }}(\left| {{{{\mathbf{d}}}_{j}}} \right|{{\tau }_{i}} + \left| {{{{\mathbf{d}}}_{i}}} \right|{{\tau }_{j}} - 2{\mathbf{\omega }}({{{\mathbf{s}}}_{1}},{{{\mathbf{\tau }}}_{i}},{{{\mathbf{\tau }}}_{j}}))$

Здесь введены обозначения для коэффициентов

$\begin{gathered} {{\alpha }_{1}} = \frac{1}{{2\pi }}\angle ({{{\mathbf{s}}}_{2}},{{{\mathbf{s}}}_{1}}),\quad {{\alpha }_{2}} = \frac{1}{{2\pi }}\angle ({{{\mathbf{s}}}_{2}},{{{\mathbf{p}}}_{1}}),\quad {{\alpha }_{3}} = \frac{1}{{2\pi }}\angle ({{{\mathbf{p}}}_{1}},{{{\mathbf{p}}}_{2}}) \\ {{\lambda }_{1}} = \frac{1}{{2\pi }}\ln \frac{{\left| {{{{\mathbf{s}}}_{1}}} \right|}}{{\left| {{{{\mathbf{s}}}_{2}}} \right|}},\quad {{\lambda }_{2}} = \frac{1}{{2\pi }}\ln \frac{{\left| {{{{\mathbf{p}}}_{1}}} \right|}}{{\left| {{{{\mathbf{s}}}_{2}}} \right|}},\quad {{\lambda }_{3}} = \frac{1}{{2\pi }}\ln \frac{{\left| {{{{\mathbf{p}}}_{2}}} \right|}}{{\left| {{{{\mathbf{p}}}_{1}}} \right|}} \\ \end{gathered} $

и вспомогательных векторов

${{{\mathbf{v}}}_{1}}{\mathbf{ = \omega }}({{{\mathbf{s}}}_{1}},{{{\mathbf{\tau }}}_{i}},{{{\mathbf{\tau }}}_{j}}),\quad {{{\mathbf{v}}}_{2}} = - {\mathbf{\omega }}({{{\mathbf{d}}}_{i}},{{{\mathbf{\tau }}}_{i}},{{{\mathbf{\tau }}}_{j}}),\quad {{{\mathbf{v}}}_{3}} = {\mathbf{\omega }}({{{\mathbf{p}}}_{2}},{{{\mathbf{\tau }}}_{i}},{{{\mathbf{\tau }}}_{j}})$

${{{\mathbf{v}}}_{4}} = \frac{1}{{2\left| {{{{\mathbf{d}}}_{j}}} \right|}}((({{{\mathbf{p}}}_{1}} + {{{\mathbf{s}}}_{1}}) \cdot {{{\mathbf{\tau }}}_{j}}){\mathbf{\omega }}({{{\mathbf{s}}}_{1}},{{{\mathbf{\tau }}}_{i}},{{{\mathbf{\tau }}}_{j}}) - {{\left| {{{{\mathbf{s}}}_{1}}} \right|}^{2}}{{{\mathbf{\tau }}}_{i}}),\quad {{{\mathbf{v}}}_{5}} = - \frac{{\left| {{{{\mathbf{d}}}_{i}}} \right|}}{{2\left| {{{{\mathbf{d}}}_{j}}} \right|}}{\mathbf{\omega }}({{{\mathbf{s}}}_{1}} + {{{\mathbf{p}}}_{2}},{{{\mathbf{\tau }}}_{j}},{{{\mathbf{\tau }}}_{j}})$

${{{\mathbf{v}}}_{6}} = - \frac{1}{{2\left| {{{{\mathbf{d}}}_{i}}} \right|}}((({{{\mathbf{s}}}_{1}} + {{{\mathbf{s}}}_{2}}) \cdot {{{\mathbf{\tau }}}_{i}}){\mathbf{\omega }}({{{\mathbf{s}}}_{1}},{{{\mathbf{\tau }}}_{i}},{{{\mathbf{\tau }}}_{j}}) - {{\left| {{{{\mathbf{s}}}_{1}}} \right|}^{2}}{{{\mathbf{\tau }}}_{j}}),\quad {{{\mathbf{v}}}_{7}} = \frac{{\left| {{{{\mathbf{d}}}_{j}}} \right|}}{{2\left| {{{{\mathbf{d}}}_{i}}} \right|}}{\mathbf{\omega }}({{{\mathbf{s}}}_{1}} + {{{\mathbf{p}}}_{2}},{{{\mathbf{\tau }}}_{i}},{{{\mathbf{\tau }}}_{i}})$

${{{\mathbf{v}}}_{8}} = \frac{1}{{12\left| {{{{\mathbf{d}}}_{i}}} \right|\left| {{{{\mathbf{d}}}_{j}}} \right|}}(2({{{\mathbf{s}}}_{1}} \cdot {\mathbf{\omega }}({{{\mathbf{s}}}_{1}} - 3{{{\mathbf{p}}}_{2}},{{{\mathbf{\tau }}}_{i}},{{{\mathbf{\tau }}}_{j}})){\mathbf{\omega }}({{{\mathbf{s}}}_{1}},{{{\mathbf{\tau }}}_{i}},{{{\mathbf{\tau }}}_{j}}) - {{\left| {{{{\mathbf{s}}}_{1}}} \right|}^{2}}({{{\mathbf{s}}}_{1}} - 3{{{\mathbf{p}}}_{2}})) - \frac{1}{4}{\mathbf{\omega }}({{{\mathbf{s}}}_{1}},{{{\mathbf{\tau }}}_{i}},{{{\mathbf{\tau }}}_{j}})$

${{{\mathbf{v}}}_{9}} = - \frac{1}{{12}}\frac{{\left| {{{{\mathbf{d}}}_{i}}} \right|}}{{\left| {{{{\mathbf{d}}}_{j}}} \right|}}{\mathbf{\omega }}({{{\mathbf{d}}}_{i}},{{{\mathbf{\tau }}}_{j}},{{{\mathbf{\tau }}}_{j}}),\quad {{{\mathbf{v}}}_{{10}}} = - \frac{1}{{12}}\frac{{\left| {{{{\mathbf{d}}}_{j}}} \right|}}{{\left| {{{{\mathbf{d}}}_{i}}} \right|}}{\mathbf{\omega }}({{{\mathbf{d}}}_{j}},{{{\mathbf{\tau }}}_{i}},{{{\mathbf{\tau }}}_{i}})$

Для соседних панелей, когда $i = j + 1$ (т.е. ${{{\mathbf{p}}}_{2}} = 0$, ${{{\mathbf{s}}}_{1}} \ne {\mathbf{0}}$), коэффициенты ${{\alpha }_{3}}$ и ${{\lambda }_{3}}$ следует положить равными нулю; в случае, когда $j = i + 1$ (${{{\mathbf{s}}}_{1}} = {\mathbf{0}}$, ${{{\mathbf{p}}}_{2}} \ne {\mathbf{0}}$), нулю следует приравнять коэффициенты ${{\alpha }_{1}}$ и ${{\lambda }_{1}}$.

В случае, когда $i = j$, соответствующие интегралы сингулярные, а их предельные значения выражаются следующим образом (формально можно считать, что все коэффициенты ${{\alpha }_{k}}$ и ${{\lambda }_{k}}$ равны нулю):

${\mathbf{I}}_{{ii}}^{{00}} = {\mathbf{I}}_{{ii}}^{{11}} = {\mathbf{0}},\quad {\mathbf{I}}_{{ii}}^{{01}} = - \frac{1}{{4\pi }}{{{\mathbf{d}}}_{i}},\quad {\mathbf{I}}_{{ii}}^{{10}} = \frac{1}{{4\pi }}{{{\mathbf{d}}}_{i}}$

4. Случай криволинейной границы профиля. Если исходная гладкая граница профиля аппроксимирована криволинейными панелями таким образом, что она представляет собой кривую класса С², можно получить приближенные выражения для коэффициентов системы (2.5). Будем считать границу параметризованной естественным параметром s, тогда базисные функции $\phi _{i}^{0}({\mathbf{r}})$ определяются первым равенством (3.1), а базисные функции $\phi _{i}^{1}({\mathbf{r}})$ имеют вид

$\phi _{i}^{1}({\mathbf{r}}) = \left( \begin{gathered} \frac{{s({\mathbf{r}}) - s({{{\mathbf{c}}}_{i}})}}{{{{L}_{i}}}},\quad {\mathbf{r}} \in {{K}_{i}}, \hfill \\ 0,\quad {\mathbf{r}} \notin {{K}_{i}} \hfill \\ \end{gathered} \right.$

Выражения для элементов диагональных матриц ${{D}^{{pq}}}$ и векторов-строк ${{L}^{p}}$ остаются такими же, как для случая прямолинейных панелей, однако процедура вычисления остальных элементов усложняется, поскольку векторы касательных и нормалей к панелям теперь изменяются вдоль них.

Для удобства введем понятие “кривизны со знаком” плоской кривой, которую определим как

$\varkappa (s) = ({\mathbf{r}}{\text{'}}(s) \times {\mathbf{r}}{\text{''}}(s)) \cdot {\mathbf{k}},$

где ${\mathbf{k}}$ – орт нормали к плоскости контура. Тогда положительные значения $\varkappa $ соответствуют выпуклым участкам контура, и для ортов касательной и внешней нормали справедливы соотношения, следующие из формул Френе:

$\frac{{d{\mathbf{\tau }}(s)}}{{ds}} = - \varkappa (s){\mathbf{n}}(s),\quad \frac{{d{\mathbf{n}}(s)}}{{ds}} = \varkappa (s){\mathbf{\tau }}(s)$

Пусть начала и концы панелей соответствуют значениям ${{s}_{i}}$ ($i = 0, \ldots ,N$) параметра $s$, тогда i-я панель соответствует значениям параметра $s \in [{{s}_{{i - 1}}},{{s}_{i}}]$, и выражение для элементов матрицы $A_{{ij}}^{{pq}}$ примет вид

$A_{{ij}}^{{pq}} = \int\limits_{{{s}_{{i - 1}}}}^{{{s}_{i}}} {\left( {\int\limits_{{{s}_{{j - 1}}}}^{{{s}_{j}}} {({\mathbf{G}}(s - \sigma ) \cdot {\mathbf{n}}(s))\varphi _{j}^{q}(\sigma )d\sigma } } \right){\kern 1pt} \varphi _{i}^{p}(s)ds} $

Будем считать, что длина $i$-й панели ${{L}_{i}} = {{s}_{i}} - {{s}_{{i - 1}}}$ мала, тогда получим приближенные формулы для $A_{{ij}}^{{pq}}$ путем интегрирования предварительно разложенных по формуле Тейлора по параметрам $s$ и $\sigma $ подынтегральных выражений. Ограничимся учетом только тех слагаемых, которые пропорциональны ${{({{L}_{i}})}^{k}}$, где $k\;\leqslant \;3$. Для диагональных элементов $A_{{ii}}^{{pq}}$ в результате получаем

$A_{{ii}}^{{00}} = \frac{{L_{i}^{2}}}{{4\pi }}{{\varkappa }_{i}},\quad A_{{ii}}^{{01}} = \frac{{L_{i}^{3}}}{{144\pi }}\varkappa _{i}^{'},\quad A_{{ii}}^{{10}} = \frac{{L_{i}^{3}}}{{72\pi }}\varkappa _{i}^{'},\quad A_{{ii}}^{{11}} = 0,$

где ${{\kappa }_{i}}$ – кривизна со знаком границы профиля в центре $i$-й панели, штрих означает производную по длине дуги.

Теперь рассмотрим внедиагональные коэффициенты, вычисление которых требует интегрирования по разным панелям ($i \ne j$). Введем вспомогательные обозначения: ${{{\mathbf{h}}}_{{ij}}} = {{{\mathbf{c}}}_{i}} - {{{\mathbf{c}}}_{j}}$ – вектор, соединяющий центры соответствующих панелей; ${{{\mathbf{\tau }}}_{i}}$, ${{{\mathbf{\tau }}}_{j}}$, ${{{\mathbf{n}}}_{i}}$, ${{{\mathbf{n}}}_{j}}$ – единичные векторы касательных и внешних нормалей в центрах $i$-й и $j$-й панелей соответственно. Тогда для элементов матриц $A_{{ij}}^{{00}}$, $A_{{ij}}^{{01}}$ и $A_{{ij}}^{{10}}$ можно получить следующие приближенные формулы:

(4.1)

$\begin{gathered} A_{{ij}}^{{00}} \approx \frac{{{{L}_{i}}{{L}_{j}}}}{{2\pi {{{\left| {{{{\mathbf{h}}}_{{ij}}}} \right|}}^{2}}}}({{{\mathbf{h}}}_{{ij}}} \cdot {{{\mathbf{n}}}_{i}}),\quad A_{{ij}}^{{01}} \approx \frac{{{{L}_{i}}L_{j}^{2}}}{{24\pi {{{\left| {{{{\mathbf{h}}}_{{ij}}}} \right|}}^{2}}}}\left( {({{{\mathbf{\tau }}}_{i}} \cdot {{{\mathbf{n}}}_{j}}) + 2\frac{{({{{\mathbf{h}}}_{{ij}}} \cdot {{{\mathbf{n}}}_{i}})({{{\mathbf{h}}}_{{ij}}} \cdot {{{\mathbf{\tau }}}_{j}})}}{{{{{\left| {{{h}_{{ij}}}} \right|}}^{2}}}}} \right), \\ A_{{ij}}^{{10}} \approx \frac{{L_{i}^{2}{{L}_{j}}}}{{24\pi {{{\left| {{{{\mathbf{h}}}_{{ij}}}} \right|}}^{2}}}}({{{\mathbf{h}}}_{{ij}}} \cdot {{{\mathbf{\tau }}}_{i}})\left( {{{\varkappa }_{i}} - 2\frac{{({{{\mathbf{h}}}_{{ij}}} \cdot {{{\mathbf{n}}}_{i}})}}{{{{{\left| {{{{\mathbf{h}}}_{{ij}}}} \right|}}^{2}}}}} \right) \\ \end{gathered} $

Коэффициентами $A_{{ij}}^{{11}}$ можно пренебречь и принять их равными нулю.

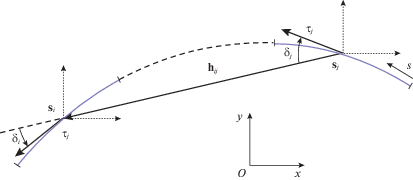
Если ввести обозначения ${{\delta }_{i}}$ и ${{\delta }_{j}}$ для углов между векторами ${{{\mathbf{\tau }}}_{i}}$, ${{{\mathbf{\tau }}}_{j}}$ и вектором ${{{\mathbf{h}}}_{{ij}}}$ соответственно, измеряемых с учетом знака таким образом, что положительный угол соответствует повороту ${{{\mathbf{h}}}_{{ij}}}$ к ${\mathbf{\tau }}$ против часовой стрелки (рис. 3), то формулы (4.1) можно записать в более компактной форме:

Рис. 3.

Две криволинейные панели и вспомогательные углы.

$A_{{ij}}^{{00}} \approx \frac{{{{L}_{i}}{{L}_{j}}}}{{2\pi {{h}_{{ij}}}}}\sin {{\delta }_{i}},\quad A_{{ij}}^{{01}} \approx \frac{{{{L}_{i}}L_{j}^{2}}}{{24\pi h_{{ij}}^{2}}}\sin ({{\delta }_{i}} + {{\delta }_{j}}),\quad A_{{ij}}^{{10}} \approx \frac{{L_{i}^{2}{{L}_{j}}}}{{24\pi h_{{ij}}^{2}}}({{h}_{{ij}}}{{\varkappa }_{i}}\cos {{\delta }_{i}} - \sin 2{{\delta }_{i}})$

При вычислении коэффициентов, которые требуют интегрирования по соседним панелям ($\left| {i - j} \right| = 1$), применение формул (4.1) может приводить к погрешности, поскольку разложение подынтегрального выражения производится в центрах панелей, и следовательно, величина $\left| {{\mathbf{r}}(s) - {\mathbf{r}}(\sigma )} \right|$ после разложения по $s$ и $\sigma $ будет иметь большу́ю относительную погрешность при приближении к общей точке смежных панелей. Поэтому для вычисления таких коэффициентов целесообразно раскладывать подынтегральное выражение по обеим переменным в окрестности их общей точки, и в результате для соседних панелей можно получить следующие приближенные формулы, которые проще и точнее по сравнению с формулами (4.1):

(4.2)

$A_{{ij}}^{{00}} = \frac{{{{L}_{i}}{{L}_{j}}}}{{4\pi }}\left( {\varkappa _{{ij}}^{'} \pm \frac{{{{L}_{j}} - 2{{L}_{i}}}}{6}\varkappa _{{ij}}^{'}} \right),\quad A_{{ij}}^{{01}} = \frac{{{{L}_{i}}L_{j}^{2}}}{{144\pi }}\varkappa _{{ij}}^{'},\quad A_{{ij}}^{{10}} = \frac{{L_{i}^{2}{{L}_{j}}}}{{72\pi }}\varkappa _{{ij}}^{'}$

Здесь ${{\varkappa }_{{ij}}}$ – кривизна со знаком границы профиля в общей точке соседних панелей, штрих означает производную по длине дуги, знак плюс в формуле для $A_{{ij}}^{{00}}$ используется, когда $j = i + 1$, а знак минус – когда $j = i - 1$.

Для интегралов (2.6), входящих в выражение для коэффициентов правой части, также могут быть получены приближенные формулы. Для коэффициентов $({{b}_{V}})_{i}^{p}$ при помощи изложенной выше методики разложения по формуле Тейлора в центре панели получаем следующие приближенные формулы:

$\begin{gathered} ({{b}_{V}})_{i}^{0} = \frac{{{{L}_{i}}}}{2}(({{{\mathbf{V}}}_{{K,i}}} - 2{{{\mathbf{V}}}_{\infty }}) \cdot {{{\mathbf{\tau }}}_{i}}) + \frac{{L_{i}^{3}}}{{48}}(({{{\mathbf{V}}}_{{K,i}}} - 2{{{\mathbf{V}}}_{\infty }}) \cdot {{{\mathbf{\tau }}}_{i}}){\text{''}} \\ ({{b}_{V}})_{i}^{1} = \frac{{L_{i}^{2}}}{{24}}(({{{\mathbf{V}}}_{{K,i}}} - 2{{{\mathbf{V}}}_{\infty }}) \cdot {{{\mathbf{\tau }}}_{i}}{\text{)'}} = \frac{{L_{i}^{2}}}{{24}}(({\mathbf{V}}_{{K,i}}^{'} \cdot {{{\mathbf{\tau }}}_{i}}) - {{\varkappa }_{i}}(({{{\mathbf{V}}}_{{K,i}}} - 2{{{\mathbf{V}}}_{\infty }}) \cdot {{{\mathbf{n}}}_{i}})) \\ \end{gathered} $

Здесь ${{{\mathbf{V}}}_{{K,i}}}$ – скорость границы профиля в центре $i$-й панели, ${{{\mathbf{\tau }}}_{i}}$ и ${{{\mathbf{n}}}_{i}}$ – единичные векторы касательной и внешней нормали в центре $i$-й панели соответственно, штрих означает производную по длине дуги.

Теперь запишем приближенные формулы для элементов $S_{{ij}}^{{pq}}$, отвечающих за учет влияния присоединенного слоя источников. Техника их получения остается принципиально той же, что и для элементов $A_{{ij}}^{{pq}}$, однако преобразования становятся более трудоемкими, поскольку подынтегральная функция при $\left| {i - j} \right| \leqslant 1$ имеет неинтегрируемую особенность и следует вычислять главные значения интегралов в смысле Коши.

Для диагональных элементов $S_{{ii}}^{{pq}}$ справедливы формулы

$S_{{ii}}^{{00}} = S_{{ii}}^{{11}} = 0,\quad S_{{ii}}^{{01}} = - S_{{ii}}^{{10}} = - \frac{1}{{4\pi }}{{L}_{i}} + \frac{{\varkappa _{i}^{2}}}{{288\pi }}L_{i}^{3}$

Для элементов, вычисление которых требует интегрирования вдоль разных панелей, как и ранее, иcпользуем обозначение ${{h}_{{ij}}} = {{{\mathbf{r}}}_{i}} - {{{\mathbf{r}}}_{j}}$ для вектора, соединяющего центры $i$-й и $j$-й панелей, тогда при $\left| {i - j} \right| > 1$ можно получить следующие приближенные формулы:

(4.3)

$\begin{array}{*{20}{c}} {S_{{ij}}^{{00}} \approx \frac{{{{L}_{i}}{{L}_{j}}}}{{2\pi {{{\left| {{{h}_{{ij}}}} \right|}}^{2}}}}({{{\mathbf{h}}}_{{ij}}} \cdot {{{\mathbf{\tau }}}_{i}}),\quad S_{{ij}}^{{01}} \approx \frac{{{{L}_{i}}L_{j}^{2}}}{{12\pi {{{\left| {{{h}_{{ij}}}} \right|}}^{2}}}}\left( {\frac{{({{{\mathbf{h}}}_{{ij}}} \cdot {{{\mathbf{\tau }}}_{i}})({{{\mathbf{h}}}_{{ij}}} \cdot {{{\mathbf{\tau }}}_{j}})}}{{{{{\left| {{{h}_{{ij}}}} \right|}}^{2}}}} - \frac{{({{{\mathbf{\tau }}}_{i}} \cdot {{{\mathbf{\tau }}}_{j}})}}{2}} \right)} \\ {S_{{ij}}^{{10}} \approx \frac{{L_{i}^{2}{{L}_{j}}}}{{12\pi {{{\left| {{{h}_{{ij}}}} \right|}}^{2}}}}\left( {\frac{1}{2} - \frac{{{{{({{{\mathbf{h}}}_{{ij}}} \cdot {{{\mathbf{\tau }}}_{i}})}}^{2}}}}{{{{{\left| {{{h}_{{ij}}}} \right|}}^{2}}}} - \frac{{({{{\mathbf{h}}}_{{ij}}} \cdot {{{\mathbf{n}}}_{i}})}}{2}{{\varkappa }_{i}}} \right),\quad S_{{ij}}^{{11}} \approx 0} \end{array}$

С учетом введенных на рис. 3 обозначений формулы (4.3) можно записать в виде

$S_{{ij}}^{{00}} \approx \frac{{{{L}_{i}}{{L}_{j}}}}{{2\pi {{h}_{{ij}}}}}\cos {{{\delta }}_{i}},\quad S_{{ij}}^{{01}} \approx \frac{{{{L}_{i}}L_{j}^{2}}}{{12\pi h_{{ij}}^{2}}}\cos ({{\delta }_{i}} + {{\delta }_{j}}),\quad S_{{ij}}^{{10}} \approx - \frac{{L_{i}^{2}{{L}_{j}}}}{{24\pi h_{{ij}}^{2}}}({{h}_{{ij}}}{{\varkappa }_{i}}\sin {{\delta }_{i}} + \cos 2{{\delta }_{i}})$

При вычислении элементов, которые требуют интегрирования по соседним панелям ($\left| {i - j} \right|$ = 1), для вычисления главных значений сингулярных интегралов следует применить прием, аналогичный описанному при получении формул (4.2); в результате получаются следующие приближенные формулы:

$S_{{ij}}^{{00}} = \pm \left( { - \frac{{{{L}_{i}}}}{{2\pi }}\ln \frac{{{{L}_{i}} + {{L}_{j}}}}{{{{L}_{i}}}} - \frac{{{{L}_{j}}}}{{2\pi }}\ln \frac{{{{L}_{i}} + {{L}_{j}}}}{{{{L}_{j}}}} + \frac{{{{L}_{i}}({{L}_{i}} + {{L}_{j}}){{L}_{j}}}}{{48\pi }}\varkappa _{{ij}}^{2}} \right)$

$S_{{ij}}^{{01}} = - \frac{{{{L}_{i}}}}{{4\pi }} + \frac{{{{L}_{i}}({{L}_{i}} + {{L}_{j}})}}{{4\pi {{L}_{j}}}}\ln \frac{{{{L}_{i}} + {{L}_{j}}}}{{{{L}_{i}}}} + \frac{{{{L}_{i}}L_{j}^{2}}}{{288\pi }}\varkappa _{{ij}}^{2}$

$S_{{ij}}^{{10}} = \frac{{{{L}_{j}}}}{{4\pi }} - \frac{{{{L}_{j}}({{L}_{i}} + {{L}_{j}})}}{{4\pi {{L}_{i}}}}\ln \frac{{{{L}_{i}} + {{L}_{j}}}}{{{{L}_{j}}}} - \frac{{L_{i}^{2}{{L}_{j}}}}{{288\pi }}\varkappa _{{ij}}^{2}$

$S_{{ij}}^{{11}} = \pm \left( {\frac{{{{L}_{i}} + {{L}_{j}}}}{{24\pi }} - \frac{{L_{i}^{2}}}{{24\pi {{L}_{j}}}}\ln \frac{{{{L}_{i}} + {{L}_{j}}}}{{{{L}_{i}}}} - \frac{{L_{j}^{2}}}{{24\pi {{L}_{i}}}}\ln \frac{{{{L}_{i}} + {{L}_{j}}}}{{{{L}_{j}}}}} \right)$

Здесь ${{\varkappa }_{{ij}}}$ – кривизна со знаком границы профиля в общей точке соседних панелей; знак плюс в формулах для $S_{{ij}}^{{00}}$ и $S_{{ij}}^{{11}}$ используется при $j = i + 1$, а минус – при $j = i - 1$.

Для учета влияния вихревых элементов, находящихся в области течения, т.е. для вычисления интегралов $({{z}_{w}})_{i}^{p}$ в формулах (2.6) введем вектор ${{{\mathbf{h}}}_{{iw}}} = {{{\mathbf{c}}}_{i}} - {{\rho }_{w}}$, который соединяет точку расположения $w$-го вихря с центром $i$-й панели.

Необходимо рассмотреть два случая. В случае малой величины отношения $\frac{{{{L}_{i}}}}{{{\text{|}}{{{\mathbf{h}}}_{{iw}}}{\text{|}}}}$, т.е. когда вихревой элемент находится достаточно далеко от панели, применимы приближенные формулы, получаемые по вышеописанной методике:

$\begin{gathered} ({{z}_{w}})_{i}^{0} = \frac{{({{{\mathbf{h}}}_{{iw}}} \cdot {{{\mathbf{n}}}_{i}})}}{{2\pi {{{\left| {{{h}_{{iw}}}} \right|}}^{2}}}}{{L}_{i}} + \frac{1}{{2\pi }}\left( {\left( {\frac{1}{4} - \frac{{{{{({{{\mathbf{h}}}_{{iw}}} \cdot {{{\mathbf{n}}}_{i}})}}^{2}}}}{{3{{{\left| {{{h}_{{iw}}}} \right|}}^{2}}}} - \frac{{\varkappa _{i}^{2}{{{\left| {{{h}_{{iw}}}} \right|}}^{2}}}}{{24}}} \right)\frac{{({\mathbf{h}}_{{iw}}^{{^{{^{{}}}}}} \cdot {{{\mathbf{n}}}_{i}})}}{{\left| {{{{\mathbf{h}}}_{{iw}}}} \right|}} + } \right. \\ \left. { + \;\left( {\frac{{\varkappa _{i}^{'}{{{\left| {{{h}_{{iw}}}} \right|}}^{2}}}}{{24}} - \frac{{{{\varkappa }_{i}}({{{\mathbf{h}}}_{{iw}}} \cdot {{{\mathbf{\tau }}}_{i}})}}{4}} \right)\frac{{({{{\mathbf{h}}}_{{iw}}} \cdot {{{\mathbf{\tau }}}_{i}})}}{{\left| {{{{\mathbf{h}}}_{{iw}}}} \right|}} + \frac{{{{\varkappa }_{i}}\left| {{{{\mathbf{h}}}_{{iw}}}} \right|}}{8}} \right)\frac{{L_{i}^{3}}}{{{{{\left| {{{{\mathbf{h}}}_{{iw}}}} \right|}}^{3}}}} \\ ({{z}_{w}})_{i}^{1} = \frac{{({{{\mathbf{h}}}_{{iw}}} \cdot {{{\mathbf{\tau }}}_{i}})}}{{12\pi \left| {{{{\mathbf{h}}}_{{iw}}}} \right|}}\left( {\frac{{{{\varkappa }_{i}}\left| {{{{\mathbf{h}}}_{{iw}}}} \right|}}{2} - \frac{{({{{\mathbf{h}}}_{{iw}}} \cdot {{{\mathbf{n}}}_{i}})}}{{\left| {{{{\mathbf{h}}}_{{iw}}}} \right|}}} \right)\frac{{L_{i}^{2}}}{{{{{\left| {{{h}_{{iw}}}} \right|}}^{2}}}} \\ \end{gathered} $

Если же вихревой элемент расположен достаточно близко к панели, получить по разработанной методике сравнительно простые и при этом достаточно точные приближенные формулы, позволяющие учитывать криволинейность границы профиля, не удается. В этом случае криволинейная панель может быть заменена на дугу соприкасающейся окружности радиусом ${{R}_{i}} = {{\left| {{{\varkappa }_{i}}} \right|}^{{ - 1}}}$, которая имеет ту же длину, что и исходная панель. При таком подходе, используя точное решение для случая окружности [17], можно получить следующую формулу, точную для дуги окружности:

$({{z}_{w}})_{i}^{0} \approx \Psi _{{iw}}^{0}\left( {{{\chi }_{i}} + \frac{{{{L}_{i}}{{\varkappa }_{i}}}}{2}} \right) - \Psi _{{iw}}^{0}\left( {{{\chi }_{i}} - \frac{{{{L}_{i}}{{\varkappa }_{i}}}}{2}} \right),$

где

$\Psi _{{iw}}^{0}(\beta ) = \frac{1}{{4\pi }}\left( {\beta - {{\theta }_{{iw}}} + 2{\text{arctg}}\left( {\frac{{{{\alpha }_{{iw}}}}}{{2 + {{\alpha }_{{iw}}}}}{\text{ctg}}\frac{{\beta - {{\theta }_{{iw}}}}}{2}} \right) - 2\pi \operatorname{sign} {{\alpha }_{{iw}}}\eta (\beta - {{\theta }_{{iw}}})} \right)$

обозначает непрерывную ветвь первообразной (по длине дуги) для соответствующей подынтегральной функции, ${{\chi }_{i}}$ – аргумент вектора $({{{\mathbf{c}}}_{i}} - {{{\mathbf{q}}}_{i}})$, т.е. угол между этим вектором и горизонтальной прямой (рис. 4), измеряемый в диапазоне $( - \pi ,\pi ]$, ${{{\mathbf{q}}}_{i}} = {{{\mathbf{c}}}_{i}} - \frac{{{{{\mathbf{n}}}_{i}}}}{{{{\varkappa }_{i}}}}$ – радиус-вектор центра соприкасающейся окружности, ${{L}_{i}}$ и ${{\varkappa }_{i}}$ – как и ранее, длина $i$-й панели и кривизна со знаком в ее центре, ${{\theta }_{{iw}}}$ – аргумент вектора $({{{\mathbf{\rho }}}_{w}} - {{{\mathbf{q}}}_{i}})$, величина которого может быть поправлена на $ \pm 2\pi $ для обеспечения выполнения условия

$ - \pi < \beta - {{\theta }_{{iw}}} \leqslant \pi \quad {\text{для}}\quad {{\chi }_{i}} - \frac{{{{L}_{i}}\left| {{{\varkappa }_{i}}} \right|}}{2} \leqslant \beta \leqslant {{\chi }_{i}} + \frac{{{{L}_{i}}\left| {{{\varkappa }_{i}}} \right|}}{2}$

${{\alpha }_{{iw}}}$ – безразмерный параметр, показывающий, насколько близко вихревой элемент расположен к дуге окружности:

${{\alpha }_{{iw}}} = \left| {{{\kappa }_{i}}} \right| \cdot \left| {{{{\mathbf{\rho }}}_{w}} - {{{\mathbf{q}}}_{i}}} \right| - 1 = \frac{{\left| {{{{\mathbf{\rho }}}_{w}} - {{{\mathbf{q}}}_{i}}} \right|}}{{{{R}_{i}}}} - {\text{1;}}\quad \eta (x) = \left\{ \begin{gathered} 1\quad при\quad x > 0 \hfill \\ 0\quad при\quad x < 0 \hfill \\ \end{gathered} \right.$

Рис. 4.

Положение вихревого элемента, криволинейной границы профиля и ее аппроксимация соприкасающейся окружностью.

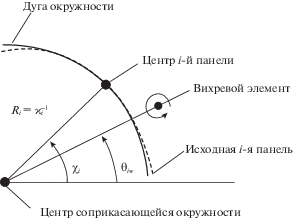
Описанный прием, однако, не позволяет вычислить коэффициент $({{z}_{w}})_{i}^{1}$, точнее, выполнить аналитическое интегрирование соответствующей функции вдоль дуги соприкасающейся окружности возможно, но результат не выражается в элементарных функциях, а дается с помощью специальной функции полилогарифма [18], что не позволяет производить практические расчеты. В этом случае можно принять еще одно упрощающее предположение и, считая ранее введенный параметр ${{\alpha }_{{iw}}}$ малым, разложить полилогарифмы по формуле Тейлора по степеням ${{\alpha }_{{iw}}}$ с учетом того, что производные могут быть выражены элементарными функциями. В результате получим приближенную формулу

$({{z}_{w}})_{i}^{1} \approx \Psi _{{iw}}^{1}\left( {{{\chi }_{i}} + \frac{{{{L}_{i}}{{\varkappa }_{i}}}}{2}} \right) - \Psi _{{iw}}^{1}\left( {{{\chi }_{i}} - \frac{{{{L}_{i}}{{\varkappa }_{i}}}}{2}} \right),$

где $\Psi _{{iw}}^{1}(\beta )$ – непрерывная ветвь первообразной; все обозначения соответствуют описанным выше:

$\begin{gathered} \Psi _{{iw}}^{1}(\beta ) = \frac{1}{{4\pi {{L}_{i}}\left| {{{\varkappa }_{i}}} \right|}}\left( {\frac{{{{{(\beta - {{\theta }_{{iw}}})}}^{2}}}}{2}} \right. + \\ + \;\left( {(\beta - {{\theta }_{{iw}}}) - 2\pi \eta ({{\alpha }_{{iw}}}) - 2\frac{{\beta - {{\theta }_{{iw}}}}}{{{{\alpha }_{{iw}}}}} - \frac{{\alpha _{{iw}}^{2}(\beta - {{\theta }_{{iw}}})}}{{\alpha _{{iw}}^{2} + {{{(\beta - {{\theta }_{{iw}}})}}^{2}}}}} \right)({{\theta }_{{iw}}} - {{\chi }_{i}}) + \\ \left. { + \;{{\alpha }_{{iw}}}(2 - {{\alpha }_{{iw}}}) - \left( {{{\alpha }_{{iw}}} - \frac{{\alpha _{{iw}}^{2}}}{2} + \frac{{\alpha _{{iw}}^{3}}}{3}} \right)\ln (\alpha _{{iw}}^{2} + {{{(\beta - {{\theta }_{{iw}}})}}^{2}}) - \frac{{\alpha _{{iw}}^{4}}}{{18}}\frac{{5{{\alpha }_{{iw}}} - 18}}{{\alpha _{{iw}}^{2} + {{{(\beta - {{\theta }_{{iw}}})}}^{2}}}}} \right) \\ \end{gathered} $

Заключение. Рассмотрено граничное интегральное уравнение относительно интенсивности свободного вихревого слоя, возникающее в вихревых методах моделирования двумерных течений. Для приближенного решения данного уравнения использован метод Галёркина с кусочно-постоянными и кусочно-линейными базисными функциями. Коэффициенты полученной линейной системы выражены интегралами, соответствующими влиянию вихревого слоя и слоя источников, расположенных на одних участках границы профиля, на другие участки, а также влиянию точечных вихрей, моделирующих вихревой след в области течения.

При аппроксимации границы профиля ломаной, состоящей из прямолинейных участков-панелей, данные интегралы вычислены точно; в случае учета криволинейности панелей разработана методика их приближенного вычисления и получены все необходимые расчетные формулы.

Работа выполнена при финансовой поддержке Российского научного фонда (проект 17-79-20445).

Список литературы

Жуковский Н.Е. О присоединенных вихрях // Тр. Отдел. физ. наук об-ва любителей естествознания. 1906. Т. 13. № 2. 14 с.
Rosenhead L., Jeffreys H. The formation of vortices from a surface of discontinuity // Proc. Roy. Soc. A. 1931. V. 134. № 823. P. 170–192.
Sarpkaya T. Computational methods with vortices – the 1988 Freeman scholar Lecture // J. Fluids Eng. 1989. V. 111. P. 5–52.
Leonard A. Vortex methods for flow simulation // J. Comput. Phys. 1980. V. 37. № 3. P. 289–335.
Cottet G.-H., Koumoutsakos P.D. Vortex Methods: Theory and Practice. Cambridge: Univ. Press, 2000. 328 p.
Lewis R.I. Vortex Element Methods for Fluid Dynamic Analysis of Engineering Systems. Cambridge: Univ. Press, 2005. 592 p.
Branlard E. Wind Turbine Aerodynamics and Vorticity-Based Methods: Fundamentals and Recent Applications. Cham: Springer, 2017. 632 p.
Головкин М.А., Головкин В.А., Калявкин В.М. Вопросы вихревой гидромеханики. Москва: Физматлит, 2009. 263 с.
Андронов П.Р., Гувернюк С.В., Дынникова Г.Я. Вихревые методы расчета нестационарных гидродинамических нагрузок. Москва: Изд-во МГУ, 2006. 184 с.
Вайникко Г.М., Лифанов И.К., Полтавский Л.Н. Численные методы в гиперсингулярных интегральных уравнениях. Москва: Янус-К., 2001. 508 с.
Yokota R. Vortex methods for the simulation of turbulent flows: review // J. Fluid Sci. Technol. 2011. V. 6. № 1. P. 14–29.
Kempka S.N., Glass M.W., Peery J.S., Strickland J.H., Ingber M.S. Accuracy considerations for implementing velocity boundary conditions in vorticity formulations // SANDIA report. SAND96-0583, UC-700. 1996.
Wu J.C., Thompson J.F. Numerical solutions of time-dependent incompressible Navier – Stokes equations using an integro-differential formulation // Comput. Fluids. 1973. V. 1. № 2. P. 197–215.
Лифанов И.К. Метод сингулярных интегральных уравнений и численный эксперимент (в математической физике, аэродинамике, теории упругости и дифракции волн). Москва: ТОО “Янус”, 1995. 520 с.
Кузьмина К.С., Марчевский И.К., Морева В.С. Определение интенсивности вихревого слоя при моделировании вихревыми методами обтекания профиля потоком несжимаемой среды // ММ. 2017. Т. 29. № 10. С. 20–34.
Кузьмина К.С., Марчевский И.К., Морева В.С., Рятина Е.П. Расчетная схема вихревых методов второго порядка точности для моделирования обтекания профилей несжимаемым потоком // Изв. вузов. Авиац. техника. 2017. № 3. С. 73–80.
Kuzmina K.S., Marchevsky I.K., Ryatina E.P. Exact solutions of boundary integral equation arising in vortex methods for incompressible flow simulation around elliptical and Zhukovsky airfoils // J. Phys. Conf. Ser., in press. 2019.
Lewin L. Polylogarithms and Associated Functions. New York: North Holland, 1981. 359 p.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал