Прикладная математика и механика, 2019, T. 83, № 3, стр. 370-376

Закрученные осесимметричные течения занимают промежуточное положение между двумерными и трехмерными течениями. С одной стороны, в них присутствует “трехмерное” взаимодействие радиально-осевого (меридионального) и окружного движений. С другой стороны, симметрия накладывает дополнительные связи на параметры движения, что упрощает исследование по сравнению с общим трехмерным случаем. Исследование закрученных осесимметричных течений представляет не только теоретический, но и практический интерес. Во-первых, поскольку некоторые реальные течения можно считать осесимметричными, например, течения в трубах и осесимметричных каналах, в смерчах и торнадо, в форсунках, в водоворотах при сливе жидкости из резервуаров, при обтекании тел вращения и т.д. Во-вторых, поскольку проверка закономерностей осесимметричных течений может быть полезна для верификации трехмерных численных схем на расчетах осесимметричных течений. Закономерности таких течений связаны с формами линий тока и вихревых линий. Интерес к закономерностям формы линий тока демонстрируют статьи [1–3] и монография [4], в которых получен ряд важных результатов. Данная статья посвящена изучению формы вихревых линий.

1. Основные обозначения и уравнения движения. Рассмотрим ламинарное осесимметричное течение однородной вязкой несжимаемой жидкости в потенциальном поле массовых сил. Далее будут использоваться следующие безразмерные переменные: ${\mathbf{V}}$ – скорость, ${\mathbf{\Omega }} = \operatorname{rot} {\mathbf{V}}$ – завихренность, $p$ – давление, отнесенное к плотности, $\Pi $ – потенциал объемных сил, $\operatorname{Re} $ – число Рейнольдса. Движение жидкости описывается уравнениями в форме Громеки–Лэмба

Введем цилиндрическую систему координат r, φ, z с началом в точке $O$ так, чтобы ось $Oz$ совпала с осью симметрии течения. Обозначим ${{{\mathbf{e}}}_{r}}$, ${{{\mathbf{e}}}_{\varphi }}$ и ${{{\mathbf{e}}}_{z}}$ правую тройку единичных векторов в радиальном, окружном и осевом направлениях. Вектор скорости имеет вид

Функции ${{V}_{r}}$, ${{V}_{\varphi }}$, ${{V}_{z}}$, $p$ и $\Pi $ будем считать зависящими только от переменных r, z и $t$. Достаточную для исследования гладкость скорости и давления будем полагать естественным свойством этих физических параметров жидкости.

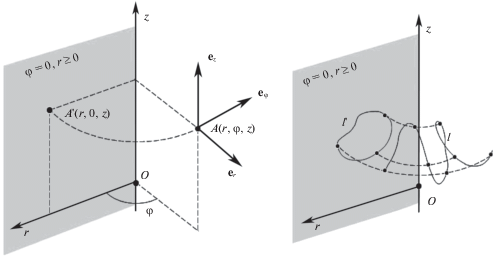
2. Линии с замкнутой $AC$-проекцией. Проекцией вдоль окружности, или $AC$-проекцией, точки $A$ с координатами $(r,\varphi ,{\kern 1pt} {\kern 1pt} {\kern 1pt} z)$ будем называть точку $A{\text{'}}$ с координатами $(r,0,{\kern 1pt} {\kern 1pt} {\kern 1pt} z)$, получаемую в результате проецирования вдоль окружности, образованной вращением точки $A$ вокруг оси симметрии, на главную меридиональную полуплоскость $\{ \varphi = 0$, $r \geqslant 0\} $ (левая часть рис. 1). Линией с замкнутой $AC$-проекцией будем называть линию, $AC$-проекция которой – гладкая граница ограниченной односвязной плоской области (контур), лежащая в полуплоскости $\{ \varphi = 0$, $r \geqslant 0\} $. При этом разные точки линии могут иметь одинаковые $AC$-проекции. В правой части рис. 1 показан контур $l{\kern 1pt} {\text{'}}$, являющийся замкнутой $AC$-проекцией незамкнутой линии $l$.

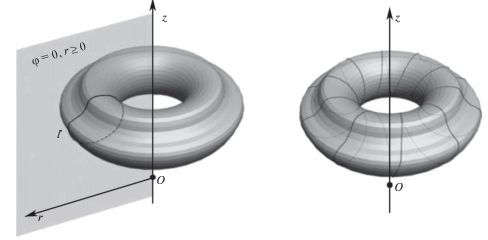
Рассмотрим подробнее, что представляет собой линия, $AC$-проекция которой – замкнутый контур. Такая линия лежит на гомеоморфной тору поверхности, образованной вращением упомянутого контура вокруг оси симметрии (левая часть рис. 2). Линия “наматывается” на поверхность и может либо, сделав конечное число оборотов, замкнуться на себя и иметь конечную длину (правая часть рис. 2), либо не замыкаться на себя ни при каком количестве оборотов, тогда она будет иметь бесконечную длину. В любом случае она будет винтовой.

Приведем пример нестационарного течения, в котором есть вихревые линии с замкнутой $AC$-проекцией. Рассмотрим осесимметричное векторное поле

где ${{J}_{0}}$ и ${{J}_{1}}$ – функции Бесселя нулевого и первого порядка соответственно.

Кроме поля скорости (2.1), для произвольного потенциала $\Pi = \Pi (r,z,t)$ зададим поле давления

Покажем, что формулы (2.1) и (2.2) дают точное решение уравнений Навье–Стокса (1.1). Проверка условия несжимаемости в случае $\frac{{\partial {\kern 1pt} }}{{\partial \varphi }} \equiv 0$ не вызывает затруднений, поскольку $(r{{J}_{1}}(r{\text{))'}}$ = $r{{J}_{0}}(r)$ (здесь и далее штрих означает дифференцирование по аргументу $r$). Проверим первое уравнение (1.1). Имеем

(учтено тождество $J_{0}^{'}(r) = - {{J}_{1}}(r)$). Следовательно, $\Omega = - \sqrt 2 V$, поэтому ${\mathbf{\Omega }} \times {\mathbf{V}} = 0$ и $\operatorname{rot} {\mathbf{\Omega }} = 2{\mathbf{V}}$. Таким образом, проверка первого уравнения (1.1) при учете равенства $\frac{{\partial {\mathbf{V}}{\kern 1pt} }}{{\partial t}}$ = = $ - \frac{2}{{\operatorname{Re} }}{\mathbf{V}}$ сводится к проверке уравнения которое выполнено в силу соотношения (2.2).

Итак, формулы (2.1) и (2.2) дают точное решение уравнений Навье–Стокса. Поскольку ${\mathbf{\Omega }} = - \sqrt 2 {\mathbf{V}}$, вихревые линии и линии тока этого решения совпадают. Поэтому $AC$-проекции вихревых линий представляют собой векторные линии меридиональной составляющей скорости

Запишем ее в виде

Пусть ${{r}_{1}}$ – первый корень уравнения ${{J}_{0}}(r)$ = 0. Для первой и второй производных функции $r{{J}_{1}}(r)$ в точке $r = {{r}_{1}}$ имеем соотношения

Поэтому в меридиональной полуплоскости в окрестности точки $(r = {{r}_{1}}$, $z = 0)$ функция ${\kern 1pt} r{{J}_{1}}(r){\kern 1pt} {\kern 1pt} {\kern 1pt} \cos z$ представляется формулой Тейлора

Следовательно, при некотором достаточно малом $\varepsilon > 0$ уравнение

задает замкнутый контур ${{C}_{\varepsilon }}$, охватывающий точку $(r = {{r}_{1}}$, $z = 0)$. Первые дифференциалы координат r и $z$ точек, расположенных на контуре ${{C}_{\varepsilon }}$, связаны соотношением которое получается из уравнения (2.4). Вместе с равенством (2.3) это соотношение означает, что $AC$-проекция одной из линий тока, а следовательно, и $AC$-проекция одной из вихревых линий совпадает с контуром ${{C}_{\varepsilon }}$.

Приведенный пример показывает, что вихревые линии нестационарного осесимметричного течения вязкой несжимаемой жидкости могут иметь замкнутую $AC$-проекцию.

Заметим, что решение (2.1), (2.2) следует считать обобщением на вязкий нестационарный случай решения, полученного Громекой для стационарного течения идеальной жидкости [5]. Решение Громеки получится из выражения (2.1), если отбросить нестационарный множитель $\exp ({{ - 2t} \mathord{\left/ {\vphantom {{ - 2t} {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }})$. Таким образом, как в нестационарных течениях вязкой жидкости, так и в стационарных течениях идеальной жидкости вихревые линии могут иметь замкнутую $AC$-проекцию.

Ниже будет показано, что в стационарном случае при наличии вязкости существование таких вихревых линий невозможно.

3. Принцип максимума окружной циркуляции. Перейдем к исследованию стационарных течений вязкой жидкости. Меридиональная составляющая завихренности ${{{\mathbf{\Omega }}}_{{rz}}}$ является ротором окружной скорости $({{{\mathbf{\Omega }}}_{{rz}}} = \operatorname{rot} {{{\mathbf{V}}}_{\varphi }})$. Окружная составляющая первого уравнения (1.1) имеет вид

Умножив это равенство скалярно на вектор $2\pi r{{{\mathbf{e}}}_{\varphi }}$, получим уравнение

Преобразуем его левую часть, используя свойство цикличности смешанного произведения векторов и выражение для ${{{\mathbf{\Omega }}}_{{rz}}}$ в цилиндрической системе координат:

Правая часть уравнения (3.1) равна

и уравнение (3.1) может быть записано в виде

Величина $\gamma = 2\pi r{{V}_{\varphi }}$ была названа [6] окружной циркуляцией. Параметр $\gamma $ тесно связан с формой вихревых линий. Это следует из легко проверяемого в цилиндрической системе координат векторного равенства

Для осесимметричных течений равенство (3.3) верно для вязкой и для невязкой жидкости. Для сжимаемой и для несжимаемой жидкости. Оно верно для стационарного и нестационарного осесимметричного течения. Из равенства (3.3) следует, что градиент $\gamma $ ортогонален векторным линиям ${{{\mathbf{\Omega }}}_{{rz}}}$, т.е. γ сохраняет свое значение на этих линиях. Но векторные линии ${{{\mathbf{\Omega }}}_{{rz}}}$ на полуплоскости $\{ \varphi = 0$, $r \geqslant 0\} $ являются $AC$-проекциями вихревых линий. Поэтому окружная циркуляция в осесимметричных течениях любого типа сохраняется на $AC$-проекциях вихревых линий. Этот факт будет использован в следующем разделе.

Последнее утверждение можно проиллюстрировать на примере точного решения (2.1), (2.2). В этом решении окружная циркуляция γ = $ - 2\pi r\sqrt 2 {{J}_{1}}(r)\cos z$. На замкнутом контуре ${{C}_{\varepsilon }}$, представляющим собой $AC$-проекцию вихревой линии, выполняется уравнение (2.5), которое означает постоянство $\gamma $ на контуре ${{C}_{\varepsilon }}$.

Уравнение (3.2) имеет эллиптический тип. Обычное средство исследования экстремальных свойств уравнений эллиптического типа – теорема Е. Хопфа [7, 8]. Эта теорема предлагает разные варианты принципа максимума для решений квазилинейных уравнений эллиптического типа в зависимости от свойств коэффициентов этих уравнений. Но в условиях теоремы есть требование ограниченности коэффициентов, а в уравнении (3.2) один из коэффициентов имеет особенность на оси симметрии (r = 0), и теорема Хопфа неприменима. Этот пробел был недавно устранен [9] и доказан принцип максимума окружной циркуляции, в котором рассматриваемая область может иметь граничные точки на оси $Oz$.

Пусть осесимметричное ламинарное течение несжимаемой жидкости с ненулевой вязкостью установилось в отсутствие внешних массовых сил и пусть $\bar {G}$ – произвольная ограниченная замкнутая область течения, лежащая в меридиональной полуплоскости $\{ r \geqslant 0$, $\varphi = 0\} $; тогда или окружная циркуляция постоянна, или ее минимум и максимум достигаются на границе и только на границе области $\bar {G}$.

4. Вихревые линии с замкнутой $AC$-проекцией в стационарном течении вязкой несжимаемой жидкости. Сформулированный выше принцип максимума позволяет доказать следующее утверждение.

В установившемся осесимметричном течении однородной вязкой несжимаемой жидкости не существует вихревых линий с замкнутой $AC$-проекцией, являющейся границей односвязной замкнутой области $\bar {G}$, целиком лежащей внутри течения.

Доказательство. Допустим, что $AC$-проекция вихревой линии представляет собой границу $\bar {G}$. Тогда, согласно равенству (3.3), на всей границе $\bar {G}$ окружная циркуляция $\gamma $ имеет одно и то же значение (см. текст после формулы (3.3)). Поэтому из принципа максимума окружной циркуляции (верного только, если коэффициент вязкости не равен нулю) следует, что величина $\gamma $ – постоянна во всей области $\bar {G}$, и внутри $\bar {G}$ выражение (3.3) дает ${{{\mathbf{\Omega }}}_{{rz}}} = 0$. Следовательно, в силу гладкости, равенство ${{{\mathbf{\Omega }}}_{{rz}}} = 0$ выполняется и на границе $\bar {G}$. Но тогда через точки границы $\bar {G}$ проходят векторные линии поля ${\mathbf{\Omega }}$ в виде окружностей, представляющих собой фигуры вращения вокруг оси симметрии. И эта граница не является $AC$-проекцией какой-либо одной вихревой линии. Утверждение доказано.

Если коэффициент вязкости равен нулю, то принцип максимума и данное доказательство не применимы. Поэтому в идеальной жидкости винтовые линии возможны, что и подтверждается решением Громеки (2.1), (2.2).

Полученный результат означает, что если вся внутренность “тора” заполнена жидкостью, то в стационарном случае в осесимметричных течениях вязкой несжимаемой жидкости невозможно существование винтовых вихревых линий, “намотанных” на такой тор.

Заключение. Показано, что в стационарном осесимметричном течении однородной вязкой несжимаемой жидкости не могут существовать винтовые вихревые линии, лежащие на такой гомеоморфной тору поверхности вращения вокруг оси симметрии, которая охватывает область, целиком лежащую внутри течения. Этот эффект существенным образом связан со стационарностью, что подтверждается приведенным примером нестационарного течения, в котором упомянутые вихревые линии существуют.