Прикладная математика и механика, 2019, T. 83, № 3, стр. 452-467
Численный анализ течений стратифицированной и однородной жидкостей около горизонтальной и наклонной пластин
Я. В. Загуменный 1, *, Ю. Д. Чашечкин 2, **
1 Институт гидромеханики НАН Украины
Киев, Украина
2 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: zagumennyi@gmail.com
** E-mail: yulidch@gmail.com
Поступила в редакцию 06.03.2019
После доработки 12.03.2019
Принята к публикации 19.03.2019
Аннотация
Изучается структура и динамика течений около горизонтальной и наклонной пластин в стратифицированной и однородной жидкостях в переходном вихревом режиме при различных углах наклона пластины к горизонту и геометрических модификациях ее передней и задней кромок. Исследование основано на высокоточном численном моделировании фундаментальной системы уравнений, которая позволяет проводить расчеты как стратифицированных, так и однородных вязких жидкостей в единой постановке. Мгновенные картины полей завихренности, градиента давления и плотности, а также значения сил и моментов, действующих на поверхность пластины, анализируются при различных углах наклона, значениях радиуса закругления передней кромки пластины и коэффициента остроты хвостовой части. Структура поля давления состоит из разномасштабных пятнистых структур с отрицательным значением давления, соответствующим положениям вихревых элементов течения, пространственные и временные масштабы, геометрические особенности, уровень проявления и скорость диссипации которых существенно зависят от угла наклона пластины к горизонту, геометрической модификации ее краев и типа жидкости. Особое внимание уделяется изучению тонкой структуры течения около передней кромки пластины, являющейся наиболее разномасштабной областью течения, в которой образуются и активно взаимодействуют как крупно-, так и мелкомасштабные вихревые структуры.
Введение. Начиная с пионерских работ Даламбера [1] и Эйлера [2], расчеты картин обтекания препятствий с оценкой сил, действующих на их поверхность, занимают ведущее место в теоретической и экспериментальной механике жидкости вследствие фундаментальности таких задач и широкого спектра практических приложений. Среди них – оптимизация конструкций по ряду критериев, расширение диапазона устойчивого полета летательных аппаратов, подводных лодок и надводных транспортных средств, разработка надежных систем управления, обеспечивающих устойчивость в широком диапазоне условий полета и окружающей среды, и мн. др.
Особое внимание уделяется расчету обтекания препятствий довольно простой формы, к примеру, пластины, цилиндра, сферы и т.д., часто изучаемых с целью проверки численных алгоритмов, совершенствования методов управления потоком [3], анализа механизмов структурирования потока и турбулентности [4] и т.п. Ввиду математической сложности задачи в начале прошлого века был разработан ряд приближенных моделей обтекания препятствий, в том числе решение Блазиуса для горизонтальной полуплоскости в пограничном слое в приближении однородной жидкости [5]. Такие подходы, как правило, не учитывают краевые эффекты, что делает такие идеализированные модели применимыми только для грубых оценок структуры течения на части поверхности довольно простой формы. Решение Блазиуса, полученное в предположении постоянного давления по нормали к поверхности без учета краевых эффектов, использовалось более ста лет для сравнения с данными лабораторных экспериментов и численного моделирования. Однако структура и динамика течения около пластины существенно зависят от ее толщины, угла наклона к горизонту, качества поверхности, что определяет поля скорости, давления и их градиентов.
Был проведен ряд экспериментальных и численных исследований течений около обтекаемых горизонтальной и наклонной пластин с целью понимания фундаментальных закономерностей формирования и развития структуры и динамики течений. Одна из самых ранних работ по исследованию вихреобразования за пластиной с острыми краями была выполнена в [6], где проанализировано поле течения около плоской пластины для 18 различных углов атаки. Численное моделирование течений за наклонной плоской пластиной с острыми кромками выполнено в работах [7–10] с использованием различных методик, включая DNS, DES, RANS и LES, в которых исследовано влияние генерированных кромками вихрей на структуру спутного течения, а также особенности формирования и развития последовательных стадий перехода от стационарного режима к хаотическому при обтекании наклонной пластины. Экспериментальные исследования по визуализации структуры течения в следе за наклонной плоской пластиной при α = 15° с использованием усредненной по фазе лазерной доплеровской анемометрии выполнены в [11], которые показали преобладание в спутном течении последовательности срывающихся с задней кромки пластины и вращающихся против часовой стрелки вихревых структур, формирование, развитие и последующий перенос которых изучаются в соответствии с последовательными этапами цикла вихреобразования.
На практике структура и динамика течений существенно зависит от геометрических неоднородностей поверхности препятствия, в частности, от толщины, качества передней и задней кромок и угла наклона пластины, что определяет поля скорости и давления, а также их градиентов. Хотя число публикаций по изучению течений в следе за пластиной, ориентированной в направлении натекающего потока, очень велико, некоторые более ранние и недавние задачи остаются все еще не решенными. Одной из наиболее актуальных задач является выбор формы и толщины передней кромки прямого крыла, которое было тонким в авиационных экспериментах О. Лилиенталя [12] и толстым в более поздней конструкции самолета братьев Райт [13], имевшем форму, подобную крыловым профилям в современной авиации. В последние годы было опубликовано много исследований о влиянии геометрической формы передних и задних кромок пластин и крыльев на структуру и динамику течения [14–16]. Большое внимание уделяется изучению вихрей, порождаемых передней кромкой при взмахах крыла, которые предположительно играют существенную роль в механизме полета насекомых [17].
В естественных условиях структура и динамика течений также зависят от реальных свойств жидкости, поскольку плотность жидкости в окружающей среде и промышленных устройствах не является постоянной вследствие неоднородности распределений концентрации растворенных веществ, взвешенных частиц, либо температуры или давления [18], что под действием силы плавучести приводит к формированию устойчивой стратификации с величиной периода плавучести, варьирующейся в диапазоне от нескольких секунд в лабораторных условиях и до десяти минут в атмосфере и гидросфере Земли [19].
В настоящей работе с использованием численного моделирования анализируется разномасштабная структура течения около наклонной пластины в переходном вихревом режиме течения на основе фундаментальной системы уравнений механики жидкости, которая позволяет изучать течения как непрерывно стратифицированных, так и однородных вязких несжимаемых жидкостей в единой постановке. Данное исследование является логическим продолжением предыдущих работ, в которых изучалась структура и динамика стратифицированных течений около неподвижной [20] и равномерно движущейся горизонтальных пластин в линейной [21] и полной нелинейной постановках [22, 23].
1. Система определяющих уравнений. Математическое моделирование задачи обтекания наклонной пластины основано на фундаментальной системе уравнений для многокомпонентной неоднородной несжимаемой жидкости в приближении Буссинеска. Учитываются эффекты плавучести и диффузии стратифицирующей компоненты, а эффектами теплопроводности и выделения энергии за счет диссипации пренебрегается [24]. Таким образом, определяющие уравнения принимают вид:
(1.1)
$\begin{gathered} \rho = {{\rho }_{0}}\left( {\exp \left( { - \frac{z}{\Lambda }} \right) + s} \right) \\ \frac{{\partial {\mathbf{v}}}}{{\partial t}} + ({\mathbf{v}} \cdot \nabla ){\mathbf{v}} = - \frac{1}{{{{\rho }_{0}}}}\nabla P + \nu \Delta {\mathbf{v}} - s{\mathbf{g}},\quad \nabla \cdot {\mathbf{v}} = 0 \\ \frac{{\partial s}}{{\partial t}} + {\mathbf{v}} \cdot \nabla s = {{\kappa }_{s}}\Delta s + \frac{{{{v}_{z}}}}{\Lambda } \\ \end{gathered} $Здесь, $s$ – возмущение солености, включая коэффициент солевого сжатия, v = = $({{v}_{x}},{{v}_{y}},{{v}_{z}})$ – вектор индуцированной скорости течения, $P$ – давление за вычетом гидростатического, $\nu = 0.01$ см2/с и ${{\kappa }_{s}}$ = $1.41 \times {{10}^{{ - 5}}}$ см2/с – коэффициенты кинематической вязкости и солевой диффузии, $\nabla $ и $\Delta $ – операторы Гамильтона и Лапласа.
Доказанная разрешимость двумерных уравнений механики жидкостей позволяет одновременно провести расчеты и для стратифицированных (сильно, когда $\Lambda = 9.8$ м, $N = 1$ c–1, ${{T}_{b}} = 6.28$ c и слабо – $\Lambda = 24$ км, $N = 0.02$ c–1, ${{T}_{b}} = 5.2$ мин), и для потенциально однородных жидкостей, в которых вариации плотности настолько малы ($\Lambda = {{10}^{8}}$ км, $N = {{10}^{{ - 5}}}$ c–1 и ${{T}_{b}} = 7.3$ дня), что не регистрируются существующими техническими средствами, но сохраняется исходная математическая постановка, а также и для актуально однородных сред ($\Lambda = \infty $, $N = 0{\kern 1pt} $ и ${{T}_{b}} = \infty $). В последнем случае фундаментальная система уравнений вырождается по части сингулярных компонентов [25].
Физически обоснованными начальными и граничными условиями являются условия прилипания и непротекания на поверхности обтекаемого препятствия для компонент скорости и полной солености, а также условия невозмущенного внешнего потока на достаточно большом удалении от обтекаемого тела:
(1.2)
$\begin{gathered} {{\left. {\mathbf{v}} \right|}_{{t \leqslant 0}}} = {{{\mathbf{v}}}_{1}}(x,z),\quad {{\left. s \right|}_{{t \leqslant 0}}} = {{s}_{1}}(x,z),\quad {{\left. P \right|}_{{t \leqslant 0}}} = {{P}_{1}}(x,z),\quad {{\left. {{{v}_{x}}} \right|}_{\Sigma }} = {{\left. {{{v}_{z}}} \right|}_{\Sigma }} = 0 \\ {{\left. {\left[ {\frac{{\partial s}}{{\partial {\mathbf{n}}}}} \right]{\kern 1pt} } \right|}_{\Sigma }} = \frac{1}{\Lambda }\frac{{\partial z}}{{\partial {\mathbf{n}}}},\quad {{\left. {{{v}_{x}}} \right|}_{{x,z \to \infty }}} = U,\quad {{\left. {{{v}_{z}}} \right|}_{{x,z \to \infty }}} = 0, \\ \end{gathered} $Система уравнений и граничные условия (1.1), (1.2) характеризуется набором параметров, имеющих размерность длины $(\Lambda ,L,h)$ и времени $({{T}_{b}}$, $T_{U}^{L} = L{\text{/}}U)$, а также содержит диссипативные коэффициенты.
Большие динамические масштабы – длина внутренней волны $\lambda = U{{T}_{b}}$ и вязкий волновой размер ${{\Lambda }_{\nu }}$ = $\sqrt[3]{{g\nu }}{\text{/}}N$ = $\sqrt[3]{{\Lambda {{{(\delta _{N}^{\nu })}}^{2}}}}$ отражают структуру поля присоединенных волн. Тонкую структуру течения характеризуют универсальные микромасштабы $\delta _{N}^{\nu }$ = = $\sqrt {{\nu \mathord{\left/ {\vphantom {\nu N}} \right. \kern-0em} N}} $, $\delta _{N}^{{{{\kappa }_{s}}}}$ = $\sqrt {{{{{\kappa }_{s}}} \mathord{\left/ {\vphantom {{{{\kappa }_{s}}} N}} \right. \kern-0em} N}} $, задаваемые диссипативными коэффициентами и частотой плавучести (аналоги масштаба Стокса на осциллирующей поверхности $\delta _{\omega }^{\nu } = \sqrt {{\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega }} $). Еще одна пара – масштабы Прандтля и Пекле – определяются диссипативными коэффициентами и скоростью тела: $\delta _{U}^{\nu } = {\nu \mathord{\left/ {\vphantom {\nu U}} \right. \kern-0em} U}$ и $\delta _{U}^{{{{\kappa }_{s}}}} = {{{{\kappa }_{s}}} \mathord{\left/ {\vphantom {{{{\kappa }_{s}}} U}} \right. \kern-0em} U}$ [21, 25].
Отношения собственных масштабов задачи задают как характерные безразмерные комбинации: числа Рейнольдса ${{\operatorname{Re} }_{U}}$ = ${{UL} \mathord{\left/ {\vphantom {{UL} \nu }} \right. \kern-0em} \nu }$ = ${L \mathord{\left/ {\vphantom {L {\delta _{U}^{\nu }}}} \right. \kern-0em} {\delta _{U}^{\nu }}} \gg 1$, внутреннего Фруда ${\text{Fr}}\;{\text{ = }}{U \mathord{\left/ {\vphantom {U {NL}}} \right. \kern-0em} {NL}}$, Пекле ${{\operatorname{Pe} }_{U}}$ = $L{\text{/}}\delta _{U}^{{{{\kappa }_{s}}}} \gg {{\operatorname{Re} }_{U}}$, коэффициент остроты ${{\xi }_{p}} = {L \mathord{\left/ {\vphantom {L h}} \right. \kern-0em} h}$, так и специфические для стратифицированных течений. В число дополнительных безразмерных отношений входит шкала масштабов ${\text{C = }}{\Lambda \mathord{\left/ {\vphantom {\Lambda L}} \right. \kern-0em} L}$ – отношением масштаба плавучести $\Lambda $ к размеру препятствия $L$, аналог обратного числа Атвуда ${\text{A}}{{{\text{t}}}^{{ - 1}}}$ = $({{\rho }_{1}} + {{\rho }_{2}}){\text{/}}({{\rho }_{1}} - {{\rho }_{2}})$ для непрерывно стратифицированных сред.
Такое разнообразие масштабов длины со значительными различиями в величинах указывает на сложность внутренней структуры даже такого медленного течения, индуцированного малыми силами плавучести, которые возникают как следствие пространственной неоднородности молекулярного потока стратифицирующего компонента. Большие масштабы задают минимальные размеры областей наблюдения и расчета, которые должны содержать изучаемые структурные элементы – опережающие возмущения, след, волны, вихри, а микромасштабы определяют размер ячейки и шага по времени. При малых скоростях пластины $U$ критическими являются микромасштабы шкалы Стокса, при больших – Прандтля.
2. Численное моделирование. Система уравнений (1.1) с граничными условиями (1.2) решается численно с использованием решателей и библиотек динамических сеток собственной разработки в рамках вычислительного пакета OpenFOAM с открытым исходным кодом на основе метода конечных объемов [26]. Для дискретизации конвективных членов и производной по времени используются, соответственно, TVD-схема с ограничением и неявная трехточечная схема второго порядка точности с разностями назад, которые обеспечивают минимальную численную диффузию, отсутствие нефизических осцилляций решения и хорошее разрешение физического процесса во времени. В ортогональных областях сетки дискретизация диффузионных членов производится на основе теоремы Гаусса, а нормальный градиент к поверхности рассчитывается по грани расчетной ячейки с использованием интерполяции второго порядка вектора, соединяющего центры двух соседних ячеек. В неортогональных областях расчетной сетки используется итеративная процедура с указываемым пользователем числом циклов для коррекции ошибок, вызванных скосом сетки.
В рамках данного численного моделирования реализовано два различных подхода. Первый состоит в задании граничных условий для свободного потока и нулевого градиента на входной и выходной границах вычислительной области, соответственно, в то время как положения ячеек расчетной сетки и препятствия остаются неизменными. Второй подход, в котором пластина совершает равномерное движение в неподвижной жидкости, реализуется с использованием методов динамических расчетных сеток в рамках пакета OpenFOAM, что позволяет точно воспроизвести условия лабораторного эксперимента, аналогичные тем, которые реализованы в Лаборатории механики жидкости Института Проблем механики РАН [27]. Такой подход также позволяет избежать появления нефизичных возмущений, возникающих на внешних границах расчетной области, и адекватно моделировать структуру и динамику течения на начальном этапе трогания пластины. Оба подхода показывают немного разные результаты на начальной стадии формирования течения, но, при этом, хорошо согласуются на больших временах, когда некоторые повторяющиеся закономерности можно выделить на фоне общей нестационарности течения.
Алгоритм построения ортогональной расчетной сетки около пластины, ориентированной под произвольным углом к горизонту, состоит в создании отдельных блоков сетки, включая внутренний цилиндр, который поворачивается вместе с пластиной при изменении ее углового положения, сеточный блок, присоединенный к цилиндру и дополняющий его до параллелепипеда, и еще два блока, с обеих его сторон соединенные с параллелепипедом. При движении наклонной пластины центральный цилиндр и примыкающие к нему сеточные блоки перемещаются вместе с пластиной, в то время как боковые сеточные блоки сжимаются и растягиваются, соответственно, так что вертикальные границы на входе и выходе остаются неизменными.
Пространственные размеры расчетных ячеек выбирались из условия адекватного разрешения наиболее мелкомасштабных компонентов течения, связанных с эффектами стратификации и диффузии, которые накладывают существенные ограничения на минимальный пространственный шаг: в высокоградиентных областях течения должны умещаться по крайней мере несколько расчетных ячеек на минимальном линейном масштабе задачи. Вычислительный шаг по времени определяется из условия Куранта: $\operatorname{Co} = \left| {\mathbf{v}} \right|\Delta t{\text{/}}\Delta r$ ≤ 1, где $\Delta r$ – минимальный размер расчетной ячейки и ${\mathbf{v}}$ – локальная скорость течения.
3. Результаты расчетов. Расчеты выполнены для четырех типов жидкостей, включая сильно ($N = 1.2$ с–1) и слабо стратифицированные ($N = 0.1$ с–1), а также потенциально ($N = {{10}^{{ - 5}}}$ с–1) и актуально ($N = 0$) однородные. Изменения плотности в потенциально однородной жидкости бесконечно малы, но исходная математическая формулировка в этом случае сохраняется, тогда как в актуально однородной жидкости плотность считается постоянной, а фундаментальная система уравнений вырождается по сингулярным компонентам [24, 25].
Структура стратифицированного течения около наклонной пластины существенно трансформируется с увеличением скорости движения пластины, начиная от многоуровневых циркуляционных течений, индуцированных диффузией, возникающих при нарушении молекулярного потока на непроницаемом неподвижном препятствии [19, 20], до сложных нестационарных вихревых и тонкоструктурных режимов при сравнительно больших числах Рейнольдса, когда все компоненты течения вовлечены в сложное нелинейное взаимодействие [22]. Можно выделить ряд характерных режимов течения в зависимости от преобладания тех или иных структурных компонентов течения, таких как вихри, которые являются общими для всех типов жидкостей, и внутренние волны, опережающие возмущения и тонкие прослойки, характерные для стратифицированных сред [23].
Наиболее практически ценными являются исследования нестационарного вихревого режима обтекания препятствий при сравнительно больших значениях числа Рейнольдса. На рис. 1 приведены мгновенные картины поля возмущения давления при различных углах наклона пластины к горизонту для двух типов жидкостей: сильно стратифицированной и потенциально однородной. Приведенные картины демонстрируют ряд общих черт, включая увеличение давления перед препятствием и падение давления в пятнистых структурах вокруг пластины, которые локализованы в центрах вихревых элементов, генерируемых передней кромкой пластины. Максимальные и минимальные значения давления и их расположение в пространстве существенно зависят от углового положения пластины относительно горизонта и типа жидкости.
Рис. 1.
Мгновенные картины поля возмущения давления около наклонной пластины для разных углов наклона к горизонту: α = 1°, 5°, 10°, 20° (а–г), левый столбец – сильно стратифицированная жидкость, правый – потенциально однородная.
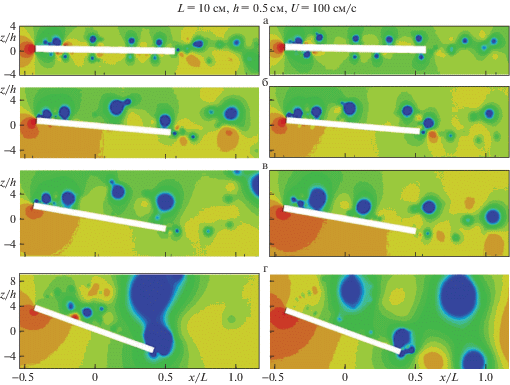
Все компоненты течения находятся в активном взаимодействии друг с другом, с тонкой структурой, и даже с присоединенными внутренними волнами, которые в этом случае существенно превышают область наблюдения. Уже даже при малых углах наклона пластины вихревая динамика заметно отличается в областях течения над и под пластиной, так что интенсивность и масштабы вихрей, генерируемых верхним краем передней кромки и дрейфующих вниз по течению вдоль ее поверхности, оказываются заметно больше в области течения над пластиной (рис. 1 (a)). При этом вихри под пластиной более четко проявлены в случае потенциально однородной жидкости, что объясняется подавляющим влиянием эффектов стратификации.
С увеличением угла наклона пластины вихревая динамика течения на ее нижней наветренной стороне подавляется влиянием набегающего потока, в то время как масштабы вихревых структур, формирующихся над верхней стороной пластины и в следе за ней, растут (рис. 1 (б–г)). Различия в интенсивности, положениях, масштабах и скоростях затухания генерируемых вихревых структур для различных типов рассматриваемых жидкостей возрастают с увеличением угла наклона пластины.
Обтекание наклонной пластины представляет собой сложный многомасштабный нестационарный физический процесс, сопровождающийся взаимодействием крупно- и мелкомасштабных компонентов между собой и с набегающим потоком. Все компоненты течения характеризуются собственной геометрией, пространственными и временными масштабами, уровнем проявления и скоростью диссипации, которые необходимо тщательно изучать как теоретически, так и экспериментально, с учетом эффектов диффузии, теплопроводности и сжимаемости, а также с контролем критерия наблюдаемости и разрешения всех разномасштабных компонент течения.
Особый научный интерес заключается в изучении тонкой структуры течения около передней кромки наклонной пластины, которая является наиболее разномасштабной областью обтекания, где образуются одновременно как крупные, так и мелкие вихревые элементы, активно взаимодействующие друг с другом. Тонкая структура течения около передней кромки наклонной пластины проиллюстрирована мгновенными картинами горизонтальной компоненты градиента плотности ${{\partial \rho } \mathord{\left/ {\vphantom {{\partial \rho } {\partial x}}} \right. \kern-0em} {\partial x}}$ и темпа бароклинной генерации завихренности $\dot {\Omega } = \nabla P \times \nabla ({{\rho }^{{ - 1}}})$, поля которых представлены на рис. 2. Увеличенный масштаб изображений в определенной области течения позволяет идентифицировать сложную мелкомасштабную структуру полей и оценивать геометрические особенности структурных элементов. Каждая физическая переменная, входящая в исходную систему уравнений, раскрывает некоторые новые важные особенности течения, способствуя лучшему пониманию общих закономерностей рассматриваемого физического процесса.
Рис. 2.
Мгновенные картины горизонтальной компоненты поля градиента плотности (а–г) и темпа бароклинной генерации завихренности (д–з) около передней кромки наклонной пластины для разных углов ее наклона к горизонту в сильно стратифицированной жидкости (сверху–вниз: α = 1°, 5°, 10°, 20°).
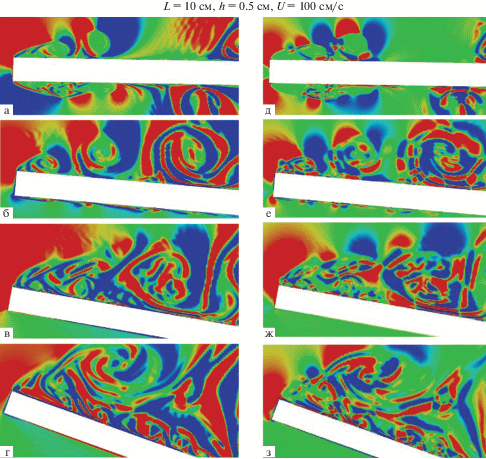
Картины поля горизонтальной компоненты градиента плотности, которая находится в линейной зависимости от коэффициента преломления света, визуализируемого в лабораторных экспериментах с помощью теневых инструментов [27], имеют сложную тонкую структуру вследствие малости отношения коэффициентов диффузии и вязкости (левая часть рис. 2). Тонкоструктурные слоистые элементы обоих знаков локализуются преимущественно на вихревых оболочках и в областях течения с интенсивными вихревыми взаимодействиями. Чем больше значение угла наклона пластины к горизонту, тем более сложна структура поля и тем больше длина наблюдаемых слоистых элементов. При $\alpha \geqslant 10^\circ $ возмущения течения на наветренной стороне пластины подавляются набегающим потоком, в то время как структура поля над подветренной стороной значительно усложняется вследствие развития процессов множественных вихревых взаимодействий, сопровождающихся слиянием, расщеплением и сложными преобразованиями разномасштабных вихревых элементов течения.
Поле темпа бароклинной генерации завихренности, картины которого представлены на рис. 2 справа, определяется согласно теореме Бьеркнеса неколлинеарностью градиентов давления и плотности. Это поле – наиболее сложное и структурированное в течениях неоднородных жидкостей. В окрестности передней кромки обтекаемой пластины и перед телом располагаются области генерации и диссипации завихренности с масштабами намного меньшими толщины пластины. С увеличением угла наклона структурные элементы становятся более тонкими и существенно усложняются – появляется ряд множественных тонкоструктурных областей усиления и затухания завихренности, постепенно удлиняющихся по мере продвижения вниз по течению. Геометрия поля темпа бароклинной генерации завихренности объясняет динамику формирования тонкой структуры вихревого потока, а также механизм расщепления полей на серию слоистых структур, отчетливо наблюдаемых на теневых изображениях стратифицированных течений в лабораторных экспериментах [21, 27].
Большой практический интерес представляет анализ структуры и динамики стратифицированного потока при нестационарном вихревом режиме, когда временные и пространственные масштабы, уровень проявления и скорость диссипации образовавшихся вихревых структур существенно зависят от геометрической формы краев пластины. Представленные ниже результаты расчетов иллюстрируют мгновенные картины полей завихренности, давления и градиента плотности, которые позволяют всесторонне проанализировать структуру и динамику течения для различных значений радиуса закругления передней и степени остроты задней кромок пластины.
Передняя и задняя кромки горизонтальной пластины представляют собой особые области течения, в которых происходит генерация вектора завихренности ${\mathbf{\Omega }} = \operatorname{rot} {\mathbf{v}}$, вследствие как общей реорганизации поля скорости, так и влияния бароклинных эффектов. Вихревые структуры формируются на передней кромке прямоугольной пластины с острыми краями с частотой около 4 Гц, затем отрываются от ее поверхности на некотором расстоянии вниз по течению и снова присоединяются к поверхности в области центра пластины (верхняя часть рис. 3 (а)). Затем вихри, генерированные передней кромкой, дрейфуют вниз по течению вдоль поверхности и взаимодействуют с вихревой дорожкой, формирующейся в следе за задней кромкой пластины с частотой осцилляций около 5 Гц. В результате множественных сложных взаимодействий двух вихревых систем в спутном течении образуется новая система с частотой следа примерно в два раза меньшей, чем у исходной вихревой дорожки. Видно, что вихри передней кромки и вихревая дорожка в следе за прямоугольной пластиной с острыми краями четко очерчены и имеют средний пространственный масштаб, сопоставимый с толщиной пластины.
Рис. 3.
Мгновенные картины поля завихренности (а–д) и давления (е–к) около горизонтальной пластины с разными геометрическими модификациями ее передней и задней кромок: $({{\tilde {r}}_{l}},\xi )$ = (0, 1), (0.4, 1), (1, 1), (1, 2), (1, 10) (а–д) и (е–к).
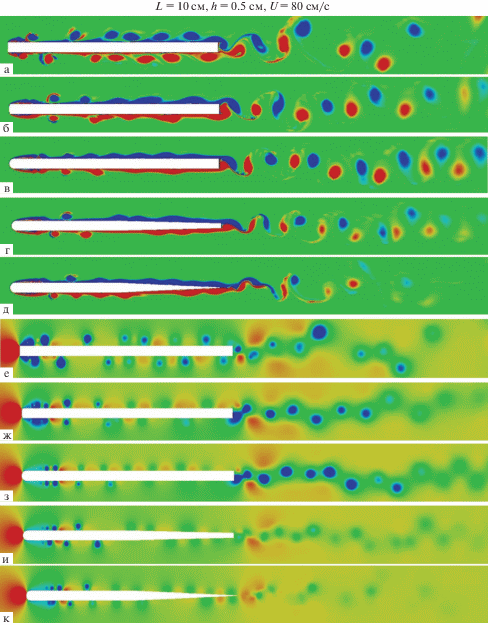
С увеличением радиуса закругления кромки вихревые структуры уменьшаются в масштабе и интенсивности, при этом принимают более размытые и вытянутые формы по мере перемещения вниз по течению (верхняя часть рис. 3 (б)). При максимальном радиусе закругления передней кромки масштабы вихрей уменьшаются практически в два раза по сравнению со случаем пластины с острыми кромками и по мере дальнейшего перемещения вниз по течению принимают форму затухающих волновых возмущений. В этом случае вихри передней кромки довольно быстро диссипируют, еще до момента достижения задней кромки пластины, и поэтому не оказывают существенного влияния на спутный след, который в данном случае сохраняет структуру первичной вихревой дорожки.
Картины поля давления для всех рассмотренных конфигураций кромок пластины (нижняя часть рис. 3) демонстрируют ряд общих черт, включая рост давления перед препятствием и падение давления в пятнистых структурах вокруг пластины, которые локализованы в центрах вихревых элементов, генерированных кромками пластины. Представленные картины показывают, что интенсивность, пространственные масштабы, уровень проявления и скорость диссипации характерных структурных элементов поля давления существенно зависят от рассматриваемой геометрической конфигурации кромок пластины.
С увеличением радиуса закругления передней кромки область высокого давления перед препятствием и пятнистые структуры низкого давления над и под пластиной значительно уменьшаются по интенсивности и масштабу благодаря сглаживающему и стабилизирующему эффекту скругленной кромки на вихревую динамику. В случае максимально закругленной передней кромки пластины (нижняя часть рис. 3 (в)) динамика спутного течения оказывается наиболее интенсивной вследствие минимального влияния дрейфующих вниз по течению вихрей передней кромки на течение в следе, в результате чего сохраняется первичная структура вихревой дорожки. В случае пластины с закругленной передней кромкой и заостренной задней (нижняя часть рис. 3 (д)), форма которой наиболее близка к характерному крыловому профилю, все возмущения поля давления практически исчезают на расстоянии от задней кромки равном около половины длины пластины, и вихревая динамика течения становится наименее интенсивной и масштабной по сравнению с другими рассмотренными геометрическими конфигурациями пластины.
Каждая отдельная физическая переменная, входящая в исходную систему уравнений, раскрывает свой собственный аспект рассматриваемого физического явления, что, в целом, способствует более полному пониманию физических механизмов, лежащих в основе формирования и развития стратифицированных течений около препятствий. Наиболее общий и полный анализ физического процесса должен быть основан на фундаментальной системе уравнений, которая наиболее всесторонне раскрывает особенности физического процесса, благодаря расширенному набору физических переменных, входящих в систему [25].
Из картин поля горизонтальной компоненты градиента плотности, представленных на рис. 4 для разных геометрических конфигураций передней и задней кромок пластины, можно получить дополнительную информацию о тонкоструктурных элементах течения, которые практически неразличимы в полях других физических переменных. Методы теневой визуализации обнаруживают большое разнообразие тонкоструктурных компонентов около движущихся тел в стратифицированной жидкости, включая лигаменты – мелкомасштабные связки, границы раздела, оболочки, волокна и т. п., которые очень похожи на наблюдаемые в рассчитанных картинах поля горизонтальной компоненты градиента плотности, которое находится в линейной зависимости от коэффициента преломления света, фиксируемого в лабораторных экспериментах [21, 25].
Рис. 4.
Мгновенные картины поля горизонтальной компоненты градиента плотности около горизонтальной пластины в непрерывно стратифицированной жидкости с разными модификациями ее передней и задней кромок: $({{\tilde {r}}_{l}},\xi )$ = (0, 1), (0.4, 1), (1, 1), (1, 2), (1, 10) (а–д).
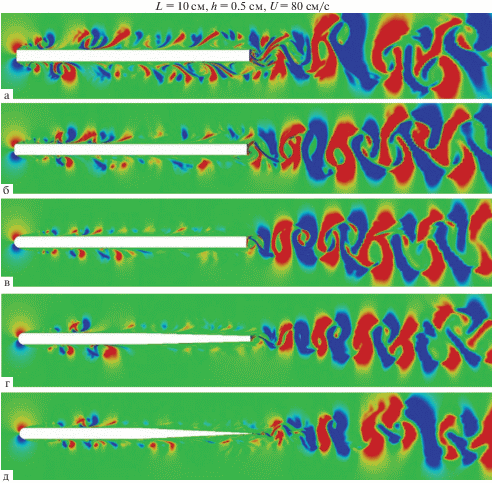
Картины поля состоят из множества мелкомасштабных многослойных структур обоих знаков, которые ориентированы преимущественно вдоль линий тока элементов вихревого течения, образуя системы спиральных завитков, типичных для вихрей. Тонкоструктурные элементы также локализованы в областях течения, где происходят активные взаимодействия различных компонентов течения друг с другом, набегающим потоком и поверхностью препятствия. Тонкость структуры поля горизонтальной компоненты градиента плотности объясняется малостью отношения коэффициента диффузии к коэффициенту кинематической вязкости.
Самые короткие и тонкие структуры сконцентрированы около прямоугольной горизонтальной пластины с острыми краями в вихревых оболочках вихрей, генерированных ее передней кромкой, в то время как в спутном течении данные структуры начинают удлиняться, утолщаться и усложняться по мере развития вниз по течению от задней кромки пластины (рис. 4 (а)). Степень закругления передней кромки влияет на количество тонкоструктурных элементов в области течения над и под пластиной в рамках заданного диапазона вариации величины горизонтальной компоненты градиента плотности (рис. 4 (б, в)). В то же время, возмущения поля хорошо выражены во всей области визуализации спутного течения при всех рассмотренных геометрических конфигурациях, в отличие от картин полей завихренности и давления, в которых в случае пластины типа крыла спутные возмущения едва различимы (верхняя часть рис. 3 и нижняя часть рис. 3 (д)).
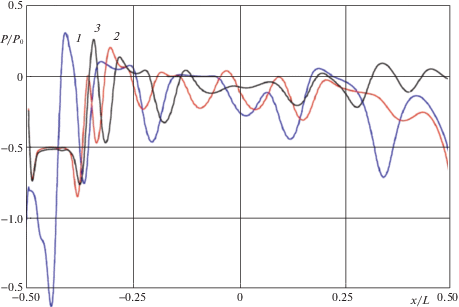
Распределения давления по верхней стороне пластины приведены на рис. 5 для трех разных геометрических конфигураций кромок пластины. Кривые распределений существенно немонотонные, отражая типичную структуру вихревого течения. В случае прямоугольной пластины с острыми краями изменения давления вблизи передней кромки примерно в три раза выше в сравнении с другими рассматриваемыми конфигурациями кромок пластины. Амплитуды колебаний давления ослабевают по мере приближения к задней кромке пластины крылового типа (кривая 3), в то время как в случае прямоугольной пластины амплитуды колебаний, наоборот, нарастают вниз по течению (кривые 1 и 2).
Рис. 5.
Распределение давления на верхней стороне горизонтальной пластины при разных модификациях ее передней и задней кромок: $L = 10$ см, $h = 0.5$ см, $U = 80$ см/с $({{\tilde {r}}_{l}},\xi )$ = (0.01, 1), (1, 1), (1, 10) (кривые1–3).
Интегральные значения коэффициентов сопротивления ${{C}_{D}}$, подъемной силы ${{C}_{L}}$ и вращающего момента ${{C}_{M}}$ приведены в таблице 1 для разных конфигураций передней и задней кромок пластины. Значения для ${{C}_{L}}$ и ${{C}_{M}}$ вычисляются путем интегрирования соответствующих локальных значений только по верхней части поверхности пластины, поскольку интегрирование по всей поверхности симметричного препятствия дает значения, сравнимые с вычислительной ошибкой. Видно, что увеличение радиуса закругления кромки и коэффициента остроты пластины приводит к монотонному уменьшению значений коэффициентов сопротивления и подъемной силы. Интегральный коэффициент вращающего момента принимает отрицательные значения, т.е. набегающий поток стремится повернуть верхнюю сторону пластины по часовой стрелке.
Таблица 1.
Интегральные значения коэффициентов сопротивления трения, подъемной силы и вращающего момента для разных модификаций передней и задней кромок пластины
| ${{\tilde {r}}_{l}}$ | ξ | CD | CL | –CM |
|---|---|---|---|---|
| 0 | 1 | 0.0322 | 0.0935 | 0.0136 |
| 0.04 | 1 | 0.0311 | 0.0912 | 0.0128 |
| 0.4 | 1 | 0.0254 | 0.0844 | 0.0106 |
| 0.8 | 1 | 0.0252 | 0.0783 | 0.0092 |
| 1 | 1 | 0.0251 | 0.0752 | 0.0083 |
| 1 | 2 | 0.0125 | 0.0743 | 0.0126 |
| 1 | 4 | 0.0110 | 0.0721 | 0.0145 |
| 1 | 10 | 0.0104 | 0.0693 | 0.0162 |
Заключение. Разработанный подход основан на численном решении системы дифференциальных уравнений несжимаемой вязкой стратифицированной жидкости с использованием решателей и библиотек собственной разработки пакета OpenFOAM, что позволяет изучать течения как непрерывно стратифицированной, так и однородной вязкой несжимаемой жидкостей в единой постановке. Каждая дополнительная физическая переменная, решаемая исходной системой уравнений, раскрывает некоторые новые важные особенности течения, что способствует лучшему пониманию изучаемых физических процессов.
Мгновенные картины поля возмущения давления за наклонной пластиной изучены в нестационарном вихревом режиме как для стратифицированной, так и для однородной жидкости при различных углах наклона пластины к горизонту. Картины состоят из многомасштабных пятнистых структур с отрицательным давлением, которые соответствуют расположению элементов вихревого потока с пространственными и временными масштабами, существенно зависящими также от угла наклона пластины к горизонту и типа жидкости.
Мгновенные картины полей завихренности, градиента давления и плотности, а также значений сил и крутящего момента, действующих на поверхность пластины, проанализированы при различных значениях радиуса закругления передней кромки и степени заостренности задней кромки пластины. Вихри, генерированные закругленной передней кромкой, имеют значительно меньшие масштабы и быстро затухают вниз по течению, так что характер следа сохраняет первичную вихревую структуру. Возмущения течения за пластиной крылового типа практически исчезают на расстоянии вниз по потоку менее половины длины пластины от задней кромки.
Картины горизонтальной составляющей поля градиента плотности, которые описывают тонкую структуру течения, состоят из множества мелкомасштабных многослойных структур обоих знаков, ориентированных, главным образом, вдоль линий тока элементов вихревого течения, а также локализованных в областях течения с активным взаимодействием различных компонентов течения с набегающим потоком и поверхностью пластины. Возмущения этого поля хорошо выражены в области спутного следа для всех рассмотренных геометрических конфигураций пластины, тогда как для случая пластины крылового типа возмущения спутного следа в структуре полей завихренности и давления проявлены относительно слабо.
Мгновенные картины исследуемых полей характеризуются собственной геометрией, пространственными и временными масштабами, уровнем проявления и скоростью диссипации, описывают структуру и динамику течения с различных физических аспектов и объясняют механизмы формирования вихревой структуры и расщепления течения на ряд тонких слоистых структур, четко наблюдаемых в экспериментах. Обтекание пластины конечной длины в общей постановке представляет собой сложный физический процесс, который требует подробного экспериментального и теоретического изучения с учетом эффектов диффузии, теплопроводности и сжимаемости, а также с контролем критериев наблюдаемости и разрешения всех разномасштабных компонентов течения.
Работа выполнена с использованием услуг и оборудования Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами МГУ имени М.В. Ломоносова, а также Центра коллективного пользования “Комплекс моделирования и обработки данных исследовательских установок мега-класса” НИЦ “Курчатовский институт” при частичной финансовой поддержке одного из авторов (Ю.Д.Ч.) средствами РФФИ (грант 18-05-00870) и государственного бюджета по госзаданию АААА-А17-117021310378-8.
Список литературы
D’Alembert J. Réflexions sur la cause générale des vents. Paris: Savid, 1747. 234 p.
Euler L. Principes généraux du mouvement des fluids // Mémoires de l’Academié royalle des sciences et belles letters, Berlin. 1757. V. 11. P. 274–315.
Гайфуллин A.М., Зубцов А.В. Асимптотическая структура нестационарного течения около полубесконечной пластины с подвижной поверхностью // Изв. РАН. МЖГ. 2013. № 1. С. 88–101.
Liu C., Yan Y., Lu P. Physics of turbulence generation and sustenance in a boundary layer // Comput. Fluids. 2014. V. 102. P. 353–384.
Шлихтинг Г. Теория пограничного слоя. Москва: Наука, 1974. 712 с.
Fage A., Johansen F. On the flow of air behind an inclined flat plate of infinite span // Brit. Aero. Res. Coun. Rep. Memo. 1927. V. 1104. P. 81–106.
Jackson C. Finite-element study of the onset of vortex shedding in flow past variously shaped bodies // J. Fluid Mech. 1987. V. 182. P. 23–45.
Lam K. Phase-locked eduction of vortex shedding in flow past an inclined flat plate // Phys. Fluids. 1996. V. 8. P. 1159–1168.
Breuer M., Jovicic N. Separated flow around a flat plate at high incidence: an LES investigation // J. Turbul. 2001. V. 2. P. 1–15.
Breuer M., Jovicic N., Mazaev K. Comparison of DES, RANS and LES for the separated flow around a flat plate at high incidence // Int. J. Num. Meth. Fluids. 2003. V. 41. P. 357–388.
Zhang J., Liu N., Lu X. Route to a chaotic state in fluid flow past an inclined flat plate // Phys. Rev. E. 2009. V. 79 (045306). P. 1–4.
Lilienthal O. Die Flugapparate, algemeine Gesichtspunkte bei deren Herstellung und Anwendung // Mayer & Müller, Berlin. 1894. 15 p.
Wright W., Wright O. Pioneering aviation works of Wright Brothers, http://www.paperlessarchives.com/wright_brothers_papers.html.
Hanson R., Buckley H., Lavoie P. Aerodynamic optimization of the flat-plate leading edge for experimental studies of laminar and transitional boundary layers // Exp. Fluids. 2012. V. 53. P. 863–871.
Hasheminejad S., Mitsudharmadi H., Winoto S. Effect of flat plate leading edge pattern on structure of streamwise vortices generated in its boundary layer // J. Flow Control. Measur. Vis. 2014. V. 2. P. 18–23.
Thomareis N., Papadakis G. Effect of trailing edge shape on the separated flow characteristics around an airfoil at low Reynolds number: a numerical study // Phys. Fluids. 2017. V. 29. P. 014101-1–014101-17.
Phillips N., Knowles K., Bomphrey R. Petiolate wings: effects on the leading-edge vortex in flapping flight // Interface Focus. 2017. V. 7. № 1. P. 20160084.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. VI. Гидродинамика. Москва: Наука, 1986. 736 с.
Chashechkin Yu., Zagumennyi Ia. Non-equilibrium processes in non-homogeneous fluids under the action of external forces // Physica Scripta. 2013. V. 155. 014010.
Загуменный Я.В., Чашечкин Ю.Д. Тонкая структура нестационарного течения, индуцированного диффузией на неподвижной пластине // Изв. РАН. МЖГ. 2013. № 3. С. 100–117.
Бардаков Р.Н., Миткин В.В., Чашечкин Ю.Д. Тонкая структура стратифицированного течения около пластины // ПМТФ. 2007. Т. 48. № 6. С. 77–91.
Загуменный Я.В., Чашечкин Ю.Д. Нестационарная вихревая картина обтекания пластины с нулевым углом атаки (двумерная задача) // Изв. РАН. МЖГ. 2016. № 3. С. 48–65.
Chashechkin Yu., Zagumennyi Ia. Formation of waves, vortices and ligaments in 2D stratified flows around obstacles // Physica Scripta. 2019. V. 94. № 5. 054003.
Чашечкин Ю.Д. Иерархия моделей классической механики неоднородных жидкостей // Морской гидрофиз. ж. 2010. Т. 5. С. 3–10.
Chashechkin Yu. Differential fluid mechanics–harmonization of analytical, numerical and laboratory models of flows. Mathematical Modeling and Optimization of Complex Structures, // Springer Ser. “Computational Methods in Applied Sciences”, 2016. V. 40. P. 61–91.
Димитриева Н.Ф., Загуменный Я.В. Численное моделирование стратифицированных течений с использованием OpenFOAM // Труды ИСП РАН. 2014. Т. 26. Вып. 5. С. 187–200.
Chashechkin Yu., Mitkin V. A visual study on flow pattern around the strip moving uniformly in a continuously stratified fluid // J. Vis. 2004. V. 7. № 2. P. 127–134.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика


