Прикладная математика и механика, 2019, T. 83, № 4, стр. 530-548

К системам механической природы относятся такие практически важные объекты автоматического управления как роботы-манипуляторы, летательные и плавательные аппараты, транспортные средства и многие другие. Общим для голономных механических систем, которые рассматриваются в данной работе, является математическая модель, составленная на основе уравнений Лагранжа второго рода [1]. Для механических объектов, функционирующих в условиях неопределенности, разработаны законы управления в форме обратной связи, обеспечивающие в замкнутой системе инвариантность по отношению к неизвестным параметрам и внешним неконтролируемым возмущениям в рамках различных подходов: с использованием ПИД-регуляторов, нейронных сетей, малых сил, c решением обратных задач динамики и др. (см, например, [2–7]).

Отдельно выделим используемые в данной работе методы синтеза систем с разрывными управлениями, функционирующих в скользящем режиме, в которых обеспечивается подавление параметрических и внешних согласованных возмущений, принадлежащих пространству управления. Однако законы разрывного управления приобретают эвристический характер при применении их в механических системах в качестве управляющих моментов [8, 9], а при их непосредственном использовании в механических системах с учетом динамики электрических исполнительных устройств не дают ожидаемого эффекта. В этом случае возмущения различной природы, действующие на механическую систему, уже не принадлежат пространству истинного управления, действующего на исполнительные устройства, и не могут быть непосредственно подавлены или скомпенсированы. Таким образом, при синтезе электромеханических систем управления возникает проблема обеспечения инвариантности по отношению к несогласованным внешним возмущениям и неопределенностям, которая требует специального рассмотрения.

Отметим еще один важный аспект: в упомянутых выше и во многих других работах, посвященных управлению механическими и электромеханическими объектами, предполагается априорное знание и использование в законах управления обобщенных координат, их скоростей, ускорений, переменных состояния исполнительных устройств, а также автономных генераторов задающих воздействий и внешних возмущений (см., например [10]). Системы с обратной связью по всему вектору состояния и внешним воздействиям обладают большими возможностями и способны отрабатывать различные технологиеские режимы, в отличие от систем со статической обратной связью только по выходным переменным (например, только по обобщенным координатам), которые не обеспечивают инвариантность и предназначены для решения узкого класса задач [11].

Однако установка полного комплекта датчиков и использование автономных динамических моделей приводит, во-первых, к увеличению стоимости и усложнению конструкции; во-вторых, к расширению динамической модели объекта управления, в частности при синтезе требуется учитывать малые динамики измерительных устройств и допускаемые ими погрешности измерений вплоть до фильтрации шумов; в-третьих, к снижению надежности, так как при выходе из строя датчиков или существенного изменения внешних воздействий, не учтенных в модели, система управления теряет работоспособность вплоть до возникновения аварийной ситуации.

Эффективное решение связано с введением в контур обратной связи динамического наблюдателя состояния. Это алгоритмы, реализуемые в вычислительной среде, которые позволяют при выполнении определенных условий получить текущие оценки неизмеряемых сигналов по измерениям части переменных вектора состояния [12–14]. Наша цель состоит в повышении надежности системы управления за счет ввода системы аналитического резервирования измерительных устройств, а также упрощении структуры регулятора за счет сокращения числа датчиков, что потребует разработки специальных подсистем наблюдения, дающих оценку не только неизмеряемых переменных состояния, но и внешних воздейстивий.

В данной работе для полноприводного электромеханического объекта управления в рамках задачи слежения представлено комплексное решение указанных проблем при измерении только обобщенных координат механической подсистемы и их задающих воздействий, и при действии на механическую подсистему внешних и параметрических возмущений. Возмущения являются несогласованными и сужают наблюдаемое пространство вектора состояния. Для преодоления проблемы большой размерности используется блочный принцип управления [12, 15–21], что позволяет декомпозировать задачу синтеза на последовательно решаемые элементарные подзадачи. В предположении о гладкости неопределенных массо-инерционных характеристик и внешних воздействий разработана процедура преобразования математической модели электромеханической системы в совместную блочную форму (СБФ) управляемости и наблюдаемости относительно ошибок слежения. Координатный базис СБФ составляют смешанные переменные – функции переменных состояния, внешних воздействий и их производных.

В отличие от блочных форм электромеханических объектов, полученных в [12, 17, 19], в данной СБФ возмущения становятся согласованными и могут быть подавлены с помощью разрывных управлений и организации скользящего режима в виртуальном пространстве смешанных переменных. Кроме того, система становится наблюдаемой относительно измерений ошибок слежения. В то же время, в силу структуры электромеханической системы матрица перед управляющими воздействиями в СБФ становится параметрически неопределенной. В условиях неопределенности входных каналов предлагается, во-первых, использовать метод иерархии управлений [8, 16, 19]. Во-вторых, для информационного обеспечения базового закона управления на основе укороченной СБФ разработан наблюдатель смешанных переменных с большими коэффициентами, в котором реализуется принцип полной декомпозиции. Предложен оригинальный метод косвенного оценивания (с помощью виртуальных корректирующих воздействий наблюдателя) смешанных переменных без использования их динамических моделей, что существенно упрощает структуру регулятора.

1. Описание объекта управления. Постановка задач. Рассматривается математическая модель полноприводного электромеханического объекта управления вида [12, 22]

где уравнениями (1.1) описывается лагранжева механическая подсистема с неопределенными массо-инерционными характеристиками; уравнениями (1.2) – динамическая модель электрических исполнительных устройств (приводов постоянного тока) с эластичными сочленениями; ${{q}_{1}} = \operatorname{col} ({{q}_{{11}}},...,{{q}_{{1n}}}) \in {{Q}_{1}} \subset {{\Re }^{n}}$ – вектор обобщенных координат механической подсистемы (вектор выходных переменных); ${{q}_{2}} = \operatorname{col} ({{q}_{{21}}}$, ..., ${{q}_{{2n}}}) \in {{Q}_{2}} \subset {{\Re }^{n}}$ – вектор обобщенных скоростей; $H({{q}_{1}}) \in {{\Re }^{{n \times n}}}$ – положительно-определенная нелинейная матрица инерции, ${{H}^{{ - 1}}}({{q}_{1}}) > 0$ $\forall {{q}_{1}} \in {{Q}_{1}}$; $C({{q}_{1}},{{q}_{2}}) \in {{\Re }^{{n \times n}}}$ – матрица центростремительных и кориолисовых сил; $f(t) = \operatorname{col} ({{f}_{1}},\,...,\,{{f}_{n}}) \in {{\Re }^{n}}$ – часть обобщенных сил (в том числе гравитационных), трактуемых как неконтролируемые возмущения; $\tau {\text{(}}t{\text{)}} \in {{\Re }^{n}}$ – вектор обобщенных сил, развиваемых исполнительными устройствами; $\omega \in {{\Re }^{n}}$ – вектор угловых скоростей роторов электроприводов; $i \in {{\Re }^{n}}$ – вектор токов цепей якорей; $K,J,L,R$, Ψ – диагональные матрицы с положительными постоянными элементами (коэффициенты крутильной жесткости, приведенные моменты инерции на валу электроприводов (подсчитанные с учетом коэффициентов передачи), индуктивности и активные сопротивления контуров якорей, магнитный поток); $u \in {{\Re }^{n}}$ – вектор управляющих напряжений якорей.

Для выходных переменных ${{q}_{1}}(t)$ объекта управления (1.1)–(1.2) рассматривается задача слежения за заданными сигналами $g(t) = \operatorname{col} ({{g}_{1}}, \ldots ,{{g}_{n}}) \in {{Q}_{1}}$ в следующих предположениях:

1) в системе (1.1)–(1.2) измеряются только обобщенные координаты ${{q}_{1}}(t)$, шумы в измерениях отсутствуют;

2) аналитический вид задающих воздействий не известен, имеются только их текущие значения $g(t)$, как следствие, нет полной информации о производных задающих воздействий, которые полагаются неизвестными, гладкими, ограниченными функциями времени;

3) внешние возмущения ${{f}_{i}}(t)$, $i = \overline {1,\,n} $ являются неизвестными гладкими ограниченными функциями времени с ограниченными производными;

4) для постоянных, положительных элементов диагональных матриц $J = \operatorname{diag} ({{J}_{i}})$, $L = \operatorname{diag} ({{L}_{i}})$, $\Psi = \operatorname{diag} ({{\psi }_{i}})$ известны только границы диапазонов, в которых находятся их значения:

5) неопределенность элементов матриц механической подсистемы $H = ({{H}_{{ij}}})$, C = $({{C}_{{ij}}})$ обусловлена неизвестными массо-инерционными характеристиками, которые могут плавно меняться в процессе эксплуатации в известных диапазонах.

С учетом особенностей среды функционирования и в силу ограничений

которые обусловлены конструкцией и запланированной мобильностью механизма в рабочем пространстве, границы диапазонов изменения неизвестных параметров системы (1.1)–(1.2), а также внешних воздействий считаются известными константами:

Для стабилизации ошибок слежения ${{e}_{1}}(t) = {{q}_{1}}(t) - g(t) \in {{\Re }^{n}}$ ставится задача синтеза динамической обратной связи, а именно, синтеза базового закона разрывного управления $u = {\text{col}}({{u}_{1}},\,{{u}_{2}},\,...,\,{{u}_{n}}) \in {{\Re }^{n}}$ и его реализации с помощью переменных динамического наблюдателя состояния.

В сделанных предположениях поставленная задача нетривиальна, поскольку наличие несогласованных внешних и параметрических возмущений, во-первых, не позволяет непосредственно использовать преимущества систем с разрывными управлениями, в которых при организации скользящего режима можно обеспечить инвариантность по отношению только к согласованным ограниченным возмущениям [8, 9, 15]. Во-вторых, при измерении только обобщенных координат теряется наблюдаемость, и в условиях параметрической неопределенности неизмеряемые переменные состояния не подлежат оцениванию даже при расширении пространства состояний за счет ввода экзогенных динамических моделей внешних воздействий [10, 12].

В следующем разделе для электромеханической системы (1.1)–(1.2) обоснован выбор нового координатного базиса, в котором составляющие модели объекта управления, трактуемые как неизвестные возмущения, становятся согласованными, и, кроме того, не сужают наблюдаемого пространства вектора состояния относительно измерений ошибок слежения.

2. Совместная блочная форма управляемости и наблюдаемости электромеханической системы. Синтез базового закона разрывного управления. Если на систему (1.1)–(1.2) внешние возмущения не действуют, то она является управляемой и наблюдаемой относительно выходных переменных ${{q}_{1}}$ в силу своей структуры [12, 15, 17]. Это позволяет выполнить диффеоморфную замену локальных переменных и представить систему (1.1)–(1.2) в эквивалентной блочной форме вход–выход, которая является совместной блочной формой управляемости и наблюдаемости относительно ошибок слежения и состоит из 5-и элементарных блоков размерности n. Согласно идеологии блочного принципа управления [12, 15–21], в каждом j-м ( j = 1, 2, 3, 4) блоке переменные следующего, ( j + 1)-го блока трактуются как фиктивные управления и последовательно, сверху вниз выбираются в виде комбинированных управлений с линейными локальными связями, обеспечивающими стабилизацию невязок между реальными и выбранными фиктивными управлениями. Сформированные локальные связи обеспечиваются с помощью реального управления в последнем блоке. Предположение о дифференцируемости элементов матриц механической подсистемы и внешних воздействий позволяет использовать в данных преобразованиях внешние воздействия и их производные. В процессе дифференцирования ошибок слежения и диффеоморфных замен локальных переменных порождаются смешанные переменные нового координатного базиса, которые являются функциями от переменных состояния исходной системы, внешних воздействий и их производных, а именно:

где

С учетом (2.1)–(2.2) имеем СБФ электромеханической системы (1.1)–(1.2) относительно ошибок слежения с линейными локальными связями вида

где ${{\bar {K}}_{j}} = {{K}_{j}} - {{K}_{{j - 1}}}$, $j = 4,3,2$, ${{\bar {K}}_{1}} = {{K}_{1}},$ ${{\bar {K}}_{j}} = \operatorname{diag} ({{\bar {k}}_{{ji}}})$, ${{\bar {k}}_{{ji}}} > 0$, а элементы смешанного вектора ${{w}_{5}} = \operatorname{col} ({{w}_{{51}}},...,w{}_{{5n}})$, трактуются как ограниченные возмущения. Диапазоны их изменения определяются с учетом (1.3)–(1.5) при выбранных коэффициентах усиления (2.2). Матрица перед истинным управлением имеет вид и содержит неопределенные параметры. Существенно, что в силу электромеханической природы объекта управления матрица В (2.5) является положительно определенной и все ее угловые миноры ${{\Delta }_{1}} = {{b}_{{11}}}$, ${{\Delta }_{2}} = {{b}_{{11}}}{{b}_{{22}}} - {{b}_{{12}}}{{b}_{{21}}}$, …, ${{\Delta }_{n}} = \det B$ строго положительные.

В отличие от системы (1.1)–(1.2) в СБФ (2.3)–(2.4) возмущения ${{w}_{5}}$ являются согласованными, т.е. принадлежат пространству истинного управления, и все неопределенности сосредоточены в последнем, пятом блоке. Как следствие, переменные состояния ${{e}_{j}} \in {{\Re }^{n}}$, $j = \overline {2,\,5} $ системы (2.3)–(2.4) являются наблюдаемыми относительно измерений ошибок слежения ${{e}_{1}}$, однако получить с помощью наблюдателя состояния текущие оценки возмущений ${{w}_{5}}(t)$ для синтеза комбинированного управления и их компенсации не представляется возможным из-за неопределенной матрицы В (2.5) [12].

Таким образом, обеспечить инвариантность замкнутой системы по отношению к внешним возмущениям можно только путем их подавления с помощью разрывного управления в форме обратной связи:

где ${{K}_{5}} = \operatorname{diag} ({{k}_{{5i}}})$, ${{k}_{{5i}}} > 0$, $i = \overline {1,\,n} .$ В замкнутой системе подсистема (2.4) имеет вид ${{\dot {e}}_{5}} = B({{w}_{5}} - {{K}_{5}}\operatorname{sign} {{e}_{5}})$.

В частном случае, когда матрица ${{H}^{{ - 1}}}({{q}_{1}})$, и, следовательно, В (2.5) являются диагональными $B = \operatorname{diag} ({{b}_{i}})$, $0 < {{\bar {b}}_{i}} \leqslant {{b}_{i}}({{q}_{1}}) \leqslant {{\bar {\bar {b}}}_{i}}({{q}_{1}})$ $\forall {{q}_{1}} \in {{Q}_{1}}$, $i = \overline {1,\,n} $, неравенства для выбора амплитуд разрывных управлений ${{k}_{{5i}}}$, $i = \overline {1,\,n} $ получим из достаточных условий [8]

При их выполнении за конечное время

возникают скользящие режимы в виртуальном пространстве смешанных переменных на поверхностях ${{e}_{{5i}}} = 0$, $i = \overline {1,\,n} $. При $t > t_{i}^{*}$ поведение переменных замкнутой системы (2.3)–(2.4), (2.6) описывается логической цепочкой экспоненциальная стабилизация ошибок слежения обеспечивается.

Заметим, что в этом частном случае моменты времени возникновения скользящих режимов $t_{i}^{*}$ на поверхностях ${{e}_{{5i}}} = 0$ не зависят друг от друга и определяются начальными условиями ${{e}_{{5i}}}(0)$ и выбором амплитуд разрывных управлений ${{k}_{{5i}}}$, $i = \overline {1,\,n} $.

В общем случае, когда матрица В (2.5) содержит неопределенные параметры, не является диагональной и не имеет преобладающей диагонали, для выбора амплитуд разрывных управлений, обеспечивающих (2.8), следует использовать метод иерархии управлений [8, 16, 19], основанный на иерархии сходимости компонент вектора ${{e}_{5}}$ в нуль, которая, например, совпадает с их порядковыми номерами:

Идея заключается в том, что для уравнений замкнутой подсистемы (2.4), (2.6) последовательно, сверху вниз составляются неравенства для выбора ${{k}_{{5i}}}$, $i = \overline {1,\,n} $, при которых за конечное время последовательно возникают скользящие режимы на поверхностях (2.9). После анализа каждого i-го уравнения согласно методу эквивалентного управления [8] из уравнения статики ${{\dot {e}}_{{5i}}}(t) = 0$ $\forall t > t_{i}^{*}$ нужно выразить эквивалентное управление ${{u}_{{ieq}}}$ и подставить в нижние уравнения с номерами i + 1, i + 2,…, n. Таким образом, управления ${{u}_{i}}$, $i = \overline {1,\,n - 1} $ последовательно исключаются из подсистемы (2.4), а матрица B будет приведена аналитически к верхнетреугольному виду $B{\text{*}}$ в режиме off-line.

Для реализации данного алгоритма нужно в символьном виде выполнить умножение матрицы B на преобразующую матрицу ${{S}_{{n \times n}}}$, $\det S \ne 0$:

где S является нижнетреугольной с единицами на главной диагонали. Получить ее можно или в результате итерационной процедуры метода Гаусса [16, 19], или непосредственно путем решения соответствующей системы линейных уравнений. Заметим, что первая строка верхнетреугольной матрицы $B{\text{*}}$ совпадает с первой строкой матрицы B (2.5), а ее диагональные элементы имеют вид

В силу (1.3)–(1.5) определяются нижние оценки диагональных и верхние оценки остальных ненулевых элементов матрицы $B{\text{*}}$ $\forall {{q}_{1}} \in {{Q}_{1}}$, $\forall t \geqslant 0$:

С учетом (2.9) уравнения $S{{\dot {e}}_{5}} = SB({{w}_{5}} - {{K}_{5}}\operatorname{sign} {{e}_{5}})$ можно представить в виде

На основе анализа системы (2.11) и достаточных условий (2.7) имеем:

После выбора численного значения ${{k}_{{5n}}}$ обратным ходом, снизу вверх на основе неравенств (2.12) последовательно выбираются численные значения ${{k}_{{5i}}}$, $i = \overline {n - 1,\,1} $. Таким образом, с помощью итерационной процедуры матрица перед управляющими воздействиями наделяется преобладающей диагональю, что обеспечивает иерархию (2.9) и устойчивость следящей системы (2.8). На проектной стадии неравенства (2.12) являются основой для выбора исполнительных устройств (ИУ), способных обеспечивать различные режимы работы системы в заданных ограничениях. На стадии эксплуатации при наличии комплектных ИУ с постоянными амплитудами неравенства (2.12) служат для анализа допустимых диапазонов изменения внешних воздействий и неопределенностей, при которых система не теряет работоспособность.

Заметим, что соотношения (2.8) справедливы, если в замкнутой системе возникнет идеальный скользящий режим и текущие значения смешанных переменных ${{e}_{{5i}}}(t)$, $i = \overline {1,n} $ точно известны $\forall t \geqslant 0$. В следующем разделе решается задача информационного обеспечения базового закона разрывного управления (2.6), а именно, для получения оценок смешанных переменных ${{\tilde {e}}_{{5i}}}(t) \approx {{e}_{{5i}}}(t)$, $i = \overline {1,n} $ вводится динамический наблюдатель состояния. Сразу заметим, что из-за наличия внешних возмущений и неопределенностей задача наблюдения может быть решена только с заданной точностью [12], а именно:

В системе с наблюдателем состояния и реализацией закона управления (2.6) в виде $u = - {{K}_{5}}\operatorname{sign} {{\tilde {e}}_{5}}$ в начальный период времени $t \in [0;\,T]$, $T < t_{1}^{*}$ в общем случае $\operatorname{sign} {{\tilde {e}}_{{5i}}}(t)$ ≠ ≠ $\operatorname{sign} {{e}_{{5i}}}(t)$ и переходные процессы переменных ${{e}_{{5i}}}(t)$, $i = \overline {1,n} $ не являются апериодическим. Области изменения смешанных переменных и их производных можно оценить следующим образом:

где области начальных условий смешанных переменных определяются в силу (2.1) с учетом ограничений на переменные исходной системы (1.3)–(1.5) при выбранных коэффициентах усиления (2.2).

При выполнении достаточных условий (2.12) в замкнутой системе слежения (2.3)–(2.4), (2.6) с наблюдателем состояния возникнет реальный скользящий режим в пограничном слое поверхностей переключения. Как следствие, ошибки слежения также сходятся в некоторые окрестности нуля и вместо асимптотической последовательности (2.8) с точностью до затухающих собственных движений имеем:

Данные неравенства следует учитывать при выборе коэффициентов усиления (2.2) и назначении желаемой точности $\delta > 0$ и времени сходимости $T > 0$ при решении задачи наблюдения.

3. Декомпозиционный синтез наблюдателя смешанных переменных пониженного порядка. В отличие от исходной системы (1.1)–(1.2), которая из-за наличия несогласованных возмущений ненаблюдаема относительно измерений ${{q}_{1}}$, в преобразованной системе (2.3)–(2.4) все неопределенности сосредоточены в последнем блоке и не сужают наблюдаемого пространства смешанных переменных относительно измерений ошибок слежения ${{e}_{1}}(t)$. Поэтому наблюдатель состояния для оценивания ${{e}_{5}}(t)$ целесообразно строить как реплику СБФ (2.3)–(2.4). При таком подходе задачи управления и наблюдения решаются относительно одних и тех же смешанных переменных, что не требует выполнения обратных замен переменных в реальном времени, а структура регулятора существенно упрощается. Для реализации данного подхода достаточно измерений только ошибок слежения.

Построение наблюдателя полной размерности 5n в данном случае затруднительно. Из-за параметрически неопределенной матрицы B (2.5) вся правая часть уравнения (2.4) в задаче наблюдения трактуется как внешние возмущения с разрывной, высокочастотной составляющей (2.6). Это не позволяет использовать стандартные методы построения наблюдателей состояния с большими коэффициентами [13, 14], которые используются для оценивания неизмерямых переменных вектора состояния при действии внешних возмущений в предположении, что внешние возмущения являются не только всюду ограниченными, но и достаточно гладкими. Поэтому в рассматриваемом случае для оценивания ${{e}_{5}}(t)$ целесообразно использовать наблюдатели пониженного порядка 4n на основе укороченной СБФ (2.3), которую представим в виде

где переменные ${{e}_{5}} \in {{\Re }^{n}}$ трактуются как внешние ограниченные возмущения с ограниченными производными (2.13), здесь и далее $O,\,I$ – нулевая и единичная матрицы соответственно размерности $n \times n$.

При синтезе наблюдателей, построенных как реплика системы (3.1), можно реализовать метод разделения движений в пространстве ошибок наблюдения не только с помощью глубоких линейных обратных связей, но и с помощью ограниченных корректирующих воздействий: разрывных [12, 16–18, 23] или их непрерывных аналогов в виде кусочно-линейных [20, 21] и S-образных нелинейных сигма-функций [24]. В отличие от стандартных методов [10, 13, 14], в рамках указанных подходов можно получить с помощью корректирующих воздействий наблюдателя оценки внешних возмущений с заданной точностью без использования в наблюдателе их динамических моделей (2.4).

Ниже представлен оригинальный метод синтеза наблюдателя пониженного порядка без корректирующих воздействий с простой настройкой параметров, в котором реализуется принцип полной декомпозиции. Основу разработанного подхода составляет принцип построения наблюдателя Луенбергера пониженного порядка [25, 26], который был распространен на линейные и нелинейные системы при действии внешних возмущений [12, 17]. В указанных работах такой наблюдатель служит для оценивания только переменных состояния. Мы предлагаем новый алгоритм, в котором, в отличие от наблюдателя Луенбергера (где отбрасывается подсистема, описывающая динамику измеряемых переменных), отбрасывается подсистема, описывающая динамику смешанных переменных, подлежащих оцениванию (2.4), а требуемые оценки обеспечивают виртуальные корректирующие воздействия наблюдателя – линейные комбинации ошибок наблюдения измеряемых переменных.

Предварительно отметим, что собственные движения переменных ${{e}_{i}}$, $i = \overline {1,4} $ в системе (3.1) устойчивые, элементы диагональной матрицы А выбираются независимо и определяют желаемые темпы сходимости ошибок слежения. В системе наблюдения, где переменная ${{e}_{5}}(t)$ трактуется как внешнее возмущение, для обеспечения сходимости ошибок наблюдения и их производных требуется использовать большие коэффициенты усиления. С целью ввода на главную диагональ матрицы системы (3.1) корректирующих матриц с большими коэффициентами выполним невырожденную замену переменных:

где матрица перехода $P$ имеет нижнетреугольную блочную структуру с квадратными диагональными матрицами размерности $n \times n$:

Элементы корректирующих матриц ${{L}_{j}}$, $j = \overline {2,\,4} $ определим позже на стадии синтеза наблюдателя. Выбор матриц ${{P}_{{31}}}$, ${{P}_{{41}}}$, ${{P}_{{42}}}$ в указанном виде (3.2) обеспечит после выполнения преобразования подобия $PA{{P}^{{ - 1}}} = \bar {A}$, $PD = D$ в матрице $\bar {A}$ нулевые матрицы в позициях (3; 2), (4; 2), (4; 3), а именно:

где

На основе системы (3.3) построим наблюдатель размерности 4n без корректирующих воздействий, но с компенсацией измеряемой переменной ${{s}_{1}} = {{e}_{1}}$ в виде:

где ${{z}_{j}} \in {{\Re }^{n}}$ $(j = \overline {1,4} )$ – вектор состояния наблюдателя, ${{L}_{1}} = \operatorname{diag} ({{l}_{{1i}}})$, ${{l}_{{1i}}} > 0$, $i = \overline {1,\,n} $. Относительно ошибок наблюдения ${{\varepsilon }_{j}} = {{s}_{j}} - {{z}_{j}} \in {{\Re }^{n}}$ получим систему с верхнетреугольной блочной матрицей

Задача синтеза наблюдателя (3.4), а именно, выбор матриц ${{L}_{j}}$, $j = \overline {1,4} $, сводится к задаче стабилизации с заданной точностью системы (3.5) и разделяется на последовательно решаемые элементарные подзадачи. В системе (3.5) на главной диагонали находятся собственные значения матрицы коэффициентов системы, поэтому, очевидно, что при выполнении (2.13) и необходимых условий ${{l}_{{ji}}} + {{\bar {k}}_{{ji}}} > {{l}_{{j + 1,i}}}$, $j = \overline {1,3} $, $i = \overline {1,n} $ $\exists {{t}_{1}} > 0:\forall t \geqslant {{t}_{1}}$ для переменных системы (3.5) с точностью до затухающих собственных движений справедливы следующие оценки:

Последовательный выбор параметров ${{l}_{{ji}}}$, $j = \overline {4,1} $, $i = \overline {1,n} $ на основе неравенств (3.6) обеспечивает стабилизацию системы (3.5) и, как следствие, решение задачи наблюдения неизмеряемых переменных ${{s}_{{ji}}}(t),$ $j = 4,3,2$, $i = \overline {1,n} $ с заданной точностью:

которую назначают с учетом $\bar {e} = {{P}^{{ - 1}}}s$ в случае, когда для синтеза обратной связи требуется получить оценки $\bar {e}(t)$.

Наша цель состоит в получении оценок “внешних возмущений” ${{e}_{5}}(t)$. С этой целью последовательно, снизу вверх, исключим из системы уравнений (3.5) переменные ${{\varepsilon }_{2}}$, ${{\varepsilon }_{3}}$, ${{\varepsilon }_{4}}$ и установим связь между “внешним возмущением” ${{e}_{5}}(t)$, измеряемой ошибкой наблюдения ${{\varepsilon }_{1}}(t) = {{e}_{1}}(t) - {{z}_{1}}(t)$ и производными переменных системы (3.5):

Таким образом, переменные

которые можно трактовать как виртуальные корректирующие воздействия наблюдателя (3.4), служат оценкой “внешнего возмущения” $\forall t > {{t}_{1}}$ в следующем смысле:

Для определения точности оценивания (3.8) составим вспомогательную систему для производных ошибок наблюдения:

для которых аналогично (3.6) имеем:

Из (3.7), (3.9) следует неравенство для ошибок оценивания переменных ${{e}_{{5i}}}$:

Неравенство (3.10) служит для выбора параметров корректирующих матриц, при которых обеспечивается желаемая точность оценивания смешанной переменной ${{e}_{5}}(t)$. Пусть, например, ${{\alpha }_{i}} = {{\delta }_{i}}{\text{/}}(4{{\bar {F}}_{i}})$, тогда

Наблюдатель (3.4) имеет меньший порядок, чем стандартные наблюдатели с большими коэффициентами [13, 14], более удобную настройку и позволяет получить оценки смешанных переменных без использования в наблюдателе их динамических моделей (2.4).

Заметим, что процесс получения модели специального вида (3.3) для построения наблюдателя (3.4) основан на выполнении алгебраических равенств (3.2) и требует полной определенности параметров преобразуемой системы. В данном случае основой для построений является искусственная модель (3.1) с известными коэффициентами регулятора. Такой подход расширяет класс наблюдаемых систем за счет параметрически неопределенных систем, приводимых к СБФ (2.3)–(2.4).

Как известно, наблюдатели с большими коэффициентами приводят к существенным всплескам вначале переходного процесса, поэтому их не рекомендуется использовать в системах с линейными регуляторами [13, 14]. В данном случае таких препятствий нет, так как используется всюду ограниченное управление. Базовый закон разрывного управления (2.6) в замкнутой системе (1.1)–(1.2) с наблюдателем (3.4) реализуется в виде

и обеспечивает заданную точность стабилизации ошибок слежения (2.14).

4. Результаты моделирования. Численное моделирование разработанных алгоритмов проводилось для математической модели трехзвенного манипулятора типа UMS-2, предназначенного для переноса объектов в цилиндрическом пространстве. Обобщенные координаты этого манипулятора ${{q}_{1}} = \operatorname{col} ({{q}_{{11}}},\,{{q}_{{12}}},\,{{q}_{{13}}})$ совершают вращательные, вертикальные линейные и горизонтальные линейные движения соответственно. Матрицы механической подсистемы (1.1) имеют вид [22]:

где ${{I}_{1}} = 0.03$ кг м² – приведенный момент инерции частей манипулятора, участвующих во вращательном движении; ${{m}_{2}} = 6.5$ кг – приведенная масса частей, участвующих в поступательном вертикальном движении; ${{I}_{2}} = 0.06$ кг м² – момент инерции этих частей, приведенный к вертикальной оси; $m_{3}^{'} = 5.5$ кг – масса руки, которая представлена однородным стержнем длиной $l = 0.9$ м; ${{m}_{3}}(t)$ = (1–3) кг – точечная масса схвата с грузом. Конструктивные ограничения:

Требовалось обеспечить движение конечной точки манипулятора в рабочем пространстве по заданной траектории, пересчитанной в программные движения обобщенных координат

с помощью разрывного управления (2.6), реализованного в виде (3.11) с помощью наблюдателя (3.4).

Моделирование проводилось в среде MATLAB–Simulink, для интегрирования использовался метод Эйлера с постоянным шагом $5 \times {{10}^{{ - 5}}}$. При моделировании возмущений были приняты следующие функции:

где $g = 9.8$ м/с² – ускорение силы тяжести. Ниже приведены параметры электрической подсистемы (1.2), коэффициентов усиления локальных (2.1) и истинных (2.6) регуляторов, а также наблюдателя (3.4) соответственно:

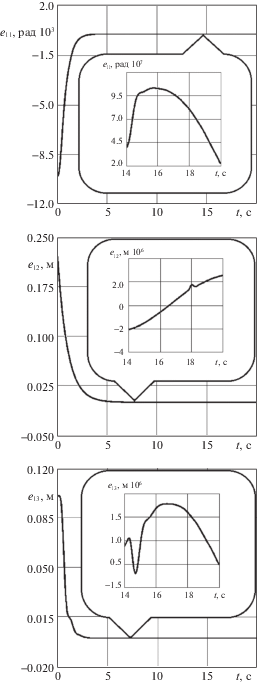
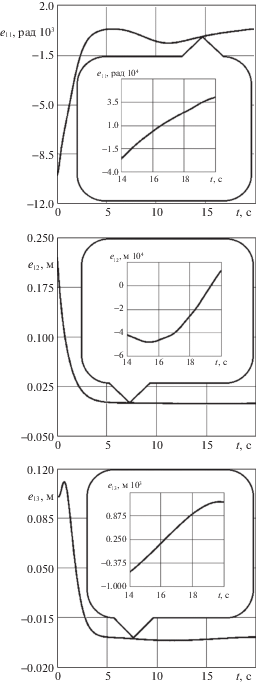
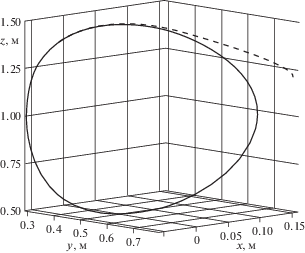
На рис. 1 показаны графики ошибок слежения по всем обобщенным координатам ${{e}_{1}} = {\text{col}}({{e}_{{11}}},\,{{e}_{{12}}},\,{{e}_{{13}}})$, ${{e}_{{1i}}}(t) = {{q}_{{1i}}}(t) - {{g}_{i}}(t)$ при использовании статической обратной связи (2.6) в предположении, что все внутренние и внешние сигналы доступны для измерения. На рис. 2 показаны графики ошибок слежения при использовании динамической обратной связи (3.11) с наблюдателем (3.4); на рис. 3 показаны соответствующий график движения конечной точки манипулятора (пунктирная линия) и заданная пространственная траектория.

Результаты моделирования подтверждают эффективность разработанного подхода. Как видно из графиков, цель управления достигается. В таблице 1 приведены времена переходных процессов ${{t}_{{пi}}}:\left| {{{e}_{{1i}}}(t)} \right| \leqslant 2 \times {{10}^{{ - 3}}}{\text{ }}$ $\forall t > {{t}_{{пi}}}$ и точности стабилизации e_yi =  $\mathop {\max \left| {{{e}_{{1i}}}\left( t \right)} \right|}\limits_{t \geqslant 10} $ для ошибок слежения ${{e}_{{1i}}}(t)$, $i = \overline {1,3} $ в системах с базовым законом управления (2.6) и динамической обратной связью (3.11) с наблюдателем состояния (3.4).

По сравнению с базовым законом в системе с наблюдателем переходные процессы протекают примерно в 2 раза дольше, и точность стабилизации ошибок слежения оказывается хуже примерно на 2 порядка. Требование к точности позиционирования конечной точки манипулятора зависит от выполняемых работ и, как правило, находится в пределах от 0.005 до 2 мм [22]. Рассчитанная на основе данных табл. 1 максимальная оценка линейной кинематической погрешности в установившемся режиме составляет 0.0086 мм и 1.038 мм для системы без наблюдателя и с наблюдателем соответственно. Таким образом, разработанные алгоритмы управления можно рекомендовать для использования, если требование к погрешности позиционирования в конкретном технологическом процессе составляет не более 1.1 мм.

Заключение. Использование в комплексе в замкнутой системе разрывного управления и наблюдателя смешанных переменных не требует полного комплекта измерительных устройств, составления динамических моделей внешних воздействий и перенастройки параметров регулятора при существенном изменении возмущающих и задающих воздействий. Разработан оригинальный декомпозиционный метод синтеза наблюдателя пониженного порядка без корректирующих воздействий. Инвариантность по отношению к внешним возмущениям и полная декомпозиция задачи синтеза наблюдателя обеспечивается с помощью линейных локальных связей с большими коэффициентами. Показано, что сигналы, пропорциональные невязкам по измеряемым ошибкам слежения, дают оценку с заданной точностью смешанных переменных, по которым формируется обратная связь. Таким образом, задачи управления и наблюдения решаются в терминах смешанных переменных СБФ, что существенно упрощает структуру регулятора. Точность позиционирования в системе с неполной информацией хуже, но при этом в полной мере удовлетворяет эксплуатационным требованиям.

Работа выполнена при частичной финансовой поддержке Российского фонда фундаментальных исследований (проект 18-01-00846A).