Прикладная математика и механика, 2019, T. 83, № 4, стр. 643-652

К ОДНОЙ ЗАДАЧЕ Я.С. УФЛЯНДА

Д. А. Пожарский^1, *

¹ Донской государственный технический университет
Ростов-на-Дону, Россия

Поступила в редакцию 29.10.2018
После доработки 28.11.2018
Принята к публикации 25.12.2018

DOI: 10.1134/S0032823519040106

Аннотация

Объясняется причина трудностей, с которыми столкнулся Я.С. Уфлянд при решении задачи теории упругости для полупространства с прямой линией раздела граничных условий, по одну сторону от которой заданы перемещения, а по другую – напряжения (перемещения оказываются неограниченными на линии раздела). Показано, что эту задачу целесообразно рассматривать как частный случай краевой задачи для пространственного клина. Описана скрытая симметрия фундаментальных решений для клина, которые должны удовлетворять теореме Бетти о взаимности работ, дано преобразование к форме с явной симметрией, возможное, если угол клина не превысил критический. При превышении такого угла решение утрачивает скрытую симметрию и становится неединственным, неограниченным на ребре клина. Единственно верным остается преобразованное решение. В задаче Уфлянда превышен критический угол. Приводится пример краевой задачи о действии силы внутри клина, когда критический угол не достигается. Решение задачи Уфлянда для несжимаемого полупространства применяется для построения асимптотического решения собственно смешанной задачи о накладке, контактирующей с границей полупространства.

Ключевые слова: упругость, краевая задача, полупространство, трехмерный клин, накладка

Как известно [1], для единственности решений краевых задач теории упругости для пространственного клина кроме граничных условий и условия убывания перемещений и напряжений в бесконечности следует ставить дополнительные условия на ребре клина: перемещения там должны быть ограниченны, а напряжения могут иметь интегрируемую особенность. Частный случай клина – полупространство с прямой линией раздела граничных условий. При решении смешанной задачи для такого полупространства, когда на одной части границы заданы перемещения, а на другой – напряжения, Я.С. Уфлянд использовал интегральное преобразование Конторовича–Лебедева (ПКЛ) в вещественной форме ([1], § 89, 90) и показал, что представление Папковича−Нейбера дает перемещения, неограниченные на линии раздела. Я.С. Уфлянд предложил блестящее решение этой проблемы, привлекая особые решения уравнения Лапласа, искусственные граничные условия для четвертой произвольной гармонической функции Папковича–Нейбера, вводя дополнительно еще 11 неизвестных функций. Тем не менее, решение получилось довольно громоздким. Более удобным при решении задач для трехмерного клина представляется ПКЛ в комплексной форме [2–4]: сдвиг контура интегрирования позволяет регулировать поведение перемещений на ребре. Ранее также изучалась задача о накладке на грани трехмерного клина при скользящей заделке другой грани [5]. Главные члены регулярного асимптотического решения этой задачи соответствуют случаю накладки на полупространстве [6].

В настоящей работе даны рекомендации для получения упругих перемещений, ограниченных на ребре клина, на основе комплексного ПКЛ. Без ограничения общности рассматривается частный случай задачи Уфлянда (несжимаемый материал, часть границы полупространства жестко заделана, на другой части приложена касательная сила). Показано, что с помощью сдвига контура интегрирования, если пренебречь возникающим вычетом, можно получить единственное фундаментальное решение, ограниченное на ребре и симметричное, т.е. удовлетворяющее теореме Бетти [7]. Это же решение можно получить как частный случай, если рассматривать более общую задачу для несжимаемого трехмерного клина (одна грань жестко заделана, на другой грани действует касательная сила). В такой задаче при острых углах клина можно сдвигать контур интегрирования без возникновения вычетов (ширина полосы регулярности обратно пропорциональна углу клина). При этом симметрия фундаментального решения в скрытой форме преобразуется к явной симметрии. Прямой угол в рассматриваемой задаче для несжимаемого клина – критический, при дальнейшем увеличении угла возникает вычет, нарушающий симметрию, единственность и теорему Бетти. Дается пример другой задачи для пространственного клина, когда критический угол не достигается. На основе фундаментального решения задачи Уфлянда для несжимаемого материала построено асимптотическое решение задачи о накладке, контактирующей с границей полупространства.

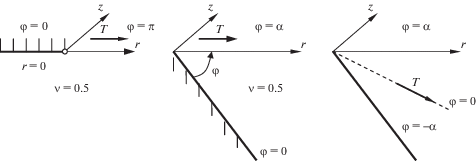
1. Частный случай задачи Уфлянда. В цилиндрических координатах r, φ, z рассмотрим несжимаемое упругое полупространство {0 ≤ r < ∞, 0 ≤ φ ≤ π, |z| < ∞} с модулем сдвига G и коэффициентом Пуассона ν = 0.5, часть границы которого φ = 0 жестко заделана, а при φ = π в радиальном направлении действует касательная сосредоточенная сила T (левая часть рис. 1), приложенная в точке r = x, z = y. Граничные условия задачи для уравнений упругого равновесия имеют вид

(1.1)

$\begin{gathered} \varphi = 0{\text{:}}\quad {{u}_{r}} = {{u}_{\varphi }} = {{u}_{z}} = 0 \\ \varphi = \pi {\text{:}}\quad {{\sigma }_{\varphi }} = {{\tau }_{{\varphi z}}} = 0,\quad {{\tau }_{{r\varphi }}} = T\delta (r - x)\delta (z - y), \\ \end{gathered} $

где δ(r) – функция Дирака. Для решения задачи (1.1) используем представление Папковича–Нейбера, которое позволяет выразить перемещения через три гармонические функции Φ_n = Φ_n(r, φ, z) (n = 0, 1, 2) в виде [1–4]

${{u}_{r}} = \frac{{\partial {{\Phi }_{0}}}}{{\partial r}} + \frac{1}{2}\frac{{\partial (r{{{\omega }}_{1}})}}{{\partial r}} - {{{\omega }}_{1}},\quad {{{\omega }}_{1}} = \sin \varphi {\text{ }}{{\Phi }_{1}} - \cos \varphi {\text{ }}{{\Phi }_{2}}$

(1.2)

${{u}_{\varphi }} = \frac{1}{r}\frac{{\partial {{\Phi }_{0}}}}{{\partial \varphi }} + \frac{1}{2}\frac{{\partial {{{\omega }}_{1}}}}{{\partial \varphi }} - {{{\omega }}_{2}},\quad {{{\omega }}_{2}} = \cos \varphi {\text{ }}{{\Phi }_{1}} + \sin \varphi {\text{ }}{{\Phi }_{2}}$

${{u}_{z}} = \frac{{\partial {{\Phi }_{0}}}}{{\partial z}} + \frac{r}{2}\frac{{\partial {{{\omega }}_{1}}}}{{\partial z}}$

Рис. 1.

Напряжения выражаются из формул (1.2) и закона Гука [1–4].

Будем искать функции Папковича–Нейбера в форме комплексных интегральных преобразований Фурье–Конторовича–Лебедева

(1.3)

$\begin{gathered} {{\Phi }_{n}}(r,\varphi ,z) = \frac{1}{{2\pi i}}\int\limits_{ - \infty }^\infty {\exp (i\beta z)} d\beta \int\limits_{\gamma - i\infty }^{\gamma + i\infty } {[{{a}_{n}}(\mu )\cos \mu \varphi + {{b}_{n}}(\mu )\sin \mu \varphi ]} {\text{ }}{{I}_{\mu }}(\left| \beta \right|r)d\mu \\ \left| {\operatorname{Re} \mu } \right| < \gamma ,\quad {{a}_{n}}( - \mu ) = - {{a}_{n}}(\mu ),\quad {{b}_{n}}( - \mu ) = {{b}_{n}}(\mu ),\quad n = 0,1,2 \\ \end{gathered} $

Двумерная дельта-функция представляется следующим образом [3]:

(1.4)

$\begin{gathered} \delta (r - x)\delta (z - y) = \frac{1}{{2{{\pi }^{2}}i}}\int\limits_{ - \infty }^\infty {\exp (i\beta (z - y))} d\beta \int\limits_{\gamma - i\infty }^{\gamma + i\infty } {\frac{\mu }{x}} {\text{ }}{{K}_{\mu }}(\left| \beta \right|x){{I}_{\mu }}\left( {\left| \beta \right|r} \right)d\mu = \\ = \frac{1}{{2{{\pi }^{2}}i}}\int\limits_{ - \infty }^\infty {\exp (i\beta (z - y))} d\beta \int\limits_{\gamma - i\infty }^{\gamma + i\infty } {\frac{\mu }{r}} {\text{ }}{{K}_{\mu }}(\left| \beta \right|x){{I}_{\mu }}(\left| \beta \right|r)d\mu \\ \end{gathered} $

В формулах (1.3) и (1.4) K_μ(x) и I_μ(x) – цилиндрические функции Бесселя, для которых при сдвиге контура интегрирования в равенстве (1.3) важную роль играют соотношения [8, 9]

(1.5)

$\begin{gathered} \frac{\partial }{{\partial r}}{{I}_{\mu }}(\left| \beta \right|r) = \frac{{\left| \beta \right|}}{2}\left[ {{{I}_{{\mu - 1}}}(\left| \beta \right|r) + {{I}_{{\mu + 1}}}(\left| \beta \right|r)} \right]{\text{,}}\quad \frac{\mu }{r}{{I}_{\mu }}(\left| \beta \right|r) = \frac{{\left| \beta \right|}}{2}\left[ {{{I}_{{\mu - 1}}}(\left| \beta \right|r) - {{I}_{{\mu + 1}}}(\left| \beta \right|r)} \right] \\ \frac{\partial }{{\partial x}}{{K}_{\mu }}(\left| \beta \right|x) = - \frac{{\left| \beta \right|}}{2}\left[ {{{K}_{{\mu - 1}}}(\left| \beta \right|x) + {{K}_{{\mu + 1}}}(\left| \beta \right|x)} \right]{\text{,}}\quad \frac{\mu }{x}{{K}_{\mu }}(\left| \beta \right|x) = \frac{{\left| \beta \right|}}{2}\left[ {{{K}_{{\mu + 1}}}(\left| \beta \right|x) - {{K}_{{\mu - 1}}}(\left| \beta \right|x)} \right] \\ \end{gathered} $

При помощи формул (1.2)–(1.5) найдем точное решение задачи (1.1):

(1.6)

${{a}_{0}} = {{a}_{1}} = {{a}_{2}} = {{b}_{1}} = 0,\quad {{b}_{0}} = {{T}_{1}}\frac{{x{{K}_{\mu }}(\left| \beta \right|x)}}{{2\cos \pi \mu }},\quad {{b}_{2}} = - {{T}_{1}}\frac{{{{K}_{\mu }}(\left| \beta \right|x)}}{{\cos \pi \mu }},\quad {{T}_{1}} = \frac{{T\exp ( - i\gamma y)}}{{\pi G}}$

Однако это решение дает неограниченные радиальные перемещения на линии раздела ($R = \sqrt {{{{(r - x)}}^{2}} + {{{(z - y)}}^{2}}} $)

(1.7)

$\begin{gathered} {{u}_{r}}(r,\pi ,z) = \frac{T}{{{{\pi }^{3}}G}}\int\limits_0^\infty {\int\limits_0^\infty {\operatorname{sh} \pi u\operatorname{th} \pi u{{K}_{{iu}}}(\beta x)\left[ {{{K}_{{iu}}}(\beta r) + (x - r)\frac{\partial }{{\partial r}}{{K}_{{iu}}}(\beta r)} \right]} } \cos (\beta (z - y))d\beta du = \\ = \left( {1 + (x - r)\frac{\partial }{{\partial r}}} \right)\frac{T}{{2{{\pi }^{2}}GR}}\left[ {\frac{\pi }{2} - {\text{arctg}}\frac{R}{{2\sqrt {xr} }}} \right], \\ \end{gathered} $

поскольку производная ${\text{arctg(1/}}\sqrt r {\text{)}}$ неограниченна при r → 0. При выводе формулы (1.7) использована связь между комплексным и вещественным ПКЛ

(1.8)

$\int\limits_{\gamma - i\infty }^{\gamma + i\infty } {F(\mu ){{I}_{\mu }}(\beta r)d\mu = \frac{2}{\pi }\int\limits_0^\infty {\operatorname{sh} \pi uF(iu){{K}_{{iu}}}(\beta r)du,\quad F( - \mu ) = - F(\mu )} } ,$

а также значения интегралов [1, 3, 9]

$\int\limits_0^\infty {\int\limits_0^\infty {\operatorname{ch} \pi u} } {{K}_{{iu}}}(\beta x){{K}_{{iu}}}(\beta r)\cos (\beta (z - y))d\beta du = \frac{{{{\pi }^{2}}}}{{4R}}$

$\int\limits_0^\infty {\int\limits_0^\infty {\frac{{\text{1}}}{{\operatorname{ch} \pi u}}} } {{K}_{{iu}}}(\beta x){{K}_{{iu}}}(\beta r)\cos (\beta (z - y))d\beta du = \frac{\pi }{{2R}}{\text{arctg}}\frac{R}{{2\sqrt {xr} }}$

Кроме того, в формуле (1.7) нарушена симметрия по x, r (перемещение вдоль линии действия силы T должно удовлетворять теореме Бетти).

Полупространство с линией раздела граничных условий – частный случай трехмерного клина с углом раствора α, когда α = π. Возможность появления неединственных, неограниченных на ребре клина решений заложена в самой структуре представления Папковича–Нейбера (1.2), а именно, в членах

(1.9)

$\frac{{\partial {{\Phi }_{0}}}}{{\partial r}},\quad \frac{1}{r}\frac{{\partial {{\Phi }_{0}}}}{{\partial \varphi }}$

Пусть в выражение (1.3) для функции Φ₀ входит интеграл

$\int\limits_{\gamma - i\infty }^{\gamma + i\infty } {F(\mu ){{K}_{{iu}}}(\beta x){{I}_{\mu }}(\beta r)d\mu } ,$

где мероморфная функция-символ F(iu) по своему асимптотическому поведению при u → 0 и u → ∞ является функцией типа th αu или cth αu, а контур интегрирования совпадает с мнимой осью или лежит чуть правее мнимой оси, но левее ближайшего к мнимой оси полюса μ₁ функции F(μ). По теории вычетов будем замыкать этот контур в правую полуплоскость. Поскольку [8]

${{I}_{\mu }}(r) = O\left( {\frac{{{{{(r{\text{/}}2)}}^{\mu }}}}{{\Gamma (\mu + 1)}}} \right),\quad r \to 0{\text{ }}(\mu \ne - 1, - 2,\; \ldots )$

главный член в поведении величин (1.9) при r → 0 будет порядка ${{r}^{{\operatorname{Re} {{\mu }_{1}} - 1}}}$. Критическим является угол клина, при превышении которого полюс μ₁ проникает в полосу 0 < < Re μ < 1. В формуле (1.7) F(μ) = tgπμ и μ₁ = 0.5 (критический угол превышен).

С целью устранения возможности появления неограниченных решений члены (1.9) должны быть преобразованы при помощи соотношений (1.5) и сдвига контура интегрирования при достаточно малых углах α, поскольку ширина полосы регулярности функции F(μ) обратно пропорциональна α. В случае (1.7) α = π и критический угол π/2 для функции-символа уже превышен. Тем не менее, скорректируем фундаментальное решение (1.7) указанным образом и отбросим возникающий вычет, несущий особенность на ребре (преобразуем только член, дающий особенность, момент отбрасывания вычетов при сдвиге контура показан стрелкой)

$x\int\limits_0^\infty {\operatorname{sh} \pi u} {\text{ }}\operatorname{th} \pi u{{K}_{{iu}}}(\beta x)\frac{\partial }{{\partial r}}{{K}_{{iu}}}(\beta r)du = \frac{{\pi \beta x}}{{4i}}\int\limits_{\gamma - i\infty }^{\gamma + i\infty } {\operatorname{tg} \pi \mu } {{K}_{\mu }}(\beta x)\left[ {{{I}_{{\mu - 1}}}(\beta r) + {{I}_{{\mu + 1}}}(\beta r)} \right]d\mu \to $

$ \to \;\frac{{\pi \beta x}}{{4i}}\int\limits_{\gamma - i\infty }^{\gamma + i\infty } {\left[ {\operatorname{tg} {\text{(}}\pi (\mu + 1){\text{)}}{{K}_{{\mu + 1}}}(\beta x) + \operatorname{tg} {\text{(}}\pi (\mu - 1)){{K}_{{\mu - 1}}}(\beta x)} \right]} {{I}_{\mu }}(\beta r)d\mu = $

(1.10)

$ = \; - x\int\limits_0^\infty {\operatorname{sh} \pi u} \operatorname{th} \pi u{{K}_{{iu}}}(\beta r)\frac{\partial }{{\partial x}}{{K}_{{iu}}}(\beta x)du$

Теперь в решении (1.7) заменим исходный интеграл (1.10) на последний интеграл (1.10). Тогда получим перемещение в виде

${{u}_{r}}(r,\pi ,z) = \frac{T}{{{{\pi }^{3}}G}}\int\limits_0^\infty {\int\limits_0^\infty {\operatorname{sh} {\text{(}}\pi u{\text{)}}\operatorname{th} {\text{(}}\pi u{\text{)}}\left( {1 - x\frac{\partial }{{\partial x}} - r\frac{\partial }{{\partial r}}} \right)} } {{K}_{{iu}}}(\beta x){{K}_{{iu}}}(\beta r)\cos (\beta (z - y))d\beta du = $

(1.11)

$ = \;u_{r}^{ * }(r,\pi ,z)\left( {1 - \frac{2}{\pi }{\text{arctg}}\frac{R}{{2\sqrt {xr} }}} \right) - \frac{{T\sqrt {xr} {{{(z - y)}}^{2}}}}{{{{\pi }^{2}}G{{R}^{2}}[{{{(r + x)}}^{2}} + {{{(z - y)}}^{2}}]}}$

$u_{r}^{ * }(r,\pi ,z) = \frac{T}{{4\pi GR}} + \frac{{T{{{(r - x)}}^{2}}}}{{4\pi G{{R}^{3}}}}$

Оно симметрично по x и r, стремится к нулю при r → 0, удовлетворяет теореме Бетти, условию жесткой заделки и уравнениям теории упругости. Кроме того, это перемещение имеет четкий механический смысл: оно строго меньше перемещения $u_{r}^{{\text{*}}}(r,\pi ,z)$, возникающего в задаче Черрути [10] для несжимаемого полупространства, когда грань φ = 0 свободна от напряжений.

Ниже будет показано, что перемещение (1.11) может быть получено как частный случай решения задачи для клина, при модификации которого при острых углах клина сдвиг контура интегрирования проводится в полосе регулярности без возникновения вычетов.

2. Задача для клина. Рассмотрим несжимаемый упругий клин {0 ≤ r < ∞, 0 ≤ φ ≤ α, |z| < ∞} с модулем сдвига G, грань которого φ = 0 жестко заделана, а на грани φ = α действует радиальная касательная сосредоточенная сила T (средняя часть рис. 1), приложенная в точке r = x, z = y. Граничные условия имеют вид (1.1), где следует заменить φ = π на φ = α. Действуя, как в предыдущей задаче, получим точное решение для клина в форме (1.2), (1.3), где

${{a}_{0}} = {{a}_{2}} = 0,\quad {{a}_{1}} = - \frac{{{{T}_{1}}}}{{{{\Delta }_{0}}(\mu )}}[\mu ({{W}_{1}}(\mu ) - 2{{\cos }^{2}}\mu \alpha {{W}_{3}}(\mu )){{K}_{\mu }} + x{{W}_{0}}(\mu ){{W}_{2}}(\mu )K_{\mu }^{'}]$

${{b}_{0}} = {{T}_{1}}\frac{{x{{K}_{\mu }}}}{{2\cos \mu \alpha }},\quad {{b}_{1}} = - {{T}_{1}}\frac{{{{W}_{0}}(\mu )}}{{{{\Delta }_{0}}(\mu )}}({{K}_{\mu }} - xK_{\mu }^{'})$

${{b}_{2}} = \frac{{{{T}_{1}}}}{{{{\Delta }_{0}}(\mu )}}[({{W}_{1}}(\mu ) - \mu {{W}_{0}}(\mu ){{W}_{2}}(\mu )){{K}_{\mu }} + 2x{{\sin }^{2}}\alpha {{W}_{3}}(\mu )K_{\mu }^{'}]$

(2.1)

${{K}_{\mu }} = {{K}_{\mu }}(\left| \beta \right|x),\quad K_{\mu }^{'} = \frac{\partial }{{\partial x}}{{K}_{\mu }}$

${{W}_{0}}(\mu ) = \sin \alpha \cos \mu \alpha {\text{,}}\quad {{\Delta }_{0}}(\mu ) = {{\cos }^{2}}\mu \alpha - {{\mu }^{2}}{{\sin }^{2}}\alpha $

${{W}_{1}}(\mu ) = \mu \sin \alpha \sin \mu \alpha + \cos \alpha \cos \mu \alpha ,\quad {{\Delta }_{1}}(\mu ) = \cos 2\mu \alpha + \cos 2\alpha $

${{W}_{2}}(\mu ) = \frac{{\sin 2\mu \alpha + \mu \sin 2\alpha }}{{{{\Delta }_{1}}(\mu )}},\quad {{W}_{3}}(\mu ) = \frac{{{{W}_{1}}(\mu )}}{{{{\Delta }_{1}}(\mu )}}$

Из формул (1.2), (1.3) и (2.1) найдем радиальное перемещение

${{u}_{r}}(r,\alpha ,z) = \frac{T}{{2{{\pi }^{2}}Gi}}\int\limits_0^\infty {\cos (\beta (z - y))d\beta \int\limits_{\gamma - i\infty }^{\gamma + i\infty } {\left\{ {x\operatorname{tg} \mu \alpha {{K}_{\mu }}(\beta x)I_{\mu }^{'}(\beta r) + } \right.} } $

(2.2)

$\left. { + \;\left( {1 - r\frac{\partial }{{\partial r}}} \right)\frac{{{{I}_{\mu }}(\beta r)}}{{{{\Delta }_{0}}(\mu )}}[\sin 2\mu \alpha {{K}_{\mu }}(\beta x) - 2{{{\sin }}^{2}}\alpha ({{W}_{4}}(\mu ){{K}_{\mu }}(\beta x) - x{{W}_{2}}(\mu )K_{\mu }^{'}(\beta x))]} \right\}d\mu $

${{W}_{4}}(\mu ) = \mu \frac{{\mu \sin 2\mu \alpha + \sin 2\alpha }}{{{{\Delta }_{1}}(\mu )}},\quad I_{\mu }^{'}(\beta r) = \frac{\partial }{{\partial r}}{{I}_{\mu }}(\beta r)$

Главный член перемещения (2.2) на ребре клина имеет символ tgμα, критический угол α = π/2. Можно показать, что правая часть первого равенства (2.2) симметрична по r, x при α < π/2 (скрытая, неочевидная симметрия) и представляет единственное фундаментальное решение, ограниченное на ребре. При α > π/2 симметрия утрачивается и формула (2.2) представляет уже неединственное решение, неограниченное на ребре (при α = π формула (2.2) совпадает с формулой (1.7)).

Преобразуем главный член в формуле (2.2), сдвигая контур интегрирования и используя соотношения (1.5), при α < π/2 (в отличие от соотношения (1.10) полоса регулярности достаточно широкая, вычеты не возникают). В результате получим перемещение

${{u}_{r}}(r,\alpha ,z) = \frac{T}{{2{{\pi }^{2}}Gi}}\int\limits_0^\infty {\cos (\beta (z - y))d\beta } \times $

$\begin{gathered} \times \;\int\limits_{\gamma - i\infty }^{\gamma + i\infty } {\left\{ {\left( {\frac{{\mu \sin 2\alpha }}{{{{\Delta }_{1}}(\mu )}} + \frac{{\sin 2\mu \alpha - 2{{{\sin }}^{2}}\alpha {{W}_{4}}(\mu )}}{{2{{\Delta }_{0}}(\mu )}}} \right)} \right.} {{K}_{\mu }}(\beta x){{I}_{\mu }}(\beta r) - \\ - \;\frac{{{{{\sin }}^{2}}\alpha }}{{{{\Delta }_{0}}(\mu )}}{{W}_{2}}(\mu )xK_{\mu }^{'}(\beta x)rI_{\mu }^{'}(\beta r) + \\ \end{gathered} $

(2.3)

$\left. { + \;\left( {\frac{{{{{\sin }}^{2}}\alpha }}{{{{\Delta }_{0}}(\mu )}}{{W}_{2}}(\mu ) - \frac{{\sin 2\mu \alpha }}{{{{\Delta }_{1}}(\mu )}}} \right)[xK_{\mu }^{'}(\beta x){{I}_{\mu }}(\beta r) + {{K}_{\mu }}(\beta x)rI_{\mu }^{'}(\beta r)]} \right\}d\mu $

с явной симметрией по r и x (после перехода к вещественной форме ПКЛ, см. формулу (1.8)), представляющее единственное фундаментальное решение при всех α, ограниченное на ребре, которое при α < π/2 совпадает с выражением (2.2), а при α = π – с формулой (1.11).

Для предельного перехода к фундаментальному решению задачи о плоской деформации клина проинтегрируем обе части формулы (2.3) по z при |z| < ∞ и вычислим возникающий интеграл с функцией Дирака, учитывая соотношение [8]

${{I}_{\mu }}(\beta r){{K}_{\mu }}(\beta x) = O\left( {\frac{{{{{(r{\text{/}}x)}}^{\mu }}}}{{2\mu }}} \right)\quad (\beta \to 0)$

Тогда получим

${{u}_{r}}(r,\alpha ) = \int\limits_{ - \infty }^\infty {{{u}_{r}}(r,\alpha ,z)dz = } \frac{T}{{8\pi Gi}}\int\limits_{\gamma - i\infty }^{\gamma + i\infty } {\frac{{\sin 2\mu \alpha + \mu \sin 2\alpha }}{{\mu {{\Delta }_{0}}(\mu )}}{\text{ }}} {{\left( {\frac{r}{x}} \right)}^{\mu }}d\mu ,$

что в точности совпадает с известным решением ([6], формула (5.3) при ν = 0.5).

3. Скрытая симметрия. Приведем пример фундаментального решения со скрытой симметрией, которое не обязательно следует приводить к форме с явной симметрией, поскольку критический угол не достигается.

Пусть радиальная сосредоточенная сила T действует в срединной полуплоскости упругого клина с углом раствора 2α, внешние грани которого находятся в условиях скользящей заделки (правая часть рис. 1). В силу симметрии по φ рассматриваем задачу для половины клина с граничными условиями

(3.1)

$\begin{gathered} \varphi = 0{\text{:}}\quad {{u}_{\varphi }} = {{\tau }_{{\varphi z}}} = 0,\quad {{\tau }_{{r\varphi }}} = \frac{T}{2}\delta (r - x)\delta (z - y) \\ \varphi = \alpha {\text{:}}\quad {{u}_{\varphi }} = {{\tau }_{{r\varphi }}} = {{\tau }_{{\varphi z}}} = 0 \\ \end{gathered} $

Эта задача также имеет точное решение [11, 12]. Перемещение вдоль линии действия силы здесь имеет вид (ν – коэффициент Пуассона)

(3.2)

$\begin{gathered} {{u}_{r}}(r,0,z) = \frac{T}{{4(1 - \nu ){{\pi }^{3}}G}}\int\limits_0^\infty {\int\limits_0^\infty {\operatorname{sh} \pi u\cos (\beta (z - y))} } \left[ {\operatorname{cth} \alpha u{\text{ }}x\frac{\partial }{{\partial r}} + } \right. \\ \left. { + \;\frac{{\operatorname{sh} 2\alpha u}}{{\operatorname{ch} 2\alpha u - \cos 2\alpha }}\left( {\kappa - r\frac{\partial }{{\partial r}}} \right)} \right]{{K}_{{iu}}}(\beta x){{K}_{{iu}}}(\beta r)dud\beta \\ \kappa = 3 - 4\nu \\ \end{gathered} $

Симметрия этого выражения по r и x является скрытой, неочевидной и может быть проверена при любых углах клина 2α (0 < α ≤ π) путем разложения в степенной ряд ([11], формулы (2.10) и (2.11), см. коэффициенты разложения в табл. 1). При α = π формула (3.2) дает фундаментальное решение Кельвина [10–12].

Причина симметрии, единственности и ограниченности на ребре фундаментального решения (3.2) заключается в том, что если в нем перейти от вещественного к комплексному ПКЛ по формуле (1.8), то возникающая главная (при r → 0) функция-символ ctg μα при 0 < α ≤ π не имеет полюсов в полосе 0 < Re μ < 1. Преобразуем главный член (при r → 0) в выражении (3.2) аналогично преобразованию (1.10):

$\int\limits_0^\infty {\operatorname{sh} \pi u} \operatorname{cth} \alpha u{{K}_{{iu}}}(\beta x)\frac{\partial }{{\partial r}}{{K}_{{iu}}}(\beta r)du = \frac{{\pi i}}{2}\int\limits_{\gamma - i\infty }^{\gamma + i\infty } {\operatorname{ctg} \alpha \mu {{K}_{\mu }}(\beta x)\frac{\partial }{{\partial r}}{{I}_{\mu }}(\beta r)d\mu } {\text{ }} = $

$\begin{gathered} = \;\frac{{\pi \beta i}}{4}\int\limits_{\gamma - i\infty }^{\gamma + i\infty } {\operatorname{ctg} \alpha \mu {{K}_{\mu }}(\beta x)\left[ {{{I}_{{\mu - 1}}}(\beta r) + {{I}_{{\mu + 1}}}(\beta r)} \right]d\mu } = \\ = \frac{{\pi \beta i}}{4}\int\limits_{\gamma - i\infty }^{\gamma + i\infty } {\left[ {\operatorname{ctg} {\text{(}}\alpha (\mu + 1){\text{)}}{{K}_{{\mu + 1}}}(\beta x) + \operatorname{ctg} {\text{(}}\alpha (\mu - 1)){{K}_{{\mu - 1}}}(\beta x)} \right]{{I}_{\mu }}(\beta r)d\mu = } \\ \end{gathered} $

$ = \; - \int\limits_0^\infty {\operatorname{sh} \pi u} {\text{ }}\frac{{\operatorname{sh} 2\alpha uK_{{iu}}^{'}(\beta x) + u\sin 2\alpha {\text{ }}{{x}^{{ - 1}}}{{K}_{{iu}}}(\beta x)}}{{\operatorname{ch} 2\alpha u - \cos 2\alpha }}{{K}_{{iu}}}(\beta r)du$

После подстановки последнего интеграла (3.3) в выражение (3.2) оно приобретает форму явной симметрии по r и x.

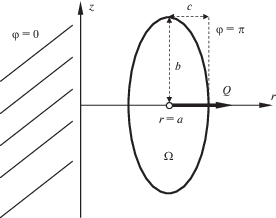
4. Задача о накладке. В качестве примера использования фундаментального решения (1.11) задачи Уфлянда рассмотрим собственно смешанную задачу о тонкой нерастяжимой абсолютно гибкой накладке, контактирующей с гранью φ = π несжимаемого полупространства (грань φ = 0 жестко заделана, рис. 2). Накладка полностью сцеплена по эллиптической области Ω = {(r – a)²/c² + z²/b² ≤ 1}, которая вытянута вдоль линии раздела r = 0 настолько, что в ней можно пренебречь касательным напряжением τ_φz, полагая σ_φ = τ_φz = 0. Вне области Ω грань φ = π не нагружена. К центру накладки вдоль оси r приложена сила Q, под действием которой накладка смещается на величину u_r = ω. Интегрируя решение (1.11) по области Ω и заменяя в нем T на неизвестное контактное напряжение τ_rφ = τ(r, z), приходим к интегральному уравнению (ИУ)

(4.1)

$\iint\limits_\Omega {\frac{{\tau (r,z)}}{G}\left[ {\frac{1}{R} + \frac{{{{{(r - x)}}^{2}}}}{{{{R}^{3}}}} + F(x,y,r,z)} \right]}dxdy = 4\pi \omega ,\quad (r,z) \in \Omega \,,$

где гладкая часть ядра имеет вид

(4.2)

$F(x,y,r,z) = \left( {x\frac{\partial }{{\partial x}} + r\frac{\partial }{{\partial r}} - 1} \right)\frac{{\text{2}}}{{\pi R}}{\text{arctg}}\frac{R}{{2\sqrt {xr} }}$

Рис. 2.

Для решения ИУ (4.1) применим регулярный асимптотический метод [3–6], эффективный для накладки, относительно удаленной от линии раздела. Введем обозначения безразмерных величин

(4.3)

$\begin{gathered} {{r}_{0}} = \frac{{r - a}}{b},\quad {{z}_{0}} = \frac{z}{b},\quad {{\omega }_{0}} = \frac{\omega }{b},\quad \lambda = \frac{a}{b} \\ \varepsilon = \frac{c}{b},\quad {{\tau }_{{\text{0}}}}({{r}_{0}},{{z}_{0}}) = \frac{{\tau (r,z)}}{{2G}},\quad {{Q}_{0}} = \frac{Q}{{2G{{b}^{2}}}} \\ \end{gathered} $

и т.д., нулевой индекс далее опускаем. Параметр λ характеризует относительную удаленность области Ω от линии раздела. Можно показать, что при $\lambda > \max (1,\sqrt 2 \varepsilon )$ гладкая часть ядра разлагается в абсолютно сходящийся ряд по отрицательным степеням λ с полиномиальными коэффициентами относительно переменных:

(4.4)

$F(x + \lambda ,y,r + \lambda ,z) = \frac{A}{\lambda } - \frac{{A(x + r)}}{{2{{\lambda }^{2}}}} + O\left( {\frac{1}{{{{\lambda }^{3}}}}} \right)\quad (\lambda \to \infty ),\quad A = - \frac{2}{\pi }$

При выводе формулы (4.4) использовано разложение в степенной ряд arctgz при |z| < 1 [8] и ряды биномиального типа.

Разыскивая решение уравнения (4.1), (4.2) при учете соотношений (4.3) и (4.4) в форме ряда по отрицательным степеням λ, приравнивая члены при одинаковых степенях λ, получим цепочку ИУ, каждое из которых решается в замкнутой форме [5, 6]. В результате получим асимптотическое решение

$\tau (r,z) = \frac{\omega }{\varepsilon }\left( {{{P}_{0}} + \frac{{{{P}_{1}}}}{\lambda } + \frac{{{{P}_{2}} + {{P}_{3}}r}}{{{{\lambda }^{2}}}} + O\left( {\frac{1}{{{{\lambda }^{3}}}}} \right)} \right){{\left[ {1 - \frac{{{{r}^{2}}}}{{{{\varepsilon }^{2}}}} - {{z}^{2}}} \right]}^{{ - 1/2}}}\quad (\lambda \to \infty )$

(4.5)

$\begin{gathered} {{P}_{0}} = \frac{1}{B},\quad {{P}_{1}} = - \frac{A}{{{{B}^{2}}}},\quad {{P}_{2}} = \frac{{{{A}^{2}}}}{{{{B}^{3}}}} \\ {{P}_{3}} = \frac{{A(2{{S}_{{20}}} - {{\varepsilon }^{2}}{{S}_{{11}}})}}{{2{{\varepsilon }^{2}}B\left[ {(2{{\varepsilon }^{2}}{{S}_{{02}}} - {{S}_{{11}}})(2{{S}_{{20}}} - {{\varepsilon }^{2}}{{S}_{{11}}}) - (3{{S}_{{11}}} - {{S}_{{01}}})(3{{\varepsilon }^{2}}{{S}_{{11}}} - {{S}_{{10}}})} \right]}} \\ \end{gathered} $

$B = {{S}_{{00}}} + {{\varepsilon }^{2}}{{S}_{{01}}},{\text{ }}{{S}_{{mn}}} = \int\limits_0^{\pi /2} {\frac{{{{{\cos }}^{{2m}}}t{{{\sin }}^{{2n}}}tdt}}{{{{{(1 - {{k}^{2}}{{{\sin }}^{2}}t)}}^{{m + n + 1/2}}}}}\quad ({{k}^{2}} = 1 - {{\varepsilon }^{2}})} $

Интегралы S_mn выражаются через полные эллиптические интегралы ([4], с. 45). Контактные напряжения (4.5) больше на той половине области контакта, которая ближе к линии раздела.

При помощи выражения (4.5) найдем связь между силой Q и перемещением ω в виде

(4.6)

$Q = \iint\limits_\Omega {\tau (r,z)drdz} = 2\pi \omega {\text{ }}\left( {{{P}_{0}} + \frac{{{{P}_{1}}}}{\lambda } + \frac{{{{P}_{2}}}}{{{{\lambda }^{2}}}} + O\left( {\frac{1}{{{{\lambda }^{3}}}}} \right)} \right)\quad (\lambda \to \infty )$

В пределе при λ → ∞ асимптотики (4.5) и (4.6) совпадают с точным решением задачи о накладке на несжимаемом полупространстве, граница которого вне области контакта свободна от напряжений [6].

Заключение. Аналогично изложенному выше может быть получено решение задачи Уфлянда при любом значении коэффициента Пуассона и произвольной заданной нагрузке при φ = π. Полупространство с линией раздела граничных условий следует рассматривать как частный случай клина, на одной грани которого заданы перемещения, а на другой – напряжения. Проблему выбора единственного решения уравнений упругого равновесия в перемещениях, ограниченного на ребре клина, можно решить, преобразуя члены (1.9) путем сдвига контура интегрирования в комплексном интеграле Конторовича–Лебедева (1.3) при достаточно малых углах раствора клина (в полосе регулярности, ширина которой обратно пропорциональна углу клина), используя соотношения (1.5). При этом перемещение вдоль линии действия силы, пропорциональное этой силе, приобретает форму явной симметрии и удовлетворяет теореме Бетти (возможность скрытой симметрии заложена в самой структуре представления Папковича–Нейбера). Преобразованные решения должны быть ограниченными на ребре и единственными при любых углах клина.

Указанное преобразование членов (1.9) рекомендуется совершать и в других краевых задачах для трехмерного клина во избежание возникновения неединственных решений, неограниченных на ребре при превышении критических углов клина. При таких углах клина происходит бифуркация фундаментального решения, представленного в форме со скрытой симметрией (в не преобразованной форме), для перемещения вдоль линии силы, характерно нарушение симметрии и теоремы Бетти, что и свидетельствует о постороннем решении.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (18-01-00017).

Список литературы

Уфлянд Я.С. Интегральные преобразования в задачах теории упругости. Л.: Наука, 1967. 402 с.
Улитко А.Ф. Метод собственных векторных функций в пространственных задачах теории упругости. Киев: Наук. думка, 1979. 263 с.
Александров В.М., Пожарский Д.А. Неклассические пространственные задачи механики контактных взаимодействий упругих тел. М.: Факториал, 1998. 288 с.
Alexandrov V.M., Pozharskii D.A. Three-dimensional Contact Problems. Dordrecht: Kluwer, 2001. 406 p.
Пожарский Д.А. Контакт со сцеплением гибких накладок и упругого клина // Изв. РАН. МТТ. 2004. № 4. С. 58–68.
Александров В.М., Сметанин Б.И., Соболь Б.В. Тонкие концентраторы напряжений в упругих телах. М.: Наука, 1993. 224 с.
Лурье А.И. Теория упругости. М.: Наука, 1970. 940 с.
Handbook of Mathematical Functions. Edited by M. Abramowitz and I. Stigan. New York: Dover, 1964.
Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Наука, 1971. 1108 с.
Hahn H.G. Elastizitätstheorie. Stuttgart: Teubner, 1985.
Александров В.М., Пожарский Д.А. Задача о включении в трехмерном упругом клине // ПММ. 2002. Т. 66. Вып. 4. С. 635–646.
Пожарский Д.А. Обобщение фундаментальных решений Миндлина и лорда Кельвина классической теории упругости // Докл. АН. 2001. Т. 380. № 4. С. 487–490.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал