1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 83, № 4, 2019

Прикладная математика и механика, 2019, T. 83, № 4, стр. 549-561

ПЕРЕДВИЖЕНИЕ ТЯЖЕЛОГО ТВЕРДОГО ТЕЛА, ПОДВЕШЕННОГО НА ТРОСЕ ПЕРЕМЕННОЙ ДЛИНЫ, С УСТРАНЕНИЕМ КОЛЕБАНИЙ

С. В. Русских 1, 2, *, Ф. Н. Шклярчук 2, 1, **

1 Московский авиационный институт (НИУ)
Москва, Россия

2 Институт прикладной механики РАН
Москва, Россия

* E-mail: sergey.russkih@rambler.ru
** E-mail: shklyarchuk@list.ru

Поступила в редакцию 25.10.2018
После доработки 23.01.2019
Принята к публикации 19.03.2019

Полный текст (PDF)

Аннотация

Рассматривается нелинейная задача конечного передвижения тяжелого твердого тела, подвешенного на нерастяжимом безынерционном тросе переменной длины с управляемым горизонтальным перемещением точки подвеса. Требуется переместить тело за определенное время из начального положения покоя в заданное конечное положение покоя с устранением колебаний в конце операции. Закон изменения длины троса считается заданным, а управляемое перемещение точки его подвеса – неизвестным. Приближенное решение задачи кинематического управления колебаниями системы, описываемой двумя нелинейными дифференциальными уравнениями с переменными коэффициентами для умеренно больших углов поворота натянутого троса и тела, ищется в рядах с неизвестными коэффициентами по методу Бубнова–Галёркина с использованием заданных базисных функций времени, удовлетворяющих некоторым начальным и конечным условиям. Ускорение точки подвеса троса ищется в виде конечного ряда по синусам с неизвестными коэффициентами. Получена связанная система нелинейных алгебраических уравнений для всех неизвестных коэффициентов, в которую входят уравнения метода Бубнова–Галёркина и нефиксированные при выборе базисных функций начальные и конечные данные. Эта система уравнений решается по методу последовательных приближений с использованием в первом приближении решений линеаризованных уравнений. На примерах системы с тросом постоянной и переменной длины выполнены расчеты с анализом точности решений путем сравнения их с численными решениями нелинейных дифференциальных уравнений прямой задачи по методу Адамса при найденных законах управления.

Ключевые слова: тело на тросе, трос переменной длины, нелинейные колебания, устранение колебаний, терминальное управление, подъемно-транспортные механизмы

Введение. Задачи управления составными трансформируемыми системами, которые совершают конечные передвижения (перемещения и повороты), актуальны при исследовании подъемно-транспортных механизмов [1, 2], манипуляционных роботов [3, 4], виброударных систем [5, 6], ракет с разделяющимися ступенями [7], космических конструкций [8–11] и пр.

Общие вопросы теории управления большими системами, включая задачи управляемого передвижения системы из одного состояния в другое, рассмотрены во многих известных монографиях ([1, 12–14] и др.). В большинстве работ упругие колебания, которые сопровождают нестационарные конечные передвижения систем или их частей, считаются малыми и в случае систем с постоянными параметрами описываются нормальными координатами, которые представляют относительные движения по собственным формам колебаний [1, 3, 15–21]. Точные решения линейных уравнений для нормальных координат записываются в виде интеграла, зависящего от неизвестных управляющих воздействий.

Для управления колебаниями по нескольким низшим собственным формам управляющие воздействия обычно ищутся в виде кусочно-линейных функций с неизвестными параметрами [1, 3] или в виде рядов заданных функций времени с неизвестными коэффициентами [15–20]. При этом в качестве заданных функций используются синусы и косинусы с частотами собственных колебаний [15–17]. В результате получаются высокочастотные, по отношению к рассматриваемому конечному времени управления, управляющие воздействия, вызывающие “ответные” колебания приводов и несущих конструкций. Кроме того, управляемая система при высокочастотном управляющем воздействии будет неробастной – малые отклонения по времени от установленного интервала управления или малые расхождения по динамическим характеристикам расчетной модели и реальной системы могут приводить к большим ошибкам. Поэтому управляющие функции должны быть достаточно простыми и гладкими, чтобы при пассивном управлении их можно было практически реализовать с помощью жестких приводов.

Был предложен [19, 20] альтернативный подход к определению силовых или кинематических управляющих воздействий при передвижении упругой системы за определенное время из одного состояния в другое с устранением упругих колебаний по нескольким низшим собственным формам. Для этого используются “простые” управляющие финитные функции (например, в виде одной волны синусоиды) при условии, что частоты подлежащих устранению собственных форм колебаний системы “настраиваются” в определенных соотношениях со временем управления. Необходимые для настройки собственные частоты получаются [21] путем минимизации квадратичного функционала с вариацией определенных параметров системы.

Рассмотрены колебания двойного маятника с вибрирующей точкой подвеса [22, 23], устойчивость управляемых движений такого маятника переменной длины [24] и управление пространственным движением многозвенного маятника [25].

Решение задач управления колебаниями упругих нелинейных систем и систем с переменными параметрами представляет большие математические и вычислительные трудности. Такие задачи обычно решаются различными приближенными и численными методами [26].

В данной работе для решения нелинейной задачи конечного перемещения за определенное время тяжелого твердого тела, подвешенного на тросе переменной длины, из одного положения покоя в другое за счет управляемого горизонтального перемещения точки подвеса предложен новый подход с одновременным использованием метода Бубнова–Галёркина и метода последовательных приближений.

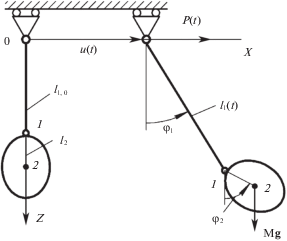
1. Постановка задачи. Рассмотрим плоскую задачу передвижения за определенное время $T$ тяжелого абсолютно твердого тела, подвешенного на тросе, из начального положения покоя в конечное положение покоя за счет заданного изменения длины троса и управляемого горизонтального перемещения точки его подвеса, рис. 1. Тело соединено с концом троса в точке 1, расположенной выше центра тяжести тела (точка 2) на расстоянии ${{l}_{2}}$. Рассматриваются два варианта пассивного управления системой: 1) динамическое (силовое) управление – определяется закон изменения горизонтальной силы $P(t)$ в точке подвеса, 2) кинематическое управление – определяется закон перемещения точки подвеса $u(t)$. В первом варианте в качестве обобщенных координат рассматриваются перемещение $u(t)$ и углы поворота натянутого троса ${{\varphi }_{1}}(t)$ и тела ${{\varphi }_{2}}(t)$, во втором варианте – только углы ${{\varphi }_{1}}(t)$ и ${{\varphi }_{2}}(t)$. Начальные условия при $t = 0$ и конечные условия при $t = T$, представляющие устойчивые положения покоя системы, записываются в виде

(1.1)
где ${{u}_{T}}$ – заданное конечное горизонтальное перемещение точки подвеса троса.

Рис. 1.

Твердое тело, подвешенное на тросе переменной длины.

Трос будем считать нерастяжимым, его инерцией будем пренебрегать и будем полагать, что его длина ${{l}_{1}}(t)$ изменяется за счет продольного перемещения верхнего конца по заданному закону при условиях

(1.2)
${{\dot {l}}_{1}}(0) = 0,\quad {{l}_{1}}(0) = {{l}_{{1,0}}},\quad {{\dot {l}}_{1}}(T) = 0,\quad {{l}_{1}}(T) = {{l}_{{1,T}}}$

Необходимо, чтобы усилие в тросе при $0 \leqslant t \leqslant T$ было растягивающим (чтобы он оставался прямолинейным). В частном случае длина троса может быть постоянной (${{l}_{1}} = const$, ${{\dot {l}}_{1}} = 0$).

Координаты центра тяжести тела при $0 \leqslant t \leqslant T$:

(1.3)
${{x}_{2}} = u + {{l}_{1}}\sin {{\varphi }_{1}} + {{l}_{2}}\sin {{\varphi }_{2}},\quad {{z}_{2}} = {{l}_{1}}\cos {{\varphi }_{1}} + {{l}_{2}}\cos {{\varphi }_{2}}$

Задача заключается в следующем: найти закон изменения управляющей силы $P(t)$ или управляющего перемещения $u(t)$, при которых тело за определенное время $T$ перемещается из начального положения покоя

${{x}_{2}} = 0,\quad {{z}_{2}} = {{l}_{{1,0}}} + {{l}_{2}},\quad {{\varphi }_{1}} = {{\varphi }_{2}} = 0\quad {\text{при}}\quad t = 0$
в заданное конечное положение покоя
${{x}_{2}} = {{u}_{T}},\quad {{z}_{2}} = {{l}_{{1,T}}} + {{l}_{2}},\quad {{\varphi }_{1}} = {{\varphi }_{2}} = 0,\quad {\text{при}}\quad t = T$
с устранением колебаний при $t \geqslant T$. Здесь эту задачу будем решать в нелинейной постановке для умеренно больших углов поворота троса и тела ($\left| {{{\varphi }_{1}}} \right|$, $\left| {{{\varphi }_{2}}} \right| < 1$ в радианах).

2. Уравнения движения. Уравнения движения рассматриваемой системы получим по методу Лагранжа в обобщенных координатах. Кинетическая энергия системы и вариация работы управляющей силы $P$ и силы тяжести тела $Mg$

$K = \frac{1}{2}M(\dot {x}_{2}^{2} + \dot {z}_{2}^{2}) + \frac{1}{2}{{J}_{2}}\dot {\varphi }_{2}^{2},\quad \delta A = P\delta u + Mg\delta {{z}_{2}}$
с учетом равенств (1.3) записываются в виде
(2.1)
$\begin{gathered} K = \frac{1}{2}M{{{\dot {u}}}^{2}} + \frac{1}{2}M[\dot {l}_{1}^{2} + l_{1}^{2}\dot {\varphi }_{1}^{2} + l_{2}^{2}\dot {\varphi }_{2}^{2} + 2\dot {u}{{{\dot {l}}}_{1}}\sin {{\varphi }_{1}} + \\ + \;2\dot {u}{{l}_{1}}{{{\dot {\varphi }}}_{1}}\cos {{\varphi }_{1}} + 2\dot {u}{{l}_{2}}{{{\dot {\varphi }}}_{2}}\cos {{\varphi }_{2}} + 2{{{\dot {l}}}_{1}}{{l}_{2}}{{{\dot {\varphi }}}_{2}}\sin ({{\varphi }_{1}} - {{\varphi }_{2}}) + 2{{l}_{1}}{{l}_{2}}{{{\dot {\varphi }}}_{1}}{{{\dot {\varphi }}}_{2}}\cos ({{\varphi }_{1}} - {{\varphi }_{2}})] + \frac{1}{2}{{J}_{2}}\dot {\varphi }_{2}^{2} \\ \delta A = P\delta u - Mg({{l}_{1}}\sin {{\varphi }_{1}}\delta {{\varphi }_{1}} + {{l}_{2}}\sin {{\varphi }_{2}}\delta {{\varphi }_{2}}), \\ \end{gathered} $
где $M$ и ${{J}_{2}}$ – масса и центральный массовый момент инерции тела, $g$ – ускорение силы тяжести.

Уравнения Лагранжа для $u$, ${{\varphi }_{1}}$ и ${{\varphi }_{2}}$ после деления их, соответственно, на $M$, $M{{l}_{1}}$ и $M{{l}_{2}}$ будут:

(2.2)
$\ddot {u} + {{\ddot {l}}_{1}}\sin {{\varphi }_{1}} + 2{{\dot {l}}_{1}}{{\dot {\varphi }}_{1}}\cos {{\phi }_{1}} + {{l}_{1}}{{\ddot {\varphi }}_{1}}\cos {{\varphi }_{1}} - {{l}_{1}}\dot {\varphi }_{1}^{2}\sin {{\varphi }_{1}} + {{l}_{2}}{{\ddot {\varphi }}_{2}}\cos {{\varphi }_{2}} - {{l}_{2}}\dot {\varphi }_{2}^{2}\sin {{\varphi }_{2}} = \frac{1}{M}P$
(2.3)
$\ddot {u}\cos {{\varphi }_{1}} + {{l}_{1}}{{\ddot {\varphi }}_{1}} + {{l}_{2}}{{\ddot {\varphi }}_{2}}\cos ({{\varphi }_{1}} - {{\varphi }_{2}}) + {{l}_{2}}\dot {\varphi }_{2}^{2}\sin ({{\varphi }_{1}} - {{\varphi }_{2}}) + 2{{\dot {l}}_{1}}{{\dot {\varphi }}_{1}} + g\sin {{\varphi }_{1}} = 0$
(2.4)
$\begin{gathered} \ddot {u}\cos {{\varphi }_{2}} + {{l}_{1}}{{{\ddot {\varphi }}}_{1}}\cos ({{\varphi }_{1}} - {{\varphi }_{2}}) + \left( {{{l}_{2}} + \frac{{{{J}_{2}}}}{{M{{l}_{2}}}}} \right){{{\ddot {\varphi }}}_{2}} - {{l}_{1}}\dot {\varphi }_{1}^{2}\sin ({{\varphi }_{1}} - {{\varphi }_{2}}) + \\ + \;2{{{\dot {l}}}_{1}}{{{\dot {\varphi }}}_{1}}\cos ({{\varphi }_{1}} - {{\varphi }_{2}}) + {{{\ddot {l}}}_{1}}\sin ({{\varphi }_{1}} - {{\varphi }_{2}}) + g\sin {{\varphi }_{2}} = 0 \\ \end{gathered} $

Для случая малых колебаний (при $\sin \varphi \approx \varphi $, $\cos \varphi \approx 1$) уравнения (2.2)–(2.4) линеаризуются и принимают, соответственно, вид

(2.5)
$\ddot {u} + {{\ddot {l}}_{1}}{{\varphi }_{1}} + 2{{\dot {l}}_{1}}{{\dot {\varphi }}_{1}} + {{l}_{1}}{{\ddot {\varphi }}_{1}} + {{l}_{2}}{{\ddot {\varphi }}_{2}} = \frac{1}{M}P$
(2.6)
$\ddot {u} + {{l}_{1}}{{\ddot {\varphi }}_{1}} + {{l}_{2}}{{\ddot {\varphi }}_{2}} + 2{{\dot {l}}_{1}}{{\dot {\varphi }}_{1}} + g{{\varphi }_{1}} = 0$
(2.7)
$\ddot {u} + {{l}_{1}}{{\ddot {\varphi }}_{1}} + \left( {{{l}_{2}} + \frac{{{{J}_{2}}}}{{M{{l}_{2}}}}} \right){{\ddot {\varphi }}_{2}} + 2{{\dot {l}}_{1}}{{\dot {\varphi }}_{1}} + {{\ddot {l}}_{1}}{{\varphi }_{1}} + (g - {{\ddot {l}}_{1}}){{\varphi }_{2}} = 0$

Если из уравнения (2.2) определить величину $\ddot {u}$ и подставить ее в уравнения (2.3) и (2.4), то после исключения $\ddot {u}$ они запишутся в виде

${{l}_{1}}{{\ddot {\varphi }}_{1}}{{\sin }^{2}}{{\varphi }_{1}} + {{l}_{2}}{{\ddot {\varphi }}_{2}}\sin {{\varphi }_{1}}\sin {{\varphi }_{2}} + 2{{\dot {l}}_{1}}{{\dot {\varphi }}_{1}}{{\sin }^{2}}{{\varphi }_{1}} + $
$ + \;{{l}_{1}}\dot {\varphi }_{1}^{2}\sin {{\varphi }_{1}}\cos {{\varphi }_{1}} + {{l}_{2}}\dot {\varphi }_{2}^{2}\sin {{\varphi }_{1}}\cos {{\varphi }_{2}} + $
$ + \;(g - {{\ddot {l}}_{1}}\cos {{\varphi }_{1}})\sin {{\varphi }_{1}} + \frac{1}{M}P\cos {{\varphi }_{1}} = 0$
${{l}_{1}}{{\ddot {\varphi }}_{1}}\sin {{\varphi }_{1}}\sin {{\varphi }_{2}} + \left( {{{l}_{2}}{{{\sin }}^{2}}{{\varphi }_{2}} + \frac{{{{J}_{2}}}}{{M{{l}_{2}}}}} \right){{\ddot {\varphi }}_{2}} + 2{{\dot {l}}_{1}}{{\dot {\varphi }}_{1}}\sin {{\varphi }_{1}}\sin {{\varphi }_{2}} + $
$ + \;{{l}_{1}}\dot {\varphi }_{1}^{2}\cos {{\varphi }_{1}}\sin {{\varphi }_{2}} + {{l}_{2}}\dot {\varphi }_{2}^{2}\sin {{\varphi }_{2}}\cos {{\varphi }_{2}} + $
$ + \;(g - {{\ddot {l}}_{1}}\cos {{\varphi }_{1}})\sin {{\varphi }_{2}} + \frac{1}{M}P\cos {{\varphi }_{2}} = 0$

Эти уравнения можно использовать при управлении системой силой $P(t)$.

Чтобы найти перемещение $u(t)$, запишем уравнение (2.2) в виде

$\ddot {u} + \frac{{{{d}^{2}}}}{{d{{t}^{2}}}}({{l}_{1}}\sin {{\varphi }_{1}} + {{l}_{2}}\sin {{\varphi }_{2}}) = \frac{1}{M}P$
и проинтегрируем его дважды с учетом начальных условий (1.1) при $t = 0$:

(2.10)
$\begin{gathered} \dot {u} = \frac{1}{M}\int\limits_0^t {P({{t}_{1}})d} {{t}_{1}} - ({{{\dot {l}}}_{1}}\sin {{\varphi }_{1}} + {{l}_{1}}{{{\dot {\varphi }}}_{1}}\cos {{\varphi }_{1}} + {{l}_{2}}{{{\dot {\varphi }}}_{2}}\cos {{\varphi }_{2}}) \\ u = \frac{1}{M}\int\limits_0^t {P({{t}_{1}})(t - {{t}_{1}})d} {{t}_{1}} - ({{l}_{1}}\sin {{\varphi }_{1}} + {{l}_{2}}\sin {{\varphi }_{2}}) \\ \end{gathered} $

Удовлетворяя конечные условия (1.1) при $t = T$, получим

(2.11)
$\int\limits_0^T {\ddot {u}(t)dt} = 0,\quad \int\limits_0^T {P(t)dt} = 0,\quad \int\limits_0^T {P(t)tdt} + {{u}_{T}} = 0$

Для случая малых колебаний при силовом управлении вместо (2.8) и (2.9) используются соответствующие им линеаризованные уравнения

(2.12)
$(g - {{\ddot {l}}_{1}}){{\varphi }_{1}} + \frac{1}{M}P = 0,\quad \frac{{{{J}_{2}}}}{{M{{l}_{2}}}}{{\ddot {\varphi }}_{2}} + (g - {{\ddot {l}}_{1}}){{\varphi }_{2}} + \frac{1}{M}P = 0$

Из первого уравнения (2.12) следует, что при малых колебаниях сила $P(t)$ должна удовлетворять таким же начальным и конечным условиям как ${{\varphi }_{1}}(t)$:

(2.13)
$P(0) = 0,\quad \dot {P}(0) = 0,\quad P(T) = 0,\quad \dot {P}(T) = 0$

Управляющая сила $P(t)$ ищется в виде финитной функции на интервале $0 \leqslant t \leqslant T$, которая удовлетворяет второму и третьему интегральным условиям (2.11) и начальным и конечным условиям (2.14). При выбранных путем проб с использованием уравнений (2.12) значениях $T$ и ${{u}_{T}}$, а также функции ${{l}_{1}}(t)$, решение при действии силы $P(t)$ должно быть физически осуществимым (трос должен оставаться натянутым и прямолинейным). Для этого усилие натяжения троса $N$, которое можно определить из уравнения равновесия его верхнего конца

(2.14)
$N\sin {{\varphi }_{1}} + P = 0$
должно быть положительным, т.е. $N(t) > 0$.

В случае кинематического управления рассматриваемой системой с помощью ускорения $\ddot {u}(t)$ задача описывается уравнениями (2.3) и (2.4). Функция $\ddot {u}(t)$ ищется в классе финитных функций при $0 \leqslant t \leqslant T$, удовлетворяющих первому условию (2.11). Кроме того, решения уравнений (2.3) и (2.4), линейно зависящих от ускорения $\ddot {u}(t)$, должны удовлетворять начальным и конечным условиям (1.1). При кинематическом управлении реакция $P(t)$ определяется из уравнения (2.2); затем из уравнения (2.14) находится усилие натяжения троса $N$. Можно получить другие тождественные выражения $N(t)$ в зависимости от параметров движения системы $u(t)$, ${{\varphi }_{1}}(t)$, ${{\varphi }_{2}}(t)$, если для преобразований использовать уравнения (2.2)–(2.4) и (2.8), (2.9). Например, умножив уравнения (2.3) на $\cos {{\varphi }_{1}}$ и вычтя из него уравнения (2.2), получим

(2.15)
$\begin{gathered} \frac{N}{M} = - \frac{P}{{M\sin {{\varphi }_{1}}}} = g\cos {{\varphi }_{1}} - {{{\ddot {l}}}_{1}} - \ddot {u}\sin {{\varphi }_{1}} + {{l}_{1}}\dot {\varphi }_{1}^{2} - \\ - \;{{l}_{2}}{{{\ddot {\varphi }}}_{2}}\sin ({{\varphi }_{1}} - {{\varphi }_{2}}) + {{l}_{2}}\dot {\varphi }_{2}^{2}\cos ({{\varphi }_{1}} - {{\varphi }_{2}}) \\ \end{gathered} $

Рассматриваемая задача пассивного управления колебаниями системы имеет множество решений при различных управляющих финитных функциях $P(t)$ или $\ddot {u}(t)$ при $0 \leqslant t \leqslant T$, удовлетворяющих интегральным условиям (2.11). При определении управляющих функций из этого класса прежде всего необходимо, чтобы они были приемлемы и удобны для практической реализации полученного расчетным путем пассивного управления с помощью “жестких” приводов. Управляющие воздействия должны быть достаточно гладкими и не содержать высокочастотных составляющих, поскольку реальные приводы обладают упругостью и инерцией и в них могут возникнуть ответные колебания, искажающие расчетные управляющие воздействия.

Для минимизации энергетических затрат на управление различные подходящие управляющие функции можно сравнивать между собой по среднеквадратичной величине (норме) и по их максимальным значениям. При оптимальном управлении наряду с решением задачи управления необходимо минимизировать определенный функционал [1, 3, 14, 22].

3. Решение уравнений. Далее рассмотрим задачу кинематического управления передвижением твердого тела на тросе переменной длины с подвижной точкой подвеса из начального положения покоя в конечное положение покоя за определенное время $T$. Для приближенного решения этой задачи, описываемой нелинейными дифференциальными уравнениями (2.3), (2.4) с управляющей функцией $\ddot {u}(t)$ и с переменными коэффициентами на конечном интервале времени $0 \leqslant t \leqslant T$ будем использовать метод Бубнова–Галёркина совместно с методом последовательных приближений. Введем безразмерное время и безразмерные параметры:

(3.1)
$\tau = \frac{t}{T},\quad {{\bar {l}}_{1}} = \frac{{{{l}_{1}}}}{{{{l}_{2}}}},\quad \bar {u} = \frac{u}{{{{l}_{2}}}},\quad \lambda = \frac{{g{{T}^{2}}}}{{{{l}_{2}}}},\quad \mu = 1 + \frac{{{{J}_{2}}}}{{Ml_{2}^{2}}}$

Уравнения (2.3) и (2.4) запишем в безразмерном виде

(3.2)
$\bar {u}{\text{''}}\cos {{\varphi }_{1}} + {{\bar {l}}_{1}}\varphi _{1}^{{''}} + \varphi _{2}^{{''}}\cos ({{\varphi }_{1}} - {{\varphi }_{2}}) + \varphi _{2}^{{'2}}\sin ({{\varphi }_{1}} - {{\varphi }_{2}}) + 2\bar {l}_{1}^{{\text{'}}}\varphi _{1}^{'} + \lambda \sin {{\varphi }_{1}} = 0$
(3.3)
$\begin{gathered} \bar {u}{\text{''}}\cos {{\varphi }_{2}} + {{{\bar {l}}}_{1}}\varphi _{1}^{{''}}\cos ({{\varphi }_{1}} - {{\varphi }_{2}}) + \mu \varphi _{2}^{{''}} - {{{\bar {l}}}_{1}}\varphi _{1}^{{'2}}\sin ({{\varphi }_{1}} - {{\varphi }_{2}}) + \\ + \;2\bar {l}_{1}^{'}\varphi _{1}^{'}\cos ({{\varphi }_{1}} - {{\varphi }_{2}}) + \bar {l}_{1}^{{''}}\sin ({{\varphi }_{1}} - {{\varphi }_{2}}) + \lambda \sin {{\varphi }_{2}} = 0, \\ \end{gathered} $
где штрихом обозначается производная по $\tau $; $0 \leqslant \tau \leqslant 1$.

Соответствующие линеаризованные уравнения (2.6) и (2.7) имеют вид:

(3.4)
$\bar {u}{\text{''}} + {{\bar {l}}_{1}}\varphi _{1}^{{''}} + \varphi _{2}^{{''}} + 2\bar {l}_{1}^{'}\varphi _{1}^{'} + \lambda {{\varphi }_{1}} = 0$
(3.5)
$\bar {u}{\text{''}} + {{\bar {l}}_{1}}\varphi _{1}^{{''}} + \mu \varphi _{2}^{{''}} + 2\bar {l}_{1}^{'}\varphi _{1}^{'} + \bar {l}_{1}^{{''}}{{\varphi }_{1}} + (\lambda - \bar {l}_{1}^{{''}}){{\varphi }_{2}} = 0$

Далее, для того чтобы при использовании метода последовательных приближений первое приближение представляло решение линеаризованных уравнений (3.4) и (3.5), их объединим, соответственно, с уравнениями (3.2) и (3.3), одновременно складывая и вычитая. Полученные уравнения запишем в виде

(3.6)
${{L}_{i}}(\bar {u},{{\varphi }_{1}},{{\varphi }_{2}}) + {{N}_{i}}(\bar {u},{{\varphi }_{1}},{{\varphi }_{2}}) = 0,\quad i = 1,2$

Здесь ${{L}_{i}}$ и ${{N}_{i}}$ – соответственно, линейные и нелинейные операторы:

${{L}_{1}} = \bar {u}{\text{''}} + {{\bar {l}}_{1}}\varphi _{1}^{{''}} + \varphi _{2}^{{''}} + 2\bar {l}_{1}^{'}\varphi _{1}^{'} + \lambda {{\varphi }_{1}}$
${{N}_{1}} = \bar {u}{\text{''}}(\cos {{\varphi }_{1}} - 1) + \varphi _{2}^{{''}}(\cos ({{\varphi }_{1}} - {{\varphi }_{2}}) - 1) + $
(3.7)
$\begin{gathered} + \;\varphi _{2}^{{'2}}\sin ({{\varphi }_{1}} - {{\varphi }_{2}}) + \lambda (\sin {{\varphi }_{1}} - {{\varphi }_{1}}) \\ {{L}_{2}} = \bar {u}{\text{''}} + {{{\bar {l}}}_{1}}\varphi _{1}^{{''}} + \mu \varphi _{2}^{{''}} + 2\bar {l}_{1}^{'}\varphi _{1}^{'} + \bar {l}_{1}^{{''}}{{\varphi }_{1}} + (\lambda - \bar {l}_{1}^{{''}}){{\varphi }_{2}} \\ \end{gathered} $
${{N}_{2}} = \bar {u}{\text{''}}(\cos {{\varphi }_{2}} - 1) + {{\bar {l}}_{1}}\varphi {{_{1}^{{''}}}_{1}}(\cos ({{\varphi }_{1}} - {{\varphi }_{2}}) - 1) - {{\bar {l}}_{1}}\varphi _{1}^{{'2}}\sin ({{\varphi }_{1}} - {{\varphi }_{2}}) + $
$ + \;2\bar {l}_{1}^{'}\varphi _{1}^{'}(\cos ({{\varphi }_{1}} - {{\varphi }_{2}}) - 1) + \bar {l}_{1}^{{''}}(\sin ({{\varphi }_{1}} - {{\varphi }_{2}}) - ({{\varphi }_{1}} - {{\varphi }_{2}})) + \lambda (\sin {{\varphi }_{2}} - {{\varphi }_{2}})$

Видно, что разложения нелинейных операторов ${{N}_{i}}$ в ряды Тейлора при малых углах ${{\phi }_{i}}$ не содержат линейных членов с ${{\varphi }_{i}}(\tau )$ и их производными.

Будем считать, что длина троса при передвижении груза изменяется по закону

(3.8)
${{\bar {l}}_{1}}(\tau ) = {{\bar {l}}_{{1,0}}} + {{\bar {\Delta }}_{1}}(\tau );\quad {{\bar {\Delta }}_{1}}(\tau ) = \frac{1}{2}({{\bar {l}}_{{1,T}}} - {{\bar {l}}_{{1,0}}})(1 - \cos \pi \tau ),$
удовлетворяющему начальным и конечным условиям (1.2).

Закон управления горизонтальным перемещением точки подвеса троса с учетом начальных и конечных условий (1.1) будем искать в виде

(3.9)
$\begin{gathered} \bar {u}{\text{''}}(\tau ) = \sum\limits_{k = 1}^n {{{b}_{k}}\sin 2k\pi \tau } ,\quad \bar {u}{\text{'}}(\tau ) = \sum\limits_{k = 1}^n {{{b}_{k}}\frac{1}{{2k\pi }}(1 - \cos 2k\pi \tau )} \\ \bar {u}(\tau ) = \sum\limits_{k = 1}^n {{{b}_{k}}\frac{1}{{2k\pi }}\left( {\tau - \frac{1}{{2k\pi }}\sin 2k\pi \tau } \right)} , \\ \end{gathered} $
где ${{b}_{k}}$ – неизвестные коэффициенты, $n$ – определенное в каждом конкретном случае число коэффициентов ${{b}_{k}}$, которое требуется, чтобы удовлетворялись все начальные и конечные условия (1.1). В частности, в конечный момент времени $\tau = 1$ должно выполняться условие для заданного перемещения точки подвеса $\bar {u}(1) = {{\bar {u}}_{T}}$, которое дает одно уравнение для коэффициентов ${{b}_{k}}$:

(3.10)
$\sum\limits_{k = 1}^n {\frac{1}{{2k\pi }}{{b}_{k}}} = {{\bar {u}}_{T}}$

Приближенное решение уравнений (3.6) с учетом равенств (3.7) и (3.9) на интервале $0 \leqslant \tau \leqslant 1$ будем искать в рядах:

(3.11)
${{\varphi }_{i}}(\tau ) = \sum\limits_{r = 0}^{{{s}_{i}}} {{{c}_{{i,r}}}{{\sigma }_{r}}(\tau )} ,\quad i = 1,2,$
где ${{c}_{{i,r}}}$ – неизвестные коэффициенты, ${{\sigma }_{r}}(\tau )$ – заданные базисные функции, удовлетворяющие части условий (1.1) для функций ${{\varphi }_{1}}(\tau )$ и ${{\varphi }_{2}}(\tau )$. Здесь будем использовать систему базисных функций при $r = 0,1,2,\; \ldots $:

(3.12)
$\begin{gathered} {{\sigma }_{r}}(\tau ) = \cos r\pi \tau - \cos (r + 1)\pi \tau \\ {{\sigma }_{r}}(0) = \sigma _{r}^{'}(0) = \sigma _{r}^{'}(1) = 0,\quad {{\sigma }_{r}}(1) = 2\cos r\pi \\ \end{gathered} $

Уравнения (3.6) удовлетворяем по методу Бубнова–Галёркина как

(3.13)
$\int\limits_0^1 [ {{L}_{i}}(\bar {u},{{\varphi }_{1}},{{\varphi }_{2}}) + {{N}_{i}}(\bar {u},{{\varphi }_{1}},{{\varphi }_{2}})]{{\sigma }_{{{{p}_{i}}}}}(\tau )d\tau = 0,\quad {{p}_{i}} = 0,1,2, \ldots ,{{s}_{i}},\quad i = 1,2$

С учетом равенств (3.7) и (3.10) эти уравнения запишем в виде

(3.14)
$\sum\limits_{r = 0}^{{{s}_{1}}} {{{\alpha }_{{i1,{{p}_{i}}r}}}{{c}_{{1,r}}}} + \sum\limits_{r = 0}^{{{s}_{2}}} {{{\alpha }_{{i2,{{p}_{i}}r}}}{{c}_{{2,r}}}} + \sum\limits_{k = 1}^n {{{\gamma }_{{{{p}_{i}}k}}}{{b}_{k}}} + {{\beta }_{{i,{{p}_{i}}}}} = 0,\quad i = 1,2$
где

(3.15)
$\begin{gathered} {{\alpha }_{{11,{{p}_{1}}r}}} = \left\langle {{{\sigma }_{{{{p}_{1}}}}}({{{\bar {l}}}_{1}}\sigma _{r}^{{''}} + 2\bar {l}_{1}^{'}\sigma _{r}^{{\text{'}}} + \lambda {{\sigma }_{r}})} \right\rangle ,\quad {{\alpha }_{{12,{{p}_{1}}r}}} = \left\langle {{{\sigma }_{p}}_{1}\sigma _{r}^{{''}}} \right\rangle \\ {{\alpha }_{{21,{{p}_{2}}r}}} = \left\langle {{{\sigma }_{{{{p}_{2}}}}}({{{\bar {l}}}_{1}}\sigma _{r}^{{''}} + 2\bar {l}_{1}^{'}\sigma _{r}^{'} + \bar {l}_{1}^{{''}}{{\sigma }_{r}})} \right\rangle \\ {{\alpha }_{{22,pr}}} = \left\langle {{{\sigma }_{p}}_{2}(\mu \sigma _{r}^{{''}} + (\lambda - \bar {l}_{1}^{{''}}){{\sigma }_{r}})} \right\rangle ,\quad {{\gamma }_{{{{p}_{i}}k}}} = \left\langle {{{\sigma }_{p}}_{i}\sin 2k\pi \tau } \right\rangle \\ {{\beta }_{{i,{{p}_{i}}}}} = \left\langle {{{N}_{i}}(\bar {u},{{\varphi }_{1}},{{\varphi }_{2}}){{\sigma }_{{{{p}_{i}}}}}} \right\rangle ,\quad i = 1,2,\quad \left\langle f \right\rangle = \int\limits_0^1 {fd\tau } \\ \end{gathered} $

Система уравнений (3.14) должна быть дополнена уравнением (3.10), а также уравнениями, представляющими невыполненные начальные и конечные условия для функций ${{\varphi }_{1}}(\tau )$ и ${{\varphi }_{2}}(\tau )$, которым не удовлетворяют заданные функции ${{\sigma }_{r}}(\tau )$.

При использовании базисных функций (3.12) дополнительные уравнения наряду с (3.10) получаются из условий ${{\varphi }_{i}}(1) = 0$ при $i = 1,2$:

(3.16)
$\sum\limits_{r = 0}^{{{s}_{i}}} {{{c}_{{i,r}}}{{\sigma }_{r}}(1) = 0} ,\quad i = 1,2$

В результате будем иметь систему $({{s}_{1}} + 1) + ({{s}_{2}} + 1) + 3$ уравнений (3.14), (3.9) и (3.16), из которых наряду с коэффициентами ${{c}_{{1,r}}}$ и ${{c}_{{2,r}}}$ можно определить $n = 3$ неизвестных коэффициентов ${{b}_{k}}$ при $k = 1,2,3$.

Для решения полученной системы алгебраических уравнений (3.14) с нелинейными членами ${{\beta }_{{i,{{p}_{i}}}}}$ используется метод последовательных приближений. В качестве первого приближения ($\nu = 1$) берется решение по методу Бубнова–Галёркина линеаризованных уравнений (3.14) при ${{\beta }_{{i,{{p}_{i}}}}} = 0$ (т.е. при ${{N}_{1}} \equiv 0$, ${{N}_{2}} \equiv 0$). В $\nu $-м приближении ($\nu = 2,3,\; \ldots $) интегралы для коэффициентов ${{\beta }_{{i,{{p}_{i}}}}}$ вычисляются численно с использованием выражений (3.7) для ${{N}_{i}}$ с функциями $\bar {u}(\tau )$ и ${{\varphi }_{i}}(\tau )$, полученными в предыдущем, $(\nu - 1)$-м, приближении как

(3.17)
$\beta _{{i,{{p}_{i}}}}^{{(\nu )}} = \left\langle {{{N}_{i}}({{{\bar {u}}}^{{(\nu - 1)}}},\varphi _{1}^{{(\nu - 1)}},\varphi _{2}^{{(\nu - 1)}}){{\sigma }_{{{{p}_{i}}}}}} \right\rangle ,\quad i = 1,2$

Приближения выполняются пока не будет достигнута требуемая точность.

4. Примеры расчета. Рассмотрим систему с безразмерными параметрами $\mu $ = 4/3, λ = = 250 (при ${{l}_{2}} = 1$ м, $M = 1000$ кг и $g \approx 10$ м/с2 это будет соответствовать ${{J}_{2}}$ = 1000/3 кг м2, $T = 5$ с). В разложениях (3.11) для углов поворота ${{\varphi }_{i}}(\tau )$ используем базисные функции (3.12) при $r = 0,1, \ldots ,7$, ${{s}_{1}} = {{s}_{2}} = 7$; соответственно этому в разложениях (3.9) полагаем $n = 3$. В результате для определения неизвестных коэффициентов ${{c}_{{i,r}}}$ и ${{b}_{k}}$ при $i = 1,2$, $r = 0,1, \ldots ,7$, $k = 1,2,3$ будем иметь систему 19-ти уравнений (3.10), (3.14), (3.16). При расчетах параметры ${{\bar {u}}_{T}}$ и ${{\bar {l}}_{1}}(\tau )$ будем подбирать такими, чтобы колебания были нелинейными с умеренно большими углами поворота ${{\varphi }_{i}}(\tau )$, т.е. (в радианах) $1{\text{/}}2 < \left| {{{\varphi }_{1}}} \right|$, $\left| {{{\varphi }_{2}}} \right| < 1$.

Точность приближенного решения задачи о нестационарных колебаниях нелинейной управляемой системы с переменными параметрами (при изменяемой по заданному закону длине троса ${{\bar {l}}_{1}}(\tau )$) оценивается путем сравнения с численным решением многошаговым конечноразностным методом Адамса прямой задачи, описываемой нелинейными дифференциальными уравнениями (3.3) с начальными условиями

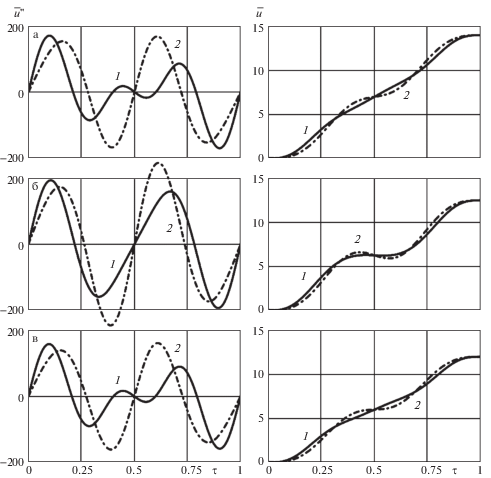
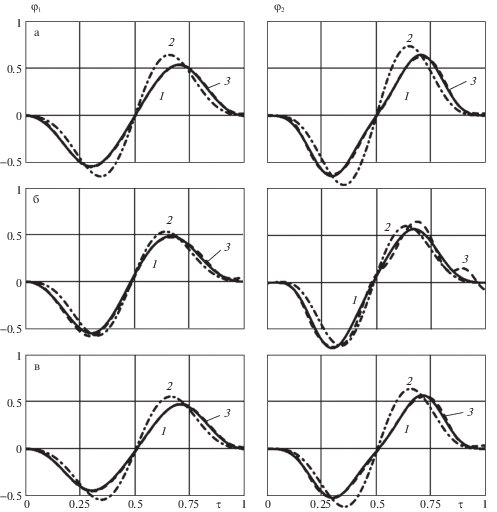
${{\varphi }_{1}}(0) = {{\varphi }_{2}}(0) = 0,\quad \varphi _{1}^{'}(0) = \varphi _{2}^{'}(0) = 0$

При этом финитная управляющая функция $\bar {u}{\text{''}}(\tau )$, $0 \leqslant \tau \leqslant 1$ берется в виде (3.9) при $n = 3$ с использованием найденных в приближенном решении коэффициентов ${{b}_{1}}$, ${{b}_{2}}$, ${{b}_{3}}$. Результаты расчетов для трех случаев перемещения тела, когда длина троса не меняется, увеличивается и уменьшается (случаи а, б и в соответственно, см. табл. 1), показаны на рисунках со следующими обозначениями: сплошные линии 1 – решения задачи в нелинейной постановке; штрихпунктирные линии 2 – решения задачи в линейной постановке (в первом приближении); штриховые линии 3 – численные решения нелинейных дифференциальных уравнений прямой начальной задачи по методу Адамса.

Таблица 1.

Исходные данные и результаты расчетов

Случай a б в
${{\bar {l}}_{{1,0}}}$ 4 4 5
${{\bar {l}}_{{1,T}}}$ – 8 4
${{\bar {u}}_{T}}$ 14 12.5 12
Линейная задача ${{b}_{1}}$ 24.44 –9.260 13.04
${{b}_{2}}$ 153.1 205.4 145.2
${{b}_{3}}$ –39.04 –44.63 –30.73
Нелинейная задача ${{b}_{1}}$ 16.22 –20.93 7.528
${{b}_{2}}$ 89.71 163.7 83.57
${{b}_{3}}$ 80.67 52.81 78.26
$\frac{{N(\tau )}}{{Mg}}$, $0 \leqslant \tau \leqslant 1$ max 1.289 1.530 1.222
min 0.658 0.454 0.696
Число последовательных приближений 91 25 45

В табл. 1 приведены исходные данные и результаты расчетов для трех вариантов (случаи а, б и в): начальная и конечная длина троса ${{\bar {l}}_{{1,0}}}$ и ${{\bar {l}}_{{1,T}}}$; величина горизонтального перемещения ${{\bar {u}}_{T}}$; значения коэффициентов ${{b}_{1}}$, ${{b}_{2}}$, ${{b}_{3}}$ для линейной и нелинейной постановки; максимальное и минимальное значение силы натяжения троса, отнесенного к силе тяжести, ${{N(\tau )} \mathord{\left/ {\vphantom {{N(\tau )} {Mg}}} \right. \kern-0em} {Mg}}$ при $0 \leqslant \tau \leqslant 1$; число последовательных приближений при решении нелинейных уравнений (3.14) с точностью 10–6. Отметим, что во всех случаях натяжение троса на всем времени интегрирования остается положительным и для случая а при $\tau = 0$ и $\tau = 1$ отношение ${{N(\tau )} \mathord{\left/ {\vphantom {{N(\tau )} {Mg}}} \right. \kern-0em} {Mg}}$ равно 1.

На рис. 2 приведены найденная управляющая функция $\bar {u}{\text{''}}(\tau )$ и соответствующее ей безразмерное перемещение точки подвеса троса $\bar {u}(\tau )$, которые определяются в виде (3.9), а на рис. 3 – углы поворота в радианах троса ${{\varphi }_{1}}(\tau )$ и тела ${{\varphi }_{2}}(\tau )$.

Рис. 2.

Ускорения и перемещения точки подвеса.

Рис. 3.

Углы поворота троса и тела.

Заключение. Предложенный новый подход для решения задач терминального управления нелинейной системы с конечным числом степеней свободы и в общем случае с переменными параметрами, который основан на одновременном применении метода Бубнова–Галёркина и метода последовательных приближений с использованием в первом приближении решений линеаризованных уравнений, позволяет аппроксимировать финитную управляющую функцию в виде ряда по синусам или косинусам. Такие вполне гладкие управляющие функции пригодны для пассивного управления системой с помощью жестких приводов. Нелинейности системы оказывают большое влияние на искомую управляющую функцию даже при умеренных амплитудах нелинейных колебаний.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 18-08-00778а).

Список литературы

  1. Черноусько Ф.Л., Акуленко Л.Д., Соколов Б.Н. Управление колебаниями. М.: Наука, 1980. 384 с.

  2. Das S.K., Utku S., Wada B.K. Inverse dynamics of adaptive space cranes with tip point adjustment // 31st Structures, Structural Dynamics and Materials Conf. 1990. P. 2367–2374.

  3. Черноусько Ф.Л., Болотник Н.Н., Градецкий В.Г. Манипуляционные роботы: динамика, управление, оптимизация. М.: Наука, 1989. 363 с.

  4. Chan J.K., Modi V.J. A Closed-form dynamical analysis of an orbiting flexible manipulator // Acta Astron. 1991. V. 25. № 2. P. 67–76.

  5. Ковалева А.С. Управление колебательными и виброударными системами. М.: Наука, 1990. 256 с.

  6. Болотник Н.Н., Зейдис И.М., Циммерманн К., Яцун С.Ф. Динамика управляемых движений вибрационных систем // Изв. РАН. Теор. и сист. упр. 2006. № 5. С. 157–167.

  7. Колесников К.С., Кокушкин В.В., Борзых С.В., Панкова Н.В. Расчет и проектирование систем разделения ступеней ракет. М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. 376 с.

  8. Nurre G.S., Ryan R.S., Scofield H.N., Sims J.I. Dynamics and control of large space structures, journal of guidance // Control and Dynamics. 1984. V. 7. № 5. P. 514–526.

  9. Дегтярев Г.Л., Сиразетдинов Т.К. Теоретические основы оптимального управления упругими космическими аппаратами. М.: Машиностроение, 1986. 216 с.

  10. Meirovitch L., Kwak M.K. Control of flexible spacecraft with time-varying configuration // J. Control, Guidance, Dyn. 1992. V. 15. № 2. P. 314–324.

  11. Русских С.В. Управляемый поворот космического аппарата с упругими панелями солнечных батарей // Изв. вузов. Машиностроение. 2016. № 12. С. 97–105.

  12. Воронов А.А. Введение в динамику сложных управляемых систем. М.: Наука, 1985. 352 с.

  13. Ганиев Р.Ф., Закржевский А.Е. Программные движения управляемых деформируемых конструкций. М.: Наука, 1995. 214 с.

  14. Матюхин В.И. Управление механическими системами. М.: Физматлит, 2009. 320 с.

  15. Бербюк В.Б. Динамика и оптимизация робототехнических систем. Киев: Наукова думка, 1989. 187 с.

  16. Кубышкин Е.П. Оптимальное управление поворотом твердого тела с гибким стержнем // ПММ. 1992. Т. 56. Вып. 2. С. 240–249.

  17. Кубышкин Е.П. Оптимальное управление поворотом системы двух тел, соединенных упругим стержнем // ПММ. 2014. Т. 78. Вып. 5. С. 656–670.

  18. Гришанина Т.В., Русских С.В., Шклярчук Ф.Н. Управление конечным поворотом упругой системы из одного состояния в другое с гашением колебаний в момент окончания операции // Уч. зап. Казан. унив. Сер. физ.-мат. науки. 2017. Т. 159. Кн. 4. С. 429–443.

  19. Гришанина Т.В. Динамика управляемого движения упругих систем при конечных перемещениях и поворотах // Изв. РАН. МТТ. 2004. № 6. С. 171–186.

  20. Гришанина Т.В., Шклярчук Ф.Н. Динамика упругих управляемых конструкций. М.: Изд-во МАИ, 2007.

  21. Гришанина Т.В., Русских С.В., Шклярчук Ф.Н. Устранение нестационарных колебаний упругой системы в момент остановки после конечного поворота по заданному закону путем настройки собственных частот // Изв. РАН. МТТ. 2018. № 4. С. 16–27.

  22. Холостова О.В. О движениях двойного маятника с вибрирующей точкой подвеса // Изв. РАН. МТТ. 2009. № 2. С. 25–40.

  23. Буланчук П.О., Петров А.Г. Параметры вибрации точки подвеса для заданного положения равновесия двойного математического маятника // Изв. РАН. МТТ. 2013. № 4. С. 31–39.

  24. Асланов B.C., Безгласный С.П. Устойчивость и неустойчивость управляемых движений двухмассового маятника переменной длины // Изв. РАН. МТТ. 2012. № 3. С. 32–46.

  25. Ананьевский И.М., Анохин Н.В. Управление пространственным движением многозвенного перевернутого маятника с помощью момента, приложенного к первому звену // ПММ. 2014. Т. 78. Вып. 6. С. 755–765.

  26. Черноусько Ф.Л., Ананьевский И.М., Решмин С.А. Методы управления нелинейными механическими системами. М.: Физматлит, 2006. 326 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал