Прикладная математика и механика, 2019, T. 83, № 4, стр. 597-607

Введение. В структуре уравнений малых колебаний механической системы традиционно выделяют диссипативные, гироскопические, позиционные потенциальные и позиционные неконсервативные силы. Исследованию различных аспектов их влияния на характер устойчивости тривиального положения равновесия посвящено огромное количество работ (например, [1–3]). В частности, анализировалось влияние структуры матриц соответствующих сил на вид собственных колебаний [4].

Диссипативные силы с полной диссипацией, как правило, оказывают стабилизирующее влияние на систему. Однако, как показывает известный парадокс Циглера, диссипативные силы даже с полной диссипацией при определенных условиях могут привести к разрушению устойчивости положения равновесия. Таким образом, их связь с устойчивостью оказывается достаточно нетривиальной, что обуславливает сохранение интереса к этой проблеме.

В частности, подробно обсуждалось дестабилизирующее влияние диссипативных сил при наличии позиционных неконсервативных сил в системах с двумя степенями свободы [5]. Эти результаты были обобщены [6] при рассмотрении влияния малых диссипативных сил, а также диссипативных сил с неполной диссипацией на устойчивость равновесия систем с двумя степенями свободы в присутствии полного набора сил. Отмечено, что это влияние может быть как стабилизирующим, так и дестабилизирующим. Кроме того, показано, что диссипативные силы, матрица которых содержит собственные числа разных знаков (т.е. имеет место частичная антидиссипация), способны не только разрушить устойчивость, но и обеспечить асимптотическую устойчивость.

Дестабилизирующее влияние различных неконсервативных сил (как диссипативных, так и позиционных) обсуждалось на примере ряда механических задач [7].

Представляется интересным исследовать влияние потенциальных сил на устойчивость равновесия в ситуации, когда в системе отсутствует полная диссипация. Отметим, что естественным источником возникновения диссипативных сил с частичной антидиссипацией (а также, вообще говоря, и позиционных неконсервативных сил) являются аэродинамические силы. Соответственно, такой анализ может быть полезен, в частности, в рамках исследования особенностей поведения механических систем, содержащих твердое тело, взаимодействующее с сопротивляющейся средой.

1. Общие замечания. Рассмотрим механическую систему с s степенями свободы. Обозначим вектор обобщенных координат через ${\mathbf{q}} = {{({{q}_{1}} \ldots {{q}_{s}})}^{T}}$. Предположим, что система имеет тривиальное положение равновесия. Тогда, как известно, уравнения движения, линеаризованные вблизи этого положения равновесия, могут быть записаны в следующем структурном виде:

Здесь ${\mathbf{A}}$, ${\mathbf{B}}$, ${\mathbf{C}}$ – матрицы $s \times s$, причем матрица ${\mathbf{A}}$ симметрическая и положительно определенная. Пусть эти матрицы таковы, что тривиальное положение равновесия асимптотически устойчиво.

Будем считать также, без ограничения общности, что уравнения представлены в безразмерной форме.

Предположим теперь, что в систему “вводится” дополнительная жесткость по одной из обобщенных координат (для определенности, ${{q}_{1}}$). Очевидно, при этом точка ${\mathbf{q}} = 0$ останется положением равновесия. Проанализируем, как изменится характер его устойчивости.

Уравнение (1.1) примет вид:

В соответствии со сделанным предположением относительно введенной дополнительной жесткости все элементы матрицы ${\mathbf{C}}{\text{'}}$ – нулевые, кроме элемента первой строки первого столбца; этот элемент равен некоторому положительному числу $c$ (имеющему смысл коэффициента жесткости).

Выполним невырожденную замену координат таким образом, чтобы сделать матрицу ${\mathbf{A}}$ единичной, сохранив матрицу ${\mathbf{C}}{\text{'}}$ диагональной. Это всегда возможно, поскольку матрица ${\mathbf{A}}$ симметрична и положительно определена. Тогда равенство (1.1) примет вид

Здесь ${\mathbf{x}}$ – вектор новых обобщенных координат, ${\mathbf{H}} = \left\| {{{h}_{{ij}}}} \right\|$ и ${\mathbf{K}} = \operatorname{diag} \{ {{k}_{{ii}}}\} $ ($i,j = 1, \ldots ,\;s$) – матрицы, полученные из матриц ${\mathbf{B}}$ и ${\mathbf{C}}$ при сделанном преобразовании.

Запишем характеристический полином системы (1.3):

Здесь для удобства обозначено $n = 2s$. Очевидно, что ${{a}_{{n - 1}}} = \operatorname{tr} {\mathbf{H}}$. Поскольку положение равновесия исходной системы асимптотически устойчиво, $\operatorname{tr} {\mathbf{H}} > 0$.

Система (1.2) в результате перехода к новым координатам примет вид

Матрица ${\mathbf{K}}{\text{'}} = \operatorname{diag} \{ k_{{ii}}^{'}\} $ получена из матрицы ${\mathbf{C}}{\text{'}}$ при сделанной замене координат. В рамках процедуры одновременной диагонализации матриц ${\mathbf{A}}$ и ${\mathbf{C}}{\text{'}}$ обе эти матрицы умножаются справа и слева на невырожденные матрицы. Такие преобразования не изменяют ранг матрицы, следовательно, $\operatorname{rank} {\mathbf{K}}{\text{'}} = \operatorname{rank} {\mathbf{C}}{\text{'}} = 1$. Соответственно, все диагональные элементы матрицы ${\mathbf{K}}{\text{'}}$, кроме одного, равны нулю. Будем считать без потери общности, что отличен от нуля первый диагональный элемент, т.е. $k_{{11}}^{'} = \kappa $.

Характеристический полином системы (1.5), как нетрудно видеть, можно представить в форме

Легко показать, что ${{b}_{{n - 2}}} = 1$ и ${{b}_{{n - 3}}} = \operatorname{tr} {\mathbf{H}} - {{h}_{{11}}}$. Суммы корней каждого многочлена (1.4) и (1.6) одинаковы и равны $ - {{a}_{{n - 1}}}$.

Если число степеней свободы равно единице, то добавление жесткости в механическую систему с одной степенью свободы не может привести к потере устойчивости (что очевидно с механической точки зрения). Действительно, в этом случае корни характеристического полинома (1.6) в принятых обозначениях имеют вид

так что при ${{h}_{{11}}} > 0$ и ${{k}_{{11}}} > 0$ асимптотическая устойчивость, разумеется, имеет место при любых $\kappa > 0$. Добавление жесткости ведет просто к увеличению частоты колебаний.

Однако в случае, когда число степеней свободы больше единицы, влияние добавленной жесткости оказывается не таким очевидным.

2. Система с двумя степенями свободы. Рассмотрим случай системы с двумя степенями свободы. Тогда достаточные условия асимптотической устойчивости тривиального положения равновесия системы (1.5) могут быть в принятых обозначениях записаны следующим образом:

Для системы с добавленной жесткостью эти условия примут вид

В данном случае, очевидно, коэффициенты характеристического полинома определяются соотношениями

Отметим, что первые четыре неравенства (2.2) выполняются заведомо при выполнении неравенств (2.1).

Если ${{a}_{3}} = {{h}_{{11}}} + {{h}_{{22}}} < 0$, то положение равновесия неустойчиво, и его нельзя стабилизировать путем введения дополнительной жесткости (такая ситуация возникает, в частности, если в обеих парциальных системах имеется антидиссипация). В дальнейшем ограничимся рассмотрением случая ${{h}_{{11}}} + {{h}_{{22}}} > 0$.

Выражение для $\Delta _{3}^{'}$ можно преобразовать следующим образом:

Оно представляет собой квадратный трехчлен относительно $\kappa $. Проанализируем его знак в зависимости от значений параметров системы.

2.1. Случай антидиссипации в одной из парциальных систем. Пусть ${{h}_{{11}}}{{h}_{{22}}} < 0$, т.е. имеет место антидиссипация по одной из обобщенных координат и диссипация по другой. В этой ситуации, очевидно, $\Delta _{3}^{'} < 0$, если величина $\kappa $ достаточно велика. Таким образом, даже если в исходной системе тривиальное положение равновесия асимптотически устойчиво, добавление достаточно большой жесткости по одной из обобщенных координат сделает его неустойчивым. Если же это положение в исходной системе неустойчиво, причем коэффициент при $\kappa $ в выражении (2.3) отрицателен, то невозможно обеспечить стабилизацию за счет увеличения жесткости по какой-либо одной обобщенной координате.

Интересно, что не важно, добавляется ли жесткость по той координате, для которой имеет место демпфирование, или по той, для которой имеет место антидиссипация.

Рассмотрим подробнее случай $\kappa \gg 1$. Тогда корни характеристического полинома системы с дополнительной жесткостью можно представить в виде

Отметим, что ${{\lambda }_{{3,4}}}$ – собственные значения парциальной системы, соответствующей второй координате.

В системе, как и следовало ожидать, присутствуют высокочастотные колебания. Если ${{h}_{{11}}} < 0$ и ${{h}_{{22}}} > 0$, то амплитуда этих колебаний, вообще говоря, возрастает. Если же ${{h}_{{11}}} > 0$ и ${{h}_{{22}}} < 0$, то эти колебания оказываются затухающими. В то же время, по крайней мере, у одного из собственных значений ${{\lambda }_{{3,4}}}$ действительная часть положительна. Таким образом, за счет увеличения жесткости в парциальной системе, отвечающей первой координате, невозможно стабилизировать вторую.

В качестве примера рассмотрим систему со следующими значениями параметров:

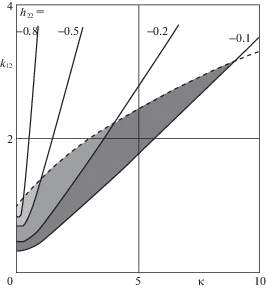
Предполагая, что позиционные неконсервативные силы отсутствуют (т.е. ${{k}_{{12}}} = {{k}_{{21}}}$), построим области асимптотической устойчивости (ОАУ) положения равновесия на плоскости параметров ($\kappa $, ${{k}_{{12}}}$) для разных значений ${{h}_{{22}}}$, $ - 1 < {{h}_{{22}}} < 0$ (так что ${{h}_{{11}}} + {{h}_{{22}}} > 0$). При этом характеристический полином (1.6) примет вид

С учетом выражений для коэффициентов полинома (2.4) и условия ${{h}_{{11}}} + {{h}_{{22}}} > 0$ ясно, что границы ОАУ образованы кривой, на которой обращается в нуль свободный член характеристического полинома (на рис. 1 изображена штриховой линией), и кривой, на которой обращается в нуль величина $\Delta _{3}^{'}$ (сплошная линия для каждого значения ${{h}_{{22}}}$); ОАУ затемнены.

Видно, что если положение равновесия устойчиво при $\kappa = 0$, то его устойчивость разрушается при достаточно большом значении дополнительной жесткости. В то же время, в некотором диапазоне значений ${{k}_{{12}}} = {{k}_{{21}}}$ увеличение $\kappa $ приводит к стабилизации положения равновесия, неустойчивого при $\kappa = 0$. Тем не менее, для достаточно больших $\kappa $ устойчивость снова теряется.

Отметим, что эффект проявляется также и в отсутствие гироскопических и позиционных неконсервативных сил.

2.2. Случай полной диссипации в обеих парциальных системах. Пусть теперь ${{h}_{{11}}} > 0$ и ${{h}_{{22}}} > 0$, т.е. колебания обеих парциальных систем затухающие. Тем не менее, одно из собственных чисел матрицы ${\mathbf{H}}$ может быть отрицательным (это означает, что в системе отсутствует полная диссипация).

Рассмотрим вначале ситуацию, когда условия (2.1) выполнены, т.е. тривиальное положение равновесия исходной системы асимптотически устойчиво. Если при этом выражение (2.3), рассматриваемое как квадратный трехчлен относительно $\kappa $, не имеет действительных корней или оба корня отрицательны, то устойчивость сохраняется при любых значениях дополнительной жесткости. Если же оба корня положительны, то это означает, что существует диапазон значений дополнительной жесткости, для которых устойчивость тривиального равновесия нарушается.

В общем случае выражение для дискриминанта указанного трехчлена достаточно громоздко. Поэтому рассмотрим частный случай.

Предположим, что в системе имеется малый параметр $\varepsilon $, причем ${{\Delta }_{3}} = \varepsilon {{\bar {\Delta }}_{3}} > 0$. Тогда при выполнении условия

существует диапазон значений $\kappa $, ${{\kappa }_{1}}$, ${{\kappa }_{2}}$, $0 < {{\kappa }_{1}} < \kappa < {{\kappa }_{2}}$, в котором $\Delta _{3}^{'} < 0$:

Отметим, что потеря устойчивости происходит уже при малых (порядка $\varepsilon $) величинах добавленной жесткости.

Неравенство (2.5) выполняется, в частности, если удовлетворяются соотношения

Пусть теперь положение равновесия исходной системы неустойчиво, причем все коэффициенты характеристического полинома положительны, а ${{\Delta }_{3}} < 0$. Тогда выражение (2.3), рассматриваемое как квадратный трехчлен относительно $\kappa $, имеет один отрицательный и один положительный корень. Это значит, что достаточно большая дополнительная жесткость обеспечивает стабилизацию положения равновесия.

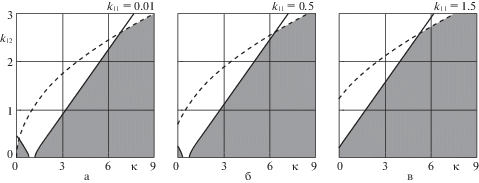
В качестве примера рассмотрим систему со следующими значениями параметров: ${{h}_{{11}}} = {{h}_{{22}}} = {{h}_{{12}}} = 0.1$, ${{h}_{{21}}} = 0.2$ (таким образом, $\det H < 0$) и ${{k}_{{22}}} = 1$. Будем считать, что позиционные неконсервативные силы отсутствуют ${{k}_{{12}}} = {{k}_{{21}}}$. При этом характеристический полином (1.6) примет вид

Нетрудно показать, что при ${{k}_{{11}}} > 0$ граница ОАУ образована кривой, на которой обращается в нуль свободный член полинома (2.7) (штриховая линия на рис. 2), и кривой, на которой обращается в нуль величина $\Delta _{3}^{'}$ (сплошная линия). Затемнены ОАУ на плоскости параметров ($\kappa $, ${{k}_{{12}}}$) для разных значений ${{k}_{{11}}}$.

Видно, что при малых ${{k}_{{11}}}$ ОАУ двусвязная при $\kappa > 0$, так что существует диапазон значений дополнительной жесткости, в котором неустойчивость имеет место при всех ${{k}_{{12}}}$. Следовательно, в этой ситуации увеличение жесткости может привести к потере устойчивости. Впрочем, если дополнительная жесткость достаточно велика, то положение равновесия снова становится асимптотически устойчивым.

Если при малых $\kappa $ тривиальное положение было неустойчивым, то оно стабилизируется за счет введения достаточно большой дополнительной жесткости. При больших ${{k}_{{11}}}$ ОАУ односвязная при $\kappa > 0$. Отметим, что если положение равновесия асимптотически устойчиво при $\kappa = 0$, то оно остается таковым при любых значениях $\kappa $. Если же оно было неустойчиво при $\kappa = 0$, то оно становится асимптотически устойчивым при введении в систему достаточно большой дополнительной жесткости.

Отметим, что для возникновения описанных эффектов наличие позиционных неконсервативных сил оказывается необязательным.

3. Система с произвольным числом степеней свободы. Пусть теперь число степеней свободы равно $s$. Предположим, что тривиальное положение исходной системы устойчиво.

Рассмотрим случай $\kappa \gg 1$. Тогда корни характеристического полинома (1.6) для системы с дополнительной жесткостью можно представить в виде следующего разложения:

где $\lambda _{{3 \ldots n}}^{'}$ являются корнями следующего уравнения ($n = 2s$):

Соответственно, имеет место равенство $\sum\nolimits_{i = 3}^n {\lambda _{i}^{'}} = - {{b}_{{n - 3}}}$. Таким образом, если ${{h}_{{11}}} < 0$ (т.е. имеет место “антидиссипация” по первой координате), то $\operatorname{Re} \left( {{{\lambda }_{{1,2}}}} \right) > 0$. Это означает, что при достаточно большом коэффициенте жесткости положение равновесия становится неустойчивым.

Аналогичная ситуация возникает и в случае, когда ${{h}_{{11}}} > 0$, но ${{b}_{{n - 3}}} = \operatorname{tr} {\mathbf{H}} - {{h}_{{11}}} < 0$: при этом среди $\lambda _{{3...n}}^{'}$ имеются величины с положительной действительной частью.

В качестве примера рассмотрим систему с тремя степенями свободы, в которой матрицы ${\mathbf{H}}$ и ${\mathbf{K}}$ имеют следующий вид:

На рис. 3 представлена эволюция корней характеристического полинома на комплексной плоскости в зависимости от $\kappa $ (направление движения изображающей точки при увеличении $\kappa $ показано стрелками).

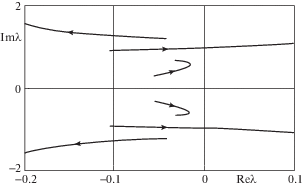
Видно, что при достаточно больших значениях $\kappa $ в системе имеется два комплексно сопряженных корня с положительной действительной частью.

Таким образом, при наличии отрицательных диагональных элементов в матрице демпфирования введение в систему достаточно большой дополнительной жесткости по одной из обобщенных координат приводит к потере устойчивости.

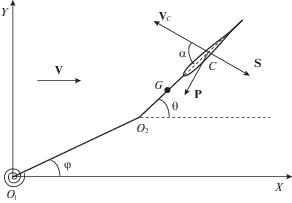
4. Двухзвенный аэродинамический маятник. Рассмотрим двухзвенный маятник, ко второму звену которого прикреплено тонкое крыло, а к первому звену – спиральная линейно-упругая пружина (см. рис. 4). Маятник помещен в поток среды, скорость которого на бесконечности постоянна и равна $V$. Оси ${{O}_{1}}$ и ${{O}_{2}}$ шарниров маятника вертикальны.

Чтобы описать аэродинамическую нагрузку на крыло, воспользуемся модифицированным квазистатическим подходом [8]: заменим систему аэродинамических сил силой лобового сопротивления S, подъемной силой P, приложенными в точке C (середине хорды крыла), а также аэродинамическим моментом ${{M}_{z}}$ относительно этой точки. Эти величины традиционно представляются в следующем виде:

Здесь $\rho $ – плотность воздуха, $\sigma $ – характерная площадь крыла, b – хорда крыла, $~{{C}_{x}}(\alpha )$, ${{C}_{y}}(\alpha )$ и ${{C}_{m}}(\alpha )$ – безразмерные коэффициенты силы лобового сопротивления, боковой силы, и аэродинамического момента, соответственно, $\alpha $ – мгновенный угол атаки, под которым будем понимать угол между воздушной скоростью ${{{\mathbf{V}}}_{C}}$ точки C и хордой крыла.

Для упрощения записи проведем обезразмеривание, выбрав в качестве “нормировочных” значений времени, массы и длины следующие величины: ${{T}_{0}} = {b \mathord{\left/ {\vphantom {b {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}$, m₀ = ${{\rho \sigma b} \mathord{\left/ {\vphantom {{\rho \sigma b} 2}} \right. \kern-0em} 2}$, ${{L}_{0}} = b$ (здесь ${{V}_{0}}$ – некоторая характерная скорость).

Тогда, с учетом (4.1), уравнения движения в безразмерной форме можно записать в следующем виде:

Здесь ${{J}_{1}}$ – момент инерции первого звена относительно неподвижной оси, ${{J}_{2}}$ – центральный момент инерции второго звена,${\text{\;}}m$ – масса второго звена, $k$ – коэффициент жёсткости пружины, r – расстояние от шарнира между звеньями до точки C, ${{l}_{1}}$ – длина первого звена, ${{l}_{2}}$ – расстояние от шарнира между звеньями до центра масс второго звена.

Величины $\alpha $ и ${{V}_{C}}$ определяются из следующих кинематических соотношений:

Уравнения (4.2) вместе с (4.3.) образуют замкнутую систему.

Динамика двухзвенного маятника рассмотрена ранее [9, 10]. Было показано, что в случае симметричного профиля крыла положение, в котором оба звена маятника вытянуты вдоль скорости набегающего потока ($\varphi \equiv \theta \equiv 0$), является положением равновесия и проанализировано влияние различных параметров системы (в том числе, жесткости пружины) на его устойчивость.

Уравнения движения (4.2), линеаризованные в окрестности тривиального положения равновесия, имеют вид, аналогичный (1.2), где

Здесь

Отметим, что $\det {\mathbf{B}} = 0$. Поскольку матрица ${\mathbf{B}}$ – сумма матрицы ${\mathbf{D}}$ диссипативных сил и матрицы ${\mathbf{G}}$ гироскопических сил, причем $\det {\mathbf{G}} > 0$, то определитель матрицы диссипативных сил отрицателен. Следовательно, в системе отсутствует полная диссипация.

Следуя описанной выше процедуре, перейдем к новым переменным:

где ${{I}_{1}} = {{J}_{1}}{{J}_{2}} + {{J}_{1}}ml_{2}^{2} + {{J}_{2}}ml_{1}^{2}$, ${{I}_{2}} = {{J}_{2}} + ml_{2}^{2}$.

Тогда компоненты матриц ${\mathbf{H}}$, ${\mathbf{K}}$ и ${\mathbf{K}}{\text{'}}$ определяются формулами

Здесь, кроме введенных выше, использованы следующие обозначения:

Видно, что при $r > {{l}_{2}} + {{r}_{0}}$ величины ${{h}_{{11}}}$ и ${{h}_{{22}}}$ положительны.

Воспользуемся тем обстоятельством, что для симметричных профилей ${{C}_{{x0}}} \ll 1$.

Тогда

Кроме того,

Пусть $r > {{r}_{0}}$. Тогда если момент инерции первого звена достаточно велик, то выражение (4.4) положительно, т.е. в отсутствие пружины в креплении имеет место асимптотическая устойчивость положения “по потоку”.

Неравенство (2.4) принимает вид:

Неравенство (4.5), очевидно, выполняется в случае, когда ${{r}_{0}} < r < {{l}_{2}} + {{{{J}_{2}}} \mathord{\left/ {\vphantom {{{{J}_{2}}} {m{{l}_{2}}}}} \right. \kern-0em} {m{{l}_{2}}}}$ и величина ${{J}_{1}}$ достаточно велика. Следовательно, при этом существует диапазон значений $0 < {{\kappa }_{1}} < \kappa < {{\kappa }_{2}}$ (определяемых выражениями (2.6)), в котором $\Delta _{3}^{'} < 0$:

Таким образом, при определенных значениях параметров установка на первое звено двухзвенного аэродинамического маятника спиральной пружины даже относительно малой жесткости приводит к потере устойчивости тривиального положения равновесия. Это подтверждается экспериментальными исследованиями [10].

Заключение. Обычно считают, что увеличение жесткости оказывает, так сказать, условно стабилизирующее воздействие на положение равновесия механической системы (делает его устойчивым или, по крайней мере, не изменяет характер устойчивости). Однако, как показано выше, при наличии отрицательных собственных чисел у матрицы диссипации это интуитивное представление является, вообще говоря, неверным. В этой ситуации влияние позиционных консервативных сил на устойчивость положения равновесия линейной системы оказывается достаточно сложным. В частности, увеличение жесткости в такой системе может привести к разрушению устойчивости равновесия. Данный эффект может оказаться существенным, в том числе, в инженерной практике.

Работа выполнена при финансовой поддержке РФФИ (гранты № 18-01-00538, 17-08-01366).