Прикладная математика и механика, 2019, T. 83, № 4, стр. 660-686

Введение. В последние десятилетия в инженерной практике широко используются композиционные материалы (КМ), имеющие пространственные структуры армирования [1–4]. Такие структуры позволяют устранить серьезный недостаток армированных в плоскости КМ – расслоение в силу ослабленного сопротивления поперечному отрыву и сдвигу, а также позволяют локализовать трещины в пределах нескольких представительных элементов композиции.

Моделировалось линейно-упругое поведение пространственно-армированных КМ [5–7]. Однако современные инженерные изделия часто подвергаются воздействию высокоинтенсивных нагрузок [2, 8], при которых компоненты КМ-конструкции деформируются упругопластически. Было показано [7], как, используя полученные там структурные соотношения, можно моделировать неупругое поведение КМ-среды в рамках теории пластичности деформационного типа. Были разработаны [9–11] структурные модели упругопластического деформирования продольно-армированных балок, перекрестно-армированных в плоскости пластин и пространственно-армированных искривленных панелей. В этих работах в качестве определяющих соотношений для компонентов композиции использовались уравнения теории пластического течения с изотропным упрочнением – теории Прандтля–Рейсса–Хилла (ТПРХ) [12]. Однако известно, что неупругое поведение многих материалов, особенно имеющих ярко выраженный предел текучести, в значительной степени зависит от скорости их деформирования [13, 14]. Имеются обзоры экспериментальных данных о влиянии скорости деформирования различных материалов на их пределы текучести, прочности и законы упрочнения [14–20], из которых следует, что предел текучести при высоких скоростях деформирования может в 2–3 раза превышать статический предел текучести. А значит, для адекватного описания неупругого поведения КМ-конструкций при их динамическом нагружении необходимо учитывать зависимость пластических и прочностных свойств компонентов композиции от скорости их деформирования. В рамках ТПРХ это обстоятельство не учитывается. Структурная теория неупругого поведения пространственно-армированных КМ-сред, использующая определяющие уравнения теории пластического течения при учете чувствительности компонентов композиции к скорости их деформирования на сегодняшний день не построена. Согласно терминологии, принятой ранее [20, 21], такую модель неупругого поведения материалов будем называть теорией упруговязкопластического деформирования, различные варианты которой для однородных материалов разработаны и обсуждались [16, 19–23].

Основные преимущества КМ – сочетание высокой прочности с легкостью – наиболее ярко проявляются в тонкостенных конструкциях типа пластин и оболочек [8, 10, 11, 24–31]. Следовательно, актуальна проблема адекватного моделирования изгибного деформирования таких элементов КМ-конструкций при учете их возможного слабого сопротивления поперечным сдвигам и при наличии высокоинтенсивного воздействия.

Поперечные сдвиги в тонкостенных КМ-элементах традиционно учитываются в рамках кинематических гипотез Рейсснера [8, 25, 27, 29, 31] или Амбарцумяна [10, 24, 26, 28, 30]. При этом в основном исследуется только линейно-упругое поведение КМ-конструкций. Лишь в отдельных работах моделировалось упругопластическое деформирование слоистых (неармированных) [27] и армированных [9–11] тонкостенных конструкций. Показано [24], что теория Амбарцумяна является асимптотически точной (в первом асимптотическом приближении получается классическая теория изгиба пластин, а во втором приближении – теория Амбарцумяна), при этом на лицевых поверхностях конструкции удается удовлетворить граничные условия по касательным силам. Теория же Рейсснера не является асимптотически точной, и никакие силовые граничные условия на лицевых поверхностях конструкции в рамках этой теории удовлетворить нельзя.

Для численного интегрирования динамических задач используют явные и неявные методы [32]. Из явных схем наиболее часто используется схема типа “крест” [9–11, 27], из неявных – методы Ньюмарка [33–35].

В связи со всем вышеизложенным настоящее исследование посвящено моделированию упруговязкопластического деформирования гибких пространственно-армированных пластин в рамках теории Амбарцумяна. Численное интегрирование возникающих при этом начально-краевых задач предполагается осуществлять с использованием явной схемы типа “крест”.

1. Модель упруговязкопластического течения. Для интегрирования упругопластических задач динамики изотропных тел с применением явной численной схемы были предложены [32] три варианта записи определяющих уравнений в рамках ТПРХ. Третий вариант записи этих уравнений соответствует схеме Уилкинса [36]. Однако для моделирования упругопластического поведения армированных тонкостенных элементов конструкций [9–11] наиболее удобным оказался второй вариант записи, имеющий вид [32]

где ${{\sigma }_{{ij}}}$ и ${{\varepsilon }_{{ml}}}$ – компоненты тензоров напряжений и деформаций, точка – производная по времени t. Выражения для компонентов тензора четвертого ранга ${{a}_{{ijml}}}$ при упругопластическом деформировании материала известны (см., например, [32], с. 238). В этом разделе по повторяющимся немым индексам проводится суммирование от 1 до 3.

Соотношения (1.1) формально совпадают с законом Гука для анизотропного тела вследствие деформационной анизотропии при пластическом деформировании изначально изотропного материала и при чисто упругом деформировании материала редуцируются в закон Гука для изотропной среды. Использование определяющих уравнений ТПРХ в форме (1.1) позволило на основе структурных соотношений, полученных для упругого случая [7], разработать модели упругопластического деформирования продольно-, плоско-перекрестно- и пространственно-армированных упругопластических сред в рамках теории пластического течения с изотропным упрочнением [9–11]. Определяющие соотношения для упруговязкопластического материала, полученные и обсуждавшиеся ранее [16, 19–23], по форме соответствуют варианту определяющих уравнений ТПРХ, использованному в схеме Уилкинса, поэтому они неудобны для моделирования упруговязкопластического поведения армированных сред. В связи с этим в настоящем разделе выведем определяющие соотношения для упруговязкопластического материала в обобщающей (1.1) форме, редуцирующиеся в соотношения (1.1) при отсутствии зависимости свойств материала от скорости его деформирования.

Как и ранее [9–11], предполагаем, что деформации ${{\varepsilon }_{{ij}}}$ малые, поэтому их можно разложить на упругие ${{e}_{{ij}}}$ и пластические ${{p}_{{ij}}}$ (несжимаемые) составляющие [20, 37]

Упругое поведение описывается соотношениями закона Гука для изотропного материала

где ${{s}_{{ij}}}$ и ${{\bar {e}}_{{ij}}}$ – компоненты тензоров-девиаторов напряжений и упругих деформаций (согласно равенству (1.3) девиатор пластических деформаций совпадает с тензором пластических деформаций), ${{\sigma }_{0}}$ и ${{\varepsilon }_{0}}$ – средние напряжение и деформация, ${{\delta }_{{ij}}}$ – символ Кронекера, E – модуль Юнга, $\nu $ – коэффициент Пуассона материала. На основании известных экспериментальных данных [20] считаем, что зависимостью упругих характеристик материала от скорости его деформирования можно пренебречь ($E = {\text{const}}$, $\nu = {\text{const}}$, $G = {\text{const}}$, $K = {\text{const}}$).

Как и ранее [20], предполагаем, что пластическое течение материала ассоциировано с поверхностью нагружения $f = 0$, которую для конкретности зададим в форме, соответствующей обобщенному на вязкопластическое деформирование условию текучести Мизеса:

или где ${{\xi }_{{ij}}}$ – компоненты девиатора скорости деформаций, T – интенсивность касательных напряжений, $\chi $ – параметр Одквиста, H – интенсивность скоростей деформаций сдвига, ${{\tau }_{s}}$ – мгновенный предел текучести при чистом сдвиге, равный значению интенсивности касательных напряжений T при определенной интенсивности скорости деформации H и накопленной пластической деформации $\chi $ в текущий момент времени t. Начальная поверхность нагружения ${{\tau }_{s}}\left( H \right) = {{\tau }_{s}}\left( {0,H} \right)$ совпадает с обычным пределом текучести, зависящим от скорости деформирования H [13, 20]. Соотношения (1.9) соответствуют традиционному предположению, что поверхность нагружения не зависит от ${{\sigma }_{0}}$ [12] (разносопротивляемость материала растяжению и сжатию в данной работе не учитывается), т.е. согласно соотношениям (1.4) и (1.5) не зависит от относительного изменения объема ${{\varepsilon }_{0}}$ элемента материала. На основании этого считаем, что поверхность нагружения не зависит и от скорости изменения относительного объема ${{\dot {\varepsilon }}_{0}}$.

Согласно ассоциированному закону пластического течения, при учете равенств (1.6) и (1.8) имеем [12, 20]

где $d\lambda $ – дифференциал неопределенного пока параметра $\lambda $. Для определения $d\lambda $ умножим все части равенств (1.10) на ${{s}_{{ij}}}$ и свернем результат по обоим индексам, тогда при учете выражений (1.8) получим

Отсюда следует выражение

подставив которое в равенства (1.10), при учете выражения (1.7) будем иметь

В рамках ТПРХ, когда ${{\tau }_{s}} = {{\tau }_{s}}\left( \chi \right)$, приращение работы пластических деформаций $d{{A}_{p}} = {{s}_{{mn}}}d{{p}_{{mn}}}$ выражают через приращение работы деформаций формоизменения

т.е. предполагают (см. [32], с. 234) где $\kappa = \kappa \left( \chi \right)$ – коэффициент пропорциональности, зависящий только от параметра Одквиста и выражающийся через модуль сдвига G и касательный модуль $\tilde {G}$ на диаграмме чистого сдвига [32], т.е. определяется свойствами материала.

Соотношения (1.13) предполагаются справедливыми при любых видах напряженно-деформированного состояния (НДС) в случае активного нагружения изотропного материала, нечувствительного к скорости деформирования. В частности, при чистом сдвиге энергетическое равенство (1.13) при учете равенств (1.8) и (1.5) принимает вид

где $\tau $ – касательное напряжение при чистом сдвиге, $\gamma $ – полная угловая деформация (например, $\gamma = 2{{\varepsilon }_{{12}}}$), ${{\gamma }_{p}}$ – пластическая составляющая величины $\gamma $.

Соотношение (1.14) справедливо при выполнении равенства (1.7), где $T = \tau $ и $\partial {{\tau }_{s}}{\text{/}}\partial H \equiv 0$. Предположим теперь, что диаграмма деформирования материала при чистом сдвиге зависит от скорости деформирования, т.е. согласно равенствам (1.7) и (1.15) имеем

где $\xi \equiv H = \left| {\dot {\gamma }} \right|$ – модуль скорости полной угловой деформации при чистом сдвиге. Используя равенство (1.16), получим энергетическое соотношение, аналогичное (1.14). Согласно равенству (1.16) при активном вязкопластическом нагружении материала в случае чистого сдвига для дифференциала касательного напряжения $\tau $ имеем выражение где ${{\tau }_{\chi }} \equiv \bar {G} = {{\tau }_{\chi }}\left( {\chi ,H} \right) = {{\tau }_{\chi }}\left( {{{\gamma }_{p}},\xi } \right)$ и ${{\tau }_{H}} = {{\tau }_{H}}\left( {\chi ,H} \right) = {{\tau }_{H}}\left( {{{\gamma }_{p}},\xi } \right)$ – известные из эксперимента функции, причем ${{\tau }_{\chi }} \equiv \bar {G}$ – касательный модуль при постоянной скорости деформирования ($\xi = {\text{const}}$) на диаграмме $\tau \sim {{\gamma }_{p}}$. (Здесь и далее для удобства предполагается, что угловые деформации $\gamma $ и ${{\gamma }_{p}}$ при проведении экспериментов на чистый сдвиг являются положительными.) Были описаны [20] методы идентификации функций ${{\tau }_{\chi }}$ и ${{\tau }_{H}}$.

С другой стороны, приращение касательного напряжения $\tau $ сопровождается приращением упругих угловых деформаций ${{\gamma }_{e}}$, поэтому на основании закона Гука (см. равенства (1.4)) имеем

где согласно равенствам (1.2)

Подставим выражение (1.19) в равенство (1.17) и учтем соотношения (1.20), тогда получим

откуда следует цепочка равенств после умножения которой на $\tau $ вытекает энергетическое соотношение или, учитывая, что при чистом сдвиге $d{{A}_{p}} = \tau d{{\gamma }_{p}}$ и $dA = \tau d\gamma $, имеем

Если материал нечувствителен к скорости деформирования (т.е. ${{\tau }_{s}} = {{\tau }_{s}}\left( \chi \right) = {{\tau }_{s}}\left( {{{\gamma }_{p}}} \right)$), то согласно соотношениям (1.18) ${{\tau }_{H}} \equiv 0$ и из равенства (1.22) вытекает соотношение (1.14), в котором $\kappa = \hat {G}$ (что полностью согласуется с выражением для $\kappa $, приведенным ранее [32]). По аналогии с ТПРХ далее предполагаем, что соотношение, аналогичное (1.23), должно быть справедливо при любых видах НДС материала в случае его активного нагружения, поэтому получаем

В случае ${{\tau }_{s}} = {{\tau }_{s}}\left( \chi \right)$, т.е. при ${{\tau }_{H}} \equiv 0$, выражение (1.24) редуцируется в равенство, заключенное в соотношениях (1.13) в скобки. Подставим выражение (1.24) в правую часть равенства (1.12), а в левой части (1.12) учтем разложение (1.2) и первое соотношение (1.4), тогда получим

Соотношение (1.25), по сути, является иной формой записи определяющих уравнений для упруговязкопластичного материала, полученных ранее [20]. Разделим обе части равенства (1.25) на дифференциал времени $dt$ и учтем соотношения (1.4) и (1.5), тогда окончательно будем иметь

где $\lambda $ – параметр Ламе (не путать с $\lambda $ в равенствах (1.10) и (1.11)), c – параметр переключения, который равен единице при активном нагружении материала и нулю при его упругом деформировании, разгрузке и нейтральном нагружении.

Если материал нечувствителен к скорости деформирования, то в равенствах (1.26) следует принять ${{\tau }_{H}} \equiv 0$, и тогда получаем соотношения вида (1.1), в которых коэффициенты ${{a}_{{ijmn}}}$ получаются из сравнения равенств (1.1) и (1.26). В этом случае выражения для ${{a}_{{ijmn}}}$ при учете соотношений (1.27) полностью совпадают с известными выражениями [32].

Определим теперь условия, при которых в равенствах (1.26) $c = 0$ или $c = 1$. Согласно равенствам (1.6) и (1.7) чисто упругое деформирование определяется условием $f < 0$, или

Начало разгрузки от поверхности нагружения характеризуется условиями $f = 0$ и $df < 0$, поэтому, используя равенство (1.6) при учете выражений (1.8) и (1.18), вычислим дифференциал функции f:

На основании второго и третьего равенств (1.8) получаем

Выражение (1.29) при учете равенств (1.30) принимает вид

Согласно соотношениям (1.31) при начале разгрузки от поверхности нагружения $f = 0$ приращения пластических деформаций отсутствуют ($d\chi = 0$), поэтому при учете условия $df < 0$ из равенства (1.32) вытекает условие начала разгрузки

В условиях нейтрального нагружения имеем

однако при этом приращения пластических деформаций опять же отсутствуют ($d\chi = 0$), поэтому из равенства (1.32) следуют условия нейтрального нагружения, аналогичные (1.33), где знак “меньше” нужно заменить знаком “равно”. В условиях активного нагружения выполняются равенства (1.34), но при этом согласно соотношениям (1.31) имеем $d\chi > 0$. Кроме того, из экспериментов известно [13, 20], что ${{\tau }_{s}} > 0$ и ${{\tau }_{\chi }} \equiv \bar {G} > 0$, поэтому из равенства (1.32) получаем условия активного нагружения

Соотношения (1.28), (1.33) и (1.35) при соответствующих переобозначениях полностью совпадают с аналогичными условиями, полученными ранее [20].

Разделим вторые соотношения в условиях (1.33) и (1.35) на дифференциал времени $dt$, тогда при учете неравенства (1.28) окончательно получим выражения для параметра переключения c в соотношениях (1.26):

Неравенство в условиях (1.35) при учете выражений (1.8) может быть переписано в виде

отсюда при учете соотношения (1.7) получаем

Так как согласно экспериментальным данным ${{\tau }_{s}} > 0$, из условий (1.35) и (1.37) после деления обеих частей неравенства (1.37) на $2{{\tau }_{s}}dt$ вытекает другая форма условия активного нагружения

Из экспериментов известно [20], что функция ${{\tau }_{H}}\left( {\chi ,H} \right) > 0$, поэтому из условий (1.38) следует: при отсутствии приращений интенсивности напряжений ($\dot {T} = 0$ или $dT = 0$) прирост пластических деформаций при активном нагружении возможен только при уменьшении скорости деформирования ($\dot {H} < 0$ или $dH < 0$), что качественно согласуется с известными экспериментальными данными [20]. Следовательно, соотношения (1.26) при учете выражений (1.27) и (1.36) также согласуются с экспериментальными результатами.

Соотношениям (1.36) можно придать несколько иную форму. Действительно, при нейтральном нагружении и разгрузке из равенств (1.26) следует ${{\dot {s}}_{{ij}}} = 2G{{\dot {\bar {\varepsilon }}}_{{ij}}}$ ($i,j = 1,2,3$). Подставив это выражение в первое условие (1.36), получим

С другой стороны, при активном нагружении согласно соотношениям (1.12) и (1.36) равенство (1.26) аналогично следующему (см. (1.24) и (1.25)):

Подставим выражение (1.40) во второе условие (1.36), тогда получим

откуда при учете обозначений (1.8) следует

Согласно постулату Друккера [12, 20], при активном нагружении имеем ${{s}_{{ij}}}{{\dot {p}}_{{ij}}} > 0$, поэтому в силу $G > 0$ из условия (1.41) вытекает редуцированное неравенство

Используя неравенства (1.39) и (1.42), выражения (1.36) можно записать в следующей форме:

Если материал нечувствителен к скорости деформирования (${{\tau }_{H}} \equiv 0$), то из соотношений (1.43) получаются выражения для параметра переключения c, полностью совпадающие с полученными ранее [32].

Таким образом, окончательно получаем, что определяющие уравнения для упруговязкопластичного материала имеют вид равенств (1.26) при учете соотношений (1.27), (1.18) и (1.43) (или (1.36)).

2. Моделирование упруговязкопластического деформирования гибкой пространственно-армированной пластины. Рассматривается пространственно-армированная пластина толщиной 2h, с которой связана декартова прямоугольная система координат так, что отсчетная плоскость $O{{x}_{1}}{{x}_{2}}$ (${{x}_{3}} = 0$) совпадает со срединной плоскостью ($\left| {{{x}_{3}}} \right| \leqslant h$), а ось $O{{x}_{3}}$ перпендикулярна отсчетной плоскости (рис. 1). Пластина усилена N семействами волокон (ND-армирована) с интенсивностями армирования ${{\omega }_{k}}$ ($1 \leqslant k \leqslant N$), причем структура армирования в поперечном направлении квазиоднородна. Относительное объемное содержание связующего в представительном элементе композиции

Так как определить реальное распределение напряжений, деформаций и их скоростей в КМ, в котором связующая матрица содержит многочисленные, достаточно произвольно ориентированные жесткие включения, весьма затруднительно [26] (особенно в случаях неупругого деформирования компонентов композиции), для получения пригодных в практических приложениях определяющих уравнений упруговязкопластического поведения рассматриваемого КМ введем исходные предпосылки, аналогичные принятым ранее [7, 9–11, 26].

1. В пределах ячейки периодичности КМ представляет собой макроскопически квазиоднородное анизотропное тело. (При достаточно густом и равномерном насыщении связующего тонкими волокнами это допущение вполне приемлемо [26].)

2. Между связующим и армирующими волокнами реализуется идеальный механический контакт.

3. В пределах ячейки периодичности, выделенной из КМ на миниуровне, деформации, напряжения и их скорости во всех компонентах и в композиции кусочно-постоянны. Эффекты более высоких порядков, связанные с изменением полей деформаций, напряжений и их скоростей на микроуровне в малых окрестностях границ контакта связующего и волокон, не учитываем.

4. Поля напряжений, деформаций и их скоростей усредняем по объему представительного элемента композиции (т.е. на основании допущения 3 – пропорционально относительному объемному содержанию ${{\omega }_{k}}$ ($0 \leqslant k \leqslant N$) каждого компонента).

5. Компоненты композиции изотропны, а их упруговязкопластическое поведение описывается определяющими уравнениями (1.26) при учете (1.18), (1.27) и (1.43), которые для удобства дальнейшего изложения перепишем в матричной форме [26] (всюду далее, если не указано иное, $k = 0,1,2,\; \ldots ,\;N$)

Здесь и далее

(выражения для ${{{\mathbf{s}}}_{k}}$ и ${{\xi }_{k}}$ получаются из первого выражения (2.3) при замене $\sigma $ на s и $\xi $ соответственно), ${{{\mathbf{Z}}}_{k}} = \left( {z_{{ij}}^{{(k)}}} \right)$ и ${{{\mathbf{Y}}}_{k}} = \left( {y_{{ij}}^{{(k)}}} \right)$ – симметричные ($6 \times 6$)-матрицы, характеризующие механическое поведение k-го компонента композиции (${{{\mathbf{Z}}}_{k}}$ можно условно трактовать как матрицу “жесткости” материала (см. (1.1))) и которые можно представить в виде ${{{\mathbf{\bar {Z}}}}_{k}} = \left( {\bar {z}_{{ij}}^{{(k)}}} \right)$ и ${{{\mathbf{\bar {\bar {Z}}}}}_{k}} = \left( {\bar {\bar {z}}_{{ij}}^{{(k)}}} \right)$ – симметричные ($6 \times 6$)-матрицы, ненулевые элементы которых определяются по формулам

Индекс T – операция транспонирования.

В соотношениях (2.3)–(2.6) все величины имеют тот же смысл, что и в разд. 1, индекс k – номер компонента композиции: $k = 0$ – связующее, $k \in [1,N]$ – арматура k-го семейства. Равенства (2.3) задают соответствия между шестью компонентами $f_{i}^{{(k)}}$ ($i = \overline {1,6} $) некоторого вектора-столбца ${{{\mathbf{f}}}_{k}}$ и компонентами соответствующего симметричного тензора второго ранга $f_{{jl}}^{{(k)}}$, $j,l = \overline {1,3} $. (Согласно введенным обозначениям (2.3), ${{\xi }_{k}} \ne {{\dot {\varepsilon }}_{k}}$.)

Как и ранее [9–11], для численного интегрирования рассматриваемой задачи используем алгоритм шагов по времени [27, 32–36], определяя значения неизвестных функций в дискретные моменты времени ${{t}_{{n + 1}}} = {{t}_{n}} + \Delta $ ($n = 0,1,2,\; \ldots $), где $\Delta = {\text{const}} > 0$ – шаг по времени. При этом считаем, что в предыдущий момент времени ${{t}_{m}}$ уже известны значения вектор-функций

Так как далее предполагаем разрабатывать явную схему типа “крест” на трехточечном шаблоне по времени (${{t}_{{n - 1}}}$, ${{t}_{n}}$, ${{t}_{{n + 1}}}$), имеющую второй порядок точности по $\Delta $ [38], то для приведения соотношения (2.2) к виду, аналогичному (1.1), преобразуем последнее слагаемое в правой части равенства (2.2), используя формулу трапеций, которая также имеет второй порядок точности по $\Delta $ [39]. Согласно формуле трапеций [39], для текущего момента времени ${{t}_{n}}$ при учете обозначений, аналогичных (2.7), имеем

откуда где

Из равенства (2.9) при учете предположений (2.7) следует, что шестикомпонентный вектор-столбец $\mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^{n - 1/2} $ в выражении (2.8) при $t = {{t}_{n}}$ уже известен.

После подстановки выражения (2.8) в равенство (2.2) получим

где $\mathop {{{{\mathbf{{\rm B}}}}_{k}}}\limits^n = \left( {\mathop {b_{{ij}}^{{(k)}}}\limits^n } \right)$ – ($6 \times 6$)-матрица, $\mathop {{{{\mathbf{p}}}_{k}}}\limits^n = \left\{ {\mathop {p_{i}^{{(k)}}}\limits^n } \right\}$ ($i,j = \overline {1,6} $) – шестикомпонентный вектор-столбец. Соотношение (2.10) в текущий момент времени ${{t}_{n}}$ представляет собой определяющее уравнение для упруговязкопластического материала k-го компонента композиции. При $t = {{t}_{n}}$ матрицы ${{{\mathbf{Z}}}_{k}}$ и ${{{\mathbf{Y}}}_{k}}$ в соотношении (2.2) (см. выражения (2.4)), а значит, согласно равенствам (2.11), $\mathop {{{{\mathbf{{\rm B}}}}_{k}}}\limits^n $и $\mathop {{{{\mathbf{p}}}_{k}}}\limits^n $, предполагаются линеаризованными по методу, аналогичному методу переменных параметров упругости [40]. Следовательно, на каждой итерации этого метода в момент времени ${{t}_{n}}$ вектор-столбец $\mathop {{{{\mathbf{p}}}_{k}}}\limits^n $ в формуле (2.10) при учете равенств (2.11) и (2.9) известен. При $\mathop {{{{\mathbf{p}}}_{k}}}\limits^n = {\mathbf{0}}$ равенство (2.10) редуцируется в соотношение (1.1).

Линеаризованные уравнения (2.10) формально совпадают с соотношениями Дюамеля–Неймана для неоднородной анизотропной среды [41], где вектор-столбец $\mathop {{{{\mathbf{p}}}_{k}}}\limits^n $ условно можно трактовать как известную в момент времени ${{t}_{n}}$ на текущей итерации скорость температурных напряжений. Поэтому, используя результаты работы [7], на основании соотношений (2.10) можно построить структурную модель упруговязкопластического деформирования пространственно-армированного КМ.

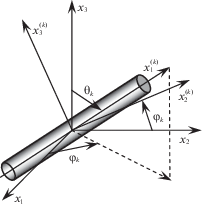
Согласно этому, с k-м семейством волокон ($1 \leqslant k \leqslant N$) свяжем свою локальную ортогональную систему координат $x_{i}^{{(k)}}$ таким образом, чтобы ось $x_{1}^{{(k)}}$ совпадала с направлением траектории армирования, а оси $x_{2}^{{(k)}}$, $x_{3}^{{(k)}}$ были перпендикулярны этим траекториям (рис. 2). Направление армирования k-м семейством волокон можно однозначно задать двумя углами сферической системы координат ${{\theta }_{k}}$ и ${{\varphi }_{k}}$. Направляющие косинусы $l_{{ij}}^{{(k)}}$ между осями $x_{i}^{{(k)}}$ и ${{x}_{j}}$ ($i,j = 1,2,3$) при этом определяются по формулам:

При переходе от глобальной системы координат ${{x}_{i}}$ к локальной системе $x_{i}^{{(k)}}$ ($i = \overline {1,3} $) выполняются следующие преобразования вектор-столбцов (см. обозначения (2.3)):

где чертой сверху обозначены величины, определенные в локальной системе координат $x_{l}^{{(k)}}$ ($l = 1,2,3$), ${{{\mathbf{G}}}_{k}} = \left( {g_{{ij}}^{{(k)}}} \right)$, ${{{\mathbf{Q}}}_{k}} = \left( {q_{{ij}}^{{(k)}}} \right)$ – ($6 \times 6$)-матрицы с элементами (см. формулы (2.12))

Невыписанные здесь компоненты матриц ${{{\mathbf{G}}}_{k}}$ и ${{{\mathbf{Q}}}_{k}}$ приведены ранее ([26], табл. (21.40) и (21.44)).

Согласно второму и третьему допущениям и условиям сопряжения полей напряжений и перемещений, на границах контакта связующего с арматурой имеем равенства (см. соотношения (2.13))

Первое из них определяет равенство удлинений арматуры k-го семейства и связующего материала в направлении траектории волокон, остальные равенства соответствуют условиям контакта между арматурой и связующим в напряжениях на боковой поверхности волокон.

Исходные предпосылки 1–5 аналогичны допущениям, принятым ранее [7, 9–11], поэтому, повторяя известные выкладки и рассуждения из [7, 9–11] при учете равенств (2.1), (2.10) и (2.15), в рассматриваемый момент времени ${{t}_{n}}$ на текущей итерации получим линеаризованное матричное соотношение, описывающее упруговязкопластическое поведение пространственно-армированного материала:

где $\dot {\sigma }$ и $\dot {\varepsilon }$ – шестикомпонентные векторы-столбцы скоростей усредненных напряжений ${{\dot {\sigma }}_{{ij}}}$ и деформаций ${{\dot {\varepsilon }}_{{ij}}}$ в композиции, аналогичные по структуре (2.3), I – единичная ($6 \times 6$)-матрица, B, ${{{\mathbf{{\rm E}}}}_{k}}$, ${{{\mathbf{C}}}_{k}}$ – ($6 \times 6$)-матрицы, ${\mathbf{D}}_{k}^{{ - 1}}$ и ${{{\mathbf{H}}}^{{ - 1}}}$ – матрицы, обратные ($6 \times 6$)-матрицам ${{{\mathbf{D}}}_{k}}$ и H, p, f, g, ${{{\mathbf{r}}}_{k}}$, ${{\varsigma }_{k}}$ – шестикомпонентные векторы-столбцы. Элементы $c_{{ij}}^{{(k)}}$ и $d_{{ij}}^{{(k)}}$ матриц ${{{\mathbf{C}}}_{k}}$ и ${{{\mathbf{D}}}_{k}}$ и компоненты $\varsigma _{i}^{{(k)}}$ векторов-столбцов ${{\varsigma }_{k}}$ при учете равенств (2.10)–(2.12), (2.14) и (2.15) определяются так: (В равенствах (2.17) и (2.18) для упрощения опущен верхний индекс n.)

Как и ранее [7, 10, 11], при выводе соотношений (2.16) и (2.17) попутно получаются линеаризованные матричные равенства

В момент времени ${{t}_{n}}$ на текущей итерации первое равенство (2.19) выражает скорости деформаций связующего ${{\dot {\varepsilon }}_{0}}$ через скорости усредненных деформаций композиции $\dot {\varepsilon }$, а второе определяет скорости деформаций волокон k-го семейства ${{\dot {\varepsilon }}_{k}}$ через скорости деформаций связующего ${{\dot {\varepsilon }}_{0}}$, т.е. в конечном итоге через $\dot {\varepsilon }$.

Согласно формулам (2.17) и (2.18), при $t = {{t}_{n}}$ на данной итерации матрицы B, ${{{\mathbf{H}}}^{{ - 1}}}$, ${{{\mathbf{E}}}_{k}}$ и векторы-столбцы p, g, ${{{\mathbf{r}}}_{k}}$ в соотношениях (2.16) и (2.19) известны.

Если материалы всех компонентов композиции нечувствительны к скорости деформирования, т.е. $\tau _{H}^{{(k)}} \equiv 0$, $0 \leqslant k \leqslant N$ (см. формулы (2.4) и (2.6)), то в соотношении (2.16) согласно формулам (2.17) и (2.18) получаем $\mathop {\mathbf{p}}\limits^n \equiv {\mathbf{0}}$, и оно редуцируется в определяющее матричное уравнение для пространственно-армированного КМ, полученное [11] в рамках ТПРХ. Следовательно, равенство (2.16) – обобщение структурных соотношений, построенных ранее [11].

Было показано [11], что в рамках ТПРХ при произвольных пространственных структурах армирования не удается разработать явную численную схему типа “крест” так, чтобы на лицевых поверхностях пластины силовые граничные условия по касательным напряжениям при использовании теории изгиба Амбарцумяна [24] были удовлетворены. Очевидно, что этот результат переносится и на данное исследование, как на более общий случай. В связи с этим, в настоящей работе рассматриваются только частные случаи пространственных структур армирования и нагружения КМ-пластин, при которых можно построить явную схему типа “крест”. Принимая это во внимание, предполагаем: структура пространственного армирования пластины такова, что если волокно k-го семейства имеет наклонную траекторию ($0 < {{\theta }_{k}} < \pi {\text{/}}2$ на рис. 2), то обязательно найдется m-е семейство наклонных волокон с параметрами армирования

изготовленных из того же материала, что и арматура k-го семейства. Такие структуры пространственного армирования часто встречаются на практике [1–4]. Так, к ним относятся пространственные структуры, изображенные на рис. 1б и 1в, а также структуры с плоско-перекрестным армированием (рис. 1а); в последнем случае формально ${{\omega }_{m}} = {{\omega }_{k}} = 0$. Кроме того, исследуется лишь частный практически важный случай нагружения КМ-пластины, когда на лицевые поверхности действуют только нормальные распределенные силы. Согласно этим предположениям, для учета возможного (например в случаях 2D- и 3D-структур армирования, изображенных на рис. 1а и 1б) слабого сопротивления КМ-пластины поперечным сдвигам используем кинематические соотношения теории Амбарцумяна [24]. Рассматривая геометрическую нелинейность задачи в приближении Кармана, для усредненных деформаций композиции ${{\varepsilon }_{{ij}}}$ и перемещений ${{U}_{i}}$ точек КМ-конструкции получим выражения [10, 24] где w – прогиб, ${{u}_{i}}$ – тангенциальные перемещения точек отсчетной плоскости (${{x}_{3}} = 0$) в направлениях ${{x}_{i}}$, $\varepsilon _{{i3}}^{0}$ – деформации поперечных сдвигов в точках отсчетной плоскости, ${{t}_{0}}$ – начальный момент времени t, ${{\partial }_{i}}$ – оператор частного дифференцирования по переменным ${{x}_{i}}$, $\Omega $ – область, занимаемая пластиной в плане. В соотношениях (2.20) и (2.21) неизвестны функции w, ${{u}_{i}}$ и $\varepsilon _{{i3}}^{0}$, зависящие от времени t и двух пространственных переменных ${{x}_{i}}$ ($i = 1,2$).

Так как моделируется механическое поведение КМ-пластины как гибкой тонкостенной системы, то напряжение ${{\sigma }_{{33}}}\left( {t,{\mathbf{r}}} \right)$ с приемлемой для инженерных приложений точностью можно аппроксимировать линейно по толщине конструкции [25]:

где $\sigma _{{33}}^{{( \pm )}}\left( {t,{\mathbf{x}}} \right) \equiv {{\sigma }_{{33}}}\left( {t,{\mathbf{x}}, \pm h} \right)$ – нормальные напряжения на нижней (–) и верхней (+) лицевых поверхностях, которые известны из соответствующих граничных условий.

Матричное равенство (2.16) представляет собой систему шести алгебраических уравнений. Согласно соотношениям соответствия, аналогичным равенствам (2.3), из третьего уравнения этой системы можно выразить скорость линейной поперечной деформации пластины:

где функция ${{\dot {\sigma }}_{3}}$ известна в момент времени ${{t}_{n}}$ после дифференцирования по t соотношения (2.22). Скорости деформаций ${{\dot {\varepsilon }}_{i}}$ в правой части равенства (2.23) определяются путем дифференцирования по времени t выражений (2.20), т.е. вычисляются через функции w, $\dot {w}$, ${{\dot {u}}_{l}}$ и $\dot {\varepsilon }_{{l3}}^{0}$ ($l = 1,2$).

Для завершения постановки задачи изгиба тонких КМ-пластин к выражениям (2.20)–(2.23) необходимо присоединить уравнения движения, граничные и начальные условия, которые общеизвестны [24], поэтому здесь не приведены (см. [10], равенства (39), (43) и [11], равенства (22), (23) и (25)).

3. Численный метод расчета. Как уже отмечалось в разд. 2, для численного интегрирования исследуемой задачи используется метод шагов по времени [9–11, 27, 32–36]. Предполагаем, что в дискретные моменты времени ${{t}_{m}}$ кроме (2.7) уже известны значения следующих функций:

Производные по времени t (за исключением левой части равенства (2.8)) аппроксимируем соответствующими центральными конечными разностями на трехточечном шаблоне [36, 38]. Это позволяет разработать явную схему численного интегрирования рассматриваемой задачи. Заменяя вторые производные по времени от кинематических переменных в уравнениях движения их конечно-разностными аналогами, при учете обозначений, подобных (3.1), получим [10]

где ${{\rho }_{0}}$ и ${{\rho }_{k}}$ – объемная плотность связующего и волокон k-го семейства, ${{\gamma }_{i}}$ – введенные для удобства функции, ${{F}_{{ij}}}$, ${{F}_{{i3}}}$, ${{M}_{{ij}}}$ – внутренние силовые факторы.

Используя предположения (3.1) и выражения (3.3), при $t = {{t}_{n}}$ можем определить все силовые факторы и внешние нагрузки, входящие в правые части соотношений (3.2), поэтому при учете необходимых граничных условий (см. [11], равенства (22) и (23)) из уравнений (3.2) можем вычислить по явной схеме значения неизвестных функций $\mathop w\limits^{n + 1} $, $\mathop {{{u}_{i}}}\limits^{n + 1} $ и $\mathop {{{\gamma }_{i}}}\limits^{n + 1} $ в следующий момент времени ${{t}_{{n + 1}}}$. Зная функции $\mathop w\limits^{n + 1} $, $\mathop {{{u}_{i}}}\limits^{n + 1} $ и $\mathop {{{\gamma }_{i}}}\limits^{n + 1} $, по формулам (2.20) при учете соотношений (3.4) можем вычислить усредненные деформации композиции $\mathop {{{\varepsilon }_{{ij}}}}\limits^{n + 1} $. Так как при $t = {{t}_{{n - 1}}}$ деформации $\mathop {{{\varepsilon }_{{ij}}}}\limits^{n - 1} $ уже известны (см. формулы (2.20) и (3.4) при учете предположений (3.1)), используя формулы численного дифференцирования по времени t и равенство (2.23), можем определить и скорости усредненных деформаций $\mathop {{{{\dot {\varepsilon }}}_{{ij}}}}\limits^n $ в каждой точке пластины в момент времени ${{t}_{n}}$. После этого по формулам (2.19) при учете обозначений (2.3) последовательно определяем скорости деформаций компонентов композиции $\mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^n $, а из равенств (2.10) и (2.8) – скорости напряжений $\mathop {{{{\dot {\sigma }}}_{k}}}\limits^n $ и ускорения деформаций $\mathop {{{{\ddot {\varepsilon }}}_{k}}}\limits^n $ ($0 \leqslant k \leqslant N$) в тех же материалах. После этого решение задачи строится совершенно так же, как и ранее [10, 11].

Как уже отмечалось, матричные соотношения (2.10), (2.16) и (2.19) предполагаются линеаризованными, поэтому в текущий момент времени ${{t}_{n}}$ в каждой точке пластины (независимо от других точек) необходимо уточнять элементы матриц ${{{\mathbf{B}}}_{k}}$, B, ${{{\mathbf{H}}}^{{ - 1}}}$, ${{{\mathbf{E}}}_{k}}$ и векторов-столбцов ${{{\mathbf{p}}}_{k}}$, p, g и ${{{\mathbf{r}}}_{k}}$ ($1 \leqslant k \leqslant N$) при учете соотношений (2.11), (2.17), (2.18), (2.23), (2.5) и (2.6). Для этого используется итерационный процесс, аналогичный методу переменных параметров упругости [40] и качественно подобный процедуре “посадки” напряженного состояния на поверхность нагружения [27, 36]. Предварительные расчеты показывают, что для получения практически приемлемых результатов вполне достаточно использовать две итерации по этому методу.

Если в момент времени ${{t}_{n}}$ итерационный процесс сошелся с требуемой точностью, т.е. известны векторы-столбцы $\mathop {{{{\dot {\sigma }}}_{k}}}\limits^n $ и $\mathop {{{{\dot {\varepsilon }}}_{k}}}\limits^n $, то, используя центральные конечные разности по времени, запишем

где правые части и векторы-столбцы $\mathop {{{\sigma }_{k}}}\limits^{n - 1} $, $\mathop {{{\varepsilon }_{k}}}\limits^{n - 1} $ уже известны (см. соотношения (2.3) и (3.1)). Следовательно, из равенств (3.5) можем определить напряжения $\mathop {{{\sigma }_{k}}}\limits^{n + 1} $ и деформации $\mathop {{{\varepsilon }_{k}}}\limits^{n + 1} $ в каждом компоненте композиции в следующий момент времени ${{t}_{{n + 1}}}$. При этом на основании закона Гука можем вычислить и упругие деформации $\mathop {e_{{ij}}^{{(k)}}}\limits^{n + 1} $ (см. равенства (1.4), (1.5) и соответствия (2.3)), а затем по формуле (1.2) – пластические деформации

Согласно последнему соотношению (1.8), для вычисления параметра Одквиста ${{\chi }^{{(k)}}}$ в момент времени ${{t}_{{n + 1}}}$ имеем равенство

где

В правых частях равенств (3.8) величины $\mathop {p_{{ij}}^{{(k)}}}\limits^{n + 1} $ и $\mathop {p_{{ij}}^{{(k)}}}\limits^n $ уже известны (см. соотношения (3.6) и предположения (3.1)), поэтому в выражении (3.7) известно последнее слагаемое. Следовательно, по формуле (3.7) при учете соотношений (3.5), (3.6) и (3.8) можно приближенно вычислить параметр Одквиста $\mathop {{{\chi }^{{(k)}}}}\limits^{n + 1} $ в каждом компоненте композиции при $t = {{t}_{{n + 1}}}$, причем не потребуется в дальнейшем уточнять значения $\mathop {{{\chi }^{{(k)}}}}\limits^{n + 1} $ в процессе итераций, организуемых в следующий момент времени ${{t}_{{n + 1}}}$, что удобно с вычислительной точки зрения.

Согласно левым частям равенств (3.2), для начала расчетов по предложенной численной схеме необходимо предварительно получить значения функций $\mathop w\limits^m $, $\mathop {{{u}_{i}}}\limits^m $ и $\mathop {{{\gamma }_{i}}}\limits^m $ ($m = 0,1$). Функции $\mathop w\limits^0 $, $\mathop {{{u}_{i}}}\limits^0 $ и $\mathop {{{\gamma }_{i}}}\limits^0 $ однозначно определяются начальными условиями, а функции $\mathop w\limits^1 $, $\mathop {{{u}_{i}}}\limits^1 $ и $\mathop {{{\gamma }_{i}}}\limits^1 $ вычисляются по формуле Тейлора [38] при использовании начальных условий и уравнений движения в начальный момент времени $t = {{t}_{0}}$ (см. [10], соотношения (58)).

Согласно формуле (2.8), при учете выражения (2.9) кроме традиционных начальных условий необходимо при $t = {{t}_{0}}$ задать и ускорения деформаций компонентов композиции $\mathop {{{{\ddot {\varepsilon }}}_{k}}}\limits^0 \left( {\mathbf{r}} \right)$. Если до начального момента времени ${{t}_{0}}$ пластина покоилась, то $\mathop {{{{\ddot {\varepsilon }}}_{k}}}\limits^0 \left( {\mathbf{r}} \right) = 0$ ($0 \leqslant k \leqslant N$).

Если область $\Omega $, занимаемая пластиной в плане, прямоугольная, то, заменяя в соотношениях (3.2) и силовых граничных условиях производные ${{\partial }_{i}}\left( \centerdot \right)$ их конечно-разностными аналогами, получим в конечном итоге явную численную схему типа “крест” [9–11, 27, 36, 38]. Если же область $\Omega $ имеет неканоническую форму, то для дискретизации равенств (3.2) по пространственным переменным ${{x}_{i}}$ ($i = 1,2$) можно использовать вариационно-разностный подход, рекомендованный ранее [27]. Необходимые условия устойчивости численной схемы типа “крест” получаются из критерия устойчивости Куранта–Фридрихса–Леви [27] и для КМ-пластины аналогичны полученным ранее неравенствам ([10], формулы (60)).

4. Обсуждение результатов расчетов. В качестве конкретных примеров рассмотрим неупругое динамическое поведение относительно толстых прямоугольных пластин

По всему контуру $\Gamma $ конструкции жестко закреплены ($w\left( {t,\Gamma } \right) = 0$, ${{u}_{i}}\left( {t,\Gamma } \right) = 0$ и ${{\gamma }_{i}}\left( {t,\Gamma } \right)$ = = 0) и в начальный момент времени $t = {{t}_{0}} = 0$ покоятся ($w\left( {{{t}_{0}},\Omega } \right) = 0$, $\dot {w}\left( {{{t}_{0}},\Omega } \right) = 0$, ${{u}_{i}}\left( {{{t}_{0}},\Omega } \right) = 0$, ${{\dot {u}}_{i}}\left( {{{t}_{0}},\Omega } \right) = 0$, ${{\gamma }_{i}}\left( {{{t}_{0}},\Omega } \right) = 0$ и ${{\dot {\gamma }}_{i}}\left( {{{t}_{0}},\Omega } \right) = 0$; $i = 1,2$). Со стороны нижних лицевых поверхностей пластины нагружаются давлением, порожденным воздушной взрывной волной [33]:

где ${{t}_{{{\text{max}}}}}$ – момент времени, в который давление $p\left( t \right)$ достигает максимального значения ${{p}_{{\max }}} > 0$, ${{t}_{{{\text{min}}}}}$ – момент времени, при котором $p\left( t \right)$ можно считать уже пренебрежимо малым по сравнению с ${{p}_{{\max }}}$ (выражению (4.2) соответствует условие $p\left( {{{t}_{{{\text{min}}}}}} \right) = 0.01{{p}_{{\max }}}$). На основании экспериментальных данных [33] в расчетах примем ${{t}_{{{\text{max}}}}} = 0.1$ мс и ${{t}_{{{\text{min}}}}} = 2$ мс, т.е. при $t > 2$ мс колебания КМ-пластин можно рассматривать как свободные.

Из экспериментов известно [8], что при интенсивном динамическом нагружении откольные явления в КМ-конструкциях возникают, если нагрузка возрастает до своего максимума за время, порядка 0.1 мкс и менее. Так как принято ${{t}_{{{\text{max}}}}}$ = 0.1 мс $ \gg $ 0.1 мкс, то в исследуемых КМ-пластинах ударно-волновые процессы не возникают и их динамическое поведение действительно можно рассматривать как движение гибких механических систем, а значит, аппроксимация (2.22) вполне обоснованно может быть использована в расчетах.

Пластины изготовлены из высокопрочного магниевого сплава ВМ65 [13] и армированы высокопрочной стальной проволокой У8А [42] (металлокомпозиция) или из эпоксидной смолы [43] и усилены стекловолокнами [42] (стеклопластик). Упругопластическое поведение материалов компонентов композиции на стадии активного нагружения при постоянстве скорости деформирования характеризуется диаграммой с линейным упрочнением

где $\sigma $ и $\varepsilon $ – осевые напряжение и деформация, $E_{{\text{s}}}^{{(k)}} = E_{{\text{s}}}^{{(k)}}\left( {\dot {\varepsilon }} \right)$ – модуль линейного упрочнения k-го компонента композиции, $\sigma _{{\text{s}}}^{{(k)}} = \sigma _{{\text{s}}}^{{(k)}}\left( {\dot {\varepsilon }} \right)$ и $\varepsilon _{{\text{s}}}^{{(k)}} = \varepsilon _{{\text{s}}}^{{(k)}}\left( {\dot {\varepsilon }} \right)$ – предел текучести и соответствующая ему деформация при значении скорости деформирования $\dot {\varepsilon } = {\text{const}}$. Физико-механические характеристики компонентов композиции приведены в табл. 1, где $a = \sqrt {E{\text{/}}\rho } $ – скорость звука в соответствующем материале, второе и третье числа в клетках соответствуют второму и третьему значению скорости деформирования $\dot {\varepsilon }$. (Имеются формулы пересчета характеристик диаграммы $\tau \sim \gamma $ при чистом сдвиге по данным диаграммы деформирования при растяжении – сжатии (4.3) [10, 32].)

Для сплава ВМ65 зависимости ${{\sigma }_{{\text{s}}}}\left( {\dot {\varepsilon }} \right)$ и ${{E}_{{\text{s}}}}\left( {\dot {\varepsilon }} \right)$ аппроксимировались степенными функциями вида $f\left( {\dot {\varepsilon }} \right) = A{{\dot {\varepsilon }}^{\mu }} + B$, постоянные A, B и $\mu $ определялись по данным, приведенным в табл. 1. Для остальных материалов использовалась линейная аппроксимация $f\left( {\dot {\varepsilon }} \right) = A\dot {\varepsilon } + B$. В силу отсутствия в литературе достоверных данных об особенностях деформирования эпоксидной смолы, стекловолокон и проволоки У8А при высоких скоростях деформирования значения ${{\sigma }_{{\text{s}}}}$ и ${{E}_{{\text{s}}}}$ для этих материалов при $\dot {\varepsilon } = 104$ с^–1 заданы условно, мало отличающимися от соответствующих значений при $\dot {\varepsilon } = 5 \times {{10}^{{ - 4}}}$ с^–1. Задание мало различающихся значений ${{\sigma }_{{\text{s}}}}$ и ${{E}_{{\text{s}}}}$ в этих случаях обосновывается известными экспериментальными фактами. Так, эпоксидная смола и стекловолокна не имеют ярко выраженного предела текучести, поэтому зависимости ${{\sigma }_{{\text{s}}}}$ и ${{E}_{{\text{s}}}}$ от $\dot {\varepsilon }$ предполагаются слабыми [20], а у высокопрочных сталей механические характеристики практически не зависят от скорости деформирования [44], поэтому данный факт учтен в табл. 1 для проволоки У8А при $\dot {\varepsilon } = 104$ с^–1. В силу указанных обстоятельств приведенные ниже результаты расчетов следует рассматривать как качественные, а не относящиеся к каким-то конкретным реальным КМ-материалам.

Структуры армирования однородные, т.е. ${{\theta }_{k}} = {\text{const}}$, ${{\varphi }_{k}} = {\text{const}}$ и ${{\omega }_{k}} = {\text{const}}$, $1 \leqslant k \leqslant N$ (см. равенства (2.1), (2.12) и рис. 2). Рассматриваются три типа структур: 1) плоское ортогональное 2D-армирование (рис. 1а), когда два ($N = 2$) семейства волокон укладываются по направлениям $O{{x}_{1}}$ и $O{{x}_{2}}$ с интенсивностями армирования ${{\omega }_{1}} = {{\omega }_{2}} = {\text{0}}{\text{.2}}$, 2) пространственное ортогональное 3D-армирование (рис. 1б), когда три ($N = 3$) семейства волокон укладываются по направлениям $O{{x}_{1}}$, $O{{x}_{2}}$ и $O{{x}_{3}}$ с плотностями армирования ${{\omega }_{1}} = {{\omega }_{3}} = {\text{0}}{\text{.1}}$ и ${{\omega }_{2}} = {\text{0}}{\text{.2}}$, 3) неортогональное пространственное 4D-армирование (рис. 1в), когда первые два семейства волокон укладываются по направлениям $O{{x}_{1}}$ и $O{{x}_{2}}$, а третье и четвертое семейства – наклонно по направлениям, определяемым углами (см. равенства (2.12) и рис. 2): ${{\theta }_{3}} = \pi {\text{/}}4$, ${{\theta }_{4}} = 3\pi {\text{/}}4$, ${{\varphi }_{3}} = {{\varphi }_{4}} = \pi {\text{/}}2$ (т.е. на рис. 1в угол $\theta = \pi {\text{/}}4$). В последнем случае интенсивности армирования имеют значения: ${{\omega }_{1}} = {\text{0}}{\text{.1}}$, ${{\omega }_{2}} = {\text{0}}{\text{.2}}$ и ${{\omega }_{3}} = {{\omega }_{4}} = {\text{0}}{\text{.05}}$. Во всех структурах армирования общий расход волокон одинаков, а суммарная плотность армирования

Для проведения расчетов в направлениях $O{{x}_{1}}$ и $O{{x}_{2}}$ вводилась равномерная сетка $\Delta {{x}_{1}} = \Delta {{x}_{2}} = 2b{\text{/}}100$ = 2 мм, а шаг по времени $\Delta $ задавался равным 0.25 мкс. При этом отношение $\Delta {{x}_{1}}{\text{/}}\Delta = 8$ км/с существенно превышает значения a, приведенные в табл. 1, поэтому необходимые условия устойчивости численной схемы типа “крест” выполняются для каждого материала компонента композиции (см. [10], неравенства (60)), а следовательно, и для соответствующих композиций, причем со значительным запасом [10].

На рис. 3 изображены поперечные осцилляции центральной точки (${{w}_{0}}\left( t \right) \equiv w\left( {t,0,0} \right)$) стеклопластиковой пластины (а, б, в) и осцилляции максимальных значений интенсивности деформаций связующего материала $\varepsilon _{ * }^{{(0)}}$ ($\varepsilon _{{\text{m}}}^{{(0)}}\left( t \right) = \mathop {\max }\limits_{\mathbf{r}} \varepsilon _{ * }^{{(0)}}\left( {t,{\mathbf{r}}} \right)$, $\left| {{{x}_{1}}} \right| \leqslant a$, $\left| {{{x}_{2}}} \right| \leqslant b$ и $\left| {{{x}_{3}}} \right| \leqslant h$) в этой конструкции (г, д, е), рассчитанные при ${{p}_{{\max }}} = 6$ МПа (см. соотношения (4.1)) и разных типах армирования: 2D-структуре (а, г), 3D-структуре (б, д) и 4D-структуре (в, е). Сплошные кривые 1 на рис. 3 определены при учете чувствительности компонентов композиции к изменению скорости их деформирования; пунктирные кривые 2 – без учета такой чувствительности (при этом расчеты проводились по данным, приведенным в табл. 1 для скорости деформирования $\dot {\varepsilon } = 5 \times {{10}^{{ - 4}}}$ с^–1).

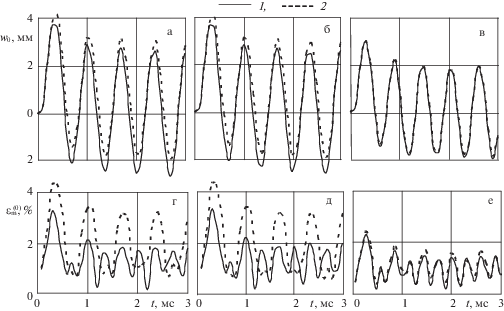
Сравнение кривых 1 и 2 на рис. 3 показывает, что неучет чувствительности компонентов композиции стеклопластиковых пластин к скорости их деформирования (кривые 2), как правило, приводит к завышению максимальных значений прогиба (${{w}_{{\max }}} = \mathop {\max }\limits_{t \geqslant 0} {{w}_{0}}\left( t \right)$) (см. рис. 3а и 3б) и максимальных значений интенсивности деформаций связующего материала ($\varepsilon _{{{\text{max}}}}^{{(0)}} = \mathop {\max }\limits_{t \geqslant 0} \varepsilon _{{\text{m}}}^{{(0)}}\left( t \right)$) (см. рис. 3г, 3д и 3е), причем на рис. 3г и 3д кривые 1 и 2 различаются значительно сильнее, чем на рис. 3а и 3б соответственно. Следовательно, неучет чувствительности компонентов композиции к скорости их деформирования в большей степени сказывается на завышении характеристик деформированного состояния компонентов композиции, чем на податливости КМ-пластины в поперечном направлении.

На рис. 3в кривые 1 и 2 визуально практически неразличимы, т.е. при структуре 4D-армирования стеклопластиковой пластины неучет чувствительности компонентов композиции к скорости их деформирования практически не оказывает влияния на определение расчетного прогиба КМ-конструкции. Однако различие зависимостей $\varepsilon _{{\text{m}}}^{{(0)}}\left( t \right)$, полученных с учетом и без учета этой чувствительности для пластины с такой структурой армирования, является достаточно значительным (см. кривые 1 и 2 на рис. 3е).

Сопоставление кривых 1 и 2 на рис. 3а и 3б и рис. 3г и 3д соответственно показывает, что для стеклопластиковой пластины замена 2D-структуры армирования (рис. 3а и 3г) на структуру 3D-армирования (рис. 3б и 3д) приводит к пренебрежительно малым уменьшениям податливости конструкции в поперечном направлении и интенсивности деформаций связующего материала. Напротив, сравнение кривых 1 и 2 на рис. 3а и 3в и рис. 3г и 3е соответственно демонстрирует, что замена 2D-структуры (рис. 3а и 3г) на структуру 4D-армирования (рис. 3в и 3е) позволяет уменьшить максимальный прогиб КМ-пластины на 18.3% при учете чувствительности компонентов композиции к скорости их деформирования и на 27.1% при неучете этой чувствительности. Значение же $\varepsilon _{{{\text{max}}}}^{{(0)}}$ в случае учета чувствительности компонентов композиции к скорости их деформирования при такой замене структуры армирования в стеклопластиковой пластине удается уменьшить на 31.2% (см. кривые 1 на рис. 3г и 3е).

Выше рассматривались стеклопластиковые пластины, для которых анизотропия композиции является ярко выраженной: ${{E}^{{(k)}}}{\text{/}}{{E}^{{(0)}}} \approx 31$ (см. табл. 1). Рассмотрим теперь динамическое поведение металлокомпозитной Mg–У8А-пластины с 3D-структурой армирования, анизотропия композиции которой является слабой: ${{E}^{{(k)}}}{\text{/}}{{E}^{{(0)}}} \approx 4.88$, $1 \leqslant k \leqslant N$ (см. табл. 1). На рис. 4 изображены зависимости ${{w}_{0}}\left( t \right)$ (а) и $\varepsilon _{{\text{m}}}^{{(0)}}\left( t \right)$ (б), определенные при тех же условиях, что и на рис. 3б и 3д соответственно, но для металлокомпозитной пластины, нагруженной согласно равенству (4.1) при ${{p}_{{\max }}} = 50$ МПа.

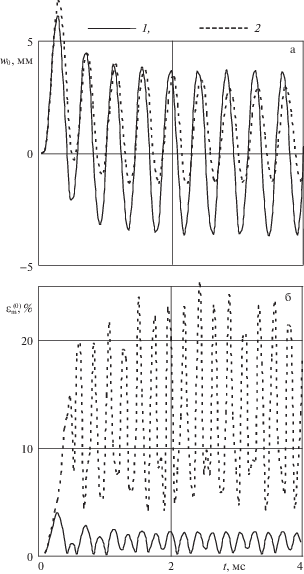
Сравнение кривых 1 и 2 на рис. 4 показывает, что и в случае рассматриваемой металлокомпозитной пластины неучет чувствительности компонентов композиции к скорости их деформирования (кривые 2) приводит к значительному завышению величин ${{w}_{{\max }}}$ и $\varepsilon _{{{\text{max}}}}^{{(0)}}$. Поведение пунктирной кривой 2 на рис. 4б свидетельствует о том, что расчетная интенсивность деформаций магниевого связующего в этом случае достигает значений порядка 20–25%, если не учитывается указанная чувствительность. Следовательно, такой расчет нужно признать некорректным с механической точки зрения, так как деформации компонентов композиции при этом являются большими, а разработанная в разд. 1 и 2 модель упруговязкопластического поведения КМ-пластин использует предположение о малости деформаций этих компонентов. Кривая же 1 на рис. 4б свидетельствует о том, что интенсивность деформаций магниевого связующего при учете чувствительности компонентов композиции от скорости их деформирования не превышает 4% от единицы, т.е. в этом случае деформации действительно малые и соответствующий расчет вполне корректен с механической точки зрения.

Выше обсуждалось неупругое динамическое поведение относительно толстых пластин ($h{\text{/min}}\left( {a,b} \right) = 1{\text{/}}10$). Дополнительные расчеты показывают, что в случае относительно тонких КМ-пластин ($h{\text{/min}}\left( {a,b} \right)$ ≤ 1/20) замена плоской структуры армирования на пространственную структуру (при сохранении общего расхода волокон), как правило, не приводит к уменьшению прогибов такой конструкции и максимальных значений интенсивности деформаций компонентов композиции. Встречаются ситуации, когда при замене плоско-перекрестной структуры армирования на пространственную структуру наблюдается увеличение податливости тонкой пластины в поперечном направлении. Однако и для относительно тонких КМ-конструкций учет и неучет чувствительности компонентов композиции к скорости их деформирования в подавляющем большинстве случаев приводит к значительному различию в результатах расчетов, особенно при определении НДС в этих компонентах.

Заключение. Анализ изгибного упруговязкопластического динамического поведения КМ-пластин показал, что неучет чувствительности компонентов композиции к изменению скорости их деформирования, как правило, приводит к значительному завышению расчетных значений интенсивности деформаций этих компонентов и прогибов конструкции. Если компоненты композиции сильно чувствительны к скорости их деформирования (например, в случаях металлических сплавов с ярко выраженными пределами текучести [13, 20]), то неучет этой чувствительности может приводить к некорректным с механической точки зрения результатам расчетов, так как в этих случаях расчетные значения деформаций могут оказаться большими (порядка 20–30%), что не согласуется с исходными положениями разработанной структурной модели неупругого деформирования КМ-пластин, в рамках которой предполагается, что деформации компонентов композиции малы. Учет же указанной чувствительности в этих случаях приводит к вполне корректным результатам расчетов (деформации компонентов композиции не превосходят 5%). Встречаются ситуации, когда при некоторых структурах армирования и уровнях нагружения конструкции учет и неучет чувствительности компонентов композиции к скорости их деформирования приводят практически к одним и тем же результатам по определению расчетного прогиба конструкции.

В случаях относительно толстых КМ-пластин (с относительной толщиной порядка 1/10), композиция которых имеет сильно выраженную анизотропию (стеклопластики), замена традиционной плоско-перекрестной структуры армирования на пространственную структуру позволяет уменьшить податливость КМ-конструкции в поперечном направлении и интенсивность деформаций связующего материала на десятки процентов. В случаях относительно толстых пластин со слабо выраженной анизотропией композиции (металлокомпозиты) замена плоской структуры армирования на пространственную, как правило, не приводит к заметному уменьшению податливости КМ-конструкции в поперечном направлении, но позволяет уменьшить интенсивность деформаций связующей матрицы. При замене плоско-перекрестных структур на пространственные структуры армирования в относительно тонких пластинах (с относительной толщиной порядка 1/20 и менее) эффект увеличения их жесткости в поперечном направлении практически не наблюдается. Наоборот, встречаются ситуации, когда такая замена приводит к увеличению прогибов тонкостенной КМ-конструкции.

Работа выполнена в рамках Программы фундаментальных научных исследований государственных академий наук на 2017–2020 годы (проект 23.4.1 – Механика деформирования и разрушения материалов, сред при механических нагрузках, воздействии физических полей и химически активных сред).