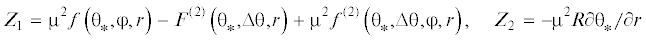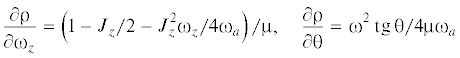Прикладная математика и механика, 2019, T. 83, № 4, стр. 615-635

1. Постановка задачи. Рассматриваются движения твердого тела вокруг неподвижной точки, близкие к случаю Лагранжа. Движение твердого тела анализируется в окрестности нижнего статически устойчивого положения равновесия, так как этот случай часто встречается в прикладных задачах. Твердое тело близко к телу вращения с вытянутым эллипсоидом инерции и характеризуется малой массовой асимметрией. Наличие малой асимметрии твердого тела является причиной возникновения резонансных эффектов, которые могут привести к динамической неустойчивости, приводящей к большому возрастанию угла нутации.

В настоящее время известно большое количество работ, в которых исследуется возмущенное движение твердых тел в случае, близком к случаю Лагранжа, например, [1–13]. Это относится как к классической задаче движения твердого тела вокруг неподвижной точки [1–8], так и к ее приложениям [9–13]. Все эти задачи характеризуются некоторым сравнительно большим восстанавливающим моментом, который обеспечивает статическую устойчивость некоторого положения равновесия, и действием малых возмущений, которые могут приводить к динамической неустойчивости движения твердого тела, в частности, за счет влияния возникающих резонансов. Во многих работах для анализа резонансных режимов движения твердых тел используются линейные по углу нутации уравнения [9–11], хотя область их применимости не оценивается. В представленной работе нелинейные уравнения резонансного движения твердого тела вокруг неподвижной точки с учетом резонансов низших порядков построены с помощью метода интегральных многообразий [14, 15]. Показано, что при малых углах нутации эти уравнения тождественно совпадают с усредненными уравнениями первого приближения, описывающими резонансное движение твердого тела в линейном случае для резонансов низшего порядка. С физической точки зрения уравнения, полученные методом интегральных многообразий, описывают “медленную” (прецессионную) составляющую решений исходных уравнений движения твердого тела, определяющую поведение системы в резонансных областях ее движения. В данной работе уравнения “медленного” движения твердого тела вокруг неподвижной точки получены при наиболее полном учете его массовой асимметрии. Массовая асимметрия твердого тела характеризуется смещением центра масс тела, его центробежными моментами инерции и разностью осевых моментов инерции относительно некоторой связанной с телом системы координат.

При наличии малой массовой асимметрии твердого тела и при изменении некоторых характеристик его движения, например, угловой скорости вращения тела вокруг его связанной продольной оси, возможно попадание системы в резонансные области (резонанс частот), при прохождении которых влияние резонансов усиливается. Известно [17], что при прохождении резонансных областей колебательные системы могут вести себя по-разному: 1) возможен “быстрый” проход через резонанс; 2) возможна реализация длительных резонансных режимов движения системы, которые поддерживаются в силу действующих возмущений (захваты в резонанс). С точки зрения движения твердого тела реализация захватов в резонанс неизбежно приводит к динамической неустойчивости движения статически устойчивого волчка Лагранжа.

В представленной работе получены и анализируются нелинейные условия захвата в резонанс, на основании которых оценивается область применимости линейных оценок, полученных с помощью метода усреднения [8]. Данная работа является развитием работы [8], в которой был проведен анализ резонансных движений волчка Лагранжа при малых углах нутации при наиболее полном учете массовой асимметрии.

Оценки условий реализации захватов в резонанс подтверждаются численным моделированием по исходным уравнениям движения твердого тела.

2. Уравнения движения. При анализе движения твердого тела близкого к телу вращения с малой массовой асимметрией часто используется форма нелинейных уравнений вида [9, 12, 16, 18]

Здесь

где ${\theta }$, ${\varphi }$ и ${\psi }$ – углы нутации, собственного вращения и прецессии твердого тела (рис. 1), $r = \left( {{{r}_{1}},{{r}_{2}}} \right)$, ${{r}_{1}} = {{K}_{z}}{\text{/}}\bar {J}$, ${{r}_{2}} = {{K}_{{z1}}}{\text{/}}\bar {J}$, ${{K}_{z}}$, ${{K}_{{z1}}}$ – проекции вектора кинетического момента твердого тела на оси связанной системы координат $Oxyz$ и неподвижной системы координат $O{{x}_{1}}{{y}_{1}}{{z}_{1}}$ (рис. 1), ${{\bar {J}}_{x}},\;{{\bar {J}}_{y}},\;{{\bar {J}}_{z}},\;{{\bar {J}}_{{xy}}},\;{{\bar {J}}_{{xz}}}$, ${{\bar {J}}_{{yz}}}$ – моменты инерции тела в связанной системе координат $Oxyz$, $\Delta x = \Delta \bar {x}{\text{/}}\Delta \bar {z},$ $\Delta y = \Delta \bar {y}{\text{/}}\Delta \bar {z}$; $\Delta \bar {x}$, $\Delta \bar {y}$, $\Delta \bar {z}$ – координаты центра масс тела в связанной системе координат $Oxyz$, $l = \Delta \bar {z}$, ${\lambda } < 0$ – параметр, характеризующий малые диссипативные моменты, действующие в связанной системе координат $Oxyz$, и пропорциональные угловым скоростям ${{{\omega }}_{x}}$, ${{{\omega }}_{y}}$, ${{{\omega }}_{z}}$.

Малый параметр ${\varepsilon }$ вводится в систему (2.1)–(2.4) формально и характеризует малую массовую асимметрию тела, малый крутящий момент ${{M}_{z}}$, действующий по оси $Oz$, и малую диссипацию (параметр ${\lambda }$). При ${\varepsilon } = 0$ имеет место невозмущенное движение статически и динамически симметричного волчка Лагранжа. В этом случае переменные ${{K}_{z}}$, ${{K}_{{z1}}}$ являются интегралами невозмущенной системы. Статическая асимметрия тела характеризуется относительной величиной смещения его центра масс по отношению к оси $Oz$, $\Delta x$, $\Delta y$. Динамическая асимметрия – центробежными моментами инерции ${{J}_{{xy}}}$, ${{J}_{{xz}}}$, ${{J}_{{yz}}}$ и разностью осевых моментов инерции $\Delta J$ (относительными величинами).

Движение твердого тела в существенной степени зависит от поведения угла собственно вращения ${\varphi }$. При быстром его изменении, когда угол ${\varphi }$ можно рассматривать как вращающуюся фазу, влияние асимметрии твердого тела на его движение невелико. Это так называемый нерезонансный случай движения твердого тела. В этом случае при использовании различных процедур метода усреднения для малых и немалых углов нутации [8–10, 19] в первом приближении слагаемые, зависящие от угла ${\varphi }$, не влияют на движение твердого тела (имеют нулевое среднее). Положение меняется, если траектория системы попадает в окрестность резонансной поверхности ${{{\omega }}_{{\varphi }}}\left( {{\theta },r} \right) = 0$. В этом случае движение тела становится более сложным, что приводит к необходимости применять специальные методы анализа резонансных режимов движения твердого тела [8, 9, 16, 19].

Уравнение поверхности ${{{\omega }}_{{\varphi }}}\left( {{\theta },r} \right) = 0$ можно записать в виде

где ${{r}_{1}}{\text{/}}{{J}_{z}} = {{{\omega }}_{z}}$ – угловая скорость вращения тела вокруг продольной оси $Oz$. В данной работе пересечение резонансной поверхности происходит за счет изменения угловой скорости ${{{\omega }}_{z}}$ при действии постоянного крутящего момента ${{M}_{z}}$ относительно оси $Oz$.

Если траектория системы принадлежит резонансной поверхности, то вращение твердого тела относительно продольной оси (частота ${{{\omega }}_{z}}$) синхронизируется с частотой прецессии твердого тела вокруг вертикали, так как ${{{\omega }}_{{\psi }}}\left( {{\theta },r} \right)\cos {\theta }$ есть проекция угловой скорости изменения угла ${\psi }$ на ось $Oz$. Для малых углов нутации, когда $\cos {\theta } \approx {\text{1}}$, имеет место совпадение частот ${{{\omega }}_{{\psi }}} \approx {{{\omega }}_{z}}$. Такое движение твердого тела иногда называют “лунным” движением, так как в этом случае тело всегда обращено одной стороной к вертикали.

Исследование резонанса ${{{\omega }}_{{\varphi }}}\left( {{\theta },r} \right) = 0$ непосредственно с помощью исходной системы (2.1)–(2.4) возможно только с помощью численных методов. Это прежде всего связано со сложным изменением угла нутации в общем случае движения твердого тела. Для получения аналитических оценок возмущений переменных при проходе через резонанс и условий захвата в резонанс используются приближенные методы анализа, основанные на асимптотических процедурах [8, 9, 16, 19] и позволяющие провести разделение (расщепление) решений системы на “медленную” и “быструю” составляющие. В этом случае для приближенного анализа поведения системы в окрестности резонансной поверхности используются “медленные” составляющие решения, что существенно упрощает задачу.

3. Применение метода интегральных многообразий. Известно, что основные явления, связанные с влиянием отдельного резонанса, как отмечено, например, в [17], происходят в $с\sqrt {\varepsilon } $ – окрестности резонансной поверхности ($с = {\text{const}} < \infty $). В этом случае вводится медленное время ${\tau } = {\mu }t$, где ${\mu } = \sqrt {\varepsilon } $, и нормированное расстояние до резонансной поверхности ${\rho }\left( {{\theta },r} \right) = {{{\mu }}^{{ - 1}}}{{{\omega }}_{{\varphi }}}\left( {{\theta },r} \right)$ [17, 20]. Тогда, используя введенное изменение масштаба и приводя систему (2.1)–(2.3) к сингулярной форме [16], получим

При записи системы (3.1)–(3.4) уравнение (2.4) не рассматривается, так как правые части уравнений (2.1)–(2.3) не зависят от угла ${\psi }$, а зависят только от производной ${\dot {\psi }} = d{\psi /}dt$.

Расщепление решений системы (3.1)–(3.4) на “медленную” и “быструю” составляющие осуществляется с использованием известной схемы метода интегральных многообразий [14–16].

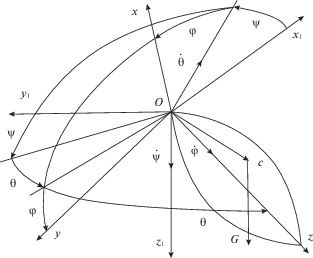
Здесь рассматриваются колебания статически устойчивого волчка Лагранжа относительно вертикали (положительного направления оси $O{{z}_{1}}$, рис. 1) с моментной характеристикой, пропорциональной $\sin {\theta }$, причем, как известно, при добавлении гироскопических членов устойчивость сохраняется. В этом случае функция $F({\theta },r)$ имеет изолированный корень ${{{\theta }}_{*}}(r)$, положение которого зависит от вектора медленно изменяющихся параметров $r$. Причем, как показано для аналогичной функции в [12], для изолированного корня выполняется условие $\partial F({\theta },r){\text{/}}\partial \theta > 0$, что подтверждает устойчивость системы.

Система (3.1)–(3.4) в окрестности корня ${{{\theta }}_{*}}$ приводится к стандартному виду метода интегральных многообразий

где ${{F}^{{(2)}}}$, ${{f}^{{(2)}}}$ – слагаемые второго и более порядка по отклонению $\Delta {\theta }$, причем матрица $A$ определена при ${\theta } = {{{\theta }}_{*}}$.

Применение к системе (3.5) классических теорем [14] метода интегральных многообразий к успеху не приводит, так как при ${\mu } = 0$ матрица $A\left( {{\xi },{\text{0}}} \right)$ имеет мнимые корни. В работе [15] метод интегральных многообразий распространен на случай, когда условие асимптотической устойчивости для присоединенной системы выполняется с учетом членов, зависящих от малого параметра ${\mu }$. В этом случае справедлива теорема [15].

Теорема. Пусть для системы (3.5) выполнены следующие условия:

1. Матрица $A\left( {{\xi },{\mu }} \right)$ определена и непрерывна при ${\xi } \in {{R}^{3}}$, ${\mu } \in \left[ {{\text{0,}}{{{\mu }}_{0}}} \right]$ и удовлетворяет по ${\xi }$ условию Липшица $\left\| {A\left( {{\xi },{\mu }} \right) - A\left( {{\bar {\xi }},{\mu }} \right)} \right\|$ ≤ $L\left\| {{\xi } - {\bar {\xi }}} \right\|$ и ограничена при всех ${\xi }$, ${\mu }$ из области определения. Существуют такие числа ${\beta }\left( {\mu } \right)$ и $N\left( {\beta } \right) > {{C}_{1}} \geqslant 0$, что для любой функции ${\xi }\left( {\tau } \right)$, имеющей непрерывную производную при ${\tau } \in \left[ { - \infty ,\infty } \right]$, фундаментальная матрица Коши $W\left( {{\tau },s,{\mu }} \right)$ уравнения ${\mu }d{\zeta /}d{\tau } = A\left( {{\xi }\left( {\tau } \right),{\mu }} \right){\zeta }$ подчиняется неравенству $\left\| {W\left( {{\tau },s,{\mu }} \right)} \right\| \leqslant N\exp \left[ { - {\beta }\left( {{\tau } - s} \right)} \right]$ при всех $ - \infty < s \leqslant {\tau } < \infty $, ${\mu } \in \left( {{\text{0,}}{{{\mu }}_{0}}} \right]$.

2. Функции X, Z определены и непрерывны в области $\Omega {\kern 1pt} {\text{\{ }}\xi $, $\zeta $, ${\mu /\xi } \in {{R}^{3}}$, $\left\| {\zeta } \right\| \leqslant {\nu }$, ${\mu } \in [{\text{0,}}{{{\mu }}_{0}}]\} $ и удовлетворяют в $\Omega $ неравенствам

где ${{a}_{k}}\left( {u,{\mu }} \right)$, ${{b}_{k}}\left( {w,{\mu }} \right)$, ${{d}_{k}}\left( {w,{\mu }} \right)$ $\left( {k = 1,2} \right)$ – неотрицательные неубывающие функции своих переменных $\left( {u = \left\| {\zeta } \right\|,w = \max \left( {\left\| {\zeta } \right\|,\left\| {{\bar {\zeta }}} \right\|} \right)} \right)$.

При выполнении условий справедливы следующее утверждения [15]:

1) для каждого ${\mu } \in \left( {{\text{0,}}{{{\mu }}_{0}}} \right]$ при ${\xi } \in {{R}^{3}},$ $\left\| {\zeta } \right\| \leqslant {\nu ,}$ $ - \infty < {\tau } < \infty $ система (3.5) имеет единственное трехпараметрическое многообразие ${\zeta } = H\left( {{\xi },\,{\mu }} \right)$, движение по которому описывается уравнением

2) траектория любого решения, начинающегося достаточно близко от интегрального многообразия, при ${\tau } \to \infty $ неограниченно приближается к некоторой траектории, лежащей на интегральном многообразии, причем скорость сближения составляет величину порядка $N\exp \left[ { - {\beta }\left( {{\tau } - s} \right)} \right]$

3) решение ${\xi }\left( {\tau } \right)$, ${\zeta }\left( {\tau } \right)$ системы (3.5), лежащее на интегральном многообразии, устойчиво (асимптотически устойчиво, неустойчиво) тогда и только тогда, когда аналогичным свойством обладает решение системы (3.6).

Система (3.5) была получена из системы (3.1)–(3.4) заменой ${\theta } = {{{\theta }}_{*}}\left( r \right) + \Delta {\theta }$. Поэтому система (3.1)–(3.4) имеет интегральное многообразие

Из приведенной теоремы следует, что если начальные условия для системы (3.1)–(3.4) выбраны достаточно близко от интегрального многообразия (3.7), то исследование устойчивости некоторого ее решения может быть проведено по системе меньшей размерности (3.6), описывающей движение по интегральному многообразию.

Константа ${\beta }$, определяющая скорость приближения траектории системы к интегральному многообразию, зависит от собственных чисел матрицы $A\left( {{\xi },{\mu }} \right)$. При достаточном малом значении параметра ${\mu }$ матрица $A\left( {{\xi },{\mu }} \right)$ имеет комплексно сопряженные собственные числа. Пусть их действительная часть удовлетворяет условию ${\lambda }{{{\mu }}^{{\text{2}}}}{\text{/}}2 < - 2{\gamma } < 0$, где ${\gamma } = O\left( {{{{\mu }}^{2}}} \right)$ – некоторая константа. Тогда для фундаментальной матрицы $W\left( {{\tau },s,{\mu }} \right)$ существует оценка [14] $\left\| {W\left( {{\tau },s,{\mu }} \right)} \right\|$ ≤ 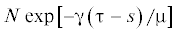, поэтому ${\beta } = O\left( {\mu } \right)$.

Согласно методу интегральных многообразий, движение системы по интегральному многообразию описывается уравнениями (3.6), которые в исходных переменных принимают вид

где переменные ${\theta ,}\,{{{\omega }}_{{\theta }}}$ определяются выражениями (3.7).

Функции ${{H}_{1}}\left( {r,{\varphi ,\mu }} \right)$, ${{H}_{2}}\left( {r,{\varphi ,\mu }} \right)$ из (3.7) находятся согласно стандартной схеме метода интегральных многообразий [15, 16] в виде ряда по малому параметру ${\mu }$, причем ${{H}_{1}}\left( {r,{\varphi ,\mu }} \right) = O\left( {\mu } \right)$, ${{H}_{2}}\left( {r,{\varphi ,\mu }} \right) = O\left( {\mu } \right)$. В этом случае угловая скорость ${{{\omega }}_{{\theta }}}$ в уравнениях (3.8)–(3.9), описывающих движение по интегральному многообразию, есть величина порядка $O\left( {\mu } \right)$ и в первом приближении не влияет на “медленные” движения системы.

С точки зрения движения волчка Лагранжа “медленные” решения описывают прецессионные движения тела, “быстрые” решения – движения, вызванные нутационными колебаниями тела, близкого к телу вращения.

Во многих работах показано, например, [9, 16], что для приближенного анализа рассматриваемого резонанса низшего порядка достаточно использования “медленного” решения, описывающего прецессионные движения твердого тела.

Для сравнения резонансных движений твердого тела в линейном (по углу нутации) [8] и в нелинейном случаях решение для ${{{\theta }}_{*}}$ удобнее определять, не используя алгебраическое нелинейное уравнение $F({{{\theta }}_{*}},r) = 0$, а из решения соответствующего дифференциального уравнения [9, 12, 16]. Тогда, дифференцируя функцию $F({\theta },r)$ и определяя производную $d{\theta }\left( {\tau } \right){\text{/}}d{\tau }$ с точностью до членов $O\left( {\mu } \right)$, получим

где точка означает скалярное произведение векторов.

Здесь для сравнения решений в резонансном случае для малых и немалых углов нутации используются уравнения движения по интегральному многообразию, в которых учтены члены в правых частях дифференциальных уравнений, пропорциональные ${\mu }$, то есть члены порядка $O\left( {{{{\mu }}^{{\text{2}}}}} \right)$ не учитываются.

Для определения движения по интегральному многообразию начальные условия при интегрировании уравнения (3.10) необходимо находить из решения нелинейного уравнения $F({\theta },r) = 0$. Причем дифференциальное уравнение для переменной ${{r}_{2}} = {{K}_{{z1}}}{\text{/}}\bar {J}$ из системы (3.8)–(3.9) можно исключить, делая замену ${{r}_{2}} \Rightarrow {{{\omega }}_{{\psi }}}$ с помощью выражения ${{r}_{2}} = {{{\omega }}_{{\psi }}}{{\sin }^{2}}{\theta } + {{r}_{1}}\cos {\theta }$ и определяя частоту ${{{\omega }}_{{\psi }}}$ из условия $F({\theta },r) = 0$ в виде

где

Если ${{{\omega }}_{z}} > 0$, то пересечение резонансной поверхности ${{{\omega }}_{{\varphi }}}\left( {{\theta },r} \right) = 0$ возможно, когда ${{{\omega }}_{{\psi }}} = {{{\omega }}_{1}}$, в противоположном случае ${{{\omega }}_{z}} < 0$ полагается ${{{\omega }}_{{\psi }}} = {{{\omega }}_{2}}$.

Таким образом, в данном случае “медленные” движения системы описываются уравнениями (3.8)–(3.10) с одной фазой ${\varphi }$. Система (3.8)–(3.10) по своей форме аналогична частично усредненной системе метода усреднения, которая обычно используется для исследования отдельного резонанса [17, 20]. Причем при движении системы в окрестности резонансной поверхности (2.5) функцию ${\rho }\left( {{\theta },r} \right)$ обычно называют расстройкой частот [20]. Следовательно, применение метода интегральных многообразий и выделение “медленной” составляющей решения позволило упростить задачу анализа поведения исходной системы при прохождении через резонансы низшего порядка.

4. Уравнения “медленного” движения тела для резонансов низших порядков. Учитывая конкретный вид функций, входящих в систему (3.1)–(3.4), запишем уравнения “медленного” движения тела (3.8)–(3.10) в форме нелинейного “маятника” с возмущениями

где штрих означает дифференцирование по медленному времени,

При анализе резонансных режимов движения твердого тела в случае малых углов нутации [8] исходная система уравнений движения была приведена стандартному виду метода усреднения с тремя фазами ${{{\psi }}_{{1,2}}}$, $\Phi $, которым соответствовали частоты ${{{\omega }}_{{1,2}}}$, ${{{\omega }}_{z}}$. При этом частично усредненная система, например, для резонанса ${{{\omega }}_{z}} = {{{\omega }}_{1}}$ определялась посредством введения резонансной фазы $\vartheta = \Phi - {{{\psi }}_{1}}$ с последующим усреднением по фазе ${{{\psi }}_{2}}$ и приведением к уравнениям нелинейного “маятника” вида (4.1)–(4.3). Система (4.1)–(4.3) записана в тех же обозначениях (с точностью до обозначения резонансной фазы), что и частично усредненная система, полученная в работе [8] для малых углов нутации, а параметры, характеризующие асимметрию ${\sigma },\Delta ,{{{\varphi }}_{1}}$, ${{{\varphi }}_{2}}$, тождественно совпадают. Причем для малых углов нутации $\left( {\sin {\theta } \approx {\theta ,}\,\cos {\theta } \approx 1} \right)$ имеем ${{F}_{{\theta }}}{\text{/}}{{f}_{{\theta }}} = 2{{{\omega }}_{a}}$, а функции ${{{\omega }}_{a}},{{{\omega }}_{{1,2}}}$, ${\omega }$ переходят в свои линейные аналоги.

Уравнения (4.1)–(4.3) построены для анализа резонанса ${{{\omega }}_{z}} - {{{\omega }}_{1}}\cos {\theta } = 0$. Аналогично могут быть записаны уравнения для резонанса ${{{\omega }}_{z}} - {{{\omega }}_{2}}\cos {\theta } = 0$, для этого достаточно поменять индексы у частот ${{{\omega }}_{{1,2}}}$. Рассматриваемым резонансам соответствуют резонансные угловые скорости вращения твердого тела относительно оси $Oz$

где ${\omega } = \sqrt {Gl\cos {\theta /}\bar {J}} $, которые получаются из условия ${{{\omega }}_{{\varphi }}}\left( {{\theta },r} \right) = 0$. Поэтому при увеличении угла нутации в момент пересечения резонанса резонансные частоты зависят от $\sqrt {\cos \theta } $ в отличие от случая малых углов нутации, для которого резонансные угловые скорости не зависят от угла ${\theta }$.

Уравнения (4.2, 4.3) – это нелинейные уравнения “маятника”, на который действуют возмущения, включая “медленно” изменяющийся угол нутации (4.1). Переход “маятника” из области вращений в область колебательного движения соответствует явлению, которое обычно называют захватом в резонанс [17]. Основное отличие “маятников”, соответствующих резонансным движениям тела при малых и немалых углах нутации, заключается в нелинейной зависимости функции $P\left( {{\theta ,\mu \rho ,\varphi }} \right)$ (производной от резонансной расстройки) от угла нутации. Это существенно усложняет анализ поведения волчка Лагранжа в резонансной области.

5. Анализ необходимых условий существования захватов в резонанс. Для анализа движения тела в резонансной области, прежде всего, рассматривается вопрос о существовании положений равновесия невозмущенного “маятника”. Уравнения движения невозмущенного “маятника” $\left( {\mu = 0} \right)$ имеют вид

“Маятник” (5.1) характеризуется “потенциальной энергией”

где $C$ – произвольная постоянная.

Необходимые условия существования положений равновесия “маятника” имеют вид [9]

Функция $P\left( {{\theta ,0,\varphi }} \right)$ записывается в виде

Здесь ${{\bar {M}}_{z}} = {{M}_{z}}{\text{/}}Gl$ – безразмерный вращающий момент, ${{K}_{{1,2}}}\left( {\theta } \right)$ – нелинейные функции угла нутации ${\theta }$, которые определяются из следующих выражений

где

В выражении (5.4) отсчет резонансной фазы выбран так, чтобы ${{{\varphi }}_{1}} = 0$. Вид функции (5.4) с точки зрения зависимости от фазы ${\varphi }$ такой же, как для линейного случая. Разница заключается лишь в том, что параметры этой функции, зависящие от угла нутации, имеют более сложный вид. Поэтому множество возможных фазовых портретов на плоскости для невозмущенного “маятника” [8] остается таким же.

Оценим влияние нелинейностей на выполнение необходимого условия (5.3) существования длительных резонансных режимов движения (областей колебательных движений невозмущенного “маятника”) с точки зрения сравнения с аналогичным условием для линейного случая.

Рассмотрим, например, частный случай асимметрии, когда $\Delta = 0$. Тогда положения равновесия “маятника” определяются из условия

где

Если $\left| {\sin {\varphi }} \right| < 1$, то на фазовой плоскости невозмущенный “маятник” имеет два положения равновесия, одно их которых устойчиво (“центр”), другое неустойчиво (“седло”). Критическая величина отношения 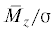, которая соответствует значению $\left| {\sin {\varphi }} \right| = 1$, будет равна 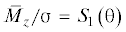, и определяется видом функции ${{S}_{1}}\left( {\theta } \right)$. Аналогичное условие для линейного случая будет иметь вид 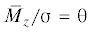(в тех же обозначениях). Функция ${{S}_{1}}\left( {\theta } \right)$ в отличие от линейного аналога зависит от параметра ${{J}_{z}}$ (5.5)–(5.6), определяющего отношение моментов инерции тела.

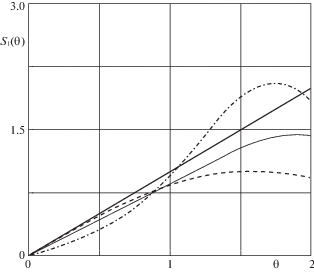
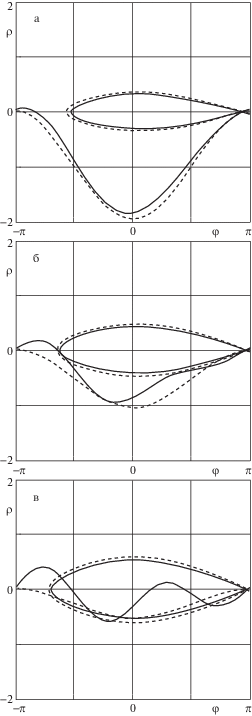
На рис. 2 проводится сравнение функции ${{S}_{1}}\left( {\theta } \right)$ с ее линейном аналогом, где жирной сплошной линией обозначена линейная функция, сплошной линией – функция ${{S}_{1}}\left( {\theta } \right)$ при ${{J}_{z}} = 0.5$, штриховой линией – функция ${{S}_{1}}\left( {\theta } \right)$ при ${{J}_{z}} = 0.01$, штрихпунктирной линией – функция ${{S}_{1}}\left( {\theta } \right)$ при ${{J}_{z}} = 0.99$. Имеет место следующее предельное соотношение ${{S}_{1}}\left( {\theta } \right) \to \sin {\theta }$ при ${{J}_{z}} \to 0$.

Результаты, приведенные на рис. 2 показывают, что линейные оценки в данном случае можно использовать, когда ${\theta } < 1$. Причем разность ${\theta } - {{S}_{1}}\left( {\theta } \right) > 0$ для всех рассматриваемых значений параметра ${{J}_{z}}$. Поэтому в этом диапазоне применение уравнений для малых углов нутации для рассматриваемого вида асимметрии дает заниженную оценку предельной величины параметра асимметрии ${{{\sigma }}_{*}}$, при которой выполняется необходимое условие. Для нелинейного случая эта оценка (при заданном крутящем моменте) будет иметь вид

Аналогичная оценка получается для другого частного случая асимметрии, когда ${\sigma } = 0$ и $\Delta \ne 0$. В этом случае имеем

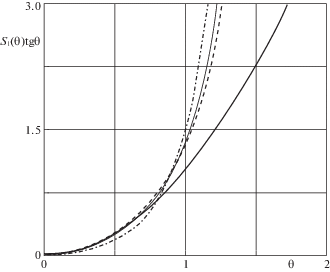
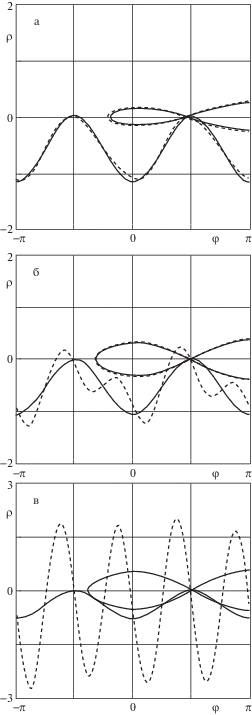
Сравнивая это выражение с его аналогом для малых углов нутации [8] sin φ = = ${{\bar {M}}_{z}}\left( {1 - {{J}_{z}}} \right){\text{/}}{{{\theta }}^{2}}\Delta $, заключаем, что влияние нелинейностей высшего порядка по углу нутации связано с заменой ${{{\theta }}^{{\text{2}}}} \Rightarrow {{S}_{1}}\left( {\theta } \right)\operatorname{tg} {\theta }$. На рис. 3 проводится сравнение функций ${{{\theta }}^{2}}$ (сплошная линия) и ${{S}_{1}}\left( {\theta } \right)\operatorname{tg} {\theta }$. Другие обозначения такие же, как на рис. 2. Так как здесь (в отличие от предыдущего случая) влияние нелинейностей более существенное, то это сужает область применения уравнений, записанных для малых углов нутации, если значения параметров асимметрии ${\sigma }$ и $\Delta $ сравнимы по величине.

Из выражения (5.9) следует следующая оценка для предельной величины параметра $\Delta $

Здесь следует отметить, что приблизительно до углов ${\theta } \approx 0.75$ оценки предельных значений ${{\Delta }_{*}}$ по линейной и нелинейной моделям близки практически во всем диапазоне параметра $0 < {{J}_{z}} < 1$. Однако при дальнейшем увеличении угла нутации графики функций ${{{\theta }}^{2}}$ и ${{S}_{1}}\left( {\theta } \right)\operatorname{tg} {\theta }$ начинают быстро расходиться (рис. 3).

Анализ необходимого условия (5.2) при сложной асимметрии, когда одновременно ${\sigma } \ne 0$ и $\Delta \ne 0$, проводится только численными методами, однако как показывают результаты численных вычислений, вывод о применимости линейных оценок при ${\theta } < 0.75$ подтверждается.

Таким образом, использование нелинейных уравнений “медленного” движения твердого тела позволило оценить диапазон применимости линейных оценок с точки зрения выполнения необходимого условия существования захватов в резонанс.

6. Оценка возможности захвата в резонанс. Если необходимое условие (5.2) выполняется, то явление захвата в резонанс в общем случае имеет вероятностный характер [13, 21, 22] и зависит от изменения полной энергии “маятника” (5.1) в силу возмущенной системы в резонансной области. При этом потенциальная энергия “маятника” отсчитывается от сепаратрисы невозмущенной задачи

где ${{П}_{с}}$ – потенциальная энергия, определенная в некоторой cедловой точке ${{{\varphi }}_{c}}$ на фазовом портрете “маятника”. Совокупность возможных фазовых портретов, соответствующих невозмущенному “маятнику” (5.4), остается такой же, как для малых углов нутации [8], так как структура функции (5.4) по резонансной фазе ${\varphi }$ не изменяется. Если ${{H}_{c}} > 0$, то система находится вне рассматриваемой области колебаний “маятника”, а если ${{H}_{c}} < 0$, то внутри области. Для оценки влияния нелинейностей на условия захвата в резонанс рассмотрим частные случаи, когда ${\sigma } \ne 0$, $\Delta = 0$ и ${\sigma } = 0$, $\Delta \ne 0$. Тогда на фазовом портрете “маятника” имеется (на одном периоде по фазе ${\varphi }$) одна петля сепаратрисы.

Переход через сепаратрису траектории системы (4.1)–(4.3) приводит к вероятностным явлениям [22], связанным с возможностью захвата в резонанс. Фазовые точки, которые в начальный момент находились на расстоянии порядка $O\left( {\mu } \right)$ друг от друга, могут в момент пересечения сепаратрисы попасть в разные области движения системы. Так как начальные условия всегда известны с некоторой погрешностью, то при ${\mu } \to {\text{0}}$ детерминированный подход теряет смысл. Однако можно рассматривать попадание системы в ту или иную область движений как случайные события и вычислять их вероятности.

Пусть ${{M}_{0}}\left( {{{{\theta }}_{0}}{\text{,}}{{{\rho }}_{0}}{\text{,}}{{{\varphi }}_{0}}} \right)$ – некоторая начальная точка, взятая в области вращений возмущенного “маятника” (4.1)–(4.3). Обозначим через 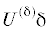– окрестность точки ${{M}_{0}}$, через $U_{v}^{{({\delta })}}$ – множество точек из 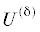, для которых траектория системы попадает в область колебаний “маятника”. Тогда плотностью вероятности захвата системы в область колебаний (или просто вероятностью захвата) называется величина [23]

где ${\text{mes}}$ обозначает некоторую меру множеств, например, объем.

Для получения аналитических оценок используется другое представление вероятности (6.2) через величины, зависящие от энергии “маятника” [23]. В ходе эволюции совокупность фазовых траекторий, соответствующая области 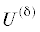, попадает в некоторую окрестность сепаратрисы невозмущенной задачи. Каждой траектории в этот момент соответствует определенное значение энергии “маятника” из некоторого диапазона. Необходимо из общего множества траекторий, выделить часть, которая соответствует переходу “маятника” в колебания. В работе [22] в качестве характеристики поведения траекторий вблизи сепаратрисы вводится величина

где $H_{c}^{'}$ – производная энергии, определенная в силу возмущенной системы (4.1)–(4.3). Величина (6.3) с точностью до знака есть приращение энергии “маятника”, вычисленное на сепаратрисе ${{l}_{c}}$ невозмущенной задачи. Поэтому при ${{\Theta }_{v}} < 0$ вероятность захвата близка к нулю и траектория “выталкивается” из колебательной области. При ${{\Theta }_{v}} > 0$ в качестве оценки вероятности захвата в резонанс при случайных начальных условиях может быть использована величина [22] где

Величина (6.4) представляет собой отношение фазового объема, входящего в область колебаний “маятника”, к полному фазовому объему, попадающему в окрестность сепаратрисы [22] за некоторый промежуток времени.

Формула основывается на утверждении о том, что фазовый объем, входящий в область колебаний “маятника” за некоторый промежуток времени пропорционален приращению энергии ${{H}_{с}}$ на сепаратрисе, ограничивающей рассматриваемую область и определенной в силу невозмущенных уравнений.

В работе [23] для систем, близких к гамильтоновым системам с медленно изменяющимися параметрами, получена оценка

где ${{{\tau }}_{*}}$ – момент времени попадания системы в окрестность сепаратрисы, $K = {\text{const}}$ < < ∞. Здесь ${{\Theta }_{v}}({{{\tau }}_{*}})$ характеризует приращение энергии, определенное на сепаратрисе, ограничивающую область, для которой определяется вероятность; ${{\Theta }_{s}}({{{\tau }}_{*}})$ – полное приращение энергии системы. Для рассматриваемой задачи [22] ${{\Theta }_{s}} = 2{\pi }\left| a \right| + {{\Theta }_{v}}{\text{/}}2$.

Поэтому важным является анализ поведения производной $H_{c}^{'}$ в резонансной области. Оценим влияние нелинейностей на величину производной энергии $H_{c}^{'}$, а значит на значение интеграла ${{\Theta }_{{v}}}$, который определяет возможность захвата в резонанс.

Производная $H_{c}^{'}$ определяется стандартным образом

где производные ${\theta ',}\,{\varphi '}$, ${\rho '}$ – это правые части уравнений (4.1)–(4.3).

Вследствие сложности и громоздкости выражения (6.6) соответствующие частные производные были определены с помощью средств символьной математики и в явном виде полная производная (6.6) не выписывалась. Однако это все же позволило провести аналитические вычисления для оценки влияния нелинейностей на величину производной (6.6) и на величину вероятности (6.4).

Сравнение оценок проводится для частных видов асимметрии ${\sigma } \ne {\text{0}}$, $\Delta = 0$ и ${\sigma } = 0$, $\Delta \ne 0$. На рис. 4, 5 приводятся петли сепаратрис и функции $H_{c}^{'}\left( {\varphi } \right)$, определенные для малых [8] и немалых углов нутации при $Gl{\text{/}}\bar {J} = 1$, ${{J}_{z}} = 0.5$, ${{\bar {M}}_{z}} = 0.005$. Рис. 4 соответствует асимметрии ${\sigma } = 0.1$, рис. 5 – асимметрии $\Delta = 0.1$. На рис. 4, 5 рассматривается случай, когда начальное значение угловой скорости $0 < {{{\omega }}_{z}}\left( 0 \right) < {{{\omega }}_{{z1}}}$ и ${{\bar {M}}_{z}} > 0$. В этом случае в соответствии с оценками, полученными в работе [8] для малых углов нутации, $H_{c}^{'} < 0$ и создаются благоприятные условия для захвата в резонанс. На рис. 4, 5 сплошными линиями показаны кривые, соответствующие оценкам данной работы, а штриховыми линиями – оценки работы [8]. Для малых углов $\left( {{\theta } = 0.3} \right)$ соответствующие кривые практически совпадают, что приводит приблизительно к одинаковым оценкам вероятности “захвата” в резонанс: ${{P}_{r}} = 0.732$, ${{P}_{{rl}}} = 0.738$ (рис. 4, а) и ${{P}_{r}} = 0.489$, ${{P}_{{rl}}} = 0.501$ (рис. 5, a), где ${{P}_{{rl}}}$ – величина вероятности, определенная по модели для малых углов нутации [8]. При увеличении угла нутации оценки начинают различаться: при ${\theta } = 0.5$ имеем ${{P}_{r}} = 0.336$, ${{P}_{{rl}}} = 0.413$ (рис. 4, б) и ${{P}_{r}} = 0.201$, ${{P}_{{rl}}} = 0.311$ (рис. 5, б); при ${\theta } = 0.75$ имеем ${{P}_{r}} = 0.223$, ${{P}_{{rl}}} = 0.327$ (рис. 4 с) и ${{P}_{r}} = 0$, ${{P}_{{rl}}} = 0.209$ (рис. 5, в). При увеличении угла нутации в окрестности резонанса действуют два противоположных фактора. С одной стороны, увеличивается размер петли сепаратрисы, с другой стороны уменьшается по модулю производная $H_{c}^{'}\left( {\varphi } \right)$, причем последний фактор в данном случае оказывается определяющим, что ведет к уменьшению вероятности захвата в резонанс. Приведенные результаты показывают, что во всех случаях оценки, соответствующие модели для малых углов нутации [8], дают завышенную величину вероятности захвата. Причем если для модели [8] при увеличении угла нутации функции $H_{c}^{'}\left( {\varphi } \right)$ всегда остаются отрицательными, то для нелинейной модели (4.1)–(4.3) функции $H_{c}^{'}\left( {\varphi } \right)$ ведут себя более сложным образом, так как при увеличении угла нутации появляются области, в которых функция $H_{c}^{'}\left( {\varphi } \right)$ положительна (рис. 4, в и рис. 5, в). Автору не удалось найти траектории, на которых имеет место захват в резонанс, для случая, когда оценка вероятности (6.4) дает ${{P}_{r}} = 0$ (рис. 5, в) по нелинейным уравнениям движения (4.1)–(4.3), например, изменяя начальную фазу – ${{{\varphi }}_{0}} \in \left[ {0,2{\pi }} \right]$, хотя при использовании модели для малых углов нутации такие траектории существуют.

Приведенные результаты также показывают, что при одном и том же уровне относительной асимметрии параметр ${\sigma }$ является более значимым, чем параметр асимметрии $\Delta $, так как при одинаковых их величинах вероятность захвата в резонанс для параметра ${\sigma }$ больше. Это также подтверждается тем, что при одних и тех же значениях параметров ${\sigma }$ и $\Delta $ размер петли сепаратрисы для параметра ${\sigma }$ больше (рис. 4 и рис. 5).

Здесь следует отметить, что приведенные оценки вероятности захвата в резонанс по формуле (6.4) имеют квазистатический характер, так как предполагают, что положение сепаратрисы при проходе через резонанс слабо изменяется. Как показывают результаты моделирования, такое предположение может не выполняться, так как при приближении к резонансной области возмущения по углу ${\theta }$ приводят соответственно к изменению положения сепаратрисы. Однако все же полученные оценки дают представление об области применения результатов, полученных по модели для малых углов нутации [8].

В общем случае для прикладных задач для оценки возможности захвата в резонанс, естественно можно применить метод статистических испытаний [24].

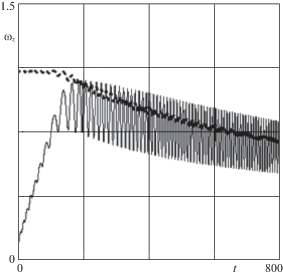
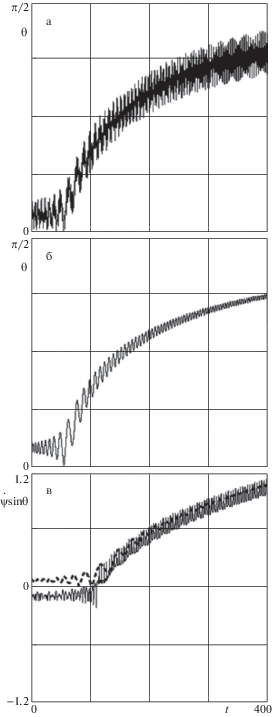
Сравнение результатов моделирования, полученных по нелинейной (4.1)–(4.3) и исходной моделям (2.1)–(2.4) показывает, что уравнения метода интегральных многообразий правильно описывают резонансные режимы движения твердого тела. В качестве примера на рис. 6, 7 приводятся зависимости, характеризующие процесс захвата в резонанс в нелинейном случае. Рассматривается сложная асимметрия вида ${\sigma } = 0.05$ и $\Delta = 0.1$. На рис. 6 штриховой линией показана резонансная скорость ${{{\omega }}_{{z1}}} > 0$, которая в отличие от случая малых углов нутации не постоянна, а уменьшается при возрастании угла нутации. При захвате в резонанс угловая скорость ${{{\omega }}_{z}}$ колеблется относительно резонансной скорости, которая изменяется. На рис. 7 показаны зависимости угла нутации, определенные по исходной (рис. 7, а) и нелинейной модели метода интегральных многообразий (рис. 7, б). Зависимость ${\theta }\left( t \right)$, определенная по методу интегральных многообразий, близка к средним значениям угла нутации, вычисленным по исходной модели. В процессе резонансной эволюции для уравнений движения по интегральному многообразию ${\theta }\left( t \right) \to {\pi /}2$, а в исходной системе угол нутации колеблется относительно этого предельного значения.

После захвата в резонанс, даже если начальные условия не взяты на интегральном многообразии, решение системы стремится к некоторому решению, лежащему на интегральном многообразии. Это иллюстрируется на рис. 7, в, где штриховой линией показана зависимость функции ${\dot {\psi }}(t)\sin {\theta }\left( t \right)$, определенная по модели (4.1)–(4.3), а сплошной линией – та же зависимость, вычисленная по исходной модели. Таким образом, при захвате в резонанс движение твердого тела стремится к прямой прецессии ${\dot {\psi }} > 0$ (${{{\omega }}_{z}} > 0$), которая описывается системой (4.1)–(4.3). Анализ резонансных режимов движения, когда ${{{\omega }}_{z}} < 0$, приводит к симметричным результатам, необходимо только в уравнениях (4.1)–(4.3) поменять индексы при ${{{\omega }}_{{1,2}}}$ местами.

Если проход через резонанс возникает за счет изменения резонансной скорости (4.4), например, $G\left( {\tau } \right)$ или $l\left( {\tau } \right)$, то этот случай сводится к предыдущему, когда ${{M}_{z}} \ne 0$, если сделать формальную замену ${{\bar {M}}_{z}} \Rightarrow {\bar {\omega }}_{l}^{'}$, где 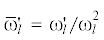, ${\omega }_{l}^{2} = Gl{\text{/}}\bar {J}$.

Заключение. Основываясь на полученных результатах, можно сделать следующие выводы:

1. Уравнения движения твердого тела с малой асимметрией, полученные методом интегральных многообразий с учетом резонансов низшего порядка (4.1)–(4.3), в случае, когда $\sin {\theta } \approx {\theta }$, совпадают с аналогичными уравнениями, построенными методом усреднения для малых углов нутации [8].

2. Оценки критических значений параметров асимметрии твердого тела, полученные для малых углов атаки с помощью необходимого условия (5.3), можно использовать, когда угол нутации ${\theta } < 0.75$. Эти оценки имеют практическое значение в прикладных задачах, связанных со стабилизацией движения космических аппаратов, например, [9–11, 13], так как позволяют исключить случаи захвата в резонанс.

3. Оценки вероятности захвата в резонанс, полученные с помощью усредненных уравнений движения твердого тела для малых углов нутации, во всех рассмотренных случаях дают завышенную величину вероятности по сравнению с вариантом, когда используются нелинейные уравнения движения, построенные методом интегральных многообразий.

Два последних вывода основываются на результатах численного моделирования.

Автор выражает благодарность д. ф.-м. н. Нейштадту А.И. за помощь и обсуждение вопросов, связанных с применением формулы (6.4) для оценки вероятности захвата в резонанс.