Прикладная математика и механика, 2019, T. 83, № 5-6, стр. 834-860
БИОМЕХАНИЧЕСКАЯ МОДЕЛЬ И ЧИСЛЕННЫЙ АНАЛИЗ РЕГЕНЕРАЦИИ ТКАНИ В ОБЪЕМЕ ПОРИСТОГО ИМПЛАНТАТА
1 Ивановский государственный энергетический университет
Иваново, Россия
2 Санкт-Петербургский политехнический университет Петра Великого
Санкт-Петербург, Россия
* E-mail: maslov@tipm.ispu.ru
Поступила в редакцию 18.08.2018
После доработки 15.01.2019
Принята к публикации 19.03.2019
Аннотация
Представлено развитие механобиологической концепции репаративной регенерации костной ткани, управляемой законом дифференциации клеток и действием внешней механической нагрузки периодического характера. Разработана математическая модель реконструкции кости в объеме пористого имплантата (скаффолда) с регулярной или хаотичной внутренней структурой на основе анализа напряженно-деформированного состояния пороупругой среды методом конечных элементов. Представлен аналитический метод нахождения эффективных упругих модулей композита, описывающего систему “кость–имплантат”, что позволяет определять пороупругие характеристики модели меняющейся сплошной среды на каждом временном шаге при расчете регенерации костной ткани в материале имплантата. Разработанные вычислительные алгоритмы применены для исследования трехмерной конечно-элементной модели остеосинтеза типичной трубчатой кости человека с помощью пористого имплантата. Проведен параметрический анализ компьютерной модели регенерации костной ткани под действием внешней стимулирующей нагрузки, изменяющейся по гармоническому закону, получены закономерности между характеристиками регенерации, параметрами внешнего воздействия и пористостью имплантата.
Введение. Задача дифференциации клеток и репаративной регенерации костной ткани в математическом виде сформулирована в работе Пауэлса 1941 года [1]. Была предложена теория, согласно которой эффект механических сил на процесс дифференциации осуществляется посредством поля упругой деформации ткани. Предполагалось, что сдвиговые компоненты тензоров напряжений и деформаций являются специфическим стимулом для развития коллагеновых волокон, т.е. фиброзной ткани, в то время как, гидростатические составляющие ответственны за формирование хрящевой ткани. На основе выдвинутых гипотез был рассмотрен процесс возникновения фиброзной, фиброзно-хрящевой и хрящевой ткани из недифференцированного вещества мезенхимальной ткани, возникающей после первоначального заживления в зоне перелома.
Впоследствии концепция Пауэлса была применена при разработке различных биомеханических моделей дифференциации тканей на основе линейной теории упругости изотропной однородной среды [2–4]. Решенные модельные задачи давали достаточно реалистичное предсказание о зоне оссификации моделируемого органа. Однако используемая статическая постановка задачи не позволяла исследовать развитие области оссификации, а классическая модель сплошной упругой среды не учитывала новые биомедицинские данные, что возмущения, вносимые механической нагрузкой в установившееся движение жидкости в транспортной системе кости могут обеспечивать передачу управляющих сигналов между клетками кости в процессе ее регенерации и перестройки.
Современный подход основан на модели двухфазной среды [5, 6] с учетом динамических нагрузок. Был введен безразмерный “механорегулирующий индекс” М, определяющий фенотип ткани, образуемой в текущей точке среды в ответ на механическую стимуляцию. Новое выражение индекса, как и ранее, представляло собой линейную комбинацию механических характеристик напряженно-деформированного состояния ткани с двумя эмпирическими константами. Однако в отличие от [1–4] в качестве основных регулирующих параметров использовались максимальные за цикл нагружения значения октаэдрической сдвиговой деформации упругого каркаса двухфазной среды и скорости потока внутритканевой жидкости в порах.
В дальнейшем [7] в механорегулирующую схему было включено диффузионное уравнение, описывающее миграцию и распределение мезенхимальных стволовых клеток (МСК), которые формируются на периостальной поверхности кости из внешних к костной мозоли мягких тканей и костного мозга. Предполагается, что МСК в каждом конечном элементе могут дифференцироваться в клетки основных фенотипов тканей: фибробласты, хондроциты и остеобласты в зависимости от среднего механического состояния элемента в текущий расчетный день. Каждый тип клеток-предшественников производит твердую фазу (упругую матрицу) двухфазного материала с определенными модулями упругости. Конечный модуль упругости сплошной среды рассчитывается на основе полученных частных значений на каждой итерации.
Указывается [8] на необходимость исследовать процессы миграции, пролиферации и дифференциации клеток различных типов при регенерации костной ткани. Предложенные математические модели [8, 9] описывают изменение концентраций мезенхимальных стволовых клеток, фибробластов, хондроцитов и остеобластов, а также временного и пространственного распределения соединительной, хрящевой и костной тканей. Деятельность указанных четырех основных типов клеток, взаимодействующих в зависимости от биохимической и механической стимуляции, характеризуется преобразованием друг в друга и в структуры тканей, включая сеть кровеносных сосудов [9].
Концепция развитая в [5–7] при незначительных модификациях применялась впоследствии и другими авторами для решения различных практических задач ортопедии и биоинженерии тканей. К основному их недостатку можно отнести то, что моделировалось действие только статической или циклической нагрузки низкой частоты (1 Гц). Поэтому, несмотря на декларируемый динамический подход, фактически задача структурной перестройки решалась в квазистатической постановке, при использовании которой инерционными эффектами пренебрегалось. Однако экспериментально показано, что динамические режимы относительно высокой частоты могут оказывать более существенный эффект при стимулировании живых тканей, чем низкочастотная периодическая нагрузка [10]. В рамках разработанных математических моделей [11, 12], развивающих подходы [5–7], было подтверждено существенное влияние частоты силового воздействия на процесс регенерации костной мозоли.
Ранее проблема регенерации рассматривалась либо в области костной мозоли, возникающей после перелома кости, либо вблизи поверхности эндопротеза сустава. Приложениями разработанных моделей к описанию процесса регенерации в пористых имплантатах, или скаффолдах, судя по публикациям, начали заниматься относительно недавно. Как одни из первых стоит отметить работы [13, 14] уже упоминавшихся авторов, в которых алгоритм компьютерного моделирования регенерации костной ткани с теми же гипотезами и числовыми параметрами [7] использован для расчета ткани в области скаффолда регулярной структуры с использованием прямого конечно-элементного моделирования гетерогенной структуры “имплантат–ткань”. Однако данный подход требует значительных вычислительных ресурсов, что позволяет анализировать лишь небольшой фрагмент кости простой формы.
За последние несколько лет появился ряд новых публикаций, посвященных применению механобиологических подходов к исследованию врастания костной ткани в пористую поверхность имплантатов. Так в работах [15–17] моделируется восстановление костной ткани в тазовом компоненте эндопротеза тазобедренного сустава, представляющем собой металлический имплантат с развитой пористой поверхностью для врастания ткани и обеспечения бесцементной фиксации в вертлюжной впадине тазовой кости. Следуя в целом устоявшейся методике расчета регенерации ткани, авторы цитируемых статей, проводят сравнение между феноменологическим подходом при моделировании заполнения остеогенными клетками исследуемой области регенерации [5–7] с подходом, учитывающим клеточные преобразования между различными типами клеток [8, 9]. Получено, что, несмотря на некоторые различия в расчетных данных, описывающих процесс дифференциации ткани в начальный период, оба алгоритма клеточных преобразований (феноменологический и клеточно-зависимый) предсказывают сходное пространственное распределение новой костной ткани при достижении равновесного состояния. Делается важный вывод о том, что феноменологический алгоритм, с вычислительной точки зрения, более быстрый, чем алгоритм решения полной задачи клеточных преобразований (миграции, дифференциации, пролиферации, апоптоза) может быть успешно использован для предсказания врастания костной ткани в пористый объем имплантата.
Параллельно рассмотренным подходам математического моделирования регенерации костной мозоли продолжает развиваться теория, максимально обобщенно описывающая процессы роста ткани. При этом, в отличие от механобиологической модели регенерации ткани как изменения фенотипа и, следовательно, физико-механических свойств заданной и неизменной в процессе расчета области сплошной среды, модели роста подразумевают наличие внутренних источников деформаций и напряжений, приводящих к изменению объема растущей ткани. Как одни из первых необходимо отметить статьи, в которых с позиций механики сплошных сред рассматривались обобщенные модели роста живой ткани [18, 19]. Важным вкладом стало введение понятия остаточных напряжений и применение мультипликативного разложения тензора трансформации на тензоры упругой и ростовой части [20, 21]. С помощью аппарата нелинейной механики сплошных сред сделаны попытки построить модели роста некоторых мягких тканей (опухоли, артерии) [22, 23]. При этом отмечалось, что для твердых тканей допустимо применение линейных соотношений теории упругости.
Несмотря на определенные успехи в построении общей теории “растущей” сплошной среды, для решения задачи “врастания” костной ткани в объем пористого имплантата теория [18–21] представляется менее соответствующей биомедицинским данным о процессах регенерации ткани, чем ранее рассмотренные подходы [6, 7, 11–14]. В данной статье в качестве основополагающей гипотезы будет предполагаться, что внутренней поровой объем имплантата заполнен тканью, содержащей клетки, способные к дифференцированию с образованием характерных фенотипов тканей, аналогично процессам, имеющим место при восстановлении костной мозоли. Тем самым будет представлена математическая модель и алгоритм расчета процесса регенерации костной ткани в объеме пористого имплантата на основе ранее предложенной механобиологической теории регенерации костной мозоли, обусловленной процессами дифференциации клеток при наличии внешнего динамического воздействия. В качестве биомеханической модели ткани и имплантата рассматривается пороупругая сплошная среда, учитывающая взаимодействие упругого каркаса и внутритканевой жидкости. Новизной решаемой задачи является анализ влияния параметров пористого имплантата и динамических характеристик приложенной силы на процесс восстановления костной ткани в объеме имплантата.
1. Концепция биомеханического моделирования. Следуя общей концепции [5, 6, 11, 12], рассмотрим схему математического подхода к описанию регенерации костной ткани в результате дифференциации клеток и действия механического стимула. В отличие от известных моделей регенерации кости в зоне перелома представленная биомеханическая модель должна учитывать наличие пористого имплантата. Это приводит к необходимости определения эффективных характеристик композитной структуры, образованной пористым имплантатом и тканью. При этом для расчета напряженно-деформированного состояния композита “имплантат–ткань” необходимо знать пороупругие характеристики сплошной среды в недренированном состоянии материала.
Предполагается, что в начальный момент времени поровое пространство имплантата и заданная область вокруг имплантата заполнено тканью гранулированного типа, содержащего некоторое количество недифференцированных клеток-предшественников (МСК). Благодаря наличию мелких кровеносных сосудов в гранулированной ткани внутри и вокруг имплантата мезенхимальные стволовые клетки могут перемещаться в направлении снижения концентрации и под действием механического стимула дифференцироваться в специфические клетки, образуя ткани определенных фенотипов (фиброзная, хрящевая, костная).
Под зоной регенерации полного объема ${{V}_{{\operatorname{reg} }}}$, ограниченного внешней поверхностью ${{S}_{{\operatorname{reg} }}}$, будем понимать внутреннее пространство поровых каналов скаффолда, объем которого учитывается величиной пористости имплантата, и некоторую область ткани вокруг имплантата. В постановке краевой задачи для объема $V$ пороупругой среды с внешней границей $S$, моделирующей полную биологическую структуру, образованную тканями и имплантатом, предполагаем, что ${{V}_{{\operatorname{reg} }}} \subset V$.
Концепция биомеханического моделирования регенерации костной ткани в объеме пористого имплантата основана на применении единой компьютерной модели исследуемой биомеханической системы (рис. 1). Основная часть математической модели описывается уравнениями динамической пороупругости, предназначенными для расчета упругих перемещений и деформаций, порового давления и потоков внутритканевой жидкости как в зоне регенерации, так и в областях сплошной среды, не участвующих в структурной перестройке. Считается, что в начальный момент времени физико-механические свойства регенерата соответствуют ткани гранулированного типа с низкими упруго-прочностными характеристиками. Динамическая нагрузка определенной частоты прикладывается пошагово по заданному временному закону, что позволяет исследовать влияние различных схем нагружения на механизм структурной перестройки кости.
После определения напряженно-деформированного состояния пороупругой среды в заданных точках модели рассчитывается значение механорегулирующего индекса $M$, определяющего фенотип ткани, образование которого стимулирует данная нагрузка [5–8]:
где $\varepsilon $ – максимальное значение октаэдрической сдвиговой деформации упругого каркаса двухфазной среды, $q$ – максимальное значение скорости потока внутритканевой жидкости в порах, а и b – эмпирические константы.В математическую модель регенерации, кроме исходной гранулированной, включены четыре вида дифференцированной ткани – фиброзная, хрящевая, незрелая костная и зрелая костная, – каждый из которых характеризуется своими значениями материальных констант (плотностью, модулем упругости, коэффициентом проницаемости и т.д.). В зависимости от значения индекса $M$, рассчитанного в точках исследуемой области, пороупругие модули ткани изменяются в соответствии с новым видом ткани, образование которого стимулирует возникающее напряженно-деформированное состояние сплошной среды.
Биомеханический критерий (1.1), введенный ранее [5, 6] на основе косвенных экспериментальных данных и наблюдений, широко используется с момента публикации до настоящего времени. Он содержит две эмпирические константы а = 0.0375, b = = 0.003 мм/с и характеризуется следующими пороговыми значениями механорегулирующего индекса [7]: 1) $M > 3$ – образование фиброзной ткани, 2) $1 < M \leqslant 3$ – образование хрящевой ткани, 3) $0.267 < M \leqslant 1$ – образование незрелой костной ткани с достаточно высокой пористостью, близкой к губчатому веществу кости, 4) 0.01 < < $M \leqslant 0.267$ – образование зрелой костной ткани, приближающейся по своим механическим характеристикам к компактному веществу кости, 5) $M \leqslant 0.01$ – резорбция костной ткани, возникающая при недостаточном механическом стимулировании.
Биологическая часть математической модели предназначена для описания миграции активных клеток-предшественников (МСК), способных к дифференциации и производству других типов клеток. Существующие математические подходы предполагают, что их доставка в область регенерации осуществляется непрерывно в течение заданного срока реконструкции по закону диффузии в соответствии со следующей постановкой начально-краевой задачи:
(1.2)
$\nabla \cdot \left( {{\mathbf{J}} \cdot \nabla \psi } \right) - \frac{{\partial \psi }}{{\partial t}} = 0,\quad t > 0,\quad {\mathbf{x}} \in {{V}_{{\operatorname{reg} }}}$(1.3)
$\psi \left( {0,{\mathbf{x}}} \right) = {{\psi }_{0}}\left( {\mathbf{x}} \right),\quad {\mathbf{x}} \in {{V}_{{\operatorname{reg} }}},\quad \psi \left( {t,{\mathbf{x}}{\text{*}}} \right) = \psi {\text{*}}\left( {t,{\mathbf{x}}{\text{*}}} \right),\quad {\mathbf{x}}* \in {{S}_{{\operatorname{reg} }}},$Уравнение (1.2) при заданных значениях функции в начальный момент времени ${{\psi }_{0}}$ и на границе области регенерации $\psi {\text{*}}$ в виде краевых условий Дирихле (1.3) позволяет определить концентрацию клеток в произвольной точке зоны регенерации в любой момент времени. Обновление значений материальных констант ткани осуществляется исходя из рассчитанной концентрации активных клеток на текущем шаге и пороупругих модулей образующегося типа ткани по критерию (1.1) в зависимости от текущего напряженно-деформированного состояния среды в области регенерации [11, 12].
После расчета характеристик образуемой в порах ткани на текущем шаге определяются эффективные модули композита, образованного пористым материалом имплантата и тканью. Затем механические свойства сплошной среды обновляются, и численная схема повторяется для следующего временного шага. По результатам вычислений на каждой итерации можно наблюдать за сходимостью процесса и стремлением изначально недифференцированной однородной ткани к преобразованию в тот или иной фенотип.
2. Численная реализация концепции. В основе биомеханической концепции регенерации костной ткани в объеме пористого имплантата лежат уравнения динамики пористого материала, насыщенного идеальной сжимаемой жидкостью [24, 25]. Моделью пороупругой сплошной среды будем описывать как фенотипы тканей, так и материал имплантата. В предыдущих работах [12, 26] численная реализация динамической задачи пороупругости методом конечных элементов описана достаточно подробно. Поэтому здесь приводятся только некоторые соотношения для демонстрации основных этапов математического моделирования структурной перестройки ткани во внутреннем пространстве скаффолда.
Начально-краевая задача теории пороупругости при использовании в качестве основных переменных упругих перемещений твердой фазы гетерогенного материала и давления поровой жидкости сводится к граничной задаче относительно изображений по Лапласу соответствующих функций ${\mathbf{\hat {u}}}$ и $\hat {p}$. При отсутствии внутренних источников жидкости уравнение динамики пороупругой среды имеет вид [12, 26]:
(2.1)
$\begin{gathered} \nabla \cdot {{{\hat {\sigma }}}_{{\operatorname{dr} }}} - {{s}^{2}}\left( {\rho {\mathbf{E}} - {{\rho }_{f}}{\mathbf{\tilde {\Gamma }}}\left( s \right)} \right) \cdot {\mathbf{\hat {u}}} - \left( {{\mathbf{{\rm A}}} - {\mathbf{\tilde {\Gamma }}}\left( s \right)} \right) \cdot \nabla \hat {p} = - {{{{\mathbf{\hat {f}}}}}_{V}},\quad {\mathbf{x}} \in V \\ {{s}^{{ - 1}}}\nabla \cdot \left( {{\mathbf{\tilde {K}}}\left( s \right) \cdot \nabla \hat {p}} \right) - {{\varphi }^{2}}{{R}^{{ - 1}}}\hat {p} - \left( {{\mathbf{{\rm A}}} - {\mathbf{\tilde {\Gamma }}}\left( s \right)} \right) \cdot \cdot {\mathbf{\hat {\varepsilon }}} = 0,\quad {\mathbf{x}} \in V, \\ \end{gathered} $Краевые условия задачи пороупругости включают в себя ограничения, наложенные на упругие перемещения и давление на поверхности, а также значения поверхностных сил ${{{\mathbf{\hat {f}}}}_{S}}$ и потоков жидкости $\hat {q}_{n}^{{\text{*}}}$ через поверхность тела:
(2.2)
$\begin{gathered} {\mathbf{\hat {u}}}\left( {\mathbf{x}} \right) = {\mathbf{\hat {u}}}{\text{*}}\left( {\mathbf{x}} \right),\quad {\mathbf{x}} \in {{S}_{u}},\quad {\mathbf{\hat {t}}}\left( {\mathbf{x}} \right) = {\mathbf{n}}\left( {\mathbf{x}} \right) \cdot {\mathbf{\hat {\sigma }}}\left( {\mathbf{x}} \right) = {{{{\mathbf{\hat {f}}}}}_{S}}\left( {\mathbf{x}} \right),\quad {\mathbf{x}} \in {{S}_{t}},\quad S = {{S}_{u}} + {{S}_{t}} \\ \hat {p}\left( {\mathbf{x}} \right) = \hat {p}{\text{*}}\left( {\mathbf{x}} \right),\quad {\mathbf{x}} \in {{S}_{p}},\quad {{{\hat {q}}}_{n}}\left( {\mathbf{x}} \right) = {\mathbf{n}}\left( {\mathbf{x}} \right) \cdot {\mathbf{\hat {q}}}\left( {\mathbf{x}} \right) = \hat {q}_{n}^{ * }\left( {\mathbf{x}} \right),\quad {\mathbf{x}} \in {{S}_{q}},\quad S = {{S}_{p}} + {{S}_{q}} \\ \end{gathered} $Для корректной постановки задачи пороупругости в каждой точке поверхности должны быть заданы четыре степени свободы, характеризующие твердую и жидкую фазы пороупругой среды. Поэтому соотношения (2.2) принимают вид комбинации условий, наложенных на механические и гидравлические переменные. Например, можно сформулировать задачу со свободной и непроницаемой для поровой жидкости частью поверхности ${{S}_{2}}$ совместно с закрепленной и полностью проницаемой частью поверхности ${{S}_{1}}$:
(2.3)
$\begin{gathered} {\mathbf{\hat {u}}}{\text{*}}\left( {\mathbf{x}} \right) = 0,\quad {\mathbf{x}} \in {{S}_{u}} = {{S}_{1}},\quad \hat {p}{\text{*}}\left( {\mathbf{x}} \right) = 0,\quad {\mathbf{x}} \in {{S}_{p}} = {{S}_{1}} \\ {{{{\mathbf{\hat {f}}}}}_{S}}\left( {\mathbf{x}} \right) = 0,\quad {\mathbf{x}} \in {{S}_{t}} = {{S}_{2}},\quad \hat {q}_{n}^{ * }\left( {\mathbf{x}} \right) = 0,\quad {\mathbf{x}} \in {{S}_{q}} = {{S}_{2}},\quad S = {{S}_{1}} + {{S}_{2}} \\ \end{gathered} $Начальные условия для используемой в дальнейшем гармонической постановки задачи не имеют существенного значения и могут быть положены равными нулю, что позволяет перейти в системе (2.1) к амплитудным значениям перемещений и давления. Заменяя параметр преобразования Лапласа на $i\omega $ для случая гармонических колебаний и применяя метод взвешенных невязок к (2.1), дифференциальные уравнения преобразуем в систему конечно-элементных уравнений [12, 26]:
(2.4)
$\begin{gathered} \left( {{\mathbf{K}}_{{\operatorname{dr} }}^{{(k)}} - {{\omega }^{2}}\left( {{{{\mathbf{M}}}^{{(k)}}} - {{{{\mathbf{\tilde {L}}}}}^{{(k)}}}\left( {i\omega } \right)} \right)} \right){{{\mathbf{U}}}^{{(k)}}} - \left( {{\mathbf{H}}_{1}^{{(k)}} + {\mathbf{\tilde {H}}}_{2}^{{(k)}}\left( {i\omega } \right)} \right){{{\mathbf{P}}}^{{(k)}}} = {{{\mathbf{F}}}^{{(k)}}} \\ - {{\left( {{\mathbf{H}}_{1}^{{(k)}} + {\mathbf{\tilde {H}}}_{2}^{{(k)}}\left( {i\omega } \right)} \right)}^{T}}{{{\mathbf{U}}}^{{(k)}}} + \left( { - {{{\mathbf{D}}}^{{(k)}}} + i{{\omega }^{{ - 1}}}{{{{\mathbf{\tilde {G}}}}}^{{(k)}}}\left( {i\omega } \right)} \right){{{\mathbf{P}}}^{{(k)}}} = - i{{\omega }^{{ - 1}}}{{{\mathbf{Q}}}^{{(k)}}}, \\ \end{gathered} $Соотношения (2.4) описывают установившиеся гармонические колебания пороупругой среды с частотой приложенных внешних сил $\omega $ в заданный момент времени ${{t}^{{(k)}}}$ (на $k$-м временном шаге). Заметим, что в (2.4) для универсальности обозначений все переменные и матрицы коэффициентов имеют зависимость от временного шага ${{t}^{{(k)}}}$ в соответствии с общей схемой математического моделирования регенерации костной ткани. Однако при численной реализации достаточно учесть только изменение свойств пороупругой среды, описывающей область регенерации. Ниже для понимания связи физико-механических характеристик образующейся ткани с результатами численного расчета приводится вид элементных матриц, образующих соответствующие глобальные матрицы системы (2.4):
(2.5)
$\begin{gathered} {{{{\mathbf{\tilde {l}}}}}^{e}} = \int\limits_{{{V}^{e}}} {\rho _{f}^{{(k)}}{{{\left( {{\mathbf{N}}_{u}^{e}} \right)}}^{T}}{{{{\mathbf{\tilde {\Gamma }}}}}^{{(k)}}}{\mathbf{N}}_{u}^{e}dV} \\ {\mathbf{h}}_{1}^{e} = \int\limits_{{{V}^{e}}} {{{{\left( {{\mathbf{B}}_{u}^{e}} \right)}}^{T}}{{{\mathbf{{\rm A}}}}^{{(k)}}}{\mathbf{N}}_{p}^{e}dV} ,\quad {\mathbf{\tilde {h}}}_{2}^{e} = \int\limits_{{{V}^{e}}} {{{{\left( {{\mathbf{N}}_{u}^{e}} \right)}}^{T}}{{{{\mathbf{\tilde {\Gamma }}}}}^{{(k)}}}{\mathbf{G}}_{p}^{e}dV} \\ \end{gathered} $В выражениях (2.5) тензоры, отвечающие за физико-механические характеристики пороупругой среды, изменяются в соответствии с математической схемой регенерации на каждом $k$-м шаге численного анализа. Алгоритм решения системы (2.4) используется как для расчета установившихся колебаний под действием гармонической силы, так и для статического анализа при постоянной нагрузке, если положить $\omega = 0$.
С точки зрения компьютерной реализации заметим, что дифференциальное уравнение (1.2), описывающее диффузию клеток, аналогично второму уравнению системы (2.1) без перекрестного слагаемого, если рассматривать его в изображениях. Это позволяет существенно упростить разработку численного алгоритма при использовании одного типа конечных элементов и, следовательно, единой конечно-элементной сетки для описания поля перемещений и распределения концентрации клеток в объеме тела. Применяя метод взвешенных невязок к уравнению (1.2) и процедуру конечно-элементной дискретизации, получим систему дифференциальных уравнений первого порядка в матричном виде:
(2.6)
${\mathbf{\dot {\Psi }}} + {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} \Psi }} = {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Q} }},$Систему обыкновенных дифференциальных уравнений (2.6) можно проинтегрировать численно с помощью разностной схемы первого порядка, что дает матричное уравнение для определения глобального узлового вектора концентрации клеток в любой момент времени:
(2.7)
${{{\mathbf{\Psi }}}^{{(k)}}} = {{{\mathbf{\Psi }}}^{{(k - 1)}}} - \Delta t{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{G} }}{{{\mathbf{\Psi }}}^{{(k - 1)}}} + \Delta t{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{Q} }},\quad k = 1,2,\; \ldots ,\;{{k}_{{\max }}},$Заметим, что расчетная схема движения клеток (2.7) применяется только для области регенерации костной ткани, которая, как правило, входит составной частью в полную конечно-элементную модель пороупругой задачи, описываемой соотношениями (2.4).
3. Определение пороупругих модулей. В уравнения (2.1), (2.4) входят упругие модули пористого материала в дренированном состоянии. Это означает, что поровые каналы материала полностью освобождены от жидкой фазы. С другой стороны для расчета композита, состоящего из пористого материала имплантата и биологической ткани, полностью заполняющей поровые каналы, необходимо учитывать недренированное состояние пороупругой среды. В общем случае связь между упругими модулями в дренированном и недренированном состояниях имеет вид [26]:
(3.1)
${{{\mathbf{C}}}_{{\operatorname{ud} }}} = {{{\mathbf{C}}}_{{\operatorname{dr} }}} + {{\varphi }^{{ - 2}}}R{\mathbf{AA}}$Методы микромеханики позволяют определить эффективные тензоры упругих модулей ${{{\mathbf{C}}}_{{\operatorname{dr} }}}$ и ${{{\mathbf{C}}}_{{\operatorname{ud} }}}$, тензор Био ${\mathbf{A}}$ и гидростатическую константу $R$ [27, 28]. Для вычисления компонент тензора эффективных модулей удобно применить метод самосогласования, основанный на применении тензора Эшелби, описывающего напряженное состояние вокруг характерного эллипсоидального включения в бесконечной среде [29]. Для произвольной двухфазной среды, состоящей из матрицы с заданным тензором упругих модулей ${{{\mathbf{C}}}_{m}}$ и включений с известным тензором ${{{\mathbf{C}}}_{{\operatorname{incl} }}}$, эффективный тензор упругих модулей гомогенизированной среды может быть записан в виде [30]:
(3.2)
${{{\mathbf{C}}}_{{\operatorname{eff} }}} = {{{\mathbf{C}}}_{m}} + \varphi {{{\mathbf{C}}}_{m}} \cdot \cdot \;{\mathbf{D}},\quad {\mathbf{D}} = {{\left( {{{{\mathbf{C}}}_{m}} + \Delta \cdot \cdot \;{\mathbf{S}}} \right)}^{{ - 1}}} \cdot \cdot \;\Delta \,,$В случае определяющих соотношений пороупругого материала для вычисления тензора эффективных модулей среды в дренированном состоянии ${{{\mathbf{C}}}_{{\operatorname{dr} }}}$ необходимо положить модули включений равными нулю: ${{{\mathbf{C}}}_{{\operatorname{incl} }}} = 0$. Вместо (3.1) для определения тензора упругих модулей в недренированном состоянии ${{{\mathbf{C}}}_{{\operatorname{ud} }}}$ можно воспользоваться соотношениями (3.2), если под включением понимать поровую жидкость: ${{{\mathbf{C}}}_{{\operatorname{incl} }}} = {{{\mathbf{C}}}_{{\operatorname{fluid} }}}$.
Расчетные формулы (3.2) дают хорошие результаты при малых значениях объемной концентрации включений. В отличие от обычного метода самосогласования дифференциальный метод позволяет аналитически определить эффективные свойства материала со сколько угодно большими значениями пористости. Рассматривая малые приращения φ и последовательно применяя формулы вычисления эффективных упругих модулей (3.2), можно получить следующее дифференциальное уравнение в тензорном виде [30]:
(3.3)
$\frac{{d{{{\mathbf{C}}}_{{\operatorname{eff} }}}}}{{d\varphi }} = \frac{{{{{\mathbf{C}}}_{{\operatorname{eff} }}} \cdot \cdot \;{\mathbf{D}}\left( {{{{\mathbf{C}}}_{{\operatorname{eff} }}}} \right)}}{{1 - \varphi }}$Макроскопический тензор Био ${\mathbf{A}}$ выражается через найденный тензор упругих модулей в дренированном состоянии ${{{\mathbf{C}}}_{{\operatorname{dr} }}}$ и тензор податливости упругого материала матрицы ${{{\mathbf{S}}}_{m}} = {\mathbf{C}}_{m}^{{ - 1}}$ [26, 27]:
(3.4)
${\mathbf{A}} = {\mathbf{E}} \cdot \cdot \;({\mathbf{I}} - {{{\mathbf{S}}}_{m}} \cdot \cdot \;{{{\mathbf{C}}}_{{\operatorname{dr} }}}),$Гидростатическая константа R, которую можно интерпретировать как эффективный модуль объемного сжатия жидкой фазы, определяется соотношением [26, 27]:
(3.5)
${{\varphi }^{2}}{{R}^{{ - 1}}} = \varphi K_{f}^{{ - 1}} + {\mathbf{E}} \cdot \cdot \;{{{\mathbf{S}}}_{m}} \cdot \cdot \left( {\varphi {\mathbf{E}} - {\mathbf{{\rm A}}}} \right)$Выражение податливости (3.5) складывается из двух слагаемых, первое из которых соответствует собственному сжатию поровой жидкости, а второе связано с деформациями упругой матрицы, влияющими на изменение пористости материала в результате его нагружения.
Формулы (3.3)–(3.5) с учетом выражений компонент тензора Эшелби для трансверсально-изотропной среды реализованы в виде программы, позволяющей рассчитать эффективные механические свойства пороупругого материала в дренированном и недренированном состояниях по заданным модулям упругости матрицы материала ${{{\mathbf{C}}}_{m}}$, пористости, форме и направлению эллипсоидальных пор [26, 31].
4. Расчет характеристик имплантата с тканью. Рассмотренный подход позволяет определять все пороупругие модули в дренированном и недренированном состояниях ткани, что необходимо для конечно-элементного моделирования. Однако наличие пористого имплантата приводит к необходимости вычисления эффективных характеристик пороупругого композита, образованного материалом имплантата и тканью, насыщенной жидкостью. При этом теория пороупругости Био имеет применение только к материалам, поровые каналы которых заполнены флюидом, совершающим хоть и малые, но собственные перемещения. В нашем случае предполагается, что ткань в поровых каналах жестко связана с материалом имплантата, что представляется достаточно реалистичным с медицинской точки зрения, поскольку именно врастание ткани с последующей остеоинтеграцией является целью любой операции по вживлению имплантатов и эндопротезов. Движение может совершать только внутритканевая жидкость, содержащаяся в порах биологических тканей. Следовательно, пороупругая модель композита “имплантат–ткань” в целом сохраняется, но для определения его эффективных характеристик требуется модифицированный алгоритм.
Пусть имплантат обладает собственной системой пор, характеризуемой пористостью ${{\varphi }_{{\operatorname{imp} }}}$, объем которых целиком заполнен биологической тканью, изменяющей свойства в процессе регенерации:
(4.1)
${{\varphi }_{{\operatorname{imp} }}} = \frac{{{{V}^{{\operatorname{tis} }}}}}{{{{V}^{{\operatorname{imp} }}}}} = \frac{{V_{s}^{{\operatorname{tis} }} + V_{f}^{{\operatorname{tis} }}}}{V},$Поскольку биологическая ткань также представляет собой пористый материал, поры которого заполнены физиологической жидкостью, то собственная пористость ткани ${{\varphi }_{{\operatorname{tis} }}}$ определяется стандартным образом:
(4.2)
${{\varphi }_{{\operatorname{tis} }}} = \frac{{V_{f}^{{\operatorname{tis} }}}}{{{{V}^{{\operatorname{tis} }}}}} = \frac{{V_{f}^{{\operatorname{tis} }}}}{{V_{s}^{{\operatorname{tis} }} + V_{f}^{{\operatorname{tis} }}}}$Тогда композитный материал, образованный имплантатом и тканью, будем рассматривать как сплошную среду с пористостью ${{\varphi }_{{\operatorname{comp} }}}$:
(4.3)
${{\varphi }_{{comp}}} = \frac{{V_{f}^{{\operatorname{tis} }}}}{{{{V}^{{imp}}}}} = {{\varphi }_{{\operatorname{tis} }}}{{\varphi }_{{imp}}}$Рассмотрим схему расчета эффективных модулей пороупругого композита “имплантат–ткань”. В качестве неизменных данных выступают свойства материала имплантата, описываемые тензором упругих модулей ${\mathbf{C}}_{s}^{{\operatorname{imp} }}$ и пористостью ${{\varphi }_{{imp}}}$ (4.1). Также к неизменным величинам относятся свойства внутритканевой жидкости и упругие модули твердой фазы каждого из рассматриваемых фенотипов ткани, описываемые тензором ${\mathbf{C}}_{s}^{{\operatorname{tis} }}$ и пористостью ${{\varphi }_{{\operatorname{tis} }}}$ (4.2).
Гомогенизация и расчет эффективных свойств гетерогенного материала по формулам (3.3)–(3.5) осуществляется дважды. На первом этапе рассматривается композит, образованный имплантатом с заданной структурой и пористостью ${{\varphi }_{{imp}}}$ и твердой фазой материала каждого из рассматриваемых фенотипов ткани. Применяя для осреднения дифференциальный метод самосогласования и рассматривая материал имплантата как матрицу с тензором упругих модулей ${{{\mathbf{C}}}_{m}}$ = ${\mathbf{C}}_{s}^{{\operatorname{imp} }}$, а ткань как включения с тензором упругих модулей твердой фазы ткани ${{{\mathbf{C}}}_{{incl}}} = {\mathbf{C}}_{s}^{{\operatorname{tis} }}$, по уравнению (3.3) для любых значений пористости имплантата ${{\varphi }_{{imp}}}$ получаем эффективные упругие модули гомогенизированной среды, которые можно трактовать как характеристики твердой фазы пороупругого композита “имплантат–ткань” с пористостью ${{\varphi }_{{comp}}}$ (4.3):
(4.4)
${\mathbf{C}}_{s}^{{\operatorname{comp} }} = f({{\varphi }_{{imp}}},{\mathbf{C}}_{s}^{{\operatorname{imp} }},{\mathbf{C}}_{s}^{{\operatorname{tis} }})$Как было отмечено, в уравнения (2.1)–(2.3) входят упругие модули среды в дренированном состоянии, коэффициенты эффективных напряжений и гидростатическая константа, учитывающие наличие поровых каналов в биологической ткани, заполняющей макропоры имплантата. Данные пороупругие характеристики, а также при необходимости упругие модули в недренированном состоянии, теперь могут быть определены для композита “имплантат–ткань” по формулам (3.3)–(3.5):
(4.5)
${\mathbf{C}}_{{dr}}^{{comp}},{\mathbf{C}}_{{undr}}^{{comp}},{{{\mathbf{A}}}^{{comp}}},{{R}^{{comp}}} = f({{\varphi }_{{comp}}},{\mathbf{C}}_{s}^{{\operatorname{imp} }},{\mathbf{C}}_{f}^{{\operatorname{tis} }})$Рассчитанные по представленному алгоритму значения материальных констант гомогенизированной среды для каждого фенотипа ткани и заданной структуры имплантата используются в схеме компьютерного моделирования регенерации ткани в объеме пористого имплантата. Они выступают как характерные значения, соответствующие определенным фенотипам ткани, по которым рассчитываются пороупругие свойства регенерата в расчетном алгоритме. На каждом временном шаге $k$ после вычисления механорегулирующего индекса получаем как значения пороупругих модулей ткани, образование которой стимулирует текущая величина нагрузки, так и эффективные материальные константы пороупругого композита “имплантат–ткань”. На следующем шаге $k + 1$ новые значения эффективных материальных констант входят в динамические уравнения среды (2.1), (2.4) и участвуют в дальнейшем расчете напряженного состояния биомеханической модели.
Подробно численная схема оценки эффективных свойств композита “имплантат–ткань” как пороупругой среды описана ранее [32], в то время как здесь приводятся только основные соотношения для понимания предложенного метода расчета. Необходимо также отметить, что поскольку в основе математического моделирования эффективных свойств неоднородного материала при большой пористости лежит разностная схема Эйлера для решения уравнений типа (3.3), то для устойчивости численного решения рекомендуется брать достаточно малый шаг по $\varphi $. Большое количество проведенных вычислительных экспериментов со сравнением результатов с аналитическими решениями, известными реферативными данными и проверкой адекватности получаемых конечных результатов известной физической картине восстановления механических свойств костной мозоли подтвердило достоверность и высокую эффективность данного метода нахождения эффективных свойств модели пороупругой среды, описывающей биологические ткани [11, 12, 25, 26, 30].
Разработанный алгоритм регенерации ткани в объеме пористого имплантата реализован в авторском программном комплексе с использованием шестистороннего конечного элемента с квадратичной интерполяцией перемещений и давления [33]. Компьютерная программа позволяет проводить имитационное моделирование восстановления физико-механических свойств кости при варьировании параметров силового воздействия и характеристик материала имплантата.
5. Численная модель пороупругой задачи. Идеализированная модель фрагмента диафиза трубчатой кости (рис. 2а), представляющая собой цилиндр длиной 84 мм, внешним диаметром 20 мм и внутренним 14 мм, образована компактным веществом 1 и костным мозгом 2. Часть диафиза длиной 34 мм замещена пористым имплантатом 4 цилиндрической формы диаметром 20 мм. Имплантат и часть кости дополнительно окружает мягкая ткань 3, также участвующая в структурной перестройке. В целом размеры модели соответствуют значениям, использованным в предыдущих работах [7, 12]. Трехмерная конечно-элементная модель учитывает симметрию относительно трех координатных плоскостей, содержит 1132 элемента и 5841 узел, имеет 23364 степени свободы. Область регенерации включает окружающую мягкую ткань 3 и объем имплантата 4 (рис. 2б).
Согласно постановке задачи пороупругости с краевыми условиями (2.3) на трех плоскостях симметрии наложены граничные условия отсутствия нормальных упругих перемещений $\hat {u}_{n}^{*} = 0$, касательных составляющих поверхностных сил ${{\hat {f}}_{{S\tau }}} = 0$ и потоков жидкости $\hat {q}_{n}^{ * } = 0$. На верхней поверхности приложена нагрузка ${{\hat {f}}_{{Sn}}}$ в точках кортикального слоя 1, а в точках костномозгового канала 2 нагрузка отсутствует ${{\hat {f}}_{S}} = 0$. Внешняя поверхность кости 1 принята непроницаемой $\hat {q}_{n}^{ * } = 0$, в то время как поверхность костной мозоли 3 и верхняя грань модели считаются абсолютно проницаемыми для внутритканевой жидкости $\hat {p}* = 0$ (рис. 2а).
В качестве распределенной силы, действующей на кость вдоль ее продольной оси, взята линейная комбинация сжимающей нагрузки, постоянной на каждой временной итерации с плавным возрастанием за период симуляции, и быстрой составляющей, изменяющейся по гармоническому закону с относительно высокой частотой $\omega $:
(5.1)
$F\left( {{{t}^{{(k)}}},\omega } \right) = {{F}_{{\operatorname{st} }}}\left( {{{t}^{{(k)}}}} \right) + {{F}_{{\operatorname{dyn} }}}\left( {{{t}^{{(k)}}}} \right){{e}^{{i\omega \tau }}},\quad {{F}_{{dyn}}}\left( {{{t}^{{(k)}}}} \right) = \beta {{F}_{{st}}}\left( {{{t}^{{(k)}}}} \right),\quad {{t}^{{(k)}}} = k\Delta t,$Согласно рекомендациям [7, 8] и предыдущим исследованиям по имитационному моделированию сращения кости [11, 12] для обеспечения стабильности расчет необходимо проводить с постепенным увеличением приложенной нагрузки. В настоящей работе, кроме варианта плавного увеличения сжимающей силы за ${{Т}_{1}}$ = 60 дней (рис. 3), с целью проверки стабильности модели врастания кости в имплантат смоделировано “мгновенное” приложение нагрузки за один временной шаг (${{Т}_{1}}$ = 1). В обоих случаях принято, что равнодействующая сила за время $0 < t \leqslant {{Т}_{1}}$ увеличивается до своего максимального значения ${{F}_{{\max }}} = 500$ Н и сохраняет достигнутую величину до конца расчетного периода равного 120 дням. Для определенности в (5.1) принято, что амплитуда гармонической нагрузки пропорциональна статической составляющей силы с заданным коэффициентом $\beta $ равным 0.1 и 0.01, что соответствует значению амплитуды 50 и 5 Н.
Напряженно-деформированное состояние среды от действия суммарной силы (5.1) в любой момент времени будет являться суперпозицией отдельных решений ввиду линейной постановки задачи. Тогда на каждом шаге нагружения $k$ для вычисления эквивалентной деформации твердой фазы пороупругой среды и потока поровой жидкости, входящих в выражение биомеханического критерия (1.1), используем сумму решений статической задачи и задачи на установившиеся гармонические колебания вязкоупругой среды.
Моделирование регенерации кости исследовалось при значениях материальных констант, приведенных в табл. 1 [11, 12]. Плотность, модули Юнга и сдвига основных видов ткани в дренированном состоянии, коэффициенты Био эффективных напряжений и гидростатическая константа были получены расчетным путем по формулам (3.3)–(3.5) исходя из типичных значений упругих модулей материала твердой и жидкой фаз и пористости материала [12, 24]. Значения гидравлической проницаемости тканей взяты из [7], а характеристика искривленности поровых каналов принята равной 1.66, что часто используется в расчетах и соответствует порам неспецифической формы [28].
Таблица 1.
Пороупругие модули биологических тканей
| Тип ткани | ${{\varphi }_{{tis}}}$ | ${{\alpha }_{{tis}}}$ | ${{\rho }_{{tis}}}$ кг/м3 | $E_{{tis}}^{{dr}}$ ГПа | $G_{{tis}}^{{dr}}$ ГПа | ${{R}_{{tis}}}$ ГПа | ${{K}_{{tis}}}$ м4/Н с |
|---|---|---|---|---|---|---|---|
| Гранулированная | 0.99 | 1.000 | 1021 | 1.36 × 10–4 | 0.57 × 10–4 | 2.29 | 1.0 × 10–14 |
| Фиброзная | 0.80 | 0.990 | 1100 | 1.15 × 10–3 | 0.47 × 10–3 | 0.21 | 1.0 × 10–14 |
| Хрящевая | 0.80 | 0.995 | 1120 | 5.82 × 10–3 | 2.35 × 10–3 | 1.07 | 5.0 × 10–15 |
| Незрелая кость | 0.65 | 0.893 | 1182 | 3.73 | 0.97 | 1.42 | 1.0 × 10–13 |
| Зрелая кость | 0.20 | 0.435 | 1416 | 13.1 | 4.5 | 0.39 | 3.7 × 10–13 |
Материал имплантата представляет собой распространенный в тканевой хирургии гидроксиапатит плотностью 3160 кг/м3 с модулем Юнга 119.5 ГПа и коэффициентом Пуассона 0.285 [34]. Принята изотропная модель распределения поровых каналов с вариацией пористости от 50 до 90%. С помощью рассмотренного алгоритма (4.4), (4.5) определены необходимые для моделирования физико-механические характеристики композита “имплантат–ткань”, в том числе эффективные упругие модули в дренированном состоянии (табл. 2) [32].
Таблица 2.
Пороупругие модули композита “имплантат–ткань”
| ${{\varphi }_{{impl}}}$ | Тип ткани, заполняющей имплантат | ${{\varphi }_{{comp}}}$ | ${{\alpha }_{{comp}}}$ | ${{\rho }_{{comp}}}$ кг/м3 | $E_{{comp}}^{{dr}}$ ГПа | $G_{{comp}}^{{dr}}$ ГПа | ${{R}_{{comp}}}$ ГПа |
|---|---|---|---|---|---|---|---|
| 0.50 | Гранулированная | 0.497 | 0.768 | 2090 | 7.407 | 3.047 | 1.074 |
| Фиброзная | 0.400 | 0.664 | 2130 | 10.62 | 4.354 | 0.851 | |
| Хрящевая | 0.400 | 0.670 | 2140 | 10.77 | 4.398 | 0.853 | |
| Незрелая кость | 0.325 | 0.611 | 2171 | 23.38 | 9.314 | 0.712 | |
| Зрелая кость | 0.100 | 0.232 | 2288 | 41.68 | 16.30 | 0.214 | |
| 0.90 | Гранулированная | 0.896 | 0.990 | 1235 | 0.012 | 0.0051 | 1.507 |
| Фиброзная | 0.720 | 0.928 | 1306 | 0.096 | 0.0396 | 0.880 | |
| Хрящевая | 0.720 | 0.954 | 1324 | 0.127 | 0.0515 | 1.149 | |
| Незрелая кость | 0.585 | 0.883 | 1380 | 3.850 | 1.552 | 1.275 | |
| Зрелая кость | 0.180 | 0.417 | 1590 | 15.14 | 5.849 | 0.362 |
6. Численная модель задачи диффузии. В используемой схеме клеточных преобразований (4.4) в качестве материальных констант присутствуют только коэффициенты диффузии по трем координатным осям, характеризующие миграцию активных клеток-предшественников (МСК). Наличие твердого скелета в пороупругой среде оказывает существенное влияние на диффузионный перенос вещества, но, тем не менее, большинство исследователей подтверждают возможность применения уравнения диффузии для описания потока вещества и концентрационного поля в пористом материале. В этом случае эффективный коэффициент диффузии выражается через пористость материала, извилистость пор и истинный коэффициент диффузии вещества (клеток) с помощью соотношения ${\mathbf{J}} = \varphi {{{\mathbf{J}}}_{{ист}}}{\text{/}}{{\tau }^{2}}$ [35].
В ранних работах значение коэффициента диффузии, входящего в уравнения типа (1.2), (2.4), (2.5), подбиралось математически из феноменологического условия, что процесс оссификации костной мозоли согласно медицинским данным о заживлении перелома обыкновенно занимает 16 недель [36], а, следовательно, активные клетки–предшественники за это время должны полностью заполнить пространство между отломками кости. Это приводит к значительному разбросу возможных значений коэффициента диффузии: 0.34–2.37 мм2/день в зависимости от начального положения фронта распространения клеток в костной мозоли [7, 37]; 0.1 мм2/день [16] при использовании диффузионной схемы [7]; 0.06–0.67 мм2/день в зависимости от расстояния между границами костных отломков [11, 12]; 10–8–10–10 см2/с (8.64 × 10–2–8.64 × × 10–4 мм2/день) для разных типов клеток на основании цитируемых источников [38].
Для исследования регенерации в объеме костного имплантата подход, основанный на косвенной оценке коэффициента диффузии по заполнению области костной мозоли, не может быть обоснованно использован, поскольку определение проникновения ткани в поровое пространство имплантата само является одной из биомедицинских задач. Глубина врастания костной ткани будет зависеть как от временно-пространственных характеристик напряженно-деформированного состояния тканей в расчетной области, так и от биохимических факторов роста. Представляется существенным, чтобы математическая модель позволяла оценивать распределение ткани в объеме пористого имплантата по некоторым независимым параметрам движения клеток. Поэтому в настоящей статье было выбрано значение коэффициента диффузии равное 0.65 мм2/день, приведенное в [8] на основании экспериментальных биомедицинских данных по скорости миграции МСК.
В расчетной схеме (4.4) глобальные векторы узловых значений описывают относительную безразмерную концентрацию клеток-предшественников. Поэтому согласно краевым условиям (1.3) на всей внешней границе ${{S}_{{reg}}}$ области регенерации (рис. 2б), совпадающей с конечно-элементной областью диффузионной задачи ${{V}_{{reg}}}$ (объем имплантата 4 и окружающей мягкой ткани 3), концентрация имеет постоянное максимальное значение $\psi * = 1$. На трех плоскостях симметрии задано отсутствие диффузионных потоков.
В начальный момент времени предполагается, что область регенерации может быть заполнена активными клетками, т.е. заданы начальные значения глобального вектора концентрации в узлах конечно-элементной сетки. Для изучения влияния предварительного наличия клеток-предшественников в зоне регенерации (рис. 2б) рассмотрены несколько вариантов значений начальной концентрации согласно начальным условиям (1.3): ${{\psi }_{0}} = 0$, 0.1, 0.3, 0.5 в поровом пространстве имплантата 4; ${{\psi }_{0}} = 0.8$ в мягкой ткани 3, окружающей имплантат. Характерные зависимости распределения концентрации клеток вдоль координатных осей X и Y показаны на рис. 4. Графики демонстрируют плавное заполнение области имплантата клетками от краев к центру. Имеет место достаточно ясная картина повышения конечной концентрации клеток в объеме при увеличении начальных значений.
7. Результаты расчета и обсуждение. Результаты расчета регенерации костной ткани в объеме пористого имплантата при шаге по времени равном одному дню и общем времени расчета в 120 дней представлены на рис. 5–9. В качестве основной переменной, характеризующей процесс регенерации, рассматривается плотность ткани, возникающей в объеме имплантата, имеющей согласно табл. 1 диапазон изменения от 1021 до 1416 кг/м3. Успешное завершение процесса регенерации характеризует выход кривых плотности на значения близкие к максимальному 1416 кг/м3. Графики показывают зависимость физико-механических свойств кости от времени в нескольких представительных точках A, B, C исследуемой области (рис. 2) при вариации ключевых параметров построенной модели: пористости имплантата, амплитуды и частоты гармонической нагрузки, времени выхода статической нагрузки на максимальное значение 500 Н.
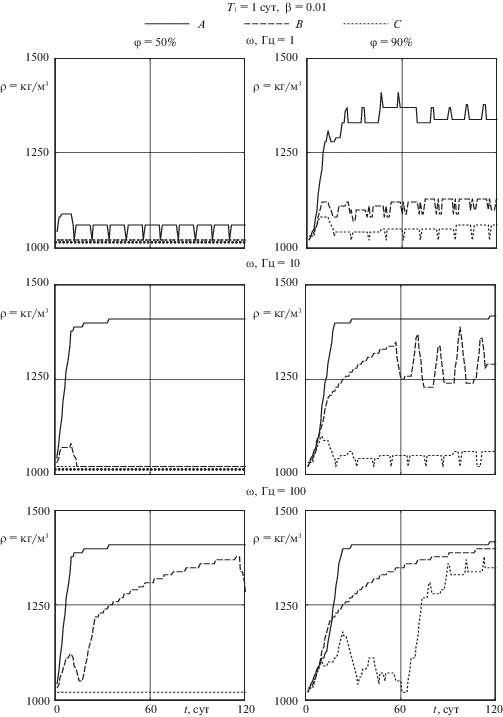
Ключевой биомедицинской задачей исследования является определение амплитуды и частоты вибрационной составляющей нагрузки, стимулирующей восстановление механических свойств ткани в объеме имплантата. Основная серия расчетов была проведена для начальных значений относительной концентрации остеогенных клеток-предшественников 0.3 и 0.8 в объеме имплантата и окружающей мягкой ткани соответственно. На рис. 5 показаны типичные графики изменения плотности образующейся ткани во времени в двух характерных случаях пористости имплантата 50% и 90% для динамической нагрузки амплитуды 50 Н с частотой 1, 10, 100 Гц. Частота порядка 1 Гц в публикациях [5, 6] трактуется как частота естественного хождения, в то время как высокочастотные колебания могут рассматриваться как вибро-стимулирующие воздействия [11, 12].
Временные зависимости (рис. 5) и распределение плотности образующейся ткани на заключительной итерации в порах имплантата (рис. 6) показывают, что процесс врастания проходит достаточно устойчиво. Несколько лучшие результаты имеют место в случаях имплантата большей пористости при вибрации с частотой 10 Гц и имплантата меньшей пористости при вибрации с частотой 100 Гц.
Однако необходимо отметить, что с медицинской точки зрения высокочастотные динамические нагрузки большой амплитуды вряд ли можно считать приемлемыми в качестве стимулирующего воздействия. Поэтому был рассмотрен вариант вибрационной составляющей нагрузки значительно меньшей амплитуды 5 Н.
Графики временных зависимостей (рис. 7) и поля распределения плотности (рис. 8) образующейся ткани демонстрируют возросшее влияние частоты приложенной гармонической нагрузки и пористости имплантата на сходимость результатов и, следовательно, на образование зрелой костной ткани. По сравнению с предыдущим случаем большой амплитуды колебаний в данном случае низкочастотное воздействие (1 Гц) не обеспечивает процесса восстановления костной ткани в имплантате. Нагрузка с частотой 10 Гц приводит к частичному врастанию ткани в некоторых областях имплантата. Повышение динамической составляющей приложенной силы до 100 Гц можно считать благоприятным фактором для остеоинтеграции кости в поровом пространстве скаффолда.
Варьирование начальных значений концентрации клеток в имплантате в диапазоне от 0 до 0.5 при фиксированных остальных параметрах модели не приводит к принципиальным изменениям в процессах регенерации, пространственно-временное распределение образующейся костной ткани качественно сохраняется. Меняется только глубина прорастания ткани в поры имплантата за установленное время расчета, соответствующая максимальному расстоянию, на которое могут продвинуться клетки-предшественники за данный период времени. Чем больше значения начальной концентрации в области регенерации, тем быстрее заполняется вся область активными клетками, участвующими в образовании ткани определенных фенотипов, тем глубже и быстрее движется фронт возникающей костной ткани при остальных благоприятных механобиологических условиях.
Существенной особенностью предыдущих исследований [7, 8, 11, 12] было постепенное увеличение приложенной нагрузки до своего максимального значения за первые 30–60 дней. Такое задание нагрузки обосновывалось тем, что если действующая сжимающая сила имеет слишком большое значение, то это приводит к значительным перемещениям и деформациям, при которых возможно образование только фиброзной ткани; тем самым процесс регенерации не реализуется. Таким образом, с математической точки зрения для обеспечения сходимости алгоритма имитационного моделирования сращения кости требуется постепенное приложение нагрузки. Однако в медицинской практике, как правило, врач осуществляет натяжение аппарата внешней фиксации сразу на максимальную величину, которую впоследствии старается поддерживать постоянной. Отмеченное несоответствие может быть предметом дальнейших исследований с целью обеспечения достоверного имитационного моделирования сращения кости.
Графики процесса регенерации ткани в объеме имплантата, имеющего заданную пористость 50 и 90%, при ${{Т}_{1}}$ = 1 для различных характерных частотах вибрационного воздействия с амплитудой 5 Н показаны на рис. 9. Видно, что в случае быстрого выхода нагрузки на свое максимальное значение численный алгоритм демонстрирует практически такую же стабильность, что и в случае плавного повышения нагрузки за первые 60 дней. К концу расчетного периода в 120 дней имеет место распределение плотности новой дифференцированной ткани соответствующее в целом плавному возрастанию силы. При этом процесс восстановления физико-механических свойств начинается раньше. Это соответствует ранее проведенным исследованиям на упрощенной полуаналитической модели регенерации ткани в объеме пористого скаффолда [32], согласно которым широкие пределы изменения ${{Т}_{1}}$ от 15 до 105 дней не повлияли на конечные значения механических характеристик ткани. В целом можно заключить, что имплантат пористостью 50–90% обеспечивает стабильность процесса остеоинтеграции.
По результатам проведенного параметрического анализа модели можно сделать также следующие выводы. Имеет место зависимость процесса восстановления свойств ткани от пористости имплантата: для более жесткого имплантата (с меньшей пористостью) для успешного восстановления требуется нагрузка большей частоты, чем для менее жесткого имплантата с большей пористостью. На рисунках не показано, но из расчета следует, что чисто статическая нагрузка, не способная генерировать вынужденные потоки внутритканевой жидкости в системе поровых каналов, не приводит к образованию костной ткани.
В отличие от ранее рассмотренных моделей регенерации костной мозоли без имплантата [11, 12], полученные кривые (рис. 5 и 7) показывают, что процесс восстановления ткани начинается не сразу, а спустя некоторое время в зависимости от времени выхода нагрузки на максимальное значение и пористости имплантата. Это связано с тем, что для начала процесса необходим определенный уровень напряженно-деформированного состояния ткани, который при малых значениях нагрузки не возникает. При этом, поскольку более жесткий имплантат воспринимает больше нагрузки, чем мягкий, то в этом случае для обеспечения необходимого по критерию уровня деформаций ткани и потоков жидкости требуется повышенное силовое воздействие, которое по расчетной схеме будет достигнуто позже. Полученный результат качественно совпадает с известными данными [13].
Конечно-элементный анализ также подтвердил, что в целом уравнение диффузии может быть применено для описания движения клеток и замыкания алгоритма регенерации ткани. Его главное достоинство – простота и наличие только одного независимого числового параметра. С другой стороны известны более сложные модели, описывающие процессы миграции, дифференциации, пролиферации и апоптоза клеток различных фенотипов [8, 9]. Их применение к исследованию регенерации ткани в объемных пористых скаффолдах, используемых в тканевой инженерии, представляется более перспективным при условии достоверного определения большого количества материальных констант, входящих в соответствующие дифференциальные уравнения.
Заключение. Представлено развитие математической модели изменяющейся пороупругой среды, описывающей процесс регенерации костной ткани под действием внешнего механического стимула периодического характера. Разработаны концепция и основные компоненты алгоритма компьютерного моделирования репаративной регенерации костной ткани, управляемой законом дифференциации клеток и действием внешней механической нагрузки периодического характера, с учетом особенностей реконструкции кости с помощью биосовместимых пористых имплантатов, или скаффолдов с регулярной или топологически произвольной внутренней структурой.
Разработана методика расчета эффективных модулей гетерогенных сред, описывающих систему “кость–имплантат”, позволяющая определять пороупругие характеристики модели регенерации костной ткани длинных трубчатых костей опорно-двигательного аппарата человека в условиях остеосинтеза пористыми имплантатами.
Математическая модель восстановления костной ткани в объеме пористого имплантата реализована в численном виде с помощью метода конечных элементов модели; проведен параметрический анализ регенерации ткани под действием внешней стимулирующей нагрузки, изменяющейся по гармоническому закону; получены теоретические закономерности между характеристиками регенерации и параметрами внешнего воздействия.
Компьютерная модель дает возможность исследовать процессы восстановления костных элементов человека, замещенных искусственными пористыми материалами, при наличии динамической нагрузки и теоретически обосновать выбор оптимального стимулирующего остеоинтеграцию воздействия на поврежденные ткани.
В частности, построенная модель позволила исследовать влияние частоты вибрационной составляющей нагрузки на процесс перестройки ткани, что слабо отражено в известных источниках, а также влияние раннего нагружения на восстановление механических свойств кости. Полученные численные результаты представляются достаточно реалистичными и соответствующими известным медицинским исследованиям процессов регенерации костной ткани.
Несомненно, полученные результаты нуждаются как в экспериментальной, так и теоретической проверке с помощью более точных моделей. Однако качественное сравнение с данными, приведенными в известных международных журналах подтверждает сопоставимость результатов, полученных с помощью разработанных моделей и признанных в зарубежной механобиологии методов.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 15-29-04825 и базовой части государственного задания Минобрнауки РФ образовательным организациям высшего образования в рамках научного проекта № 2.7557.2017/8.9.
Список литературы
Pauwels F. Grundriess einer Biomechanik der Frakturheilung // 34th Kongress der Deutschen Orthopadischen Gesellschaft. Stuttgart: Ferdinand Enke Verlag, 1941. P. 62–108.
Carter D.R. Mechanical loading history and skeletal biology // J. Biomech. 1987. V. 20. P. 1095–1109.
Carter D.R., Beaupre G.S., Giori N.J. et al. Mechanobiology of skeletal regeneration // Clin. Orthop. Relat. Res. 1998. V. 355. № 10 (suppl.) P. 41–55.
Giori N.J., Ryd L., Carter D.R. Mechanical influence on tissue differentiation at bone-cement interfaces // J. Arthropl. 1995. V. 10. P. 514–522.
Huiskes R., van Driel W.D., Prendergast P.J., et al. A biomechanical model for periprosthetic fibrous-tissue differentiation // J. Mat. Sci.: Materials in Medicine. 1997. V. 8. P. 785–788.
Prendergast P.J., Huiskes R., Soballe K. Biophysical stimuli on cells during tissue differentiation at implant interfaces // J. Biomech. 1997. V. 30. № 6. P. 539–548.
Lacroix D., Prendergast P.J. A mechano-regulation model for tissue differentiation during fracture healing: analysis of gap size and loading // J. Biomech. 2002. V. 35. № 8. P. 1163–1171.
Isaksson H., van Donkelaar C.C., Huiskes R. et al. A mechano-regulatory bone-healing model incorporating cell-phenotype specific activity // J. Theor. Biol. 2008. V. 252. P. 230–246.
Кирпичев И.В., Коровин Д.И., Маслов Л.Б. и др. Математическая модель клеточных преобразований при регенерации костной ткани в условиях изменяющейся биохимической среды с возможной механорегуляцией // Рос. журн. биомех. 2016. Т. 20. № 3. С. 220–235.
Goodship A.E., Lawes T.J., Rubin C.T. Low-magnitude high-frequency mechanical signals accelerate and augment endochondral bone repair: Preliminary evidence of efficacy // J. Orthop. Res. 2009. V. 27. № 7. P. 922–930.
Маслов Л.Б. Математическая модель структурной перестройки костной ткани // Рос. журн. биомех. 2013. Т. 17. № 2. С. 39–63.
Маслов Л.Б. Математическое моделирование восстановления механических свойств костной мозоли // ПММ. 2015. Т. 79. № 2. С. 286–303.
Byrne D.P., Lacroix D., Planell J.A., et al. Simulation of tissue differentiation in a scaffold as a function of porosity, Young’s modulus and dissolution rate: application of mechanobiological models in tissue engineering // Biomaterials. 2007. V. 28. P. 5544–5554.
Lacroix D., Planell J.A., Prendergast P.J. Computer-aided design and finite-element modelling of biomaterial scaffolds for bone tissue engineering // Phil. Trans. R. Soc. A. 2009. V. 367. P. 1993–2009.
Mukherjee K., Gupta S. The effects of cellular activities on acetabular cup fixation: a parametric study using three-dimensional finite element analysis // The Bone & Joint J. 2016. V. 98-B. № 8 (suppl.). P. 12–22.
Mukherjee K., Gupta S. Bone ingrowth around porous-coated acetabular implant: a three-dimensional finite element study using mechanoregulatory algorithm // Biomech. Model. Mechanobiol. 2016. V. 15. № 2. P. 389–403.
Mukherjee K., Gupta S. Mechanobiological simulations of peri-acetabular bone ingrowth: a comparative analysis of cell-phenotype specific and phenomenological algorithms // Med. Biol. Eng. Comput. 2017. V. 55. № 3. P. 449–465.
Штейн А.А. О континуальных моделях растущего материала // Мех. композит. мат. 1979. № 6. С. 1105–1110.
Регирер С.А., Штейн А.А. Методы механики сплошной среды в применении к задачам роста и развития биологических тканей // Совр. пробл. биомех. 1985. Вып. 2. С. 5–37.
Yavari A. A geometric theory of growth mechanics // J. Nonlin. Sci. 2010. V. 20. № 12. P. 781–830.
Ciarletta P., Destrade M., Gower A.L. et al. Morphology of residually stressed tubular tissues: Beyond the elastic multiplicative decomposition // J. Mech. Phys. Solids. 2016. V. 90. № 5. P. 242–253.
Ambrosi D., Pezzuto S., Riccobelli D. et al. Solid tumors are poroelastic solids with a chemo-mechanical feedback on growth // J. Elast. 2017. V. 129. № 1–2. P. 107–124.
Ciarletta P., Destrade M., Gower A.L. On residual stresses and homeostasis: an elastic theory of functional adaptation in living matter // Sci. Rep. 2016. V. 6. Article № 24390.
Biot M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid, part I: low frequency range // J. Acoust. Soc. Am. 1956. V. 28. № 2. P. 168–178.
Маслов Л.Б. Исследование вибрационных характеристик пороупругих механических систем // Изв. РАН. МТТ. 2012. № 2. С. 78–92.
Маслов Л.Б. Конечно-элементные пороупругие модели в биомеханике. Санкт-Петербург: Лань, 2013. 240 с.
Dormieux L., Kondo D., Ulm F.-J. Microporomechanics. N.Y.: Wiley, 2006. 328 p.
Coussy O. Poromechanics. N.Y.: Wiley, 2004. 315 p.
Устинов К.Б. Об определении эффективных упругих характеристик двухфазных сред. Случай изолированных однородностей в форме эллипсоидов вращения // Успехи механики. 2003. № 2. С. 126–168.
Арсеньев Д.Г., Зинковский А.В., Маслов Л.Б. Эффективные упругие характеристики анизотропной модели пористого биологического материала, насыщенного жидкостью // Науч.-техн. ведомости СПбГПУ. 2008. № 3 (59). С. 230–236.
Sevostianov I., Yilmaz N., Kushch V. et al. Effective elastic properties of matrix composites with transversely-isotropic phases // Int. J. Sol. Struct. 2005. V. 42. № 2. P. 455–476.
Маслов Л.Б. Математическая модель регенерации костной ткани в пористом имплантате // Мех. композ. мат. 2017. Т. 53. № 3. С. 567–590.
Программа конечно-элементного расчета физико-механических характеристик костной ткани при реконструкции пористыми имплантатами: прогр. ЭВМ 2017612467 Рос. Федерация / Маслов Л.Б.; заявитель и правообладатель Маслов Л.Б. № 2016664806; заяв. 30.12.16; зарег. в Реестре программ для ЭВМ 22.02.17.
Rapacz-Kmita A., Ślósarczyk A., Paszkiewiczet Z. Mechanical properties of HAp–ZrO2 composites // J. Eur. Ceram. Soc. 2006. V. 26. P. 1481–1488.
Аксельруд В.А., Лысянский В.М. Экстрагирование (система твердое тело–жидкость). Ленинград: Химия, 1974. 256 с.
Frost H.M. The biology of fracture healing. An overview for clinicians. Part I // Clin. Orthop. Relat. Res. 1989. V. 248. № 11. P. 283–293.
Lacroix D., Prendergast P.J., Li G. et al. Biomechanical model to simulate tissue differentiation and bone regeneration: application to fracture healing // Med. Biol. Eng. Comput. 2002. V. 40. P. 14–21.
Geris L., Gerisch A., Sloten J.V. et al. Angiogenesis in bone fracture healing: A bioregulatory model // J. Theor. Biol. 2008. V. 251. № 1. P. 137–158.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика