Прикладная математика и механика, 2019, T. 83, № 5-6, стр. 691-703

Существование стационарных режимов вращения (регулярных прецессий) динамически симметричного спутника-твердого тела на круговой орбите установлено около 60-ти лет назад в работах [1, 2]. Эти работы затем были продолжены в статьях [3–7]. Имеется история исследования стационарных вращений [8–10]. Для движений, отвечающих стационарным вращениям, ось симметрии спутника занимает фиксированное положение в орбитальной системе координат (ОСК), а сам спутник вращается вокруг оси симметрии с постоянной угловой скоростью. Показано, что существует три типа стационарных вращений: для одного из них ось симметрии перпендикулярна плоскости орбиты (цилиндрическая прецессия), для второго типа она лежит в плоскости, перпендикулярной радиус-вектору центра масс (гиперболоидальная прецессия), а для третьего типа ось симметрии спутника находится в плоскости, перпендикулярной вектору скорости центра масс (коническая прецессия). Все три типа прецессий, очевидно, неустойчивы по отношению к возмущениям угла собственного вращения.

В статье изучается устойчивость по отношению к возмущениям положения оси симметрии в орбитальной системе координат и скоростям изменения этих возмущений. Причем исследование ограничивается только задачей об устойчивости цилиндрической прецессии. При помощи методов Ляпунова и КАМ-теории [11–13] эта задача рассмотрена довольно подробно в целом ряде работ [1–7, 14–18]. Но строгое и полное решение задачи для всех физически допустимых значений параметров до сих пор не получено. Ниже излагаются результаты исследования, дополняющие упомянутые работы [1–7, 14–18] и вместе с ними дающие ответ на вопрос об устойчивости цилиндрической прецессии для всех значений параметров. Кроме того, иногда даются уточнения опубликованных численных результатов, а в некоторых случаях приводятся более простые доказательства сделанных ранее выводов об устойчивости и неустойчивости.

1. Введение. Рассмотрим движение спутника в центральном ньютоновском гравитационном поле. Линейные размеры спутника предполагаем малыми по сравнению с размерами орбиты. Поэтому влиянием вращения спутника относительно его центра масс $O$ на орбиту самого центра масс можно пренебречь [8]. Спутник будем считать твердым телом, центральный эллипсоид которого является эллипсоидом вращения, орбиту центра масс предполагаем круговой.

Пусть $OXYZ$ – орбитальная система координат (ОСК), ось $OZ$ которой направлена вдоль радиус-вектора центра масс спутника, $OX$ – по трансверсали, а $OY$ – по нормали к плоскости орбиты. Система координат $Oxyz$ образована главными центральными осями инерции спутника (ось $Oz$ направлена вдоль его оси динамической симметрии). Положение связанной системы координат относительно ОСК задается при помощи углов Эйлера $\theta ,\;\psi ,\;\varphi $ ($\theta $ – угол нутации, $\psi $ – угол прецессии, $\varphi $ – угол собственного вращения).

Проекция $r$ абсолютной угловой скорости спутника на его ось симметрии постоянна во все время движения $(r = {{r}_{0}} = {\text{const)}}$. Это позволяет [8–10] свести систему дифференциальных уравнений шестого порядка вращательного движения спутника относительно центра масс к системе четвертого порядка, описывающей движение оси симметрии $Oz$ спутника относительно ОСК $OXYZ$. Обобщенными координатами при этом будут углы $\theta $ и $\psi $, соответствующие им канонически сопряженные импульсы обозначим через ${{p}_{\theta }}$ и ${{p}_{\psi }}$. За независимую переменную примем безразмерную величину $\nu = {{\omega }_{0}}t$, где $t$ – время, а ${{\omega }_{0}}{\text{ }}$ – угловая скорость в круговом движении центра масс спутника.

Цилиндрической прецессии спутника отвечает [8–10] частное решение уравнений движения, в котором $\theta = \pi {\text{/}}2$, $\psi = \pi $, ${{p}_{\theta }} = {{p}_{\psi }} = 0$. Для этого решения ось симметрии спутника перпендикулярна плоскости орбиты, а спутник вращается вокруг оси симметрии с постоянной угловой скоростью $d\varphi {\text{/}}dt$, равной ${{r}_{0}} - {{\omega }_{0}}{\text{ }}$.

Для исследования устойчивости введем возмущения ${{q}_{i}},{{p}_{i}}$ ${\text{(}}i = {\text{1,2)}}$, положив

Функция Гамильтона возмущенного движения имеет вид [10]

Здесь через $\alpha $ и $\beta $ обозначены безразмерные параметры задачи:

Соответствующие функции (1.1) уравнения движения допускают обобщенный интеграл энергии $H = h = {\text{const}}$. На невозмущенном движении $h = - \alpha \beta {\text{ }}$.

Функция Гамильтона (1.1) представима в виде сходящегося ряда

Несущественная аддитивная постоянная $ - \alpha \beta $ здесь отброшена, а ${{H}_{{2k}}}$ – формы степени $2k$ относительно ${{q}_{1}}$, ${{q}_{2}}$, ${{p}_{1}}$, ${{p}_{2}}$. Далее разложение (1.3) потребуется с точностью до форм восьмой степени включительно. Здесь для краткости приведем только выражения для форм второй и четвертой степеней:

Введем обозначения

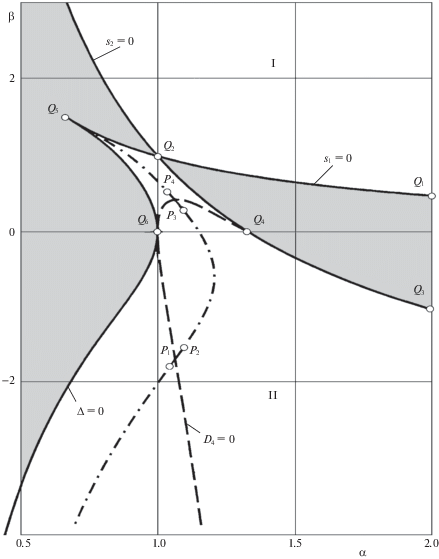
В плоскости параметров $\alpha ,\beta $ существует (см. рис. 1) две области I и II устойчивости в первом приближении, которые задаются соответственно неравенствами ${{s}_{1}} > 0$, ${{s}_{2}} > 0$ и ${{s}_{1}} < 0$, ${{s}_{2}} < 0$, $\Delta > {\text{0}}$ [1–7].

Граница области I состоит из участков гипербол: один участок (${{s}_{1}} = 0$) соединяет точки ${{Q}_{1}}{\text{(2,1/2)}}$ и ${{Q}_{2}}{\text{(1,1)}}$, а другой (${{s}_{2}} = 0$), начавшись в точке ${{Q}_{2}}{\text{(1,1)}}$, идет при возрастании $\beta $ влево и вверх, приближаясь к асимптоте $\alpha = 0$.

Граница области II образована тремя участками. Один является частью гиперболы ${{s}_{2}} = 0$ и соединяет точки ${{Q}_{3}}(2, - 1)$ и ${{Q}_{2}}{\text{(1,1)}}$, этот участок пересекает ось $\beta = 0$ в точке ${{Q}_{4}}{\text{(4/3,0)}}$. Другой участок является частью гиперболы ${{s}_{1}} = 0$, он соединяет точки ${{Q}_{2}}{\text{(1,1)}}$ и ${{Q}_{5}}{\text{(2/3,3/2)}}$. Третий участок границы области II задается уравнением $\Delta = 0$, он начинается в точке ${{Q}_{5}}{\text{(2/3,3/2)}}$ и при уменьшении $\beta $ проходит через точку ${{Q}_{{\text{6}}}}{\text{(1,0)}}$ оси $\beta = 0$, а далее при $\beta \to - {\text{ }}\infty $ приближается к вертикальной асимптоте $\alpha = 0$.

Если параметры $\alpha $, $\beta $ не лежат внутри областей I и II или на их границах, то цилиндрическая прецессия неустойчива, так как [11] характеристическое уравнение линеаризованных уравнений возмущенного движения (им отвечает квадратичная часть (1.4) функции Гамильтона (1.3)) имеет хотя бы один корень с положительной вещественной частью. На рис. 1 области неустойчивости закрашены серым цветом.

Внутри областей I и II и на их границах частоты ${{\omega }_{1}}$ и ${{\omega }_{2}}$ (${{\omega }_{1}} \geqslant {{\omega }_{2}} \geqslant 0$) малых колебаний оси симметрии спутника определяются уравнением

На границах областей I и II либо ${{\omega }_{1}} = {{\omega }_{2}}$ (участок $\Delta = 0$ границы области II), либо меньшая из частот ${{\omega }_{2}}$ обращается в нуль, либо сразу обе частоты ${{\omega }_{1}}$ и ${{\omega }_{2}}$ равны нулю; последнее реализуется в точке ${{Q}_{5}}(2{\text{/}}3,{\text{ }}3{\text{/}}2)$ пересечения кривых ${{s}_{1}} = 0$ и $\Delta = 0$. Во всех граничных точках цилиндрическая прецессия спутника неустойчива в первом (линейном) приближении [10, 16].

2. Результаты нелинейного анализа устойчивости в области I и на ее границах. Из проведенного ранее нелинейного анализа следует, что внутри области I и во всех точках ее границы цилиндрическая прецессия устойчива. Для точек, лежащих внутри области I, это впервые показано [5] при помощи второго метода Ляпунова. Устойчивость на границах области I была показана в статье [16] при помощи методов КАМ-теории. Ниже дается иной способ доказательства устойчивости, который применим как для внутренних точек области I, так и для ее граничных точек. Доказательство опирается только на теорему Ляпунова об устойчивости движения [11].

Запишем функцию Гамильтона (1.1) в лагранжевых переменных ${{q}_{i}}$, ${{\dot {q}}_{i}}$ $(i = 1,2)$ (точкой обозначается производная по независимой переменной $\nu $).

Проделав хорошо известные выкладки [19], получим следующее выражение для обобщенного интеграла энергии (интеграла Якоби):

где

При получении выражения (2.1) для удобства записи к функции $H$ добавлена несущественная аддитивная постоянная $\alpha \beta $.

Из интеграла (2.1) и теоремы Ляпунова следует, что если функция (2.2) будет определенно-положительной в окрестности точки ${{q}_{1}} = {{q}_{2}} = 0$, то имеет место устойчивость. Разложение функции (2.2) в ряд имеет вид

где многоточием обозначена совокупность членов выше третьей степени относительно ${{q}_{1}}$, ${{q}_{2}}$. Из выражения (2.3) видно, что при выполнении неравенств ${{s}_{1}} > 0$, ${{s}_{{\text{2}}}} > 0$ функция $W$ будет определенно-положительной. Поэтому, как и следовало ожидать [5], внутри области I цилиндрическая прецессия устойчива.

На участке ${{s}_{1}} = 0$ границы области I (т.е. когда $\beta = 1{\text{/}}\alpha $, $\alpha \geqslant 1$) функция (2.2), очевидно, определенно-положительна. А на участке ${{s}_{2}} = 0$ (когда $\beta = 4{\text{/}}\alpha - 3$, $\alpha \leqslant 1$) эту функцию можно преобразовать к виду

откуда следует, что при $\alpha \leqslant 1$ функция ${\text{ }}W$ является определенно-положительной. Таким образом, в согласии с известным результатом [16], показано, что на границе области I цилиндрическая прецессия устойчива.

3. Об устойчивости на границе области II. Сначала рассмотрим левую границу $\Delta = 0$ области II, а затем – ее правую границу, состоящую из участков ${{Q}_{3}}{{Q}_{{\text{2}}}}$ и ${{Q}_{2}}{{Q}_{{\text{5}}}}$.

3.1. Случай $\Delta = 0$. Здесь $ - \infty < \beta \leqslant 3{\text{/}}2$, ${\text{ }}{{\omega }_{{\text{1}}}} = {{\omega }_{{\text{2}}}} = \omega $, причем ω – монотонно убывающая функция β ${\text{(}}0 \leqslant \omega < 2.147709)$. Ранее показано [16], что на интервалах ($ - \infty < \beta $ < < 0) и ($0 < \beta < {\text{3/2}}$), на которые точка ${{Q}_{{\text{6}}}}{\text{(1,0)}}$ разбивает кривую $\Delta = 0$, цилиндрическая прецессия устойчива.

О неустойчивости в точке ${{Q}_{{\text{6}}}}{\text{(1,0)}}$. При $\beta = 0$ цилиндрическая прецессия представляет собой поступательное движение спутника в абсолютном пространстве, когда его ось симметрии $Oz$ перпендикулярна плоскости орбиты. В точке ${{Q}_{{\text{6}}}}{\text{(1,0)}}$ это движение, очевидно, неустойчиво [16] (следствие того, что при $\alpha = 1$ центральный эллипсоид инерции спутника – сфера и гравитационный момент обращается в нуль). Поэтому при $\alpha = 1$, $\beta = 0$ возмущенное движение спутника представляет собой его равномерное вращение вокруг неизменного направления вектора угловой скорости спутника в абсолютном пространстве. При таком движении ось $Oz$ с течением времени может отклониться на конечный угол от направления нормали к плоскости орбиты, как бы ни была мала величина угловой скорости возмущенного движения спутника.

О неустойчивости в точке ${{Q}_{{\text{5}}}}{\text{(2/3,3/2)}}$. В этой точке обе частоты малых колебаний спутника обращаются в нуль ${\text{(}}{{\omega }_{1}} = {{\omega }_{2}} = 0)$. При помощи теоремы Четаева о неустойчивости показано [16], что в точке ${{Q}_{{\text{5}}}}{\text{(2/3,3/2)}}$ цилиндрическая прецессия неустойчива. Ниже приводится доказательство неустойчивости, менее громоздкое, предложенного ранее [16].

Сделаем в функции Гамильтона возмущенного движения (1.3) каноническое унивалентное преобразование ${{q}_{1}},{{q}_{2}},{{p}_{1}},{{p}_{2}} \to {{x}_{1}},{{x}_{2}},{{y}_{1}},{{y}_{2}}$, приводящее эту функцию к ее простейшей (нормальной) форме до членов четвертой степени включительно. Вычисления показывают, что эту замену можно представить в виде последовательности двух канонических преобразований. Первое преобразование ${{q}_{1}},{{q}_{2}},{{p}_{1}},{{p}_{2}} \to {{\xi }_{1}},{{\xi }_{2}},{{\eta }_{1}},{{\eta }_{2}}$ – линейное и задается [10] равенствами

а вторая замена ${{\xi }_{1}},{{\xi }_{2}},{{\eta }_{1}},{{\eta }_{2}} \to {{x}_{1}},{{x}_{2}},{{y}_{1}},{{y}_{2}}$ – нелинейная, близкая к тождественной. Она задается неявно при помощи соотношений где ${{S}_{4}}$ – форма четвертой степени относительно ${{\xi }_{1}},\;{{\xi }_{2}},\;{{y}_{1}}$, ${{y}_{2}}$:

В новых переменных ${{x}_{1}},\;{{x}_{2}},\;{{y}_{1}}$, ${{y}_{2}}$ функция Гамильтона (1.3) принимает вид

где многоточием обозначена совокупность членов выше пятой степени относительно ${{x}_{1}},\;{{x}_{2}},\;{{y}_{1}}$, ${{y}_{2}}$.

Укороченная система, определяемая только первыми тремя слагаемыми в нормальной форме (3.1), допускает [16] частное, неограниченно возрастающее решение:

Для доказательства неустойчивости возьмем функцию Четаева в виде

где а за область $V > 0$ примем область, в которой ${{y}_{2}} > 0$, а

Для производной функции $V$ в силу уравнений движения с полной (неукороченной) функцией Гамильтона (3.1) получаем в области (3.2) такое выражение:

где $P(u)$ – многочлен шестой степени относительно $u$ вида

Легко проверить, что в области $V > 0$ этот многочлен положителен, а его минимальное значение равно 46.69931 (достигается при b = ±0.819997). Поэтому функция (3.3) определенно-положительна в области $V > 0$. Неустойчивость доказана.

3.2. Об устойчивости на правой границе области II. Сначала рассмотрим участки ${{Q}_{3}}{{Q}_{4}}$, ${{Q}_{4}}{{Q}_{{\text{2}}}}$ и ${{Q}_{2}}{{Q}_{{\text{5}}}}$ правой границы, а затем отдельно рассмотрим точку ${{Q}_{4}}{\text{(4/3,0)}}$.

Об устойчивости на участках ${{Q}_{3}}{{Q}_{4}}$, ${{Q}_{4}}{{Q}_{{\text{2}}}}$ и ${{Q}_{2}}{{Q}_{{\text{5}}}}$. Здесь ${{\omega }_{2}} = 0$, а ${{\omega }_{1}} = \sqrt {9{{\alpha }^{2}} - 15\alpha + 7} $ на участках ${{Q}_{3}}{{Q}_{4}}$ и ${{Q}_{4}}{{Q}_{{\text{2}}}}$ и ${{\omega }_{1}} = \sqrt {3\alpha - 2} $ на участке ${{Q}_{2}}{{Q}_{{\text{5}}}}$. При помощи канонической замены переменных ${{q}_{i}}$, ${{p}_{i}} \to {{u}_{i}}$, $v{}_{i}$ $(i = 1,2)$ функция Гамильтона (1.3) приводится к нормальной форме вида

где ${{O}_{{m + 2}}}$ – совокупность членов не ниже $(m + 2)$-й степени относительно ${{u}_{1}}$, ${{u}_{2}}$, ${{v}_{1}}$, ${{v}_{2}}$, величина $\delta = \pm 1$, ее конкретное значение определяется в процессе линейной нормализации квадратичной части (1.4) функции Гамильтона [10]. Нелинейная нормализация проводится до такой степени $m$, чтобы коэффициент ${{a}_{{m,0}}}$ нормальной формы (3.4) был отличен от нуля. Согласно известному результату [20], при $\delta {{a}_{{m,0}}} > 0$ имеет место устойчивость, а при $\delta {{a}_{{m,0}}} < 0$ – неустойчивость.

Вычисления показали [10, 16], что на всех трех рассматриваемых участках правой границы величина δ равна –1. Для величины же ${{a}_{{4,0}}}$ на участках ${{Q}_{3}}{{Q}_{4}}$, ${{Q}_{4}}{{Q}_{{\text{2}}}}$ и ${{Q}_{2}}{{Q}_{{\text{5}}}}$ можно получить [16] соответственно такие выражения:

Поэтому на участке ${{Q}_{3}}{{Q}_{4}}$ цилиндрическая прецессия устойчива, а на участках ${{Q}_{4}}{{Q}_{{\text{2}}}}$ и ${{Q}_{2}}{{Q}_{{\text{5}}}}$ неустойчива [16].

Анализ устойчивости в точке ${{Q}_{4}}(4{\text{/}}3,0)$. После линейной канонической замены переменных

и последующего нелинейного канонического преобразования ${{\xi }_{i}}$, ${{\eta }_{i}} \to {{u}_{i}}$, $v{}_{i}$ $(i = 1,2)$, нормализующего члены четвертой степени в функции Гамильтона, получим функцию (3.4) в следующем виде:

Так как ${{a}_{{4,0}}} = 0$, то вопрос об устойчивости не решается рассмотрением членов до четвертой степени включительно в разложении (1.3). Требуется, вообще говоря, нормализация членов более высоких степеней. Но в рассматриваемой конкретной задаче можно без этого обойтись. Дело в том, что при $\alpha = 4{\text{/}}3$, $\beta = {\text{0}}$ положение равновесия $\theta = \pi {\text{/}}2$, $\psi = \pi $, отвечающее цилиндрической прецессии, не является изолированным, так как при указанных параметрах существует семейство положений равновесия $\theta = {{\theta }_{0}} = {\text{const}}$, $\psi = \pi $, где ${{\theta }_{0}}$ – любое значение угла нутации из интервала $(0,{\text{ }}\pi )$; эти равновесия отвечают конической прецессии спутника. Было показано [18], что в таких ситуациях реализуется трансцендентный случай в задаче об устойчивости: коэффициент ${{a}_{{m,0}}}$ в нормальной форме (3.4) равен нулю для любого значения $m$. Там же показано, что в трансцендентном случае имеет место неустойчивость.

Таким образом, в точке ${{Q}_{4}}(4{\text{/}}3,0)$ цилиндрическая прецессия спутника неустойчива.

4. Исследование устойчивости для значений параметров, лежащих внутри области II. В области II функция Гамильтона (1.3) знакопеременна. Исследование устойчивости цилиндрической прецессии для значений параметров $\alpha ,\;\beta $ из этой области проводилось ранее [14, 15, 17]. Это исследование требует громоздких вычислений и проведено не полностью. Осталась, например, нерассмотренной часть области II, в которой $\beta < - 20$. Ниже кратко излагаются результаты анализа устойчивости во всей области II. Анализ опирается на результаты по устойчивости автономных гамильтоновых систем с двумя степенями свободы [12, 13, 17] и на алгоритмы компьютерных символьных вычислений.

Если нет резонанса до порядка $2m$ включительно (т.е. ${{k}_{1}}{{\omega }_{1}} \ne {{k}_{2}}{{\omega }_{2}}$ для натуральных ${{k}_{1}}$ и ${{k}_{2}}$, удовлетворяющих неравенству $0 < {{k}_{1}} + {{k}_{2}} \leqslant 2m$), то при помощи преобразования Биркгофа $q{}_{i}$, ${{p}_{i}} \to q_{i}^{'}$, $p_{i}^{'}$ функция Гамильтона (1.3) приводится к нормальной форме вида

Если величина

отлична от нуля, то начало координат ${{q}_{i}} = {{p}_{i}} = {\text{0}}$ ${\text{(}}i = {\text{1,2)}}$ устойчиво [12, 13].

Если же реализуется резонанс порядка $2m$, то к функции (4.1) добавляются резонансные слагаемые $r_{1}^{{{{k}_{1}}/2}}r_{2}^{{{{k}_{2}}/2}}({{a}_{{{{k}_{1}}{{k}_{2}}}}}\sin \varphi $ + ${{b}_{{{{k}_{1}}{{k}_{2}}}}}\cos \varphi )$, где $\varphi = {{k}_{1}}{{\varphi }_{1}} + {{k}_{2}}{{\varphi }_{2}}$. Положим

Начало координат будет устойчивым, если величина (4.3) положительна, и неустойчивым, если она отрицательна [13]. Если же ${\text{ }}{{f}_{{{{k}_{1}}{{k}_{2}}}}} = 0$, то надо вычислять нормальную форму функции Гамильтона до членов, степень которых относительно $q_{i}^{'}$, $p_{i}^{'}$ превосходит $2m$. Например, при резонансе четвертого порядка ${{\omega }_{1}} = 3{{\omega }_{2}}$ функция Гамильтона, нормализованная до членов шестой степени включительно, имеет вид

И для исследования устойчивости в случае ${\text{ }}{{f}_{{{\text{13}}}}} = {\text{ 0}}$, следует [17] вычислить величину $e$ по формуле

При $e > 0$ имеет место устойчивость, а при $e < 0$ – неустойчивость.

О кривых ${{D}_{4}} = 0$ и ${{\omega }_{1}} = 3{{\omega }_{2}}$. Отсутствие форм нечетных степеней в разложении (1.3) функции Гамильтона возмущенного движения сильно упрощает вычисления, необходимые для получения ее нормальной формы. Например, наличие резонанса третьего порядка ${{\omega }_{1}} = 2{{\omega }_{2}}$ не влияет на структуру нормальной формы (4.1) при $m = 2$. Вычисления показывают, что для величины (4.2) при $m = 2$ справедливо выражение

Кривая ${{D}_{4}} = 0$ изображена на рис. 1 штриховой линией. В области положительных значений $\beta $ кривая соединяет точки ${{Q}_{{\text{6}}}}{\text{(1,0)}}$ и ${{Q}_{4}}(4{\text{/}}3,0)$ и имеет экстремум в точке (1.073499, 0.426688). При малых значениях ${\text{|}}\beta {\text{|}}$ в окрестности точки ${{Q}_{{\text{6}}}}{\text{(1,0)}}$ кривая ${{D}_{4}} = 0$ представима рядом вида

а вблизи точки ${{Q}_{4}}(4{\text{/}}3,0)$ – рядом

При $\beta \to - \infty $ кривая ${{D}_{4}} = 0$ имеет вертикальную асимптоту $\alpha = 5{\text{/}}3$, причем

Кривая ${{\omega }_{1}} = 3{{\omega }_{2}}$ резонанса четвертого порядка показана на рис. 1 штрихпунктирной линией и задается уравнением

Его можно представить в параметрической форме

где $0 \leqslant \tau < {{\tau }_{*}}$, а ${{\tau }_{*}}$ = 2.166504 – корень уравнения $9{{\tau }^{8}} - 136{{\tau }^{4}} - 300{{\tau }^{2}} + 36 = 0$.

Кривая ${{\omega }_{1}} = 3{{\omega }_{2}}$ начинается в точке ${{Q}_{5}}(2{\text{/}}3,{\text{ }}3{\text{/}}2)$, ось $\beta = 0$ она пересекает при α = = $(20\sqrt {13} - 41){\text{/}}27$ = 1.152260, в точке (1.207392, –0.587632) имеет вертикальную касательную, а при $\beta \to - \infty $ кривая стремится к асимптоте $\alpha = 0$:

Используя хорошо известные алгоритмы теории многочленов [21], можно показать, что в области II кривые ${{D}_{4}} = 0$ и ${{\omega }_{1}} = 3{{\omega }_{2}}$ пересекаются только в двух точках: (1.062223, 0.424015) и (1.064888, –1.677124) (см. рис. 1).

Согласно сформулированным в начале раздела условиям устойчивости и неустойчивости, можно утверждать, что если параметры $\alpha $, $\beta $ не лежат на кривой резонанса четвертого порядка ${{\omega }_{1}} = 3{{\omega }_{2}}$ и на кривой ${{D}_{4}} = 0$, то цилиндрическая прецессия устойчива [14, 15, 17]. Устойчивость при значениях параметров, лежащих на этих кривых, требует отдельного рассмотрения.

Об устойчивости при резонансе ${{\omega }_{1}} = 3{{\omega }_{2}}$. Используя параметрическое представление (4.8) кривой ${{\omega }_{1}} = 3{{\omega }_{2}}$, можно показать, что равенство ${\text{ }}{{f}_{{{\text{13}}}}} = {\text{0}}$ для функции ${\text{ }}{{f}_{{{{k}_{{\text{1}}}}{{k}_{2}}}}}$ из (4.3) приводится к уравнению $F(\tau ) = {\text{0}}$, где $F(\tau ) = G{\text{(}}\tau {\text{)}}G( - \tau {\text{)}}$, а $G{\text{(}}\tau {\text{)}}$ – многочлен двадцатой степени относительно τ с целочисленными коэффициентами:

Анализ показывает, что на допустимом интервале $0 < \tau < {{\tau }_{*}}$ изменения параметра ${\text{ }}\tau $ существуют ровно четыре корня уравнения $F(\tau ) = {\text{0}}$. Этим корням соответствуют четыре точки кривой ${{\omega }_{1}} = 3{{\omega }_{2}}$ (см. рис. 1):

Они выделяют на резонансной кривой интервалы ${{P}_{1}}{{P}_{2}}$ и ${{P}_{3}}{{P}_{4}}$, в которых функция ${\text{ }}{{f}_{{{\text{13}}}}}$ отрицательна и, следовательно, имеет место неустойчивость. Вне этих интервалов ${\text{ }}{{f}_{{{\text{13}}}}} > 0$, и там будет устойчивость. Концевые точки ${{P}_{i}}$ $(i = 1,...,4)$ интервалов, в которых ${\text{ }}{{f}_{{{\text{13}}}}} = 0$, отвечают критическому случаю резонанса четвертого порядка, когда для исследования устойчивости необходимо в разложении (1.3) учитывать члены выше четвертой степени и получать нормальную форму вида (4.4).

Обозначим через ${{e}_{i}}$ значение величины (4.5), вычисленной в точке ${{P}_{i}}$. Вычисления показали, что

поэтому [17] цилиндрическая прецессия спутника в точках ${{P}_{1}}$ и ${{P}_{4}}$ устойчива, а в точках ${{P}_{2}}$ и ${{P}_{3}}$ неустойчива.

Таким образом, задача об устойчивости цилиндрической прецессии решена для всех значений параметров, лежащих на резонансной кривой ${{\omega }_{1}} = 3{{\omega }_{2}}$.

Анализ устойчивости на кривой ${{D}_{4}} = 0$. Для завершения исследования осталось рассмотреть устойчивость для параметров, лежащих на кривой ${{D}_{4}} = 0$. На этой кривой есть четыре точки (1.025959, 0.360377), (1.026302, –0.847311) и (1.126083, 0.384775), (1.134791, –3.233129), в которых реализуются два резонанса шестого порядка: $2{{\omega }_{1}} = 4{{\omega }_{2}}$ и ${{\omega }_{1}} = 5{{\omega }_{2}}$ соответственно. Первый из них, на самом деле, является резонансом третьего порядка, но, как отмечалось выше, из-за отсутствия в разложении (1.3) формы ${{H}_{3}}$ наличие этого резонанса проявляется при учете в (1.3) форм не ниже шестой степени. Аналогично, резонансы пятого порядка: ${{\omega }_{1}} = 4{{\omega }_{2}}$ и $2{{\omega }_{1}} = 3{{\omega }_{2}}$, которые реализуются на кривой ${{D}_{4}} = 0$ (в двух точках каждый), не играют роли при нормализации функции Гамильтона до членов шестой степени.

Проведенные ранее вычисления [15] показали, что во всех четырех точках кривой ${{D}_{4}} = 0$, отвечающих резонансам шестого порядка, величина (4.3) положительна, поэтому в этих точках имеет место устойчивость.

Вне точек резонансов шестого порядка и вне резонанса ${{\omega }_{1}} = 3{{\omega }_{2}}$ на кривой ${{D}_{4}} = 0$ функция Гамильтона (1.3) приводится к нормальной форме, задаваемой равенством (4.1), в котором $m = 3$. Для решения вопроса об устойчивости надо рассмотреть функцию ${{D}_{6}}$, определяемую формулой (4.2). На кривой ${{D}_{4}} = 0$ для функции ${{D}_{6}}$ справедливы такие аналитические представления:

Если $\beta \to - \infty $ вдоль кривой ${{D}_{4}} = 0$, то

Вычисления показали, что на кривой ${{D}_{4}} = 0$ есть только две точки: R₁(1.066320, –1.707488) и R₂(1.063991, 0.424808), в которых функция ${{D}_{6}}$ обращается в нуль. Эти точки лежат очень близко к точкам пересечения кривых ${{D}_{4}} = 0$ и ${{\omega }_{1}} = 3{{\omega }_{2}}$. На рис. 1 они не показаны. Существование точки ${{R}_{2}}$ отмечалось ранее в статье [15], точка же ${{R}_{1}}$ там не была обнаружена из-за недостаточной точности вычислений.

В точках ${{R}_{1}}$ и ${{R}_{2}}$ имеем соответственно ${{\omega }_{1}} = 2.874051$, ${{\omega }_{2}} = 0.946201$ и ${{\omega }_{1}}$ = 1.160814, ${{\omega }_{2}} = 0.380520$. Отсюда видно, что резонансы до восьмого порядка в этих точках не реализуются, поэтому нормальной формой функции Гамильтона (1.3) будет функция вида (4.1), в которой $m = 4$. Вычисления показывают, что величина ${{D}_{8}}$ в точках ${{R}_{1}}$ и ${{R}_{2}}$ равна соответственно 1.900220 и 4.508041. Так как ${{D}_{8}} \ne 0$, то в обеих точках имеет место устойчивость.

Следовательно, внутри области II неустойчивость имеет место на интервалах ${{P}_{1}}{{P}_{2}}$ и ${{P}_{3}}{{P}_{4}}$ кривой ${{\omega }_{1}} = 3{{\omega }_{2}}$ и в двух концевых точках ${{P}_{2}}$ и ${{P}_{3}}$ этих интервалов. Во всех остальных точках области II цилиндрическая прецессия устойчива.

Заключение. Таким образом, вопрос об устойчивости цилиндрической прецессии решен для всех физически допустимых значений параметров $\alpha ,\;\beta $.

Работа выполнена за счет гранта Российского научного фонда (проект № 19-11-00116) в Московском авиационном институте (Национальном исследовательском университете) и в Институте проблем механики им. А.Ю. Ишлинского РАН.