1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 84, № 1, 2020

Прикладная математика и механика, 2020, T. 84, № 1, стр. 26-43

ОБ ЭВОЛЮЦИИ ДВИЖЕНИЙ СПУТНИКА-БАЛЛОНА В ПЛОСКОЙ ОГРАНИЧЕННОЙ ПЛАНЕТНОЙ ЗАДАЧЕ ЧЕТЫРЕХ ТЕЛ С УЧЕТОМ СВЕТОВОГО ДАВЛЕНИЯ

А. В. Доброславский 1, *, П. С. Красильников 1, **

1 Московский авиационный институт
Москва, Россия

* E-mail: a.dobroslavskiy@gmail.com
** E-mail: krasil06@rambler.ru

Поступила в редакцию 14.06.2019
После доработки 20.10.2019
Принята к публикации 30.10.2019

Полный текст (PDF)

Аннотация

Рассмотрена плоская ограниченная задача четырех тел с учетом сил светового давления, когда орбита Земли – кеплеровский эллипс с фокусом в Солнце, орбита Луны – кеплеровский эллипс с фокусом в Земле, спутник-баллон – пассивно гравитирующее тело. Получена усредненная силовая функция задачи в оскулирующих элементах в нерезонансном случае, когда невозмущенная орбита спутника Земли принадлежит внешней сфере гравитационного влияния Земли, расположенной за лунной сферой Хилла. Показано, что интегралами усредненных уравнений в оскулирующих элементах являются большая полуось орбиты спутника и среднее значение силовой функции. Исследованы стационарные режимы колебаний, их бифуркация в зависимости от коэффициента светового давления и большой полуоси невозмущенной орбиты спутника. Построены фазовые портреты колебаний при разных значениях коэффициента светового давления. Проведены расчеты либрационных и ротационных движений спутника в плоскости эклиптики.

Ключевые слова: ограниченная планетная задача четырех тел, световое давление, усредненные уравнения в оскулирующих элементах

Впервые фактор светового давления в ограниченной задаче трех тел был исследован в работе Радзиевского [1], в которой рассмотрен фотогравитационный случай, полученный введением коэффициента редукции. Практический интерес к проблеме появился в связи с исследованием движения спутника Vanguard 1, деградация орбиты которого не соответствовала расчетным значениям. Объяснение этому было дано в работах Мюзена [2] и Паркинсона [3] – было учтено влияние сил светового давления на спутник в первом приближении классической теории возмущений. Расчет орбит спутников-баллонов Echo 1, Echo 2 и PAGEOS, обладавших большим отношением миделева сечения к массе, потребовал учитывать заход спутника в земную тень. В работе Козаи [4] это было учтено решением уравнения тени. Интересной находкой стало введение теневой функции в работе Феррас-Мелло [5], что позволило использовать уравнения теории возмущений. В дальнейшем, в работах Вашковьяк [6, 7] функция тени была представлена в виде ряда по полиномам Лежандра и выражена через элементы орбиты спутника, в результате чего были получены вековые и долгопериодические возмущения элементов орбиты под влиянием солнечного давления и сжатия Земли у полюсов. В монографии Аксенова [8] исследовано влияние светового давления и земной тени на эволюцию кеплеровских элементов орбиты в первом приближении метода малого параметра. В работе Кривова и др. [9] возмущения от сил светового давления, наряду с возмущениями от зональных гармоник, используются в решении задачи о движении космического мусора. Эта же задача, но дополненная возмущениями от электромагнитных сил, рассматривается в работе Гамильтона и Кривова [10].

Брайант [11], используя идеи метода усреднения, описал явное изменение большой полуоси орбиты за период обращения спутника по орбите с учетом эффекта тени. Он показал также, что при отсутствии тени большая полуось орбиты спутника сохраняет свое невозмущенное значение. Было получено решение плоской ограниченной эллиптической задачи трех тел методом двойного усреднения без учета сил светового давления [12, 13]: показано, что усредненные уравнения движения допускают два первых интеграла, исследованы траектории движения спутника, в частности траектории падения спутника на центральное тело. Исследованы периодические орбиты пассивно гравитирующей точки в фотогравитационной прямолинейной ограниченной задаче четырех тел [14, 15]. Изучены положения относительного равновесия пассивно гравитирующей точки в поле притяжения трех массивных материальных точек, находящихся в вершинах треугольника Лагранжа, при условии, что одно из тел является источником излучения [16]. Рассмотрены движения спутника под воздействием уже трех излучающих тел, находящихся в вершинах равностороннего треугольника [17]. Методом двойного усреднения решалась ограниченная задача четырех тел [18], в частности использовалась техника, впервые примененная Гауссом, следуя которой Луна представляется материальным кольцом, при этом были рассмотрены как орбиты спутника, находящиеся внутри лунной орбиты, так и вовне. Заметим также, что метод усреднения эффективно используется и в задачах о вращательных движениях спутников на неэволюционирующих орбитах. Из всего множества работ на эту тему укажем лишь некоторые – [19–23].

Цель статьи – исследовать эволюционные эффекты в движении спутника-баллона в ограниченной задаче четырех тел с учетом сил светового давления. Анализ движений проводится на асимптотически больших интервалах времени на основе тройного усреднения оскулирующих уравнений движения, записанных в кеплеровских элементах орбиты, при этом эффект тени учитываться не будет. Такая постановка задачи вполне оправдана для системы Земля–Луна–Солнце–спутник, когда невозмущенная орбита спутника – кеплеровский эллипс с фокусом в Земле. В этом случае эффектом тени можно пренебречь, так как время нахождения спутника в зоне земной тени мало.

1. Постановка задачи. Рассмотрим движение спутника-баллона большой парусности на асимптотически больших промежутках времени, когда орбиты спутника находятся во внешней сфере гравитационного влияния Земли, расположенной за лунной сферой Хилла.

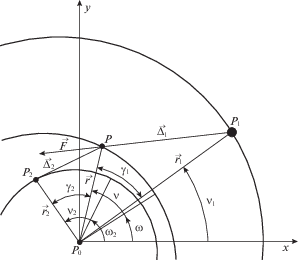
Поскольку орбита Луны составляет малый угол с плоскостью эклиптики, будем считать, что все тела движутся в одной плоскости (рис. 1). Введем декартову неинерциальную систему координат, с центром в ${{P}_{0}}$ (Земле) и осью ${{P}_{0}}x$, направленной в перицентр орбиты Солнца, при этом тело ${{P}_{1}}$ массы ${{m}_{1}}$ (Солнце) обращается вокруг тела ${{P}_{0}}$ по эллиптической орбите c заданными большой полуосью ${{a}_{1}}$ и эксцентриситетом ${{e}_{1}}$. Тело ${{P}_{2}}$ массы ${{m}_{2}}$ (Луна), также движется по эллиптической орбите вокруг ${{P}_{0}}$ c заданной большой полуосью ${{a}_{2}}$, эксцентриситетом ${{e}_{2}}$ и аргументом перицентра ${{\omega }_{2}}$. Считаем также, что невозмущенная орбита пассивно-гравитирующего тела $P$ (спутника-баллона) есть кеплеровский эллипс с фокусом в точке ${{P}_{0}}$, большой полуосью $a$ и эксцентриситетом $e$. На спутник действуют гравитационные силы со стороны массивных тел ${{P}_{0}}$, ${{P}_{1}}$ (вектор ${{\vec {\Delta }}_{1}}$) и ${{P}_{2}}$ (вектор ${{\vec {\Delta }}_{2}}$). Помимо этого, будем учитывать силу светового давления $\vec {F}$ со стороны тела ${{P}_{1}}$, считая, что спутник имеет значительную площадь миделева сечения при небольшой массе. Будем считать также, что большая полуось орбиты спутника существенно превосходит радиус лунной орбиты ($a \approx 6.15 \times {{10}^{{ - 3}}}$ а.е.). В этом случае можно пренебречь эффектом земной тени, так как, согласно проведенным расчетам, конус земной тени начинает влиять на орбиту спутника при эксцентриситете $e < 0.38$, а в предельном случае $e = 0$ пребывание в тени составляет менее 0.12% периода обращения.

Рис. 1.

Постановка задачи.

Отметим, что в силу постановки задачи траектории возмущающих тел ${{P}_{1}}$, ${{P}_{2}}$ рассматриваются как кеплеровские эллипсы. Такое допущение вполне оправдано, так как спутник находится на значительном удалении как от ${{P}_{1}}$, так и от ${{P}_{2}}$, поэтому возмущения в кеплеровских элементах орбит этих тел дают пренебрежимо малый вклад в силовую функцию задачи.

Пусть ${{\gamma }_{1}}$ – угол между векторами $\vec {r}$ и ${{\vec {r}}_{1}}$, имеющий выражение через параметры орбитального движения:

(1.1)
${{\gamma }_{1}} = \nu + \omega - {{\nu }_{1}}$

Здесь $\nu $, $\omega $ – соответственно, истинная аномалия и аргумент перицентра тела $P$, а ${{\nu }_{1}}$ – истинная аномалия орбиты тела ${{P}_{1}}$. Обозначим ${{\gamma }_{2}}$ угол между векторами $\vec {r}$ и ${{\vec {r}}_{2}}$, тогда

(1.2)
${{\gamma }_{2}} = {{\nu }_{2}} + {{\omega }_{2}} - \nu - \omega \,{\kern 1pt} ,$
где ${{\nu }_{2}}$, ${{\omega }_{2}}$ – истинная аномалия и аргумент перицентра тела ${{P}_{2}}$.

2. Возмущающая функция. Выражение для возмущающей силовой функции представим в виде:

(2.1)
$R = {{R}_{1}} + {{R}_{\lambda }} + {{R}_{2}}$

Здесь ${{R}_{1}}$ – силовая функция гравитационного возмущения от Солнца, имеющая вид

${{R}_{1}} = \frac{{f{{m}_{1}}}}{{{{r}_{1}}}}\sum\limits_{k = 2}^\infty {{{{\left( {\frac{r}{{{{r}_{1}}}}} \right)}}^{k}}{{P}_{k}}\left( {\cos {{\gamma }_{1}}} \right)} $
$f$ – гравитационная постоянная, ${{P}_{k}}$ – полиномы Лежандра.

${{R}_{\lambda }}$ – возмущенная функция светового давления на спутник:

${{R}_{\lambda }} = - \delta \left( {\frac{{{{r}_{0}}^{2}}}{{r_{1}^{2}}}r\cos {{\gamma }_{1}} + \frac{{r_{0}^{2}}}{{{{r}_{1}}}}\sum\limits_{k = 2}^\infty {{{{\left( {\frac{r}{{{{r}_{1}}}}} \right)}}^{k}}{{P}_{k}}\left( {\cos {{\gamma }_{1}}} \right)} } \right),$
где ${{r}_{0}}$ – среднее расстояние от Земли до Солнца, $\delta $ – коэффициент светового давления на сферический спутник:

(2.2)
$\delta = \frac{{\varkappa \pi {{\rho }^{2}}{{E}_{0}}}}{{mc}}$

Здесь $\rho $ – радиус спутника, $m$ – его масса, $\varkappa $ – коэффициент поверхности спутника, равный 1 для полного поглощения/отражения света, и 1.44 для диффузного рассеивания, ${{E}_{0}}$ – солнечная постоянная, определенная как мощность светового потока на поверхности Земли без учета поглощения в атмосфере (приблизительно 1367 Вт/м2), $с$ – скорость света в вакууме.

Далее, ${{R}_{2}}$ – силовая функция гравитационного возмущения со стороны тела ${{P}_{2}}$ (Луны), которая, для случая внешней сферы гравитационного влияния Земли, находящейся за сферой Хилла Луны, имеет вид [24]:

${{R}_{2}} = f{{m}_{2}}\left( {\frac{1}{r} + \frac{{r_{2}^{3} - {{r}^{3}}}}{{{{r}^{2}}r_{2}^{2}}}\cos {{\gamma }_{2}} + \frac{1}{r}\sum\limits_{k = 2}^\infty {{{{\left( {\frac{{{{r}_{2}}}}{r}} \right)}}^{k}}{{P}_{k}}\left( {\cos {{\gamma }_{2}}} \right)} } \right)$

Здесь ${{r}_{2}} < r$, $3 \times {{10}^{{ - 3}}} < r < 6.21 \times {{10}^{{ - 3}}}$ а.е.

3. Усредненная возмущающая функция. Быстрыми переменными задачи являются средняя аномалия $M$ невозмущенного движения спутника, а также средние аномалии ${{M}_{1}}$, ${{M}_{2}}$ тел ${{P}_{1}}$, ${{P}_{2}}$. Всюду ниже предполагаем, что отсутствуют резонансы между частотами средних аномалий.

Возмущающую функцию (2.1) усредним по $M$, полагая ${{r}_{2}} < r$:

$R* = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\left( {{{R}_{1}} + {{R}_{\lambda }} + {{R}_{2}}} \right)dM} {\text{,}}\quad dM = \frac{{{{r}^{2}}}}{{{{a}^{2}}\sqrt {1 - {{e}^{2}}} }}d\nu $

Здесь $a$ и $e$ – большая полуось и эксцентриситет невозмущенной орбиты тела $P$. Вычисления показывают, что

(3.1)
$\begin{gathered} R* = \frac{3}{2}\frac{{r_{0}^{2}}}{{r_{1}^{2}}}\delta ea\cos \left( {\omega - {{\nu }_{1}}} \right) + \frac{{f{{m}_{1}} - \delta r_{0}^{2}}}{{{{r}_{1}}}}\sum\limits_{k = 2}^\infty {r_{1}^{{ - k}}R_{{k + 2,k}}^{*}\left( {{{\nu }_{1}} - \omega } \right)} + \\ + \;f{{m}_{2}}\left( {\frac{1}{a} + \frac{3}{2}ea\cos \left( {{{\nu }_{2}} + {{\omega }_{2}} - \omega } \right) + \sum\limits_{k = 2}^\infty {r_{2}^{k}R_{{1 - k,k}}^{*}\left( {{{\nu }_{2}} + {{\omega }_{2}} - \omega } \right)} } \right) \\ \end{gathered} $

Здесь использованы следующие обозначения:

$\begin{gathered} R_{{m,k}}^{*}\left( \xi \right) = \frac{{{{a}^{m}}{{{\left( {1 + e} \right)}}^{m}}}}{{{{a}^{2}}\sqrt {1 - {{e}^{2}}} }}\left( {{{F}_{{2,1}}}\left( {\frac{1}{2},\;m;\;1;\;\frac{{2e}}{{e - 1}}} \right){{{\left( {P_{k}^{{\left( 0 \right)}}\left( 0 \right)} \right)}}^{2}}} \right. + \\ + \;\left. {2\sum\limits_{i = 1}^k {\frac{{\left( {k - i} \right)!}}{{\left( {k + i} \right)!}}{{{\left( {P_{k}^{{\left( i \right)}}\left( 0 \right)} \right)}}^{2}}F_{{3,2}}^{{reg}}\left( {\frac{1}{2},\;1,\;m;\;1 - i,\;1 + i;\;\frac{{2e}}{{e - 1}}} \right)\cos i\xi } } \right) \\ \end{gathered} $
$P_{k}^{{\left( i \right)}}\left( 0 \right)$ – присоединенные функции Лежандра в нуле [25]:
$P_{k}^{{\left( i \right)}}\left( 0 \right) = \left\{ \begin{gathered} {{\left( { - 1} \right)}^{{\left( {k - i} \right)/2}}}\frac{{\left( {k + i} \right)!}}{{{{2}^{k}}\left( {\frac{{k - i}}{2}} \right)!\left( {\frac{{k + i}}{2}} \right)!}},\quad k - i = 2m,\quad m \in Z \hfill \\ 0,\quad k - i = 2m + 1,\quad m \in Z \hfill \\ \end{gathered} \right.$
${{F}_{{2,1}}}$ – гипергеометрическая функция, $F_{{{\text{3,2}}}}^{{{\text{reg}}}}$ – регуляризованная гипергеометрическая функция, имеющая вид
$F_{{3,2}}^{{{\text{reg}}}}\left( {{{\alpha }_{1}},{{\alpha }_{2}},{{\alpha }_{3}};{{\beta }_{1}},{{\beta }_{2}};z} \right) = \sum\limits_{n = 0}^\infty {\frac{{{{{\left( {{{\alpha }_{1}}} \right)}}_{n}}{{{\left( {{{\alpha }_{2}}} \right)}}_{n}}{{{\left( {{{\alpha }_{3}}} \right)}}_{n}}}}{{\Gamma \left( {{{\beta }_{1}} + n} \right)\Gamma \left( {{{\beta }_{2}} + n} \right)}}\frac{{{{z}^{n}}}}{{n!}}} \,,$
$\Gamma $ – гамма-функция, ${{\left( x \right)}_{n}}$ – символ Похгаммера:

${{\left( x \right)}_{n}} = \frac{{\Gamma \left( {x + n} \right)}}{{\Gamma \left( x \right)}}$

Усредняя (3.1) по ${{M}_{1}}$, получим

(3.2)
$\begin{gathered} R{\text{**}} = \left( {f{{m}_{1}} - \delta r_{0}^{2}} \right)\sum\limits_{k = 2}^\infty {R_{{1 - k,k + 2,k}}^{{{\text{**}}}}\left( \omega \right)} + \\ + \;f{{m}_{2}}\left( {\frac{1}{a} + \frac{3}{2}ea\cos \left( {{{\nu }_{2}} + {{\omega }_{2}} - \omega } \right) + \sum\limits_{k = 2}^\infty {r_{2}^{k}R_{{1 - k,k}}^{{\text{*}}}\left( {{{\nu }_{2}} + {{\omega }_{2}} - \omega } \right)} } \right), \\ \end{gathered} $
где

(3.3)
$\begin{gathered} R_{{s,m,k}}^{{{\text{**}}}}\left( \eta \right) = \frac{{a_{1}^{s}{{{\left( {1 + {{e}_{1}}} \right)}}^{s}}}}{{a_{1}^{2}\sqrt {1 - e_{1}^{2}} }}\frac{{{{a}^{m}}{{{\left( {1 + e} \right)}}^{m}}}}{{{{a}^{2}}\sqrt {1 - {{e}^{2}}} }}\left( {{{F}_{{2,1}}}\left( {\frac{1}{2},\;s;\;1;\;\frac{{2{{e}_{1}}}}{{{{e}_{1}} - 1}}} \right){{F}_{{2,1}}}\left( {\frac{1}{2},\;m;\;1;\;\frac{{2e}}{{e - 1}}} \right){{{\left( {P_{k}^{{\left( 0 \right)}}\left( 0 \right)} \right)}}^{2}} + } \right. \\ + \;2\sum\limits_{i = 1}^k {\frac{{\left( {k - i} \right)!}}{{\left( {k + i} \right)!}}F_{{3,2}}^{{{\text{reg}}}}\left( {\frac{1}{2},\;1,\;s;\;1 - i,\;1 + i;\;\frac{{2{{e}_{1}}}}{{{{e}_{1}} - 1}}} \right)} \times \\ \left. {^{{^{{^{{}}}}}} \times \;F_{{3,2}}^{{{\text{reg}}}}\left( {\frac{1}{2},\;1,\;m;\;1 - i,\;1 + i;\;\frac{{2e}}{{e - 1}}} \right){{{\left( {P_{k}^{{\left( i \right)}}\left( 0 \right)} \right)}}^{2}}\cos i\eta } \right) \\ \end{gathered} $

Усредним $R{\text{**}}$ по ${{M}_{2}}$. Учитывая, что ${{M}_{2}}$ входит (через ${{\nu }_{2}}$) только в последние два члена формулы (3.2), получим

(3.4)
$\begin{gathered} R{\text{***}} = \left( {f{{m}_{1}} - \delta r_{0}^{2}} \right)\sum\limits_{k = 2}^\infty {R_{{1 - k,k + 2,k}}^{{{\text{**}}}}\left( \omega \right)} + \\ + \;f{{m}_{2}}\left( {\frac{1}{a} - \frac{3}{2}e{{e}_{2}}a\cos \left( {\omega - {{\omega }_{2}}} \right) + \sum\limits_{k = 2}^\infty {R_{{k + 2,1 - k,k}}^{{{\text{***}}}}\left( {\omega - {{\omega }_{2}}} \right)} } \right), \\ \end{gathered} $
где $R_{{1 - k,k + 2,k}}^{{{\text{**}}}}\left( \omega \right)$ вычисляется по формуле (3.3), а $R_{{k + 2,1 - k,k}}^{{{\text{***}}}}\left( {\omega - {{\omega }_{2}}} \right)$ по формуле (3.5), представленной ниже:

(3.5)
$\begin{gathered} R_{{t,m,k}}^{{{\text{***}}}}\left( \zeta \right) = \frac{{a_{2}^{t}{{{\left( {1 + {{e}_{2}}} \right)}}^{t}}}}{{a_{2}^{2}\sqrt {1 - e_{2}^{2}} }}\frac{{{{a}^{m}}{{{\left( {1 + e} \right)}}^{m}}}}{{{{a}^{2}}\sqrt {1 - {{e}^{2}}} }}\left( {{{F}_{{2,1}}}\left( {\frac{1}{2},\;t;\;1;\;\frac{{2{{e}_{2}}}}{{{{e}_{2}} - 1}}} \right){{F}_{{2,1}}}\left( {\frac{1}{2},\;m;\;1;\;\frac{{2e}}{{e - 1}}} \right){{{\left( {P_{k}^{{\left( 0 \right)}}\left( 0 \right)} \right)}}^{2}} + } \right. \\ + \;2\sum\limits_{i = 1}^k {\frac{{\left( {k - i} \right)!}}{{\left( {k + i} \right)!}}F_{{3,2}}^{{{\text{reg}}}}\left( {\frac{1}{2},\;1,\;t;\;1 - i,\;1 + i;\;\frac{{2{{e}_{2}}}}{{{{e}_{2}} - 1}}} \right)} \times \\ \left. { \times \;F_{{3,2}}^{{{\text{reg}}}}\left( {\frac{1}{2},\;1,\;m;\;1 - i,\;1 + i;\;\frac{{2e}}{{e - 1}}} \right){{{\left( {P_{k}^{{\left( i \right)}}\left( 0 \right)} \right)}}^{2}}\cos i\zeta } \right) \\ \end{gathered} $

4. Первые интегралы уравнений движения. В случае плоского движения с учетом того, что функция $R{\text{***}}$ не зависит от средней аномалии $M$, усредненные оскулирующие уравнения Лагранжа имеют вид:

(4.1)
$\begin{gathered} \frac{{da}}{{dt}} = 0 \\ \frac{{de}}{{dt}} = - \frac{{\sqrt {1 - {{e}^{2}}} }}{{en{{a}^{2}}}}\frac{{\partial R{\text{***}}}}{{\partial \omega }} \\ \frac{{d\omega }}{{dt}} = \frac{{\sqrt {1 - {{e}^{2}}} }}{{en{{a}^{2}}}}\frac{{\partial R{\text{***}}}}{{\partial e}} \\ \frac{{dM}}{{dt}} = n - \frac{{1 - {{e}^{2}}}}{{en{{a}^{2}}}}\frac{{\partial R{\text{***}}}}{{\partial e}} \\ \end{gathered} $

Здесь $n$ – среднее движение тела $P$. Уравнения по $e$, $\omega $ имеют канонический вид с автономной функцией Гамильтона $R{\text{***}}$, поэтому система допускает два первых интеграла:

$a = \operatorname{const} ,\quad R{\text{***}}\left( {e,\omega } \right) = \operatorname{const} $

5. Качественный анализ. Для проведения качественного анализа рассмотрим усеченный ряд (3.4), в котором ограничимся первыми тремя членами, взятыми для гравитационного возмущения со стороны Солнца ($r{\text{/}}{{r}_{1}}{\text{ }} \ll {\text{ }}1$) и со стороны Луны (${{r}_{2}}{\text{/}}r{\text{ }} \ll {\text{ }}1$). Тогда, после преобразований, получим следующее выражение для усеченной силовой функции:

(5.1)
$\begin{gathered} {{R}^{{\left( {3,3} \right)}}} = \left( {f{{m}_{1}} - \delta r_{0}^{2}} \right)\left( {\frac{{{{a}^{2}}\left( {3{{e}^{2}} + 2} \right)}}{{8{{a}^{3}}{{{\left( {1 - e_{1}^{2}} \right)}}^{{3/2}}}}} - \frac{{15{{e}_{1}}{{a}^{3}}\left( {3{{e}^{3}} + 4e} \right)}}{{64a_{1}^{4}{{{\left( {1 - e_{1}^{2}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}\cos \omega } \right) + \\ + \;f{{m}_{2}}\left( {\frac{1}{a} + \frac{{a_{2}^{2}\left( {3e_{2}^{2} + 2} \right)}}{{8{{a}^{3}}{{{\left( {1 - {{e}^{2}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}} - 3e{{e}_{2}}\left( {\frac{a}{2} + \frac{{5a_{2}^{3}\left( {3e_{2}^{2} + 4} \right)}}{{64{{a}^{4}}{{{\left( {1 - {{e}^{2}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}} \right)\cos \left( {\omega - {{\omega }_{2}}} \right)} \right) \\ \end{gathered} $

Найдем стационарные точки уравнений (4.1):

(5.2)
$\begin{gathered} \frac{{\partial {{R}^{{\left( {3,3} \right)}}}}}{{\partial e}} = \left( {f{{m}_{1}} - \delta r_{0}^{2}} \right)\left( {\frac{{3e{{a}^{2}}}}{{4a_{1}^{3}{{{\left( {1 - e_{1}^{2}} \right)}}^{{3/2}}}}} - \frac{{15{{e}_{1}}{{a}^{3}}\left( {9{{e}^{2}} + 4} \right)}}{{64a_{1}^{4}{{{\left( {1 - e_{1}^{2}} \right)}}^{{5/2}}}}}\cos \omega } \right) + \\ {\text{ + }}\;f{{m}_{2}}\left( {\frac{{3ea_{2}^{2}\left( {3e_{2}^{2} + 2} \right)}}{{8{{a}^{3}}{{{\left( {1 - {{e}^{2}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}} - 3{{e}_{2}}\left( {\frac{{5a_{2}^{3}\left( {4{{e}^{2}} + 1} \right)\left( {3e_{2}^{2} + 4} \right)}}{{64{{a}^{4}}{{{\left( {1 - {{e}^{2}}} \right)}}^{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0em} 2}}}}}} + \frac{a}{2}} \right)\cos \left( {\omega - {{\omega }_{2}}} \right)} \right) = 0 \\ \frac{{\partial {{R}^{{\left( {3,3} \right)}}}}}{{\partial \omega }} = \left( {f{{m}_{1}} - \delta r_{0}^{2}} \right)\frac{{15{{e}_{1}}{{a}^{3}}\left( {3{{e}^{3}} + 4e} \right)}}{{64a_{1}^{4}{{{\left( {1 - e_{1}^{2}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}\sin \omega + \\ {\text{ + }}\;3f{{m}_{2}}e{{e}_{2}}\left( {\frac{{5a_{2}^{3}\left( {3e_{2}^{2} + 4} \right)}}{{64{{a}^{4}}{{{\left( {1 - {{e}^{2}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}} + \frac{a}{2}} \right)\sin \left( {\omega - {{\omega }_{2}}} \right) = 0 \\ \end{gathered} $

Одним из решений второго уравнения в системе (5.2) является $e = 0$. Более того, из системы уравнений (4.1) следует, что одномерное многообразие $e = 0$ является интегральным, при этом $\omega $ – его локальная координата ($\omega $ теряет физический смысл как угол, задающий положение перигея оскулирующего эллипса в плоскости ${{P}_{0}}xy$).

Подставив $e = 0$ в первое уравнение системы (5.2), получим выражение для нахождения $\omega $:

$\frac{{5{{e}_{1}}{{a}^{2}}\left( {f{{m}_{1}} - \delta r_{0}^{2}} \right)}}{{8a_{1}^{4}{{{\left( {1 - e_{1}^{2}} \right)}}^{{5/2}}}}}\cos \omega - f{{m}_{2}}{{e}_{2}}\left( {\frac{{5a_{2}^{3}\left( {3e_{2}^{2} + 4} \right)}}{{32{{a}^{5}}}} + 1} \right)\cos \left( {\omega - {{\omega }_{2}}} \right) = 0$

Отсюда находим значения стационарных точек $\omega = {{\omega }_{*}}$ на интервале $\left[ {0,\;2\pi } \right)$: ${{\omega }_{*}} = \left\{ {\pi {\text{/}}2,\;3\pi {\text{/}}2} \right\}$ при ${{\omega }_{2}} = \left\{ {0,\pi } \right\}$ и, если аргумент перицентра орбиты Луны отличен от $\pi m$, имеем два значения ${{\omega }_{{\text{*}}}}$, как функции параметров задачи (их явные выражения опускаем). Одна из стационарных точек устойчива, вторая неустойчива на многообразии $e = 0$. Нестационарный режим (0, $\omega \left( t \right)$) описывает асимптотическое стремление к устойчивой точке.

Таким образом, круговая невозмущенная орбита спутника-баллона сохраняет свою форму под действием возмущений от Солнца, Луны и светового давления, но при этом угловая скорость движения спутника по орбите меняется на малую величину $\dot {\omega }$, зависящую от времени и параметров возмущений. Влияние Луны проявляет себя в том, что возмущения $\omega \left( t \right)$ в полярном угле $\nu + \omega $ радиус-вектора спутника имеют предельный режим $\mathop {\lim }\limits_{t \to \infty } \omega \left( t \right) = {{\omega }_{{\text{*}}}}$, отличный от $\pi {\text{/}}2$, $3\pi {\text{/}}2$ при ${{\omega }_{2}} \ne \pi m$.

Для исследования движений спутника при значениях $e \ne 0$ заметим, что система (5.2) линейна относительно $\sin \omega $ и $\cos \omega $. Из второго уравнения и тождества ${{\cos }^{2}}\omega + {{\sin }^{2}}\omega $ = 1 выразим $\sin \omega $ и $\cos \omega $:

(5.3)
$\sin \omega = \pm \frac{{M\left( {e,a} \right)\sin {{\omega }_{2}}}}{{Q\left( {e,a,\delta ,{{\omega }_{2}}} \right)}},\quad \cos \omega = \pm \frac{{M\left( {e,a} \right)\cos {{\omega }_{2}} + S\left( {e,a,\delta } \right)}}{{Q\left( {e,a,\delta ,{{\omega }_{2}}} \right)}},$
где знаки перед выражением следует брать согласованно. Здесь

$S\left( {e,a,\delta } \right) = \frac{{5{{e}_{1}}{{a}^{3}}\left( {3{{e}^{2}} + 4} \right)}}{{16a_{1}^{4}{{{\left( {1 - e_{1}^{2}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}}\left( {f{{m}_{1}} - \delta r_{0}^{2}} \right),\quad M\left( {e,a} \right) = f{{m}_{2}}{{e}_{2}}\left( {\frac{{5a_{2}^{3}\left( {3e_{2}^{2} + 4} \right)}}{{16{{a}^{4}}{{{\left( {1 - {{e}^{2}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}} + 2a} \right)$
$Q\left( {e,a,\delta ,{{\omega }_{2}}} \right) = \sqrt {{{M}^{2}}\left( {e,a} \right) + {{S}^{2}}\left( {e,a,\delta } \right) + 2M\left( {e,a} \right)S\left( {e,a,\delta } \right)\cos {{\omega }_{2}}} $

Подставив (5.3) в первое уравнение системы (5.2), исключим $\omega $, получив уравнение относительно эксцентриситета $e$:

(5.4)
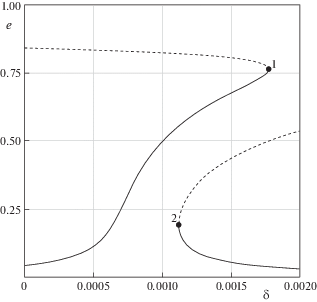
$\begin{gathered} \frac{{{{a}^{2}}\left( {f{{m}_{1}} - \delta r_{0}^{2}} \right)}}{{a_{1}^{3}{{{\left( {1 - e_{1}^{2}} \right)}}^{{3/2}}}}}\left( {e \mp \frac{{5a{{e}_{1}}\left( {9{{e}^{2}} + 4} \right)}}{{16{{a}_{1}}\left( {1 - e_{1}^{2}} \right)}}\left( {\frac{{M\left( {e,a} \right)\cos {{\omega }_{2}} + S\left( {e,a,\delta } \right)}}{{Q\left( {e,a,\delta ,{{\omega }_{2}}} \right)}}} \right)} \right) + \\ {\text{ + }}\;f{{m}_{2}}\left( {\frac{{a_{2}^{2}e\left( {3e_{2}^{2} + 2} \right)}}{{2{{a}^{3}}{{{\left( {1 - {{e}^{2}}} \right)}}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}} \mp {{e}_{2}}\left( {\frac{{5a_{2}^{3}\left( {4{{e}^{2}} + 1} \right)\left( {3e_{2}^{2} + 4} \right)}}{{16{{a}^{4}}{{{\left( {1 - {{e}^{2}}} \right)}}^{{7/2}}}}} + 2a} \right)\left( {\frac{{M\left( {e,a} \right) + S\left( {e,a,\delta } \right)\cos {{\omega }_{2}}}}{{Q\left( {e,a,\delta ,{{\omega }_{2}}} \right)}}} \right)} \right) = 0 \\ \end{gathered} $

Уравнение (5.4) исследуем численно для системы Земля–Луна–Солнце: $a = 2.67$ × × 10–3 а.е., ${{a}_{1}} = 1$ а.е., ${{a}_{2}} = 2.57 \times {{10}^{{ - 3}}}$ а.е., ${{e}_{1}}$ = 0.01671123, ${{e}_{2}} = 0.0549$, ${{\omega }_{2}} = 0$, рассматривая δ как независимый параметр. На рис. 2 изображены кривые равновесий в координатах ($\delta $, $e$), где непрерывной линией отмечены устойчивые, а штриховой – неустойчивые положения равновесия. На левой ветви кривой равновесия, соответствующей знаку минус в уравнении (5.4), отмечена точка бифуркации (1) с координатами $(\delta _{{\text{*}}}^{{(1)}},e_{*}^{{(1)}})$ = $(1.77 \times {{10}^{{ - 3}}}$, 0.762). На правой ветви расположена точка бифуркации (2) с координатами $(\delta _{*}^{{\left( 2 \right)}},e_{*}^{{\left( 2 \right)}})$ = $(1.12 \times {{10}^{{ - 3}}}$, 0.192), соответствующей плюсу в уравнении (5.4).

Рис. 2.

Бифуркационная диаграмма $e(\delta )$.

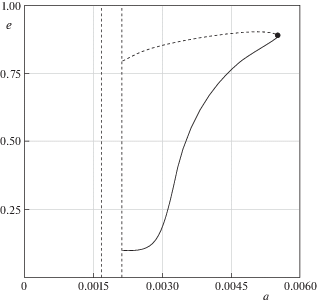
Исследуем также уравнение (5.4) при фиксированном $\delta = 5 \times {{10}^{{ - 4}}}$, рассматривая $a$ как независимый параметр. На рис. 3 представлена кривая равновесия в координатах ($a$, $e$), где непрерывной линией отмечены устойчивые, а штриховой – неустойчивые положения равновесия. Вертикальными штриховыми линиями на рисунке отмечена лунная сфера Хилла. Точка бифуркации имеет координаты $({{a}_{*}},{{e}_{*}})$ = $(5.52 \times {{10}^{{ - 3}}}$, 0.887).

Рис. 3.

Бифуркационная диаграмма $e(a)$.

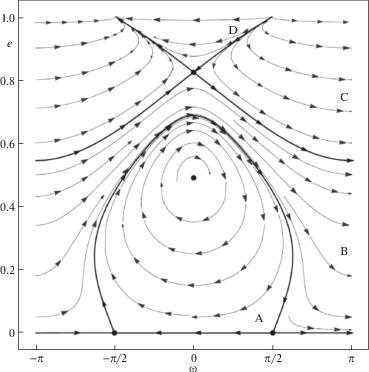
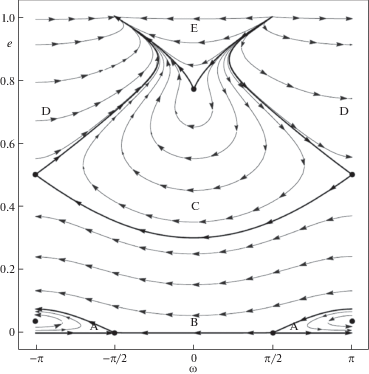
Построим фазовые портреты колебаний по ($\omega $, $e$), используя прежние значения параметров. На рис. 4 представлен фазовый портрет при $\delta = 1 \cdot {{10}^{{ - 3}}}$ (случай $\delta < \delta _{*}^{{\left( 2 \right)}}$). Здесь видим область ограниченных колебаний A с гетероклиническими границами. Фазовые кривые внутри области B охватывают цилиндр ${{S}^{1}} \times {{R}^{1}} = \left[ {0,1} \right) \times \left[ { - \pi ,\pi } \right)$, сохраняя значение $e < 1$, тогда как в областях C и D они покидают область $e < 1$. Заметим, что ряды для усредненной силовой функции задачи расходятся при $e = 1$, поэтому достоверность расчетов в окрестности $e = 1$ низкая.

Рис. 4.

Фазовый портрет при $\delta = 1 \times {{10}^{{ - 3}}}$.

При бифуркационном значении $\delta = \delta _{*}^{{\left( 2 \right)}}$ появляется дополнительная неустойчивая стационарная точка возвратного типа, принадлежащая гомоклинической кривой, охватывающей цилиндр (рис. 5).

Рис. 5.

Фазовый портрет при $\delta = \delta _{*}^{{(2)}}$.

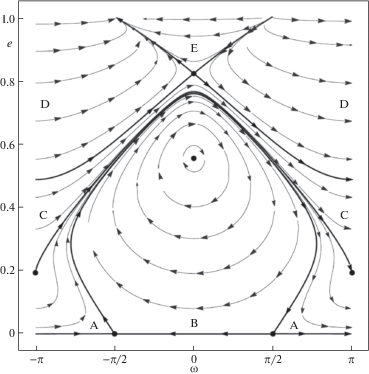
Наиболее интересная картина колебаний отвечает случаю $\delta \in (\delta _{*}^{{\left( 2 \right)}},\delta _{*}^{{\left( 1 \right)}})$, приведенному на рис. 6 (фазовый портрет построен при $\delta = 1.5 \times {{10}^{{ - 3}}}$). Здесь имеем четыре стационарные точки, а фазовый портрет состоит из областей либрационных движений A и D в окрестности устойчивых равновесий, области ротационных колебаний В и областей неограниченных движений С, Е и F, когда фазовая точка выходит на траектории параболического типа, преодолевая значения $e = 1$. Указанные области разделены сепаратрисами, при этом сепаратрисы, ограничивающие область C, асимптотически сливаются в бесконечно удаленной точке при $t \to \pm \infty $.

Рис. 6.

Фазовый портрет при $\delta = 1.5 \times {{10}^{{ - 3}}}$.

Еще раз подчеркнем, что в малой окрестности $e = 1$ достоверность расчетов падает в силу расходимости рядов. Так удержание большего числа членов ряда (3.4) (до 10-ти включительно) показало, что решение задачи Коши в малой окрестности $e = 1$ некорректно: существенно меняется поведение траектории спутника в осях ${{P}_{0}}xy$ при появлении новых членов ряда и недопустимо быстро возрастает скорость колебаний по эксцентриситету орбиты спутника. Высокая точность расчетов гарантируется для $e \leqslant 0.8$.

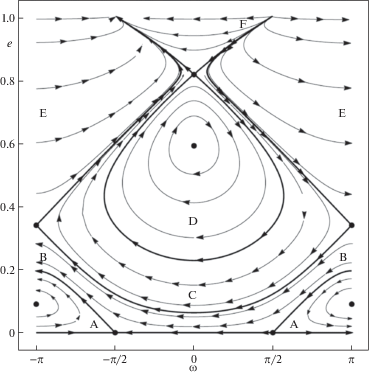
Рисунки 7 и 8 описывают колебания при $\delta \in [\delta _{*}^{{\left( 1 \right)}}, + \infty )$. Видно, что область либрации D (см. рис. 6) сжимается в точку равновесия при $\delta = \delta _{*}^{{(1)}}$ на рис. 7 и полностью исчезает при $\delta > \delta _{*}^{{(1)}}$ на рис. 8 (для построения фазового портрета использовалось значение $\delta = 2 \times {{10}^{{ - 3}}}$).

Рис. 7.

Фазовый портрет при $\delta = \delta _{*}^{1}$.

Рис. 8.

Фазовый портрет при $\delta = 2 \times {{10}^{{ - 3}}}$.

6. Численный расчет траекторий движения. Для построения оскулирующего эллипса в декартовых координатах воспользуемся следующей параметризацией:

(6.1)
$x = r\cos \theta ,\quad y = r\sin \theta ,\quad r = a\left( {1 - e\cos E} \right)$

Здесь $\theta $ – полярный угол, получаемый из соотношений:

$\theta = \nu + \omega ,\quad \nu = 2\operatorname{arctg} \left( {\sqrt {\frac{{1 + e}}{{1 - e}}} \operatorname{tg} \frac{E}{2}} \right)$
$E$ – эксцентрическая аномалия, представимая рядом Фурье [24]:

$E = M\left( t \right) + 2\sum\limits_{k = 1}^\infty {\frac{{{{J}_{k}}\left( {ke\left( t \right)} \right)}}{k}\sin kM\left( t \right)} $

Здесь ${{J}_{k}}$ – функция Бесселя, $M$ – средняя аномалия.

Подставив в (6.1) известные выражения для $\cos \nu $ и $\sin \nu $ через эксцентрическую аномалию $E$ и эксцентриситет $e$

$\cos \nu = \frac{{\cos E - e}}{{1 - e\cos E}},\quad \sin \nu = \frac{{\sin E\sqrt {1 - {{e}^{2}}} }}{{1 - e\cos E}}$
получим

(6.2)
$\begin{gathered} x = a\left( {\cos \omega \left( {\cos E - e} \right) - \sin \omega \sin E\sqrt {1 - {{e}^{2}}} } \right) \\ y = a\left( {\cos \omega \sin E\sqrt {1 - {{e}^{2}}} + \sin \omega \left( {\cos E - e} \right)} \right) \\ \end{gathered} $

Далее, численно интегрируя систему (4.1), с учетом усеченной силовой функции (5.1), получим $e\left( t \right)$, $\omega \left( t \right)$ и $M\left( t \right)$.

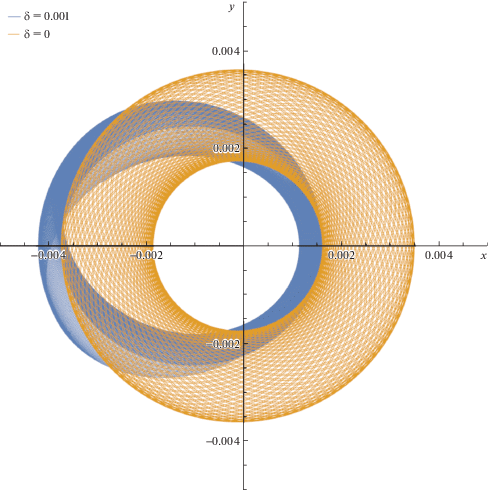
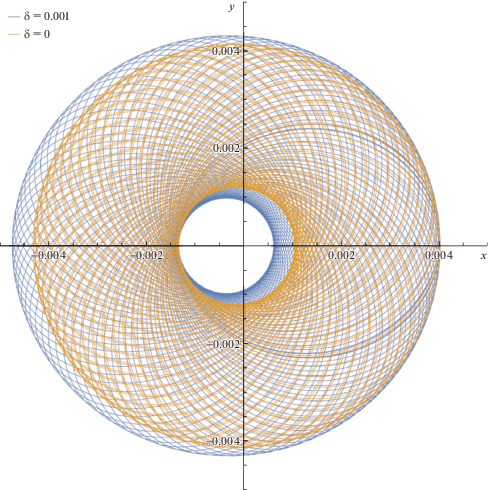
Рассмотрим фазовые траектории в области $A$ (рис. 4). Для этого случая проведем численное моделирование траекторий движения, задав параметры $\delta = 1 \times {{10}^{{ - 3}}} < \delta _{*}^{{\left( 2 \right)}}$, $a = 2.67 \times {{10}^{{ - 3}}}$, ${{\omega }_{2}} = 0$ и начальные значения фазовых переменных $e\left( 0 \right) = 0.4$, $\omega \left( 0 \right) = 0$, $M\left( 0 \right) = 0$. Интегрируя систему (4.1) на промежутке времени в 3650 дней получим возмущенные траектории “либрационного” типа (рис. 9) как для случая чисто гравитационных возмущений от Солнца и Луны (траектории, отвечающие $\delta = 0$), так и с учетом совместного влияния светового и гравитационного воздействий (траектории, отвечающие $\delta = 0.001$). Поскольку оскулирующие аргумент перицентра и эксцентриситет меняются слабо, возмущенная орбита близка к “стационарной орбите”, отвечающей стационарной точке фазового портрета. Заметим, что “стационарная орбита” сохраняет значения своих кеплеровских элементов $a = 2.67 \times {{10}^{{ - 3}}}$, $e = 0.497$, $\omega = 0$ во все время движения.

Рис. 9.

Траектории либрационного типа.

Для начальных значений $e\left( 0 \right) = 0.5$, $\omega \left( 0 \right) = \pi $, $M\left( 0 \right) = 0$, отвечающих случаю вековых возмущений по $\omega $, имеем траектории ротационного типа, представленные на рис. 10. Для расчетов использовался промежуток времени 2700 дней. Этим траекториям отвечает область $B$ на фазовом портрете системы (см. рис. 4).

Рис. 10.

Траектории ротационного типа.

В заключение отметим, что точность, с которой решения усредненной системы приближают решения строгих уравнений движения спутника-баллона, определяется на основе обобщенной теоремы Н.Н. Боголюбова [27, 28] поскольку строгие уравнения движения содержат три независимых малых параметра: $\delta $, $\varepsilon = {{\left( {r{\text{/}}{{r}_{1}}} \right)}^{2}} \approx {{a}^{2}}$ (здесь ${{r}_{1}} \approx 1$) и $\mu = {{m}_{2}}$ (${{m}_{1}} = 1$). Метод усреднения с тремя независимыми малыми параметрами гарантирует точность приближения первого порядка малости по малым параметрам на асимптотически большом промежутке времени в нерезонансном случае. Это значит, что для любых малых величин ${{\sigma }_{1}} > 0$, ${{\sigma }_{2}} > 0$, ${{\sigma }_{3}} > 0$ существуют три константы ${{\gamma }_{i}}\left( {{{\sigma }_{1}},{{\sigma }_{2}},{{\sigma }_{3}}} \right) > 0$ такие, что

$\left\| {u\left( t \right) - \nu \left( t \right)} \right\| \leqslant {{\gamma }_{1}}\delta + {{\gamma }_{2}}\varepsilon + {{\gamma }_{3}}\mu \,,$
когда $t\sim {1 \mathord{\left/ {\vphantom {1 {\left\| {\delta ,\varepsilon ,\mu } \right\|}}} \right. \kern-0em} {\left\| {\delta ,\varepsilon ,\mu } \right\|}}$, $0 \leqslant \delta \leqslant {{\sigma }_{1}}$, $0 \leqslant \varepsilon \leqslant {{\sigma }_{2}}$, $0 \leqslant \mu \leqslant {{\sigma }_{3}}$. Здесь $u\left( t \right)$ – вектор строгих решений уравнений движения, $\nu \left( t \right)$ – вектор усредненных уравнений.

Заключение. Исследована эволюция высоких орбит спутника Земли, принадлежащих плоскости эклиптики, под действием гравитационных возмущений от Солнца, Луны и светового давления. Из анализа нерезонансных усредненных уравнений движения в оскулирующих элементах следует, что большая полуось $a$ не эволюционирует, эволюция по $e$ и $\omega $ описывается интегралом энергии. В отличие от задачи трех тел, когда пренебрегают притяжением Луны [26], здесь существуют (при фиксированных параметрах $a = 2.67 \times {{10}^{{ - 3}}}$ а.е., ${{a}_{1}} = 1$ а.е., ${{a}_{2}} = 2.57 \times {{10}^{{ - 3}}}$ а.е., ${{e}_{1}} = 0.01671123$, ${{e}_{2}}$ = = 0.0549, ${{\omega }_{2}} = 0$) два бифуркационных значения $\delta _{*}^{{\left( 1 \right)}} = 1.77 \times {{10}^{{ - 3}}}$, $\delta _{*}^{{\left( 2 \right)}} = 1.12 \times {{10}^{{ - 3}}}$ коэффициента светового давления $\delta $. При $\delta \in [0,\delta _{*}^{{\left( 2 \right)}}) \cup (\delta _{*}^{{\left( 1 \right)}}, + \infty )$ имеем два положения равновесия, на интервале $\delta \in (\delta _{*}^{{\left( 2 \right)}},\delta _{*}^{{\left( 1 \right)}})$ – четыре равновесия, в точках бифуркации – три равновесия. Бифуркация равновесий наблюдается также в плоскости параметров ($a$, $e$) при фиксированном $\delta = 5 \times {{10}^{{ - 4}}}$ (рис. 3). Поэтому фазовые портреты колебаний (рис. 4–8) имеют гораздо более сложный вид, чем в задаче трех тел.

Показано, что существует два типа эволюционирующих орбит: орбиты либрационного и ротационного типов. Для орбит первого типа оскулирующие аргумент перицентра и эксцентриситет меняются периодически, но с малыми амплитудами, орбита близка к траектории, отвечающей стационарной точке и сохраняющей значения своих невозмущенных кеплеровских элементов во все время движения.

Орбиты второго типа имеют непрерывно возрастающий аргумент перицентра, и, как следствие, медленное вращение линии апсид оскулирующего эллипса, на которое накладывается медленное периодическое изменение эксцентриситета.

Притяжение спутника точкой ${{P}_{2}}$ массы ${{m}_{2}}$ (Луной) сильно осложняет проведение расчетов в окрестности $e = 1$, так как коэффициенты ряда (3.4) быстро возрастают по величине при $e \to 1$ (см. (5.4)) и ряд расходится. Поэтому, в отличие от плоской ограниченной задачи трех тел [26], численный счет не подтвердил наличие орбит столкновения с Землей, для которых эксцентриситет близок к единице.

Описаны дополнительные эффекты, вызванные световым давлением: смещение ограниченной траектории спутника как целого относительно траектории классической задачи четырех тел в область, более удаленную от Солнца (на рис. 9 и рис. 10 Солнце находится в правой полуплоскости).

Авторы признательны рецензентам за сделанные замечания.

Исследования выполнены в Московском авиационном институте при поддержке гранта РФФИ № 18-01-00820 А.

Список литературы

  1. Радзиевский В.В. Ограниченная задача трех тел с учетом светового давления // Астрон. ж. 1950. Т. 27. № 4. С. 250–256.

  2. Musen P. The influence of the solar radiation pressure on the motion of an artifical satellite // J. Geophys. Res. 1960. V. 65. № 5. P. 1391–1396.

  3. Parkinson R.W., Jones H.M., Shapiro I.I. Effects of solar radiation pressure on Earth satellite orbits // Science. 1960. V. 131. P. 920–921.

  4. Kozai Y. Effect of solar radiation pressure on the motion of an artificial satellite // Smiths. Astrophys. Obs. Special Rept. 1961. V. 56. P. 25–34.

  5. Ferraz-Mello S. Analytical study of the Earth’s shadowing effects on satellite orbits // Celest. Mech. 1972. V. 5. P. 80–101.

  6. Вашковьяк С.Н. Функция тени в задаче о влиянии светового давления на движение искусственных спутников Земли // Вестн. Моск. ун-та. Сер. 3. Физ. Астрон. 1974. № 5. С. 584–590.

  7. Вашковьяк С.Н. Изменение орбит спутников-баллонов под действием светового излучения // Астрон. ж. 1976. Т. 53. № 5. С. 1085–1094.

  8. Аксенов Е.П. Теория движения искусственных спутников Земли. М.: Наука, 1977. 360 с.

  9. Krivov A.V., Sokolov L.L., Dikarev V.V. Dynamics of Mars-orbiting dust: Effect of light pressure and planetary oblateness // Celest. Mech. Dyn. Astron. 1995. V. 63. Iss. 3–4. P. 313–339.

  10. Hamilton D.P., Krivov A.V. Circum planetary dust dynamics: effect of solar gravity, radiation pressure, planetary oblatness, and electromagnetism // Icarus. 1996. V. 123. P. 503–523.

  11. Bryant R.W. The effect of solar radiation pressure on the motion of an artificial satellite // Astron. J. 1961. V. 66. P. 430–432.

  12. Аксенов Е.П. Двукратно осредненная эллиптическая ограниченная задача трех тел // Астрон. ж. 1979. Т. 56. № 2. С. 419–426.

  13. Аксенов Е.П. Траектории в двукратно осредненной эллиптической ограниченной задаче трех тел // Астрон. ж. 1979. Т. 56. № 3. С. 623–631.

  14. Kalvouridis T.J., Arribas M., Elipe A. Parametric evolution of periodic orbits in the restricted four-body problem with radiation pressure // Planet. Space Sci. 2007. V. 55. P. 475–493.

  15. Kalvouridis T.J., Hadjifotinou K.G. Bifurcations from planar to three-dimensional periodic orbits in the photo-gravitational restricted four-body problem // Intern. J. Bifurc. Chaos. 2008. V. 18. № 2. P. 465–479.

  16. Papadouris J.P., Papadakis K.E. Equilibrium points in the photogravitational restricted four-body problem // Astrophys. Space Sci., 2013. V. 344. P. 21–38.

  17. Mittal A., Agarwal R., Suraj M.S., Arora M. On the photo-gravitational restricted four-body problem with variable mass // Astrophys. Space Sci. 2018. V. 363. P. 109.

  18. Ash M.E. Doubly averaged effect of the Moon and Sun on high altitude Earth satellite orbit // Celest. Mech. 1976. V. 14. P. 209–238.

  19. Krasil’nikov P. Fast non-resonance rotations of spacecraft in restricted three body problem with magnetic torques // Int. J. Non-Linear Mech. 2015. V. 73. P. 43–50.

  20. Тихонов А.А. О вековой эволюции ротационного движения заряженного ИСЗ на регрессирующей орбите // Космич. исслед. 2005. Т. 43. № 2. С. 111–125.

  21. Тихонов А.А. Уточнение модели “наклонный диполь” в задаче об эволюции вращательного движения заряженного тела в геомагнитном поле // Космич. исслед. 2002. Т. 40. № 2. С. 171–177.

  22. Амелькин Н.И., Холощак В.В. Эволюция вращательного движения динамически симметричного спутника с внутренним демпфированием на круговой орбите // ПММ. 2019. Т. 83. № 1. С. 3–15.

  23. Амелькин Н.И., Холощак В.В. Вращательное движение несимметричного спутника с демпфером на круговой орбите // ПММ. 2019. Т. 83. № 1. С. 16–31.

  24. Мюррей К., Дермотт С. Динамика солнечной системы, М.: Физматлит, 2010. 556 с.

  25. Дубошин Г.Н. Небесная механика. Основные задачи и методы, М.: Наука, 1968. 800 с.

  26. Доброславский А.В., Красильников П.С. Об эволюции движений спутника-баллона в плоской ограниченной задаче трех тел с учетом светового давления // Письма в астрон. ж. 2018. Т. 44. № 8–9. С. 618–630.

  27. Красильников П.С. Прикладные методы исследования нелинейных колебаний. М.; Ижевск: Инст. компьют. исслед., 2015. 528 с.

  28. Красильников П.С. О нелинейных колебаниях маятника переменной длины на вибрирующем основании // ПММ. 2012. Т. 76. № 1. С. 36–51.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал