Прикладная математика и механика, 2020, T. 84, № 1, стр. 13-25
ОБ ОДНОМ АНАЛОГЕ ИСТОЛКОВАНИЯ ПУАНСО РЕШЕНИЯ ЭЙЛЕРА В ЗАДАЧЕ О ДВИЖЕНИИ ТВЕРДОГО ТЕЛА В ПОТЕНЦИАЛЬНОМ ПОЛЕ СИЛ
Г. В. Горр *
Институт прикладной математики и механики
Донецк, Украина
* E-mail: gvgorr@gmail.com
Поступила в редакцию 25.09.2019
После доработки 21.11.2019
Принята к публикации 02.12.2019
Аннотация
Рассмотрена задача о движении твердого тела с неподвижной точкой под действием потенциальных сил. Получены условия существования трех инвариантных соотношений уравнений движения. Найдены зависимости от времени основных переменных задачи. Исследовано движение эллипсоида инерции тела в неподвижном пространстве. Установлен некоторый аналог результата Пуансо в истолковании решения Эйлера – в статье движение тела представлено как качение без скольжения эллипсоида инерции по касательной к нему плоскости в неподвижном пространстве.
Введение. Исследование движения твердого тела, как правило, заключается в комплексном подходе, который состоит в получении аналитического решения уравнений движения и последующего истолкования движения с помощью различных геометрических методов. Известно, что в общем случае уравнения движения тела под действием потенциальных и гироскопических сил не интегрируемы в квадратурах по Якоби (уравнений Эйлера–Пуассона [1–3] и уравнений Кирхгофа–Пуассона [4, 5]). Первые дополнительные интегралы уравнений динамики твердого тела получены при определенных ограничениях на параметры распределения масс (см. обзоры [6–9]).
Изучение свойств движения тела относится к заключительному этапу в исследовании решений уравнений динамики. Классический результат Л. Пуансо [10] в истолковании движения тела в случае Эйлера [11] изложен в монографиях Э. Рауса [12], Г.К. Суслова [6], К. Магнуса [13], А.В. Борисова и И.С. Мамаева [8] и других авторов. В силу важности изучения движения свободного твердого тела в приведенных монографиях подробно рассмотрены и результаты И. Мак-Куллага, Ж. Сильвестра, Г. Дарбу, Н.Б. Делоне, Ж. Кенига. В качестве обзорных работ по исследованию других решений уравнений Эйлера–Пуассона наравне с приведенными выше можно отметить публикации А.О. Домогарова [14], П.В. Харламова [15]. Значение геометрического анализа свойств движения тела с неподвижной точкой высоко оценивал Н.Е. Жуковский [16]. Он предлагал и свой метод истолкования движения тела, который основан на свойствах вектора кинематического момента, а работа [17] по истолкованию движения гироскопа Гесса занимает особое место в динамике твердого тела.
Теорема Л. Пуансо о представлении движения тела с помощью качения без скольжения подвижного аксоида вектора угловой скорости по неподвижному аксоиду наибольшее применение получила после того, как П.В. Харламов [18] вывел новые уравнения неподвижного годографа. Хотя формально уравнения неподвижного годографа можно найти, используя углы Эйлера, но процедура получения уравнений неподвижного годографа при таком подходе приводит к значительным трудностям в нахождении вспомогательных переменных, которые в прямом методе Пуансо не используются. Благодаря применению уравнений П.В. Харламова [18] к настоящему времени практически во всех решениях уравнений динамики установлено истолкование движения тела прямым методом Пуансо (см. монографии П.В. Харламова [15], И.Н. Гашененко, Г.В. Горра, А.М. Ковалева [19], Г.В. Горра, А.М. Ковалева [20]).
После того, как была накоплена информация о геометрических свойствах движения тела с помощью различных методов, актуальной стала задача о комплексном подходе в истолковании движения твердого тела с неподвижной точкой. Для его получения автор данной статьи предложил модифицированный метод Пуансо [21], основанный на введении вектора, который коллинеарен вектору угловой скорости. Он позволяет представлять не только движение тела с помощью качения без скольжения подвижного аксоида этого вектора по неподвижному аксоиду, но и, в зависимости от целей исследования, выбирать в качестве подвижного годографа или неподвижного годографа плоские направляющие линии. Данный подход, как показано [21–24], приносит новую информацию о движении тела, упрощая в ряде случаев истолкование движения тела. Кроме этого, данный подход позволяет исследовать движение различных геометрических объектов, связанных с телом, в неподвижном пространстве. Например, с его помощью можно получить свойства движения сферы, эллипсоида инерции и других поверхностей в неподвижном пространстве. То есть в этом варианте модифицированного метода имеет место обобщение подхода Э. Рауса [13], который он использовал при рассмотрении сфероконических и эллипсоидоконических сечений в решении Эйлера. Однако его исследования были основаны на достаточно сложных приемах сферической тригонометрии. Определенное преимущество комплексного подхода по сравнению с методом Пуансо связано, прежде всего, со структурой решения уравнений движения тела. Данная статья посвящена исследованию движения эллипсоида инерции тела в решении [25], уравнений движения тела под действием потенциальных сил. Это решение получено на основании применения метода инвариантных соотношений [26, 27], особенности которого изучены ранее [28], и метода изучения обратных задач динамики твердого тела [29]. Показано, что движение тела можно представить качением без скольжения эллипсоида инерции по касательной плоскости, которая неподвижна в пространстве. Таким образом, установлен аналог результата Пуансо, полученного им в истолковании решения Эйлера.
1. Постановка задачи. Вид решения. Рассмотрим уравнения движения твердого тела, имеющего неподвижную точку, в потенциальном поле сил [6, 30, 31]:
(1.1)
${{A}_{1}}{{\dot {\omega }}_{1}} = ({{A}_{2}} - {{A}_{3}}){{\omega }_{2}}{{\omega }_{3}} + {{\nu }_{3}}\frac{{\partial U({{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}})}}{{\partial {{\nu }_{2}}}} - {{\nu }_{2}}\frac{{\partial U({{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}})}}{{\partial {{\nu }_{3}}}}$(1.2)
${{A}_{2}}{{\dot {\omega }}_{2}} = ({{A}_{3}} - {{A}_{1}}){{\omega }_{3}}{{\omega }_{1}} + {{\nu }_{1}}\frac{{\partial U({{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}})}}{{\partial {{\nu }_{3}}}} - {{\nu }_{3}}\frac{{\partial U({{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}})}}{{\partial {{\nu }_{1}}}}$(1.3)
${{A}_{3}}{{\dot {\omega }}_{3}} = ({{A}_{1}} - {{A}_{2}}){{\omega }_{1}}{{\omega }_{2}} + {{\nu }_{2}}\frac{{\partial U({{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}})}}{{\partial {{\nu }_{1}}}} - {{\nu }_{1}}\frac{{\partial U({{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}})}}{{\partial {{\nu }_{2}}}}$(1.4)
${{\dot {\nu }}_{1}} = {{\omega }_{3}}{{\nu }_{2}} - {{\omega }_{2}}{{\nu }_{3}},\quad {{\dot {\nu }}_{2}} = {{\omega }_{1}}{{\nu }_{3}} - {{\omega }_{3}}{{\nu }_{1}},\quad {{\dot {\nu }}_{3}} = {{\omega }_{2}}{{\nu }_{1}} - {{\omega }_{1}}{{\nu }_{2}}$Уравнения (1.1)–(1.4) при заданной силовой функции $U = U({{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}})$ допускают первые интегралы
(1.5)
$\nu _{1}^{2} + \nu _{2}^{2} + \nu _{3}^{2} = 1,\quad {{A}_{1}}{{\omega }_{1}}{{\nu }_{1}} + {{A}_{2}}{{\omega }_{2}}{{\nu }_{2}} + {{A}_{3}}{{\omega }_{3}}{{\nu }_{3}} = k$(1.6)
${{A}_{1}}\omega _{1}^{2} + {{A}_{2}}\omega _{2}^{2} + {{A}_{3}}\omega _{3}^{2} - 2U({{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}}) = 2E,$Условия существования дополнительных первых интегралов уравнений (1.1)–(1.4) изучали Д.Н. Горячев [30], Х.М. Яхья [32, 33]. Обзор результатов, полученных в этой задаче, подробно изучен в монографии А.В. Борисова и И.С. Мамаева [8], в которой отмечены статьи И.В. Комарова и В.Б. Кузнецова [34, 35], имеющие большое значение для квантовой механики.
Ранее [25] автором рассмотрены условия существования у системы (1.1)–(1.4) трех инвариантных соотношений
(1.7)
${{\omega }_{1}} = \nu _{3}^{{n - 1}}\left( { - \frac{{{{\mu }_{1}}n}}{{n + 2}}{{\nu }_{1}} + {{\beta }_{1}}{{\mu }_{2}}} \right),\quad {{\omega }_{2}} = \nu _{3}^{{n - 1}}\left( { - \frac{{{{\mu }_{1}}n}}{{n + 2}}{{\nu }_{2}} + {{\beta }_{2}}{{\mu }_{2}}} \right),\quad {{\omega }_{3}} = {{\mu }_{1}}\nu _{3}^{n},$(1.8)
$U({{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}}) = \frac{1}{2}\left[ {{{A}_{1}}\omega _{1}^{2}({{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}}) + {{A}_{2}}\omega _{2}^{2}({{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}}) + {{A}_{3}}\omega _{3}^{2}({{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}})} \right] - E,$Рассмотрим одно из решений [25]. Оно характеризуется следующими условиями на моменты инерции, постоянную $k$ и параметры $\beta _{1}^{{}}$, $\beta _{2}^{{}}$, ${{\mu }_{1}}$, ${{\mu }_{2}}$:
(1.10)
$\mu _{1}^{2}n_{{}}^{2} = \mu _{2}^{2}\kappa _{0}^{2}(n + 2)_{{}}^{2}\quad (\kappa _{0}^{2} = \beta _{1}^{2} + \beta _{2}^{2})$Запишем вид исследуемого решения [25]:
(1.11)
${{\omega }_{2}}({{\nu }_{3}}) = \frac{{{{\mu }_{2}}(n + 1)\nu _{3}^{n}}}{n}\left( {{{\beta }_{2}}{{\nu }_{3}} - {{\beta }_{1}}\sqrt {\lambda _{0}^{2} - \nu _{3}^{2}} } \right)$(1.12)
$\begin{gathered} {{\nu }_{1}}({{\nu }_{3}}) = \frac{1}{{\kappa _{0}^{{}}}}\left[ {\beta _{1}^{{}}\left( {n - (n + 1)\nu _{3}^{2}} \right) - \beta _{2}^{{}}(n + 1)\nu _{3}^{{}}\sqrt {\lambda _{0}^{2} - \nu _{3}^{2}} } \right] \\ {{\nu }_{2}}({{\nu }_{3}}) = \frac{1}{{\kappa _{0}^{{}}}}\left[ {\beta _{2}^{{}}\left( {n - (n + 1)\nu _{3}^{2}} \right) + \beta _{1}^{{}}(n + 1)\nu _{3}^{{}}\sqrt {\lambda _{0}^{2} - \nu _{3}^{2}} } \right], \\ \end{gathered} $(1.13)
$\int\limits_{\nu _{3}^{{(0)}}}^{{{\nu }_{3}}} {\frac{{d{{\nu }_{3}}}}{{\nu _{3}^{n}\sqrt {\lambda _{0}^{2} - \nu _{3}^{2}} }} = - \frac{{{{\mu }_{1}}(n + 1)}}{{n + 2}}(t - t_{0}^{{}})} $В соотношениях (1.11)–(1.13) через $\lambda _{0}^{{}}$ обозначена постоянная
а переменная ${{\nu }_{3}}$ изменяется на отрезкеОчевидно, что $\lambda _{0}^{{}}$ из (1.14) удовлетворяет условию $0 < \lambda _{0}^{{}} < 1$, при котором решение (1.11)–(1.13) на отрезке (1.15) является действительным (значение $\nu _{3}^{{(0)}} = 0$ исключается из рассмотрения). В дальнейшем полагаем ${{\mu }_{1}} > 0$, ${{\mu }_{2}} > 0$, что не ограничивает общности задачи истолкования движения.
Отметим, что интерес в исследовании инвариантных соотношений (1.7) (ИС) состоит в том, что уравнения (1.4) на ИС (1.7)
(1.16)
$\begin{gathered} {{{\dot {\nu }}}_{1}} = \nu _{3}^{n}\left( {\frac{{2(n + 1)}}{{n + 2}}\mu _{1}^{{}}{{\nu }_{2}} - \beta _{2}^{{}}\mu _{2}^{{}}} \right), \\ {{{\dot {\nu }}}_{2}} = \nu _{3}^{n}\left( { - \frac{{2(n + 1)}}{{n + 2}}\mu _{1}^{{}}{{\nu }_{1}} + \beta _{1}^{{}}\mu _{2}^{{}}} \right),\quad {{{\dot {\nu }}}_{3}} = \mu _{2}^{{}}\nu _{3}^{{n - 1}}\left( {\beta _{2}^{{}}{{\nu }_{1}} - \beta _{1}^{{}}\nu _{2}^{{}}} \right), \\ \end{gathered} $(1.17)
$\beta _{2}^{{}}{{\nu }_{1}} + \beta _{1}^{{}}\nu _{2}^{{}} = \frac{{\kappa _{0}^{{}}}}{n}\left[ {n - (n + 1)\nu _{3}^{2}} \right],$Приведем вид силовой функции (1.8) на ИС (1.7) при выполнении условий (1.9), (1.10):
(1.18)
$\begin{gathered} U({{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}}) = \frac{{\mu _{1}^{{}}A_{3}^{{}}\nu _{3}^{{2(n - 1)}}}}{{2(n + 2)}}\left[ {2\mu _{1}^{{}}n_{{}}^{2} - \mu _{1}^{{}}(n + 1)(n - 2)\nu _{3}^{2} - } \right. \\ \left. { - \;2\mu _{2}^{{}}n(n + 2)\left( {\beta _{1}^{{}}{{\nu }_{1}} + \beta _{2}^{{}}\nu _{2}^{{}}} \right)} \right] \\ \end{gathered} $В силу результатов [28] следует, что в выражении для силовой функции из (1.18) нельзя использовать равенство (1.17).
2. Истолкование движения тела в решении (1.11)–(1.13) прямым методом Пуансо. Рассмотрим интеграл (1.13). Пусть $n = 1$, тогда ИС (1.7) принимают вид
(2.1)
${{\omega }_{1}} = - \frac{{{{\mu }_{1}}n}}{{n + 2}}\nu _{1}^{{}} + {{\beta }_{1}}{{\mu }_{2}},\quad {{\omega }_{2}} = - \frac{{{{\mu }_{1}}n}}{{n + 2}}\nu _{2}^{{}} + {{\beta }_{2}}{{\mu }_{2}},\quad {{\omega }_{3}} = {{\mu }_{1}}\nu _{3}^{{}}$В случае (2.1) силовая функция (1.18) имеет квадратичный порядок. То есть уравнения (1.1)–(1.3) описывают движение твердого тела под действием центральных ньютоновских сил. Условие (1.9) при $n = 1$ таково
Линейные ИС для уравнений движения исследовались многими авторами (см., например, [9]). Однако случай (2.2) ими отдельно не рассматривался.
Положим в (1.13) $n = 1$. Сделаем замену $\lambda _{0}^{2} - \nu _{3}^{2} = z_{{}}^{2}$. Тогда, учитывая, что
(2.3)
$\int\limits_{\nu _{3}^{{(0)}}}^{{{\nu }_{3}}} {\frac{{d{{z}_{{}}}}}{{\lambda _{0}^{2} - z_{{}}^{2}}} = \frac{{2{{\mu }_{1}}}}{3}(t - t_{0}^{{}})} ,$(2.4)
$\nu _{3}^{2} = \frac{{3e_{{}}^{w}}}{{{{{(e_{{}}^{w} + 1)}}^{2}}}},\quad \left( {w = \frac{{2{{\mu }_{1}}(t - t_{0}^{{}})}}{{\sqrt 3 }}} \right)$Запишем равенства (1.12), (2.1) при $n = 1$:
(2.5)
$\begin{gathered} {{\nu }_{1}}({{\nu }_{3}}) = \frac{1}{{\kappa _{0}^{{}}}}\left[ {\beta _{1}^{{}}\left( {1 - 2\nu _{3}^{2}} \right) - \beta _{2}^{{}}\nu _{3}^{{}}\sqrt {3 - 4\nu _{3}^{2}} } \right] \\ {{\nu }_{2}}({{\nu }_{3}}) = \frac{1}{{\kappa _{0}^{{}}}}\left[ {\beta _{2}^{{}}\left( {1 - 2\nu _{3}^{2}} \right) + \beta _{1}^{{}}\nu _{3}^{{}}\sqrt {3 - 4\nu _{3}^{2}} } \right] \\ \end{gathered} $(2.6)
${{\omega }_{1}}({{\nu }_{3}}) = {{\mu }_{2}}({{\beta }_{1}} - \kappa _{0}^{{}}\nu _{1}^{{}}),\quad {{\omega }_{2}}({{\nu }_{3}}) = {{\mu }_{2}}({{\beta }_{2}} - \kappa _{0}^{{}}\nu _{2}^{{}}),\quad {{\omega }_{3}}({{\nu }_{3}}) = {{\mu }_{1}}\nu _{3}^{{}}$На основании равенств (2.4)–(2.6) можно сделать заключение о том, что при $t \to \infty $ функции ${{\nu }_{3}} \to 0$, ${{\nu }_{1}} \to \frac{{{{\beta }_{1}}}}{{{{\kappa }_{0}}}}$, ${{\nu }_{2}} \to \frac{{{{\beta }_{2}}}}{{{{\kappa }_{0}}}}$, ${{\omega }_{i}} \to 0$ ($i = \overline {1,3} $). То есть при неограниченном возрастании времени движение тела стремится к состоянию покоя.
Покажем, что и при $n > 1$ движение тела носит асимптотический характер. Выберем начальное значение $\nu _{3}^{{(0)}} > 0$. Из интеграла (1.13) следует, что $\frac{{d\nu _{3}^{{}}}}{{dt}} < 0$ при $\nu _{3}^{{}} = \nu _{3}^{{(0)}}$, то есть на отрезке (1.15) переменная $\nu _{3}^{{}}$ убывает и достигает значения $\nu _{3}^{{}} = 0$ за бесконечный промежуток времени, так как интеграл (1.13) расходится. Из равенств (1.11) следует, что ${{\omega }_{i}} \to 0$ ($i = \overline {1,3} $) при $\nu _{3}^{{}} \to 0$. Данные свойства доказывают высказанное выше утверждение.
Для построения подвижного годографа обратимся к равенствам (1.11). Исключим из них переменную $\nu _{3}^{{}}$:
(2.7)
$\begin{gathered} (n + 2)(\omega _{1}^{2} + \omega _{2}^{2}) - n\omega _{3}^{2} = 0 \\ \mu _{2}^{n}(n + 2)_{{}}^{{2n}}(\beta _{1}^{{}}\omega _{1}^{{}} + \beta _{2}^{{}}\omega _{2}^{{}})_{{}}^{n} - \mu _{1}^{{2n}}n_{{}}^{n}(n + 1)_{{}}^{n}\omega _{3}^{{n - 1}} = 0 \\ \end{gathered} $Таким образом, в силу (2.7) подвижный годограф вектора угловой скорости – линия пересечения конуса второго порядка и алгебраической поверхности $n$-го порядка.
Уравнения неподвижного годографа угловой скорости для решения (1.11), (1.12) находим с помощью уравнений П.В. Харламова [15]
(2.8)
${{\omega }_{\xi }}({{\nu }_{3}}) = \frac{{{{\mu }_{1}}(n + 1)}}{{n + 2}}\nu _{3}^{n}\sqrt {\lambda _{0}^{2} - \nu _{3}^{2}} ,\quad {{\omega }_{\eta }}({{\nu }_{3}}) = {{\mu }_{1}}\nu _{3}^{n},\quad {{\omega }_{\zeta }}({{\nu }_{3}}) = \frac{{{{\mu }_{1}}(n + 1)}}{{n + 2}}\nu _{3}^{{n + 1}}$Откуда следует, что при ${{\nu }_{3}} \to 0$ функции ${{\omega }_{\xi }} \to 0$, ${{\omega }_{\eta }} \to 0$, ${{\omega }_{\zeta }} \to 0$.
Покажем, что, кроме свойства асимптотичности, движение тела имеет и свойство изоконичности движения. Изоконическими движениями называются движения тела, для которых подвижный и неподвижный аксоиды вектора угловой скорости симметричны относительно касательной к ним плоскости, проходящей через начало координат [36].
Изоконические движения в динамике тяжелого твердого тела имеют место в решениях Ж. Лагранжа [37], Д. Гриоли [38], В.А. Стеклова [39]. Например, изоконические движения в решении В.А. Стеклова рассмотрены Р. Фаббри [40, 41], Е.И. Харламовой и Г.В. Мозалевской [42]. В полях сложной структуры они изучены в [43, 44].
Выполним в решении (1.11) замену переменных: вместо ${{\omega }_{1}}$, ${{\omega }_{2}}$, ${{\omega }_{3}}$ введем переменные
(2.9)
${{\Omega }_{1}} = \frac{1}{{\kappa _{0}^{{}}}}\left( {\omega _{1}^{{}}\beta _{2}^{{}} - \omega _{2}^{{}}\beta _{1}^{{}}} \right),\quad {{\Omega }_{2}} = \frac{1}{{\kappa _{0}^{{}}}}\left( {\omega _{1}^{{}}\beta _{1}^{{}} + \omega _{2}^{{}}\beta _{2}^{{}}} \right),\quad {{\Omega }_{3}} = \omega _{3}^{{}}$Замена (2.9) означает поворот подвижной системы координат вокруг третьей координатной оси. Подставим ${{\omega }_{1}}$, ${{\omega }_{2}}$, ${{\omega }_{3}}$ из (1.11) в равенства (2.9). Тогда получим
(2.10)
${{\Omega }_{1}}({{\nu }_{3}}) = \frac{{{{\mu }_{1}}(n + 1)}}{{n + 2}}\nu _{3}^{n}\sqrt {\lambda _{0}^{2} - \nu _{3}^{2}} ,\quad {{\Omega }_{2}}({{\nu }_{3}}) = \frac{{{{\mu }_{1}}(n + 1)}}{{n + 2}}\nu _{3}^{{n + 1}},\quad {{\Omega }_{3}}({{\nu }_{3}}) = {{\mu }_{1}}\nu _{3}^{n}$Из соотношений (2.8) и (2.10) следует
3. Применение модифицированного метода Пуансо в истолковании движения тела. Для исследования движения эллипсоида инерции в неподвижном пространстве необходимо получить матрицу перехода от подвижного базиса к неподвижному базису. Введем углы Эйлера $\phi $, $\psi $, $\theta $, используя равенства
(3.1)
$\begin{gathered} {{\nu }_{1}} = \sin \theta \sin \phi ,\quad {{\nu }_{2}} = \sin \theta \cos \phi ,\quad {{\nu }_{3}} = \cos \theta \\ {{\omega }_{1}} = \dot {\psi }\sin \theta \sin \phi + \dot {\theta }\cos \phi ,\quad {{\omega }_{2}} = \dot {\psi }\sin \theta \cos \phi - \dot {\theta }\sin \phi ,\quad {{\omega }_{3}} = \dot {\phi } + \dot {\psi }\cos \theta \\ \end{gathered} $Обозначим единичные векторы подвижной системы координат через ${\mathbf{i}}_{1}^{{}}$, ${\mathbf{i}}_{2}^{{}}$, ${\mathbf{i}}_{3}^{{}}$, а неподвижной системы координат – через ${\mathbf{э}}_{1}^{{}},{\mathbf{э}}_{2}^{{}},{\mathbf{э}}_{3}^{{}} = {\mathbf{\nu }}$. Из (3.1) следуют очевидные равенства
(3.2)
$\phi (t) = {\text{arctg}}\frac{{{\mathbf{\nu }}(t) \cdot {{{\mathbf{i}}}_{1}}}}{{{\mathbf{\nu }}(t) \cdot {{{\mathbf{i}}}_{2}}}},\quad \theta (t) = {\text{arccos}}({\mathbf{\nu }} \cdot {{{\mathbf{i}}}_{3}}),\quad \psi (t) = \int\limits_{{{t}_{0}}}^t {\frac{{\left( {{\mathbf{\omega }}(\tau ) \times {{{\mathbf{i}}}_{3}}} \right) \cdot \left( {{\mathbf{\nu }}(\tau ) \times {{{\mathbf{i}}}_{3}}} \right)}}{{{{{\left( {{\mathbf{\nu }}(\tau ) \times {{{\mathbf{i}}}_{3}}} \right)}}^{2}}}}d\tau } $Поскольку полярный угол неподвижного годографа можно определить из соотношений (2.8)
(3.3)
$\alpha ({{\nu }_{3}}) = {\text{arctg}}\frac{{n + 2}}{{(n + 1)\sqrt {\lambda _{0}^{2} - \nu _{3}^{2}} }},$(3.4)
${\text{tg}}\left( {\alpha ({{\nu }_{3}}) - \psi ({{\nu }_{3}})} \right) = \frac{{\left( {{\mathbf{\omega }}({{\nu }_{3}}) \times {\mathbf{\nu }}({{\nu }_{3}})} \right) \cdot \left( {{\mathbf{\nu }}({{\nu }_{3}}) \times {{{\mathbf{i}}}_{3}}} \right)}}{{{{{\mathbf{i}}}_{3}} \cdot \left( {{\mathbf{\omega }}({{\nu }_{3}}) \times {\mathbf{\nu }}({{\nu }_{3}})} \right)}}$На основании равенств (1.11) и (1.12), а также (3.3) и (3.4) получим
(3.5)
$\psi ({{\nu }_{3}}) = - {\text{arctg}}(n + 1)\sqrt {\lambda _{0}^{2} - \nu _{3}^{2}} + {{\psi }_{0}}$Запишем первые два соотношения из (3.2), принимая ${{\nu }_{3}}$ за вспомогательную переменную:
(3.6)
$\phi ({{\nu }_{3}}) = {\text{arctg}}\frac{{\beta _{1}^{{}}\left[ {n - (n + 1)\nu _{3}^{2}} \right] - \beta _{2}^{{}}(n + 1)\nu _{3}^{{}}\sqrt {\lambda _{0}^{2} - \nu _{3}^{2}} }}{{\beta _{2}^{{}}\left[ {n - (n + 1)\nu _{3}^{2}} \right] + \beta _{1}^{{}}(n + 1)\nu _{3}^{{}}\sqrt {\lambda _{0}^{2} - \nu _{3}^{2}} }}$Применим к исследованию решения (1.11)–(1.13) модифицированный метод [21]. Пусть ${\mathbf{b}}({{\nu }_{3}}) = b({{\nu }_{3}}){\mathbf{\omega }}({{\nu }_{3}})$, где
Функция (3.8) определена на отрезке (1.15), исключая точку ${{\nu }_{3}} = 0$. Тогда из (1.11), (1.12), (2.8) и (3.8) имеем
(3.9)
${\mathbf{b}}_{\Pi }^{{}}({{\nu }_{3}}) = b_{1}^{{}}({{\nu }_{3}}){\mathbf{i}}_{1}^{{}} + b_{2}^{{}}({{\nu }_{3}}){\mathbf{i}}_{2}^{{}} + b_{3}^{{}}({{\nu }_{3}}){\mathbf{i}}_{3}^{{}}$(3.10)
${\mathbf{b}}_{{\text{H}}}^{{}}({{\nu }_{3}}) = b_{\xi }^{{}}({{\nu }_{3}}){\mathbf{э}}_{1}^{{}} + b_{\eta }^{{}}({{\nu }_{3}}){\mathbf{э}}_{2}^{{}} + b_{\zeta }^{{}}({{\nu }_{3}}){\mathbf{э}}_{3}^{{}}$,(3.11)
$\begin{gathered} b_{1}^{{}}({{\nu }_{3}}) = \frac{{{{\mu }_{1}}(n + 1)}}{{n + 2}}\left( {\beta _{1}^{{}}{{\nu }_{3}} + \beta _{2}^{{}}\sqrt {\lambda _{0}^{2} - \nu _{3}^{2}} } \right) \\ b_{2}^{{}}({{\nu }_{3}}) = \frac{{{{\mu }_{1}}(n + 1)}}{{n + 2}}\left( {\beta _{2}^{{}}{{\nu }_{3}} - \beta _{1}^{{}}\sqrt {\lambda _{0}^{2} - \nu _{3}^{2}} } \right),\quad b_{3}^{{}}({{\nu }_{3}}) = {{\mu }_{1}} \\ \end{gathered} $(3.12)
$b_{\xi }^{{}}({{\nu }_{3}}) = \frac{{{{\mu }_{1}}(n + 1)}}{{n + 2}}\sqrt {\lambda _{0}^{2} - \nu _{3}^{2}} ,\quad b_{\eta }^{{}}({{\nu }_{3}}) = {{\mu }_{1}},\quad b_{\zeta }^{{}}({{\nu }_{3}}) = \frac{{{{\mu }_{1}}(n + 1)}}{{n + 2}}$Подвижный и неподвижный годографы (3.9) и (3.10) – конгруэнтные плоские кривые; в алгебраической форме в силу (3.11) и (3.12) их координаты определяются уравнениями
(3.13)
$\begin{gathered} b_{1}^{2}({{\nu }_{3}}) + b_{2}^{2}({{\nu }_{3}}) = \frac{{\mu _{1}^{2}n}}{{n + 2}},\quad b_{\zeta }^{{}}({{\nu }_{3}}) = {{\mu }_{1}} \\ b_{\xi }^{2}({{\nu }_{3}}) + b_{\eta }^{2}({{\nu }_{3}}) = \frac{{\mu _{1}^{2}n}}{{n + 2}},\quad b_{\eta }^{{}}({{\nu }_{3}}) = {{\mu }_{1}} \\ \end{gathered} $Таким образом, применение модифицированного метода [21] позволяет представить движение тела качением без скольжения двух конусов (3.13). В силу структуры (3.13) данный подход имеет несомненные преимущества перед прямым методом Пуансо, так как уравнения подвижного и неподвижного годографов (2.7) и (2.8) содержат одно алгебраическое уравнение, степень которого зависит от параметра $n$. Это обстоятельство существенно скажется на построении годографов. В отличие от этого свойства, годографы (3.13) векторов (3.9) и (3.10) для любых $n$ являются плоскими кривыми (уравнение плоскости не зависит от $n$) и только радиусы окружностей зависят от $n$.
Рассмотрим движение эллипсоида инерции в решении (1.11)–(1.13). Данная задача решается следующим образом. Рассмотрим уравнение эллипсоида инерции тела, используя равенства из (1.9):
где $x$, $y$, $z$ – координаты точек эллипсоида (3.14), $\sigma _{0}^{{}}$ – постоянная. Непосредственной подстановкой значений ${{b}_{i}}$ ($i = \overline {1,3} $) из (3.11) в уравнение (3.14) убеждаемся в том, что конец подвижного годографа вектора ${\mathbf{b}}_{\Pi }^{{}}$ из (3.9) принадлежит поверхности (3.14) при $\sigma _{0}^{2} = \mu _{1}^{2}(n + 1)$. То есть при обкатывании поверхностей с направляющими ${\mathbf{b}}_{\Pi }^{{}}$, ${\mathbf{b}}_{{\rm H}}^{{}}$ получим движение эллипсоида инерции. Остается выяснить свойство расположения эллипсоида инерции в неподвижном пространстве. Покажем, что эллипсоид инерции тела на кривой (3.11) касается неподвижной плоскости $b_{\eta }^{{}}({{\nu }_{3}}) = {{\mu }_{1}}$.Запишем уравнение (3.14) в переменных ${{b}_{i}}$ ($i = \overline {1,3} $):
(3.15)
$\Phi (b_{1}^{{}},b_{2}^{{}},b_{3}^{{}}) = (n + 2)(b_{1}^{2} + b_{2}^{2}) + b_{3}^{2} - \mu _{1}^{2}(n + 1) = 0$Запишем матрицу перехода от подвижной системы координат к неподвижной системе [13]:
(3.16)
$\begin{gathered} L(\phi ,\psi ,\theta ) = \\ = \left( {\begin{array}{*{20}{c}} {\cos \phi \cos \psi - \sin \phi \sin \psi \cos \theta }&{ - \sin \phi \cos \psi - \cos \phi \sin \psi \cos \theta }&{\sin \psi \sin \theta } \\ {\cos \phi \sin \psi + \sin \phi \cos \psi \cos \theta }&{ - \sin \phi \sin \psi + \cos \phi \cos \psi \cos \theta }&{ - \cos \psi \sin \theta } \\ {\sin \phi \sin \theta }&{\cos \phi \sin \theta }&{\cos \theta } \end{array}} \right), \\ \end{gathered} $(3.17)
$\begin{gathered} \cos \theta = {{\nu }_{3}},\quad \sin \theta = \sqrt {1 - \nu _{3}^{2}} ,\quad \sin \phi = \frac{{{{\nu }_{1}}({{\nu }_{3}})}}{{\sqrt {1 - \nu _{3}^{2}} }},\quad \cos \phi = \frac{{{{\nu }_{1}}({{\nu }_{3}})}}{{\sqrt {1 - \nu _{3}^{2}} }} \\ \sin \psi = \frac{{\sqrt {\lambda _{0}^{2} - \nu _{3}^{2}} }}{{\sqrt {1 - \nu _{3}^{2}} }},\quad \cos \psi = - \frac{1}{{(n + 1)\sqrt {1 - \nu _{3}^{2}} }} \\ \end{gathered} $Вычислим градиент поверхности (3.15) на кривой ${\mathbf{b}}_{\Pi }^{{}}({{\nu }_{3}})$:
(3.18)
$\overline {grad} \,\Phi \left| {_{{{\mathbf{b}}_{\Pi }^{{}}({{\nu }_{3}})}}} \right. = \frac{1}{{{{\nu }_{3}}}}\left[ { - {{\mu }_{1}}n{{\nu }_{1}} + {{\beta }_{1}}(n + 2){{\mu }_{2}}} \right]{\mathbf{i}}_{1}^{{}} + \frac{1}{{{{\nu }_{3}}}}\left[ { - {{\mu }_{1}}n{{\nu }_{2}} + \beta _{2}^{{}}(n + 2)} \right]{\mathbf{i}}_{2}^{{}} + {{\mu }_{1}}{\mathbf{i}}_{3}^{{}}$Используя равенства (3.16)–(3.18), вычислим значение вектора (3.18) в неподвижной системе координат:
(3.19)
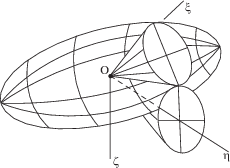
${{\left. {\overline {{\text{grad}}} \,\Phi } \right|}_{{{\mathbf{b}}_{\Pi }^{{}}({{\nu }_{3}})}}} = {{\mu }_{1}}(n + 1){\mathbf{э}}_{2}^{{}}$Равенство (3.19) показывает, что при движении эллипсоида инерции в неподвижном пространстве он катается по плоскости $b_{\eta }^{{}}({{\nu }_{3}}) = {{\mu }_{1}}$ по кривым (3.9), (3.10). Эскиз движения эллипсоида показан на рис. 1. Поскольку при $t \to \infty $ ${{\nu }_{3}} \to 0$, а точка ${{\nu }_{3}} = 0$ исключена из рассмотрения, то по непрерывности можно сделать заключение, что при $t \to \infty $ эллипсоид инерции в неподвижном пространстве стремится к состоянию покоя.
Заключение. Исследовано движение эллипсоида инерции тела в одном решении задачи о движении тела под действием потенциальных сил. Установлен определенный аналог истолкования Пуансо в решении Эйлера: движение тела представлено качением без скольжения эллипсоида инерции тела по неподвижной в пространстве плоскости, которая является касательной плоскостью к эллипсоиду инерции. Доказано, что данное касание происходит на кривой неподвижного годографа вспомогательного вектора, коллинеарного вектору угловой скорости. На основе модифицированного метода Пуансо, предложенного автором данной статьи [21], движение тела можно представить посредством качения подвижного годографа вспомогательного вектора по неподвижному годографу этого вектора. Преимущество данного результата, по сравнению с результатом истолкования прямым методом, состоит в том, что направляющие линии соответствующих аксоидов являются окружностями одинакового радиуса, что означает свойство изоконичности движения тела.
Автору статьи известен только один аналогичный случай, установленный И.Н. Гашененко [45], в случае А. Брессана [46] для решения В. Гесса [47]. Однако, для этого варианта представления движения с помощью качения эллипсоида инерции по плоскости не выполняется свойство изоконичности движения гироскопа Гесса, так как кривая, по которой происходит качение эллипсоида, является трансцендентной кривой.
Статья посвящается памяти моего учителя Павла Васильевича Харламова.
Список литературы
Зиглин С.Л. Ветвление решений и несуществование первых интегралов в гамильтоновых системах // Функц. анализ и его приложения. 1983. Т. 17. № 1. С. 8–23.
Зиглин С.Л. Расщепление сепаратрис, ветвление решений и несуществование интеграла в динамике твердого тела // Тр. Моск. матем. об-ва. 1980. Т. 41. С. 287–303.
Козлов В.В. О несуществовании аналитических интегралов канонических систем, близких к интегрируемым // Вестн. Моск. ун-та. Сер. 1. Математика и механика. 1974. № 2. С. 77–82.
Борисов А.В. Необходимые и достаточные условия интегрируемости уравнений Кирхгофа // Reg. & Chaot. Dyn. 1996. V. 1. № 2. P. 61–73.
Козлов В.В., Онищенко Д.А. Неинтегрируемость уравнений Кирхгофа // Докл. АН СССР. 1982. Т. 266. № 6. С. 1298–1300.
Суслов Г.К. Теоретическая механика. М.; Л.: Гостехиздат, 1946. 655 с.
Горр Г.В., Кудряшова Л.В., Степанова Л.А. Классические задачи динамики твердого тела. Киев: Наук. думка, 1978. 294 с.
Борисов А.В., Мамаев И.С. Динамика твердого тела. М.; Ижевск: Регулярная и хаотическая динамика, 2001. 384 с.
Горр Г.В., Мазнев А.В. Динамика гиростата, имеющего неподвижную точку. Донецк: ДонНУ, 2010. 364 с.
Poinsot L. Thèorie nouvelle de la rotation des corps // J. Math. Pures et Appl. 1851. Bd. 1. № 16. P. 289–336.
Euler L. Du mouvement de rotation des corps solides autour d’un axe variable // Ibid. 1758, 1765. V. 14. P. 154–193.
Раус Э.Дж. Динамика системы твердых тел. М.: Наука, 1983. Т. 1. 464 с.; Т. 2. 544 с.
Магнус К. Гироскоп. Теория и применение. М.: Мир, 1974. 526 с.
Домогаров А.С. О свободном движении гиростата. СПб., 1893. 175 с.
Харламов П.В. Лекции по динамике твердого тела. Новосибирск: Изд-во Новосиб. гос. ун-та, 1965. 221 с.
Жуковский Н.Е. О значении геометрического истолкования в теоретической механике // Собр. соч.: в 7 т. М.-Л.: Гостехиздат, 1950. Т. 7. С. 9–15.
Жуковский Н.Е. Локсодромический маятник Гесса // Собр. соч.: В 7 т. М.; Л.: Гостехиздат, 1948. Т. 1. С. 257–274.
Харламов П.В. Кинематическое истолкование движения тела, имеющего неподвижную точку // ПММ. 1964. Т. 28. Вып. 3. С. 502–507.
Гашененко И.Н., Горр Г.В., Ковалев А.М. Классические задачи динамики твердого тела. Киев: Наук. думка, 2012. 401 с.
Горр Г.В., Ковалев А.М. Движение гиростата. Киев: Наук. думка, 2013. 408 с.
Горр Г.В. Об одном подходе в применении теоремы Пуансо кинематического истолкования движения тела с неподвижной точкой // Механика твердого тела. 2012. Вып. 42. С. 26–36.
Горр Г.В., Щетинина Е.К. О движении тяжелого твердого тела в двух частных случаях решения С.В. Ковалевской // Нелинейная динамика. 2018. Т. 14. № 1. С. 123–138.
Горр Г.В., Синенко А.И. О кинематическом истолковании движения тяжелого твердого тела с неподвижной точкой // ПММ. 2014. Т. 28. Вып. 3. С. 334–345.
Горр Г.В., Данилюк Д.А., Ткаченко Д.Н. О кинематическом истолковании движения тела в частном случае решения Д.Н. Горячева–С.А. Чаплыгина // Ж. Теор. Прикл. Мех. (ДонНУ). № 3–4 (60). 2017. С. 19–32.
Горр Г.В. О трех инвариантных соотношениях уравнений движения тела в потенциальном поле сил // ПММ. 2019. Т. 83. № 2. С. 202–214.
Леви-Чивита Т., Амальди У. Курс теоретической механики. В 2-х т. Т. 2. Ч. 2. М.: Изд-во иностр. лит., 1951. 555 с.
Харламов П.В. Об инвариантных соотношениях системы дифференциальных уравнений // Механика твердого тела. 1974. Вып. 6. С. 15–24.
Горр Г.В. Инвариантные соотношения уравнений динамики твердого тела (теория, результаты, комментарии). М.; Ижевск: Институт компьютерных исследований, 2017. 424 с.
Галиуллин А.С. Обратные задачи динамики тяжелого твердого тела с одной закрепленной точкой // Диффер. уравн. 1972. Т. 8. № 8. С. 1357–1362.
Горячев Д.Н. Некоторые общие интегралы в задаче о движении твердого тела. Варшава: Тип. Варш. уч. округа, 1910. 62 с.
Горячев Д.Н. Новые случаи движения твердого тела вокруг неподвижной точки // Варшав. унив. изв. 1915, кн. 3. С. 1–11.
Yehia H.M. Transformations of mechanical systems with cyclic coordinates and new integrable problems // J. Phys. A: Math.-Con. 2001. V. 34. P. 11167–11183.
Yehia H.M. Kovalevskaya’s integrable case: generalizations and related new results // Reg. Chaot. Dyn. 2003. V. 8. № 3. P. 337–348.
Комаров И.В., Кузнецов В.Б. Обобщенный гиростат Горячева–Чаплыгина в квантовой механике // Дифференциальная геометрия, группы Ли и механика. Зап. научн. сем. ЛОМИ АН СССР. 1987. Т. 9. С. 134–141.
Комаров И.В., Кузнецов В.Б. Квазиклассическое квантование волчка Ковалевской // Теор. и мат. физ. 1987. Т. 73. № 3. С. 335–347.
Горр Г.В., Илюхин А.А., Ковалев А.М., Савченко А.Я. Нелинейный анализ поведения механических систем. Киев: Наук. думка, 1984. 285 с.
Klein F., Sommerfeld A. Über die Theorie des Kreisels. N.Y.: Johnson Reprint Corp., 1965. 966 p.
Grioli G. Esistenza e determinazione delle precessioni regolari dinamicamente possibili per un solido pesante asimmetrico // Ann. di Matem. pura ed Applic. 1947. S. 4. V. 24, f. 3–4. P. 271–281.
Стеклов В.А. Новое частное решение дифференциальных уравнений движения твердого тела, имеющего неподвижную точку // Тр. отд-ния физ. наук Об-ва любителей естествознания. 1899. Т. 10. № 1. С. 1–3.
Fabbri R. Sopra una soluzione particolare delle equazioni del moto di un solido pesante ad un punto fisso // Atti. Accad. Naz. Lincei, Cl. Sci. Fis. Mat. e Nat. 1934. V. 19. № 6. P. 407–415, 495–502, 872–873.
Fabbri R. Sui coni di Poinsot in una particolare rotazione dei solidi pesanti // Atti. Accad. naz. Lincei. Rend. Cl. sci. fis., mat. e natur. 1934. Ser. 6. V. 19. P. 872–873.
Харламова Е.И., Мозалевская Г.В. Интегродифференциальное уравнение динамики твердого тела. Киев: Наук. думка, 1986. 296 с.
Верховод Е.В., Горр Г.В. Прецессионно-изоконические движения твердого тела с неподвижной точкой // ПММ. 1993. Т. 57. Вып. 4. С. 31–39.
Верховод Е.В., Горр Г.В. Новые случаи изоконических движений в обобщенной задаче динамики твердого тела с неподвижной точкой // ПММ. 1993. Т. 57. Вып. 5. С. 25–34.
Гашененко И.Н. Кинематическое представление по Пуансо движения тела в случае Гесса // Механика твердого тела. 2010. Вып. 40. С. 12–20.
Bressan A. Sulle precessini d’un corpo rigido costituenti moti di Hess // Rend. Semin. Mat. Univ. Padova. 1957. V. 27. P. 276–283.
Hess W. Über die Euler’schen Bewegungsgleichungen und über eine neue partikuläre Lösung des Problems der Bewegung eines starren schweren Körpers um einen festen Punkt // Math. Ann. 1890. B. 37. H. 2. S. 153–181.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика