Прикладная математика и механика, 2020, T. 84, № 1, стр. 122-136

Покрытия находят широкое применение в современной технике как эффективное средство снижения трения и износа деталей узлов трения. В процессе эксплуатации покрытие изнашивается, и это оказывает влияние на технические характеристики узла трения. Кроме того, износ покрытия является главным фактором, определяющим его долговечность. Все это обуславливает актуальность задачи расчета кинетики изнашивания покрытия.

Существуют различные подходы к моделированию изнашивания покрытий [1–4]. Детальное описание кинетики изнашивания покрытия предполагает использование решения соответствующей износоконтактной задачи [5], в рамках которой покрытие представляется полосой (двумерная постановка) или слоем (трехмерная постановка). При таком подходе в каждый момент времени решается контактная задача для покрытия, толщина $h$ которого изменяется вследствие его изнашивания. Поведение покрытия в условиях контактного взаимодействия определяется на основе деформационной модели, связывающей контактные напряжения и граничные перемещения.

Простейшая деформационная модель покрытия постоянной толщины $h = {{h}_{0}}$ устанавливает прямо пропорциональную зависимость нормального граничного перемещения ${v}$ от контактного давления $p$ и имеет вид модели Винклера ${v} = - B{{h}_{0}}p$ с постоянным коэффициентом податливости $B{{h}_{0}}$. Подобная модель использовалась в ряде работ в связи с расчетом кинетики изнашивания покрытия [6].

Ввиду того, что толщина $h$ покрытия обычно мала и сравнима с его износом $W$, возникает необходимость применения уточненных деформационных моделей, учитывающих формоизменение покрытия вследствие его изнашивания. В качестве такой модели в работах [7–9] использовалась модель Винклера ${v} = - Bhp$, $h = {{h}_{0}} - W$ с изменяющимся в процессе изнашивания коэффициентом податливости $Bh$. Следует отметить, что использование уточненных деформационных моделей приводит к нелинейным постановкам износоконтактной задачи.

В данной работе наряду с указанными моделями рассматривается уточненная деформационная модель покрытия, учитывающая искривленность границы покрытия [10]. С использованием различных деформационных моделей в рамках двумерной постановки износоконтактной задачи выполняются расчеты кинетики изнашивания покрытия, которые свидетельствуют о важности учета фактора формоизменения покрытия в процессе его изнашивания.

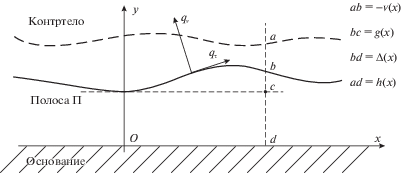
1. Основные уравнения износоконтактной задачи для покрытия формулируются далее в рамках двумерной теории упругости (плоское деформированное состояние). В этом случае покрытие представляется в виде упругой полосы $\Pi $ переменной ширины, сцепленной с абсолютно жестким основанием (рис. 1). Свяжем систему координат $Oxy$ с основанием, как это показано на рис. 1, и обозначим через $h(x)$ ширину полосы.

Считается, что к верхней границе полосы приложены касательное ${{q}_{\tau }}$ и нормальное ${{q}_{\nu }}$ напряжения, обусловленные ee контактным взаимодействием с контртелом. Соответствующие перемещения верхней границы полосы вдоль осей $x$ и $y$ обозначим через $u$ и ${v}$. В качестве контртела выступает абсолютно жесткое цилиндрическое тело, образующая которого перпендикулярна плоскости $Oxy$. Контртело может скользить по покрытию вдоль своей образующей (продольное скольжение) или перпендикулярно ей (поперечное скольжение).

Деформационная модель покрытия определяет связь напряжений ${{q}_{\tau }}$, ${{q}_{\nu }}$ и перемещений $u$, ${v}$. Подобная связь устанавливается путем решения соответствующей краевой задачи теории упругости для неканонической области (полосы $\Pi $) и в общем виде реализуется с использованием достаточно сложных алгоритмов [11]. Однако в случае тонкого покрытия, используя асимптотический подход, удается представить деформационную модель в виде простых алгебраических соотношений [6, 12]. Для полосы переменной ширины использование такого подхода приводит к следующим соотношениям [10]:

в которых $\unicode{230} = 3\, - \,4\nu $, $\nu $ – коэффициент Пуассона, $G$ – модуль сдвига, штрих у символа функции означает производную по координате $x$, при этом полоса считается асимптотически тонкой и слабоискривленной. Последнее означает, что изменение $\Delta A \approx A{\text{'}}h$ любой величины $A$ вдоль оси $x$ на расстоянии $h$ мало по сравнению с самой величиной $A$, т.е. где $\varepsilon $ – малый параметр, $\varepsilon \ll 1$. В качестве величины $A$ здесь может выступать сама ширина $h$ полосы, граничные перемещения $u$, ${v}$, контактные напряжения ${{q}_{\tau }}$, ${{q}_{\nu }}$. В частности, при $A = h$ условие (1.2) означает, что $\left| {h{\text{'}}} \right|\sim \varepsilon \ll 1$. Правые части соотношений (1.1) содержат слагаемые, порядок малости которых, согласно условию (1.2), не превышает $O({{\varepsilon }^{2}})$.

Учитывая фрикционный характер контактного взаимодействия покрытия с контртелом, допустим, что контактные напряжения ${{q}_{\tau }}$, ${{q}_{\nu }}$ связаны друг с другом законом трения Кулона [13]

в котором $0 < p = - {{q}_{\nu }}$ – контактное давление, $0 \leqslant \mu $ – коэффициент трения, $0 \leqslant {{\tau }_{0}}$ – адгезионная составляющая трения. Запись (1.3) закона Кулона при неотрицательных значениях $p$, $\mu $ и ${{\tau }_{0}}$ предполагает, что скольжение контртела происходит в направлении оси $x$.

Подстановка в равенство (1.3) правых частей соотношений (1.1) позволяет найти выражение для перемещения $u$ через перемещение ${v}$. В свою очередь, такое выражение позволяет исключить перемещение $u$ из второго соотношения (1.1) и получить следующую деформационную модель покрытия

где $B = (1 - 2\nu ){{[2(1 - \nu )G]}^{{ - 1}}}$. При выводе зависимости (1.4) выполнялась оценка получаемых слагаемых с использованием условия (1.2) и удерживались только слагаемые, порядок малости которых не превышает $O({{\varepsilon }^{2}})$. Если же в (1.4) пренебречь слагаемыми порядка $\varepsilon $, то можно прийти к вышеупомянутой модели Винклера:

В случае постоянной ширины $h = {{h}_{0}}$ полосы зависимость (1.4) принимает вид деформационной модели

которая использовалась ранее для расчета трения и износа подвижных сопряжений с покрытиями [14, 15]. Пренебрегая в левой части равенства (1.6) последним слагаемым, имеющим порядок малости $\varepsilon $, получим модель Винклера с постоянным коэффициентом податливости: которая также упоминалась выше.

Замечание 1. Величина $ - {v}$ представляет собой упругое сжатие полосы, которое не может превышать ее ширину, т.е. $ - {v} < h$. Применительно к деформационным моделям (1.5) и (1.7) это условие принимает вид неравенства

Замечание 2. Общая деформационная модель покрытия (1.4) содержит производную $h{\text{'}}$, т.е. учитывает искривленность границы покрытия. Кроме того, эта модель содержит в качестве параметров коэффициент трения $\mu $ и адгезионную составляющую трения ${{\tau }_{0}}$. Более простая деформационная модель (1.6) содержит только коэффициент трения $\mu $, тогда как модели (1.5) и (1.7) винклеровского типа вообще не учитывают трение.

Записанные выше соотношения имеют место в каждый момент времени $t$ процесса изнашивания покрытия, обусловленного его контактным взаимодействием с контртелом. В процессе изнашивания толщина $h$ покрытия уменьшается на величину $W$ линейного износа, так что

где ${{h}_{{{\kern 1pt} 0}}}$ – начальная толщина покрытия. Здесь и далее аргументом $t$ обозначается зависимость рассматриваемых величин от времени.

Считается, что скорость износа покрытия при неизменной скорости скольжения контртела линейно зависит от контактного давления [13]. Представим эту зависимость в виде закона изнашивания

в котором $\alpha $ – параметр износостойкости материала покрытия, точка над символом функции означает производную по времени $t$, причем первое равенство (1.10) является следствием соотношения (1.9).

Граничное перемещение ${v}$, присутствующее в вышеуказанных деформационных моделях, связано с шириной полосы и геометрией контртела условием контакта (рис. 1):

где – зазор между контртелом и основанием, ${{\Delta }_{c}}(t) = \Delta (0,t)$, функция $g(x)$ описывает форму контртела, $g(0) = 0$, $\delta (t)$ – внедрение контртела в покрытие относительно некоторого, произвольно заданного уровня $y = {{y}_{{{\kern 1pt} 0}}}$.

При условии, что $\left| {h{\text{'}}} \right| \sim \varepsilon \ll 1$, нормальная (вдоль оси $y$) нагрузка $P$ на контртело, приходящаяся на единицу длины его образующей, связана с контактным давлением $p$ согласно условию равновесия

Здесь и далее отрезок $[ - a,b]$ задает область контакта контртела и покрытия в плоскости $Oxy$.

Задача расчета кинетики изнашивания покрытия состоит в нахождении функций $h(x,t)$ и $p(x,t)$, удовлетворяющих уравнениям (1.10) и (1.11), при использовании той или иной деформационной модели покрытия. В дальнейшем эта задача будет конкретизирована для трех случаев, различающихся кинематикой скольжения и геометрией контакта контртела и покрытия.

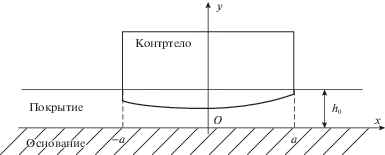
2. Продольное скольжение контртела. Допустим, что контртело скользит вдоль своей образующей (перпендикулярно плоскости $Oxy$) при фиксированной области контакта $[ - a,a]$, а толщина ${{h}_{0}}$ покрытия в начальном состоянии постоянна (рис. 2). Для описания упругого поведения покрытия в процессе его изнашивания воспользуемся деформационной моделью (1.5). Не ограничивая общности, внедрение $\delta $ контртела в покрытие будем отсчитывать от уровня $y = {{h}_{{{\kern 1pt} 0}}}$, т.е. положим в выражении (1.12): ${{y}_{0}} = {{h}_{{{\kern 1pt} 0}}}$.

Исключим с помощью условия контакта (1.11) граничное перемещение ${v}$ из соотношения (1.5) и заменим в полученном равенстве контактное давление $p$ комбинацией $ - \dot {h}{\text{/}}\alpha $ согласно закону изнашивания (1.10). В результате можно прийти к следующему уравнению кинетики изнашивания покрытия:

Уравнение (2.1) представляет собой нелинейное дифференциальное уравнение Абеля второго рода, и его решение при произвольной правой части может быть построено только приближенно численными методами. В дальнейшем будет рассматриваться случай линейной зависимости внедрения контртела от времени:

в котором уравнение (2.1) имеет точное решение [16]. С учетом начального условия $h(x,0) = {{h}_{0}}$ это решение представляется в параметрическом виде: где $\xi $ – параметр решения, ${{\xi }_{0}}$ – значение $\xi $, отвечающее моменту $t = 0$,

Определив из равенств (2.2) производную $\dot {h}$ и воспользовавшись законом изнашивания (1.10), можно получить параметрическое выражение для контактного давления:

Ввиду того, что контактное давление $p$ принимает только положительные значения, и должно выполняться неравенство (1.8), правая часть равенства (2.4) задает диапазон допустимых значений параметра $\xi $:

Согласно равенствам (2.3) вид функции $\varphi (\xi )$ в значительной степени определяется наличием корней у квадратного трехчлена $R(\xi )$, что, в свою очередь, зависит от значения параметра ${{\Delta }_{1}}$. Рассмотрим для определенности случай

когда квадратный трехчлен $R(\xi )$ не имеет корней, будучи положительным. Тогда [17] и, в силу первого неравенства (2.3): $1{\text{/}}4 < {{\Delta }_{1}} < {{\xi }_{0}}$.

Как показывает анализ первого равенства (2.2) с функцией $\varphi (\xi )$ вида (2.6), с течением времени $t$ параметр $\xi $ возрастает. Это означает, что неравенства (2.3) обеспечивают выполнение условия (2.5).

При использовании вместо (1.5) более простой деформационной модели (1.7) получается линейное уравнение кинетики изнашивания покрытия, которое совпадает с уравнением (2.1), если в последнем заменить первый член на $B{\text{/}}\alpha {{h}_{0}}\dot {h}$. Решение $h$ такого уравнения и соответствующее контактное давление $p$, определяемое из закона изнашивания (1.10), имеют вид

причем $D(x) = g(x) - {{\delta }_{0}} + {{\delta }_{1}}{\text{/}}\eta $, $\eta = \alpha {\text{/}}(B{{h}_{0}})$.

Полученные выше равенства позволяют выполнить расчет кинетики изнашивания покрытия. Это было сделано при

в случае плоского контртела ($g(x) \equiv 0$), когда отсутствуют зависимости величин $h$ и $p$ от координаты $x$. При использовании деформационной модели (1.5) расчет выполнялся на основе равенств (2.2), (2.4) и (2.6), а при использовании модели (1.7) – по формулам (2.7).

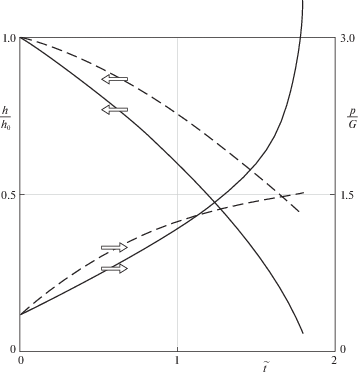
На рис. 3 показаны расчетные зависимости толщины покрытия $h$ и контактного давления $p$ от безразмерного времени $\tilde {t} = \eta t$. Сплошные и штриховые линии отвечают деформационным моделям (1.5) и (1.7), соответственно.

Показанные зависимости свидетельствуют о том, что использование уточненной деформационной модели (1.5), учитывающей формоизменение покрытия, может существенным образом изменить результаты расчета кинетики его изнашивания.

3. Поперечное скольжение контртела (конечная область контакта). Рассмотрим гладкое выпуклое контртело, которое скользит по покрытию перпендикулярно своей образующей (в плоскости $Oxy$, рис. 4). Как и прежде, неизношенное покрытие имеет постоянную толщину ${{h}_{0}}$ и описывается деформационной моделью (1.5).

Свяжем с подвижным контртелом систему координат $Oxy$ (рис. 4) и допустим, что в ней существуют стационарные распределения контактного давления $p(x)$, износа $W(x)$, толщины $h(x)$ покрытия, а область контакта представляется отрезком $[ - a,b]$. В подвижной системе координат закон изнашивания (1.10) имеет вид [18]

причем

По аналогии с предыдущей задачей, исключим граничное перемещение ${v}$ из соотношения (1.5) с помощью условия контакта (1.11), записанного в подвижной системе координат, полагая ${{y}_{0}} = {{h}_{0}}$. Затем заменим в полученном равенстве контактное давление $p$ комбинацией $h{\text{'/}}\alpha $ согласно закону изнашивания (3.1). В результате придем к следующему уравнению кинетики изнашивания покрытия в подвижной системе координат:

Путем дифференцирования по $x$ уравнения (3.3) при учете закона изнашивания (3.1) можно получить уравнение для контактного давления

Уравнения (3.3) и (3.4) представляют собой нелинейные дифференциальные уравнения Абеля второго и первого рода, соответственно [16]. Их решения могут быть построены только в приближенном виде численными методами.

Отметим, что найденное из уравнения (3.4) контактное давление $p(x)$ позволяет определить толщину $h(x)$ изношенного покрытия по формулам

которые вытекают из закона изнашивания (3.1), при этом последнее равенство получается с учетом условия равновесия (1.13).

Для гладкого контртела имеют место равенства ${v}( - a) = {v}(b) = 0$, из которых в силу соотношения (1.5) следует, что

При наличии равенств (3.2) и ${v}(b) = 0$ условие контакта (1.11) позволяет установить связь $g(b) = \delta $ размера $b$ области контакта с внедрением $\delta $ контртела. Для определения размера $a$ области контакта служит первое равенство (3.5). Последнее обстоятельство обуславливает целесообразность использования уравнения (3.4) для расчета кинетики изнашивания покрытия.

При использовании вместо (1.5) более простой деформационной модели (1.7) получается линейное уравнение кинетики изнашивания покрытия, которое совпадает с уравнением (3.3), если в последнем заменить первый член на $ - B{\text{/}}\alpha {{h}_{0}}h{\text{'}}$. Контактное давление при использовании деформационной модели (1.7) описывается линейным уравнением

решение которого, удовлетворяющее второму равенству (3.5), имеет вид причем, как и прежде, $\eta = \alpha {\text{/}}(B{{h}_{0}})$.

Расчет кинетики изнашивания покрытия выполнялся на основе дифференциального уравнения (3.4) (деформационная модель (1.5)) и формулы (3.6) (деформационная модель (1.7)) в случае параболического контртела $g(x) \equiv k{{x}^{2}}$. Для решения уравнения (3.4) применялся численный метод Рунге–Кутты четвертого порядка точности [19], при этом контролировалось выполнение неравенства (1.8).

Расчет проводился при $k = 0.05$ м^–1, значения параметров $G$, $\nu $, ${{h}_{0}}$, $\alpha $ принимались такими же, как для задачи с продольным скольжением контртела (раздел 2).

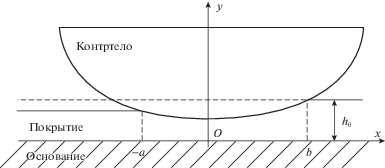
На рис. 5 показаны расчетные зависимости отношения $\rho = b{\text{/}}a$, характеризующего асимметрию области контакта, от внедрения $\delta $ контртела в покрытие. Сплошные и штриховые линии, как и прежде, отвечают деформационным моделям (1.5) и (1.7), соответственно.

Показанные зависимости свидетельствуют о том, что использование уточненной деформационной модели (1.5), учитывающей формоизменение покрытия, может существенно повлиять на контактные характеристики изнашиваемого покрытия.

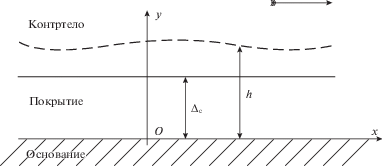
4. Поперечное скольжение контртела (бесконечная область контакта). Рассмотрим бесконечно протяженное плоское контртело, которое скользит по покрытию перпендикулярно своей образующей (в плоскости $Oxy$), в результате чего покрытие изнашивается (рис. 6). В отличие от предыдущих случаев, будем считать, что в начальном (неизношенном) состоянии покрытие имеет переменную толщину ${{h}_{0}}(x)$ и его упругое поведение описывается более сложной деформационной моделью (1.4).

В рассматриваемом случае плоского контртела: $\Delta (x,t) = {{\Delta }_{c}}(t)$ (рис. 6). Учитывая это равенство, исключим с помощью условия контакта (1.11) граничное перемещение ${v}$ из соотношения (1.4) и заменим в полученном равенстве контактное давление $p$ комбинацией $ - \dot {h}{\text{/}}\alpha $ согласно закону изнашивания (1.10). В результате можно прийти к следующему уравнению кинетики изнашивания покрытия

где ${{\mu }_{1}} = \mu \unicode{230} {\text{/}}(\unicode{230} - 1)$, ${{A}_{1}} = 2(\mu + B{{\tau }_{0}})$. Для уравнения (4.1) имеет место начальное условие

Уравнение (4.1) относится к классу квазилинейных уравнений в частных производных, и для нахождения его общего решения применим метод характеристик [20]. Однако, первые интегралы, получаемые при использовании этого метода, не позволяют эффективно реализовать известную процедуру решения задачи Коши (4.1), (4.2) [20]. В связи с этим, выполним линеаризацию уравнения (4.1), ограничив дальнейшее рассмотрение случаем малого износа покрытия. А именно, будем считать, что $W{\text{/}}{{h}_{0}}\sim \varepsilon \ll 1$ и примем во внимание условие малости деформаций покрытия: $\left| {v} \right|{\text{/}}h\sim \varepsilon \ll 1$. При таких ограничениях, используя в качестве искомой величины износ $W$, связанный с толщиной $h$ соотношением (1.9), и пренебрегая членами порядка ${{\varepsilon }^{2}}$ в уравнении (4.1), получим из него линейное уравнение

с начальным условием

Здесь

причем считается, что

Согласно определению (4.5) величины $\gamma $, последнее неравенство выполняется, если

Воспользуемся для решения уравнения (4.3) вышеупомянутым методом характеристик и составим соответствующую характеристическую систему

Далее ограничимся случаем постоянного зазора между контртелом и основанием:

Для такого случая процедура построения решения задачи Коши (4.3), (4.4) с использованием первых интегралов системы (4.7) формально повторяет выкладки работы [15], поэтому выпишем сразу это решение, справедливость которого можно проверить прямой подстановкой в равенства (4.3) и (4.4):

где $L(y)$ – функция, обратная к $K(x)$: $L\left( {K(x)} \right) = x$. Существование этой функции обеспечивается тем, что $K(x)$ – монотонно возрастающая функция в силу своего определения (4.10) и неравенства (4.6). Отметим, что функция $X(x,t)$ представляет собой первый интеграл характеристической системы (4.7). Здесь и далее $X = X(x,t)$, если не указано иное.

Определив производную $\dot {W}$ путем дифференцирования выражения (4.9) по времени $t$, можно на основе закона изнашивания (1.10) найти контактное давление:

где – начальное распределение контактного давления, $S(x,L) = R(x) - R(L) > 0$, причем последнее неравенство обуславливается монотонным возрастанием функций $R(x)$ и $L(y)$.

Согласно выражению (4.11), контактное давление принимает положительные значения и выполняется неравенство (1.8), если $0 < B{{p}_{0}}(x) < 1$, что, согласно выражению (4.12), имеет место при условии $0 < \psi (x) < {{h}_{0}}(x)$. С учетом определения (4.10) функции $\psi (x)$, можно установить, что последние неравенства выполняются, если

Замечание 3. Значения функции ${{p}_{0}}\left( {L(X(x,t))} \right)$, присутствующей в выражении (4.11), постоянны вдоль характеристик $X(x,t) = {\text{const}}$. Это позволяет описать эволюцию контактного давления $p(x,t)$ во времени $t$ как смещение начального распределения ${{p}_{0}}(x)$ вдоль оси координат со скоростью $\dot {x} = {{[K{\kern 1pt} {\text{'}}(x)]}^{{ - 1}}}$, обеспечивающей выполнение условия $X(x,t) \equiv K(x) - t = {\text{const}}$, с уменьшением значений этого распределения в ${{e}^{{S(x,L(X))}}}$ раз. Подобное описание дает основание интерпретировать величину

как фазовую скорость эволюции контактного давления. Аналогичное поведение контактного давления наблюдается в случае изнашивания волнистого штампа, скользящего по упругому покрытию постоянной толщины [14, 15].

Замечание 4. В случае, когда начальная толщина покрытия описывается периодической функцией

функции $K$, $R$ и $L$ обладают квазипериодическими свойствами

Эти свойства позволяют установить, что в случае (4.13) износ $W$ и контактное давление $p$, определяемые по формулам (4.9) и (4.11), представляют собой периодические функции:

При использовании вместо (1.4) более простой деформационной модели (1.5) уравнение кинетики изнашивания покрытия имеет прежний вид (4.1) за тем исключением, что в его левой части отсутствует член с производной $h{\text{'}}$, а в правой части стоит функция

Уравнение такого вида, как и прежде, можно линеаризовать в случае малого износа покрытия и прийти к уравнению (4.3), в левой части которого отсутствует член с производной $W{\kern 1pt} '$, а в правой части стоит функция $\hat {\psi }$. При условии (4.8) это уравнение имеет решение

которому, в силу закона изнашивания (1.10), соответствует контактное давление

Полученные выше равенства позволяют выполнить расчет кинетики изнашивания покрытия. Это было сделано для покрытия, имеющего первоначально волнистую форму

где ${{\bar {h}}_{0}}$ – средняя толщина покрытия, ${{h}_{{{\kern 1pt} 1}}}$ и $\lambda $ – амплитуда и длина волны формы покрытия. При использовании деформационной модели (1.4) расчет выполнялся на основе формул (4.9) и (4.11), а при использовании модели (1.5) – по формулам (4.14) и (4.15).

Использовались следующие значения параметров: ${{\bar {h}}_{0}} = 1$ мм, ${{h}_{1}} = 0.1{{\bar {h}}_{0}}$, $\lambda = 4{{\bar {h}}_{0}}$, ${{\Delta }_{{c0}}} = 0.7$ мм, $\mu = 0.3$, ${{\tau }_{0}} = 1.05$ ГПа, которым, согласно выражению (4.16), отвечает слабоискривленное покрытие: ${\text{|}}h_{0}^{'}(x{\text{)|}} < 0.16$. Значения параметров $G$, $\nu $, $\alpha $ принимались такими же, как для задачи с продольным скольжением контртела (раздел 2).

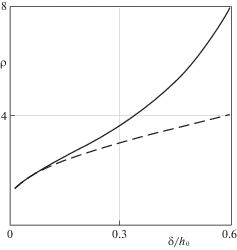
На рис. 7 показаны расчетные зависимости толщины покрытия h(x, t) = = ${{h}_{0}}(x) - W(x,t)$ (а) и контактного давления $p(x,t)$ (б) от координаты $x$ в различные моменты безразмерного времени $\tilde {t}$: 0 (кривые 1), 1 (кривые 2), 2.5 (кривые 3), причем $\tilde {t} = \bar {\eta }t$, $\bar {\eta } = \alpha {\text{/}}(B{{\bar {h}}_{0}})$. Сплошные и штриховые линии отвечают деформационным моделям (1.4) и (1.5), соответственно.

Показанные зависимости свидетельствуют о том, что использование уточненной деформационной модели (1.4) вместо более простой модели (1.5) может существенно изменить результаты расчета кинетики его изнашивания. В частности, при использовании модели (1.4) наблюдается сдвиг по фазе волнистых форм границы покрытия и распределения контактного давления (см. Замечание 3), который отсутствует при использовании модели (1.5).

5. Выводы.

1. Рассмотрены уточненные деформационные модели изнашиваемого покрытия, в том числе деформационная модель, учитывающая искривленность границы покрытия и трение. Использование таких моделей приводит к нелинейным уравнениям кинетики изнашивания покрытия.

2. На основе уточненных деформационных моделей выполнены расчеты эволюции толщины покрытия и контактного давления в рамках двумерной постановки износоконтактной задачи. Для некоторых частных случаев получены аналитические решения задачи.

3. Показано, что использование уточненных деформационных моделей покрытия, учитывающих изменение его формы, может существенно изменить результаты расчета кинетики изнашивания покрытия.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (17-01-00352).