Прикладная математика и механика, 2020, T. 84, № 2, стр. 208-233

1. Введение. Основными проблемами, возникающими при отработке угольных месторождений подземным способом, являются геодинамические события. К наиболее опасным из них относятся горные удары, внезапные выбросы угля и газа [1]. При этом смещения контура выработок достигают огромных размеров, что, как правило, приводит к аварийным и катастрофическим последствиям. 

Подавляющее большинство этих событий происходит в окрестности выработок, проходимых по угольному пласту (пластовых выработок), и сопровождаются переходом пласта и окружающих пород в предельное состояние с образованием зон неупругого деформирования (предельно напряженных зон). Эти зоны относятся к зонам опорного давления и на границах с упругими областями концентрация напряжений в них достигают максимальных значений [2, 3].

В зависимости от характеристик прочности угольного пласта, вмещающих пород и глубины ведения горных работ их переход в предельное состояние при отработке пласта происходит по-разному. В одних случаях наступление предельного состояния вмещающих пород с последующим их обрушением происходит при сравнительно небольших размерах выработанного пространства и, как правило, не вызывает проблем при ведении горных работ.

Наибольшую опасность представляют случаи отработки пластов с прочными вмещающими пласт горными породами, образующими перед обрушением огромные выработанные пространства. При этом параметры опорного давления (размер предельно напряженной зоны ${{L}_{p}}$ и коэффициент концентрации напряжений ${{k}_{\sigma }}$ – отношение максимального вертикального напряжения к гравитационным напряжениям в массиве до ведения горных работ) достигают значительных величин. Зависание пород над выработкой вызывает большие смещения пород в ее кровле, а при их обрушении возникает значительная аэродинамическая волна сжатия, способная опрокинуть вентиляционную струю шахтного проветривания. Эти обстоятельства приводят к авариям и как следствие к нарушениям нормального функционирования работы горного предприятия.

В этой связи для предотвращения опасных последствий геодинамических явлений в зонах ведения горных работ применяют различные методы принудительного обрушения прочной (“тяжелой”) кровли, и наиболее эффективным среди них является метод направленного гидроразрыва. Метод заключается в искусственном нарезании щели, называемой зародышевой трещиной, в трудно обрушаемой кровле угольного пласта и последующей подачей в нее под давлением жидкости (флюида), которая, создавая высокую концентрацию напряжений у краев щели, инициирует появление и развитие трещины в прочных вмещающих породах [4]. В конечном итоге трещина полностью пересекает всю толщу прочного слоя горных пород, что и приводит к его обрушению.

Зародышевая щель образуется путем искусственного нарезания на поверхности скважины двух небольших канавок (выемок), называемых пропилами, на всю длину скважины [4]. Они расположены на противоположных концах ее диаметра (рис. 1).

Проблема эффективного использования способа гидроразрыва состоит в том, чтобы заложить рациональные параметры зародышевой трещины с целью ее оптимального распространения в породах кровли для обеспечения их регулируемого обрушения.

Поскольку необходимо обрушить прочный и мощный слой породы кровли пласта, в основном представляющей однородный и изотропный материал, то на траекторию трещины, движущейся в этом слое, наиболее существенное влияние оказывает неоднородное поле напряжений, обусловленное наличием горной выработки.

Особенно остро проблема встает на больших глубинах, когда размеры предельно напряженных зон угольного пласта значительны, а коэффициент концентрации напряжений в них достигает больших величин, намного превышающих единицу. Поэтому распределение напряжений около трещины может оказать существенное влияние на ее траекторию, значительно изменяя направление по отношению к направлению зародышевой трещины.

В этой связи разработка математической модели о состоянии углепородного массива, вмещающего пластовую выработку и трещину гидроразрыва, является важной научной и производственной задачей, позволяющей решать проблемы безопасности горных работ и повышения производительности труда на угледобывающих предприятиях.

Одной из первых работ, послуживших началом бурного применения метода гидроразрыва, является работа Ю.П. Желтова и С.А. Христиановича, обосновавших возможность и эффективность применения гидроразрыва в нефтегазовой промышленности для повышения дебета нефтеносной скважины [5]. Основываясь на методах механики деформируемого твердого тела, они успешно решили задачу о распространении трещины гидроразрыва нефтеносного пласта и ее влиянию на окружающий скважину массив.

В настоящее время имеется обширная библиография фундаментальных работ, посвященных применению гидроразрыва пластов, в том числе и направленного гидроразрыва массива горных пород [6–12], где приведены оригинальные фундаментальные решения задач гидроразрыва, построенные на методах механики твердого деформируемого тела [6–8], включая и методы гидромеханики [9–11]. Однако в подавляющем большинстве исследования касаются распространения трещин с началом у поверхности нагнетающей скважины. Полагается, что она находится в гравитационном однородном поле напряжений массива и никаких других горных объектов, создающих неоднородное поле напряжений, нет. Теоретических исследований, посвященных распространению трещин гидроразрыва в гравитационном поле напряжений массива, искаженном наличием в нем горных выработок, немного, и в них влияние выработки учитывается достаточно утрированно. Так, например, в [12] авторы производят расчет направления развития трещины в окрестности пластовой выработки, используя устаревшие представления об образовании около выработки свода давления с эллиптической формой. Полагая этот свод арочной конструкцией, они получают напряжения в ней методами строительной механики стержневых систем и используют их при расчете трещин гидроразрыва, отыскивая также и направление движения трещины. Такой подход является довольно грубым приближением в расчетах трещины, поскольку не учитывает в расчетах ни физико-механических свойств массива, ни свойств угольного пласта.

Ниже представлена модель и приведены результаты решения в плоской постановке задачи распространения трещины гидроразрыва в окрестности горной выработки, пройденной по угольному пласту.

2. Постановка и построение решения задачи о геомеханическом состоянии массива, вмещающего пластовую выработку и трещину гидроразрыва. Задача формулируется следующим образом (рис. 1). В массиве горных пород, моделируемом невесомой плоскостью, имеется выработка 1 прямоугольного сечения размерами ${{b}_{{v}}} \times {{h}_{{v}}}$, пройденная на глубине $H$ по угольному пласту 2 на всю его мощность. В кровле и почве выработки приложена реакция крепи $f$. Характеристики прочности угольного пласта (${{\sigma }_{0}}$ – предел прочности на одноосное сжатие, $K$ – коэффициент сцепления, ρ – угол внутреннего трения) меньше, чем характеристики прочности пород вмещающего массива, но больше, чем характеристики ($K{\kern 1pt} '$ – коэффициент сцепления, $\rho {\kern 1pt} '$ – угол внутреннего трения) по контактам пласта с остальным массивом. Массив нагружен гравитационным давлением сверху и снизу $\gamma H$ (γ – средневзвешенный объемный вес налегающих пород), а с боков – $\lambda \gamma H$ (λ – коэффициент бокового давления). В краевых частях пласта образуются зоны неупругого деформирования 3 шириной ${{L}_{p}}$. В окрестности выработки для инициирования трещины в прочных породах кровли пласта пробурена скважина 4 радиусом ${{r}_{{sk}}}$ с двумя треугольными выемками-пропилами 5, расположенными на противоположных концах диаметра скважины. Размеры выемки, предназначенной для концентрации напряжений и, следовательно, инициирования трещины, ${{h}_{{tr}}}$, ${{b}_{{tr}}}$. Зародышевая трещина наклонена к горизонту под углом ${{\theta }_{{tr}}}$, а давление жидкости в ней $p$. Система координат $yOz$ совпадает с центральными осями выработки. Координаты скважины ${{y}_{{sk}}}$, ${{z}_{{sk}}}$. Вдоль линии APB (рис. 1) строятся графики опорного давления (эпюры напряжений) на краевую часть пласта.

В процессе решения задачи полагается:

1) трасса выработки и ось скважины параллельны, а их размеры вдоль абсциссы x значительно превосходят размеры в плоскости $Oyz$, в силу чего, можно считать, что породы в окрестности выработки и скважины находятся в условиях плоской деформации;

2) прочность пласта значительно ниже прочности вмещающих его пород;

3) сжимающие нормальные напряжения положительны, а растягивающие отрицательны;

4) трещина гидроразрыва распространяется в прочных, однородных и изотропных породах, и она не изменяет поля напряжений в окрестности выработки;

5) процессы фильтрации жидкости в массиве и другие ее утечки не учитываются.

В ходе решения задачи рассматриваются случаи распространения трещины в прочных породах, расположенных над пластом, для ряда глубин заложения выработки и значений начального давления ${{p}_{0}}$ в ней.

2.1. Постановка задачи о предельно напряженном состоянии пласта. Особенность задачи о напряженном состоянии массива с пластовой выработкой заключается в том, что прочность окружающих горных пород, как правило, существенно выше прочности пласта, по которому пройдена выработка. Поэтому если горные породы деформируются еще упруго, то краевые части пласта шириной ${{L}_{p}}$ уже находятся в предельном состоянии.

Предельно напряженные зоны пласта начинают развиваться с его обнажения в бортах выработки при достижении вертикальным главным напряжением ${{\sigma }_{1}}$ (главное напряжение ${{\sigma }_{3}}$ на обнажении равно нулю) значения ${{\sigma }_{0}}$. При увеличении ${{\sigma }_{1}}$ зона неупругих деформаций распространяется вглубь пласта, и в этой зоне он деформируется не только по направлению его мощности, но главным образом в плоскости контактов между пластом и окружающими породами, где происходит его проскальзывание. Поскольку вдоль контактов пласта с окружающими породами возможно нарушение сплошности, проявляющееся в виде проскальзывания, то в ней будут одновременно существовать два предельных состояния равновесия: общее или обыкновенное (состояние самого пласта) и специальное (состояние по контакту пласта с окружающим массивом) [13, 14].

В этой связи в строгой математической постановке необходимо использовать два критерия перехода его в предельное состояние: общий и специальный. Эти критерии чаще всего применяются в формах с прямолинейными огибающими кругов предельных состояний по пласту и по поверхностям ослаблений (по контакту пласта с массивом), на которых характеристики прочности ниже, чем по пласту [2, 13, 14]. Эти условия совместно с дифференциальными уравнениями равновесия образуют систему разрешающих уравнений о напряженном состоянии краевой зоны угольного пласта. В задаче о состоянии пласта, находящегося в условиях плоского деформированного состояния, эта система может быть сведена к одному нелинейному дифференциальному уравнению гиперболического типа, которое решается методом характеристик [13]. В этом методе интегрируются дифференциальные уравнения, имеющие на характеристических линиях достаточно простую структуру. В механике деформируемого твердого тела эти линии совпадают с линиями скольжения материала [13].

Несмотря на относительно простой вид полученных дифференциальных уравнений, их интегрирование в замкнутом виде получается только на участках пласта, расположенных в непосредственной близости к его обнажению. На остальных участках его предельно напряженной зоны решение можно получить только путем вычислительной процедуры, последовательно решая три краевые задачи механики предельного равновесия сыпучих сред для ряда характерных участков этой зоны.

Из-за сложностей в решении краевых задач чаще всего для описания предельно напряженного состояния угольного пласта используют подход, разработанный Г.Л. Фисенко [2]. Он основан на многочисленных экспериментах, проведенных на многих шахтах ряда угольных месторождений, учитывает важнейшие характеристики прочности горных пород, а распределения напряжений в пласте представляются аналитическими выражениями.

Согласно этому подходу вертикальные нормальные напряжения вдоль оси пласта в предельно напряженной зоне изменяются по экспоненциальному закону

где

Недостаток этого подхода состоит в том, что формула для ${{\sigma }_{z}}$ основана на экспериментальных данных и по сути дела является эмпирической. Другой существенный недостаток этого подхода заключается в том, что нормальные и касательные напряжения на контакте пласта с окружающим массивом напрямую он не определяет, и это обстоятельство затрудняет решение упругопластической задачи о напряженном состоянии массива в окрестности выработки.

В данной статье впервые для расчета напряжений в предельно напряженной зоне пласта был использован более строгий и фундаментальный метод характеристик, реализованный путем численного решения краевых задач для ряда характерных участков этой зоны, включая участки, примыкающие к обнажению. Результаты решения изложены в работе [15].

В ней показано, что графики распределения нормальных и касательных напряжений могут быть построены как вдоль контакта пласта с окружающим массивом, так и вдоль оси пласта и представляют собой комбинацию поочередно сменяющих друг друга участков с постоянными и нелинейно возрастающими напряжениями. Для дальнейших исследований о напряженном состоянии массива горных пород эти графики следует аппроксимировать аналитическими зависимостями, в частности, полиномами. Такая замена облегчает решение упругопластической задачи при определении параметров опорного давления. Коэффициенты полинома определяются из решения системы алгебраических уравнений, число которых совпадает с количеством участков в предельно напряженной зоне слоя. Правые части уравнений этой системы равны значениям найденных напряжений на границах участков этой зоны [15].

Сравнительные оценки результатов расчета напряжений, полученные методом характеристик, с результатами расчетов напряжений по экспоненциальной формуле [2], показывают их близость лишь на достаточно узком участке предельно напряженной зоны. С увеличением длины участка разница в напряжениях существенно возрастает и может достигать значительных величин, доходя на расстоянии $4.44{{h}_{{v}}}$ до 85% [15].

2.2. Постановка упругопластической задачи о пластовой выработке. Зная характер распределения линий скольжения и напряжений на них, можно определить напряжения в любой точке предельно напряженной зоны пласта, в том числе и на границе (контакте) пласта с окружающим массивом. В этой связи замена краевой части пласта, находящейся в предельном состоянии, действующими на контакте пласта с массивом нормальными и касательными напряжениями ${{\sigma }_{{p.y}}}$, ${{\sigma }_{{p.z}}}$, ${{\tau }_{{p.yz}}}$, ${{\tau }_{{p.zy}}}$ позволяет сформулированную задачу свести к краевой задаче теории упругости. В отличие от классической задачи граничные условия формулируются не по контуру выработки, а по замкнутому контуру, включающему кровлю, почву выработки и контакт пласта с окружающим массивом на участке предельной зоны. Так, по горизонтальным участкам этого контура проекции ${{p}_{z}}$, ${{p}_{y}}$ полного напряжения соответственно равны напряжениям ${{\sigma }_{z}}$ и ${{\tau }_{{yz}}}$. Тогда в граничном интегральном сингулярном уравнении краевой задачи теории упругости [16, 17] интегрирование производится по замкнутому контуру, охватывающему кровлю, почву выработки и контур предельно напряженной зоны. Это уравнение в форме, представленной в [16], принимает следующий вид [18, 19]

где $L$ – внешний контур, охватывающий почву, кровлю выработки и границы предельно напряженной зоны; ${{L}_{{op}}}$ – суммарный контур предельно напряженной зоны; ${{L}_{b}}$ – контур, охватывающий почву и кровлю выработки, индексы $q$, $m$ попеременно принимают значения 2, 3 (индекс 2 соответствует оси $y$, 3 – оси $z$); ${{Q}_{O}}$, ${{M}_{O}}$ – точки на поверхности этой области; $d{{O}_{{MO}}}$ – дифференциал поверхности в окрестности точки ${{M}_{O}}$; ${{\Phi }_{{qm}}}({{Q}_{O}},{{M}_{O}})$ – тензор Грина; ${{n}_{m}}({{Q}_{O}})$ – вектор нормали к поверхности выработки в точке ${{Q}_{O}}$; ${{a}_{q}}$, ${{a}_{m}}$ – компоненты вектора фиктивной нагрузки; $f({{Q}_{O}})$ – обобщенный вектор нагрузки, приложенный к поверхности выработки изнутри; ${{\sigma }_{{e.qm}}}$ – компоненты тензора естественного поля в нетронутом горными работами массиве, которые при отсутствии тектонических напряжений представляются в виде

В основе численного решения интегрального уравнения (2.1) лежит метод механических квадратур [17, 20]. Для его реализации контур выработки (область ${{L}_{b}}$) разбивается на ${{N}_{b}}$ элементов (граничных элементов), а контур предельно напряженной зоны (область ${{L}_{{op}}}$) на ${{N}_{p}}$ элементов. Далее производится нумерация центров тяжестей этих элементов от 1 до $N$ (${{N}_{b}} + {{N}_{p}}$) и замена интеграла в уравнении суммой. Произвольная точка Q_O контура области обозначается через $i$, а точка ${{M}_{O}}$ – через $k$. Тогда уравнение (2.1) в компонентной форме принимает вид

В уравнении (2.2) $\Delta {{L}_{k}}$ – размер $k$-го участка контура границы области интегрирования (размер граничного элемента); $\Delta {{L}_{k}} = \Delta {{L}_{{bk}}}$ при $k = 1, \ldots ,{{N}_{b}}$, $\Delta {{L}_{k}} = \Delta {{L}_{{pk}}}$ при $k = 1, \ldots ,{{N}_{p}}$.

Интегрирование выражения (2.2) по каждому элементу при условии, что ${{\sigma }_{{e.qm}}}$, ${{\sigma }_{{p.qm}}}{{f}_{q}}$, ${{a}_{q}}$ постоянны в пределах каждого из них [17, 19], приводит к векторному уравнению

Входящие в уравнение (2.3) величины обозначают результирующие усилия, приложенные в центрах граничных элементов:

Векторному уравнению (2.3) соответствуют два уравнения относительно координат этого вектора, и для их определения следует решить систему алгебраических уравнений $2({{N}_{b}} + {{N}_{p}}) \times 2({{N}_{b}} + {{N}_{p}})$.

После решения системы уравнений напряжения в произвольной точке $j$ массива определяются суммированием напряжений от действия фиктивной нагрузки и напряжений исходного гравитационного поля напряжений:

где ${{\sigma }_{{qmt}}}$ – компоненты фундаментального тензора третьего ранга, являющегося решением задачи Кельвина о действии сосредоточенной силы на бесконечную среду [16, 17, 21].

В разрешающих уравнениях (2.1), (2.3) сформулированной задачи кроме неизвестной интенсивности фиктивной нагрузки неизвестным остается также и суммарный размер предельно напряженной, входящей в область интегрирования $L$ уравнения (2.1). Эти неизвестные находятся в ходе реализации итерационной процедуры метода последовательных приближений, реализованной ранее [18, 19].

Описанный выше подход к решению задач о геомеханическом состоянии без учета предельно напряженных зон применялся в оценке геомеханического состояния анизотропного массива, вмещающего выработки, причем задачи решались как в двумерной постановке [22], так и в трехмерной [23, 24].

2.3. Задача о распространении трещины гидроразрыва в окрестности пластовой выработки и последовательность ее решения. Известно, что при теоретическом анализе проблемы прочности и распространения трещин в твердых деформируемых телах при квазистатических процессах используется уравнение Ирвина [25–27]

где ${{k}_{n}}$, ${{k}_{t}}$ – коэффициенты интенсивности напряжений, обусловленные действием нормальной (расклинивающей) ${{p}_{n}}$ и касательной ${{p}_{t}}$ нагрузок на берегах трещины; $E$ – модуль продольной упругости, а μ, как и ранее, – коэффициент Пуассона пород массива. Γ – плотность энергии разрушения материала, необходимой для образования единицы поверхности, ${{K}_{{1C}}}$ – коэффициент трещиностойкости материала (справочные данные для некоторых типов горных пород приведены в [28]).

Для определения давления жидкости, при котором происходит рост трещины на определенную (заданную) величину, необходимо учесть тот факт, что приращение трещины происходит значительно быстрее, чем его заполнение жидкостью. Таким образом, пока жидкость занимает часть трещины длиной $2b$, сама длина трещины стала равна $2a = 2(b + \Delta l)$.

Существует несколько методов определения коэффициентов интенсивности напряжений на концах трещины, находящейся в плоскости с “удаленными” границами, в которой поле напряжений неоднородное. Если трещина мала по сравнению с размерами плоскости и располагается внутри нее, то в качестве одного из вариантов вычисления коэффициента интенсивности напряжений могут быть взяты соотношения из [25–27]

В выражениях (2.6), (2.7) функция ${{p}_{n}}$ равна напряжению, которое было бы перпендикулярным плоскости трещины, если бы она была закрыта; следовательно, напряжение находится аналитически или численно для тела без трещины. Аналогично может быть определен коэффициент интенсивности напряжений от касательного напряжения ${{p}_{t}}$.

При постоянных значениях ${{p}_{n}}$, ${{p}_{t}}$ выражения для ${{k}_{n}}$, ${{k}_{t}}$ после интегрирования принимают следующий вид

После подстановки ${{k}_{n}}$ и ${{k}_{t}}$ в уравнение (2.5) значение внутреннего давления в трещине, соответствующее ее продвижению на заданную величину $\Delta l$, принимает следующий вид

Значение ${{p}_{{{\text{кр}}}}}$, определяемое зависимостью (2.9), называется критическим давлением (“трещинодвижущей” силой) и оно соответствует устойчивому росту трещины [25].

Отклонения трещины от начального направления в изотропной среде следует ожидать при ${{k}_{t}} \ne 0$ [26, 27].

В этой связи направление продвижения трещины происходит под таким углом $\theta = {{\theta }_{с}}$ относительно начального ее положения, которое совпадает с направлением площадки с максимальным растягивающим напряжением. Известно, что по этой площадке отсутствует касательное напряжение, нормальное напряжение по ней является главным напряжением ${{\sigma }_{3}}$, а сама площадка называется главной площадкой.

Угол ${{\theta }_{с}}$ определяется из решения следующего тригонометрического уравнения относительно угла $\theta $, отсчитываемого от направления трещины в момент ее “страгивания” [26, 27]

Входящие в уравнение (2.10) коэффициенты интенсивности ${{k}_{n}}$ и ${{k}_{t}}$ определяются согласно зависимостям (2.8), в которых нормальная и касательная нагрузки по поверхности трещины, связанные с компонентами поля напряжений (2.4), определяются по известным соотношениям напряжений по наклонным площадкам

Следовательно, в окрестности выработки, где поле напряжений в массиве неоднородно, трещина в общем случае распространяется не прямолинейно. С каждым новым приращением длины (циклом роста), она меняет и свое направление.

Поскольку трещина распространяется в неоднородном поле напряжений, то напряжения ${{p}_{n}}$ и ${{p}_{t}}$ на ее берегах в двух ее развивающихся направлениях будут различны.

Для трещины, распространяющейся прямолинейно, интегралы в выражениях (2.6), (2.7) следует представить суммой интегралов по каждому отдельному направлению

В выражениях (2.13), (2.14) $p{{1}_{n}}$, $p{{1}_{t}}$, $p{{2}_{n}}$, $p{{2}_{t}}$ – напряжения на поверхности трещины по разные стороны от середины, причем, $p{{1}_{n}}$, $p{{1}_{t}}$ – напряжения на левой ее ветви, а $p{{2}_{n}}$, $p{{2}_{t}}$ – на правой.

При $j$ циклах трещина представляет собой ломаную линию в виде совокупности прямолинейных отрезков, в пределах которых напряжения ${{p}_{n}}$ и ${{p}_{t}}$ приняты постоянными величинами.

Если эта линия незначительно отклонятся от прямой линии, выражения (2.13), (2.14) можно представить в следующем виде

где $\Delta {{l}_{i}}$ – длина $i$-го участка (отрезка) трещины (приращение трещины).

После интегрирования выражения (2.15)

Аналогично интегрируется выражение (2.14)

С учетом (2.16), (2.17) выражения интенсивности напряжений для трещины с несколькими участками принимают следующий вид

После подстановки зависимостей (2.15) в выражение (2.5) и преобразования из него может быть получено выражение для критического давления для трещины с числом участков, равным $j$

В выражениях (2.9), (2.13)–(2.19)

Условием, соответствующим началу развития зародышевой трещины, ее “страгивания” является условие превышения коэффициентом интенсивности ${{k}_{n}}$ значения коэффициента трещиностойкости ${{k}_{{1C}}}$. У кончика зародышевой трещины ${{k}_{n}}$ определяется по формуле

где ${{F}_{{tr}}}$ – коэффициент, зависящий от условий нагружения тела с круговым отверстием, содержащим трещину [27].

Для зародышевых трещин, расположенных на противоположных концах диаметра скважины, коэффициент ${{F}_{{tr}}}$ зависит от размера ${{b}_{{tr}}}$ и диаметром скважины [27].

Очевидно также, что развитие трещины гидроразрыва возможно, если давление жидкости $p$, подаваемое по скважине в трещину, превысит критическое давление, определяемое по формуле (2.19). При этом его минимальное значение соответствует случаю равенства величин $a$ и $b$, т.е. началу “страгивания” трещины. Из выражения (2.19) получаем

Коэффициенты интенсивности напряжений ${{k}_{n}}$ и ${{k}_{t}}$ при этом определяются по следующим формулам, вытекающим из выражения (2.18)

Очевидно, что для осуществления процедуры гидроразрыва необходим предварительный выбор насосного оборудования. В первую очередь это касается его характеристики напора ${{p}_{0}}$.

При выполнении гидроразрыва прочных пород, вмещающих угольный пласт, как правило, используют насосные установки с жесткими характеристиками напор ${{p}_{0}}$, расход жидкости в единицу времени $Q$. К установкам с жесткими характеристиками относят насосы, у которых один из параметров $Q$ практически не меняется при изменении другого ${{p}_{0}}$. Такие характеристики обеспечивают насосы поршневого или плунжерного типов.

В процессе гидроразрыва необходимо учитывать изменение давления жидкости при прохождении ее по трещине, обусловленное динамической вязкостью η и параметрами самой трещины: раскрытием $w$ перед очередным циклом прорастания и ее длиной.

Градиент давления (падение давления) вдоль направления распространения трещины и расход вязкой жидкости при ламинарном движении в плоском канале связан известным законом Пуазейля [5, 10]

в котором раскрытие трещины определяется по формуле [29] где ${{x}_{{tr}}}$ – абсцисса, отсчитываемая от середины трещины вдоль ее оси $l$.

Замена градиента давления в соотношении (2.22) конечноразностным выражением через конечное давление ${{p}_{1}}$ и начальное ${{p}_{0}}$ на некотором интервале $\Delta l$ по формуле

позволяет выразить конечное давление на интервале приращения трещины через начальное давление и ряд других параметров: трещины, жидкости и окружающего породного массива. Так, например, для участка $j$ растущей трещины из формулы (2.24) следует выражение давления в виде

Процесс образования и развития трещины может быть представлен двумя этапами. На первом этапе развитие трещины происходит при постепенном повышении давления жидкости, начиная с нуля. Достигнув значения ${{p}_{{{\text{кр}}}}}_{{.\min }}$, определяемого по формуле (2.20), трещина “страгивается”, при этом направление ее движения совпадает с направлением зародышевой трещины, поскольку на ее кончике действует только давление жидкости. При дальнейшем увеличении давления на $\Delta p$ до некоторого текущего значения $p$ трещина должна увеличить свой размер на $\Delta l$. Это приращение может быть найдено из решения трансцендентного уравнения

в котором второе слагаемое является значением критического давления, определяемого формулой (2.19) и соответствующим росту трещины. В этом уравнении значение $b$ следует положить равным ${{b}_{{tr}}}$ и после этого найти величину $a$. Его решение может производиться последовательными приближениями, например, увеличивая на каждом шаге итерации размер a на малую величину до тех пор, пока не будет выполнено условие (2.26). Приращение $\Delta l$ определится как разность между конечной величиной a итерационного процесса и значением $b = {{b}_{{tr}}}$. После этого по формуле (2.23) вычисляется значение $w$, в котором ${{x}_{{tr}}}$ следует положить, равным ${{b}_{{tr}}}$. Затем по формуле (2.25) вычисляется новое значение $p$, к нему добавляется очередное приращение давления $\Delta p$ и начинается новый цикл первого этапа расчета трещины.

На новом цикле размер $b$ становится равным размеру $a$ предыдущего цикла. По формулам (2.4) вычисляются компоненты напряжений на участке приращения трещины, а по формулам (2.11), (2.12) определяются компоненты ${{p}_{n}}$ и ${{p}_{t}}$, в которых $\theta = {{\theta }_{{tr}}}$. Далее в ходе итерационного процесса решения уравнения (2.26) определяются параметры $a$, $b$. Затем по формуле (2.23) вычисляется параметр $w$, в котором абсцисса ${{x}_{{tr}}}$ равна значению $b$ этого цикла. Далее по формуле (2.25) вычисляется $p$, потом к нему добавляется $\Delta p$, по формулам (4) компоненты напряжений, а по формулам (2.11), (2.12) определяются компоненты ${{p}_{n}}$ и ${{p}_{t}}$.

Следующий цикл начинается с присвоения новому значению $b$ значения $a$ предыдущего этапа. Затем по формулам (2.21), в которых ${{p}_{{{\text{кр}}}}}_{{.\min }}$ полагается равным давлению $p$, вычисленному в конце предыдущего цикла, находятся ${{k}_{n}}$, ${{k}_{t}}$ и подставляются в уравнение (2.10), из решения которого определяется угол θ между направлением трещины предыдущего цикла и новым направлением. Далее методом последовательных приближений решается уравнение (26) и определяется размер $a$, затем вычисляются параметры $w$, $p$, ${{p}_{n}}$, ${{p}_{t}}$, ${{k}_{n}}$, ${{k}_{t}}$, θ. Следующие циклы расчета трещины реализуются аналогично. Процесс счета продолжается до тех пор, пока давление жидкости в системе не достигнет своего конечного значения ${{p}_{0}}$, определяемого техническими характеристиками насосного оборудования.

Второй этап расчета трещины соответствует росту трещины при $p = {{p}_{0}}$. К этому моменту ее полудлина сравнима с радиусом скважины. В этом случае вполне правомерна замена отверстия трещиной и тогда ее полудлиной считается сумма полудлины трещины, полученной на первом этапе роста, и значение радиуса скважины [27]. А коэффициент ${{F}_{{tr}}}$ следует принять равным единице.

Циклы второго этапа выполняются таким же образом, как и циклы первого этапа, но следует учесть, что на втором этапе прироста давления $\Delta p$ нет.

Рост трещины прекращается в том случае, если давление в ней стало меньше напряжений в нетронутом массиве (на бесконечности), либо в случае прекращения подачи жидкости в трещину, ограничившись определенным числом циклов.

В ранее опубликованных работах автора [31, 32] была разработана модель распространения трещины, в которой механизм развития трещины принимался следующим. При достижении нагнетаемой жидкостью давления, определяемого формулой (2.20), трещина, полудлина которой b принимается равной сумме радиуса скважины и ширине пропила, находится в неустойчивом равновесии и для ее прорастания на $\Delta l$ необходимо повысить давление до значения ${{p}_{{{\text{кр}}}}}$, вычисляемого по формуле (2.19). Тогда ее край скачком переместится в соседнюю точку. При этом направление скачка (угол $\theta = {{\theta }_{1}}$) определяется из решения уравнения (2.10), в котором ${{k}_{n}}$, ${{k}_{t}}$ определяются по формулам (2.21). Новое направление трещины составит с горизонтом угол ${{\theta }_{2}} = {{\theta }_{{tr}}} + {{\theta }_{1}}$. Для прорастания трещины еще на величину $\Delta l$ давление жидкости также должно определяться по формуле (2.19), в которой $a = b + 2\Delta l$, а $b = b + \Delta l$. Новое направление скачка (угол ${{\theta }_{3}}$) находится из решения уравнения (2.10), в котором ${{k}_{n}}$, ${{k}_{t}}$ находятся снова по формулам (2.21), но уже с учетом нового значения $b$. Таким образом, давление жидкости в трещине в процессе ее роста изменяется между значениями критического давления, определяемого формулами (2.20) и (2.19). Следующие циклы в развитии трещины повторяются по описанному алгоритму.

Изложенный подход при расчете траектории трещины имеет ряд существенных недостатков. Во-первых, в нем не учитываются характеристики жидкости. Во-вторых, не входят параметры насосного оборудования. В-третьих, величина прорастания трещины принята постоянной величиной.

Разработанная и представленная в статье модель лишена отмеченных недостатков, и она наиболее полно отражает механизм развития трещины гидроразрыва.

3. Анализ полученных результатов. В рамках рассматриваемой модели проведен вычислительный эксперимент, за исходные данные в котором приняты следующие параметры массива, выработки и зародышевой трещины: $\lambda = 1$, $\gamma = 25$ кН/м³, $K = 0$, $\rho = 20^\circ $, $\rho {\kern 1pt} ' = 10^\circ $, ${{\sigma }_{0}} = 10$ МПа, ${{K}_{{1C}}} = 1.66$ МПа м^1/2 ($\Gamma = 12.92 \times {{10}^{{ - 5}}}$ МПа м), ${{b}_{v}} = 5$ м, ${{h}_{v}} = 3$ м, $f = 2$ кH/м², ${{r}_{{sk}}} = 0.021$ м, ${{b}_{{tr}}} = 0.008$ м, $\eta = 13.04 \times {{10}^{{--10}}}$ МПа с, ${{\theta }_{{tr}}} = --30^\circ $, ${{y}_{{sk}}} = 3$ м, ${{z}_{{sk}}} = 10$ м, $Q = 0.005$ м³/с. Другие параметры в ходе вычислений изменялись.

На рис. 2 представлена компьютерная модель сетки линий скольжения в предельно напряженной зоне состояния угольного пласта, полученная по результатам численного решения задачи о состоянии пласта на основе общего и специального критериев предельного состояния. На этом рисунке участок 1 – зона выпирания, участки 2 – зоны Прандтля, а участки 3 являются областями, в которых выполняются специальные условия предельного состояния. Линии скольжения и распределение напряжений в них могут быть получены в аналитическом виде. При этом зона 1 построена по результатам решения первой, а зоны Прандтля построены по результатам решения второй краевых задач предельного состояния. Линии скольжения на остальных участках построены в ходе численного решения третьей краевой задачи предельного состояния.

На рис. 3 графики 1–4 представляют собой эпюры напряжений ${{\sigma }_{z}}$ и ${{\tau }_{{yz}}}$, построенные при $H = 800$ м в кровле пласта (вдоль линии APB на рис. 1) в предельно напряженной зоне (графики 1, 3) и в упругой области (графики 2, 4). Графики в предельной зоне построены путем аппроксимации полиномами графиков, поученных в результате численного решения краевых задач предельного состояния для ряда участков этой зоны. Из анализа графиков вытекает, что значения напряжений в упругой области и предельно напряженной зоне совпадают на их границе в точке $P$ (рис. 1), абсцисса которой равна размеру ${{b}_{v}}{\text{/}}2 + {{L}_{p}}$, а ординатой является значение ${{\sigma }_{z}}$ на границе предельной и упругой областей (в точке $P$ на рис. 1). Отнесенная к $\gamma H$ она равна коэффициенту концентрации напряжений ${{k}_{\sigma }}$. Из графиков следует, что размер предельно наряженной зоны составляет ${{L}_{p}} = 4.9$ м, а коэффициент концентрации ${{k}_{\sigma }} = 1.582$.

На рис. 4а показана траектория трещины гидроразрыва, построенная в окрестности этой выработки. Давление жидкости в скважине p₀ составляет 30 МПа. Кружками на траектории показаны номера циклов ее роста. Цифрой 1 обозначена выработка, цифрой 2 – предельно напряженные зоны, 3 – зародышевая трещина, 4 – ветви траектории трещины.

Как следует из рисунка, при данных горнотехнических параметрах траектория трещины не совпадает с направлением зародышевой трещины, а очень существенно отклоняется от его направления, стремясь проникнуть в кровлю выработки по кратчайшему расстоянию. На рис. 4б показана часть траектории, примыкающая к скважине при первых семи циклах ее роста. Из этих рисунков следует, что траектория трещины представляет собой кривую линию, довольно сильно изменяющую направление зародышевой трещины в начале своего развития.

На рис. 5 построен график изменения давления в трещине в зависимости от числа циклов при ее прорастании. Кружки на графике также как и на рис. 4 соответствуют номерам циклов. Из рисунка следует, что рост трещины происходит в два этапа. На первом этапе рост начинается с давления ${{p}_{{{\text{кр}}}}}_{{.\min }} = 5.72$ МПа, и за семь циклов давление достигает значения ${{p}_{0}} = 30$ МПа, при этом полудлина трещины прорастает до 0.0158 м. На втором этапе ее развитие сопровождается падением давления за счет вязкости жидкости. Из рисунка следует, что общее число циклов при росте полудлины трещины до 8.02 м составляет 36 циклов, а давление на конечном этапе снизилось до 28 МПа. Как показывают результаты вычислительного эксперимента, предельное давление ${{p}_{0}}$ на глубине 800 м, меньше которого рост трещины не происходит, составляет 28 МПа.

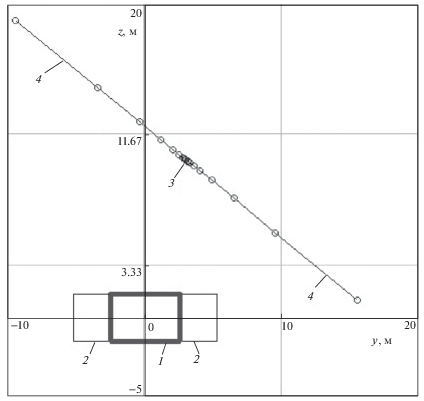
На рис. 6–8 показаны траектории трещины гидроразрыва, построенные при других глубинах заложения выработки и давлении ${{p}_{0}} = 30$ МПа. Цифры на них обозначают те же объекты, что и на рис. 4а.

На рис. 6 расчеты произведены для глубины $H = 700$ м. Видно, что траектория трещины изменяется плавно, но, как и в предыдущем случае, значительно изменяет первоначальное направление на начальных циклах роста, хотя и менее круто по сравнению с рис. 4а, и она также стремится к контуру выработки. Ее полудлина достигает значения 9.7 м за 27 циклов, а расчеты показывают, что конечное давление составляет 29 МПа, снизившись в процессе роста трещины на 1 МПа.

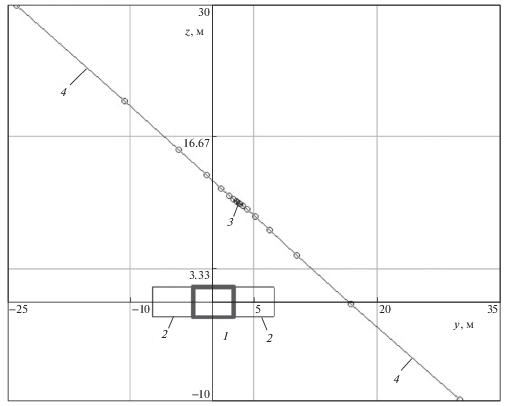
На рис. 7 траектория трещины гидроразрыва построена около выработки, расположенной на глубине $H = 600$ м. Она также криволинейна, но изменяет свое первоначальное направление более плавно и не так круто как в предыдущих двух случаях. Конечной точкой трещины оказывается точка на контакте массива с пластом в его предельно напряженной зоне. Ее полудлина 9.1 м, и она достигает этого значения за 23 цикла.

Для оценки результатов по расчету траектории трещины со значительным изменением исходного положения произведен их сравнительный анализ с результатами решения классической задачи, в которой трещина криволинейна. В качестве такой задачи выбрана задача о коэффициентах интенсивности напряжений около дугообразной трещины, расположенной в плоскости, нагруженной равнокомпонентным полем напряжений. Крайние радиальные сечения трещины образуют угол 2α [30].

В этой связи участки траектории на рис. 4а, 6 и 7, на которых происходит существенное отклонение от направления зародышевой трещины, приняты дугами окружностей разных радиусов.

Из результатов расчета, по которым построен рис. 4а, следует, что трещина за первые восемь циклов второго этапа своего развития изменяет на сто сорок градусов исходное направление на полудлине в 0.739 м. Эта полудлина по принятому допущению соответствует дуге окружности, радиус которой получается равным 0.302 м.

При угле 2α = 140° и напряжении на сторонах плоскости в 20 МПа коэффициенты интенсивности напряжений, подсчитанные по аналитическим формулам с дугообразной трещиной [30], равны: ${{k}_{n}}$ = 11.648 МПа м^1/2, ${{k}_{t}}$ = 8.156 МПа м^1/2. Эти же коэффициенты, полученные с помощью формул (2.15), принимают значения: ${{k}_{n}}$ = 21.533 МПа м^1/2, ${{k}_{t}}$ = 0. Как видно, разница в результатах значительна. Следовательно эффект кривизны трещины существенно сказывается на результаты расчета интенсивности напряжений.

Для участка трещины гидроразрыва длиной 0.739 м, показанной на рис. 4а, рассчитанные коэффициенты интенсивности напряжений принимают следующие значения: ${{k}_{n}}$ = 14.314 МПа м^1/2, ${{k}_{t}}$ = 0.667 МПа м^1/2. Если предположить, что реальное соотношение между коэффициентами ${{k}_{n}}$, ${{k}_{t}}$ у гидротрещины будет такого же порядка, как и в примере с дугообразной трещиной в равнокомпонентном поле напряжений, то полученные с помощью формул (2.15) значения коэффициентов интенсивности напряжений, далеки от их реальных значений. В связи с этим, и картина развития трещины на рис. 4а скорее всего не соответствует действительности.

Из результатов расчета графика на рис. 6, следует, что трещина за двенадцать циклов изменяет на угол 2α = 67° свое исходное направление на полудлине в 1.289 м, соответствующей дуге окружности радиуса 1.102 м. Рассчитанные коэффициенты интенсивности напряжений принимают следующие значения: ${{k}_{n}}$ = 21.002 МПа м^1/2, ${{k}_{t}}$ = = 3.946 МПа м^1/2. Коэффициенты интенсивности напряжений, подсчитанные по аналитическим формулам с дугообразной трещиной [30], получаются равными ${{k}_{n}}$ = = 24.447 МПа м^1/2, ${{k}_{t}}$ = 7.358 МПа м^1/2. Видно, что значения коэффициента ${{k}_{t}}$ и в этом случае значительно отличаются друг от друга.

Из результатов расчета графика на рис. 7, следует, что трещина за четырнадцать циклов изменяет на угол 2α = 58° свое исходное направление на полудлине в 6.875 м, соответствующей дуге окружности радиуса 6.792 м. Рассчитанные коэффициенты интенсивности напряжений принимают следующие значения: ${{k}_{n}}$ = 55.581 МПа м^1/2, ${{k}_{t}}$ = = 9.161 МПа м^1/2. Коэффициенты интенсивности напряжений, подсчитанные по аналитическим формулам с дугообразной трещиной [30], получаются равными ${{k}_{n}}$ = = 58.602 МПа м^1/2, ${{k}_{t}}$ = 15.155 МПа м^1/2. В этом случае значения коэффициентов ${{k}_{n}}$ отличаются друг от друга в пределах шести процентов, тогда как значения ${{k}_{t}}$, по-прежнему, далеки друг от друга.

Таким образом, в расчетах траектории трещины, существенно меняющей свое направление на начальном этапе развития, формулы (2.15), не учитывающие эффекта кривизны трещины, значительно искажают результаты и для расчета не пригодны.

На рис. 8 траектория трещины построена около выработки, расположенной на глубине 400 м. Из рисунка следует, что трещина распространяется практически прямолинейно и ее траектория совпадает с направлением зародышевой трещины. Полудлина трещины равна 10.5 м и соответствует 16 циклам, при этом давление в трещине уменьшается незначительно, всего на 0.04 МПа. Трещина на четырех первых циклах изменила исходное направление на угол α = 3.2°. При этом ее полудлина составляет 0.836 м, а соответствующий ей радиус равен 14.969 м. Коэффициенты интенсивности равны: ${{k}_{n}}$ = 24.639 МПа м^1/2, ${{k}_{t}}$ = 0.35 МПа м^1/2. Коэффициенты интенсивности напряжений, вычисленные по формулам для дугообразной трещины [30], получаются равными ${{k}_{n}}$ = = 22.911 МПа м^1/2, ${{k}_{t}}$ = 0.32 МПа м^1/2. Сравнение результатов показывает их незначительное расхождение, а потому подтверждает пригодность формул (2.15) для случаев развития трещины с малыми отклонениями исходного состояния.

Из рис. 8 следует, что при прямолинейном распространении трещины отношение давления жидкости ${{p}_{0}}$ к гравитационному давлению $\gamma H$ равно трем. Исходя из этого факта, можно предположить, что при других значениях ${{p}_{0}}$ и $\gamma H$ прямолинейному росту трещины также соответствует ${{p}_{0}}{\text{/}}\gamma H = 3$.

В этой связи ниже на рис. 9, 10 представлены результаты расчетов трещины гидроразрыва для ряда глубин $H$ и значений давления ${{p}_{0}}$, в которых ${{p}_{0}}{\text{/}}\gamma H = 3$. Число циклов роста трещины, как и в предыдущем случае, принято равным девяти. Цифры на них обозначают те же объекты, что и на предыдущих рисунках, на которых изображены траектории трещин.

На рис. 9 показана траектория трещины гидроразрыва, распространяющейся около выработки, расположенной на глубине 500 м. Давление жидкости в скважине составляет 37.5 МПа, что в три раза выше гравитационного. Траектория трещины практически прямолинейна, и ее полудлина составляет 15.3 м.

На рис. 10 траектория трещины, растущая вблизи выработки, построена на глубине 800 м и давлении жидкости в скважине, равном 60 МПа. Соотношение ${{p}_{0}}{\text{/}}\gamma H = 3$ также равно трем, и трещина распространяется прямолинейно, достигая при заданном числе циклов полудлины 33.5 м.

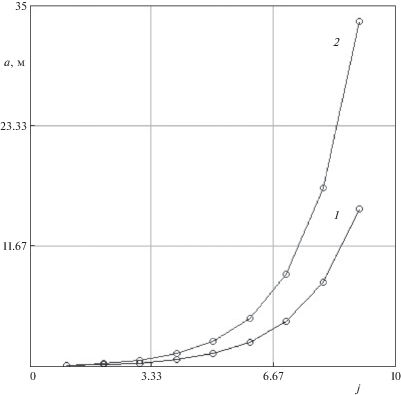
На рис. 11 построены графики изменения полудлины трещины $a$ в зависимости от числа циклов ее роста $j$ для траекторий, представленных на рис. 9, 10. Из анализа графиков следует, что, во-первых, они нелинейны, во-вторых, на последних циклах их значения резко возрастают. Как показывает анализ роста трещины, изменение ее полудлины с увеличением числа циклов довольно точно описывается показательной функцией

где $N$ – конечное число циклов, ${{a}_{N}}$ – конечная полудлина трещины.

Из сравнения графиков, представленных на рис. 8–10, следует, что при равных соотношениях ${{p}_{0}}{\text{/}}\gamma H = 3$ полудлины трещины на разных глубинах имеют разные величины. В этой связи проведена количественная оценка сравнения полудлин трещин, распространяющихся прямолинейно на разных глубинах.

В качестве показателя этой оценки на рис. 12 построен график изменения отношения полудлины трещины, распространяющейся вблизи выработки на глубине $H$, к этой глубине в зависимости от давления жидкости ${{p}_{0}}$, соответствующего прямолинейному росту трещины. Этот график имеет вид слабовыпуклой кривой, незначительно отличающейся от прямой линии. Кружки на графике соответствуют глубине $H$, равной 400 м, 500 м, 600 м, 700 м и 800 м.

Заключение. 1. Задача о геомеханическом состоянии массива горных пород, вмещающего выработку, пройденную по угольному пласту, сведена ко второй внешней краевой задаче теории упругости для интегрального сингулярного уравнения. Особенность этой задачи заключается в том, что в краевых частях выработки образуются предельно напряженные зоны пласта и их замена действующими в них напряжениями, найденными в ходе численного решения краевых задач теории предельного состояния, вполне может рассматриваться как краевая задача теории упругости. Решение интегрального уравнения получено методом механических квадратур и с помощью процедуры последовательных приближений. Поле напряжений построено на основе фундаментальных решений Кельвина.

2. Особенностью распространения трещины в массиве горных пород является неоднородное поле напряжений, обусловленное наличием выработки, расположенной вблизи трещины. Это поле играет важную роль в расчетах траектории распространения трещины, и при определенных условиях может существенно повлиять на траекторию трещины гидроразрыва.

3. Анализ полученных результатов показал:

а) принятое допущение об отсутствии влияния друг на друга интенсивности напряжений не всегда справедливо. Так, при отношении начального давления жидкости в скважине к величине гравитационного давления в массиве, равном 1.5, трещина гидроразрыва довольно резко меняет первоначальное направление. С ростом этого отношения траектория становится плавной, а ее направление в меньшей степени отклоняется от направления зародышевой трещины. В тех случаях, когда трещина на начальных этапах своего развития меняет свое первоначальное положение более чем на десять градусов, для расчета ее параметров необходимо использование зависимостей, учитывающих и компоненты неоднородного поля напряжений, и изменения формы и направления траектории. В этом случае задача существенно усложняется. Однако во многих случаях важно установить рациональные соотношения между соответствующими параметрами, обеспечивающими прямолинейное развитие трещины, и для расчета воспользоваться более простыми зависимостями.

б) при отношении начального давления жидкости в скважине к величине гравитационного давления в массиве, равном трем и более, траектория трещины практически прямолинейна, и она незначительно отклоняется от направления зародышевой трещины, а ее полудлина растет нелинейно, увеличиваясь по закону показательной функции;

в) при прямолинейном распространении трещины гидроразрыва давление жидкости оказывает большее влияние на ее длину, чем глубина расположения трещины. Изменение отношения полудлины трещины к глубине ее расположения с ростом давления жидкости происходит практически линейно.

Исследование выполнено за счет гранта Российского научного фонда (проект № 17-17-01143).