Прикладная математика и механика, 2020, T. 84, № 2, стр. 196-207

Определение резонансных частот и форм колебаний деформируемых твердых тел (ДТТ) – классическая задача механики, имеющая множество практических приложений [1, 2]. Применительно к МКЭ данная проблематика освещена в большом количестве публикаций, начиная с классического труда [3]. В большинстве случаев решение таких задач ищется в приближении отсутствия диссипации на основе метода Ланцоша [4–7].

Наличие в ДТТ вязкой диссипации делает задачу поиска резонансных частот нелинейной, что существенно осложняет процедуру нахождения комплексных резонансных частот и форм колебаний. Существуют различные подходы к линеаризации и решению таких задач [8, 9]. Однако сравнение алгоритмов, представленных в современных CAE (computer-aided engineering) системах, например, ПО “ANSYS”, показывает, что вычисление резонансных частот с учетом вязкого трения требует на порядок больших временных и вычислительных затрат, нежели модовый анализ недиссипативных систем по методу Ланцоша. По этой причине в большинстве случаев вязкими потерями в высокодобротных системах пренебрегают, ссылаясь, в том числе и на то, что затухание вносит пренебрежимо малую поправку в абсолютное значение резонансной частоты, а сами по себе параметры и модели потерь для разных материалов априори не известны.

Тем не менее, в акустике для механоакустических систем “ДТТ-сжимаемая жидкость” величина потерь, связанных с акустическим излучением объектом звуковых волн, является хоть и малой, но принципиально важной в части оценки шумоизлучающей способности ДТТ. Вместе с тем, даже при отсутствии потерь на излучение, само по себе нахождение резонансных частот тел, погруженных в жидкость, не реализовано должным образом в современных программах численного моделирования, и вычисления сопровождаются критической потерей точности и расходимостью решения.

В связи с перечисленными выше ограничениями в данной работе представлена попытка адаптации метода Ланцоша под узкий класс задач нахождения собственных чисел механоакустических систем в приближении малости величины потерь на акустическое излучение.

1. Формулировка задачи на собственные числа для механоакустической системы. Конечно-элементное моделирование искомых гармонических виброакустических процессов традиционно осуществляется в пространстве двух переменных: поля перемещений u колеблющегося с частотой ω ДТТ, и потенциала перемещений θ, описывающего динамику жидкой среды. В такой постановке задача нахождения отклика на заданные силовые b воздействия в дискретном виде может быть описана системой линейных уравнений с симметричными матричными элементами, которая аналогична ранее представленной авторами [10]:

где ${{{\mathbf{K}}}_{s}}$ и ${{{\mathbf{M}}}_{s}}$ – матрицы жесткости и масс деформируемого твердого тела, ${{{\mathbf{M}}}_{F}}$ и ${{{\mathbf{G}}}_{F}}$ – матрицы, описывающие перетекание и сжимание жидкости, ${{{\mathbf{M}}}_{{FSI}}}$ и ${{{\mathbf{Z}}}_{F}}$ – матрицы, определяющие граничные условия непротекания на поверхности контакта ДТТ-жидкость и отсутствия отражения акустических волн от границ расчетной области соответственно. Алгоритмы формирования матричных компонент ${{{\mathbf{K}}}_{s}}$, ${{{\mathbf{M}}}_{s}}$, ${{{\mathbf{M}}}_{F}}$ и ${{{\mathbf{G}}}_{F}}$ можно найти в классических трудах [3, 11, 12]. С процедурой эффективного формирования матрицы ${{{\mathbf{M}}}_{{FSI}}}$, которая устанавливает зависимость между ${\mathbf{u}}$ и θ, можно ознакомиться в [10].

Решение уравнений (1.1) для заданных внешних сил ${\mathbf{b}}$ может быть найдено как непосредственно на фиксированной сетке частот, так и с помощью разложения полей ${\mathbf{u}}$ и θ по собственным векторам ${\mathbf{q}}$, которые являются решением однородной задачи на собственные числа $\lambda = \omega _{{рез}}^{2}$, где ${{\omega }_{{рез}}}$ – резонансные частоты механоакустической системы.

Первым очевидным препятствием к решению задачи (1.1) с помощью процедур модового анализа является нелинейность задачи на собственные числа относительно $\omega _{{рез}}^{2}$, определяющаяся членами ${{\omega }^{4}}{{{\mathbf{G}}}_{F}}$ и $i{{{\mathbf{Z}}}_{F}}(\omega )$.

Матрица $[{{{\mathbf{Z}}}_{F}}\left( \omega \right)]$ имеет ненулевые элементы только для узлов на внешней границе расчетной области. Существует целый ряд методов описания выхода акустических волн за границы расчетной области [13–16] с использованием различных вариантов связи между значением потенциала θ и его производной по нормали к границе расчетной области θ_n. В наиболее простой, используемой ниже, импедансной формулировке такая связь может быть представлена в виде: ${{\theta }_{n}} = i\omega \theta {\text{/}}c$, где $с$ – скорость звука в среде. Данное соотношение предполагает, что акустические волны выходят сквозь внешнюю жидкую границу конечно-элементной модели (КЭМ) в направлении близком к нормали. Применение более точного описания внешней границы могло бы внести поправку к оценке излучающей способности мод твердого тела, однако сама форма мод определяется достаточно точно уже в таком приближении границы КЭМ. С другой стороны импедансное соотношение обладает простой зависимостью от частоты, что позволяет записать ${{{\mathbf{Z}}}_{F}}$ в следующем виде:

где импедансная матрица $[Z]$ является частотно независимой. В предположении, что потери на излучение вносят слабое возмущение в формы резонансных колебаний ДТТ, для соотношения (1.2) можно допустить разложение ${{\omega }^{3}}$ по степеням ${{\omega }^{2}}$ и ${{\omega }^{4}}$ на заранее определенном интервале поиска решений $[{{\omega }_{m}}_{{in}};{{\omega }_{{\max }}}]$. Это позволяет приближенно отнести часть потерь в матрицы масс и сжимаемости жидкости. В совокупности с использованием дополнительной переменной (как это показано ранее [19]): и замены $\mu = 1{\text{/}}\left( {\lambda --s} \right)$, такой подход позволяет для решения (1.1) получить линейную задачу на собственные числа и вектора, аналогичную по своему виду описанной в [4]: где величина $s$ – спектральный сдвиг, определяющий область поиска собственных чисел. Матрицы $\left[ {\mathbf{M}} \right]$, $[{\mathbf{K}}]$ и собственный вектор $\{ q\} $ равны:

При этом модифицированные демпфированием материала $\chi $ и потерями на излучение матричные компоненты ${{{\mathbf{K}}}_{{SM}}}$, ${{{\mathbf{M}}}_{{FM}}}$ и ${{{\mathbf{G}}}_{{FM}}}$ определяются следующими соотношениями:

Величины коэффициентов ${{a}_{\omega }}$ и ${{b}_{\omega }}$ определяются исходя из ширины частотного интервала, в котором матрица ${{{\mathbf{Z}}}_{F}}(\omega )$ разлагается в ряд. Например, для использованных авторами значений ${{\omega }_{m}}_{{in}}{\text{/}}{{\omega }_{{max}}} = 0.5$ (октава) по методу наименьших квадратов можно получить: ${{a}_{\omega }} = 0.364$ и ${{b}_{\omega }} = 0.662$. При этом максимальная погрешность описанного выше разложения ${{\omega }^{3}}$ не превысит 7% в октаве.

2. Модифицированный сдвинутый блочный метод Ланцоша и особенности его применения к механоакустическим системам. В работе [4] описан сдвинутый блочный метод Ланцоша, применяемый для уравнений вида (1.4) в задачах строительной механики. Ограничение, присущее методу [4] и ряду аналогичных, заключается в использовании действительных значений переменных. В настоящей статье метод модифицирован и обобщен для комплекснозначных матриц и векторов. Для этого повторяется последовательность из тех же алгебраических операций, что и в классическом методе, но для комплекснозначных переменных. Правомерность данного подхода для слабодиссипативных систем подтверждается на практике большим объемом проведенных численных экспериментов.

Метод Ланцоша (как классический, так и модифицированный) позволяет приближенно представить исходную задачу на собственные числа большой размерности (1.3) приближенной задачей в виде [17]:

где $\mu {\text{*}}$ – приближенные значения искомой части собственных чисел исходной задачи, а $\left[ {\mathbf{T}} \right]$ – симметричная ленточная блочно-трехдиагональная матрица, состоящая из симметричных квадратных блоков ${{[{\mathbf{a}}]}_{j}}$ и верхнетридиагональных блоков ${{[{\mathbf{b}}]}_{j}}$:

Размеры $k$ каждого блока $[{\mathbf{a}}]$ и $[{\mathbf{b}}]$ подбираются исходя из оптимизации времени расчета. Авторами в расчетах использовались блоки при $k = 3$.

Матрица $\left[ {\mathbf{T}} \right]$ формируется методом последовательных приближений, и имеет размерность существенно (на несколько порядков) меньше, чем у исходной системы. Благодаря тому, что $\left[ {\mathbf{T}} \right]$ имеет меньшую размерность и специальный вид, нахождение ее собственных чисел оказывается более простой вычислительной операцией, чем нахождение собственных значений исходной системы.

С учетом (1.4–2.2) модифицированный алгоритм Ланцоша, развитый авторами настоящей статьи для решения акустических задач, может быть представлен в следующем виде:

1. Начало

2. Создаются ${{[{\mathbf{v}}]}_{0}}$ – нулевая и ${{[{\mathbf{r}}]}_{1}}$ – случайная матрицы (число строк соответствует числу степеней свободы, число столбцов – размеру блока, равному $k$)

3. Декомпозиция ${{[{\mathbf{r}}]}_{1}}$ создается таким образом, чтобы получить ${{\left[ {\mathbf{v}} \right]}_{1}}$ и ${{\left[ {\mathbf{b}} \right]}_{1}}$, удовлетворяющие условию: ${{[{\mathbf{v}}]}_{1}}^{T}[{\mathbf{M}}]{{[{\mathbf{v}}]}_{1}} = [{\mathbf{I}}]$, ${{[{\mathbf{v}}{\text{]}}}_{{\text{1}}}}{{{\text{[}}{\mathbf{b}}]}_{1}} = {{[{\mathbf{r}}{\text{]}}}_{1}}$ и ${{\left[ {\mathbf{b}} \right]}_{1}}$ – верхнетреугольная матрица размерности $k$ (Используется метод модифицированного QR-разложения)

4. Присвоение $j = 1$, выполнение факторизации матрицы $[{{{\mathbf{G}}}_{{\mathbf{s}}}}]$

5. Цикл Ланцоша

5.1. $[{\mathbf{V}}] = [{\mathbf{V}},{{{\mathbf{v}}}_{j}}]$ (Дополнение матрицы $[{\mathbf{V}}]$ блоком, полученным на предыдущем этапе)

5.2. Вычисление ${{[{\mathbf{h}}]}_{j}} = {{[{{{\mathbf{G}}}_{{\mathbf{s}}}}]}^{{ - 1}}}[{{{\mathbf{M}}}_{{\mathbf{0}}}}]{{[{\mathbf{v}}]}_{j}}$ для степеней свободы ${\mathbf{u}}$ и $p$, исходя из (2.5)

5.3. Вычисление ${{[{\mathbf{h}}]}_{j}}$ для степеней свободы θ с использованием выражения (2.4), которое будет дано ниже

5.4. ${{\left[ {\mathbf{h}} \right]}_{j}} = {{\left[ {\mathbf{h}} \right]}_{j}} - {{\left[ {\mathbf{v}} \right]}_{j}}_{{ - 1}}\left[ {\mathbf{b}} \right]_{j}^{T}$

5.5. ${{\left[ {\mathbf{a}} \right]}_{j}} = \left[ {\mathbf{v}} \right]_{j}^{T}\left[ {\mathbf{M}} \right]{{\left[ {\mathbf{h}} \right]}_{j}}$

5.6. ${{[{\mathbf{r}}]}_{{j + }}}_{1} = {{[{\mathbf{h}}]}_{j}} - {{[{\mathbf{r}}]}_{j}}{{[{\mathbf{a}}]}_{j}}$

5.7. Поиск независимых объемов жидкости $i$ на основе анализа суммы строк матрицы ${{\left[ {{{M}_{{FM}}}} \right]}_{{\theta i}}}$. Вычитание из ${{r}_{{\theta i}}}$ его среднего значения

5.8. Ортогонализация ${{[{\mathbf{r}}]}_{j}}_{{ + 1}} = {{[{\mathbf{r}}]}_{j}}_{{ + 1}} - [{\mathbf{V}}]({{[{\mathbf{V}}]}^{T}}[{\mathbf{M}}]{{[{\mathbf{r}}]}_{j}}_{{ + 1}})$

5.9. Декомпозиция ${{[{\mathbf{r}}]}_{j}}_{{ + 1}}$ аналогично п. 3, таким образом, что $[{\mathbf{v}}]_{{j + 1}}^{T}[{\mathbf{M}}]{{[{\mathbf{v}}]}_{{j + 1}}} = [{\mathbf{I}}]$, ${{[{\mathbf{v}}]}_{{j + 1}}}{{[{\mathbf{b}}]}_{{j + 1}}} = {{[{\mathbf{r}}]}_{{j + 1}}}$ и ${{\left[ {\mathbf{b}} \right]}_{{j + 1}}}$ – верхнетреугольная матрица

5.10. Внесение $j$-х блоков в систему:

5.10.1. Дополнение матрицы $[{\mathbf{T}}]$ блоками ${{[{\mathbf{a}}]}_{j}}$ и ${{\left[ {\mathbf{b}} \right]}_{j}}$ в соответствии с (2.2), расчет и проверка сходимости собственных чисел задачи $[{\mathbf{T}}]\{ {\mathbf{W}}\} = \mu {\text{*}}\{ {\mathbf{W}}\} $

5.10.2. Расчет собственных чисел $\mu {\text{*}}$ для “текущей версии” $[{\mathbf{T}}]$. Сначала блочная матрица сводится к трехдиагональной методом итераций, на каждой итерации исключается одна ненулевая диагональ. Далее для трехдиагональной матрицы используется один из стандартных методов нахождения собственных чисел

5.10.3. Проверка сходимости собственных чисел задачи $[{\mathbf{T}}]\{ {\mathbf{W}}\} = \mu {\text{*}}\{ {\mathbf{W}}\} $. Каждая $j$-я итерация приводит к своему набору собственных чисел $\mu {\text{*}}$, наибольшие из $\mu {\text{*}}$ должны слабо меняться от итерации к итерации. Это является критерием выхода из цикла

5.11. Конец цикла при положительном результате проверки

6. Расчет собственных векторов системы: $\left[ {\mathbf{Q}} \right] = [{\mathbf{V}}][{\mathbf{W}}]$

7. Расчет ${{q}_{\theta }} = s \cdot {{q}_{p}}{\text{/}}\lambda $, исходя из найденных $[{\mathbf{Q}}]$ и соответствующих им ${\mathbf{\lambda }}$

8. Конец

Важно перечислить основные отличия приведенного алгоритма от классической схемы [4, 17] (кроме применения комплексных переменных).

Во-первых, классический алгоритм, примененный к системе уравнений (1.4), будет содержать следующую операцию вместо п. 5.2 и 5.3:

Такая операция требует факторизации плохо обусловленной матрицы $([{\mathbf{K}}] - {{s}^{2}}[{\mathbf{M}}])$ в силу сингулярности отдельных блоков матрицы $\left[ {{{{\mathbf{M}}}_{{FM}}}} \right]$. Нужно отметить, что сингулярные блоки матрицы $\left[ {{{{\mathbf{M}}}_{{FM}}}} \right]$ присущи изолированным объемам жидкости, не имеющим граничных условий в виде заданного потенциала или поглощения акустической энергии, например, жидкость со всех сторон окруженная деформируемой оболочкой.

Пусть строки векторов $\left\{ h \right\}$ и $\{ v\} $, соответствующие степеням свободы $u$, $\theta $, $p$ обозначаются: $\{ {{h}_{u}}\} $, $\left\{ {{{h}_{\theta }}} \right\}$, $\left\{ {{{h}_{p}}} \right\}$ и $\{ {{v}_{u}}\} $, $\{ {{v}_{\theta }}\} $, $\{ {{v}_{p}}\} $. Тогда выражение (2.3), по сути, представляет собой решение уравнения:

Из последнего уравнения следует, что

и в таком случае два первых уравнения преобразуются к виду: где

При этом матрица $[{{{\mathbf{G}}}_{s}}]$ уже не имеет сингулярных элементов и численное решение системы уравнений (2.5) становится возможно получить методами стандартных библиотек линейной алгебры, что нельзя было сделать для системы (2.3). Кроме того, сделанное преобразование позволяет существенно сэкономить ресурсы при вычислениях на компьютере.

Во-вторых, сингулярность отдельных $i$ блоков матрицы $\left[ {{{{\mathbf{M}}}_{{FM}}}} \right]$ приводит к невозможности обеспечения ортогональности между используемыми в цикле Ланцоша векторами $r$. Пусть ${{r}_{{\theta i}}}$ – фрагмент вектора $r$, характеризующий $\theta $ степени свободы для i-го независимого объема жидкости КЭМ. Пусть при этом строки и столбцы матрицы [M_FM]_θi, соответствующие $\theta $ степеням свободы данного i-го объема жидкости, образуют сингулярную матрицу в силу того, что построчная сумма их элементов равна нулевому вектору. Тогда, если вектора ${{r}_{{\theta i}}}$ и ${{{v}}_{{\theta i}}}$ ортогональны друг другу, т.е. выполняется равенство:

для любого значения константы будет выполняться аналогичное равенство:

На практике это приводит к тому, что пространство Крылова, строящееся на основе ортогональных векторов $r$, определяется не однозначно, а лишь с точностью до постоянной (в пространстве) величины, которая бесконечно возрастает на каждом шаге алгоритма Ланцоша. Это в итоге приводит к потере точности и появлению нефизичных решений $\mu * \to \infty $ или $\omega \to s$.

Для того чтобы избежать данного обстоятельства можно искусственно вычесть из векторов ${{r}_{{\theta i}}}$ их среднее значение (п. 5.7 алгоритма) и восстановить удаленное среднее значение потенциала уже после выполнения цикла Ланцоша и с учетом (1.3) (п. 7 алгоритма).

Важно отметить, что по результатам работы алгоритма можно получить коэффициенты ${{\zeta }_{j}}$, характеризующие потери энергии, возникающие вследствие акустического излучения, которое генерируется колебаниями ДТТ на резонансной частоте ${{\omega }_{{резj}}}$ при $\chi = 0$:

3. Синтез амплитудно-частотной характеристики по результатам модового анализа механоакустических систем. Найденные по результатам работы приведенного алгоритма собственные числа $\lambda $ и вектора ${\mathbf{q}}$ могут использоваться для численного воспроизведения амплитудно-частотной характеристики (АЧХ) колебаний, возбуждаемых в механоакустической системе внешним силовым воздействием ${\mathbf{b}}$ путем синтеза мод. В основе данной процедуры лежит вычисление коэффициентов возбуждения ${{\gamma }_{j}}$ мод. Каждый такой $j$ коэффициент с учетом ортогонализации, обеспеченной при решении задачи на собственные числа (1.4), может быть записан в виде:

Здесь ${{{\mathbf{q}}}_{{uj}}}$ – выборка из j-го собственного вектора, отвечающая степеням свободы ${\mathbf{u}}$. При этом поле перемещений ДТТ может быть найдено в виде:

Представление величины звукового давления в виде совокупности возбужденных мод, вследствие сингулярности ${{{\mathbf{M}}}_{F}}$, приводит к необходимости определения постоянной $C$ в выражении:

Постоянная $C$ может быть рассчитана исходя из анализа поведения механоакустической системы при $\omega \to 0$, путем выделения у данной механоакустической системы $k$ ($k$ не более 6) твердотельных степеней свободы – форм колебаний тела с нулевой частотой (${{\lambda }_{k}} = 0$), при которых оно не деформируется и имеет перемещения ${{{\mathbf{u}}}_{Т}}$. Учитывая, что для $\omega \to 0$ соотношение между ${\mathbf{u}}$ и $p$ может быть записано в виде:

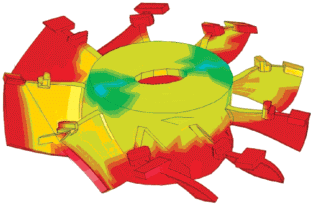
где $\left\{ {{{{\mathbf{m}}}_{{FSI}}}} \right\}$ и $\{ {{{\mathbf{g}}}_{{FM}}}\} $ – суммы столбцов матриц ${{{\mathbf{M}}}_{{FSI}}}$ и ${{{\mathbf{G}}}_{{FM}}}$ соответственно. Исходя из этого, выражение для $C$ может быть представлено следующим образом: где $g$ – сумма элементов вектора $\{ {{{\mathbf{g}}}_{{FM}}}\} $, $i$ – номер деформационной моды (${{\lambda }_{i}} > 0$).

4. Апробация алгоритма. В качестве примера апробации предложенных технологий модового анализа для прогнозирования АЧХ колеблющегося в безграничной жидкости тела ниже рассмотрен расчет звукового давления вблизи макета гребного винта (см. рис. 1). Модель представляет собой несколько пластин, размещенных равномерно на конической обечайке. Вокруг данного тела смоделирована жидкость, внешняя акустически прозрачная граница которой – куб – имеет габариты втрое большие, чем габариты тела.

Анализ результатов модального анализа показывает, что для подобных механоакустических систем собственные моды формируют три группы:

− моды, описывающие собственные резонансные колебания тела и сопутствующие процессы излучения звуковых волн на резонансных частотах во внешнюю среду. Пример таких колебаний приведен на рис. 1. Данные моды характеризуются малой величиной мнимой части собственной частоты ($\zeta \ll 0.1$), а также высокой сходимостью при их расчете по приведенному выше алгоритму;

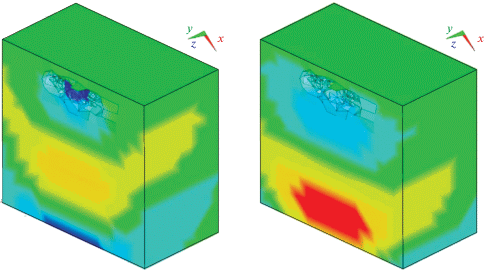
− моды, позволяющие описать произвольное поле давления в объеме жидкости с помощью разложения по дискретному набору бегущих акустических волн. Пример таких форм колебаний приведен на рис. 2 (слева – действительная часть моды, справа – мнимая). Данные моды характеризуются большой величиной мнимой части собственной частоты ($0.1 < \zeta < 0.5$) и невысокой сходимостью при их расчете по приведенному выше алгоритму;

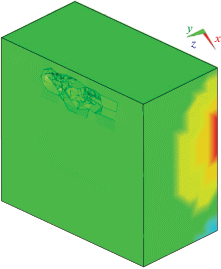
− моды, описывающие разложение поля давления на импедансных границах жидкости. Пример таких колебаний приведен на рис. 3. Данные моды характеризуются высокой величиной мнимой части собственной частоты ($\zeta > 0.5$), плохой сходимостью при их расчете по приведенному выше алгоритму, а также крайне малыми значениями уровней виброакустических полей на удалении от импедансных границ расчетной области. По-видимому существование данных мод определяется исходной математической формулировкой решаемой задачи и не несет значимого физического смысла.

Важно отметить, что моды каждого описанного выше типа характеризуются различным распределением энергии колебаний между водной средой и упругими колебаниями твердого тела. Наибольшим образом упругие колебания проявляются в модах первого типа. Такие моды при расчете АЧХ определяют акустическое поле в среде в окрестности резонансных частот. Напротив, упругие колебания твердых тел в модах третьего типа отсутствуют, что делает их ненужными для прогнозирования АЧХ. Моды второго типа, занимая промежуточное положение, вносят незначительный вклад в форму АЧХ, позволяя уточнить уровень излучения в межрезонансной области. Поэтому необходимость учета мод второго типа напрямую зависит от решаемой задачи.

Примечательно, что в качестве критерия принадлежности той или иной моды к конкретной группе выступает единственный параметр – величина потерь на излучение $\zeta $. Таким образом, вводя в модифицированный алгоритм ограничение на $\zeta $ сверху, можно существенно сэкономить временные ресурсы, избавляясь от необходимости расчета плохо сходящихся мод.

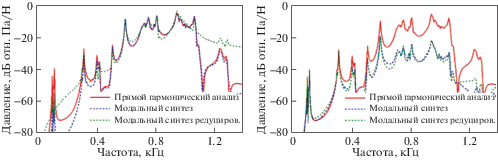
Например, на рис. 4 представлен результат прогнозирования АЧХ звукового давления для описанной выше модели в точке, лежащей на удалении от тела на импедансной границе жидкости при возбуждении макета лопасти нормальной силой. На обоих рисунках красной кривой приведены результаты прямого гармонического расчета звукового давления (без использования модального анализа). Синей пунктирной кривой представлены результаты прогнозирования звукового давления с использованием синтеза мод по описанному алгоритму, при учете мод с $\zeta < 0.5$. Зеленой пунктирной кривой также показаны результаты использования модального синтеза, но при учете лишь мод первой группы ($\zeta < 0.1$). Под прямым гармоническим анализом, результат которого был приведен на рис. 4, следует понимать явное решение системы (1.1) с ненулевой правой частью. Для получения кривой АЧХ производится перебор значений $\omega $ с достаточно мелким шагом, при этом решение (1.1) находится независимым образом для каждого из $\omega $. Для решения (1.1) при прямом гармоническом анализе применяется метод решения СЛАУ с использованием LDL^T-факторизации.

Важно отметить, что графики приведены, в том числе, для демонстрации корректности изложенного метода аппроксимации потерь на излучение. Так, на рис. 4, слева аппроксимация при расчете мод выполнялась в диапазоне 512…1024 Гц, а на рис. 4, справа – в диапазоне 64…128 Гц.

Как видно из рисунков, использование модального синтеза является корректным только в том диапазоне, в котором осуществляется аппроксимация потерь на излучение, и влияет на результат гораздо сильнее, чем увеличение порога по $\zeta $. Увеличение порога $\zeta $ с 0.1 до 0.5 приводит к уточнению результатов между резонансов в данном случае лишь на величину менее 3 дБ.

Оценить эффективность алгоритма можно следующим образом. Прямой гармонический анализ требует значительных временных ресурсов для расчета распределения поля для каждой заданной частоты ω, затрачиваемое время ${{T}_{{\operatorname{harm} }}}$ приближенно определяется выражением:

где ${{N}_{\omega }}$ – количество расчетных частот, а ${{T}_{{\operatorname{fact} }}}$ – время факторизации матрицы левой части уравнения (1.1).

При использовании вышеописанного модального алгоритма время решения задачи ${{T}_{{\operatorname{modal} }}}$ определяется временем нахождения мод, а дальнейший синтез АЧХ производится за время, пренебрежимо малое по сравнению с ${{T}_{{\operatorname{modal} }}}$ и ${{T}_{{\operatorname{harm} }}}$. Количество мод ${{N}_{\lambda }}$ заранее неизвестно, но, как правило, для инженерных расчетов ${{N}_{\lambda }} \ll {{N}_{\omega }}$. Таким образом, ${{T}_{{\operatorname{modal} }}}$ определяется: количеством мод ${{N}_{\lambda }}$, количеством выполняемых спектральных сдвигов ${{N}_{s}}$, временем факторизации матрицы ${{G}_{s}}$ (п. 4 алгоритма), средним временем выполнения одной итерации Ланцоша (п. 5 алгоритма) ${{T}_{{\operatorname{iter} }}}$ и количеством необходимых итераций: $\sim {\kern 1pt} \alpha $ итераций на одну моду.

Выполненные расчеты показывают, что для матриц значительной размерности справедлива приближенная оценка ${{T}_{{\operatorname{iter} }}} \gg 0.1{{T}_{{\operatorname{fact} }}}$, хотя для каждой последующей итерации величина ${{T}_{{\operatorname{iter} }}}$ слабо линейно возрастает из-за увеличения размерности ортогонолизируемых матриц (п.п. 5.1 и 5.8 алгоритма), т.е. можно записать:

Значение величин ${{N}_{s}}$ и $\alpha $ существенно зависят от дискретных свойств исследуемой механоакустической системы (заполненность и размерность исходных матриц) и ширины частотного диапазона. Для задач, представляющих практический интерес справедлива оценка: $4 < \alpha < 10$ и ${{N}_{s}} < 5$.

Сравнивая выражения (3.4) и (3.5) можно убедиться, что модальный анализ будет эффективен по сравнению с прямым гармоническим анализом при ${{N}_{\omega }} > {\text{ }}(5{\text{ }} + {{N}_{\lambda }})$, что, как правило, выполняется в практических приложениях. Кроме этого, данный алгоритм актуален для ряда приложений, например, [18], в которых требуется представление виброакустических характеристик систем именно в виде мод, а не в виде отклика на конкретное воздействие.

Заключение. Разработан модифицированный метод Ланцоша, позволяющий производить расчет излучающих звук форм и комплексных величин собственных частот резонансных колебаний взаимодействующих с жидкостью деформируемых тел с учетом моделирования потерь на акустическое излучение.

По результатам апробации метода установлено, что метод позволяет с высокой точностью воспроизвести АЧХ звукового давления, излучаемого ДТТ в рамках заданной октавной полосы. Метод обладает высокой численной сходимостью при отношении между мнимой и действительной частями резонансной частоты $\zeta < 0.1$, что достаточно для определения величины резонансного шумоизлучения колеблющегося ДТТ.

Представленный метод может быть использован в акустическом проектировании при исследовании виброакустических характеристик корпусных конструкций.

Авторы выражают благодарность руководителю Центра гидроакустики ИПФ РАН П.И. Коротину за обсуждение результатов работы. Работа выполнена в рамках программы фундаментальных научных исследований государственных академий наук, тема № 0035-2019-0018.