Прикладная математика и механика, 2020, T. 84, № 2, стр. 256-268

Введение. Одним из наиболее распространенных методов модификации поверхностей является нанесение на них различного типа покрытий. В условиях контактного взаимодействия между телами возникают силы адгезии, которые могут быть как пренебрежимо малыми, так и существенными. На микро и нано уровне, как правило, адгезионное взаимодействие необходимо учитывать. Покрытия толщиной меньше микрона не являются редкостью и используются, например, в микро-электро-механических системах (МЕМС) [1]. Кроме того, механические свойства покрытий в настоящее время определяются методами наноиндентирования, с использованием диапазонов сил и внедрений, при которых не учитывать адгезию нельзя [2]. Еще одним примером могут являться покрытия из материалов, таких как некоторые виды полимеров, которые проявляют адгезионные свойства на макроуровне. Таким образом, решение контактных задач для слоистых тел с учетом адгезии является актуальной задачей механико-математического моделирования.

Одна из наиболее распространенных моделей адгезионного взаимодействия разработана Джонсоном, Кендаллом и Робертсом (JKR), в ее основе лежит принцип баланса энергии, а силы адгезии действуют внутри области контакта. Упрощенная модель JKR применима в случае высоких значений поверхностной энергии, причем для податливых поверхностных слоев. Контакт упругих слоистых тел при наличии адгезии исследовался в работах [3–6] с использованием моделей на основе теории JKR. При этом в них применялись энергетические подходы, позаимствованные из механики разрушений, такие как скорость высвобождения энергии [3, 4] и коэффициент интенсивности напряжений [5]. Контакт жесткого индентора произвольной формы с упругим полупространством, покрытым упругим слоем, исследовался с помощью метода граничных элементов в [6]. Для решения использовался алгоритм быстрых преобразований Фурье. В перечисленных выше исследованиях [3–6] использовался метод граничных элементов. Были получены [7–9] полуаналитические решения задач о контакте слоистых упругих оснований с использованием моделей адгезии, основывающихся на теории JKR. Для этой же модели адгезии построено асимптотическое решение контактной задачи о нагружении поперечно-изотропного упругого слоя [10].

В случае контакта податливых покрытий на жестком основании может быть эффективным применение одномерной модели материала. Преимущество такого подхода – возможность использовать более точные формы потенциала адгезионного взаимодействия, рассматривать задачи со сложной геометрией контакта, а также минимизировать численную составляющую решения задачи. Так, например, было получено [11] решение периодической контактной задачи о скольжении волнистого индентора по вязкоупругому слою Кельвина при учете адгезии, описываемой моделью Можи–Дагдейла [12]. В рамках этой модели адгезионное давление аппроксимируется постоянным значением, действующим внутри области адгезионного взаимодействия, которая определяется величиной зазора между поверхностями. Применимость одномерной модели ограничена требованиями к свойствам материала подложки. Помимо того, что моделируемый слой должен быть значительно мягче основания, указанная модель не подходит для описания мягких покрытий с большим значением коэффициента Пуассона, например, резиновых.

Рассмотрена [13] уточненная постановка контактной задачи, где считается, что силы адгезии прикладываются не к границе деформируемого тела как контактное давление, а к точкам внутри тела, причем граница тела свободна от нагрузок. Получены решения для тонкого упругого слоя на жестком основании и для упругого полупространства.

Модель Можи–Дагдейла использовалась для решения осесимметричной контактной задачи для слоистых тел при наличии адгезии [14, 15]. При этом использовалось упрощающее предположение об отсутствии влияния адгезии на размер площадки контакта. Получено [14] полуаналитическое решение задачи о контакте с адгезией жесткого сферического индентора и упругого основания, сцепленного с упругим слоем. С помощью интегральных преобразований Ханкеля было построено решение для случая нескольких слоев, сцепленных с упругим основанием.

Целью данной работы является решение контактной задачи для упругого двухслойного основания и индентора произвольной формы при наличии адгезии, на основе которого можно проанализировать совместное влияние адгезионных сил и различной податливости материалов покрытия и подложки на результаты индентирования, а также рассмотреть напряженное состояние, возникающее в покрытии и подложке.

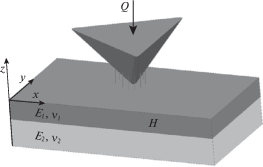
1. Постановка задачи. Рассмотрим задачу о внедрении жесткого гладкого индентора произвольной формы под действием нормальной силы Q в двухслойное основание, состоящее из упругого слоя, сцепленного с упругим полупространством (рис. 1).

Система координат $(x,y,z)$ связана с индентором, начало системы координат находится в точке первоначального касания индентора и слоя. Материалы слоя и полупространства характеризуются модулем Юнга и коэффициентом Пуассона ${{E}_{i}}$, ${{\nu }_{i}}$ ($i = 1$ для слоя и $i = 2$ для полупространства). Адгезионное взаимодействие между поверхностью слоя и индентором зависит от зазора $\delta $ и описывается моделью Можи–Дагдейла:

Рассматриваются следующие граничные условия при $z = 0$:

Здесь $\Omega $ – область контакта, $\Omega {\text{*}}$ – область адгезионного взаимодействия, $w(x,y)$ – вертикальные смещения поверхности слоя, $D$ – внедрение индентора, ${{\sigma }_{z}}$, ${{\tau }_{x}}_{z}$, ${{\tau }_{y}}_{z}$ – нормальные и касательные напряжения. Форма индентора описывается функцией $f(x,y)$. Контактные давления $p(x,y) = - {{\sigma }_{z}}(x,y)$ и области $\Omega ,\;\Omega {\text{*}}$ неизвестны.

Зазор в (1.1) определяется соотношением:

Выполняется также условие равновесия

и условие равенства $p{\text{*}}$ нормальных напряжений на границе области контакта $\Omega $.

Условия на нижней границе слоя ($z = - H$, где H – толщина слоя) соответствуют полному сцеплению:

Здесь $u_{x}^{{(i)}}$, $u_{y}^{{(i)}}$ – горизонтальные перемещения материала слоя ($i = 1$) и полупространства ($i = 2$).

2. Метод решения. Рассмотрим сначала пространственную контактную задачу без учета сил адгезии. Аналогичная задача о контакте осесимметричного гладкого индентора с двухслойным упругим основанием подробно рассмотрена [16] с использованием интегрального преобразования Ханкеля, метода граничных элементов и итерационной процедуры. Подобный подход использован и для решения более сложной задачи с граничными условиями (1.2)–(1.5) при $p{\text{*}} = 0$.

Рассмотрим сначала задачу о действии постоянной нагрузки q, распределенной внутри квадрата со стороной 2a, на двухслойное упругое основание. Условия на верхней границе слоя имеют вид

Эта задача решена в [17] с помощью методов, основанных на использовании двойных интегральных преобразований Фурье, которые позволяют рассчитать напряжения и упругие перемещения в слое и полупространстве. В частности, показано, что нормальные перемещения на верхней границе слоя определяются соотношением

Здесь ${{x}_{a}}$, ${{y}_{a}}$, ${{w}_{a}}$ – безразмерные координаты и нормальные смещения поверхности, отнесенные к полуширине квадрата $a$; ${{E}_{1}}{\text{ }}$ и ${{\nu }_{1}}$ – модуль Юнга и коэффициент Пуассона материала слоя, соответственно; $\chi = \tfrac{{{{E}_{1}}(1 + {{\nu }_{2}})}}{{{{E}_{2}}(1 + {{\nu }_{1}})}}$ – отношение приведенных модулей упругости слоя и упругого полупространства; $\gamma $, $\varphi $ – координаты в пространстве двойных интегральных преобразований Фурье; $\lambda = H{\text{/}}a$ – безразмерная толщина слоя. Функция $\Delta (\gamma ,\varphi ,\lambda ,\chi )$ получена в результате решения системы линейных функциональных уравнений, полученных из граничных условий (1.5), (2.1) в результате использования бигармонических функций для определения напряжений и перемещений, а также примененного к постоянной нагрузке двойного интегрального преобразования Фурье. Общий вид $\Delta (\gamma ,\varphi ,\lambda ,\chi )$ является громоздким и здесь не приводится, но важно отметить, что эта функция линейно зависит от $\bar {q}$ – результата применения двойного преобразования Фурье к постоянному давлению $q$:

В связи с тем, что постоянное давление $q$ линейно входит в функцию $\Delta (\gamma ,\varphi ,\lambda ,\chi )$ и может быть вынесено за знак интеграла, соотношение (2.2) может быть взято за основу при решении контактной задачи – определении контактного давления $p\left( {x,y} \right)$ в виде кусочно-постоянной функции.

Из условий (1.2) и (1.4) можно получить следующее уравнение для определения контактного давления:

где ${{p}_{1}}...{{p}_{N}}$ – неизвестные постоянные давления в каждом из $N$ элементов, ${{f}_{1}}...{{f}_{N}}$ определяются формой индентора. Коэффициенты $k_{i}^{j}$ получены из соотношения (2.2):

Здесь ${{(x_{{ij}}^{2} + y_{{ij}}^{2})}^{{1/2}}}$ – расстояние между центрами элементов-квадратов, $\Delta {\kern 1pt} '(\gamma ,\chi ,\varphi ,\lambda )$ = = $\Delta (\gamma ,\chi ,\varphi ,\lambda ){\text{/}}q$.

Решение уравнения (2.4) в произвольной, априори превышающей искомую, области контакта включает, вообще говоря, отрицательные давления в некоторых элементах-квадратах. На следующей итерации давление в этих элементах полагается нулевым, ранг матрицы системы (2.4) сокращается за счет данных нулевых элементов, и система решается заново. В результате итерационного процесса определяется положительное контактное давление $p\left( {x,y} \right)$ и область контакта $\Omega $.

Для решения контактной задачи с учетом сил адгезии применяется процедура, похожая на цикл нагружение–разгрузка. Сначала решается задача без адгезии, при этом индентор нагружен силой ${{Q}_{0}}$, такой, что область контакта $\Omega _{0}^{*}$ заведомо включает в себя искомую область адгезионного взаимодействия $\Omega {\text{*}}$ и область контакта $\Omega $ для задачи с адгезией при нагрузке $Q < {{Q}_{0}}$. Затем нагрузка уменьшается на шаг $\Delta Q$, определяется новая область контакта, давление, а также вертикальные смещения границы подложки. С учетом вертикальных смещений, а также положения границы области $\Omega _{0}^{*}$, происходит поиск элементов поверхности, соответствующих геометрическим критериям возникновения адгезионного взаимодействия в выражении (1.1), затем пересчет значений вертикальных перемещений поверхности, а также определение силы притяжения индентора к поверхности ${{Q}_{{adh}}}$. Система линейных уравнений с учетом сил адгезии приобретает следующий вид:

где ${{Q}_{{adh}}} = \sum\nolimits_{i = 1}^N {4p_{i}^{*}{{a}^{2}}} $, $\left( {\begin{array}{*{20}{c}} {w_{1}^{{adh}}} \\ \vdots \\ {w_{N}^{{adh}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {k_{1}^{1}}& \cdots &{k_{N}^{1}} \\ \vdots & \ddots & \vdots \\ {k_{1}^{N}}& \cdots &{k_{N}^{N}} \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} {p_{1}^{*}} \\ \vdots \\ {p_{N}^{*}} \end{array}} \right)$

Здесь k – номер итерации, ${{w}_{{adh}}}$ – перемещения, вызванные действием адгезионных сил ($p_{i}^{*}$ может принимать значение $p{\text{*}}$ либо 0 в зависимости от выполнения условия (1.1)). Нагрузка уменьшается пошагово до тех пор, пока не достигнет значения $Q$, необходимого по условиям задачи. В результате определяется область контакта, область адгезионного взаимодействия и распределение контактного давления. Затем полученные на поверхности распределения нормальных напряжений используются для определения внутренних напряжений подобно тому, как подобный расчет проводился для аналогичной задачи без адгезии [18].

3. Результаты расчетов. Разработанный метод решения может быть использован для решения пространственных задач для тел с покрытиями при произвольной форме гладкого индентора. С практической точки зрения наиболее востребованной является задача о вдавливании пирамиды Берковича при малых нагрузках в двухслойное упругое полупространство. Этот тип головок широко используется при наноиндентировании, он представляет собой трехгранную пирамиду с закругленным концом (по ГОСТ Р. 8.904-2015 радиус закругления может быть до 50 нм, в ходе эксплуатации увеличивается). При исследовании тонких пленок все чаще индентирование происходит в упругом режиме, что не позволяет определять твердость исследуемых материалов, но может дать информацию об их упругих свойствах.

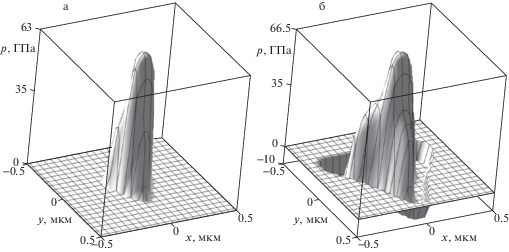
Для демонстрации возможностей метода было исследовано вдавливание силой $Q = 0.002$ Н трехгранной пирамиды, геометрия которой определяется ГОСТ Р. 8.904-2015, но радиус закругления составляет 0.3 мкм, в покрытие толщиной 0.1 мкм с модулем Юнга 350 ГПа, нанесенное на подложку с модулем 70 ГПа. Коэффициенты Пуассона для материалов слоя и полупространства полагались равными 0.3 и 0.4, соответственно. Адгезионное взаимодействие характеризовалось параметрами $p{\text{*}} = 10{\kern 1pt} $ ГПа, $\delta {\text{*}} = 2$ нм. Выбор величины критического зазора обусловлен характерным радиусом действия сил Ван-дер-Ваальса, значение $p{\text{*}}$ является достаточно высоким, чтобы получить при расчетах результаты, демонстрирующие влияние адгезии. На рис. 2 приведены распределения контактного давления под индентором, причем на рис. 2а представлен результат, полученный с учетом взаимного притяжения поверхностей, а на рис. 2б – без учета сил адгезии. Сложная форма индентора приводит к тому, что в центре площадки контакта (под скруглением) распределение давления близко к осесимметричному, ближе к границе контактные давления имеют значительный градиент под гранями пирамиды; форма области контакта близка к треугольной. При наличии адгезии на периферии области контакта имеет место отрицательное давление, и, в соответствии с соотношением (1.1), в зазоре, не превышающем $\delta {\text{*}}$, имеет место постоянное отрицательное давление. При наличии адгезии площадь области контакта и максимальное значение контактного давления больше, что соответствует выполнению условия равновесия (1.3) при наличии априори неизвестных адгезионных сил.

Другим распространенным типом наконечника при индентировании является скругленный конус либо сфера. В связи с меньшим количеством геометрических параметров в этом случае более удобно провести полный анализ совместного влияния сил адгезии и слоистой структуры основания на решение контактной задачи и распределение внутренних напряжений. С этой целью введем систему безразмерных параметров, характеризующих как входные данные, использованные при расчетах, так и результаты. Используем безразмерные координаты $(x{\kern 1pt} ',y{\kern 1pt} ') = (x,y){\text{/}}R$, где $R$ – радиус сферы, безразмерные смещения поверхности слоя $w'(x{\kern 1pt} ',y{\kern 1pt} ') = {{w}^{{(1)}}}(x,y){\text{/}}R$, безразмерную нагрузку $Q' = Q{\text{/}}{{R}^{2}}{{E}_{1}}{\text{ }}$, относительную жесткость слоя $\chi = {{E}_{1}}{\text{/}}{{E}_{2}}$, его относительную толщину $\lambda = H{\text{/}}R$, а также безразмерные константы в модели Можи–Дагдейла (1.1): ${{p}_{a}}{\text{/}}{{E}_{1}}$, $\delta {\text{*/}}R$. Безразмерные контактные давления отнесены к модулю Юнга слоя $p{\kern 1pt} '(x,y)$ = $p(x,y){\text{/}}{{E}_{1}}$, подобным образом вводятся и безразмерные напряжения.

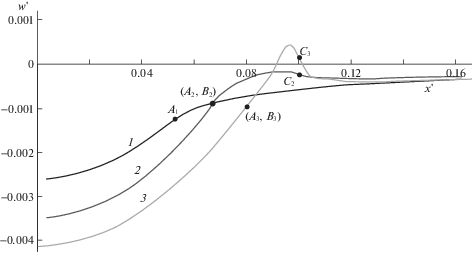
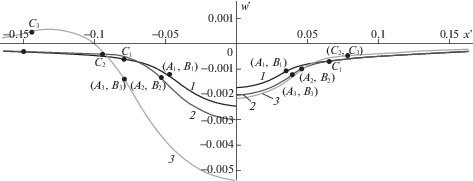
На рис. 3–5 представлены результаты расчета нормального смещения поверхности в условиях контактного взаимодействия для упругого полупространства (рис. 3), относительно мягкого (рис. 4) и относительно жесткого слоя (рис. 5). Решение для упругого полупространства было получено при $\chi = 1$ с целью верификации модели и последующего сравнения результатов. Результаты, представленные на рис. 3, получены при $\nu = 0.3$, $Q' = {\text{0}}{\text{.238}} \times {\text{1}}{{{\text{0}}}^{{ - 3}}}$, $\delta {\text{*/}}R = {\text{0}}{\text{.6667}} \times {\text{1}}{{{\text{0}}}^{{ - 3}}}$ и ${{p}_{a}}{\text{/}}{{E}_{1}} = 0$, 0.0143, 0.0714 для кривых 1–3 соответственно. Здесь и далее на кривых литерой А обозначена точка нулевого значения контактного давления, литерой B – граница области контакта, C – внешняя граница области $\Omega {\text{*}}$, в которой действуют силы адгезии. В некоторых случаях точки А и В расположены очень близко, что связано с большим градиентом давления вблизи границы области контакта. Зависимость вертикального смещения от координаты, монотонная для случая без адгезии (кривая 1), имеет максимум при наличии адгезии, причем, чем больше значение ${{p}_{a}}$, тем больше величина этого максимума. Также увеличивается размер площадки контакта, при этом ширина зоны адгезионного взаимодействия вне области контакта (между точками В и С) с увеличением значения ${{p}_{a}}$ сначала растет, затем уменьшается. Последний результат находится в соответствии с выводом Можи [12], что при больших значениях адгезионного давления ширина этой зоны стремится к нулю.

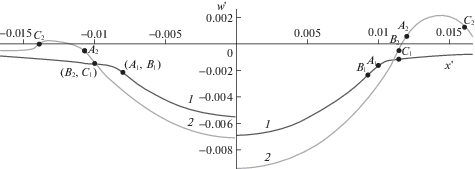
Рис. 4 иллюстрирует влияние величины адгезионного давления на смещение поверхности слоя, более податливого, чем основание, ($\chi = 0.1$) для двух вариантов его толщины: $H{\text{/}}R = 0.017$ (левая часть) и $H{\text{/}}R = 0.083$ (правая часть). Для расчетов использовались следующие значения параметров: ${{\nu }_{1}} = 0.4$, ${{\nu }_{2}} = 0.3$, $\delta {\text{*/}}R = {\text{0}}{\text{.6667}}$ × 10^–3, $Q' = {\text{0}}{\text{.159}} \times {\text{1}}{{{\text{0}}}^{{ - 2}}}$. Кривые 1, 2 построены для ${{p}_{a}}$ = 0.0143, 0.0714, соответственно. Влияние адгезионных сил на форму поверхности в целом проявляется так же, как и для однородного полупространства, но следует отметить, что для более тонкого слоя ширина кольцевой области $\Omega {\text{*}}$, в которой действуют силы адгезии, меньше, чем для толстого, особенно для относительно высоких значений ${{p}_{a}}$.

На рис. 5 представлены аналогичные результаты для относительно жестких покрытий $\chi = 5$ толщиной $H{\text{/}}R = 0.017$ (левая часть) и $H{\text{/}}R = 0.05$ (правая часть). Расчет проводился для следующих значений безразмерных параметров:

Кривые 1, 2, 3 соответствуют ${{p}_{a}} = {\text{0}}{\text{.143}} \times {\text{1}}{{{\text{0}}}^{{ - 2}}}$, ${\text{0}}{\text{.286}} \times {\text{1}}{{{\text{0}}}^{{ - 2}}}$, ${\text{0}}{\text{.571}} \times {\text{1}}{{{\text{0}}}^{{ - 2}}}$. Характерной особенностью является отсутствие немонотонной зависимости нормальных смещений поверхности жесткого слоя от координаты, зафиксированных для полупространства и податливого слоя на относительно жесткой подложке. Единственным исключением является кривая 3 в левой части рисунка. В этом случае радиус пятна контакта почти в пять раз превышает толщину слоя, что приводит к относительному уменьшению влияния слоя на результат решения задачи. Интересно отметить, что для относительно тонкого слоя имеет место существенное различие кривых 2 и 3, в то время как для более толстого слоя эти кривые достаточно близки.

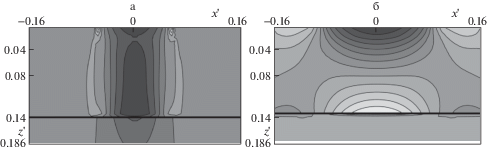
Результаты решения контактной задачи при наличии адгезии были использованы для расчета напряженного состояния в слое и основании, представленного на рис. 6–9 для относительно жестких ($\chi = 5$, $H{\text{/}}R = 0.0833$, ${{\nu }_{1}} = 0.35$, ${{\nu }_{2}} = 0.35$, $\delta {\text{*/}}R = {\text{0}}{\text{.333}}$ × × 10^–3, $Q' = {\text{0}}{\text{.158}} \times {\text{1}}{{{\text{0}}}^{{ - 3}}}$) и относительно податливых ($\chi = 0.01$, $H{\text{/}}R = 0.017$, ${{\nu }_{1}} = 0.4$, ${{\nu }_{2}} = 0.35$, $H{\text{/}}R = {\text{0}}{\text{.0166}}$, $\delta {\text{*/}}R = {\text{0}}{\text{.166}} \times {\text{1}}{{{\text{0}}}^{{ - 3}}}$, $Q' = {\text{0}}{\text{.198}} \times {\text{1}}{{{\text{0}}}^{{ - 2}}}$) упругих слоев при различных значениях ${{p}_{a}}$. На рис. 6 представлена общая картина распределения растягивающих-сжимающих напряжений, полученная при ${{p}_{a}} = 1.14 \times {{10}^{{ - 1}}}$ (рис. 6а), ${\text{2}}{\text{.85}} \times {\text{1}}{{{\text{0}}}^{{ - 2}}}$ (рис. 6б) для относительно податливых (рис. 6а) и относительно жестких (рис. 6б) слоев. Наиболее светлыми являются области растяжения (отрицательные значения напряжений), темные области соответствуют сжатию. Если для относительно жестких покрытий реализуется напряженное состояние, характерное для изгиба, которое отличается от случая взаимодействия без адгезии только количественными показателями, то в случае относительно податливых покрытий за счет адгезионного взаимодействия на периферии области контакта и под областью $\Omega {\text{*}}$ возникают растягивающие напряжения, которых нет при ${{p}_{a}} = 0$.

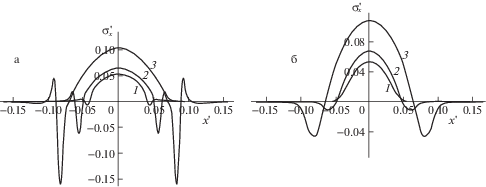
Анализ влияния величины параметра ${{p}_{a}}$ на растягивающие–сжимающие напряжения $\sigma _{x}^{'}$ на поверхности слоя и на границе раздела покрытия с подложкой можно провести на основе кривых, представленных на рис. 7, 8 (относительно податливый и жесткий слои, соответственно). Кривые 1–3 (рис.7) получены при ${{p}_{a}}{\text{/}}{{E}_{1}}$ = 0.071, 0.143, 0.286. На поверхности (рис. 7а) возникает интересный эффект резкого перехода от сжатия к растяжению вблизи границы области контакта. В области $\Omega {\text{*}}$ происходит переход растягивающих напряжений в сжимающие с локальным максимумом на внешней границе $\Omega {\text{*}}$. Описанные выше эффекты тем более выражены, чем больше величина ${{p}_{a}}$. На границе раздела слоя с основанием (рис. 7б) максимальные сжимающие напряжения в центре области контакта передаются почти в полном объеме, а растягивающие напряжения значительно меньше, чем на поверхности. Для ${{p}_{a}}{\text{/}}{{E}_{1}} = 0.071$ (кривая 1) имеет место только сжатие.

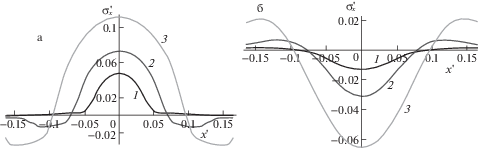
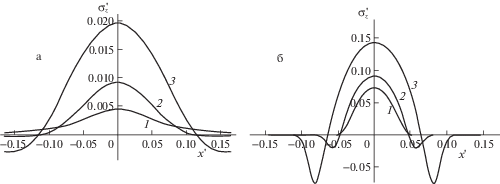
При определении напряжений в относительно жестком слое были использованы значения${{p}_{a}}{\text{/}}{{E}_{1}} = 0.286 \times {{10}^{{ - 2}}}$, $0.143 \times {{10}^{{ - 1}}}$, $0.286 \times {{10}^{{ - 1}}}$ для кривых 1–3, соответственно. При малых значениях ${{p}_{a}}$, аналогично случаю без адгезии, на поверхности (рис. 8а) имеет место только сжатие. С увеличением ${{p}_{a}}$ возникают зоны растяжения с локальными максимумами, не привязанными непосредственно к границам областей $\Omega $ или $\Omega {\text{*}}$ (в отличие от случая относительно податливых покрытий). На границе раздела слоя с основанием (рис. 8б) за счет изгиба слоя происходит зеркальное отражение картины распределения напряжений на поверхности. Как и при отсутствии адгезии, максимальное растяжение реализуется на границе раздела слоя с основанием под центром области контакта, и значение максимума тем больше, чем больше значение ${{p}_{a}}$.

Концентрация растягивающих напряжений может служить причиной образования трещины в материале слоя. Другой причиной разрушения композиции слой-основание могут быть отрицательные нормальные напряжения, стремящиеся отделить слой от основания. Подобный результат был получен при решении задачи для относительно жесткого слоя без адгезии [16] при некоторой комбинации входных параметров задачи, но в этом случае максимальные значения напряжений составили не более 3% от максимального значения контактного давления. Распределение $\sigma _{z}^{'}$ на границе раздела слоя и основания представлено на рис. 9 для относительно податливого (рис. 9а) и относительно жесткого (рис. 9б) слоев. Все параметры расчета аналогичны использованным при построении кривых рис. 6, 7. Результаты в данном случае являются предсказуемыми. При малых значениях параметра ${{p}_{a}}$ для обоих типов слоев напряжений, работающих на отрыв слоя, не обнаружено. С увеличением значений ${{p}_{a}}$ появляются отрицательные нормальные напряжения, более локальные в случае относительно податливого слоя.

Заключение. В данном исследовании предложен численно-аналитический метод расчета контактных давлений и внутренних напряжений, возникающих в двухслойном упругом полупространстве при вдавливании гладкого индентора произвольной формы с учетом адгезионного взаимодействия между индентором и поверхностью слоя. Используется модель Можи–Дагдейла, в которой адгезия определяется априори неизвестной формой зазора между контактирующими телами и в то же время влияет на результаты решения контактной задачи. Метод не имеет ограничений по соотношению модулей упругости слоя и основания.

Проанализировано совместное влияние сил адгезии и свойств упругого слоя – его относительной жесткости и толщины – на решение контактной задачи и распределение внутренних напряжений. Анализ результатов для относительно жестких и относительно податливых слоев показал, что:

Для относительно податливых покрытий имеет место немонотонная зависимость нормальных смещений поверхности слоя от расстояния до центра области контакта. Подобный эффект прилипания материала слоя к индентору наблюдается и для упругого полупространства, но отсутствует в случае относительно жестких слоев, за исключением очень тонких, когда слой мало влияет на решение контактной задачи.

При анализе напряженного состояния основное внимание было уделено растягивающим–сжимающим напряжениям, концентрация которых может служить причиной образования трещины в материале слоя, а также нормальным напряжениям на границе раздела слоя и полупространства. В результате адгезии на поверхности относительно податливых слоев возникает эффект резкого перехода от сжатия к растяжению вблизи границы области контакта и обратно вблизи границы области адгезионного взаимодействия. В случае отсутствия адгезии при тех же входных параметрах задачи растяжения на поверхности слоя нет. На поверхности относительно жестких слоев также могут возникать области растяжения при достаточно больших значениях адгезионного давления, но максимальные растягивающие напряжения имеют место на границе раздела слоя и полупространства под центром области контакта. Они также растут с ростом адгезионных сил.

На границе раздела слоя с основанием при наличии на поверхности адгезионных сил имеют место отрицательные нормальные напряжения, стремящиеся отделить слой от основания. В случае относительно податливых слоев эти напряжения сконцентрированы под областями отрицательных давлений на поверхности, а в случае жестких слоев они распределены более равномерно, но, в целом, меньше (по отношению к максимальному значению контактного давления).

Работа выполнена при поддержке гранта РНФ № 18-19-00574.