Прикладная математика и механика, 2020, T. 84, № 3, стр. 304-310

При обтекании однородным сверхзвуковым потоком тела с затупленной носовой частью перед ним формируется отошедший скачок уплотнения, поверхность которого искривлена, вследствие чего течение газа за ним вихревое. Связь формы скачка и завихренности на его поверхности известна [1, 2]. В течении за скачком справедливы закономерности вихревых течений для общего (без предположения о какой-либо симметрии) 3D случая. Наиболее важные из них представлены в работах [3–6]. Все они обобщают инварианты, известные для баротропных течений. При этом рассматриваются “обобщенные” циркуляции и поля “обобщенных” скорости и завихренности, что делает упомянутые законы сохранения труднообозримыми. Однако при дополнительном предположении об изоэнергетичности вихревого течения (которое выполняется в течениях за отошедшим скачком) обнаруженные закономерности получаются более обозримыми особенно для плоских и осесимметричных течений. В первую очередь необходимо упомянуть результат Крокко [7]. Он состоит в том, что в плоском случае вдоль линий тока сохраняется отношение завихренности к давлению ${{I}_{1}} = \Omega {\text{/}}p$, а в осесимметричном – инвариант ${{I}_{2}} = \Omega {\text{/}}(pr)$, где $r$ – расстояние от оси симметрии. Также можно указать на формулу, связывающую завихренность на поверхности осесимметричного тела (при нулевом угле атаки) с минимальным радиусом кривизны скачка [8].

Кроме законов сохранения представляют интерес и закономерности формы тех линий, которые определяются полем течения. Так, например, для несжимаемой жидкости изучались закономерности формы линий тока [9, 10], а также использовались [11, 12] и исследовались [13] закономерности формы вихревых линий.

В последнее время появились результаты [14, 15], относящиеся к общему (несимметричному) 3D случаю течений за отошедшим скачком уплотнения. Было предложено [14] точку, в которой вектор нормали к поверхности скачка параллелен скорости набегающего потока, называть лидирующей точкой. Для общего 3D случая показано, во-первых, что во всех точках линии тока, начинающейся в лидирующей точке, завихренность равна нулю (линия нулевой завихренности), а во всех остальных точках течения за скачком завихренность отлична от нуля. Во-вторых, что вихревые линии за скачком замкнуты и один раз охватывают линию нулевой завихренности. Для общего 3D случая показано [15], что при обтекании гладких выпуклых носовых частей линия торможения (линия тока, которая заканчивается в передней точке торможения) начинается в лидирующей точке скачка (и, следовательно, совпадает с линией нулевой завихренности). В данной статье продолжается поиск закономерностей течений за отошедшим скачком в общем 3D случае. Исследуются векторные линии векторного произведения скорости и градиента энтропии. Интерес к форме этих линий связан с вопросом существования (и возможности построения) таких систем ортогональных криволинейных координат на изоэнтропийных поверхностях за скачком, в которых линии тока являются координатными линиями (система естественных координат). Для таких систем координат исследуемые в данной статье линии представляют собой второе семейство координатных линий. Если хотя бы одна такая линия, начавшись в точке $A $ на одной из линий тока и сделав один оборот по изоэнтропийной поверхности, окажется на той же линии тока в точке $B \ne A$, то существование системы координат окажется невозможным (поскольку координатные линии не должны иметь двух точек пересечения). Ниже будет показано, что если линия делает один оборот, то всегда $B = A$, и построение системы координат возможно.

1. Основные обозначения и уравнения движения. Рассмотрим течение газа за отошедшим скачком уплотнения, образовавшимся при стационарном обтекании тела с затупленной носовой частью однородным сверхзвуковым потоком. Кроме отошедшего скачка ниже по течению могут существовать другие скачки и тангенциальные разрывы. Пусть ${{G}_{0}}$ – область, расположенная за отошедшим головным скачком, в которой отсутствуют какие-либо разрывы и точки торможения. И пусть при этом часть границы ${{G}_{0}}$, лежащая на скачке, содержит лидирующую точку скачка. Давление $p$ и плотность $\rho $ газа связаны соотношением $p = \sigma {\kern 1pt} {\kern 1pt} {{\rho }^{k}}$, где $k$ – показатель адиабаты, $\sigma $ – энтропийная функция, которая постоянна вдоль линий тока, но в области ${{G}_{0}}$ может принимать разные значения на различных линиях тока. Скорость газа ${\mathbf{V}}$ связана с плотностью уравнением неразрывности: $\operatorname{div} (\rho {\mathbf{V}}) = 0$. Газ предполагается идеальным: $p = R\rho T$, где $T$ – температура, $R$ – отношение универсальной газовой постоянной к молярной массе. Поскольку набегающий сверхзвуковой поток однороден, течение за скачком остается изоэнергетическим. Это значит, что полная энтальпия $k{{(k - 1)}^{{ - 1}}}p{{\rho }^{{ - 1}}}$ + ${{V}^{2}}{\text{/}}2$, где $V = {\text{|}}{\mathbf{V}}{\text{|}}$, всюду одинакова. Поэтому уравнения Эйлера, записанные в форме Крокко [16], имеют вид

В области ${{G}_{0}}$ газодинамические функции ${\mathbf{V}}$, $\rho $ и $p$ предполагаются дважды непрерывно дифференцируемыми по пространственным координатам и допускающими вместе со своими производными до второго порядка включительно непрерывное продолжение на поверхность скачка. Все дальнейшие рассуждения будут относиться к области ${{G}_{0}}$ и к той части скачка, которая является частью границы ${{G}_{0}}$. Под значениями завихренности и энтропийной функции на скачке будем понимать непрерывные продолжения $\Omega $ и $\sigma $ из области ${{G}_{0}}$ на эту поверхность.

2. Завихренность на поверхности скачка. Как отмечено во введении, поскольку скачок имеет искривленную форму, завихренность непосредственно за скачком принимает ненулевое значение. Расположим прямоугольную декартову систему координат $Oxyz$ с началом в произвольной точке $O$ на скачке так, чтобы ось $z$ совпала с нормалью к поверхности скачка. Учитывая условие непрерывности (при пересечении скачка) касательной составляющей скорости, несложно убедиться, что тем же свойством обладает $z$-компонента завихренности (нормальная к скачку компонента завихренности). Поскольку в набегающем сверхзвуковом потоке завихренность равна нулю, нормальная составляющая завихренности по обе стороны скачка также равна нулю, т.е. вихревые линии лежат на скачке. Поэтому поток вектора $\Omega $ через любую поверхность, лежащую на скачке, равен нулю.

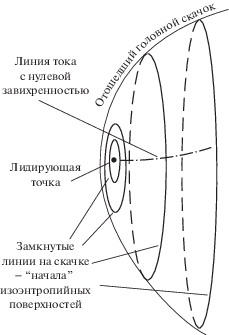
3. Циркуляция скорости газа по контуру, лежащему на изоэнтропийной поверхности за отошедшим скачком уплотнения. Из условий на косом скачке уплотнения [16, 17] следует, что энтропийная функция $\sigma $ на поверхности скачка имеет одно и то же значение на линии (лежащей на скачке), вдоль которой нормаль к скачку составляет один и тот же угол с вектором скорости набегающего потока. Такие линии, лежащие на скачке гладкой выпуклой формы, замкнуты и охватывают лидирующую точку, в которой вектор нормали параллелен скорости набегающего потока (рис. 1).

Рис. 1.

Поверхности тока, начинающиеся на упомянутых замкнутых линиях, охватывают линию тока, начинающуюся в лидирующей точке (линию нулевой завихренности), и представляют собой изоэнтропийные поверхности $\sigma = \operatorname{const} $.

Теорема 1. Пусть в течении за отошедшим головным скачком контур лежит на поверхности $\sigma = \operatorname{const} $ и один раз охватывает линию нулевой завихренности. И пусть на части этой поверхности, расположенной между скачком и контуром, отсутствуют какие-либо разрывы. Тогда циркуляция скорости газа по такому контуру равна нулю.

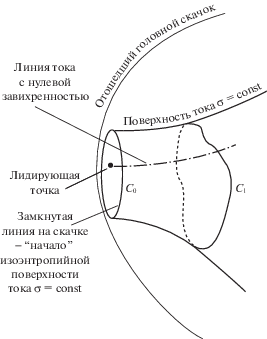
Доказательство. Пусть ${{С}_{1}}$ – произвольный контур, лежащий на одной из поверхностей $\sigma = \operatorname{const} $ и один раз охватывающий линию нулевой завихренности (рис. 2). Контур, лежащий на скачке и представляющий собой начало этой поверхности, обозначим ${{С}_{0}}$. Рассмотрим две поверхности. ${{S}_{0}}$ – лежащая на скачке поверхность, ограниченная контуром ${{С}_{0}}$ и ${{S}_{1}}$ – часть поверхности $\sigma = \operatorname{const} $, расположенная между контурами ${{С}_{0}}$ и ${{С}_{1}}$. Объединение ${{S}_{0}} \cup {{S}_{1}}$ представляет собой поверхность, ограниченную контуром ${{С}_{1}}$. Поэтому, согласно теореме Стокса, циркуляция скорости ${\mathbf{V}}$ по контуру ${{С}_{1}}$ есть поток вектора $\Omega $ через поверхность ${{S}_{0}} \cup {{S}_{1}}$. В предыдущем разделе показано, что поток вектора $\Omega $ через поверхность ${{S}_{0}}$ равен нулю. Из уравнения (1.1) следует, что вихревые линии лежат на поверхностях вида $\sigma = \operatorname{const} $. Поэтому поток вектора $\Omega $ через поверхность ${{S}_{1}}$ также равен нулю. Следовательно, циркуляция скорости ${\mathbf{V}}$ по контуру ${{С}_{1}}$ равна нулю. Теорема 1 доказана.

Рис. 2.

4. Существование системы ортогональных криволинейных координат. Рассмотрим поле вектора ${\mathbf{a}} = {\mathbf{V}} \times \nabla \sigma $. Из уравнения (1.1) следует, что в области ${{G}_{0}}$ этот вектор равен нулю только на линии нулевой завихренности. Поэтому во всех остальных точках ${{G}_{0}}$ определено семейство векторных линий вектора $a$. Эти линии в каждой точке ортогональны линиям тока (поскольку $a$ и ${\mathbf{V}}$ ортогональны). Согласно уравнению (1.1), каждая такая линия лежит на одной из поверхностей вида $\sigma = \operatorname{const} $.

Теорема 2. Пусть в течении за отошедшим головным скачком часть ${{С}_{{AB}}}$ векторной линии вектора ${\mathbf{a}} = {\mathbf{V}} \times \nabla \sigma $, лежащая на поверхности $\sigma = \operatorname{const} $ (не являющейся линией нулевой завихренности), делает один оборот вокруг линии нулевой завихренности и при этом начинается и заканчивается на одной и той же линии тока l в точках $A$ и $B$. И пусть на части поверхности $\sigma = \operatorname{const} $, расположенной между скачком, линией ${{С}_{{AB}}}$ и криволинейным отрезком линии тока l между точками $A$ и $B$, отсутствуют какие-либо разрывы и точки торможения. Тогда точки $A$ и $B$ совпадают.

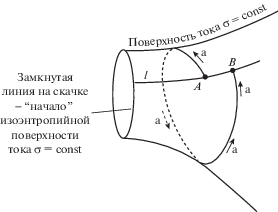
Доказательство проведем методом “от противного”. Допустим, что $B \ne A $(рис. 3).

Рис. 3.

Обозначим ${{С}_{{BA}}}$ – часть линии тока l, заключенная между точками $B$ и A. Вместе кривые ${{С}_{{AB}}}$ и ${{С}_{{BA}}}$ представляют собой контур, лежащий на поверхности $\sigma = \operatorname{const} $ и один раз охватывающий линию нулевой завихренности. В предыдущем разделе было показано, что циркуляция скорости ${\mathbf{V}}$ по такому контуру равна нулю. С другой стороны, на ${{С}_{{AB}}}$ скорость ${\mathbf{V}}$ ортогональна $a$ (и, следовательно, вклад в циркуляцию на этой части контура равен нулю), а на ${{С}_{{BA}}}$ скорость ${\mathbf{V}}$ не равна нулю и параллельна l, что означает ненулевой вклад в циркуляцию. Следовательно, циркуляция по контуру не равна нулю. Полученное противоречие означает, что $B = A$, и векторная линия $a$ замкнута. Теорема 2 доказана.

Векторная линия $a$, начавшись в точке $A$, может заканчиваться или на скачке или ниже по течению на границе области ${{G}_{0}}$, не пересекая второй раз линию тока $l$. Существование такой линии не противоречит возможности построения системы ортогональных криволинейных координат на изоэнтропийной поверхности $\sigma = \operatorname{const} $, в которой линии тока являются координатными линиями. Поэтому теорема 2 означает существование (и возможность построения) системы ортогональных криволинейных координат на каждой поверхности $\sigma = \operatorname{const} $ в области ${{G}_{0}}$.

Заключение. В работе проведен анализ полных уравнений Эйлера для 3D стационарных течений идеального газа в области между отошедшим головным скачком и носовой частью обтекаемого однородным сверхзвуковым потоком тела без предположения о какой-либо симметрии. Показано существование такой системы ортогональных криволинейных координат на каждой изоэнтропийной поверхности $\sigma = \operatorname{const} $, в которой линии тока есть координатные линии (теорема 2). В качестве промежуточного результата показано, что циркуляция скорости по контурам, лежащим на изоэнтропийных поверхностях равна нулю (теорема 1). Этот факт можно использовать для верификации численных расчетов, полученных не только схемами высокого, но и схемами первого порядка (поскольку при проверке отсутствует необходимость вычислять производные).