Прикладная математика и механика, 2020, T. 84, № 3, стр. 280-303
К ЗАДАЧЕ ОПТИМИЗАЦИИ СТРУКТУРЫ РАКЕТЫ-НОСИТЕЛЯ
1 ОАО “Газпром – космические системы”
Щелково М.О., Россия
2 Московский физико-технический институт
Долгопрудный М.О., Россия
3 Томский государственный университет
Томск, Россия
* E-mail: branets.07@mail.ru
Поступила в редакцию 18.10.2019
После доработки 25.02.2020
Принята к публикации 11.03.2020
Аннотация
Несмотря на большой прогресс в ракетной технике и практический опыт создания ряда ракетно-космических систем (ракет-носителей (РН)), задача оптимизации структуры РН не потеряла своего значения. Еще в фундаментальной работе известных американских ученых [1] в 1965 году ставился, в частности, вопрос об оптимизации распределения топлива между ступенями многоступенчатой конфигурации носителя. Было предложено его приближенное решение: авторы показали, что при одинаковых удельных импульсах ракетных двигателей последовательно работающих ступеней РН, оптимальным является равное распределение характеристических скоростей для каждой ступени. Позднее в учебном пособии, вышедшем в России [2], такой же вывод был повторен. В монографии [3], вышедшей в США в 2004 году, также упоминавших этот результат, кроме того было сказано, что другого более общего решения пока не найдено. В предлагаемой работе делается попытка найти новые подходы к решению этой и других смежных задач, связанных с оптимизацией ракеты-носителя.
Введение. Предлагаемая схема исследования основана на трех идейных предпосылках. Первая состоит в применении схемы “обратного полета”, когда процесс выведения рассматривается при обращении знака времени, т.е. выполняемом как бы в обратном порядке. Вследствие этого положения анализ процесса выведения РН начинается с последней ступени притом, что начальными условиями становятся условия нахождения ракетной ступени с полезным грузом на круговой орбите ИСЗ (окончание процесса реального выведения). Вторая предпосылка позволяет рассматривать виртуальную модель ракетной ступени с переменным количеством топлива и, соответственно, переменным весом топливных баков. Представляется, что поиск оптимального распределения топлива между ракетными ступенями носителя нужно искать при сравнении виртуальных РС. Третья – использует весьма наглядный и понятный параметр эффективности расходования топлива, являющийся производной от характеристической скорости ракетной ступени по расходуемому топливу. В статье проводится последовательно массово-весовой анализ РН и определяются условия для границ распределения топлива между ракетными ступенями, далее выполняется исследование динамики движения последней ступени, что совместно с требованиями к первой ступени позволяет во многом определить структуру РН. В заключительной части проводится анализ существующих ракет-носителей, иллюстрирующих полученные выводы.
1. Распределение топлива между РС. Исходные определения и аналитика. Проведем массово весовой анализ РН и поиск подходов к поставленной задаче распределения топлива (и характеристических скоростей) между РС, следуя работе [3] и используя обозначения этой работы. Главным объектом анализа является ракетная ступень ракеты-носителя. Положим, что каждая РС состоит из ракетного двигателя РД, имеющего массу ${{m}_{{рд}}}$, баков для хранения топлива массой ${{m}_{б}}$, и рядом служебных систем РС массой ${{m}_{\operatorname{s} }}$, так что вес “сухой” ракетной ступени равен ${{m}_{{рд}}} + {{m}_{б}} + {{m}_{\operatorname{s} }}$; массу полезного груза обозначим ${{m}_{{пг}}}$, конечная масса РС будет ${{m}_{{кон}}} = {{m}_{{рд}}} + {{m}_{б}} + {{m}_{\operatorname{s} }} + {{m}_{{пг}}}$, измеряемая в килограмах. Вес топлива РС обозначим ${{m}_{т}}$; величина тяги РД зависит от массового расхода и удельного импульса ${{R}_{{уд}}}$ в секундах:
где $g$ – гравитационное ускорение Земли, и тяга измеряется в Н. Потери тяги двигателя из-за атмосферного давления на малой высоте – будем учитывать в величине удельного импульса РД. Основным “выходным” параметром рассматриваемой $k$-й ракетной ступени будем считать приращение скорости $\Delta {{V}_{k}}$, получаемой за счет тяги ракетного двигателя, т.е. интеграла от ускорения, сообщаемого этим двигателем на полном интервале работы РД в условиях отсутствия внешних сил; эту величину называют характеристической скоростью РС. Для работы $k$-й ракетной ступени будем использовать далее известное соотношение для величины получаемого приращения скорости (формула Циолковского–Мещерского):(1.2)
$\Delta {{V}_{i}} = \int\limits_{{{m}_{{кон}}}}^{{{m}_{{нач}}}} {g{{R}_{{уд{\kern 1pt} }}}_{i}{{{\left( {\frac{{dm}}{m}} \right)}}_{i}}} = g{{R}_{{уд{\kern 1pt} }}}_{i}\ln MR{{{\kern 1pt} }_{i}}\; = {{V}_{{ист}}}{{{\kern 1pt} }_{i}}\ln {{\left( {1 + \frac{{{{m}_{т}}}}{{{{m}_{{кон}}}}}} \right)}_{i}},$Сумма $\Delta {{V}_{\Sigma }}$ всех ступеней даст полную скорость, которую может сообщить полезному грузу РН. Скорость для выведения на низкую круговую орбиту ИСЗ, хорошо известна, представим ее суммой $\Delta {{V}_{i}}$ в виде их выражения (1.2), можно видеть, что при равных удельных импульсах РД всех ракетных ступеней, суммарная скорость будет определяться произведением $MR{{{\kern 1pt} }_{i}}$ под знаком логарифма. Очевидно, что максимальное значение этого произведения при том, что сумма $\Delta {{V}_{{{\kern 1pt} i}}}$ фиксирована, будет тогда, когда значения всех составляющих будут одинаковы (и равно 1/3 для трехступенчатой РН, 1/2 – для двухступенчатой РН и т.д.). Выше мы и упоминали этот результат работы [1], и его будем рассматривать как первое приближение в решении поставленной задачи.
Построим проектную кривую обратного метода функциональной зависимости скорости $\Delta V$ обратного по знаку ускорения в функции от расходуемого топлива. Рассмотрение начнем с последней ступени, которой дадим номер $i$ (для простоты изложения индекс дальше использовать не будем, когда идет рассмотрение одной ступени РН). Особенностью этой проектной кривой будет формирование того же самого массового отношения начальной массы к конечной для вычисления приращения скорости в соответствии с соотношением (1.2) в функции текущего значения расходуемой массы топлива. Обозначим текущую (изменяющуюся во времени) массу РС
(1.3)
${{m}_{\operatorname{c} }}\left( t \right) = {{m}_{{пг}}} + {{m}_{{рд}}} + {{m}_{б}} + {{m}_{\operatorname{s} }} + {{m}_{т}}$На начальный момент времени реального полета ${{m}_{\operatorname{c} }} = {{m}_{{нач}}}$, и массовое отношение будет переменным во времени:
(1.4)
$MR\left( t \right) = \frac{{{{m}_{с}}}}{{{{m}_{{кон}}}}} = 1 + \frac{{{{m}_{т}}}}{{{{m}_{{пг}}} + {{m}_{{рд}}} + {{m}_{\operatorname{s} }} + {{m}_{б}}}}$В предлагаемом здесь обратном методе эта зависимость $\Delta V$ начинается с $MR\left( 0 \right)$ = 1, ($\Delta V = 0$) при ${{m}_{\operatorname{c} }} = {{m}_{{кон}}}$, и продолжается до ${{m}_{\operatorname{c} }} = {{m}_{{нач}}}$.
Безразмерные соотношения и виртуальная РС. Помимо величины массового отношения (1.4) введем понятие виртуальной ракетной ступени, которая будет отличаться от исходной тем, что запас топлива в ней не фиксирован, как в реальной РС. Этот переменный запас топлива будем обозначать той же переменной ${{m}_{т}}$, такие соотношения нам потребуются при анализе массовых параметров для переменных величин $\Delta V$ ракетной ступени, характеризуемых переменным количеством топлива.
Можно видеть, что все весовые составляющие для виртуальной РС могут при этом оставаться такими же, как в реальной РН, кроме веса баков для топлива. Положим простейшую линейную модель, когда вес баков пропорционален весу хранящегося в них топлива с неким коэффициентом $\mu $, т.е. ${{m}_{б}} = \mu {{m}_{{\text{т}}}}$ (не составляет труда использовать более точную весовую модель баков). Тогда имеем
(1.5)
$M{{R}_{{врт}}} = \frac{{{{m}_{с}}}}{{{{m}_{{кон}}}}} = 1 + \frac{{{{m}_{т}}}}{{{{m}_{{пг}}} + {{m}_{{рд}}} + {{m}_{\operatorname{s} }} + \mu {{m}_{т}}}}$В формулах (1.1), (1.4) и (1.5) масса всех составляющих входит в виде их отношения, т.е. имеется возможность представить формулы в безразмерном виде. Поскольку для нас самой важной является масса полезного выводимого груза, будем относить все массовые составляющие к этой массе. Введем безразмерные обозначения: $x = {{{{m}_{т}}} \mathord{\left/ {\vphantom {{{{m}_{т}}} {{{m}_{{пг}}}}}} \right. \kern-0em} {{{m}_{{пг}}}}}$ – основной параметр, определяющий запасы топлива в рассматриваемой ракетной ступени. Далее обозначим ${{a}_{k}} = {{\left( {{{m}_{{рд}}} + {{m}_{\operatorname{s} }}} \right)} \mathord{\left/ {\vphantom {{\left( {{{m}_{{рд}}} + {{m}_{\operatorname{s} }}} \right)} {{{m}_{{пг}}}}}} \right. \kern-0em} {{{m}_{{пг}}}}}$ – некий массовый конструктивный коэффициент, учитывающий вес РД и конструкции РС и ее систем, являющийся для выбранной ступени постоянным. Тогда получим для массового отношения (1.5) такую формулу
В качестве примера определим введенные коэффициенты в формуле (1.6) для третей ступени РН “Протон-К”, параметры которой представлены в следующей таблице 1.
Таблица 1.
Основные характеристики РН “Протон-К”
| Ступень | Первая | Вторая | Третья |
|---|---|---|---|
| Тяга двигателя, кН | 9500 | 2300 | 583 |
| Масса с топливом, кгс | 450 510 | 167 828 | 50 747 |
| Масса сухая, кгс | 31 000 | 11 750 | 4150 |
| Удельный импульс, с | 288 | 320 | 325 |
| Полезный груз, кг | 20 700 |
Используя числовые данные:
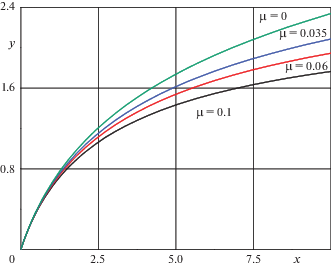
На рис. 1 представлены зависимости виртуального массового отношения (1.6) на основе числовых данных, когда ${{a}_{k}} = 0.067$ и различных значений бакового коэффициента $\mu $. Из этого графика и формулы (1.6) видно, что конструктивный параметр ${{a}_{k}}$ определяет наклон прямой (соответствует $\mu = 0$), и он тем выше, чем меньше весовые значения составляющих сухого веса ступени. Влияние же веса баков иллюстрируется семейством кривых. Представим безразмерные зависимости самого главного для нас параметра $\Delta V$, который запишем тоже в безразмерном виде, отнесенным к скорости истечения массы из ракетного двигателя
Рис. 1.
Зависимость $M{{R}_{{врт}}}$ от запасаемого топлива $x = {{{{m}_{т}}} \mathord{\left/ {\vphantom {{{{m}_{т}}} {{{m}_{{пг}}}}}} \right. \kern-0em} {{{m}_{{пг}}}}}$.
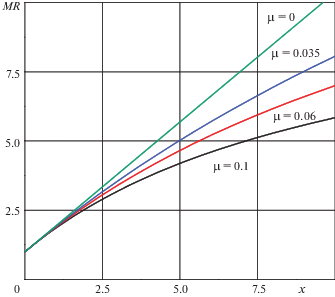
На рис. 2 представлены зависимости (1.2) для $\Delta V$ в безразмерном виде, справедливые, как для реальных, так и для виртуальных массовых отношений:
Функция $y\left( x \right)$ представляет $\Delta V\left( x \right)$ в единицах скорости истечения газов ракетного двигателя ${{V}_{{ист}}}$. Эти кривые дают представление о том, как вариации параметров ракетной ступени – $\mu $, ${{a}_{k}}$, ${{m}_{т}}$ влияют на основную ее характеристику – величину доставляемой ракетной ступенью приращения скорости $\Delta V$. Представленные зависимости очень показательны: во-первых, они относятся ко всем ступеням РН с любыми ракетными двигателями. Во-вторых, видно, что близко к началу координат существует область почти линейной зависимости $\Delta V$ от затраченного топлива: именно в этой области и работают все ракетные ступени. Так при $x \leqslant 2$ (${{m}_{т}} \leqslant 2{{m}_{{пг}}}$), величина $y$ достигает 1, тогда как последующее увеличение скорости, к примеру, в два раза потребует затрат топлива почти на порядок больше. Этим определяется тот факт, что очень трудно сделать одноступенчатую ракету, так как для этого потребуется массовое отношение не менее $у \sim \;3$. Даже при самом высоком удельном импульсе (в рассматриваемом примере, ${{R}_{{уд}}} = 325$ с, для третьей ступени РН), потребуется топлива в сотни раз больше веса полезного груза. Основное влияние здесь оказывает баковый коэффициент, которой сделать малым для конструкции с исходным большим весом практически возможным не представляется. Разделив потребную для выведения характеристическую скорость на три, т.е. рассматривая трехступенчатую РН, мы получим условия для каждой ступени в благоприятной зоне приемлемых характеристик.
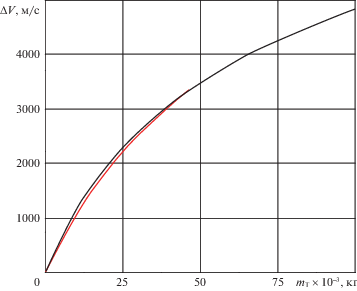
На рис. 3 представлены две зависимости $\Delta V\left( {{{m}_{т}}} \right)$, построенные для существующих параметров третьей ступени РН “Протон-К”: реальная зависимость, вычисленная по формуле (1.2) с использованием $MR$ формулы (1.4), которая заканчивается при ${{m}_{т}}$, равном 46.562 т (заправка РС) и виртуальная кривая, которая не ограничена. Как и следовало ожидать, начало и конец зависимости для третьей ступени лежат на виртуальной кривой $\Delta V\left( {{{m}_{т}}} \right)$. Отсюда можно сделать вывод, что виртуальная зависимость является огибающей семейства таких зависимостей для семейства РС, отличающихся различными объемами запасаемого топлива.
Рис. 3.
Реальная и виртуальная зависимости $\Delta V\left( {{{m}_{т}}} \right)$ для третьей ступени РН “Протон”.
Показатель эффективности расходования топлива. Зависимости $y\left( x \right)$ рис. 2 показывают, что эффективность преобразования ракетного топлива в скорость ракетной ступени сильно изменяется от самой высокой в начале графика (реально это конец работы РС), быстро снижающейся по мере увеличения запасаемого топлива.
Введем понятие эффективности расходования топлива (ЭРТ) ракетной ступенью, как величину производной от скорости $\Delta V$ по расходу топлива, то есть будем рассматривать производную ${{d\Delta V} \mathord{\left/ {\vphantom {{d\Delta V} {d{{m}_{т}}}}} \right. \kern-0em} {d{{m}_{т}}}}$. Дифференцируя соотношение (1.2), получаем
(1.9)
$\frac{{d\Delta V}}{{d{{m}_{т}}}} = \frac{{d\Delta V}}{{dMR}}\frac{{dMR}}{{d{{m}_{т}}}} = \frac{{g{{R}_{{уд}}}}}{{MR}}\frac{{dMR}}{{d{{m}_{т}}}}$Будем рассматривать производные от реальных (1.4) и виртуальных (1.5) массовых отношений
(1.10)
$\frac{{d\Delta V}}{{d{{m}_{т}}}} = \frac{{g{{R}_{{уд}}}}}{{{{m}_{\operatorname{c} }}}},\quad \frac{{d\Delta {{V}_{{врт}}}}}{{d{{m}_{т}}}} = \frac{{g{{R}_{{уд}}}}}{{{{m}_{с}}}}\frac{{{{m}_{{пг}}} + {{m}_{{рд}}} + {{m}_{\operatorname{s} }}}}{{{{m}_{{пг}}} + {{m}_{{рд}}} + {{m}_{\operatorname{s} }} + \mu {{m}_{т}}}}$Поскольку нас интересуют рассматриваемые величины производных в двух точках начала и конца работы ступени, то в начале: $\mu {{m}_{т}} = {{m}_{б}}$ и ${{m}_{с}} = {{m}_{н}}$, в конце: mc = = ${{m}_{{пг}}} + {{m}_{{рд}}} + {{m}_{\operatorname{s} }}$, то в этих точках имеем такие соотношения между виртуальной и реальной приращениями скоростей
(1.11)
$\begin{gathered} \frac{{d\Delta {{V}_{{врт}}}}}{{d{{m}_{т}}}} = k\frac{{d\Delta V}}{{d{{m}_{т}}}} - в начале \\ \frac{{d\Delta {{V}_{{врт}}}}}{{d{{m}_{т}}}} = \frac{1}{k}\frac{{d\Delta V}}{{d{{m}_{т}}}} - в конце \\ \end{gathered} $Именно это различие в производных показано на рис. 3. Сравнение этих производных показывает следующее. В начале обратного полета (конец выведения) виртуальная производная (1.10) будет в $k$ раз больше реальной, тогда как в конце она становится в k раз меньше, таким образом, виртуальная зависимость $\Delta {{V}_{{тек}}}\left( {{{m}_{т}}} \right)$ является действительно огибающей реальных кривых зависимостей $\Delta V\left( {{{m}_{т}}} \right)$ для различных вариантов этой ступени, отличающихся величиной запасаемого топлива. Заметим, что ранее [4] была сделана попытка (от которой впоследствии отказались) построить алгоритм нахождения оптимальной границы перехода с помощью этого коэффициента.
Для дальнейшего анализа будет нужен в основном реальный показатель эффективности расходования топлива (ЭРТ), обозначим его символом $\zeta $; можно видеть, что эта величина есть отношение ускорения РС к массовому расходу топлива, в итоге из соотношений (1.9) и (1.10) получаем
(1.13)
$\zeta = \frac{{d\Delta V}}{{d{{m}_{т}}}} = \frac{{d\Delta V}}{{dt}}\frac{{dt}}{{d{{m}_{т}}}} = \frac{F}{{{{m}_{c}}}}\frac{1}{{{{{\dot {m}}}_{т}}}} = \frac{{g{{R}_{{уд}}}}}{{{{m}_{\operatorname{c} }}}}$Этот показатель не зависит от тяги РД, расхода топлива и определяется только удельным импульсом и текущей массой ракетной ступени. Заметим, что вторая формула (1.10) иллюстрирует падение эффективности РС по мере увеличения размеров запасаемого топлива и самой ступени для виртуальной зависимости.
Можно видеть, что данных таблицы 1 достаточно, чтобы построить зависимость показателя ЭРТ для каждой РС, а тем самым и для всей РН. На рис. 4 и 5 представлены такие зависимости для РН “Протон-К” и “Зенит” (последняя советская РН); на графиках даны две зависимости: кривые показателя $\zeta $, являющиеся гиперболами, и текущая масса РН, точки разрыва кривых – это переход от одной ступени к другой, происходящий из-за отбрасывания массы пустой РС. Данные для РН “Зенит” представлены в таблице 2.
Рис. 4.
РН “Протон”, показатель ЭРТ $\zeta $ в функции от текущей массы РС ${{m}_{c}}$; слева – кривая 3 ступени, затем второй, и далее – первой. По оси абсцисс – масса РН в кг, по оси ординат – показатель ЭРТ в м/с кг. Заметим, что характеристические скорости ракетных ступеней суть: $\Delta {{V}_{1}}$ = (2615/2900) м/с (для предельных значений ${{R}_{{уд}}}$), $\Delta {{V}_{2}} = 3327$ м/с и $\Delta {{V}_{3}} = 3366$ м/с.
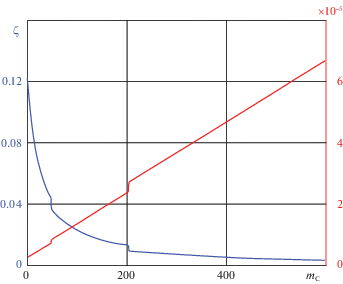
Рис. 5.
РН “Зенит”, зависимости $\zeta $ от ${{m}_{\operatorname{c} }}$. Слева кривые второй ступени, далее – первой: точка разрыва – переход от первой ступени ко второй. Характеристические скорости ступеней этой РН: $\Delta {{V}_{1}}$ = 3637/3966 м/с (предельные значения ${{R}_{{уд}}}$), $\Delta {{V}_{2}} = 5167$ м/с.
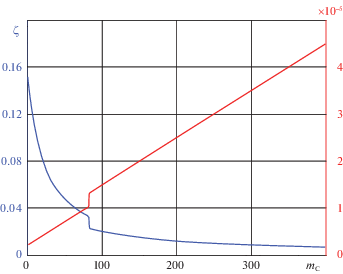
Таблица 2.
Основные характеристики РН “Зенит-2”
| Ступень | Первая | Вторая |
|---|---|---|
| Тяга двигателя, кН | 7259 | 834 |
| Масса с топливом, кг | 352 700 | 89 900 |
| Удельный импульс, сек | 337.2 | 350 |
| Масса сухая, кг | 33 900 | 9300 |
| Масса полезного груза, кг | 13 700 | |
Ход кривых ЭРТ на представленных рисунках показывает, что показатель ЭРТ начала работ последующей ступени выше, чем конца работы предыдущей. Эта информация позволяет искать решение задачи оптимизации перераспределения топлива между ступенями РС в поиске возможности использования более высоких показателей ЭРТ. Совершенно очевидно, что желательно большее количество топлива израсходовать там, где выше коэффициент $\zeta $, т.е. переместить как можно большее количество топлива в РС в сторону последней ступени. При этом по мере увеличения топлива в более эффективной РС кривая зависимости $\zeta $ изменяется; она увеличивается по длине и “проседает”, но по-разному: меньше всего в начале координат (увеличение массы баков), и больше – к границе перехода к смежной РС (баки и топливо). Такое “перераспределение” топлива должно закончиться при выравнивании показателей ЭРТ на границе двух РС. По сути дела этот вывод и есть решение задачи об оптимальном распределении топлива между ракетными ступенями, который нужно дополнить естественными ограничениями, существующими для различных участков полета.
Тем самым, может быть создан некоторый новый методический подход к решению поставленной задачи оптимизации: нужно построить компьютерный алгоритм поиска границы по массе топлива при переходе от одной ступени к другой, таким образом, чтобы исключить “разрывы” в кривой ЭРТ между соседними РС, кроме, может быть, той, которая вызвана сбросом массы отработанной ступени РН.
Обсуждение результатов и выводы. В качестве примера рассмотрим более детально один такой переход, скажем от второй к третьей РС РН “Протон-К”. Значение показателя ЭРТ конца работы второй ступени в конце ее работы равен (используем данные таблицы 1 такие: ${{\zeta }_{{2k}}} = 0.0377$ м/с кг, тогда как в начале работы третьей ступени этот показатель равен ${{\zeta }_{{30}}} = 0.04458$ м/с кг. Если допустить увеличение запасов топлива, т.е. и характеристической скорости третьей ступени $\Delta {{V}_{3}}$ на $\delta V = 1$ м/с, и уменьшение на такую же величину $\Delta {{V}_{2}}$, то получим выигрыш в массе топлива $\delta m = \delta V\left( {{1 \mathord{\left/ {\vphantom {1 {{{\zeta }_{{2k}}} - {1 \mathord{\left/ {\vphantom {1 {{{\zeta }_{{30}}}}}} \right. \kern-0em} {{{\zeta }_{{30}}}}}}}} \right. \kern-0em} {{{\zeta }_{{2k}}} - {1 \mathord{\left/ {\vphantom {1 {{{\zeta }_{{30}}}}}} \right. \kern-0em} {{{\zeta }_{{30}}}}}}}} \right) = 4.093$ кг, т.е. такой проектный процесс передачи топлива к более эффективной РС имеет смысл. Величину массы топлива третьей ступени можно увеличивать, к примеру, до тех пор, пока ${{\zeta }_{{30}}}$ не уменьшится до конечного значения ${{\zeta }_{{2k}}} = 0.0377$ м/с кг, откуда получим в линейном приближении, что массу третьей ступени можно увеличить на 13 035 кг, и это эквивалентно увеличению скорости на $\delta {{V}_{3}} = 535$ м/с. Из рассмотрения кривых показателя ЭРТ рис. 4 и 5 видно, что такие же соображения можно применить и ко всем другим точкам перехода от одной РС к другой. Заметим, что примерно такие расчеты были приведены в работах [5–7].
Более внимательный анализ показывает, что такая линейная экстраполяция вряд ли справедлива для больших изменений в распределении масс и скоростей. Дело в том, что изменяя параметры ракетной ступени (массу ее топлива), мы должны переходить к виртуальной ее модели, при этом вся кривая ЭРТ этой ступени меняется в целом. Обратимся к безразмерному соотношению для массового отношения РС (1.6) и попробуем выразить величину параметра ЭРТ через переменные $x = {{{{m}_{т}}} \mathord{\left/ {\vphantom {{{{m}_{т}}} {{{m}_{{пг}}}}}} \right. \kern-0em} {{{m}_{{пг}}}}}$ и $y$ в безразмерных равенствах (1.7). Имеем
(1.14)
$y = \ln M{{R}_{{врт}}},\quad \zeta = \frac{{d\Delta V}}{{d{{m}_{т}}}} = \frac{{g{{R}_{{уд}}}}}{{{{m}_{{пг}}}}}\frac{{dy}}{{dx}}\quad {\text{и}}\quad \frac{{dy}}{{dx}} = \frac{{1 + {{а}_{k}}}}{{\left( {1 + {{а}_{k}} + \mu x} \right)\left( {1 + {{а}_{k}} + x + \mu x} \right)}}$При малых значениях $x$ показатель ЭРТ равен $\zeta = \frac{{g{{R}_{{уд}}}}}{{{{m}_{{пг}}}}}\frac{1}{{1 + {{a}_{k}}}}$, но как только величина $x$ возрастает, начинается падение ЭРТ, которое затем происходит не по обычной, а по квадратичной гиперболе, тем самым граница искомого перехода, когда эффективности выравниваются, действительно всегда существует. Схема использования запасов топлива при $х \leqslant 2$ для всех ступеней соответствует упомянутому выше критерию равных характеристических скоростей [1–3]. Появление трехступенчатых РН в истории объясняется тем, что все они были получены из межконтинентальных баллистических ракет добавлением третьей ступени, которая действительно сильно увеличила ее суммарную эффективность.
Как показала практика, при проектировании уже ракеты-носителя для выведения на низкую круговую орбиту (НОО), все равно переходили к использованию двухступенчатой РН, когда последняя ступень взяла на себя задачи второй и третьей из-за ее более высокой эффективности. Точно такой же процесс можно было бы себе представить и на границе перехода от второй к первой ступени, однако требования к первой ступени, которые мы рассмотрим дальше, являются уникальными и не могут быть исполнены последующими ступенями. Можно видеть, что перераспределение скоростей (или топлива) между РС возможно, и оно, безусловно, может привести к положительному результату. Найти простые аналитические соотношения в поставленной задаче – не удалось, даже с использованием виртуальной модели. Не вызывает сомнений, что можно и нужно построить компьютерный алгоритм нахождения рационального распределения характеристических скоростей между ракетными ступенями, о чем говорилось выше.
2. Динамика выведения последней ступени. Применим метод обратного полета к исследованию динамики движения последней ступени. Такая задача имеет особый интерес с точки зрения исследования возможности для построения РН с двумя ступенями, когда последняя ступень выполняет основной набор орбитальной скорости оптимальным образом. При этом, естественно выгодно использование на последней ступени РД с самыми высокими удельными импульсами, какие имеют кислородно-водородные двигатели, хотя проведенное рассмотрение будет справедливым для любых других РД.
Исследование оптимальной траектории. При торможении орбитальной скорости возникает особый случай: при достаточно энергичном горизонтальном ускорении РС успевает выдать достаточно большой импульс приращения скорости при малом изменении высоты полета.
Обратимся к уравнениям движения и запишем их в проекциях скорости движение ракетной ступени на оси орбитальной системы координат [3]. Пусть $\alpha $ представляет собой угол к линии горизонта направления вектора тяги РД, ${{V}_{\theta }}$ и ${{V}_{r}}$ – компоненты горизонтальной и вертикальной составляющих скорости, $r$ – геоцентрический радиус РС; при отсутствии аэродинамических сил уравнения движения примут вид:
(2.1)
$\begin{gathered} \frac{{d{{V}_{\theta }}}}{{dt}} = \frac{{F\cos \alpha }}{m} \\ \frac{{d{{V}_{r}}}}{{dt}} = \frac{{F\sin \alpha }}{m} - \left( {g - \frac{{V_{\theta }^{2}}}{r}} \right) \\ \end{gathered} $Максимальная эффективность импульса тяги РД получается при его использовании только в целях гашения (т.е. набора в реальном полете) орбитальной скорости ${{V}_{\theta }}$. Примем для дальнейшего анализа угол $\alpha = 0$, при этом получаем такие уравнения:
(2.2)
$\frac{{d{{V}_{\theta }}}}{{dt}} = \frac{F}{m},\quad \frac{{d{{V}_{r}}}}{{dt}} = - g + \frac{{V_{\theta }^{2}}}{r},$(2.3)
${{V}_{\theta }}\left( t \right) = V_{\theta }^{0} - \Delta V = V_{\theta }^{0} - g{{R}_{{уд}}}\ln \left[ {MR\left( t \right)} \right] = V_{\theta }^{0} - g{{R}_{{уд}}}\ln \left( {1 + \frac{{{{{\dot {m}}}_{т}}t}}{{{{m}_{к}}}}} \right)$Аналогичным образом может быть получено соотношение с участием виртуального изменения скорости, позволяющее оценить процесс торможения для любого выбранного переменного запаса топлива этой ступени. Уменьшение орбитальной скорости (2.3) приводит к появлению вертикального ускорения, вследствие чего появляется вертикальная скорость снижения. Подставляя это значение во второе уравнение (2.2), получаем:
(2.4)
$\frac{{d{{V}_{r}}}}{{dt}} = - g + \frac{{{{{\left( {V_{\theta }^{0} - \Delta V} \right)}}^{2}}}}{r} \simeq - \frac{{\Delta V}}{r}\left( {2V_{\theta }^{0} - \Delta V} \right) = g\frac{{\Delta V}}{{V_{\theta }^{0}}}\left( {\frac{{\Delta V}}{{V_{\theta }^{0}}} - 2} \right),\quad \dot {r}\left( t \right) = {{V}_{r}}$В этих уравнениях будем считать на начальном участке движения изменение высоты полета $r$ малым, так что $V_{\theta }^{{{{0}^{2}}}} = gr$ и величину гравитационного ускорения будем считать постоянной. Можно видеть, что вертикальная составляющая скорости получается интегрированием уравнения (2.4) при соотношении для $\Delta V\left( t \right)$ в виде (1.2) в первом разделе этой работы и нулевых начальных условиях по скоростям:
Однако, в целях получения достаточно общих соотношений для любых параметров РС, нам удобнее будет представить зависимости высоты и скорости вертикального снижения в функции от безразмерной переменной $w = \Delta V{\text{/}}V_{\theta }^{0}$. Эта переменная представляет собой долю полной орбитальной скорости, получаемую за счет работы рассматриваемой ракетной ступени. Для анализа вертикального движения преобразуем первое уравнение (2.4) следующим образом:
(2.5)
$\frac{{d{{V}_{r}}}}{{dw}} = \frac{g}{a}\left[ {w\left( {w - 2} \right)} \right] = \frac{{{{m}_{к}}}}{{{{R}_{{уд}}}{{{\dot {m}}}_{т}}}}\exp \left( {\Delta V{\text{/}}\left( {g{{R}_{{уд}}}} \right)} \right)\left[ {w\left( {w - 2} \right)} \right],$(2.6)
$\frac{{d{{V}_{r}}}}{{dw}} = \frac{g}{{{{a}_{0}}}}V_{\theta }^{0}{{e}^{{\eta w}}}\left[ {w\left( {w - 2} \right)} \right] = \frac{{V_{\theta }^{0}}}{{{{n}_{0}}}}{{e}^{{\eta w}}}w\left( {w - 2} \right)$Второе уравнение для вертикального расстояния $r\left( t \right)$ (2.4) приведем к этим же переменным: ${{V}_{r}} = \frac{{dr}}{{dt}}$ = $\frac{{dr}}{{d\Delta V}}\frac{{d\Delta V}}{{dt}}$ = $\frac{{dr}}{{dw \cdot V_{\theta }^{0}}}{{a}_{0}}{{e}^{{ - \eta w}}}$, откуда получаем
Интегрируя (2.6) с учетом начальных условий по скорости $V_{r}^{0} = 0$, имеем
(2.8)
${{V}_{r}}{\text{/}}V_{\theta }^{0} = \frac{1}{{{{n}_{0}}\eta }}\left\{ {{{e}^{{\eta w}}}w\left[ {w - 2\left( {1 + \frac{1}{\eta }} \right)} \right] + \frac{2}{\eta }\left( {1 + \frac{1}{\eta }} \right)\left( {{{e}^{{\eta w}}} - 1} \right)} \right\}$Подставляя полученное решение в (2.7) с учетом начального условиея по высоте вида ${{r}_{0}} = V_{\theta }^{{{{0}^{2}}}}{\text{/}}g$, получаем
(2.9)
$\frac{r}{{{{r}_{0}}}} = 1 + \frac{1}{{2n_{0}^{2}{{\eta }^{2}}}}\left\{ {{{e}^{{2\eta w}}}w\left( {w - 2 - \frac{3}{\eta }} \right) + \frac{1}{\eta }\left( {3 + \frac{7}{{2\eta }}} \right)\left( {{{e}^{{2\eta w}}} - 1} \right) - \frac{4}{\eta }\left( {1 + \frac{1}{\eta }} \right)\left( {{{e}^{{\eta w}}} - 1} \right)} \right\}$Как следует из полученных решений, траектория определяется параметрами $\eta $, зависящим как от $g{{R}_{{уд}}}$, так и от ${{n}_{0}} = {{a}_{0}}{\text{/}}g$ – величины перегрузки в начале обратного полета. Можно видеть, что для уменьшения вертикальной скорости и уменьшения снижения высоты полета ее следует выбрать максимальной. С учетом конструктивных ограничений для полезной нагрузки это максимальное значение может быть взято порядка ${{n}_{0}} \leqslant 4$, именно эта величина ниже используется при построении графиков.
Анализ возможностей. Полученные аналитические зависимости дают представление о поведении основных параметров траектории выведения: можно видеть, что для уменьшения вертикальной скорости и уменьшения снижения высоты полета существует ее значительный участок, определяемый начальной высотой целевой орбиты. Формула (2.9) показывает условие (т.е. накладывает требование) на уровень тяги ракетного двигателя последней ступени: его величину желательно сделать как можно больше, этим данный участок ракетного полета отличается от орбитального полета, где величина тяги РД может быть, в том числе, и очень малой. Более того, перегрузка от тяги РД соотносится с величиной земного ускорения.
Заметим, что STS “Спейс Шаттл” имеет перегрузку в конце выведения, равную 3, такая перегрузка уменьшает на порядок высотную “просадку” траектории по сравнению, скажем, с перегрузкой, равной 1. Можно себе представить, что при перегрузке в 0.1 “просадка” траектории становится на три порядка больше.
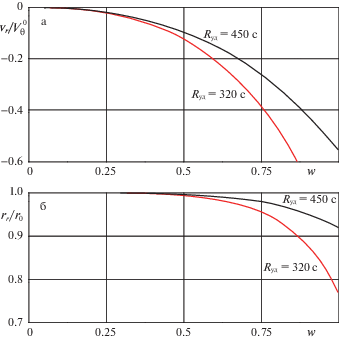
На рис. 6 представлена зависимость ${{V}_{r}}\left( w \right)$, и $r\left( w \right)$ в безразмерном виде (8.2) и (9.2) для двух величин удельного импульса. Используя представление ${{e}^{{\eta w}}} \approx 1 + \eta w$ + $\frac{1}{2}{{\eta }^{2}}{{w}^{2}}$ + + $\frac{1}{6}{{\eta }^{3}}{{w}^{3}}$ + …, выразим приближение формулы (8.2) в виде степенного ряда:
(2.10)
$\frac{{{{V}_{r}}}}{{V_{\theta }^{0}}} = - \frac{1}{{{{n}_{0}}}}\left( {{{w}^{2}} + \frac{2}{3}\eta {{w}^{3}} + ...} \right)$Точно так же для высоты полета, отсчитываемой от круговой орбиты ${{r}_{0}}$, справедливо следующее приближенное представление формулы (2.9):
(2.11)
$\frac{r}{{{{r}_{0}}}} = 1 - \frac{1}{{n_{0}^{2}}}\left\{ {\frac{1}{3}{{w}^{3}} + \left( {\frac{5}{{12}}\eta - \frac{1}{{12}}} \right){{w}^{4}} + ...} \right\}$Степенные функции (2.10) и (2.11), графиков рис. 6 и 7, а также и сами решения (2.8), (2.9) позволяют проанализировать зависимость траектории полета от параметров РС. Уменьшение высоты полета для рассматриваемой нами модели движения возможно только до расстояния ~80 км, ниже которого нужно будет учитывать влияние атмосферы.
График изменения высоты рис. 6 показывает, что имеется возможность использовать рассматриваемую оптимальную схему
набора орбитальной скорости до достаточно больших импульсов $\Delta V$. Однако, для реализации такой траектории РС должна получить от предыдущей (первой)
ступени требуемую составляющую вертикальной скорости, представленную на этом же рисунке.
Безразмерный параметр $\eta = V_{\theta }^{0}{\text{/}}\left( {g{{R}_{{уд}}}} \right)$ изменяется в пределах от 1.78 до 2.67 (от ${{R}_{{уд}}} = 450$ с до ${{R}_{{уд}}} = 300$ с). Траектория торможения при ${{R}_{{уд}}} = 450$ с с учетом только первых двух членов разложения (2.11) проходит 80 км уже при $w \simeq 0.63$, что соответствует  $\Delta V = 4950$ м/с. Вертикальная составляющая скорости в конце такой траектории должна быть ~ –900
м/с, которую нужно рассматривать как требование к конечным параметрам траектории первой
ступени.
$\Delta V = 4950$ м/с. Вертикальная составляющая скорости в конце такой траектории должна быть ~ –900
м/с, которую нужно рассматривать как требование к конечным параметрам траектории первой
ступени.
Как видно из представленных зависимостей изменения высоты, динамика движения в принципе позволяет реализацию оптимального гашения скорости до достаточно больших значений $w$. Можно видеть далее, что для высокого удельного импульса задача достижения как можно большей скорости для последней ступени решается существенно легче.
Поставим вопрос о возможности увеличения импульса торможения, для чего необходимо в первую очередь обеспечить сохранение высоты полета для больших значений $w$. Вертикальное ускорение согласно соотношению (2.4) равно $gw\left( {2 - w} \right)$ и в нашем распоряжении имеется возможность изменения ориентации вектора тяги РД. Пусть вектор активного ускорения ${\mathbf{a}}$ расположен под углом $\alpha $ к линии горизонта вверх, тогда уравнения (2.1) будут иметь такой вид:
(2.12)
$\frac{{d{{V}_{r}}}}{{dt}} = a\sin \alpha + gw\left( {w - 2} \right),\quad \frac{{d{{V}_{\theta }}}}{{dt}} = a\cos \alpha $При этом уравнение гашения орбитальной скорости (2.3) изменится на такое:
(2.13)
${{V}_{\theta }}\left( t \right) = V_{\theta }^{0} - \int a \cos \alpha dt = V_{\theta }^{0} - \Delta V + \int {a\left( {1 - \cos \alpha } \right)} dt$Первой идеей может оказаться желание компенсировать вертикальное ускорение, т.е. выбрать угол наклона вектора тяги $\sin \alpha \approx gw\left( {2 - w} \right)$. При этом условии угол $\alpha $ быстро становится большим, уравнения (2.14) интегрируются, но уже член первого порядка относительно переменной $w$ имеет вид
Следующий подход к решению задачи состоит в том, что будем полагать вариации угла $\alpha $ небольшими, вызывающими малые отклонения рассматриваемой траектории торможения. Обозначим вариации скорости вертикального движения и расстояния переменными $\Delta {{V}_{r}}$ и $\Delta r$ соответственно. Поскольку в уравнения вертикального движения ускорение $a\sin \alpha $ входит аддитивно, то уравнения для варьируемых параметров примут следующий вид:
Переходя к переменным w, η, получаем
(2.15)
$\frac{{d\Delta {{V}_{r}}}}{{dw}} = V_{\theta }^{0}\sin \alpha ,\quad \frac{{d\Delta r}}{{dw}} = \frac{1}{{{{a}_{0}}}}V_{\theta }^{0}{{e}^{{\eta w}}}\Delta {{V}_{r}}$При интегрировании первого уравнения (2.15) предположим, что в начальной точке обратного полета имеется вертикальная составляющая скорости $V_{r}^{0}$ (не поясняя, как она появилась), тогда изменение вертикальной скорости и высоты получим в таком виде
(2.16)
$\frac{{\Delta {{V}_{r}}}}{{V_{\theta }^{0}}} = \frac{{\Delta V_{r}^{0}}}{{V_{\theta }^{0}}} + w\sin \alpha $(2.17)
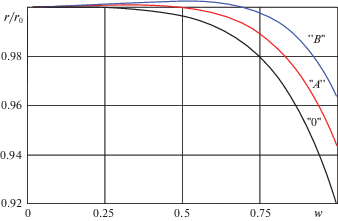
$\frac{{\Delta r}}{{{{r}_{0}}}} = \frac{{\Delta V_{r}^{0}}}{{V_{\theta }^{0}}}\frac{{({{e}^{{\eta w}}} - 1)}}{{{{n}_{0}}\eta }} + \frac{{\sin \alpha }}{{{{n}_{0}}\eta }}\left\{ {w{{e}^{{\eta w}}} - \frac{{({{e}^{{\eta w}}} - 1)}}{\eta }} \right\}$Полученные формулы дают возможность проследить отдельно влияние начальной составляющей скорости и активного ускорения на желаемое увеличение высоты траектории. На рис. 7 представлены вычисленные зависимости $(r + \Delta r)$ (2.17), показывающие влияние порознь компоненты, зависящей от начальной скорости (кривая “А”) и компоненты малого угла наклона к горизонту (кривая “В”) относительно опорной траектории (кривая “О”), представленной ранее на рис. 6 для самого высокого удельного импульса.
Представим для дальнейшего анализа формулу (2.17) в виде степенного ряда
(2.18)
$\frac{{\Delta r}}{{{{r}_{0}}}} = \frac{{\Delta V_{r}^{0}}}{{V_{\theta }^{0}{{n}_{0}}}}\left( {w + \frac{1}{2}\eta {{w}^{2}} + \frac{1}{6}{{\eta }^{2}}{{w}^{3}} + ...} \right) + \frac{{\sin \alpha }}{{{{n}_{0}}}}\left( {\frac{1}{2}{{w}^{2}} + \frac{2}{3}\eta {{w}^{3}} + ...} \right)$Рассмотрим сначала влияние начальной скорости $\Delta V_{r}^{0}$. Согласно формуле (2.16) эта компонента “сдвигает” вверх профиль скоростей рис. 6. Это означает, что такая величина приращения скорости должна быть добавлена к ${{V}_{r}}$ в начале работы последней ступени (т.е. за счет предыдущей ступени), а затем “погашена” в конце ее работы. Несмотря на то, что эти приращения выполняются в конце работы как предыдущей, так и последней ступени, когда имеют место максимальные ускорения, т.е. минимальные гравитационные потери, тем не менее, такие потери существенно увеличивают величину затрачиваемой характеристической скорости.
Положим, что добавка высоты $\Delta r$ в соответствии с формулой (2.17) дает приращение параметру $w$ на величину $\Delta w$. Поварьируем основное уравнение для высоты полета (2.11) с учетом только первого порядка величины $\Delta w$:
(2.19)
$\frac{{\Delta r}}{{{{r}_{0}}}} = - \frac{{\Delta w}}{{n_{0}^{2}}}\left\{ {{{w}^{2}} + \left( {\frac{5}{3}\eta - \frac{1}{3}} \right){{w}^{3}} + ...} \right\}$Последнее равенство может рассматриваться как уравнение для определения $\Delta w$ при его приравнивании соотношениям (2.18). Заметим, что поскольку $\eta w$ не является малой величиной, предлагаемая оценка может дать представление о порядке величин в решении задачи. Оценим сначала влияние члена $\Delta V_{r}^{0}$, из сравнения (2.19) и (2.18) получаем
(2.20)
$\Delta w \simeq {{n}_{0}}\frac{{\Delta V_{r}^{0}}}{{V_{\theta }^{0}}}\left[ {{{\left( {w + \frac{1}{2}\eta {{w}^{2}} + \frac{1}{6}\eta {{w}^{3}} + ...} \right)} \mathord{\left/ {\vphantom {{\left( {w + \frac{1}{2}\eta {{w}^{2}} + \frac{1}{6}\eta {{w}^{3}} + ...} \right)} {\left( {{{w}^{2}} + \left( {\frac{5}{3}\eta - \frac{1}{3}} \right){{w}^{3}} + ...} \right)}}} \right. \kern-0em} {\left( {{{w}^{2}} + \left( {\frac{5}{3}\eta - \frac{1}{3}} \right){{w}^{3}} + ...} \right)}}} \right]$Возьмем, для примера $\Delta V_{r}^{0} = 40$ м/с $(0.005V_{\theta }^{0})$, и при основном значении $w = 0.63$ получим зависящий от $w$ множитель в равенстве (2.19) равным 1.63, что в итоге дает значение $\Delta w = 0.032$. Эта оценка с учетом того, что реальная $\Delta V{\kern 1pt} '$ за счет гравитационных потерь будет заметно больше данной $\Delta V_{r}^{0}$, показывает низкую эффективность метода “А”.
Оценку влияния составляющей ускорения (метод “В”) получим таким же образом:
(2.21)
$\Delta w = \frac{{{{n}_{0}}\sin \alpha }}{2}\left[ {{{\left( {{{w}^{2}} + \frac{4}{3}\eta {{w}^{3}} + ...} \right)} \mathord{\left/ {\vphantom {{\left( {{{w}^{2}} + \frac{4}{3}\eta {{w}^{3}} + ...} \right)} {\left( {{{w}^{2}} + \left( {\frac{5}{3}\eta - \frac{1}{3}} \right){{w}^{3}} + ...} \right)}}} \right. \kern-0em} {\left( {{{w}^{2}} + \left( {\frac{5}{3}\eta - \frac{1}{3}} \right){{w}^{3}} + ...} \right)}}} \right]$Для примера возьмем $\sin \alpha = 0.1$, множитель, зависящий от $w$ в равенстве (2.21) равен 1.64, откуда получаем значение $\Delta w = 0.328$. Гравитационные потери (2.14) при этом составят $V_{\theta }^{0}\left( {1 - \cos \alpha } \right)$ = $0.005V_{\theta }^{0}$ ≤ 30 м/с. Таким образом, именно этот метод является более эффективным и может быть предложен для увеличения времени и характеристической скорости работы последней ступени.
Кривая зависимости снижения высоты рис. 7 показывает, что в этой области горизонтальных скоростей ($w \approx 1$) вертикальное движение является близким к свободному падению с высоты, равной радиусу целевой круговой орбиты под действием силы притяжения Земли. Это обстоятельство позволяет сформулировать требования к конечным параметрам траектории движения первой ступени носителя.
Требования к первой ступени. В свете изложенных выше идей одним из основных требований к первой ступени является:
• Обеспечение вертикальной составляющей движения, позволяющей осуществить выход за пределы атмосферы и достижению номинальной высоты орбиты (в данном случае 185 км) и возможному попутному набору некоторой горизонтальной скорости за счет профиля выведения по углу тангажа. Потенциальная энергия подъема на эту высоту, т.е. требование чтобы траектория “коснулась” конечной круговой орбиты, определяет по законам механики (${{V}^{2}} = 2gh$) эквивалентную скорость в 1900 м/с.
Следует заметить, что в реальном проекте при формировании профиля выведения последней ступени начало “оптимального” горизонтального разгона может быть начато сразу после выхода РС из атмосферы, т.е. существенно ранее достижения высоты в ${r \mathord{\left/ {\vphantom {r {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}} \geqslant 0.98$, как это было рассмотрено выше. Такая возможность имеется для любой РН, и она позволяет еще увеличить время работы РД и величину разгонного импульса последней ступени. Имеет смысл напомнить здесь и другие требования к РС1:
• Для первой ступени совершенно необходима большая тяга РД: нужно значительное вертикальное ускорение, существенно превосходящее начальный вес РН. Основные потери характеристической скорости первой ступени создает гравитационное ускорение Земли, уменьшающее величину вертикальной проекции ускорения от работы реактивных двигателей, величина этих потерь определяется временем их работы (см. [2, 7, 8]). Оценки гравитационных потерь лежат в интервале 1000–1300 м/с;
• Потери в эффективности работы РД создает атмосферное давление, которое снижает тягу ракетных двигателей: величина удельного импульса, учитывающая их работу на малой высоте ниже того, что могут дать эти двигатели, находящиеся в вакууме. Оценки таких потерь составляют 120–180 м/с [3, 4, 5];
• Наличие атмосферы создает весьма существенное аэродинамическое сопротивление (скоростной напор), действующий на находящуюся в полете РН; такие потери оцениваются в 150–250 м/с. Помимо этого, преодоление атмосферного сопротивления требует выполнения ориентации РН строго против вектора скорости. Тем самым внешние условия в полете первой ступени приводят к потерям реальной скорости полета от той, которую обеспечивают ракетные двигатели (характеристической скорости). Согласно учебным пособиям [3, 4, 5] суммарные потери характеристической скорости первой ступени лежат в пределах 1200–1650 м/с. Все эти обстоятельства определяют необходимую величину характеристической скорости первой ступени РН.
Оптимизация траектории выведения рекомендует одновременно осуществлять достижение высоты и горизонтальной скорости [3, 6], для этого предполагается непрерывный активный участок полета с разворотом изделия в плоскости орбиты по углу тангажа, создающего проекцию ускорения в сторону орбитального движения. Тем самым во время вертикального подъема осуществляется набор некоторой части горизонтальной скорости. Однако, можно видеть, что низкая ЭРТ первой ступени может поставить ограничения альтернативной схеме набора горизонтальной скорости последующей РС, имеющей более высокое ЭРТ. Другими словами, набор горизонтальной скорости РС-1 оправдан, если он по показателю ЭРТ приближается к последней ступени (в начале ее работы).
Перечисленные здесь задачи первой ступени не могут быть перенесены для исполнения последующими ступенями, в этом смысле величина ее характеристической скорости полностью определяется поставленными выше требованиями. Оптимизация расходов топлива первой ступени состоит в возможном сокращении ее участия в том, что может быть сделано следующими ступенями и совокупностью конструктивных и системных технических решений для этой РС.
В известном смысле происходит разделение задач, когда достижение орбитальной скорости становится основным требованием к последней ступени, тогда как выход за атмосферу и достижение высоты целевой орбиты – задача первой ступени. Низкая эффективность первой ступени – вынужденная плата за решение задачи выведения на орбиту.
Естественно, что при более углубленном исследовании этой задачи потребуется применение численного моделирования для определения оптимизации распределения и профилей выведения.
3. Анализ существующих РН. Первая ступень является самой важной и сложной составляющей РН; основным ее компонентом является ракетный двигатель (двигатели) большой тяги. Создание такого ракетного двигателя, равно как конструктивных и технических решений РС-1, минимизирующих ее массу, всегда является уникальной разработкой, определяющей саму возможность создания РН и ее пользовательские качества (т.е. длительность ее использования).
Аналитические оценки всех этих потерь возможны и существуют, но их одновременное действие можно оценить только при компьютерном моделировании процесса выведения; оно зависит от многих факторов, в том числе и от профиля выведения, т.е. от самой траектории выведения (изменение угла наклона вектора тяги к горизонту и уровня тяги РД). Проектирование ракетной системы для выведения на орбиту – весьма сложная задача, требующая учета массы факторов, влияющих на ее совершенство: это и конструктивные параметры РН и ее составляющих, характеристики ракетных двигателей и работы бортовых систем и приборов. Во всем этом многообразии данных не существует четкого алгоритма, позволяющего выстроить ясно обоснованную схему достижения наилучшего решения. Тем не менее, успешные главные конструкторы РН достигли выдающихся результатов в такой сложной разработке, какой является создание РН, в основном за счет своих уникальных качеств инженера и руководителя. Их разработки дают нам возможность провести аналитические оценки уровня совершенства ракеты-носителя в целом, которые нам предоставляет история ракетной техники, опираясь на ряд показателей, которые мы рассмотрим далее. Данные по реальным ракетным системам, взятым из практики, показывают их различную эффективность, т.е. деятельность главных конструкторов имеет непреходящую и большую ценность. Сделаем попытку показать эти аналитические оценки на примерах.
Показатель эффективности РН и влияние конструктивной схемы. На практике существует очень важный показатель эффективности РН, определяемый отношением веса выводимого полезного груза (речь идет о низкой орбите) к начальному весу ракеты-носителя: $\lambda = {{{{m}_{{пг}}}} \mathord{\left/ {\vphantom {{{{m}_{{пг}}}} {\left( {{{m}_{{нач}}} - {{m}_{{пг}}}} \right)}}} \right. \kern-0em} {\left( {{{m}_{{нач}}} - {{m}_{{пг}}}} \right)}}$. По сути дела, этот параметр достаточно полно характеризует совершенство РН. Совместно с такими параметрами, как удельный импульс РД, суммарное значение характеристических скоростей ракетных ступеней РН – все эти данные создают некоторое “поле” аналитических оценок.
Первыми ракетными двигателями большой тяги для межконтинентальной двухступенчатой баллистической ракеты дальнего действия Р-7 главного конструктора С.П. Королева, положившими начало созданию ракет-носителей, явились РД 107 и РД 108 главного конструктора В.П. Глушко. Эти РД имели тягу на поверхности Земли в 83.5/100.24 т и 79.3/99.3 т соответственно (здесь и далее в знаменателе приведена тяга этого же двигателя в вакууме). Ракета Р7 имела хорошо известную теперь пакетную схему из 4-х боковых ускорителей и центрального блока большего размера (длины), который являлся второй ступенью, все РД этих ступеней начинают работу со старта. Этот носитель в двухступенчатом варианте имел начальный стартовый вес 270–280 т, он позволил в октябре 1957 года вывести на орбиту Земли первый искусственный спутник весом в 80 кг, через полгода таким же РН был выведен третий ИСЗ весом в 1700 кг (вес полезного груза МБР Р7 был около 5.0 т). Установка третьей ступени на эту ракету дала возможность довести величину полезного груза до величины более 5.5 т, так появилось понятие ракеты-носителя (эта РН получила название “Восток”, и на этой ракете был выполнен первый полет человека в космос). Впоследствии был осуществлен ряд модификаций этой ракеты: РН “Союз” – так был назван носитель, использованный для пилотируемого корабля “Союз” 7К-ОК. Вес выводимого на низкую орбиту полезного груза был доведен до 6.8 т, на этой ракете появилась более мощная третья ступень, стартовый вес РН увеличился до 306 т. Пилотируемые корабли “Союз” нашего времени имеют вес до 7.2 т, они летают на модификации РН “Союз-2”, модернизация этой РН продолжается. Рассмотренный здесь период времени занимает более 60 лет, за это время конструкция РД сильно не менялась. Уровень тяги РД первой ступени поднялся до 86.6/104 т и 80.8/94 т соответственно, за счет увеличения удельного импульса с 252/313 с (РД 107) и 252/313.6 с (РД 108) до значений 263/320 с и 257.7/320.6 с соответственно.
Показатель эффективности РН для первых “Союзов” оказался равным 0.0217, для “Союза ФГ” (носитель эпохи станции “Мир”, стартовая масса РН 308 т) он равен 0.023, и для “Союза-2” (эпоха МКС, стартовая масса РН 313 т) – 0.0246. Величина начального ускорения на этой серии РН сохранилась на уровне 1.34 g. Из этих данных видно, что усовершенствование характеристик РН – весьма трудный и длительный процесс.
Рассмотренная выше РН “Протон” (главный конструктор В.Н. Челомей, двухступенчатая межконтинентальная баллистическая ракета УР-500, первый полет 1965 год) относится к классу тяжелых РН, она прошла аналогичный “Союзу” длительный путь модернизации и превращения из двухступенчатой ракеты в трехступенчатую РН. Первый пуск “Протона-К” – трехступенчатой РН – состоялся в марте 1967 года. При массе полезного груза, выводимого на низкую круговую орбиту в 20.7 т показатель эффективности этого носителя составляет $\lambda = 0.03$ (у тяжелых РН, как правило, конструктивные показатели лучше). Последняя его модификация – РН “Протон-М”, начавшая полеты с 2001 года, имеет ${{m}_{{пг}}} = 23.7$ т и показатель эффективности $\lambda = 0.0336$. Разность в показателях эффективности “Союза” и “Протона” объясняется в основном применением в РН “Союз” пакетной конструктивной схемы, сравнительно с классической тандемной в случае “Протона”. По конструктивному совершенству пакетная схема заметно уступает тандемной схеме, имеющей общие топливные баки.
Упоминавшийся РН “Зенит-2” (РН среднего класса) имеет показатель $\lambda = 0.03$. Заметим, что эта ракета сделана по тандемной конструктивной схеме.
Аналогом РН среднего класса, близкий к “Союзу”, является американская РН “Атлас-5”, прошедшая также длительный период своих модернизаций. Первая РН “Атлас Д” была одноступенчатой, она вывела в космос на незамкнутую орбиту (суборбитальный полет) первый американский пилотируемый корабль “Меркурий” (май 1961 г.); модификация этой РН, содержащая две ступени, обеспечила несколько орбитальных полетов этого корабля, начиная с февраля 1962 года. Существующая модификация имеет вторую ступень, использующую водородное топливо (на первой ступени кислород – керосин). При начальном весе в 334.5 т эта РН выводит на низкую орбиту 9.8 т полезного груза. В качестве РД первой ступени используется российский РД-180 (изготовитель НПО “Энергомаш”, созданный на основе ракетных двигателей РН “Энергия” и “Зенит-2”) – с тягой 390.2/423 т, имеющий удельный импульс – 311.3/337.8 с. На второй ступени используется РД RL – 10A-4-2 (американская компания Rocketdyne) с тягой 10.1 т на топливе жидкий кислород и жидкий водород с удельным импульсом в 451 с. Показатель эффективности этой РН равен $\lambda = 0.03$, получаемый, в том числе за счет более высоких характеристик используемых РД (водородное топливо), за счет орбиты меньшего наклонения из-за места старта, имеющего близкую к экватору широту точки старта.
Тяжелые носители. Общепризнано, что самый большой и эффективной РН является “Сатурн-5”, главного конструктура Вернера Фон Брауна, первый полет которой состоялся в 1967 году. На этой РН были осуществлены полеты человека на Луну, она имела стартовую массу в 2965 т, две ступени этой ракеты выводили на низкую (порядка 185 км) круговую орбиту вес более 140 т (третью ступень и лунный комплекс). В первой ступени этой ракеты использовались пять параллельно работающих ракетных двигателей F-1 с тягой в 690/790 т, каждый, имевших удельный импульс ${{R}_{{уд}}} = 264{\text{/}}304$ с (топливо–кислород–керосин), вторая ступень имела пять РД J-2 с тягой по 100.7 т каждый и удельным импульсом в ${{R}_{{уд}}} = 421$ с (кислородно-водородное топливо). Такой же РД был установлен на третьей ступени, предназначенной для выведения лунного комплекса с низкой околоземной орбиты на траекторию полета к Луне. Показатель эффективности этой РН выведения на низкую земную орбиту равен $\lambda = 0.0495$ – самый высокий на сегодняшний день в ракетной практике.
В Советском Союзе тяжелой ракетой-носителем, подобной “Сатурну-5” является РН “Энергия” (главный конструктор В.П. Глушко). Первый полет этой РН состоялся в 1987 году, она имела стартовый вес 2419 тонн, вес выводимого на низкую орбиту ПГ – 105 тонн. Ракета имела две ступени: центральный блок и четыре боковых ускорителя с кислородно-керосиновыми РД 170 (главный конструктор РД – В.П. Глушко, тяга 740.5/806 т, удельный импульс 309.5/337.2 с). Центральный блок являлся второй ступенью, он работал со старта и имел четыре РД 0120, использующий кислородно-водородное топливо (РД тягой по 155/190 т, удельный импульс 360/455 с, производство воронежского КБ Химавтоматики, главный конструктор А.Д. Конопатов). Показатель эффективности этой РН $\lambda = 0.043$.
Казалось бы, прогресс в совершенствовании ракетных двигателей, произошедший за время от программы “Аполлон” полетов к Луне до программы “Буран” (около 20 лет) должен был привести к увеличению показателя эффективности рассматриваемой тяжелой РН, но этого не случилось. На мой взгляд, причиной этого явилось применение в РН “Энергия” так называемой пакетной схемы, повторявшей, по сути, конструктивную схему ракеты Р-7 С.П. Королева. Конструктивные издержки сильно влияют на итоговые показатели РН. Нужно сказать, что выбор пакетной схемы в начале космической эры был оправдан, так как в то время достижение уровня тяги РД в 100 тонн было осуществлено с использованием 4-камерного ракетного двигателя, имевшего вследствие этого существенный диаметр, не позволявший разместить на ограниченном по размеру ракетном блоке более одного такого РД.
Размещение на первой ступени при общих топливных баках нескольких ракетных двигателей, работающих параллельно, началось практически одновременно у нас и в Америке. Первые старты ракеты носителя “Сатурн-1” Вернера фон Брауна (эта ракета предназначалась для отработки кораблей лунного комплекса на орбите Земли), начались в 1964 году. На большом диаметре первой ступени (размером 6.52 м) главный конструктор разместил 8 РД фирмы Rocketdyne, работающих на кислородно-керосиновом топливе тягой по 86 т каждый, взятых с военной ракеты. Для последующих ступеней было принято решение делать их на кислородно-водородном топливе; той же компании были заказаны две модификации такого РД: RL-10 с тягой 6–8 т (первая) и затем J-2 с тягой в 100 т. РН “Сатурн-1” имел три ракетных ступени: на второй было установлено 6 двигателей RL-10, а на третьей два таких двигателя, всего в программе было 10 таких РН. Следующая модификация этого носителя “Сатурн-1В” начала полеты в 1966 году, она была двухступенчатой с использованием одного двигателя J-2 для второй ступени, что позволило увеличить выводимый вес почти в два раза. В лунной программе было 6 таких ракет, и еще 3 для полетов к орбитальной станции “Скайлэб”. Показатели эффективности этих РН были $\lambda = 0.0194$ для “Сатурна-1” и $\lambda = 0.0314$ для “Сатурна 1В” (хорошая иллюстрация, почему 2-ступенчатая РН эффективней 3-ступенчатой).
На этой же ракете Вернер фон Браун применил еще одно важное новшество: в каждый РД была встроена автоматика, анализирующая правильность работы двигателя, в случае нарушения функционирования двигатель отключался. Были проведены специальные натурные испытания с имитацией таких отказов. Оказалось, что даже при исключении из работы одного–двух РД, первая ступень РН “Сатурн” выполняла задачу выведения (в частности, благодаря этому мероприятию все пуски РН “Сатурн” были успешными, несмотря на то, что отказы РД в программе “Аполлон” имели место).
В Советском Союзе ракета УР-500 и созданные на ее основе упоминавшийся в этой работе РН “Протон-К и “Протон-М”, имели на первой ступени шесть параллельно работающих РД-253 разработки В.П. Глушко тягой по 150 т каждый (на последней модификации РН – используются РД-276).
Тяжелая ракета-носитель С.П. Королева Н-1, разработка которой не была завершена, имела на первой ступени 26 реактивных двигателей НК-33 тягой по 150–160 т, и могла вывести на низкую орбиту 75 т полезного груза. В процессе разработки проект дорабатывался, и число РД было увеличено до 30 РД, такая ракета должна была выводить на низкую орбиту до 95 т полезного груза. Показатели эффективности РН Н-1 (проектные) были на уровне $\lambda = 0.034$. Эта РН имела четыре испытательных пуска, закончившихся неудачами вследствие недостаточности наземной отработки.
Влияние начального ускорения. Рассмотрим сравнительный пример двух советских РН середины 60-х (“Протон-К”) и двадцать лет спустя, середины 80-х (“Зенит-2”). В результате проведенных оценок параметров $\Delta V$ трех ступеней РН “Протон К”, которые можно сделать, используя приведенные данные по этой РН и формулу для характеристической скорости (2.1).
Имеем следующие величины: $\Delta {{V}_{1}} = 2615{\text{/}}2900$ м/с, $\Delta {{V}_{2}} = 3327$ м/с и $\Delta {{V}_{3}} = 3366$ м/с, т.е. суммарное приращение скорости всех трех ступеней этой РН $\Delta {{V}_{\Sigma }}$ = 9308/9533 м/с, тогда как первая космическая скорость на высоте 185 км составляет $V_{\theta }^{0} = 8020$ м/с (заметим, что две цифры величин скорости первой ступени соответствуют двум значениям удельного импульса: на поверхности Земли и в вакууме, реальное ее значение лежит внутри этого интервала, и может быть определено при компьютерном расчете траектории выведения). Таким образом, получаем первую оценку (достаточно грубую) величины потерь в 1288/1513 м/с (в среднем 1430 м/с), которые будем относить к потерям первой ступени.Заметим, что ракета-носитель “Союз ФГ” – одна из последних модификаций, используемая для пилотируемых полетов, имеет ускорение ${{a}_{0}} = 1.34g$, составляющие характеристических скоростей $\Delta {{V}_{1}}$ = 2615/2900 м/с, $\Delta {{V}_{2}} = 2611$ м/с, $\Delta {{V}_{3}} = 3865$ м/с, $\Delta {{V}_{\Sigma }} = 9404$ м/с, т.е. примерно такое же значение, как и для РН “Протон”.
В более современной РН “Зенит-2”, разработка которой была выполнена в рамках программы “Энергия”–“Буран” в конце 90-х годов ХХ столетия, была применена двухступенчатая структура носителя, выбранная благодаря более высокой эффективности ракетных двигателей. Аналогичные вычисления с использованием данных по этой РН, дают $\Delta {{V}_{1}}$ = 3637/3966 м/с и $\Delta {{V}_{2}}$ = 5167 м/с, т.е. полная характеристическая скорость этой РН составляет $\Delta {{V}_{\Sigma }}$ = 8804/9133 м/с, и величина потерь становится (в среднем) около 1048.5 м/с. Разницу в величинах полной скорости можно объяснить в первую очередь разными стартовыми ускорениями этих ракет и профилями выведения: если для РН “Протон-К” оно равно ${{a}_{0}} = 1.32$, то у РН “Зенит-2” оно составляет ${{a}_{0}} = 1.61$. Из физических соображений понятно, что чем выше вертикальное ускорение, тем быстрее закончится решение задачи выведения, меньшее время потребуется работы РД и меньше будут гравитационные потери. Однако, увеличение скорости в более плотной атмосфере увеличивает аэродинамические потери, еще раз хочу подчеркнуть, что четкой аналитической зависимости между стартовым ускорением и величиной суммарных потерь первой ступени не существует.
Применение твердотопливных ускорителей (ТТРД). В 1981 г. стартовал корабль многоразового использования “Спейс шаттл”, на котором были применены ускорители первой ступени, работающие на твердом топливе. Такой ускоритель SRB (Solid Rocket Booster) при весе в 570 т развивал тягу в 1360–1501 т, и имел удельный импульс 269 с у Земли, и длительность работы 124 с. Главными жидкостными ракетными двигателями этого корабля (Space Shuttle Main Engine) – были три кислородно-водородных двигателя тягой по 170 т на старте и 212 т в вакууме, они имели максимальный удельный импульс 455 с и осуществляли основной набор орбитальной скорости, работая в течение 480 с. Стартовый вес корабля составлял 2050 т, т.е. начальное ускорение ${{a}_{0}} = 1.59\;g$, вес выведенного на низкую орбиту космического самолета – 122.5 т, в этом весе на полезный груз выделено 24.4 т. Если показатель эффективности рассчитывать по полному весу STS на низкой орбите, то он будет таким: $\lambda = 0.061$ (надо признать, что это самый высокий на сегодня показатель для РН!). Если же его считать по полезному грузу, доставляемому STS на орбиту, то показатель будет равен $\lambda = 0.012$.
Еще до полета “Спейс шаттла” американские компании “Локхид Мартин” (семейство РН “Атлас”) и “Мак-Дональд Дуглас” (впоследствии компания “Боинг”, семейство РН “Дельта”) начали применять твердотопливные ускорители (ТТУ) на обычных одноразовых ракетах-носителях.
Применение ТТУ оказалось весьма эффективным по целому ряду показателей. Первое неоспоримое преимущество состоит в существенно более высокой надежности ТТУ (на порядок и выше в сравнении с ракетными двигателями основной РН). Это обстоятельство позволяет применять несколько параллельно работающих ускорителей в связке без заметного снижения надежности РН в целом. Второе достоинство заключается в возможности за счет выбора числа ТТУ достаточно простым способом увеличивать стартовую тягу РД первой ступени, т.е. начальное ускорение РН при старте, что влияет на величину потерь на начальном участке полета. При этом не обязательно время работы ТТУ должно совпадать с временем работы основного РД ракеты: здесь важно преодолеть начальный участок большого стартового веса с приемлемым начальным ускорением.
Так, в упоминавшемся выше РН “Атлас-5” существует модификация варианта “heavy”, когда при старте используются дополнительные боковые твердотопливные ускорители (от 2-х до 5). Каждый из них имеет тягу в 172.1 т (1688 кН), ${{R}_{{уд}}} = 279.3$ с, время горения 94 с (при времени работы основного РД-180 в 253 с), вес каждого ТТУ равен 5.761 т (сухой) при 41 т горючего. Эта РН в своем максимальном варианте при стартовом весе в 546.7 т выводит на низкую орбиту вес полезного груза в 18.8 т, т. е. почти в два раза больший вес. При этом, естественно масса топлива второй ступени увеличивается, и такая РН имеет показатель эффективности $\lambda = 0.0356$.
Последние достижения. Рассмотрения раздела 2 настоящей статьи показывает, что можно говорить о минимальной величине вертикальной составляющей импульса тяги первой ступени, определяемого тем, что траектория выведения должна “достичь” высоты круговой орбиты (в рассматриваемом случае – 185 км). Основной набор орбитальной скорости может быть выполнен второй ступенью. Здесь совершенно не обязательно иметь непрерывный процесс разгона РН с переходом на вторую РС, хотя такой порядок работы РД, как правило, всегда выполняется. Важно получить условия сопряжения конца работы первой ступени с началом работы второй ступени. Вторая же ступень должна обеспечить основную составляющую орбитальной скорости для достижения целевой орбиты (вплоть до значения 0.9 или более), условием же оптимальности (отсутствие “просадки” траектории по высоте, т.е. гравитационных потерь) является величина уровня тяги РД второй ступени, создающей перегрузку в ${{n}_{0}} \geqslant 3{\kern 1pt} - {\kern 1pt} 4$ единицы в конце участка выведения.
На настоящий день ближе всего к изложенным в этих статьях идеям оказалась последняя американская ракета-носитель “Falkon 9”, руководителем этой разработки явился талантливый инженер и изобретатель Илон Маск. Регулярные полеты начались с 2005 года, к настоящему времени выполнено четыре модификации этой РН с последовательным увеличением выводимого полезного груза, и эти работы продолжаются. Инновационное и техническое содержание этих разработок свидетельствует, что их руководитель является реальным главным конструктором уровня Вернера фон Брауна и С.П. Королева. Одна из последних модификаций этой РН “Falkon 9 FT” при стартовой массе в 549 т, начальном ускорении в ${{a}_{0}} = 1.37\;g$, выводит на НОО – 22.8 т полезного груза (здесь надо учесть малое наклонение этой орбиты и место стартового полигона, близкое к экватору). По имеющейся информации на этой РН горизонтальная составляющая скорости в конце работы первой ступени существенно меньше той, которая рекомендована в классических трудах [3, 9].
Такие решения вызваны тем, что после отделения первой ступени предполагалось затем гасить эту скорость для осуществления ее посадки. Тем самым, основную часть орбитальной скорости обеспечивает именно последняя ступень: ракетный двигатель этой ступени имеет вакуумное сопло, высокий удельный импульс ${{R}_{{уд}}} = 348$ с при достаточно большой тяге РД в 95 т, создающий, по-видимому, перегрузку в конце выведения ${{n}_{0}} \geqslant 3$. Ракета-носитель имеет рекордный показатель эффективности $\lambda = 0.0415$, при том, что все ракетные двигатели этой РН используют кислородно-керосиновое топливо.
В этой же ракете осуществлена возможность мягкой посадки первой ступени на полигон старта или плавающую платформу с использованием собственного реактивного двигателя – одно из самых смелых и уникальных достижений в ракетной технике.
В исполнении Илона Маска получила определенные преимущества и рассмотренная в этом разделе пакетная схема построения первой ступени: все три РС тяжелого носителя “Falkon-9 Heavy” выполняют мягкую посадку в целях их последующего применения.
В заключение в таблице 3 приведены сводные статистические данные о ракетах-носителях, эксплуатируемых в настоящее время.
Таблица 3.
Современные тяжелые носители
| Ракета- носитель | Первый полет | Кол-во пусков в год (всего) | Широта СК | Стартовая масса, т | Масса ПН, т | Диаметр ГО. м | λ | Цена пуска, млн $ | ||
|---|---|---|---|---|---|---|---|---|---|---|
| НОО | ГПО | ГСО | ||||||||
| “Протон-М” – “Бриз-М”  |
2001 | 8–12 (98) | 46° | 705 | 23 | 6.35 | 3.25 | 4.35 | 0.0336 | 65–70 |
“Зенит-3SL”  |
1999 | 4–5 (36) | 0° | 473 | 13.7 | 6.06 | 2.6 | 4.15 | 0.03 | 80 |
Ariane 5 ECA  |
2002 | 6 (36) | 5° | 780 | 20 | 10 | 5.4 | 0.0265 | 220 | |
Delta IV Heavy
 |
2004 | 1 (6) | 35° и 28° | 732 | 23 | 10.75 | 6.57 | 5.1 | 0.0314 | 265 |
Delta IV M+(5.4)
 |
2009 | 2–3 (2) | 35° и 28° | 399 | 13.5 | 5.5 | 3.12 | 5.1 | 0.0348 | 170 |
Atlas V 521  |
2003 | 2 (2) | 35° и 28° | 419 | 13.49 | 4.88 | 2.63 | 5.4 | 0.0333 | 160 |
Atlas V 551  |
2006 | 1 (3) | 35° и 28° | 541 | 18.8 | 6.86 | 3.90 | 5.4 | 0.0356 | 190 |
Falcon 9 FT  |
2015 | 18–20 (54) | 28° | 549 | 22.8 | 5.5–8.3 | 5.2 | 0.0415 | 62 | |
Falcon Heavy  |
2018 | 1–2 (3) | 28° | 1421 | 63.8 | 8.0–26.7 | 5.2 | 0.047 | 90–150 | |
H-IIB
 |
2009 | 2 (5) | 30° | 531 | 19 | 8 | 5.1 | 0.0348 | 182 | |
CZ-3B
 |
1996 | 4 (22) | 28° | 426 | 11.2 | 5.1 | 2 | 4.2 | 0.0263 | 50–70 |
CZ-5
 |
2016 | 1 (2) | 19.6° | 687 | 20 | 14 | 11 | 3.35 | 0.0261 | |
Список литературы
Hill P.G., Peterson C.R. Mechanics and Thermodynamics of Propulsion. Reading MA: Addison-Wesley Publ., 1965. 565 p.
Куренков В.И., Юмашев Л.П. Выбор основных проектных характеристик и конструктивного облика ракет носителей. Самара: Самарский гос. аэрокосмический университет, 2005.
Griffin M.D., French J.R. Space Vehicle Design AIAA Education Series. Reston VA: AIAA, 2004. 687 p.
Алифанов О.М., Андреев А.Н., Гущин В.Н. Баллистические ракеты и ракеты-носители. М.: Дрофа, 2004. 512 с.
Бранец В.Н. Об оптимизации структуры ракеты-носителя // Полет. 2012. № 9. С. 21–35.
Бранец В.Н. Новые подходы к задачам оптимизации структуры ракеты-носителя // Доклад на XII съезде механиков, (секция механика космических полетов), Уфа, 2019 г. (в печати).
Бранец В.Н. К вопросу оптимизации структуры ракеты-носителя // Космонавтика и ракетостроение. 2014. № 1. С. 201–215.
Павлюк Ю.C. Баллистическое проектирование ракет. Челябинск: Изд. ЧГТУ, 1996. 92 с.
Охоцимский Д.Е., Энеев Т.М. Некоторые вариационные задачи, связанные с запуском искусственного спутника Земли // УФН. 1957. Т. 63. Вып. 1а. С. 5–32.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика