Прикладная математика и механика, 2020, T. 84, № 3, стр. 327-340

ВОЛНЫ, ЗАХВАЧЕННЫЕ ПОЛУБЕСКОНЕЧНОЙ ПЛАСТИНОЙ КИРХГОФА НА УЛЬТРАНИЗКИХ ЧАСТОТАХ

С. А. Назаров^1, *

¹ Санкт-Петербургский государственный университет
Санкт-Петербург, Россия

Поступила в редакцию 06.08.2019
После доработки 16.03.2020
Принята к публикации 02.04.2020

DOI: 10.31857/S0032823520030066

Аннотация

Рассмотрена полубесконечная пластина Кирхгофа со свободным краем, частично лежащая на винклеровском основании (задача Неймана для бигармонического оператора, возмущенного малым свободным членом с компактным носителем). Показано, что для любого малого $\varepsilon > 0$ можно построить (неединственным образом) переменный коэффициент податливости основания порядка $\varepsilon $, при котором пластина приобретает собственное число ${{\varepsilon }^{4}}$, вкрапленное в непрерывный спектр, а соответствующая собственная функция экспоненциально затухает на бесконечности. Проверено, что более одного малого собственного числа быть не может. Примечательно то, что у акустического волновода (задача Неймана для оператора Лапласа) малое положительное возмущение не может спровоцировать появление собственного числа около точки отсечки непрерывного спектра.

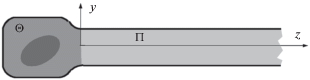
Ключевые слова: полубесконечная пластина Кирхгофа, винклеровское основание, малое возмущение, пороговый резонанс, околопороговое собственное число в непрерывном спектре

1. Постановка задачи. Пластина $\Omega \subset {{\mathbb{R}}^{2}}$ состоит из единичной (произвели масштабирование) полуполосы-волновода $\Pi = \{ x = (y,z)$: $z \geqslant 0$, $y \in ( - 1{\text{/}}2,1{\text{/}}2)\} $ и “резонатора” $\Theta \subset \{ x{\kern 1pt} :\;z < 0\} $, ограниченной области в нижней полуплоскости $\mathbb{R}_{ - }^{2}$ (тонирована на рис. 1). Границу $\partial \Omega $ считаем гладкой, класса ${{C}^{\infty }}$ для простоты. В области $\Omega $ рассмотрим задачу о собственных колебаниях пластины Кирхгофа [1, § 30], лежащей частично на винклеровском основании [2, 3] малой переменной податливости

(1.1)

$\begin{array}{*{20}{c}} {{{\Delta }^{2}}{{u}_{\varepsilon }}(x) + {{a}_{\varepsilon }}(x){{u}_{\varepsilon }}(x) = {{\lambda }_{\varepsilon }}{{\rho }_{\varepsilon }}(x){{u}_{\varepsilon }}(x),\quad x \in \Omega } \end{array}$

(1.2)

$\begin{array}{*{20}{c}} {{{N}^{q}}(x,\nabla ){{u}_{\varepsilon }}(x) = 0,\quad x \in \partial \Omega \quad (q = 2,3)} \end{array}$

Рис. 1.

Здесь ${{u}_{\varepsilon }}$ – прогиб пластины, ${{\lambda }_{\varepsilon }} = {{D}^{{ - 1}}}\omega _{\varepsilon }^{2}$ – спектральной параметр, причем ${{\omega }_{\varepsilon }} > 0$ – частота колебаний, $D > 0$ – цилиндрическая жесткость пластины, а плотность пластины

(1.3)

$\begin{array}{*{20}{c}} {{{\rho }_{\varepsilon }}(x) = 1 + {{\varepsilon }^{{ - 2}}}\rho (x),\quad \,{\kern 1pt} \rho (x) = 0,\quad \,x \in \Pi } \end{array}$

содержит большой параметр ${{\varepsilon }^{{ - 2}}}$ и гладкую в $\overline \Theta $ функцию $\rho \geqslant 0$ (резонатор утяжелен), причем постоянная плотность однородного волновода $\Pi $ сведена к единице. Кроме того, $\nabla = \operatorname{grad} $, $\Delta = \nabla \cdot \nabla $ – оператор Лапласа, а ${{N}^{q}}(x,\nabla )$ – дифференциальные операторы краевых условий, отвечающих свободному краю пластины [1, 4]

(1.4)

$\begin{gathered} {{N}^{3}}(x,\nabla ) = {{\partial }_{n}}\Delta - (1 - \nu )({{\partial }_{s}}\kappa (s){{\partial }_{s}} - \partial _{s}^{2}{{\partial }_{n}}) \\ {{N}^{2}}(x,\nabla ) = \Delta - (1 - \nu )(\partial _{s}^{2} - \kappa (s){{\partial }_{n}}) \\ \end{gathered} $

При этом $\nu \in [0,1{\text{/}}2)$ – коэффициент Пуассона, $\kappa $ – кривизна дуги $\partial \Omega $, ${{\partial }_{n}} = \partial {\text{/}}\partial n$, ${{\partial }_{s}} = \partial {\text{/}}\partial s$, а $(n,s)$ – локальная система криволинейных координат, $n$ – ориентированное расстояние до границы, $n > 0$ вне $\Omega $, $s$ – длина дуги на $\partial \Omega $, измеренная против часовой стрелки. На прямых участках границы $\{ x:y = \pm 1{\text{/}}2$, $z > 0\} $ имеем

(1.5)

$\begin{gathered} N_{ \pm }^{3}(\nabla ) = \pm {{\partial }_{y}}(\partial _{y}^{2} + (2 - \nu )\partial _{z}^{2}),\quad N_{ \pm }^{2}(\nabla ) = \partial _{y}^{2} + \nu \partial _{z}^{2} \\ {{\partial }_{n}} = \pm {{\partial }_{y}} = \pm \partial {\text{/}}\partial y,\quad {{\partial }_{s}} = \mp {{\partial }_{z}} = \mp \partial {\text{/}}\partial z \\ \end{gathered} $

Наконец, $D{{a}_{\varepsilon }}$ – коэффициент податливости винклеровского основания $\Theta $ (пластина не контактирует с основанием вдоль полуполосы $\Pi $ – носители функций ${{a}_{\varepsilon }}$ и $\rho $ глубоко тонированы на рис. 1), который будем искать в виде

(1.6)

$\begin{array}{*{20}{c}} {{{a}_{\varepsilon }}(x) = {{\varepsilon }^{2}}{{a}_{0}}(x) + {{\varepsilon }^{3}}\sum\limits_{j = 0,1,2} {{\tau }_{{j\varepsilon }}}{{b}_{j}}(x)} \end{array}$

Здесь и далее $\varepsilon > 0$ – фиксированный малый параметр, а ${{\tau }_{j}}$ – дополнительные параметры, подбор которых обеспечит существование собственного числа рассматриваемой задачи

(1.7)

$\begin{array}{*{20}{c}} {{{\lambda }_{\varepsilon }} = {{\varepsilon }^{4}}} \end{array}$

Вариационная формулировка задачи (1.1), (1.2)

(1.8)

$\begin{array}{*{20}{c}} {2E({{u}_{\varepsilon }},v;\Omega ) + {{{({{a}_{\varepsilon }}{{u}_{\varepsilon }},v)}}_{\Omega }} = {{\lambda }_{\varepsilon }}{{{({{\rho }_{\varepsilon }}{{u}_{\varepsilon }},v)}}_{\Omega }}\quad v \in {{H}^{2}}(\Omega )} \end{array}$

осуществляется на пространстве Соболева ${{H}^{2}}(\Omega )$ и включает скалярное произведение ${{( \cdot ,\; \cdot )}_{\Omega }}$ в пространстве Лебега ${{L}^{2}}(\Omega )$, а также функционал энергии пластины Кирхгофа [1, § 30]

(1.9)

$\begin{array}{*{20}{c}} {E(u,u;\Omega ) = \frac{1}{2}\int\limits_\Omega \left[ {{\text{|}}\Delta u{{{\text{|}}}^{2}} + 2(1 - \nu )\left( {{{{\left| {\frac{{{{\partial }^{2}}u}}{{\partial y\partial z}}} \right|}}^{2}} - \frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}}\frac{{{{\partial }^{2}}u}}{{\partial {{z}^{2}}}}} \right)} \right]dx} \end{array}$

(1.10)

$\begin{array}{*{20}{c}} {E(u,v;\Omega ) = \frac{1}{4}(E(u + v,u + v;\Omega ) - E(u - v,u - v;\Omega ))} \end{array}$

Поскольку билинейная форма (1.10) в левой части интегрального тождества (1.8) симметрична, положительна и замкнута в гильбертовом пространстве ${{H}^{2}}(\Omega )$, задаче (1.1), (1.2) отвечает [5, Гл. 10] самосопряженный положительный оператор ${{A}^{\varepsilon }}$ в пространстве ${{L}^{2}}(\Omega )$ с областью определения

$D({{A}^{\varepsilon }}) = \{ u \in {{H}^{4}}(\Omega ){\kern 1pt} :\;{{N}^{q}}u = 0\;на\;{\kern 1pt} \partial \Omega ,\;q = 2,3\} $

Непрерывный спектр $\sigma _{c}^{\varepsilon }$ этого оператора и соответственно дифференциальной (1.1), (1.2) или вариационной (1.8) задач занимает полуось ${{\bar {\mathbb{R}}}_{ + }}$ = $[0, + \infty )$, но в нем могут возникнуть собственные числа, образующие точечный спектр $\sigma _{p}^{\varepsilon }$, вкрапленные в непрерывный спектр и потому обладающие природной неустойчивостью. Именно последнее свойство требует применения процедуры “точной настройки” [6, 7] параметров задачи для образования точечного спектра.

Появление малого собственного числа (1.7) – необычный феномен: например, в подобной рассматриваемой задаче Неймана для оператора Лапласа, описывающей акустический волновод, малое возмущение не может вызвать возникновение собственного числа на интервале $(0,{{t}_{\Theta }})$, верхний край ${{t}_{\Theta }} > 0$ которого определяется формой и размерами резонатора $\Theta $ (см. разд. 7). В обоих случаях на нижнем краю ${{\lambda }_{\dag }} = 0$ непрерывного спектра задач реализуются пороговые резонансы [8–11], однако их качество различается, так как в задаче Неймана с $\lambda = 0$ имеется одна стоячая (не переносящая энергию) волна ${{w}^{0}}(x) = 1$, а в задаче Кирхгофа их три

(1.11)

$\begin{array}{*{20}{c}} {{{v}_{0}}(x) = {{w}^{{10}}}(x) = 1,\quad {{v}_{1}}(x): = {{w}^{{20}}}(x) = z,\quad {{v}_{2}}(x): = {{w}^{{11}}}(x) = y} \end{array}$

Именно линейно растущая волна ${{v}_{1}}$ и обуславливает возможность построения экспоненциально затухающей собственной функции на ультронизкой частоте.

Еще раз укажем основное отличие представленного далее результата от всех опубликованных ранее исследований дискретного и непрерывного спектров разнообразных краевых задач для бигармонического оператора: посредством малых, физически осмысленных, возмущений дифференциальных операторов собственное число медленно поднимается с нижнего порога спектра и, погружаясь в непрерывный спектр, становится неустойчивым и нуждается в тщательном подборе нескольких свободных параметров пластины.

2. Статическая задача. Рассмотрим неоднородное бигармоническое уравнение

(2.1)

$\begin{array}{*{20}{c}} {{{\Delta }^{2}}u(x) = f(x),\quad x \in \Omega } \end{array}$

с краевыми условиями

(2.2)

$\begin{array}{*{20}{c}} {{{N}^{q}}(x,\nabla )u(x) = {{g}^{q}}(x),\quad x \in \partial \Omega \quad (q = 2,3)} \end{array}$

Правые части $f$ и ${{g}^{q}}$ экспоненциально затухают при $z \to + \infty $, т.е. ${{e}^{{\beta z}}}f \in {{L}^{2}}(\Omega )$ при некотором $\beta > 0$, а ${{g}^{q}}$ – след на $\partial \Omega $ функции ${{G}^{q}}$, причем ${{e}^{{\beta z}}}{{G}^{q}}$ ∈ ${{H}^{{4 - q}}}(\Omega )$ и

$\left\| {(f,{{g}^{2}},{{g}^{3}});{{W}_{\beta }}(\Omega )} \right\|: = \left\| {{{e}^{{\beta z}}}f;{{L}^{2}}(\Omega )} \right\| + \sum\limits_{q = 2,3} inf\left\{ {\left\| {{{e}^{{\beta z}}}{{G}^{q}};{{H}^{{4 - q}}}(\Omega )} \right\|{\kern 1pt} :\;{{g}^{q}} = {{G}^{q}}\;на\;\partial \Omega } \right\}$

Установлено [12, 13], что найдется величина $\beta (\nu ) > 0$, при которой в случае $\beta \in (0$, β(ν)) три условия ортогональности

(2.3)

$\begin{array}{*{20}{c}} {{{J}_{p}}(f,{{g}^{2}},{{g}^{3}}): = {{{(f,{{\upsilon }_{p}})}}_{\Omega }} - {{{({{g}^{3}},{{\upsilon }_{p}})}}_{{\partial \Omega }}} + {{{({{g}^{2}},{{\partial }_{n}}{{\upsilon }_{p}})}}_{{\partial \Omega }}} = 0\quad (p = 0,1,2)} \end{array}$

обеспечивают существование единственного решения $u$ задачи (2.1), (2.2) в весовом пространстве Соболева $W_{\beta }^{4}(\Omega )$ с нормой $\left\| {u;W_{\beta }^{4}(\Omega )} \right\|$ = = $\left\| {{{e}^{{\beta z}}}u;{{H}^{4}}(\Omega )} \right\|$ и оценку

$\left\| {u;W_{\beta }^{4}(\Omega )} \right\| \leqslant c\left\| {(f,{{g}^{2}},{{g}^{3}});{{W}_{\beta }}(\Omega )} \right\|$

Это решение далее обозначаем

(2.4)

$\begin{array}{*{20}{c}} {u = {{R}_{\beta }}(f,{{g}^{2}},{{g}^{3}})} \end{array}$

Приведем несколько утверждений, вытекающих из общих результатов [13] и полиномиального свойства [14] квадратичной формы (1.9): для любой ограниченной области $\Xi \subset {{\mathbb{R}}^{2}}$ справедливо высказывание

(2.5)

$\begin{array}{*{20}{c}} {E(u,u;\Xi ) = 0,\;u \in {{H}^{2}}(\Xi ) \Leftrightarrow u(x) = {{c}_{0}} + {{c}_{1}}z + {{c}_{2}}y} \end{array}$

Еще один факт, нужный для всех выводов: у однородной ($f = 0$ и ${{g}^{q}} = 0$) задачи (2.1), (2.2) нет решений в классе ${{H}^{2}}(\Omega )$.

Модельная задача для бигармонического уравнения в бесконечной полосе $( - 1{\text{/}}2,1{\text{/}}2) \times \mathbb{R}$ помимо линейных функций (1.11) имеет решения

(2.6)

$\begin{array}{*{20}{c}} {{{w}^{{12}}}(x) = \frac{1}{2}({{z}^{2}} - \nu {{y}^{2}}),\quad {{w}^{{21}}}(x) = yz,\quad {{w}^{{13}}}(x) = \frac{1}{6}{{z}^{3}} - \frac{\nu }{2}{{y}^{2}}z} \end{array}$

Других, линейно независимых (относительно указанных), решений с не более чем степенным ростом на бесконечности нет.

Решения (1.11), (2.6) связаны соотношениями

(2.7)

$\begin{array}{*{20}{c}} {{{\partial }_{z}}{{w}^{{pq + 1}}}(x) = {{w}^{{pq}}}(x),\quad q = 0, \ldots ,{{\tau }_{p}} - 1,\quad {{\partial }_{z}}{{w}^{{p0}}}(x) = 0,{\kern 1pt} \quad p = 1,2} \end{array}$

Здесь ${{\tau }_{1}} = 4$ и ${{\tau }_{2}} = 2$ – длины жордановых цепочек

(2.8)

$\begin{array}{*{20}{c}} {{{W}^{{10}}}(y) = 1,{\kern 1pt} \quad {{W}^{{11}}}(y) = 0,\quad {{W}^{{12}}}(y) = - \frac{\nu }{2}{{y}^{2}},\quad {{W}^{{13}}}(y) = 0} \end{array}$

(2.9)

$\begin{array}{*{20}{c}} {{{W}^{{20}}}(y) = y,\quad {{W}^{{21}}}(y) = 0.} \end{array}$

Жордановы цепочки составлены из собственных и присоединенных векторов (скалярных функций в рассматриваемом случае) операторного пучка

(2.10)

$\begin{array}{*{20}{c}} {\theta \mapsto \left\{ {\partial _{y}^{4} + 2{{\theta }^{2}}\partial _{y}^{4} + {{\theta }^{4}},{{{\left. {N_{ \pm }^{3}({{\partial }_{y}},\theta )} \right|}}_{{y = \pm 1/2}}},{{{\left. {N_{ \pm }^{2}({{\partial }_{y}},\theta )} \right|}}_{{y = \pm 1/2}}}} \right\}} \end{array}$

и отвечают нулевому собственному числу $\theta = 0$. По цепочкам выстраиваются полиномиальные решения задачи Кирхгофа в полосе $( - 1{\text{/}}2,1{\text{/}}2) \times \mathbb{R}$

${{w}^{{pq}}}(y,z) = \sum\limits_{k = 0}^q {\kern 1pt} \frac{1}{{k!}}{{z}^{k}}{{W}^{{pq - k}}}(y)$

Длины ${{\tau }_{p}}$ можно предсказать [13, 15] на основе характеристик (2.5) и (2.7) функций (1.11).

При нарушении условий ортогональности (2.3) задача (2.1), (2.2) все-таки имеет решение, обладающее степенным ростом на бесконечности, определенное с точностью до линейного слагаемого и допускающее представление

(2.11)

$\begin{array}{*{20}{c}} {u(x) = \tilde {u}(x) + \chi (z)\sum\limits_{p = 1}^2 {\kern 1pt} \sum\limits_{q = 0}^{{{\tau }_{p}} - 1} {\kern 1pt} {{c}_{{pq}}}{{w}^{{pq}}}(x)} \end{array}$

Здесь остаток ${{\tilde {u}}_{0}}$ экспоненциально затухает при $z \to + \infty $, т.е. ${{e}^{{\beta z}}}\tilde {u} \in {{H}^{4}}(\Omega )$, и $\chi $ – гладкая срезающая функция

(2.12)

$\begin{array}{*{20}{c}} {\chi (z) = 1\quad при\quad z > 2l,\quad \chi (z) = 0\quad при\quad z < l,\quad 0 \leqslant \chi \leqslant 1} \end{array}$

Коэффициенты ${{c}_{{10}}}$, ${{c}_{{20}}}$, ${{c}_{{11}}}$ в представлении (2.11) произвольны, а коэффициенты ${{c}_{{12}}}$, ${{c}_{{21}}}$, ${{c}_{{13}}}$ вычисляются по формулам

(2.13)

$\begin{gathered} {{c}_{{pq}}} = {{\alpha }_{{pq}}}{{({{(f,{{w}^{{p{{\tau }_{p}} - q}}})}_{\Omega }} - {{({{g}^{3}},{{w}^{{p{{\tau }_{p}} - 1 - q}}})}_{{\partial \Omega }}} + ({{g}^{2}},{{\partial }_{n}}{{w}^{{p{{\tau }_{p}} - 1 - q}}}))}_{{\partial \Omega }}}) \\ {{\alpha }_{{23}}} = - {{\alpha }_{{13}}} = (1 - {{\nu }^{2}}{{)}^{{ - 1}}},\quad {{\alpha }_{{21}}} = (2(1 - \nu {{))}^{{ - 1}}} \\ \end{gathered} $

Интегральные представления (2.13) выводятся согласно методу [16] при помощи подстановки функций ${{u}_{0}}$ и ${{w}^{{p{{\tau }_{p}} - 1 - q}}}$ в тождество

(2.14)

$\begin{gathered} {{({{\Delta }^{2}}u,w)}_{{{{\Omega }_{R}}}}} - {{(u,{{\Delta }^{2}}w)}_{{{{\Omega }_{R}}}}} - {{({{N}^{3}}u,w)}_{{{{{(\partial \Omega )}}_{R}}}}} + {{({{N}^{2}}u,{{\partial }_{n}}w)}_{{{{{(\partial \Omega )}}_{R}}}}} - \\ - \;{{({{\partial }_{n}}u,{{N}^{2}}w)}_{{{{{(\partial \Omega )}}_{R}}}}} + {{(u,{{N}^{3}}w)}_{{{{{(\partial \Omega )}}_{R}}}}} = \\ = \int\limits_{ - 1/2}^{1/2} {{\left. {(u(x){{N}^{3}}(\nabla )w(x) - {{\partial }_{z}}u(x){{N}^{2}}(\nabla )w(x) + {{\partial }_{z}}w(x){{N}^{2}}(\nabla )u(x) - w(x){{N}^{3}}(\nabla )u(x))} \right|}_{{z = R}}}dz - \\ - \;2(1 - \nu )\sum\limits_ \pm \pm \left( {u\left( { \pm \frac{1}{2},R} \right)\frac{{{{\partial }^{2}}w}}{{\partial y\partial z}}\left( { \pm \frac{1}{2},R} \right) - w\left( { \pm \frac{1}{2},R} \right)\frac{{{{\partial }^{2}}u}}{{\partial y\partial z}}\left( { \pm \frac{1}{2},R} \right)} \right) \\ \end{gathered} $

и предельного перехода $R \to + \infty $; при этом ${{\Omega }_{R}} = \{ x \in \Omega {\kern 1pt} :\;z < R\} $ – усеченный волновод с краем ${{(\partial \Omega )}_{R}}$ = $\{ x \in \partial \Omega {\text{:}}\;z < R\} $, а операторы (1.4) на сечении $\{ x \in \Pi {\kern 1pt} :\;{\kern 1pt} z = R\} $ принимают вид

${{N}^{3}}(\nabla ) = \frac{{{{\partial }^{3}}}}{{\partial {{z}^{3}}}} + (2 - \nu )\frac{{{{\partial }^{3}}}}{{\partial z\partial {{y}^{2}}}},\quad {{N}^{2}}(\nabla ) = \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}} + \nu \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}}$

Формула Грина (2.14) включает внеинтегральные члены, происходящие от интегрирования вдоль контура $\partial {{\Omega }_{R}}$ с угловыми точками $( \pm 1{\text{/}}2,R)$ [1, 17], и поэтому ее следует признать обобщенной.

3. Волны на ультранизких частотах. Построим решения

(3.1)

$\begin{array}{*{20}{c}} {{{w}_{\varepsilon }}(y,z) = {{e}^{{\varepsilon {{\theta }_{\varepsilon }}z}}}{{W}_{\varepsilon }}(y),\quad {{v}_{\varepsilon }}(y,z) = {{e}^{{{{\varepsilon }^{2}}{{\tau }_{\varepsilon }}z}}}{{V}_{\varepsilon }}(y)} \end{array}$

задачи в бесконечной полосе с параметром (1.7)

(3.2)

$\begin{gathered} {{\Delta }^{2}}w(x) = {{\varepsilon }^{4}}w(x),\quad x \in ( - 1{\text{/}}2,1{\text{/}}2) \times \mathbb{R} \\ {{N}_{q}}(\nabla )w( \pm 1{\text{/}}2,z) = 0,\quad z \in \mathbb{R}\quad (q = 2,3) \\ \end{gathered} $

Волна ${{w}_{\varepsilon }}$ отвечает изгибным колебаниям полосы; после подстановки выражения для ${{w}_{\varepsilon }}$ в соотношения (3.2) приходим к краевой задаче для обыкновенного дифференциального уравнения, которую следует интерпретировать как операторный пучок из-за полиномиального вхождения параметра ${{\theta }_{\varepsilon }}$

(3.3)

$\begin{gathered} \partial _{y}^{4}{{W}_{\varepsilon }}(y) + 2{{\varepsilon }^{2}}\theta _{\varepsilon }^{2}\partial _{y}^{2}{{W}_{\varepsilon }}(y) + {{\varepsilon }^{4}}\theta _{\varepsilon }^{4}{{W}_{\varepsilon }}(y) = {{\varepsilon }^{4}}{{W}_{\varepsilon }}(y),\quad y \in ( - 1{\text{/}}2,1{\text{/}}2) \\ \pm \partial _{y}^{3}{{W}_{\varepsilon }}( \pm 1{\text{/}}2) \pm (2 - \nu ){{\varepsilon }^{2}}\theta _{\varepsilon }^{2}{{\partial }_{y}}{{W}_{\varepsilon }}( \pm 1{\text{/}}2) = 0,\quad \partial _{y}^{2}{{W}_{\varepsilon }}( \pm 1{\text{/}}2) + \nu {{\varepsilon }^{2}}\theta _{\varepsilon }^{2}{{W}_{\varepsilon }}( \pm 1{\text{/}}2) = 0 \\ \end{gathered} $

Известны [18] разложения

(3.4)

$\begin{gathered} {{W}_{\varepsilon }}(y) = \sum\limits_{j = 0}^3 {\kern 1pt} {{\varepsilon }^{j}}\theta _{\varepsilon }^{j}{{W}^{{1j}}}(y) + {{\varepsilon }^{4}}W{\text{'}}(y) + {{\varepsilon }^{6}}W{\kern 1pt} ''(y) + \ldots \\ {{\theta }_{\varepsilon }} = {{\theta }_{0}} + {{\varepsilon }^{2}}\theta {\kern 1pt} ''\; + \ldots \\ \end{gathered} $

Здесь ${{W}^{{1j}}}$ – собственные и присоединенные векторы (2.8), (2.9), числа ${{\theta }_{0}}$, $\theta {\kern 1pt} '' \in \mathbb{C}$ и функции $W{\text{'}}$, $W{\text{''}}$ подлежат определению, а многоточие обозначает младшие асимптотические члены. В задаче (3.3) заменим величины ${{W}_{\varepsilon }}$ и ${{\theta }_{\varepsilon }}$ их разложениями (3.4) и соберем множители при одинаковых степенях малого параметра $\varepsilon $. Суммы коэффициентов при ${{\varepsilon }^{j}}\theta _{\varepsilon }^{j}$, $j = 0, \ldots ,3$, обращаются в нуль согласно определению собственных и присоединенных векторов (этот факт проверяется непосредственно), а коэффициенты при ${{\varepsilon }^{4}}$ формируют задачу

(3.5)

$\begin{gathered} \partial _{y}^{4}W{\kern 1pt} '(y) = F{\kern 1pt} '(y): = {{W}^{{10}}}(y) - \theta _{0}^{4}(2\partial _{y}^{2}{{W}^{{12}}}(y) + {{W}^{{10}}}(y)),\quad y \in ( - 1{\text{/}}2,1{\text{/}}2) \\ \pm \partial _{y}^{3}W{\kern 1pt} '( \pm 1{\text{/}}2) = G_{{3 \pm }}^{'}: = \mp (2 - \nu )\theta _{0}^{4}{{\partial }_{y}}{{W}^{{12}}}( \pm 1{\text{/}}2) \\ \partial _{y}^{2}W{\kern 1pt} '( \pm 1{\text{/}}2) = G_{{2 \pm }}^{'}: = - \nu \theta _{0}^{4}{{W}^{{12}}}( \pm 1{\text{/}}2) \\ \end{gathered} $

Условия разрешимости задачи (3.5)

(3.6)

$\begin{array}{*{20}{c}} {\int\limits_{ - 1/2}^{1/2} F{\kern 1pt} '(y){{W}^{{p0}}}(y)dy - \sum\limits_ \pm \left( {G_{{3 \pm }}^{'}{{W}^{{p0}}}\left( { \pm \frac{1}{2}} \right) \mp G_{{2 \pm }}^{'}{{\partial }_{y}}{{W}^{{p0}}}\left( { \pm \frac{1}{2}} \right)} \right) = 0} \end{array}$

при $p = 2$ выполнено, а в случае $p = 1$ оно эквивалентно алгебраическому уравнению

(3.7)

$\begin{array}{*{20}{c}} {1 - \theta _{0}^{4}(1 - {{\nu }^{2}}) = 0} \end{array}$

Корни уравнения (3.7) имеют вид

(3.8)

$\begin{array}{*{20}{c}} {\theta _{ \pm }^{{{\text{re}}}} = \pm \left| \theta \right|,\quad \theta _{ \pm }^{{{\text{im}}}} = \pm i\left| \theta \right|\quad (\left| \theta \right| = {{{(1 - {{\nu }^{2}})}}^{{ - 1/4}}})} \end{array}$

Теперь задача (3.5) имеет решение $W{\text{'}}$, и оно становится единственным при соблюдении условий ортогональности

(3.9)

$\begin{array}{*{20}{c}} {\int\limits_{ - 1/2}^{1/2} W{\text{'}}(y){{W}^{{p0}}}(y)dy = 0\quad (p = 1,2)} \end{array}$

Итак, определены главные члены разложений (3.4). Поскольку ${{W}^{{11}}} = {{W}^{{13}}} = 0$, поправки $W{\text{''}}$ и $\theta {\text{''}}$ находятся из задачи

(3.10)

$\begin{gathered} \partial _{y}^{4}W{\kern 1pt} ''(y) = F{\kern 1pt} ''(y): = \theta _{0}^{2}{{W}^{{12}}}(y) - 4\theta {\kern 1pt} ''{\kern 1pt} \theta _{0}^{3}(2\partial _{y}^{2}{{W}^{{12}}}(y) + {{W}^{{10}}}(y)) - \\ - \;\theta _{0}^{2}(2\partial _{y}^{2}W{\kern 1pt} '(y) + \theta _{0}^{4}{{W}^{{12}}}(y)),\quad y \in ( - {\text{1/2}},{\text{1/2}}) \\ \pm \partial _{y}^{3}W{\kern 1pt} ''( \pm {\text{1/2}}) = G_{{3 \pm }}^{{''}}: = \mp 4(2 - \nu )\theta {\kern 1pt} ''{\kern 1pt} \theta _{0}^{3}{{\partial }_{y}}{{W}^{{12}}}( \pm {\text{1/2}}) \mp (2 - \nu )\theta _{0}^{4}{{\partial }_{y}}W{\kern 1pt} '( \pm {\text{1/2}}) \\ \partial _{y}^{2}W{\kern 1pt} ''( \pm {\text{1/2}}) = G_{{2 \pm }}^{{''}}: = - 4\nu \theta {\kern 1pt} ''{\kern 1pt} \theta _{0}^{3}{{W}^{{12}}}( \pm {\text{1/2}}) - \nu \theta _{0}^{4}W{\kern 1pt} '( \pm {\text{1/2}}) \\ \end{gathered} $

Условие (3.6) разрешимости этой задачи превращается в линейное уравнение

(3.11)

$\begin{array}{*{20}{c}} { - 4\theta {\text{''}}\theta _{0}^{3}(1 - {{\nu }^{2}}) + t({{\theta }_{0}}) = 0} \end{array}$

дающее величину $\theta {\text{''}}$ для каждого корня (3.8). Наконец, задача (3.9), (3.10) приобретает единственное решение $W{\text{''}}$, подчиненное условиям ортогональности (3.9).

Асимптотическая процедура может быть продолжена, однако ни младшие члены, ни выражения $W{\text{'}}$, $W{\text{''}}$ и $\theta {\text{''}}$, в частности, слагаемое $t({{\theta }_{0}})$ в уравнении (3.11), востребованы не будут. Понадобятся построенные главные члены асимптотики и известный [18] факт: функции

$[0,{{\varepsilon }_{0}}) \mathrel\backepsilon \varepsilon \mapsto \theta _{{\varepsilon \pm }}^{{\operatorname{re} /\operatorname{im} }},\quad [0,{{\varepsilon }_{0}}) \mathrel\backepsilon \varepsilon \mapsto W_{{\varepsilon \pm }}^{{\operatorname{re} /\operatorname{im} }}(y)$

аналитические при некотором ${{\varepsilon }_{0}} > 0$.

Вторая волна (3.1) отвечает крутильным колебаниям пластины, а ее ингредиенты отыскиваются из аналогичной (3.3) краевой задачи на отрезке $( - 1{\text{/}}2,1{\text{/}}2)$ в виде

(3.12)

$\begin{gathered} {{V}_{\varepsilon }}(y) = {{W}^{{20}}}(y) + {{\varepsilon }^{2}}{{\vartheta }_{\varepsilon }}{{W}^{{21}}}(y) + {{\varepsilon }^{4}}V{\text{'}}(y) + \ldots = y + {{\varepsilon }^{4}}V{\text{'}}(y) + \ldots \\ {{\vartheta }_{\varepsilon }} = {{\vartheta }_{0}} + \ldots \\ \end{gathered} $

В итоге условия (3.6) разрешимости задачи

$\partial _{y}^{4}V{\kern 1pt} '(y) = F{\kern 1pt} '(y): = y,\quad y \in ( - {\text{1/2}},{\text{1/2}})$

$ \pm \partial _{y}^{3}V{\kern 1pt} '( \pm {\text{1/2}}) = G_{{3 \pm }}^{3} = \mp (2 - \nu )\vartheta _{0}^{2},\quad \partial _{y}^{2}V{\kern 1pt} '( \pm {\text{1/2}}) = \mp \nu \vartheta _{0}^{2}{\text{/}}2$

приводят к квадратному уравнению

$\frac{1}{{12}} + 2(1 - \nu )\vartheta _{0}^{2} = 0$

с чисто мнимыми корнями

(3.13)

$\begin{array}{*{20}{c}} {{{\vartheta }_{ \pm }} = \pm i\left| \vartheta \right|\quad (\left| \vartheta \right| = (24(1 - \nu {{{))}}^{{ - 1/2}}})} \end{array}$

Величины ${{\vartheta }_{{\varepsilon \pm }}}$ и ${{W}_{{\varepsilon \pm }}}$, включающие построенные главные асимптотические члены, аналитически зависят от переменной ${{\varepsilon }^{2}} \in [0,\varepsilon _{0}^{2})$.

4. Формальная асимптотика захваченной волны. В отличие от осциллирующих крутильных волн, заданных формулами (3.1) и (3.12), (3.13), среди четырех изгибных волн $w_{{\varepsilon \pm }}^{{\operatorname{im} /\operatorname{re} }}$ с ингредиентами (3.11) волна $w_{{\varepsilon - }}^{{\operatorname{re} }}$ исчезает при $z \to + \infty $ хоть и с малой, но экспоненциальной скоростью. Волны $w_{{\varepsilon \pm }}^{{\operatorname{im} }}$ медленно осциллируют, а волна $w_{{\varepsilon + }}^{{\operatorname{re} }}$ растет при $z \to + \infty $. Именно затухающую волну возьмем в качестве основного члена конструкции захваченной волны

(4.1)

$\begin{array}{*{20}{c}} {u_{\varepsilon }^{{{\text{tr}}}}(y,z) = \chi (z)w_{{\varepsilon - }}^{{\operatorname{re} }}(y,z) + {{u}_{\varepsilon }}(y,z)} \end{array}$

Функция $w_{{\varepsilon - }}^{{\operatorname{re} }}$ определена только в единичной полосе и потому умножена на срезающую функцию (2.12), а дополнительное слагаемое ${{u}_{\varepsilon }}$, которое компенсирует невязки, оставленные произведением $\chi w_{{\varepsilon - }}^{{\operatorname{re} }}$ в уравнении (1.1) и краевых условиях (1.2), исчезает на бесконечности, однако в отличие от $w_{{\varepsilon - }}^{{\operatorname{re} }}$ с большой скоростью, т.е. ${{e}^{{\beta z}}}{{u}_{\varepsilon }} \in {{H}^{4}}(\Omega )$ (ср. разд. 2). Сам остаток будем искать в виде

(4.2)

$\begin{array}{*{20}{c}} {{{u}_{\varepsilon }}(x) = {{u}_{0}}(x) + \varepsilon {{u}_{1}}(x) + {{\varepsilon }^{2}}{{u}_{2}}(x) + {{\varepsilon }^{3}}{{u}_{3}}(x) + {{\varepsilon }^{3}}u_{\varepsilon }^{'}(x)} \end{array}$

Слагаемые ${{u}_{j}}$ экспоненциально затухают на бесконечности и удовлетворяют задаче (2.1), (2.2) с некоторыми правыми частями ${{f}_{j}}$ и $g_{j}^{q}$, имеющими компактные носители.

Учитывая разложения (3.4) и формулы (2.8), видим, что на резонаторе $\Theta $ справедливо разложение

(4.3)

$\begin{gathered} w_{{\varepsilon - }}^{{\operatorname{re} }}(y,z) = 1 - \varepsilon \left| \theta \right|z + {{\varepsilon }^{2}}{{\left| \theta \right|}^{2}}\frac{1}{2}({{z}^{2}} - \nu {{y}^{2}}) - {{\varepsilon }^{3}}\left( {{{{\left| \theta \right|}}^{3}}\frac{z}{2}\left( {\frac{{{{z}^{2}}}}{3} - \nu {{y}^{2}}} \right) - \left| \theta \right|\theta {\kern 1pt} ''{\kern 1pt} z} \right) + \tilde {w}_{{\varepsilon - }}^{{re}}(y,z) \\ \tilde {w}_{{\varepsilon - }}^{{re}}(y,z) = O({{\varepsilon }^{4}}),\quad (y,z) \in \bar {\Theta } \\ \end{gathered} $

Поэтому, обозначив $[{{\Delta }^{2}},\chi ]$ и $[{{N}^{q}}(\nabla ),\chi ]$ коммутаторы бигармонического оператора и дифференциальных операторов (1.5) со срезающей функцией (2.12), находим

(4.4)

$\begin{gathered} {{f}_{0}} = - [{{\Delta }^{2}},\chi ]1,\quad g_{0}^{q} = - [{{N}^{q}}(\nabla ),\chi ]1 \\ {{f}_{1}} = \left| \theta \right|[{{\Delta }^{2}},\chi ]z,\quad g_{1}^{q} = \left| \theta \right|[{{N}^{q}}(\nabla ),\chi ]z \\ \end{gathered} $

Операторы (1.4) аннулируют линейные функции (1.11). Следовательно, первые два слагаемых в сумме (4.2) принимают вид

(4.5)

$\begin{array}{*{20}{c}} {{{u}_{0}}(x) = 1 - \chi (z),\quad {{u}_{1}}(x) = - \left| \theta \right|(1 - \chi (z))z} \end{array}$

и обладают компактными носителями, т.е. заведомо затухают на бесконечности. При учете соотношения (1.6) выводим выражения для правых частей задачи (2.1), (2.2) для слагаемого ${{u}_{2}}$

(4.6)

$\begin{gathered} {{f}_{2}}(x) = \rho (x) - {{a}_{0}}(x) - \frac{{{{{\left| \theta \right|}}^{2}}}}{2}[{{\Delta }^{2}},\;\chi (z)]({{z}^{2}} - \nu {{y}^{2}}) \\ g_{2}^{q}(x) = - \frac{{{{{\left| \theta \right|}}^{2}}}}{2}[{{N}^{q}}(\nabla ),\;\chi (z)]({{z}^{2}} - \nu {{y}^{2}}) \\ \end{gathered} $

Решение ${{u}_{2}}$ экспоненциально затухает на бесконечности при выполнении трех условий разрешимости (2.3). В силу соотношений (2.13), (3.8) и обобщенной формулы Грина (2.14) получаем

(4.7)

$\begin{gathered} {{J}_{2}}({{f}_{2}} - \rho + {{a}_{0}},g_{2}^{2},g_{2}^{3}) = - \frac{{{{{\left| \theta \right|}}^{2}}}}{2}\mathop {lim}\limits_{R \to + \infty } \left( {\int\limits_{{{\Omega }_{R}}} z{{\Delta }^{2}}\left( {\chi (z)({{z}^{2}} - \nu {{y}^{2}})} \right)dx} \right. - \\ - \;\left. {\int\limits_{{{{(\partial \Omega )}}_{R}}} \left( {z{{N}^{3}}(x,\nabla )({{z}^{2}} - \nu {{y}^{2}}) - {{\partial }_{n}}z{{N}^{2}}(x,\nabla )({{z}^{2}} - \nu {{y}^{2}})} \right){\kern 1pt} d{{s}_{x}}} \right) = \\ = - \frac{{{\text{|}}\theta {{{\text{|}}}^{2}}}}{2}\mathop {lim}\limits_{R \to + \infty } {{\left. {\int\limits_{ - 1/2}^{1/2} {\kern 1pt} \left( {z{{N}^{3}}(\nabla )({{z}^{2}} - \nu {{y}^{2}}) - {{N}^{2}}(\nabla )({{z}^{2}} - \nu {{y}^{2}})} \right)} \right|}_{{z = R}}}dy = \\ = {\text{|}}\theta {{{\text{|}}}^{2}}(1 - {{\nu }^{2}}) = \sqrt {1 - {{\nu }^{2}}} \\ \end{gathered} $

Нетрудно подобрать нетривиальные неотрицательные функции ${{a}_{0}}$ и $\rho $, для которых

(4.8)

$\begin{array}{*{20}{c}} {\int\limits_\Theta {\kern 1pt} z\left( {\rho (x) - {{a}_{0}}(x)} \right)dx = - \sqrt {1 - {{\nu }^{2}}} ,\quad \int\limits_\Theta \left( {\rho (x) - {{a}_{0}}(x)} \right){\kern 1pt} dx = \int\limits_\Theta y\left( {\rho (x) - {{a}_{0}}(x)} \right)dx = 0} \end{array}$

В итоге находим единственное исчезающее на бесконечности решение ${{u}_{2}}$ задачи (2.1), (2.2) с правыми частями (4.6). Согласно разложениям (5.1) и (1.6) правые части задачи для функции ${{u}_{3}}$ принимают вид

(4.9)

$\begin{gathered} {{f}_{3}}(x) = \left| \theta \right|z(\rho (x) - {{a}_{0}}(x)) + \sum\limits_{j = 0}^2 {\kern 1pt} {{\tau }_{{j0}}}{{b}_{j}}(x) + [{{\Delta }^{2}},\chi (z)]\left( {\frac{{{{{\left| \theta \right|}}^{3}}}}{2}\left( {\frac{1}{3}{{z}^{3}} - \nu {{y}^{2}}z} \right) - \left| \theta \right|\theta {\kern 1pt} ''{\kern 1pt} z} \right) \\ g_{3}^{q}(x) = [{{N}^{q}}(\nabla ),\chi (z)]\left( {\frac{{{{{\left| \theta \right|}}^{3}}}}{2}\left( {\frac{1}{3}{{z}^{3}} - \nu {{y}^{2}}z} \right) - \left| \theta \right|\theta {\kern 1pt} ''{\kern 1pt} z} \right)\quad (q = 2,3) \\ \end{gathered} $

Для того чтобы соблюсти условия разрешимости (2.3) в случае выражений (4.9), подчиним слагаемые ${{b}_{j}}$ в представлении (1.6) коэффициента податливости ${{a}_{\varepsilon }}$ двум требования. Во-первых, введем условия биортогональности

(4.10)

$\int\limits_\Theta {{b}_{j}}(x){{{v}}_{k}}(x)dx = {{\delta }_{{j,k}}}$

Здесь $j,k = 0,1,2$ и ${{\delta }_{{j,k}}}$ – символ Кронекера. Во-вторых, считаем, что при некотором $\delta > 0$ носители слагаемых содержатся во множестве $\{ x:{\kern 1pt} \,{{a}_{0}}(x) \geqslant \delta \} $. В результате суммарный нормированный коэффициент податливости (1.6) остается положительным при малом $\varepsilon > 0$. Наконец, соотношения (4.10) позволяют удовлетворить упомянутые условия разрешимости за счет выбора главных членов ${{\tau }_{{j0}}}$ представлений

(4.11)

$\begin{array}{*{20}{c}} {{{\tau }_{{j\varepsilon }}} = {{\tau }_{{j0}}} + \tau _{{j\varepsilon }}^{'}} \end{array}$

Точные значения величин ${{\tau }_{{j0}}}$ востребованы не будут.

Итак, задача (2.1), (2.2) с правыми частями (4.9) имеет единственное решение ${{u}_{3}}(y,z)$, затухающее при $z \to + \infty $. Отделенные члены асимптотики (4.2) захваченной волны $w_{\varepsilon }^{{{\text{tr}}}}$ построены. Попутно определены (заведомо не единственным способом) главные члены представления (1.6) коэффициента податливости винклеровского основания. Намеченную процедуру можно было бы продолжить и найти младшие асимптотические члены, однако проверить сходимость полученных формальных рядов затруднительно. Поэтому изберем иной путь и применим процедуру точной настройки параметров волновода.

5. Доказательство существования захваченной волны. Сформируем задачу для остатка $u_{\varepsilon }^{'}$ из представления (4.1)

(5.1)

$\begin{gathered} {{\Delta }^{2}}u_{\varepsilon }^{'}(x) = f_{\varepsilon }^{'}(x;u_{\varepsilon }^{'},\tau _{\varepsilon }^{'}),\quad x \in \Omega \\ {{N}^{q}}(x,\nabla )u_{\varepsilon }^{'}(x) = {{g}^{{q'}}}(x;u_{\varepsilon }^{'},\tau _{\varepsilon }^{'}),\quad x \in \partial \Omega \quad (q = 2,3) \\ \end{gathered} $

Здесь $\tau {\kern 1pt} ' = (\tau _{{0\varepsilon }}^{'},\tau _{{1\varepsilon }}^{'},\tau _{{2\varepsilon }}^{'})$ – набор остатков в разложениях (4.11) и (1.6). При учете соотношений (4.3), (4.4)–(4.7), (4.9) преобразуем правые части задачи (5.1) следующим образом

$f{\kern 1pt} '(x;u_{\varepsilon }^{'},\tau _{\varepsilon }^{'}) = - \sum\limits_{j = 0}^2 \tau _{j}^{'}{{b}_{j}}(x) + \tilde {f}_{\varepsilon }^{'}(x;u_{\varepsilon }^{'},\tau _{\varepsilon }^{'})$

$\tilde {f}_{\varepsilon }^{'}(x;u_{\varepsilon }^{'},\tau _{\varepsilon }^{'}) = \varepsilon ({{u}_{0}}(x) + \varepsilon {{u}_{1}}(x) + {{\varepsilon }^{2}}{{u}_{2}}(x) + {{\varepsilon }^{3}}{{u}_{3}}(x) + {{\varepsilon }^{3}}u{\text{'}}(x)) + $

(5.2)

$ + \;(\rho (x) - {{a}_{0}}(x))(\chi (z){{\varepsilon }^{{ - 1}}}(w_{{\varepsilon - }}^{{\operatorname{re} }}(x) - 1 + \varepsilon {\text{|}}\theta {\text{|}}z) + \varepsilon {{u}_{2}}(x) + {{\varepsilon }^{2}}{{u}_{3}}(x) + {{\varepsilon }^{2}}u{\text{'}}(x)) - $

$ - \;\sum\limits_{j = 0}^2 ({{\tau }_{{j0}}} + \tau _{{j\varepsilon }}^{'}){{b}_{j}}(x)(\chi (z)(w_{{\varepsilon - }}^{{\operatorname{re} }}(x) - 1) + {{\varepsilon }^{2}}{{u}_{2}}(x) + {{\varepsilon }^{3}}{{u}_{3}}(x) + {{\varepsilon }^{3}}u_{\varepsilon }^{'}(x))$

$g_{\varepsilon }^{{q'}}(x;u_{\varepsilon }^{'},\tau _{\varepsilon }^{'}) = {{\varepsilon }^{{ - 3}}}[{{N}^{q}}(x,\nabla ),\chi (z)]\tilde {w}_{{\varepsilon - }}^{{{\kern 1pt} re}}(x)$

В силу предположения (4.10) условия разрешимости (2.3) задачи (5.1) в классе функций, исчезающих на бесконечности, принимают вид

(5.3)

$\begin{array}{*{20}{c}} {\tau {\text{'}} = J(\tilde {f}_{\varepsilon }^{'},g_{\varepsilon }^{{2'}},g_{\varepsilon }^{{3'}})} \end{array}$

Здесь $J = ({{J}_{1}},{{J}_{2}},{{J}_{3}})$ – вектор функционалов (2.3).

Заменим в формуле (5.2) коэффициенты $\tau _{{j\varepsilon }}^{'}$ их выражениями (5.3) и согласно обозначению (2.4) получим решения $u_{\varepsilon }^{'} \in W_{\beta }^{4}(\Omega )$ задачи (5.1)

(5.4)

$u_{\varepsilon }^{'} = {{R}_{\beta }}(\tilde {f}_{\varepsilon }^{'},g_{\varepsilon }^{{2'}},g_{\varepsilon }^{{3'}})$

Положим

$\mathcal{F}_{\varepsilon }^{'}(u_{\varepsilon }^{'},\tau _{\varepsilon }^{'}) = (f_{\varepsilon }^{'},g_{\varepsilon }^{{2'}},g_{\varepsilon }^{{3'}},J(\tilde {f}_{\varepsilon }^{'},g_{\varepsilon }^{{2'}},g_{\varepsilon }^{{3'}}))$

и заметим, что

(5.5)

$\begin{gathered} \left\| {\mathcal{F}_{\varepsilon }^{'}(0,0);{{W}_{\beta }} \times {{\mathbb{R}}^{3}}} \right\| \leqslant c\varepsilon \\ \left\| {\mathcal{F}_{\varepsilon }^{'}(u_{\varepsilon }^{'},\tau _{\varepsilon }^{'}) - \mathcal{F}_{\varepsilon }^{'}(v_{\varepsilon }^{'},t_{\varepsilon }^{'});{{W}_{\beta }} \times {{\mathbb{R}}^{3}}} \right\| \leqslant c\varepsilon \left\| {(u{\kern 1pt} '\; - v_{\varepsilon }^{'},\tau _{\varepsilon }^{'} - t_{\varepsilon }^{'});W_{\beta }^{4}(\Omega ) \times {{\mathbb{R}}^{3}}} \right\| \times \\ \times \;\left( {1 + \left\| {(u_{\varepsilon }^{'},\tau _{\varepsilon }^{'});W_{\beta }^{4}(\Omega ) \times {{\mathbb{R}}^{3}}} \right\| + \left\| {(v_{\varepsilon }^{'},t_{\varepsilon }^{'});W_{\beta }^{4}(\Omega ) \times {{\mathbb{R}}^{3}}} \right\|} \right) \\ \end{gathered} $

Перепишем соотношения (5.3), (5.4) как абстрактное уравнение

(5.6)

$\begin{array}{*{20}{c}} {(u_{\varepsilon }^{'},\tau _{\varepsilon }^{'}) = \mathcal{Q}_{\beta }^{\varepsilon }(u_{\varepsilon }^{'},\tau _{\varepsilon }^{'})\quad {\text{в}}\quad {{\mathcal{H}}_{\beta }} = W_{\beta }^{4}(\Omega ) \times {{\mathbb{R}}^{3}}} \end{array}$

В силу неравенств (5.5) при $\varepsilon \in (0,{{\varepsilon }_{r}})$ оператор $\mathcal{Q}_{\beta }^{\varepsilon }$ – сжимающий оператор на шаре

${{\mathcal{B}}_{r}} = \{ (u,\tau ) \in {{\mathcal{H}}_{\beta }}{\kern 1pt} :\;\left\| {(u,\tau );{{\mathcal{H}}_{\beta }}} \right\| \leqslant r\} $

в гильбертовом пространстве ${{\mathcal{H}}_{\beta }}$. Здесь $r$ и ${{\varepsilon }_{r}}$ – положительные, вообще говоря, малые числа. В итоге известный [19] принцип Банаха сжимающих отображений дает единственное решение $(u_{\varepsilon }^{'},\tau _{\varepsilon }^{'}) \in {{\mathcal{B}}_{r}}$ уравнения (5.6), к тому же допускающее оценку

$\left\| {(u_{\varepsilon }^{'},\tau _{\varepsilon }^{'});{{\mathcal{H}}_{\beta }}} \right\| \leqslant c\varepsilon $

При этом $u_{\varepsilon }^{'} \in W_{\beta }^{4}(\Omega )$ – решение задачи (5.1), а значит, функция (4.1), экспоненциально затухающая на бесконечности согласно формулам (3.1) и (3.6), удовлетворяет задаче (1.1), (1.2) с коэффициентом податливости (1.6). Искомая захваченная волна построена.

6. Единственность захваченной волны на ультранизких частотах. Предположим, что нашлась бесконечно малая положительная последовательность $\{ {{\varepsilon }_{k}}\} _{{k = 1}}^{\infty }$, при которой у задачи (1.1), (1.2) с ингредиентами (1.3), (1.6), (1.7) есть решение ${{u}_{{{{\varepsilon }_{k}}}}} \in {{H}^{4}}(\Omega )$, т.е. захваченная волна. Далее нижний индекс $k$ у $\varepsilon = {{\varepsilon }_{k}}$ не пишем и считаем, что

(6.1)

$\begin{array}{*{20}{c}} {{\text{|}}{{a}_{\varepsilon }}(x){\text{|}} \leqslant c{{\varepsilon }^{2}},\quad {\text{|}}{{\rho }_{\varepsilon }}(x) - 1{\text{|}} \leqslant c{{\varepsilon }^{{ - 2}}},\quad x \in \Theta ,\quad {{a}_{\varepsilon }}(x) = 0,\quad {{\rho }_{\varepsilon }}(x) = 1,\quad x \in \Pi } \end{array}$

Нормируем функции ${{u}_{\varepsilon }}$ в пространстве ${{L}^{2}}(\Theta )$. Функция ${{u}_{\varepsilon }} \in {{H}^{4}}(\Omega )$, разумеется, принадлежит пространству $W_{{ - \beta }}^{4}(\Omega )$ функций с экспоненциальным ростом при $z \to + \infty $, на котором для решения $u \in W_{{ - \beta }}^{4}(\Omega )$ задачи (2.1), (2.2) доказана [12, 20] весовая оценка

(6.2)

$\begin{array}{*{20}{c}} {\left\| {u;W_{{ - \beta }}^{4}(\Omega )} \right\| \leqslant c\left( {\left\| {f,{{g}^{2}},{{g}^{3}});{{\mathcal{W}}_{{ - \beta }}}(\Omega )} \right\| + \left\| {u;{{L}^{2}}(\Theta )} \right\|} \right)} \end{array}$

Неравенство (6.2) с не зависящим от $\varepsilon \in (0,{{\varepsilon }_{0}})$ множителем $c$ сохраняется и при возмущении бигармонического оператора ${{\Delta }^{2}}$ малым оператором ${{S}_{\varepsilon }} = {{a}^{\varepsilon }} - {{\varepsilon }^{4}}(1 + {{\varepsilon }^{{ - 2}}}\rho )$, т.е.

$\left\| {{{u}_{\varepsilon }};W_{{ - \beta }}^{4}(\Omega )} \right\| \leqslant c\left\| {{{u}_{\varepsilon }};{{L}^{2}}(\Theta )} \right\| = c$

Итак, существует слабый в $W_{{ - \beta }}^{4}(\Omega )$ и сильный в ${{L}^{2}}(\Theta )$ предел ${{u}_{0}}$ последовательности ${{\{ {{u}_{{{{\varepsilon }_{k}}}}}\} }_{{k = 1}}}$. При этом, во-первых,

(6.3)

$\begin{array}{*{20}{c}} {\left\| {{{u}_{0}};{{L}^{2}}(\Theta )} \right\| = 1} \end{array}$

и, во-вторых, ${{u}_{0}} \in W_{{ - \beta }}^{4}(\Omega )$ – решение однородной ($f = 0$, ${{g}^{2}} = {{g}^{3}} = 0$) задачи (2.1), (2.2), которое ввиду медленного роста (показатель $\beta > 0$ можно взять любым) превращается в линейную функцию

${{u}_{0}}(x) = {{c}_{0}} + {{c}_{1}}z + {{c}_{2}}y$

Убедимся в том, что ${{c}_{1}} = {{c}_{2}} = 0$, и тем самым установим, что на малой частоте ${{\omega }_{\varepsilon }} = \sqrt D {{\varepsilon }^{2}}$ (ср. формулу (1.7)) имеется только одна захваченная волна, так как ${{c}_{0}} \ne 0$ в силу нормировки (6.3). С этой целью подставим в формулу Грина (2.14), переделанную для полосы $\Pi $, экспоненциально затухающую функцию ${{u}_{\varepsilon }} \in {{H}^{4}}(\Omega )$ и одну из ограниченных относительно переменной $z$ функций

$w_{\varepsilon }^{{(1)}}(x) = {{\varepsilon }^{{ - 2}}}(2w_{{\varepsilon - }}^{{\operatorname{re} }}(x) - (1 + i)w_{{\varepsilon + }}^{{\operatorname{im} }}(x) - (1 - i)w_{{\varepsilon - }}^{{\operatorname{im} }}(x))$

$w_{\varepsilon }^{{(2)}}(x) = {{\varepsilon }^{{ - 1}}}(v_{{\varepsilon + }}^{{\operatorname{im} }}(x) - v_{{\varepsilon - }}^{{\operatorname{im} }}(x))$

Перечисленные функции удовлетворяют однородному уравнению с оператором ${{\Delta }^{2}} - {{\varepsilon }^{4}}$ в полуполосе $\Pi $ и краевым условиям (1.2) на ее боковых сторонах. Таким образом, формула Грина принимает вид

(6.4)

$\begin{gathered} 0 = \int\limits_{ - 1/2}^{1/2} ({{u}_{\varepsilon }}(x){{N}^{3}}(\nabla )w_{\varepsilon }^{{(p)}}(x) + {{\partial }_{z}}{{u}_{\varepsilon }}(x){{N}^{2}}(\nabla )w_{\varepsilon }^{{(p)}}(x) + \\ + \;{{\partial }_{z}}w_{\varepsilon }^{{(p)}}(x){{N}^{2}}(\nabla ){{u}_{\varepsilon }}(x) + w_{\varepsilon }^{{(p)}}(x){{N}^{3}}(\nabla ){{u}_{\varepsilon }}(x)){{{\text{|}}}_{{z = 0}}}dy + \\ + \;2(1 - \nu )\sum\limits_ \pm \pm \left( {{{u}_{\varepsilon }}\left( { \pm \frac{1}{2},0} \right)\frac{{{{\partial }^{2}}w_{\varepsilon }^{{(p)}}}}{{\partial y\partial z}}\left( { \pm \frac{1}{2},0} \right) - w_{\varepsilon }^{{(p)}}\left( { \pm \frac{1}{2},0} \right)\frac{{{{\partial }^{2}}{{u}_{\varepsilon }}}}{{\partial y\partial z}}\left( { \pm \frac{1}{2},0} \right)} \right) \\ \end{gathered} $

Слабая сходимость ${{u}_{\varepsilon }} \cdot {{u}_{0}}$ в ${{H}^{4}}(\Theta )$ влечет за собой сильную сходимость в пространстве Соболева ${{H}^{3}}( - 1{\text{/}}2,1{\text{/}}2)$ на торце полуполосы $\Pi $. Кроме того, согласно полученным в разд. 3 асимптотическим разложениям имеем

$w_{\varepsilon }^{{(j)}}(x) = w_{0}^{{(j)}} + O(\varepsilon )\quad (j = 1,2)$

$w_{0}^{{(1)}}(x) = 2{\text{|}}\theta {{{\text{|}}}^{2}}({{z}^{2}} - \nu {{y}^{2}}),\quad w_{0}^{{(2)}}(x) = 2i\vartheta yz$

При учете соотношений (6.1) предельный переход $\varepsilon \to + 0$ в равенстве (6.4) дает соотношение

(6.5)

$\begin{gathered} \int\limits_{ - 1/2}^{1/2} {{\left. {\left( {{{u}_{0}}(x){{N}^{3}}(\nabla )W_{0}^{{(j)}}(x) + {{\partial }_{z}}{{u}_{0}}(x){{N}^{2}}(\nabla )w_{0}^{{(j)}}(x)} \right)} \right|}_{{z = 0}}}dy + \\ + \;2(1 - \nu )\sum\limits_ \pm \pm {{u}_{0}}\left( { \pm \frac{1}{2},0} \right)\frac{{{{\partial }^{2}}w_{0}^{{(j)}}}}{{\partial y\partial z}}\left( { \pm \frac{1}{2},0} \right) = 0 \\ \end{gathered} $

В силу формул (2.13) выводим, что левая часть соотношения (6.5) равна $2\left| \theta \right|{{\alpha }_{{23}}}{{c}_{2}}$ и $2i\left| \vartheta \right|{{\alpha }_{{21}}}{{c}_{1}}$ соответственно при $j = 1$ и $j = 2$. Таким образом, равенства ${{c}_{1}} = {{c}_{2}} = 0$ доказаны.

7. Формулировка результатов и пояснения к ним. 1°. Изгибные колебания. В предыдущих разделах доказано следующее утверждение: найдутся такие положительные величины ${{\varepsilon }_{0}}$ и ${{\delta }_{0}}$, что в случае $\varepsilon \in (0,{{\varepsilon }_{0}})$ при правильном выборе коэффициентов (1.3) и (1.6) у краевой задачи (1.1), (1.2) (или (1.8) в вариационной постановке) появляется собственное число (1.7), вкрапленное в непрерывный спектр. Кроме того, обнаруженное собственное число простое, и на интервале $(0,{{\varepsilon }^{4}}(1 + {{\delta }_{0}}))$ других собственных чисел нет. Соответствующая собственная функция экспоненциально затухает на бесконечности, и ее поведение при $\varepsilon \to + 0$ описывается асимптотическими разложениями (4.1), (4.2), т.е. согласно формулам (2.8) и (3.1), (3.4) в главном реализуется как изгибные колебания пластины.

2°. Упрощения. Для того чтобы соблюсти физически осмысленное требование

(7.1)

$\begin{array}{*{20}{c}} {{{a}_{\varepsilon }}(x) \geqslant 0} \end{array}$

пришлось придать локальное, но значительное возмущение плотности ${{\rho }_{\varepsilon }}$ – иначе не удается удовлетворить два первых ограничения (4.8) одновременно. Если отказаться от условия (7.1) и, утратив прикладной характер спектральной задачи, допустить коэффициент ${{a}_{\varepsilon }}$ переменного знака, то по прежней схеме можно построить собственное число (1.7) и при $\rho = 0$ в формуле (1.3).

3°. Крутильные колебания. В предположениях о симметрии области $\Omega $ относительно оси абсцисс и четности функций ${{a}_{\varepsilon }}$, ${{\rho }_{\varepsilon }}$ можно искать собственные функции задачи (1.1), (1.2), нечетные по переменной $y$. Соответствующая постановка спектральной задачи сводится к сужению уравнения (1.1) и краевых условий (1.2) на половину волновода ${{\Omega }_{ + }} = \{ x = (y,z) \in \Omega :y > 0\} $

(7.2)

$\begin{gathered} {{\Delta }^{2}}{{u}_{\varepsilon }}(x) + {{a}_{\varepsilon }}(x){{u}_{\varepsilon }}(x) = {{\lambda }_{\varepsilon }}{{\rho }_{\varepsilon }}(x){{u}_{\varepsilon }}(x),\quad x \in {{\Omega }_{ + }} \\ {{N}^{q}}(x,\nabla ){{u}_{\varepsilon }}(x) = 0,\quad x \in {{(\partial \Omega )}_{ + }}\quad (q = 2,3) \\ \end{gathered} $

и постановки искусственных краевых условий

(7.3)

$\begin{array}{*{20}{c}} {{{w}_{\varepsilon }}(0,z) = 0,{\kern 1pt} {\kern 1pt} \partial _{y}^{2}{{w}_{\varepsilon }}(0,z) = 0,\quad (0,z) \in \Omega } \end{array}$

Условия (7.3) имитируют свободно опёртый край пластины, и им удовлетворяет только вторая волна (3.1), порожденная жордановой цепочкой (2.9) с длиной два. Рассуждения и выкладки из разд. 6 показывают, что у задачи (7.2), (7.3) нет малых собственных чисел.

4°. Акустический волновод. В задаче Неймана для оператора Гельмгольца $\Delta + {{\varepsilon }^{4}}$ в полосе $( - 1{\text{/}}2,1{\text{/}}2) \times \mathbb{R}$ возникают две осциллирующие волны

${{w}_{{\varepsilon \pm }}}(y,z) = {{e}^{{ \pm i{{\varepsilon }^{2}}z}}}$

Эти волны порождены жордановой цепочкой {1, 0} с длиной два, порожденной нулевым собственным числом аналогичного (2.10) операторного пучка

$\theta \mapsto \left\{ { - {{{\left. {\partial _{y}^{2} - {{\theta }^{2}}, \pm {{\partial }_{y}}} \right|}}_{{y = \pm 1/2}}}} \right\}$

Таким образом, свойства решений задачи Неймана

(7.4)

$\begin{gathered} - \Delta {{u}_{\varepsilon }}(x) + \varepsilon {{a}_{0}}(x){{u}^{\varepsilon }}(x) = {{\lambda }^{\varepsilon }}{{u}^{\varepsilon }}(x),\quad x \in \Omega \\ {{\partial }_{n}}{{u}^{\varepsilon }}(x) = 0,\quad x \in \partial \Omega \\ \end{gathered} $

с малым спектральным параметром ${{\lambda }^{\varepsilon }}$ похожи на свойства решений видоизмененной задачи Кирхгофа (7.2), (7.3). В частности, у задачи (7.4) не может быть малых положительных собственных чисел.

5°. Один открытый вопрос. При помощи минимального принципа (см., например, [5]) нетрудно убедиться в том, что в случае

(7.5)

$\begin{array}{*{20}{c}} {{{a}_{0}}(x) \leqslant 0,\quad x \in \Theta ,\quad \int\limits_\Theta {{a}_{0}}(x)dx < 0,\quad {{a}_{0}}(x) = 0,\quad x \in \Pi ,} \end{array}$

задача Неймана (7.4) обладает отрицательным собственным числом. При малом $\varepsilon > 0$ у задачи (7.4) нет других собственных чисел около начала координат, так как пороговый резонанс реализуется только на пространстве постоянных функций. Впрочем ограничения (7.5) противоречат физическому смыслу задачи и вводятся здесь с чисто математической целью.

Аналогичный вывод о существовании отрицательного собственного числа можно сделать и в задаче (1.1), (1.2) при плотности ${{\rho }_{\varepsilon }} = 1$ (способ возмущения существенно упрощается: утяжеление (1.3) “резонатора” не требуется и коэффициенте ${{a}_{\varepsilon }}(x) = \varepsilon {{a}_{0}}(x)$, подчиненном соотношениям (7.5). Остался открытым вопрос о построении коэффициентов ${{\rho }_{\varepsilon }}$ и ${{a}_{\varepsilon }}$, обеспечивающих максимально возможное количество собственных чисел – двух отрицательных в дискретном спектре и одного положительного в непрерывном или трех отрицательных.

Работа выполнена при финансовой поддержке Российского научного фонда (проект 17-11-01003).

Список литературы

Михлин С.Г. Вариационные методы в математической физике. М.: Наука, 1970.
Крылов А.Н. О расчете балок, лежащих на упругом основании. Ленинград: изд-во АН СССР, 1931.
Hetenyi M. Beams on Elastic Foundation. Michigan: Univ. Press, 1946.
Бирман М.Ш. O вариационном методе Треффца для уравнения ${{\Delta }^{2}}u = f$ // Докл. АН СССР. 1955. Т. 101. № 2. С. 201–204.
Бирман М.Ш., Соломяк М.З. Спектральная теория самосопряженных операторов в гильбертовом пространстве. Л.: изд-во Ленингр. ун-та, 1980.
Назаров С.А. Асимптотика собственных чисел на непрерывном спектре регулярно возмущенного квантового волновода // Теоретическая и математическая физика. 2011. Т. 167. № 2. С. 239–262.
Назаров С.А. Принудительная устойчивость простого собственного числа на непрерывном спектре волновода // Функциональный анализ и его приложения. 2013. Т. 47. № 3. С. 37–53.
Molchanov S., Vainberg B. Scattering solutions in networks of thin fibers: small diameter asymptotics // Comm. Math. Phys. 2007. V. 273. № 2. P. 533–559.
Grieser D. Spectra of graph neighborhoods and scattering // Proc. London Math. Soc. 2008. V. 97. № 3. P. 718–752.
Pankrashkin K. Eigenvalue inequalities and absence of threshold resonances for waveguide junctions // J. Math. Anal. Appl. 2017. V. 449. № 1. P. 907–925.
Бахарев Ф.Л., Назаров С.А. Критерии отсутствия и наличия ограниченных решений на пороге непрерывного спектра в объединении квантовых волноводов // Алгебра и анализ. (в печати)
Nazarov S.A., Plamenevsky B.A. Elliptic Problems in Domains with Piecewise Smooth Boundaries. Berlin: Walter de Gruyter. 1994.
Назаров С.А. Полиномиальное свойство самосопряженных эллиптических краевых задач и алгебраическое описание их атрибутов // Успехи матем. наук. 1999. Т. 54. № 5. С. 77–142.
Назаров С.А. Самосопряженные эллиптические краевые задачи. Полиномиальное свойство и формально положительные операторы // Проблемы матем. анализа. Вып. 16. СПб.: изд-во СПбГУ. 1997. С. 167–192.
Назаров С.А. Несамосопряженные эллиптические задачи с полиномиальным свойством в областях, имеющих цилиндрические выходы на бесконечность // Записки научн. семинаров петербург. отделения матем. института РАН. 1997. Т. 249. С. 212–230.
Мазья В.Г., Пламеневский Б.А. О коэффициентах в асимптотике решений эллиптических краевых задач в области с коническими точками // Math. Nachr. 1977. Bd. 76. S. 29–60.
Назаров С.А. Асимптотика собственных колебаний длинной двумерной пластины Кирхгофа с переменным сечением // Матем. сб. 2018. Т. 209. № 9. С. 35–86.
Вайнберг М.М., Треногин В.А. Теория ветвления решений нелинейных уравнений. М.: Наука, 1969.
Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.: Наука, 1976.
Кондратьев В.А. Краевые задачи для эллиптических уравнений в областях с коническими или угловыми точками // Тр. Московск. матем. общества. 1963. Т. 16. С. 219–292.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал