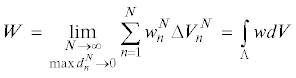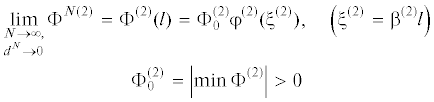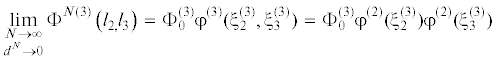Прикладная математика и механика, 2020, T. 84, № 3, стр. 387-404

Введение. Явление адгезии твердых тел играет как положительную, так и отрицательную роль. Для количественного описания адгезионного взаимодействия твердых тел используется целый ряд моделей (например [1–9]). В основе адгезии, как физического явления, лежат дальнодействующие потенциальные взаимодействия частиц материалов твердых тел [9–13]. В рамках механики твердого тела модели адгезии учитывают это обстоятельство различными способами. Во всех случаях зависимость характеристик адгезии от свойств материалов определяется набором параметров, который надо найти экспериментально или теоретически (например [14]).

Твердый материал под влиянием внешних воздействий в различных условиях проявляет различные свойства. Между этими свойствами существует взаимосвязь. Она обусловлена атомно-молекулярным взаимодействием.

Взаимосвязь различных свойств должна выражаться во взаимосвязи групп параметров, соответствующих их проявлениям. Например, известно [8, 10, 15–18], что для упругих материалов модули Юнга и сдвига – с одной стороны, и характеристики адгезионного взаимодействия – с другой стороны, вычисляются через изменение потенциальной энергии взаимодействия тел или их атомов. Потенциальная энергия и ее изменения рассчитываются с помощью тех или иных модельных потенциалов. Для получения информации об их параметрах из эксперимента в физике применяется способ расчета измеряемой характеристики через неизвестные параметры модельного потенциала [18]. При этом предполагается, что измеряемое свойство (явно или неявно) связано с величиной межмолекулярного потенциала, а, следовательно, может быть представлено как функция его параметров. Для реальных материалов с их сложными химическим составом и атомно-молекулярной структурой сделать это трудно, хотя выражение одних макропараметров через другие можно пытаться реализовать методом частиц [19, 20].

В данной работе предпринята попытка установить связь между параметрами Ламэ с энергией $\Delta \,{{f}_{{\left( {12} \right)}}}$ адгезии вдоль поверхности ${{A}_{{\left( {12} \right)}}}$ двух тел ${{B}_{{\left( 1 \right)}}}$ и ${{B}_{{(2)}}}$ с помощью нелокальной модели сплошных упругих материалов. В качестве иллюстрации выявленной связи показано, как установить, возможна или нет адгезия, зная механические свойства вступивших в контакт материалов.

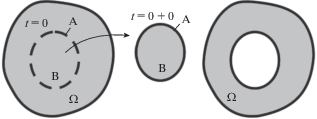
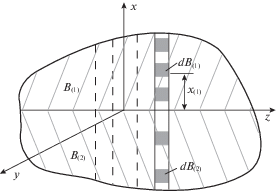
1. Основные положения о взаимодействующих телах. Нелокальная модель сплошной упругой среды. Для построения нелокальной модели вводится ряд допущений. Допускается, что сплошные тела B получены сначала мысленным, с помощью поверхности $A$, в момент времени $t = 0$, а затем реальным, в момент $t = 0 + 0$, мгновенным выделением из бесконечно протяженных, однородных, изотропных сплошных упругих сред Ω с конфигурацией ${{\Lambda }_{\infty }}$, температурой Θ. Конфигурация ${{\Lambda }_{0}}$ тела B при мысленном выделении является отсчетной. Допущение введено для исключения влияния границ на свойства тел $B$ в отсчетном состоянии (рис. 1).

Тело B после выделения ввиду изменения окружающих условий (удаление воздействия со стороны $\Omega {\backslash }B$, контакт с другим телом и т.д.), приобретает текущую конфигурацию Λ, которая с течением времени t может меняться.

Распределения температур Θ и плотностей ρ материала как в Ω, так и в B в любой момент времени t считаются равномерными, значения Θ и ρ известны. Для упрощения рассуждений допускается, что в актуальной (текущей) конфигурации $\Lambda $ тело B находится в равновесии.

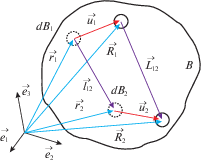
Центры инерции частиц dB произвольного тела B в отсчетной конфигурации ${{\Lambda }_{0}}$ имеют радиус-векторы $\vec {r} = {{x}_{j}}{{\vec {e}}_{j}}$, $\,{{\vec {e}}_{j}}$ ($j = 1,2,3$) – ортонормированный базис. Положение частицы $d{{B}_{2}} \subset B$ относительно другой частицы $d{{B}_{1}} \equiv dB \subset B$ определяется вектором ${{\vec {l}}_{2}}$ = ${{\vec {r}}_{2}} - {{\vec {r}}_{1}}$ ≡ ${{\vec {r}}_{2}} - \vec {r}$. Его длина равна ${{l}_{2}} = \left| {{{{\vec {l}}}_{2}}} \right|$ = $\left| {{{{\vec {r}}}_{2}} - \vec {r}} \right|$. При движении тела B его частицы dB приобретают новые положения (рис. 2). Они характеризуются радиус-вектором $\vec {R}$ = ${{X}_{j}}{{\vec {e}}_{j}}$ и вектором перемещения $\vec {u}\, = \vec {R} - \vec {r}$. Вектор перемещений определен с точностью до жестких движений.

Положение частицы $d{{B}_{1}} \equiv dB$ относительно частицы $d{{B}_{j}} \equiv dB$, $j \geqslant 2$ в текущей конфигурации определяться вектором

с длиной ${{L}_{j}} = \left| {{{{\vec {L}}}_{j}}} \right| = \left| {{{{\vec {R}}}_{j}} - \vec {R}} \right|$. Здесь $\Delta {{\vec {u}}_{{1j}}} \equiv \Delta {{\vec {u}}_{j}} = {{\vec {u}}_{j}} - \vec {u}$ – смещение частицы $d{{B}_{j}}$ относительно частицы $d{{B}_{1}} \equiv dB$ (рис. 2).

В данной работе рассматриваются только малые деформации, когда

Здесь $\left\| {{{\nabla }^{n}}\vec {u}} \right\|$ – сумма квадратов компонент $n$-го ($n = 1,\;2$) градиента вектора $\vec {u}$; $D$ – характерный размер области, где необходим учет ${{\nabla }^{2}}\vec {u}$.

В приближении малых деформаций (1.1) допускается представление вектора $\Delta \vec {u}$ в виде суммы

В рамках (1.1) и (1.2) $\nabla = d{\text{/}}d\vec {r} = d{\text{/}}d\vec {l}$ – оператор Гамильтона, ${{\nabla }^{2}} = \nabla \nabla $ и ${{\vec {l}}^{2}} = \vec {l}{\kern 1pt} \vec {l}$ – внешние произведения.

Считается, что тело $B$ имеет внутреннюю потенциальную энергию $W$

Для упрощения рассуждений далее для интегральных сумм рассматриваются только такие $N$ разбиения тела $B$ на элементарные части $\Delta B_{n}^{N}$, при которых объемы $\Delta V_{n}^{N}$ равны между собой. При этом $\Delta V_{n}^{N}$ = $\Delta {{V}^{N}} = V{\text{/}}N$, где $V$ – объем области $\Lambda $, занимаемой телом $B$.

Энергии $W_{n}^{N} = w_{n}^{N}\Delta V_{n}^{N}$ частиц $\Delta B_{n}^{N}$ рассматриваются как потенциальные энергии взаимодействия материальных точек $b_{n}^{N}$ из некоторого дискретного тела ${{\hat {B}}^{N}} = \left\{ {\,b_{n}^{N}} \right\}$ со всеми другими точками $b_{m}^{N} \in {{\hat {B}}^{N}}$ ($m \ne n$) того же тела. При этом энергия $W$ тела $B$ является потенциальной энергии ${{W}^{N}}$ нелокального взаимодействия его частей $\Delta B_{n}^{N}$.

Материальные точки $b_{n}^{N}$ находятся в точках $\vec {R}_{n}^{N}$ – в текущей конфигурации, и $\vec {r}_{n}^{N}$ – в отсчетной конфигурации, занимаемых центрами инерции частиц $\Delta B_{n}^{N}$. Для дискретного тела ${{\hat {B}}^{N}} = \left\{ {\,b_{n}^{N}} \right\}$ его потенциальная энергия ${{W}^{N}}$, равная энергии $W$ сплошного тела $B$ (${{W}^{N}} = W$), является функцией положения точек $b_{n}^{N}$: ${{W}^{N}} = {{W}^{N}}(\vec {R}_{1}^{N}$, …, $\vec {R}_{N}^{N})$. В соответствии с [21], для этой функции справедливо представление в виде суммы всех одно-, двух-, трех и так далее точечных функций. Рассматриваются только парные и тройные взаимодействия. Поэтому

Здесь $W_{i}^{N}$ – потенциальная энергия одной из частиц $b_{i}^{N}$ со всеми другими частицами системы $\left\{ {b_{n}^{N}} \right\}$, $W_{{ij}}^{N}$ – потенциал взаимодействия пары частиц $b_{i}^{N}$и $b_{j}^{N}$, $W_{{ijk}}^{N}$ – потенциал взаимодействия тройки частиц $b_{i}^{N}$, $b_{j}^{N}$ и $b_{k}^{N}$.

Потенциалы $W_{{ij}}^{N}$ и $W_{{ijk}}^{N}$ (как и $W_{n}^{N}$) считаются пропорциональными объемам взаимодействующих частиц сплошного тела

Принято, что коэффициенты $\Phi _{{}}^{{N(2)}}$ и $\Phi _{{}}^{{N(3)}}$ (потенциалы) зависят только от межчастичных расстояний $l$ – расстояния между парой частиц с любыми номерами в отсчетной конфигурации, и параметров $l_{0}^{N}$ = $\sqrt[3]{{\Delta {{V}^{N}}}}$ = $\sqrt[3]{{V{\text{/}}N}}$, ${{\beta }^{{(2)}}}$ и $\Phi _{0}^{{(2)}}$. Считаются справедливыми равенства

При ${{\xi }_{0}} = {{\beta }^{{(2)}}}{{l}_{0}} \to 0$ функция ${{\varphi }^{{(2)}}}({{\xi }^{{(2)}}})$ имеет вид:

Для непрерывных и дифференцируемых необходимое число раз функции $\varphi _{{}}^{{(21)}}\left( \xi \right)$ и $\varphi _{{}}^{{(22)}}\left( \xi \right)$ справедливы равенства

Эти выражения соответствуют требованию устойчивой дискретной системы, свидетельствующей о наличии в ней отталкивательной “сердцевины” и стремящимся к нулю “хвоста”, описывающим притяжение [21, 22]. Гарантией устойчивости [21] является положительность и ограниченность суммы всех парных взаимодействий частиц. Это получится, если

Здесь $\Lambda _{1}^{N}$ – область вокруг одной из материальных точек $b_{1}^{N}$, которая взаимодействует с другими точками $b_{2}^{N}$ системы $\left\{ {b_{n}^{N}} \right\}$ с характерным межчастичным расстоянием ${{l}_{0}} \equiv l_{0}^{N}$; ${{\varphi }^{{(22)}}}(\xi )$ = ${{e}^{{ - 2(\xi - {{\xi }_{0}})}}}$ – $2{{e}^{{ - (\xi - {{\xi }_{0}})}}}$ (${{\xi }_{0}} < \xi < + \infty $) – потенциал Морзе [18]; функция $\varphi _{{}}^{{(21)}}\left( \xi \right)$ ($0 \leqslant \xi \leqslant {{\xi }_{0}}$) может быть любой, удовлетворяющей перечисленным свойствам.

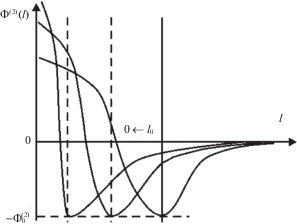
При ${{l}_{0}} \to 0$ ($N \to \infty $) область $\Lambda _{1}^{N}$ стягивается к точке – центру инерции частицы $dB$. Зависимость $\Phi _{{}}^{{(2)}}\left( l \right)$ становится похожей на дельта-функцию Дирака (рис. 3). Получающееся при этом равенство

является условием отсутствия взаимного проникания бесконечно малых частиц сплошного материала при их неограниченном сближении (рис. 3).

Существует целый ряд способов описания тройных потенциальных взаимодействий (например [23–26]). В данной работе трехчастичный потенциал выбирается в виде, который учитывает, что (следующие за парными в схеме Майера [27]) одна частица $dB \equiv d{{B}_{1}}$ взаимодействует сразу с двумя другими не взаимодействующими между собой частицами $d{{B}_{2}}$ и $d{{B}_{3}}$

Здесь $\xi _{j}^{{(3)}} = {{\beta }^{{(3)}}}{{l}_{{j\,}}}$, $0 < \xi _{j}^{{(3)}} < \infty $; ${{\beta }^{{(3)}}}$ и $\Phi _{0}^{{(3)}}$ – параметры, характеризующие механические свойства материала.

Трехчастичные взаимодействия влияют на характер потенциальных взаимодействий [23, 28, 29]. При их учете необходима проверка устойчивости систем частиц. Для дискретной системы $\left\{ {b_{n}^{N}} \right\}$ можно использовать методы статистической механики [21]. Для сплошной среды условием устойчивости является положительная определенность квадратичной формы для энергии малых упругих деформаций линейной теории упругости, полученной на основании рассматриваемой нелокальной модели.

При ${{l}_{0}} \to 0$ ($N \to \infty $) выражение (1.4), записанное для дискретных систем, преобразуется в свой аналог для сплошных сред. В текущей конфигурации $\Lambda $ тела $B$ оно приобретают вид

Здесь $Y_{{}}^{{(2)}} = {{\beta }^{{(2)}}}L$, $L$ – расстояние между двумя произвольными частицами, $Y_{j}^{{(3)}}$ = = β⁽³⁾L_j ($j = 2,\,3$), ${{L}_{j}}$ – расстояние между частицей $dB \equiv d{{B}_{1}}$ и частицами $d{{B}_{2}}$ и $d{{B}_{3}}$.

Выражения (1.13) и (1.14) позволяют вычислить потенциальную энергию всего твердого деформируемого тела B, а также объемную плотность ее распределения путем суммирования потенциальных энергий всех пар и троек бесконечно его малых частиц как в отсчетной конфигурации, когда $w = {{w}_{0}} = w(\vec {r})$, так и в текущей конфигурации. Это используется далее для построения локальных моделей тела B.

2. Локальные модели. Связь нелокальных и локальных характеристик механических свойств. Для выбора модели, в рамках которой предлагается определять характеристики механических свойств упругих материалов на основании экспериментальных данных, сначала вводятся характеристики кинематики произвольной бесконечно малой частицы $dB \subset B$ [30]. Используются первый $\nabla \vec {u}$ и второй ${{\nabla }^{2}}\vec {u}$ градиенты ее перемещений. Искомая модель предполагается линейной. В ее рамках изменение объемной плотности $\Delta w$ потенциальной энергии, вызванное внешними воздействиями, является полиномом второй степени относительно обобщенных перемещений $\nabla \vec {u}$ и ${{\nabla }^{2}}\vec {u}$ частицы $dB \subset B$, а обобщенные силы – тензоры внутренних напряжений ${{P}^{{(1)}}} = \partial w{\text{/}}\partial (\nabla \vec {u})$ и ${{P}^{{(2)}}} = \partial w{\text{/}}\partial ({{\nabla }^{2}}\vec {u})$, которые совершают работу на вариациях $\nabla \vec {u}$ и ${{\nabla }^{2}}\vec {u}$, – полиномы их первой степени. Коэффициенты этих полиномов должны быть определены экспериментально. Вместе с тем, те же коэффициенты с помощью допущений (1.1) и (1.2) выражаются через параметры ($\Phi _{0}^{{(2)}}$, ${{\beta }^{{(2)}}}$, $\Phi _{0}^{{(3)}}$, ${{\beta }^{{(3)}}}$) потенциалов ${{\Phi }^{{(2)}}}$ и ${{\Phi }^{{(3)}}}$ следующими действиями.

В текущей конфигурации используются потенциалы ${{\Phi }^{{(2)}}} = \Phi _{0}^{{(2)}}{{\varphi }^{{(2)}}}({{\beta }^{{(2)}}}L)$ и ${{\Phi }^{{(2)}}} = \Phi _{0}^{{(3)}}{{\varphi }^{{(3)}}}({{\beta }^{{(3)}}}{{L}_{2}}$, ${{\beta }^{{(3)}}}{{L}_{3}})$. Они получаются путем замены в функциях ${{\varphi }^{{(2)}}}({{\beta }^{{(2)}}}l)$ и ${{\varphi }^{{(3)}}}({{\beta }^{{(3)}}}{{l}_{2}},\,{{\beta }^{{(3)}}}{{l}_{3}})$, определенных равенствами (1.7)–(1.9), (1.12), аргументов $l \equiv {{l}_{2}}$ и ${{l}_{3}}$ на $L \equiv {{L}_{2}} = \left| {{{{\vec {L}}}_{2}}} \right|$ и ${{L}_{3}} = \left| {{{{\vec {L}}}_{3}}} \right|$, в которых ${{\vec {L}}_{j}} = {{\vec {l}}_{j}} + \Delta {{\vec {u}}_{j}}$. Для $\Delta {{\vec {u}}_{j}}$ справедлива оценка (1.1). Поэтому зависимости ${{\varphi }^{{(2)}}}(\vec {L})$ и ${{\varphi }^{{(3)}}}({{\vec {L}}_{2}},\,{{\vec {L}}_{3}})$ представлены полиномами второй внешней степени относительно $\Delta \vec {u} \equiv \Delta {{\vec {u}}_{2}}$ и $\Delta {{\vec {u}}_{3}}$. Их коэффициенты – это коэффициенты разложения ${{\varphi }^{{(2)}}}(\vec {L})$ и ${{\varphi }^{{(3)}}}({{\vec {L}}_{2}},\,{{\vec {L}}_{3}})$ по внешним степеням $\Delta \vec {u} \equiv \Delta {{\vec {u}}_{2}}$ и $\Delta \,{{\vec {u}}_{3}}$ в окрестности ${{\vec {L}}_{j}} = {{\vec {l}}_{j}}$. Вследствие этого выражение (1.14) также окажется полиномом второй степени относительно $\Delta {{\vec {u}}_{j}}$ (представлено в [31]). Подстановка в полученное выражение вектора $\Delta {{\vec {u}}_{j}}$ в виде полинома (1.2) второй степени по внешним степеням вектора ${{\vec {l}}_{j}}$ приводит его к виду, который соответствует представлению о линейной модели упругого материала второго порядка.

Тензоры напряжений ${{P}^{{(1)}}}$ и ${{P}^{{(2)}}}$ при этом определяются равенством

Коэффициенты полиномов (2.1) и (2.2) выражаются через параметры ($\Phi _{0}^{{(2)}}$, ${{\beta }^{{(2)}}}$, $\Phi _{0}^{{(3)}}$, ${{\beta }^{{(3)}}}$) путем интегрирования соответствующих выражений, содержащих первый и второй градиенты потенциалов ${{\Phi }^{{(2)}}} = \Phi _{0}^{{(2)}}{{\varphi }^{{(2)}}}({{\beta }^{{(2)}}}l)$ и ${{\Phi }^{{(2)}}} = \Phi _{0}^{{(3)}}{{\varphi }^{{(3)}}}({{\beta }^{{(3)}}}{{l}_{2}}$, ${{\beta }^{{(3)}}}{{l}_{3}})$ по области, занимаемой телом $B$ в отсчетной конфигурации ${{\Lambda }_{0}}$

Здесь ${{\nabla }_{j}} \equiv d \ldots {\text{/}}d{{\vec {l}}_{j}} = \nabla $, ${{P}^{{0\left( n \right)}}}$ и ${{C}^{{\left( {m,n} \right)}}}$ – тензоры начальных напряжений и характеристик механических свойств.

Для бесконечно протяженного тела $\Omega $, когда влиянием близости границ области интегрирования на их значения можно пренебречь, тензоры $P_{{}}^{{0(2)}}$, ${{C}^{{(1,2)}}}$ и ${{C}^{{(2,1)}}}$ обращаются в нуль. Выражение (2.1) приобретает вид $\Delta w = \Delta {\text{*}}w$ + $P_{{}}^{{0(1)}} \cdot \cdot {{\left( {\nabla \vec {u}} \right)}^{T}}$, характерный для модели Джеремилло [30], в рамках которой прирост $\Delta {\text{*}}w$ величины $\Delta w$ определяется равенствами:

При этом получаются равенства матриц компонент соответствующих тензоров: $C_{{ijkm}}^{{J(1,1)}}$ = $C_{{ijkm}}^{{(1,1)}}$, $C_{{ijkmnl}}^{{J(2,2)}}$ = $C_{{ijkmnl}}^{{(2,2)}}$. В этих равенствах правые части определяются выражениями (2.4) (при условии ${{C}^{{(1,2)}}} = {{C}^{{(2,1)}}} = 0$), зависящими от ($\Phi _{0}^{{(2)}}$, ${{\beta }^{{(2)}}}$, $\Phi _{0}^{{(3)}}$, ${{\beta }^{{(3)}}}$), а левые части – зависящими от ($\lambda $, $\mu $, $С_{1}^{J}$, $С_{2}^{J}$) выражениями (2.7) и (2.8). В каждой из матриц линейно независимыми компонентами оказываются только две. Так что, приравняв выбранные пары соответственных компонент тензоров $C_{{ijkm}}^{{J(1,1)}}$ и $C_{{ijkm}}^{{(1,1)}}$, $C_{{ijkmnl}}^{{J(2,2)}}$ и $C_{{ijkmnl}}^{{(2,2)}}$, можно построить систему четырех уравнений для неизвестных ($\Phi _{0}^{{(2)}}$, ${{\beta }^{{(2)}}}$, $\Phi _{0}^{{(3)}}$, ${{\beta }^{{(3)}}}$), считая ($\lambda $, $\mu $, $С_{1}^{J}$, $С_{2}^{J}$) известными.

Из равенств $C_{{1212}}^{{(1,1)}} = C_{{1212}}^{{J(1,1)}}$ и $C_{{1122}}^{{(1,1)}} = C_{{1122}}^{{J(1,1)}}$ следует система уравнений:

где неизвестными величинами являются

Коэффициенты ${{\Psi }_{{ij}}}$ ($i{\text{,}}j = 1,2$) определяются с помощью расчета в сферической системе координат необходимых компонент тензора $C_{{}}^{{(1,1)}}$ [32].

Видно, что учет только парных взаимодействий приводит к условию: $\lambda = \mu $.

Компоненты $С_{{^{{111111}}}}^{{(2{\text{,2)}}}}$ и $С_{{^{{112211}}}}^{{(2{\text{,2)}}}}$ связаны с параметрами ($\Phi _{0}^{{(2)}}$, ${{\beta }^{{(2)}}}$, $\Phi _{0}^{{(3)}}$, ${{\beta }^{{(3)}}}$) соотношениями

Здесь неизвестными являются ($1{\text{/}}{{\beta }^{{(2)2}}}$) и ($1{\text{/}}{{\beta }^{{(3)2}}}$). Величины ${{Z}^{{(2)}}}$ и ${{Z}^{{(3)}}}$ определены при решении системы (2.9). Коэффициенты ${{\Gamma }_{{km}}}$ являются результатом вычислений в сферической системе координат с началом в центре инерции частицы $dB \equiv d{{B}_{1}}$ компонент тензора $С_{{}}^{{(2{\text{,2)}}}}$

В то же время компоненты $С_{{^{{111111}}}}^{{J(2{\text{,2)}}}}$ и $С_{{^{{112211}}}}^{{J(2{\text{,2)}}}}$ (на основании (2.8)) связаны с $С_{1}^{J}$ и $С_{2}^{J}$ равенствами $С_{{^{{111111}}}}^{{J(2{\text{,2)}}}}$ = $9С_{1}^{J}$ + $6С_{2}^{{J(2{\text{,2)}}}}$, $С_{{^{{112211}}}}^{{J(2{\text{,2)}}}}$ = $С_{1}^{J}$ + $2С_{2}^{{J(2{\text{,2)}}}}$. Следствием этого и (2.13) является приведение системы (2.12) к виду

Очевидно, что система имеет решение лишь тогда, когда $С_{1}^{J} = С_{2}^{J} = С_{{}}^{J}$ в предположении о том, что ${{\beta }^{{(2)}}} = {{\beta }^{{(3)}}} = \beta $. Значит, нелокальная модель соответствует такому варианту модели Джеремилло, в котором неклассические свойства материала характеризуются только одним параметром. При этом совпадают параметры ${{\beta }^{{(2)}}}$ и ${{\beta }^{{(3)}}}$, характеризующие “скорость” изменения потенциалов парного и тройного взаимодействий.

Предполагается, что $\lambda $, μ и ${{С}^{J}}$ определяются на основании данных экспериментов по определению классических механических свойств однородных, изотропных, линейно упругих материалов, а также экспериментов по описанию нелинейности акустических ветвей дисперсионного закона для плоских продольных волн высокой частоты, в однородных, изотропных, линейно упругих материалах [32, 33].

Результатом проделанных рассуждений является аналитическая связь параметров $\lambda $, μ и ${{С}^{J}}$ локальной модели с параметрами $\Phi _{0}^{{(2)}}$, $\Phi _{0}^{{(3)}}$ и $\beta $ нелокальной модели того же материала. Видна также необходимость использования второго градиента перемещений.

3. Метод определения параметров межчастичных потенциалов из разных материалов. Явление адгезии связано с нелокальным потенциальным взаимодействием частиц из разных материалов. Вместе с тем изложенная выше возможность определения параметров межчастичных потенциалов взаимодействия через значения классических характеристик локального упругого состояния относится только к однородным по своим свойствам материалам. Для определения параметров потенциалов взаимодействия разных материалов через характеристики каждого из них проведены следующие рассуждения.

Предполагается, что независимо от того, рассматриваются взаимопроникающие материалы или каждый из этих материалов сконцентрирован в двух разных, не имеющих общих частей объемах, частицы этих материалов взаимодействуют между собой по одним и тем же законам, не зависящим от того, каким материалом окружены соответствующая пара или тройка. Значит вид потенциалов парных и тройных взаимодействий в обоих случаях один и тот же. Характеристики твердого раствора, создаваемого взаимопроникающими материалами, могут быть измерены или рассчитаны, например, по модели Рейсса. Это дает возможность определить характеристики потенциалов взаимодействия частиц разных материалов.

Рассматривается материал, являющийся объединением двух взаимно проникающих сред (их смесь [34]), моделирующих реальные материалы тел ${{B}_{{(1)}}}$ и ${{B}_{{(2)}}}$. Пусть ${{B}_{{(s)}}} = {{B}_{{(1)}}} \cup {{B}_{{(2)}}}$ – тело, получившееся за счет взаимного проникновения тел ${{B}_{{(1)}}}$ и ${{B}_{{(2)}}}$; ${{\Lambda }_{{(1)}}} = {{\Lambda }_{{(2)}}} = {{\Lambda }_{{(s)}}}$ – общая конфигурация ${{B}_{{(s)}}}$, ${{B}_{{(1)}}}$ и ${{B}_{{(2)}}}$. Пусть $d{{B}_{s}}$ = $d{{B}_{{(1)}}} \cup d{{B}_{{(2)}}}$ – частица рассматриваемого объединенного тела. Она имеет объем $d{{V}_{{(s)}}}$. Часть его $d{{V}_{{(1)}}} = {{c}_{{(1)}}}d{{V}_{s}}$ занимает материал частицы $d{{B}_{{(1)}}}$, а часть $d{{V}_{{(2)}}} = {{c}_{{(2)}}}d{{V}_{{(s)}}}$ – материал частицы $d{{B}_{{(2)}}}$. Здесь ${{c}_{{(1)}}}$ и ${{c}_{{(2)}}}$ – объемные концентрации материалов ${{B}_{{(1)}}}$ и ${{B}_{{(2)}}}$ в материале ${{B}_{{(s)}}}$, ${{c}_{{(1)}}} + {{c}_{{(2)}}} = 1$.

Материал тела ${{B}_{{(s)}}}$ считается однородным, изотропным, линейно упругим. Вид потенциалов парных и тройных межчастичных взаимодействий в материале ${{B}_{{(s)}}}$ описывается зависимостями (1.6)–(1.12). При любых ${{c}_{{(1)}}}$ и ${{c}_{{(2)}}}$ справедливы установленные для таких материалов связи между группами параметров (${{\lambda }_{{(s)}}}$, ${{\mu }_{{(s)}}}$, $С_{{(s)}}^{J}$) и ($\Phi _{{0(s)}}^{{(2)}}$, $\Phi _{{0(s)}}^{{(3)}}$, ${{\beta }_{{(s)}}}$). Концентрационные зависимости для модулей Юнга ${{E}_{{(s)}}}$ и сдвига ${{G}_{{(s)}}}$ этого материала определяются экспериментально или теоретически. Один из вариантов соответствует модели Рейсса.

Допускается, что частицы $d{{B}_{{(1)}}}$ и $d{{B}_{{(2)}}}$, входящие в состав частиц $d{{B}_{{(s)}}}$, испытывают адгезионное взаимодействие. Оно характеризуется потенциалами

Здесь греческие буквы в скобках нижнего индекса является перечнем номеров взаимодействующих материалов – первого или второго: $\alpha $, $\beta $, $\gamma = 1,2$, при этом, хотя бы два номера не совпадают; цифры вне скобок – номера взаимодействующих частиц, так что ${{L}_{{\,(12)\,j}}}$ – расстояние между частицами $d{{B}_{{(1)}}} \equiv d{{B}_{{(1)1}}}$ и $d{{B}_{{(2)j}}}$ ($j = 2,3$) в текущей конфигурации.

Неизвестные параметры ($\Phi _{{0(12)}}^{{(2)}}$, $\Phi _{{0(112)}}^{{(3)}}$, $\Phi _{{0(122)}}^{{(3)}}$, $\beta _{{(12)}}^{{}}$) потенциалов (3.2) выражены через параметры ($\Phi _{{0(s)}}^{{(2)}}$, $\beta _{{(s)}}^{{}}$, $\Phi _{{0(s)}}^{{(3)}}$).

Потенциальная энергия взаимодействия двух бесконечно близких друг к другу частиц $d{{B}_{{(s)j}}}$ ($j = 1,\;2$), имеющих объемы $d{{V}_{{(s)j}}}$ = $d{{V}_{{(\alpha )j}}} + d{{V}_{{(\beta )j}}}$ = ${{с}_{{(\alpha )}}}d{{V}_{{(s)j}}}$ + ${{c}_{{(\beta )}}}d{{V}_{{(s)j}}}$, с одной стороны, равна $\Phi _{{(s)0}}^{{(2)}}d{{V}_{{(s)1}}}d{{V}_{{(s)2}}}$. С другой стороны эта величина равна потенциалу взаимодействия частиц однородных материалов, входящих в состав частицы твердого раствора$\sum\nolimits_{\alpha ,\beta = 1}^2 {\Phi _{{(\alpha \beta )0}}^{{(2)}}d{{V}_{{(\alpha )1}}}d{{V}_{{(\beta )2}}}} $. Поэтому справедливо равенство

Для трех бесконечно близких друг к другу частиц $d{{B}_{{(s)p}}}$ ($p = 1,2,3$) аналогично можно получить:

Вычисление объемной плотности потенциальной энергии всех парных и тройных взаимодействий произвольной частицы $d{{B}_{{(s)}}} \equiv d{{B}_{{(s)1}}}$ с ее окружением внутри ${{\Omega }_{{(s)}}}$ приводит к равенствам

Один из возможных способов решения системы (3.3)–(3.6) опирается на аппроксимацию концентрационных зависимостей для ($\Phi _{{({\text{s}})0}}^{{{\text{(2)}}}}$, $\Phi _{{({\text{s}})0}}^{{{\text{(2)}}}}{\text{/}}\beta _{{{\text{(s)}}}}^{{\text{3}}}$) и ($\Phi _{{({\text{s}})0}}^{{{\text{(3)}}}}$, $\Phi _{{({\text{s}})0}}^{{{\text{(3)}}}}{\text{/}}\beta _{{{\text{(s)}}}}^{{\text{6}}}$), полученных с использованием выражений (2.9), (2.14) и (3.1), полиномами для (3.5) второй и для (3.6) третьей степени относительно концентраций ${{с}_{{(1)}}}$ и ${{с}_{{(2)}}}$.

4. Адгезионное взаимодействие двух тел. Одной из характеристик адгезионного взаимодействия твердых тел ${{B}_{{\left( 1 \right)}}}$ и ${{B}_{{\left( 2 \right)}}}$ является энергия адгезии. Суммарная энергия адгезии равна изменению их свободной энергии $\Delta {{f}_{{\left( {12} \right)}}}$, произошедшему в изотермическом обратимом процессе вступления их в адгезионное взаимодействие. Если ${{B}_{{\left( 1 \right)}}}$ и ${{B}_{{\left( 2 \right)}}}$ полубесконечны, ограничены параллельными плоскостями, то говорят об энергии адгезии ${{F}_{a}}$, приходящейся на единицу площади их противоположных участков [35]. При отсутствии контакта говорят о зависимости энергии адгезии от расстояния между ${{B}_{{\left( 1 \right)}}}$ и ${{B}_{{\left( 2 \right)}}}$ (например [36]). Предлагается способ расчета энергии адгезии, который удобно использовать в случаях, когда участки поверхностей${{A}_{{\left( 1 \right)}}}$ и ${{A}_{{\left( 2 \right)}}}$, вдоль которых тела ${{B}_{{\left( 1 \right)}}}$ и ${{B}_{{\left( 2 \right)}}}$ вступают в адгезионный контакт, конгруэнтны, так что добиваться этой конгруэнтности путем соответствующего деформирования не требуется.

Допускается, что тела ${{B}_{{\left( 1 \right)}}}$ и ${{B}_{{\left( 2 \right)}}}$ выделяются мысленно в бесконечно протяженных средах ${{\Omega }_{{\left( 1 \right)}}}$ и ${{\Omega }_{{\left( 2 \right)}}}$, имеющих одинаковые температуры ${{\Theta }_{{\left( 1 \right)}}}$ и ${{\Theta }_{{\left( 2 \right)}}}$, поверхностями ${{A}_{{\left( 1 \right)}}}$ и ${{A}_{{\left( 2 \right)}}}$. В момент $t = 0$ они выделяются реально и мгновенно. Также одновременно в момент времени $t = 0 + 0$ они вступают вдоль поверхности ${{A}_{{\left( {12} \right)}}}$ в адгезионный контакт. Это допущение равносильно мгновенной замене тела ${{С}_{{\left( 1 \right)}}} = {{\Omega }_{{(1)}}}{\backslash }{{B}_{{(1)}}}$, контактирующей с мысленно выделенным телом ${{B}_{{\left( 1 \right)}}}$ вдоль ${{A}_{{\left( 1 \right)}}}$, состоящим из другого материала телом ${{B}_{{\left( 2 \right)}}}$, контактирующим с ${{B}_{{\left( 1 \right)}}}$ вдоль части ${{A}_{{\left( {12} \right)}}}$ поверхности ${{A}_{{\left( 1 \right)}}}$.

Мгновенность такой замены сохраняет в момент $t = 0 + 0$ положения всех частиц $d{{B}_{{\left( 1 \right)}}}$ и $d{{B}_{2}}$ относительно центров инерции тел ${{B}_{{\left( 1 \right)}}}$ и ${{B}_{{\left( 2 \right)}}}$. Однако при этом в каждом из этих тел нарушается равновесие и начинается их деформирование в общем случае сопровождаемое тепловыми изменениями. Если ими пренебречь, а процесс образования тела $B = {{B}_{{\left( 1 \right)}}} \cup {{B}_{{(2)}}}$ и последующего деформирования до установления равновесия будет адиабатическим, то возникшее в момент $t = 0 + 0$ изменение $\Delta \,{{f}_{{(12)}}}$ свободной энергии тел ${{B}_{{\left( 1 \right)}}}$ и ${{B}_{{\left( 2 \right)}}}$ с течением времени меняться не будет. Следовательно, значение $\Delta {{f}_{{(12)}}}$, вычисленное в момент $t = 0 + 0$ с использованием расчета нелокальных потенциальных взаимодействий для отсчетных конфигураций тел ${{B}_{{\left( 1 \right)}}}$ и ${{B}_{{\left( 2 \right)}}}$, будет равно энергии упругих деформаций, возникших в объединенном теле ${{B}_{{(12)}}} = {{B}_{{\left( 1 \right)}}} \cup {{B}_{{(2)}}}$ к моменту перехода его в равновесное состояние.

Пусть ${{W}_{{\left( \alpha \right)}}}$ и ${{W}_{{\left( {12} \right)}}}$потенциальные энергии взаимодействия частиц тел ${{B}_{{\left( \alpha \right)}}}$ (c номерами $\alpha = 1,2$) и ${{B}_{{(12)}}}$ соответственно. Тогда равное суммарной энергии адгезии изменение свободной энергии (в соответствии с ее определением [35])

где ${{f}_{{(12)}}}$, ${{f}_{{(1)}}}$ и ${{f}_{{(2)}}}$ соответственно свободные энергии объединенного тела ${{B}_{{(12)}}}$ и его составляющих ${{B}_{{(1)}}}$ и ${{B}_{{(2)}}}$ до вступления в адгезионный контакт.

Если это равенство записывается для момента времени $t = 0 + 0$, то для проведения конкретных расчетов в соответствии с изложенными в разделе 1 допущениями можно получить следующее выражение [37]

Сказанное свидетельствует о том, что при сделанных допущениях об изотермичности и обратимости адгезионного взаимодействия тел ${{B}_{{\left( 1 \right)}}}$ и ${{B}_{{\left( 2 \right)}}}$ энергия этого взаимодействия при их фиксированной конфигурации зависит от потенциалов межчастичных взаимодействий, параметры которых, как следует из результатов первого и второго разделов, определяются механическими свойствами материалов ${{B}_{{\left( \alpha \right)}}}$ – параметрами ${{\lambda }_{{(\alpha )}}}$, ${{\mu }_{{(\alpha )}}}$, $С_{{(\alpha )}}^{J}$. Очевидно, что при одинаковых конфигурациях тел ${{B}_{{\left( 1 \right)}}}$ и ${{B}_{{\left( 2 \right)}}}$ и их взаимной ориентации, но разных их материалах, то есть разных наборах значений ${{\lambda }_{{(\alpha )}}}$, ${{\mu }_{{(\alpha )}}}$, $С_{{(\alpha )}}^{J}$ энергия адгезии, как и ее распределение, окажутся разными.

Приводимый далее пример иллюстрирует использование оценки потенциальной энергии парных и тройных взаимодействий, соответствующих моменту $t = 0 + 0$, на основании выражения (4.2).

5. Пример оценки влияния механических свойств материалов на их адгезионные свойства. Для исключения “схватывания” скользящих друг относительно друга деталей различных устройств используются твердые смазки. Актуальным является теоретически обоснованные рекомендации по выбору их материала на основании информации о механических свойствах трущихся материалов. Предлагаемый пример иллюстрирует возможность получения такой рекомендации в рамках предложенной модели адгезии.

Вывод о наличии или отсутствии адгезии строится, как и в теории взаимодействий Ван-дер-Ваальса [23], на результатах сопоставления величины и знака сил парных и тройных взаимодействий.

Выражение (3.2) свидетельствует о том, что воздействие одного из тел на другое тело является суммой двух видов воздействий слагающих их частиц. Одно из них обусловлено парными взаимодействиями, а другое – тройными. На примере анализа взаимодействия тел ${{B}_{{(1)}}}{\kern 1pt} $: $0 < x$ ≡ ${{x}_{{(1)}}} < + \infty $, ${{B}_{{(2)}}}{\kern 1pt} $: $ - \infty < {{x}_{{(2)}}} < 0$ (рис. 4) предлагается оценка роли каждого из видов взаимодействия тел ${{B}_{{(1)}}}$ и ${{B}_{{(2)}}}$ в ответе на вопрос о наличии или отсутствии адгезии между ними в зависимости от их механических свойств.

Для упрощения математических рассуждений считается, что силы адгезии со стороны тела ${{B}_{{(2)}}}$ на частицы ${\text{d}}{{B}_{{(1)}}} \subset {{B}_{{(1)}}}$ ориентированы перпендикулярно плоскости адгезионного контакта ${{A}_{{(12)}}}{\kern 1pt} $: $x \equiv {{x}_{{(1)}}} = {{x}_{{(2)}}} = 0$ тел ${{B}_{{(1)}}}$ и ${{B}_{{(2)}}}$ и зависят только от расстояния $x \equiv {{x}_{{(1)}}}$ от ${{A}_{{(12)}}}$. Предположение аналогично предположению работ [39, 40].

Учитывая это, взаимодействующие тела можно мысленно разделить на цилиндрические части одинакового бесконечно малого сечения, перпендикулярные плоскости контакта ${{A}_{{(12)}}}{\kern 1pt} $: $x = 0$. Так что учитываются только те силы взаимодействия, которые возникают между частицами разных материалов, принадлежащих соосным цилиндрам (рис. 4).

На основании выражения (4.2), с учетом сделанных допущений, получено выражение, которое определяет значение приходящейся на единицу объема частицы $d{{B}_{{(1)}}}$, величины ${{w}_{{(1)}}} = w_{{(1)}}^{{(2)}} + w_{{(1)}}^{{(3)}}$ потенциальной энергии ее парных $w_{{(1)}}^{{(2)}}$ и тройных $w_{{(1)}}^{{(3)}}$ взаимодействий с частицами тел ${{B}_{{(1)}}}$ и ${{B}_{{(2)}}}$

Параметры потенциалов $\Phi _{{(12)}}^{{(2)}}$, $\Phi _{{(112)}}^{{(3)}}$ $\Phi _{{(122)}}^{{(3)}}$ и $\beta _{{(12)}}^{{}}$ определены выражениями (3.3)–(3.6).

В соответствии с принятым предположением об их цилиндрической структуре расстояние между частицами отсчитывается вдоль нормали к поверхности контакта ${{B}_{{(1)}}}$ и ${{B}_{{(2)}}}$. В примере рассматривается взаимодействие только одной частицы $d{{B}_{{(1)}}}$ со всеми частицами $d{{B}_{{(2)}}}$ из находящегося напротив нее цилиндра бесконечно малого сечения в теле ${{B}_{{(2)}}}$ (рис. 4). Поэтому в расчетах первое слагаемое в выражении $w_{{(1)}}^{{(3)}}$, определяющее взаимодействие частицы $d{{B}_{{(1)}}} \equiv d{{B}_{{(1)1}}}$ с другими частицами $d{{B}_{{(1)2}}} \in {{B}_{{(1)}}}$, отсутствует. Частица $d{{B}_{{(1)}}}$ находится на расстоянии $x \equiv {{x}_{{(1)}}}$ от поверхности контакта. С ней взаимодействуют все частицы $d{{B}_{{(2)}}}$, расстояние от которых до $d{{B}_{{(1)}}}$ не менее $x \equiv {{x}_{{(1)}}}$. Несмотря на то, что координаты частиц $d{{B}_{{(2)2}}}$ и $d{{B}_{{(2)2}}}$ отсчитываются вдоль одной оси – оси цилиндра, которому они принадлежат, интегралы в последнем слагаемом выражения (4.1) вычисляются независимо друг от друга. В результате получена зависимость ${{w}_{{(1)}}}$ от безразмерного расстояния $\xi = {{\beta }_{{(12)}}}x$ между частицей $d{{B}_{{(1)}}}$ и телом ${{B}_{{(2)}}}$

Для частицы $d{{B}_{{(1)}}}$, которая контактирует с цилиндром, $\xi = {{\beta }_{{(12)}}}x \to 0$. Поэтому

Сила, действующая на частицу $d{{B}_{{(1)}}} \equiv d{{B}_{{(1)1}}}$ со стороны других частиц $d{{B}_{{(1)2}}} \subset {{B}_{{(1)}}}$, а также частиц $d{{B}_{{(2)}}}$ определяется равенством

Здесь ${{\vec {l}}_{{(21)}}}$ – радиус-вектор частицы $d{{B}_{{(1)}}}$ относительно $d{{B}_{{(2)}}}$. Векторы ${{\vec {l}}_{{(21)}}}$ и ${{\vec {F}}_{{(21)}}}$ параллельны и направлены в одну сторону (значение ${{F}_{{(21)}}}$, $\vec {F}_{{(21)}}^{{(2)}}$, $\vec {F}_{{(21)}}^{{(3)}}$ > 0) в случае отталкивания, направлены в разные стороны (значение ${{F}_{{(21)}}}$, $\vec {F}_{{(21)}}^{{(2)}}$, $\vec {F}_{{(21)}}^{{(3)}}$ < 0) в случае притяжения.

При отсутствии учета $\Phi _{{(112)}}^{{(3)}}$ выражение для расчета значения ${{F}_{{(21)}}}$ в рассматриваемом примере приобретает следующий вид

Объемная плотность силы воздействия цилиндра на частицу определяется равенством:

Просуммировав воздействие стержня из ${{B}_{{(2)}}}$ на все частицы стержня из ${{B}_{{(1)}}}$, контактирующего с ним, можно получить приходящуюся на единицу площади ${{A}_{{(12)}}}$ силу ${{\sigma }_{{(1)}}}$ действия тела ${{B}_{{(2)}}}$ на тело ${{B}_{{(1)}}}$

В выражениях (5.2), (5.3), (5.5), (5.6) слагаемые, содержащие параметр $\Phi _{{0(122)}}^{{(3)}}$, характеризуют влияние тройных взаимодействий. Поэтому при $\Phi _{{0(122)}}^{{(3)}} = 0$ и $\Phi _{{0(12)}}^{{(2)}} > 0$ – тройные взаимодействия не учитываются, а парные взаимодействия таковы, что находясь на любых расстояниях $x \equiv {{x}_{{(1)}}}$ от тела ${{B}_{{(2)}}}$ частица $d{{B}_{{(1)}}}$ притягивается к нему, так как ${{\sigma }_{{(1)}}}(\xi ) < 0$. Если $\Phi _{{0(12)}}^{{(2)}} > 0$ и $\Phi _{{0(122)}}^{{(3)}} > 0$, это утверждение сохраняется.

При $\Phi _{{0(12)}}^{{(2)}} > 0$, $\Phi _{{0(122)}}^{{(3)}} < 0$ видно, что составляющая силы $\sigma _{{(1)}}^{{(3)}}$ = $(9{\text{/}}4)( - \Phi _{{0(122)}}^{{(3)}}{\text{/}}\beta _{{(12)}}^{6})$ = = $(9{\text{/}}4)\left| {\Phi _{{0(122)}}^{{(3)}}{\text{/}}\beta _{{(12)}}^{6}} \right|$ > 0, порожденная тройными взаимодействиями, уменьшает действие силы притяжения $\sigma _{{(1)}}^{{(2)}}$ = $( - 3{\text{/}}2)(\Phi _{{0(12)}}^{{(2)}}{\text{/}}\beta _{{(12)}}^{3})$ < 0, порожденной парными взаимодействиями, и при выполнении неравенства

окажется, что сила ${{\sigma }_{{(1)}}} = \sigma _{{(1)}}^{{(2)}} + \sigma _{{(1)}}^{{(3)}}$ становится отталкивающей. Значит, между телом ${{B}_{{(2)}}}$ частицей $d{{B}_{{(1)}}}$ адгезии нет.

Выразив параметры $\left( {\Phi _{{0(12)}}^{{(2)}}{\text{/}}\beta _{{(12)}}^{3}} \right)$ и $\left( {\Phi _{{0(122)}}^{{(3)}}{\text{/}}\beta _{{(12)}}^{6}} \right)$ потенциалов межчастичных взаимодействий, входящие в выражения (5.2)–(5.7), через модули Юнга и сдвига контактирующих материалов методами данной работы, можно получить условия, связывающие эти модули, как в случае хорошей адгезии материалов, так и при ее отсутствии.

С помощью этой величины сделана оценка возможности адгезии некоторых пар материалов. Результат сопоставляется с имеющейся информацией о взаимодействии материалов этих пар.

Существует целый ряд анизотропных материалов, у которых в одном из направлений $\nu \leqslant 0$ (определяется методами работы [41]), обладающих антиадгезионными свойствами: тальк, графит, дисульфиды молибдена (MoS₂) и вольфрама (WS₂) и т.д. [42]. Это учтено в расчете приходящейся на единицу площади поверхности контакта тел B₍₁₎ и B₍₂₎ силы взаимодействия ${{\sigma }_{{(1)}}}$ для пар: Тальк – Cu, Тальк – Fe, Cu – Fe. Для первой пары получено: ${{\sigma }_{{(1)}}} = 65 \times {{10}^{9}}$ Н/м² > 0. Медь отталкивает тальк, адгезии между ними нет. Для второй пары: ${{\sigma }_{{(1)}}} = 523 \times {{10}^{9}}$ Н/м² > 0. Железо отталкивает тальк, адгезии нет. Для третьей пары: ${{\sigma }_{{(1)}}} = - 53 \times {{10}^{9}}$ Н/м² < 0. Медь притягивает сталь, адгезия есть.

В качестве исходных приняты следующие значения модуля Юнга $E$ и коэффициента Пуассона $\nu $ характеристик упругого состояния контактирующих материалов: тальк [42]: $E = 0.16 \times {{10}^{{11}}}$ Н/м², $\nu = 0$; медь [43]: $E = 1.10 \times {{10}^{{11}}}$ Н/м², $\nu = 0.31$; железо [43]: $E = 2.12 \times {{10}^{{11}}}$ Н/м², $\nu = 0.26$.

Полученные выводы соответствуют известным из технической и технологической практики выводам об адгезионном взаимодействии рассмотренных пар материалов.

Заключение. В работе представлены рассуждения, позволяющие выразить характеристики адгезионного взаимодействия однородных, изотропных, линейно упругих материалов через их классические характеристики упругого состояния – параметры Ламэ, а также неклассические – параметры полностью симметричной модели материалов второго порядка Джеремилло, которые можно определить с помощью экспериментов по исследованию нелинейности дисперсионного закона плоских акустических волн. Представленные результаты позволяют теоретически подобрать такие сочетания материалов с известными механическими свойствами, которые будут обладать заданными адгезионными свойствами, в том числе и антиадгезионными.