1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 84, № 3, 2020

Прикладная математика и механика, 2020, T. 84, № 3, стр. 311-326

АСИМПТОТИЧЕСКОЕ РАЗЛОЖЕНИЕ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ЖИДКОСТИ ПРИ ДВИЖЕНИИ В НЕЙ ДВУХ СФЕР ПЕРЕМЕННЫХ РАДИУСОВ ВБЛИЗИ ИХ КОНТАКТА

Ш. В. Сандуляну 1, 2, *

1 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

2 Московский физико-технический институт
Долгопрудный, Россия

* E-mail: shtefan.sanduleanu@gmail.com

Поступила в редакцию 30.09.2019
После доработки 02.03.2020
Принята к публикации 16.03.2020

Полный текст (PDF)

Аннотация

Рассматриваются два сферических пузырька переменных радиусов в идеальной жидкости при их движении вдоль линии центров. Получено точное выражение для кинетической энергии жидкости. Для этого найдена функция тока Стокса в бисферических координатах в разложении по полиномам Гегенбауэра. С помощью функции тока определены точные ряды коэффициентов квадратичной формы кинетической энергии. Проведено сравнение известных рядов с новыми рядами и доказана их тождественность. Преимущество новой формы рядов состоит в возможности вывода разложений их по малому зазору между пузырьками до произвольного порядка точности, включая все первые известные члены разложения, и изучена их сходимость. Полученные результаты могут быть использованы для описания динамики пузырьков вблизи контакта и определения условий их слияния при акустическом воздействии на них.

Ключевые слова: взаимодействие пузырьков, сила Бьеркнеса, функция тока Стокса, кинетическая энергия жидкости, осевая симметрия, асимптотическое разложение

Введение. Проблема взаимодействия сферических газовых пузырьков в пульсирующем поле давления является предметом изучения большого числа как теоретических, так и экспериментальных работ, начиная с работ Бьеркнесов 19 века [1] и кончая работами последних лет [2–5]. Бьеркнес установил, что сила взаимодействия между пульсирующими сферами, находящимися на больших расстояниях, обратно пропорциональна квадрату расстояния между ними. Данная зависимость была подтверждена экспериментально [6, 7].

Аналитически исследована [8–10] динамика сфер переменных радиусов на большом расстоянии. Уточнение результатов Бьеркнеса связано с получением разложения для силы гидродинамического взаимодействия по обратным степеням расстояния между центрами сфер. Кинетическая энергия найдена с точностью до членов порядка ${{r}^{{ - 3}}}$ [11, 12] и до ${{r}^{{ - 4}}}$ [13], а само решение с точностью до ${{r}^{{ - 5}}}$ [14] и до ${{r}^{{ - 6}}}$ [3].

Однако, как теоретически [3, 15], так и экспериментально [4, 16–19], показано, что при приближении к контакту эта зависимость не применима и ее следует находить из решения задачи взаимодействия двух пульсирующих сфер в точной постановке.

Задачу взаимодействия газовых пузырьков в акустическом поле волны удобно исследовать методом обобщенных координат Лагранжа. Основным слагаемым функции Лагранжа является кинетическая энергия. Для сферических пузырьков возникает задача вычисления кинетической энергии, как функции радиусов сфер, расстояния между центрами сфер и скоростей изменения радиусов и центров.

Для построения точного решения этой задачи существует два наиболее эффективных метода. Первым из них является метод отражений, с помощью которого Хикс построил точное решение для движения двух сфер постоянных радиусов [20]. Этим же методом получено точное решение для сфер переменных радиусов [21–23], хотя попытки были предприняты и раньше [24–26]. В случае постоянных радиусов кинетическая энергия является квадратичной формой двух скоростей центров сфер и имеет три коэффициента, найденных Хиксом. В случае переменных радиусов квадратичная форма содержит десять коэффициентов [21, 23], включая три коэффициента Хикса.

Второй метод заключается в том, чтобы представить решение в бисферических координатах [27]. Такое направление исследований проведено в случае постоянных радиусов [28–30] и в случае переменных радиусов [8, 31].

Следует заметить, что из рядов коэффициентов кинетической энергии, полученные первым методом, были найдены их трехчленные разложения вблизи контакта сфер как в случае сфер постоянных радиусов [32], так и для случая переменных радиусов [33]. Для рядов, полученных вторым методом в случае сфер постоянных радиусов [28, 29], был разработан алгоритм получения разложения до любого порядка по малому зазору [34]. Для случая сфер переменных радиусов такое разложение в литературе отсутствует. Цель данной работы устранить этот пробел.

В настоящем исследовании приведен вывод точного выражения в бисферических координатах кинетической энергии для случая переменных радиусов. А также вывод асимптотических разложений вблизи контакта. Исследование проводится в три этапа. Первый этап: построение точного решения краевой задачи для функции тока; второй этап: вычисление кинетической энергии и третий этап: построение асимптотических разложений для коэффициентов кинетической энергии.

1.Функция тока. Рассматривается потенциальное осесимметричное течение несжимаемой идеальной жидкости плотности ${{\rho }_{l}}$ в области ограниченной изнутри двумя сферами. Течение жидкости вызывают две сферы радиусов ${{R}_{1}}$, ${{R}_{2}}$, меняющиеся со скоростями ${{\dot {R}}_{1}}$, ${{\dot {R}}_{2}}$. Центры сфер на оси $z$ имеют координаты ${{z}_{1}}$, ${{z}_{2}}$ (${{z}_{1}} > {{z}_{2}}$) и двигаются со скоростями ${{u}_{1}} = - {{\dot {z}}_{1}}$, ${\kern 1pt} {{u}_{2}} = {{\dot {z}}_{2}}$, направленными на встречу друг другу (рис. 1). Расстояние между центрами сфер $r = {{z}_{1}} - {{z}_{2}}$, расстояние между поверхностями сфер (зазор) $h = r - {{R}_{1}} - {{R}_{2}}$.

Рис. 1.

Постановка задачи.

Компоненты скорости жидкости ${{v}_{\rho }}$, ${{v}_{\theta }}$, ${{v}_{z}}$, в цилиндрической системе координат $\rho $, $\theta $, z ($x = \rho cos\theta $, $y = \rho sin\theta $) выражаются через функцию тока $\psi $:

(1.1)
${{v}_{\rho }} = \frac{1}{\rho }\frac{{\partial \psi }}{{\partial z}},\quad {{v}_{\theta }} = 0,\quad {{v}_{z}} = - \frac{1}{\rho }\frac{{\partial \psi }}{{\partial \rho }}$

Уравнение для функции тока $\psi $ вытекает из условия потенциальности поля скорости и имеет вид [35]:

(1.2)
$\frac{\partial }{{\partial \rho }}\left( {\frac{1}{\rho }\frac{{\partial \psi }}{{\partial \rho }}} \right) + \frac{\partial }{{\partial z}}\left( {\frac{1}{\rho }\frac{{\partial \psi }}{{\partial z}}} \right) = 0$

Функция тока должна удовлетворять граничным условиям, следующим из условия равенства нормальных скоростей жидкости ${{v}_{n}}$ и поверхности сфер ${{w}_{n}}$

(1.3)
$({{{\mathbf{v}}}_{i}},{\mathbf{n}}) = ({{{\mathbf{w}}}_{i}},{\mathbf{n}}),\quad i = 1,2$

Для решения краевой задачи (1.2), (1.3) удобно перейти к бисферическим координатам ξ, ζ, θ ($x = \rho cos\theta $, $y = \rho sin\theta $):

(1.4)
$\rho = c\frac{{sin\zeta }}{{\operatorname{ch} \xi - cos\zeta }}\quad z = c\frac{{sh\xi }}{{\operatorname{ch} \xi - cos\zeta }}$

Тогда поверхности сфер радиусов ${{R}_{1}}$ и ${{R}_{2}}$ задаются уравнениями

(1.5)
$\xi = {{\tau }_{1}} = \operatorname{const} ,\quad \xi = - {{\tau }_{2}} = \operatorname{const} ,\quad \zeta \in [0,\pi ],\quad \theta \in [0,2\pi ],$
при этом ${{R}_{i}}\operatorname{sh} {{\tau }_{i}} = c$, $r = {{R}_{1}}\operatorname{ch} {{\tau }_{1}} + {{R}_{2}}\operatorname{ch} {{\tau }_{2}}$.

Таким образом, можно определить поверхности сфер с помощью параметров ${{\tau }_{1}}$, ${{\tau }_{2}}$ и $c$, которые выражаются через ${{R}_{1}}$, ${{R}_{2}}$ и малый зазор $h$ следующим образом

(1.6)
${{\tau }_{i}} = \sqrt {2hp} {\text{/}}{{R}_{i}} + O\left( {{{h}^{{3/2}}}} \right),\quad c = \sqrt {2hp} + O\left( {{{h}^{{3/2}}}} \right),\quad p = {{R}_{1}}{{R}_{2}}{\text{/}}({{R}_{1}} + {{R}_{2}})$

Функцию тока будем искать в виде [27, 29]

(1.7)
$\begin{gathered} \psi (\xi ,\zeta ) = {{\left( {\operatorname{ch} \xi - cos\zeta } \right)}^{{ - 1/2}}}\sum\limits_{n = 0}^\infty {{U}_{n}}(\xi )C_{n}^{{ - 1/2}}(cos\zeta ) \\ {{U}_{n}}(\xi ) = \frac{{{{\alpha }_{n}}\operatorname{sh} \left( {(n - 1{\text{/}}2)(\xi + {{\tau }_{2}})} \right) + {{\beta }_{n}}\operatorname{sh} \left( {(n - 1{\text{/}}2)({{\tau }_{1}} - \xi )} \right)}}{{\operatorname{sh} \left( {(n - 1{\text{/}}2)\tau } \right)}},\quad \tau = {{\tau }_{1}} + {{\tau }_{2}}, \\ \end{gathered} $
где $C_{n}^{{ - 1/2}}(\mu )$ – полиномы Гегенбауэра [36], $\mu = cos\zeta $.

Коэффициенты ${{\alpha }_{n}}$, ${{\beta }_{n}}$ находятся из граничных условий (1.3) на поверхностях сфер при $\xi = {{\tau }_{1}}$ и $\xi = - {{\tau }_{2}}$

(1.8)
$({{{\mathbf{v}}}_{i}},{\mathbf{n}}) = \frac{1}{\rho }\frac{{\partial \psi }}{{\partial \zeta }}\frac{{\operatorname{ch} {{\tau }_{i}} - cos\zeta }}{c} = ( - {{1)}^{i}}\left( {{{u}_{i}}\left( { - \frac{{\operatorname{ch} {{\tau }_{i}}cos\zeta - 1}}{{\operatorname{ch} {{\tau }_{i}} - cos\zeta }}} \right) + {{{\dot {R}}}_{i}}} \right) = ({{{\mathbf{w}}}_{i}},{\mathbf{n}})$

После интегрирования уравнения (1.8) по $\zeta $ получаем

(1.9)
$\psi ({{\tau }_{1}},\zeta ) = {{u}_{1}}{{c}^{2}}\frac{1}{2}\frac{{1 - {{\mu }^{2}}}}{{{{{\left( {\operatorname{ch} {{\tau }_{1}} - \mu } \right)}}^{2}}}} + {{\dot {R}}_{1}}{{c}^{2}}\frac{1}{{\operatorname{ch} {{\tau }_{1}} - \mu }} + \left( {\frac{{{{{\dot {R}}}_{2}}{{c}^{2}}}}{{{{{\operatorname{sh} }}^{2}}{{\tau }_{2}}}} - \frac{{{{{\dot {R}}}_{1}}{{c}^{2}}\operatorname{ch} {{\tau }_{1}}}}{{{{{\operatorname{sh} }}^{2}}{{\tau }_{1}}}}} \right),\quad \mu = cos\zeta $

Выражение для $\psi ( - {{\tau }_{2}},\zeta )$ получается перестановкой индексов 1 на 2 и заменой знака выражения $\psi ({{\tau }_{1}},\zeta )$. С помощью тождеств [29] при $\tau > 0$ и $ - 1 \leqslant \mu \leqslant 1$

${{\left( {\operatorname{ch} \tau - \mu } \right)}^{{1/2}}} = \sum\limits_{n = 0}^\infty \tfrac{{C_{n}^{{ - 1/2}}(\mu )}}{{\sqrt 2 }}{{e}^{{ - (n - 1/2)\tau }}}$
$\frac{1}{{{{{\left( {\operatorname{ch} \tau - \mu } \right)}}^{{1/2}}}}} = \sum\limits_{n = 0}^\infty C_{n}^{{ - 1/2}}(\mu )\frac{{ - (n - 1{\text{/}}2)\sqrt 2 }}{{\operatorname{sh} \tau }}{{e}^{{ - (n - 1/2)\tau }}}$
$\frac{1}{2}\frac{{1 - {{\mu }^{2}}}}{{{{{\left( {\operatorname{ch} \tau - \mu } \right)}}^{{3/2}}}}} = \sum\limits_{n = 0}^\infty C_{n}^{{ - 1/2}}(\mu )\sqrt 2 n(n - 1){{e}^{{ - (n - 1/2)\tau }}}$
находятся выражение для ${{\alpha }_{n}}$
(1.10)
${{\alpha }_{n}} = \left( {{{u}_{1}}2n(n - 1) - {{{\dot {R}}}_{1}}\frac{{2n - 1}}{{\operatorname{sh} {{\tau }_{1}}}} + \left( {\frac{{{{{\dot {R}}}_{2}}}}{{{{{\operatorname{sh} }}^{2}}{{\tau }_{2}}}} - \frac{{{{{\dot {R}}}_{1}}\operatorname{ch} {{\tau }_{1}}}}{{{{{\operatorname{sh} }}^{2}}{{\tau }_{1}}}}} \right)} \right)\frac{{{{c}^{2}}}}{{\sqrt 2 }}{{e}^{{ - (n - 1/2){{\tau }_{1}}}}},$
выражение для ${{\beta }_{n}}$ получается перестановкой индексов 1 на 2 и заменой знака ${{\alpha }_{n}}$.

Следует отметить, что в случае движения сфер постоянных радиусов (${{\dot {R}}_{i}} = 0$) суммирование в разложении (1.7) начинается с $n = 2$ [29] ввиду того, что коэффициенты ${{\alpha }_{n}}$, определяемые формулой (1.10) равны нулю при $n = 0$ и 1. Однако множество полиномов Гегенбауэра с $n \geqslant 2$ не образует полного базиса. Последнее обстоятельство играет существенную роль и в случае движения сфер переменных радиусов. При начале суммирования от $n = 2$, необходимо предварительно выделить некоторую функцию [8], а остаток найти в виде разложения по полиномам Гегенбауэра с $n \geqslant 2$. Однако разложение по полному базису (1.7) начинается с $n = 0$, что исключает необходимость выделения отдельной функции. Данное преимущество также имеет место при решении задачи вязкого взаимодействия двух сфер переменных радиусов.

Выражение для функции тока (1.7) с точностью до константы тождественно с выражением, полученным в [8], однако в упомянутой работе были обнаружены несколько опечаток. Выбор константы не принципиален, однако он влияет на вид коэффициентов кинетической энергии, которые находятся в следующем разделе.

2. Кинетическая энергия. Кинетическая энергия жидкости выражается через интеграл от ${{{v}}^{2}}$ по области вне двух сфер:

(2.1)
$T = \frac{{{{\rho }_{l}}}}{2}\iiint \,{{v}^{2}}dV$

С помощью формулы Грина, интеграл (2.1) может быть найден по формуле [29]

(2.2)
$\frac{T}{{\pi {{\rho }_{l}}}} = \oint \,\psi \frac{1}{\rho }\psi _{\zeta }^{'}d\xi - \psi \frac{1}{\rho }\psi _{\xi }^{'}d\zeta = \int\limits_{\xi = - {{\tau }_{2}}}^{{{\tau }_{1}}} \left. {\psi \frac{1}{\rho }\psi _{\zeta }^{'}} \right|_{{\zeta = 0}}^{{\zeta = \pi }}d\xi + \int\limits_{\zeta = 0}^\pi \left. {\psi \frac{1}{\rho }\psi _{\xi }^{'}} \right|_{{\xi = - {{\tau }_{2}}}}^{{\xi = {{\tau }_{1}}}}d\zeta $

Следует заметить то, что в случае сфер постоянных радиусов функция тока равна нулю на оси симметрии [29] и первый интеграл вклада не дает. Используя выражение для функции тока (1.7), получаем кинетическую энергию в виде квадратичной формы по скоростям

$T = 2\pi {{\rho }_{l}}\left\{ {\sum\limits_{j = 1}^2 {\left( {{{A}_{j}}u_{j}^{2} + {{D}_{j}}{{{\dot {R}}}_{j}}^{2} + \sum\limits_{i = 1}^2 {{{C}_{{ij}}}{{{\dot {R}}}_{j}}{{u}_{i}}} } \right)} + 2\left( {B{{u}_{1}}{{u}_{2}} + E{{{\dot {R}}}_{1}}{{{\dot {R}}}_{2}}} \right)} \right\}$
${{A}_{1}} = \tfrac{{R_{1}^{3}}}{6} + {{c}^{3}}\,\sum\limits_{n = 2}^\infty \tfrac{{{{{(2n - 1)}}^{2}} - 1}}{{2{{Q}_{n}}\left( {{{\tau }_{1}}} \right)\left( {{{Q}_{n}}\left( \tau \right) - 1} \right)}},\quad B = \frac{{{{c}^{3}}}}{2}\sum\limits_{n = 2}^\infty \tfrac{{{{{(2n - 1)}}^{2}} - 1}}{{{{Q}_{n}}\left( \tau \right) - 1}}$
(2.3)
${{C}_{{11}}} = 2{{c}^{3}}\,\sum\limits_{n = 2}^\infty \tfrac{{{{S}_{n}}({{\tau }_{1}})}}{{{{Q}_{n}}\left( {{{\tau }_{1}}} \right)\left( {{{Q}_{n}}\left( \tau \right) - 1} \right)}},\quad {{C}_{{12}}} = 2{{c}^{3}}\,\sum\limits_{n = 2}^\infty \tfrac{{{{S}_{n}}({{\tau }_{2}})}}{{{{Q}_{n}}\left( \tau \right) - 1}}$
${{D}_{1}} = R_{1}^{3} + {{c}^{3}}\,\sum\limits_{n = 2}^\infty \frac{2}{{{{{(2n - 1)}}^{2}} - 1}}\frac{{S_{n}^{2}({{\tau }_{1}})}}{{{{Q}_{n}}\left( {{{\tau }_{1}}} \right)\left( {{{Q}_{n}}\left( \tau \right) - 1} \right)}}$
$E = \tfrac{{{{{({{R}_{1}}{{R}_{2}})}}^{2}}}}{r} + {{c}^{3}}\,\sum\limits_{n = 2}^\infty \frac{2}{{{{{(2n - 1)}}^{2}} - 1}}\frac{{{{S}_{n}}({{\tau }_{1}}){{S}_{n}}({{\tau }_{2}})}}{{{{Q}_{n}}\left( \tau \right)\left( {{{Q}_{n}}\left( \tau \right) - 1} \right)}},$
где ${{Q}_{n}}\left( x \right)$ = $\exp \left( {\left( {2n - 1} \right)x} \right)$ и введено обозначение ${{S}_{n}}(x)$ = $({{Q}_{n}}\left( x \right)$ – $(2n - 1)\operatorname{sh} x$ – $\operatorname{ch} x){\text{/}}{{\operatorname{sh} }^{2}}x$, а коэффициенты ${{A}_{2}}$, ${{C}_{{21}}}$, ${{C}_{{22}}}$ и ${{D}_{2}}$ получаются перестановкой 1 на 2 в формулах для ${{A}_{1}}$, ${{C}_{{12}}}$, ${{C}_{{11}}}$, ${{D}_{1}}$. Кроме того ряды (2.3) можно выразить через исходные параметры ${{R}_{1}}$, ${{R}_{2}}$, r, подставив
(2.4)
$c = \sqrt {{{{\left( {{{r}^{2}} - R_{1}^{2} - R_{2}^{2}} \right)}}^{2}} - 4R_{1}^{2}R_{2}^{2}} {\text{/}}(2r),\quad {{e}^{{ - {{\tau }_{1}}}}} = b - \sqrt {{{b}^{2}} - 1} ,$
где $b = ({{r}^{2}} + R_{1}^{2} - R_{2}^{2}){\text{/}}(2r{{R}_{1}})$. Аналогично можно выразить экспоненты ${{e}^{{ - {{\tau }_{2}}}}}$ и ${{e}^{{ - \tau }}}$.

Если коэффициенты кинетической энергии (2.3) представить в виде рядов по экспонентам, то они полностью совпадут с рядами [20] и [15, 21, 23], что доказывает достоверность проведенных вычислений.

Кинетическая энергия была найдена в виде ряда по обратным степеням $r$ [3]. Сравнение с точным решением показывает совпадение членов до ${{r}^{{ - 6}}}$, однако следующие по порядку члены не совпадают.

При рассмотрении взаимодействия двух пузырьков переменных радиусов с фиксированными центрами [37, 38] коэффициенты кинетической энергии оказались отличны от точных (2.3), так как задача решалось в предположении постоянства потенциала скоростей на поверхности сфер. Такая неточность не влияет на главную асимптотику силы Бьеркнеса при больших расстояниях между сферами.

В несколько ином виде коэффициенты кинетической энергии можно получить из выражений для гидродинамических сил [8]. С учетом небольших опечаток они согласуются с выражениями (2.3).

Следует заметить, что ряды [15, 20–23] более удобны для получения разложений на больших расстояниях $r \gg {{R}_{1}}$, ${{R}_{2}}$. Вблизи контакта, при малых $h \ll {{R}_{1}}$, ${{R}_{2}}$, из этих рядов было получено [32, 33] только трехчленное разложение. Следующие члены разложения удобно получить из рядов (2.3). Алгоритм их получения представлен в следующем разделе.

3. Асимптотическое разложение. 3.1. Асимптотическое разложение вблизи контакта. Для получения асимптотического разложения кинетической энергии жидкости вблизи контакта, воспользуемся методикой работы [34]. В этой работе методика представлена для сфер постоянных радиусов, то есть для коэффициентов ${{A}_{1}}$, ${{A}_{2}}$, B. Предлагается развитие этой методики для случая переменных радиусов, то есть для остальных семи коэффициентов.

Коэффициент ${{A}_{1}}$ запишем в виде:

(3.1)
$\begin{array}{*{20}{l}} {{{A}_{1}} = \tfrac{{R_{1}^{3}}}{6} + {{c}^{3}}\,\sum\limits_{n = 2}^\infty \frac{{{{e}^{{ - \left( {1 + {{\lambda }_{1}}} \right)t}}}}}{{1 - {{e}^{{ - t}}}}}\frac{{{{{(2n - 1)}}^{2}} - 1}}{2},\quad t = \left( {2n - 1} \right)\tau ,\quad {{\lambda }_{1}} = {{\tau }_{1}}{\text{/}}\tau } \end{array}$

Подставляя под знаком суммы преобразование Меллина и выполняя суммирование по $n$, имеем

(3.2)
${{A}_{1}} = \frac{{R_{1}^{3}}}{6} + \frac{{{{c}^{3}}}}{2}\frac{1}{{2\pi i}}\int\limits_{\sigma - i\infty }^{\sigma + i\infty } {{\tau }^{{ - s}}}\Gamma (s)Z\left( s \right)\zeta \left( {s,1 + {{\lambda }_{1}}} \right)ds,\quad \sigma > 3,$
где
$Z(s) = \sum\limits_{n = 2}^\infty {{\left( {2n - 1} \right)}^{{ - s}}}\left( {{{{(2n - 1)}}^{2}} - 1} \right) = \zeta (s - 2)\left( {1 - {{2}^{{ - (s - 2)}}}} \right) - \zeta (s)\left( {1 - {{2}^{{ - s}}}} \right),$
$\zeta (s,a)$ – дзета функция Гурвица, $\zeta (s) = \zeta (s,1)$ – дзета функция Римана [36].

Вычислим интеграл (3.2), воспользовавшись теоремой вычетов. Для этого необходимо найти полюса подынтегральной функции. Они расположены в точках: 3, 1, –1, … и определяют порядки членов асимптотического разложения. Вычет в первой точке определяет главный член разложения, во второй точке – следующий и т.д. Учитывая значения вычетов в точках 3, 1, –1, …, –2l + 1, получим следующее разложение:

(3.3)
$\begin{gathered} {{A}_{1}} = \frac{{R_{1}^{3}}}{6} + \frac{{{{c}^{3}}}}{2}\left( {\frac{{\zeta (3,1 + {{\lambda }_{1}})}}{{{{\tau }^{3}}}} + \frac{1}{{2\tau }}\left( {ln\frac{\tau }{2} + \psi (1 + {{\lambda }_{1}}) + \frac{1}{6}} \right) - } \right. \\ \left. { - \;\sum\limits_{k = 1}^l \frac{{{{\tau }^{{2k - 1}}}}}{{(2k - 1)!}}Z( - 2k + 1)\zeta ( - 2k + 1,1 + {{\lambda }_{1}})} \right) + r_{{{{A}_{1}}}}^{{2l - 1}}, \\ \end{gathered} $
где $\psi (x) = \Gamma {\kern 1pt} '(x){\text{/}}\Gamma (x)$ – дигамма функция [36], а остаточный член имеет вид:

(3.4)
$r_{{{{A}_{1}}}}^{m} = \frac{{{{c}^{3}}}}{2}\frac{1}{{2\pi i}}\int\limits_{{{\sigma }_{m}} - i\infty }^{{{\sigma }_{m}} + i\infty } {{\tau }^{{ - s}}}\Gamma (s)Z\left( s \right)\zeta \left( {s,1 + {{\lambda }_{1}}} \right)ds,\quad - {\kern 1pt} m - 1 < {{\sigma }_{m}} < - m$

Аналогично для коэффициента $B$ получаем [34]

(3.5)
$B = \frac{{{{c}^{3}}}}{{4\tau }}\left( {\frac{{2\zeta (3)}}{{{{\tau }^{2}}}} + ln\frac{\tau }{2} + \left( {\psi (1) + \frac{1}{6}} \right) - 2\,\sum\limits_{k = 1}^n \frac{{{{\tau }^{{2k}}}}}{{(2k - 1)!}}Z( - 2k + 1)\zeta ( - 2k + 1)} \right) + r_{B}^{{2l - 1}},$
где $r_{B}^{{2l - 1}}$ определяется аналогично $r_{{{{A}_{1}}}}^{{2l - 1}}$.

Приведем асимптотические разложения остальных коэффициентов:

(3.6)
$\begin{gathered} {{C}_{{1j}}} = \frac{{2{{c}^{3}}}}{{{{{\operatorname{sh} }}^{2}}{{\tau }_{j}}}}\left( {\frac{{2\tau - \zeta (2,1 + {{\lambda }_{1}}(2 - j))}}{{2{{\tau }^{2}}}}\operatorname{sh} {{\tau }_{j}} + \sum\limits_{k = 0}^m \frac{{{{{\left( { - \tau } \right)}}^{k}}}}{{k!}}{{Z}_{{{{C}_{{1j}}}}}}( - k,{{\lambda }_{1}}) + } \right. \\ \left. { + \;{{{\left( { - 1} \right)}}^{{j - 1}}}\frac{{\gamma {{{\operatorname{ch} }}^{{j - 1}}}{{\tau }_{j}} + {{{\operatorname{ch} }}^{{2 - j}}}{{\tau }_{j}}{\kern 1pt} \psi \left( {{{\lambda }_{1}} + 2 - j} \right)}}{{2\tau }} + \frac{{\operatorname{ch} {{\tau }_{j}} - 1}}{\tau }\left( {1 + \frac{1}{2}ln\frac{\tau }{2}} \right)} \right) + r_{{{{C}_{{1j}}}}}^{m}, \\ j = 1,2 \\ \end{gathered} $
где $\gamma \approx 0.577216$ – постоянная Эйлера и

(3.7)
$\begin{gathered} {{Z}_{{{{C}_{{1j}}}}}}(s,{{\lambda }_{j}}) = \left( {\zeta (s,\lambda _{1}^{{j - 1}}) - \zeta (s,{{{\left( {1 + {{\lambda }_{1}}} \right)}}^{{2 - j}}})\operatorname{ch} {{\tau }_{j}}} \right)\left( {\zeta (s)(1 - {{2}^{{ - s}}}) - 1} \right) - \\ - \;\zeta (s,{{\left( {1 + {{\lambda }_{1}}} \right)}^{{2 - j}}})\operatorname{sh} {{\tau }_{j}}\left( {\zeta (s - 1)(1 - {{2}^{{ - (s - 1)}}}) - 1} \right), \\ j = 1,2 \\ \end{gathered} $

Для коэффициентов ${{D}_{1}}$, E вывод асимптотического разложения существенно сложнее

(3.8)
${{D}_{1}} = R_{1}^{3} + \frac{{2{{c}^{3}}}}{{{{{\operatorname{sh} }}^{4}}{{\tau }_{1}}}}\sum\limits_{k = - 1}^n \mathop {{\text{res}}}\limits_{s = - k} \left( {{{\tau }^{{ - s}}}\Gamma (s){{Z}_{{{{D}_{1}}}}}(s,{{\lambda }_{1}})} \right) + r_{{{{D}_{1}}}}^{m}$
(3.9)
$E = \frac{{{{{\left( {{{R}_{1}}{{R}_{2}}} \right)}}^{2}}}}{r} + \frac{{2{{c}^{3}}}}{{{{{\operatorname{sh} }}^{2}}{{\tau }_{1}}{{{\operatorname{sh} }}^{2}}{{\tau }_{2}}}}\sum\limits_{k = - 1}^n \mathop {{\text{res}}}\limits_{s = - k} {\kern 1pt} \left( {{{\tau }^{{ - s}}}\Gamma (s){{Z}_{E}}(s,{{\lambda }_{1}},{{\lambda }_{2}})} \right) + r_{E}^{m}$
где
${{Z}_{{{{D}_{1}}}}}(s,{{\lambda }_{1}}) = {{\operatorname{sh} }^{2}}{{\tau }_{1}}\zeta (s,1 + {{\lambda }_{1}})H(s - 2) + \left( {\operatorname{sh} \left( {2{{\tau }_{1}}} \right)\zeta (s,1 + {{\lambda }_{1}}) - 2\operatorname{sh} {{\tau }_{1}}\zeta (s)} \right)H(s - 1) + $
$ + \;\left( {\zeta (s,1 - {{\lambda }_{1}}) - 2\operatorname{ch} {{\tau }_{1}}\zeta (s) + {{{\operatorname{ch} }}^{2}}{{\tau }_{1}}\zeta (s,1 + {{\lambda }_{1}})} \right)H(s)$
${{Z}_{E}}(s,{{\lambda }_{1}},{{\lambda }_{2}}) = \operatorname{sh} {{\tau }_{1}}\operatorname{sh} {{\tau }_{2}}\zeta (s,2)H(s - 2) - $
$ - \;\left( {\operatorname{sh} {{\tau }_{1}}\zeta (s,1 + {{\lambda }_{1}}) + \operatorname{sh} {{\tau }_{2}}\zeta (s,1 + {{\lambda }_{2}}) - \operatorname{sh} \tau \zeta (s,2)} \right)H(s - 1) + $
$ + \;\left( {\zeta (s) - \operatorname{ch} {{\tau }_{1}}\zeta (s,1 + {{\lambda }_{1}}) - \operatorname{ch} {{\tau }_{2}}\zeta (s,1 + {{\lambda }_{2}}) + \operatorname{ch} {{\tau }_{1}}\operatorname{ch} {{\tau }_{2}}\zeta (s,2)} \right)H(s),$
а функция $H(s)$ имеет вид:

$H(s) = \sum\limits_{n = 2}^\infty \tfrac{{{{{\left( {2n - 1} \right)}}^{{ - s}}}}}{{{{{\left( {2n - 1} \right)}}^{2}} - 1}}$

Учитывая рекуррентное соотношение

$H(s) = H(s + 2) + \zeta (s + 2)\left( {1 - {{2}^{{ - (s + 2)}}}} \right) - 1,$
а также, то, что $H(0) = 1{\text{/}}4$ и $H(1) = 3{\text{/}}4 - ln2$, после взятия вычета асимптотическое разложение для коэффициентов ${{D}_{1}}$ и $E$ окончательно принимает вид
(3.10)
$\begin{gathered} {{D}_{1}} = R_{1}^{3} + \frac{{2{{c}^{3}}}}{{{{{\operatorname{sh} }}^{4}}{{\tau }_{1}}}}\left\{ { - \frac{{\operatorname{ch} {{\tau }_{1}} - 1}}{{2\tau }}{{{\left( {\psi (1 + {{\lambda }_{1}}) - \operatorname{sh} {{\tau }_{1}} + 2 + \operatorname{ch} {{\tau }_{1}}{{{\left( {\psi (1 + {{\lambda }_{1}}) + } \right.}}^{{^{{}}}}}} \right.}}^{{^{{}}}}}} \right. \\ \left. { + \;\left. {ln\tau - 1 + 3ln2} \right) + ln\left( {\frac{\tau }{2}} \right)} \right) + \left. {\sum\limits_{k = 0}^m \frac{{{{{( - \tau )}}^{k}}}}{{k!}}{{W}_{{{{D}_{1}}}}}(k,{{\lambda }_{1}})} \right\} + r_{{{{D}_{1}}}}^{m} \\ \end{gathered} $
(3.11)
$\begin{gathered} E = \frac{{{{{({{R}_{1}}{{R}_{2}})}}^{2}}}}{r} + \frac{{{{c}^{3}}}}{{\tau {{{\operatorname{sh} }}^{2}}{{\tau }_{1}}{{{\operatorname{sh} }}^{2}}{{\tau }_{2}}}}\left\{ {\operatorname{sh} {{\tau }_{1}}\operatorname{sh} {{\tau }_{2}}\left( { - ln(2\tau ) - \frac{3}{2} + \gamma } \right) + \frac{1}{2}(\operatorname{sh} \tau - \operatorname{sh} {{\tau }_{1}}{{ - }^{{^{{^{{^{{}}}}}}}}}} \right. \\ - \;\operatorname{sh} {{\tau }_{2}}) + \left( {\frac{3}{2} - 2ln2} \right)(\operatorname{ch} {{\tau }_{1}} - 1)(\operatorname{ch} {{\tau }_{2}} - 1) - \left. {2\,\sum\limits_{k = 0}^m \frac{{{{{( - \tau )}}^{{k + 1}}}}}{{k!}}{{W}_{E}}(k,{{\lambda }_{1}},{{\lambda }_{2}})} \right\} + r_{E}^{m}, \\ \end{gathered} $
причем функции ${{W}_{{{{D}_{1}}}}}$ и ${{W}_{E}}$ определены как
${{W}_{{{{D}_{1}}}}}(k,{{\lambda }_{1}}) = \sum\limits_{j = - 1}^1 {(3{{j}^{2}} - 2)\zeta ( - k,1 + j{{\lambda }_{1}}){{{\operatorname{ch} }}^{{j + 1}}}{{\tau }_{1}}} G(k) + $
$ + \;\operatorname{sh} {{\tau }_{1}}\left[ {2\left( {\operatorname{ch} {{\tau }_{1}}\zeta ( - k,1 + {{\lambda }_{1}}) - \zeta ( - k)} \right)G(k + 1) + \operatorname{sh} {{\tau }_{1}}\zeta ( - k,1 + {{\lambda }_{1}})G(k + 2)} \right] + $
$ + \;\frac{1}{4}\left[ {{{F}_{k}}\left( {0,1 - {{\lambda }_{1}}} \right) + {{F}_{k}}\left( {2{{\tau }_{1}},1 + {{\lambda }_{1}}} \right) - 2{{F}_{k}}\left( {{{\tau }_{1}},1} \right)} \right]$
${{W}_{E}}(k,{{\lambda }_{1}},{{\lambda }_{2}}) = \left( {\operatorname{sh} {{\tau }_{1}}\operatorname{sh} {{\tau }_{2}}G(k + 2) + \operatorname{sh} \tau G(k + 1) + \operatorname{ch} {{\tau }_{1}}\operatorname{ch} {{\tau }_{2}}G(k)} \right)\zeta ( - k,2) - $
$ - \;\sum\limits_{j = 1}^2 {\left( {\operatorname{sh} {{\tau }_{j}}\zeta ( - k,1 + {{\lambda }_{j}})G(k + 1) + \left( {\operatorname{ch} {{\tau }_{j}}\zeta ( - k,1 + {{\lambda }_{j}}) - \tfrac{1}{2}\zeta ( - k)} \right)G(k)} \right)} + $
$ + \;\frac{1}{4}\left[ {{{F}_{k}}\left( {0,1} \right) + {{F}_{k}}\left( {\tau ,2} \right) - {{F}_{k}}\left( {{{\tau }_{1}},1 + {{\lambda }_{1}}} \right) - {{F}_{k}}\left( {{{\tau }_{2}},1 + {{\lambda }_{2}}} \right)} \right],$
где

${{F}_{k}}\left( {x,y} \right) = \left\{ {{{\zeta }^{{(1,0)}}}( - k,y) + L(k)\zeta ( - k,y)} \right\}\left\{ {\left( {1 + {{{\left( { - 1} \right)}}^{k}}} \right)\operatorname{sh} x + \left( {1 - {{{\left( { - 1} \right)}}^{k}}} \right)\operatorname{ch} x} \right\}$
$G(k) = \frac{1}{2}\left\{ {\frac{1}{2} - k + \left( {1 - {{{\left( { - 1} \right)}}^{k}}} \right)\left( { - ln2 + \sum\limits_{j = 1}^{(k - 1)/2} \zeta (1 - 2j)\left( {1 - {{2}^{{ - (1 - 2j)}}}} \right)} \right)} \right\}$
$L(k) = \sum\limits_{j = 1}^k \,{{j}^{{ - 1}}} - ln\frac{\tau }{2}$

Как отмечалось ранее, коэффициенты ${{A}_{2}}$, ${{C}_{{22}}}$, ${{C}_{{21}}}$, ${{D}_{2}}$ находятся перестановкой индексов.

3.2. Сравнение асимптотического разложения. Для случая сфер постоянных радиусов асимптотическое разложение кинетической энергии [34] находится в согласии с трехчленным разложением [32]. Также в согласии находятся полученные выше асимптотические разложения кинетической энергии, для случая сфер переменных радиусов, с трехчленным разложением [33].

3.3. Оценка остаточного члена. Разложение $X = \sum\nolimits_{n = 0}^m {{{X}_{n}}(\varepsilon )} + R_{X}^{m}(\varepsilon )$ является по Пуанкаре [36] асимптотическим по параметру $\varepsilon $, если $\mathop {lim}\limits_{\varepsilon \to 0} {\kern 1pt} \left| {R_{X}^{m}{\text{/}}{{X}_{m}}} \right| = 0$. Для определенности рассмотрим разложение ${{A}_{1}}$ (3.3). Представим его в виде

(3.12)
${{A}_{1}} = x_{{{{A}_{1}}}}^{0} + \sum\limits_{k = 1}^l \,x_{{{{A}_{1}}}}^{{2k - 1}} + r_{{{{A}_{1}}}}^{{2l - 1}},$
где

$x_{{{{A}_{1}}}}^{{2k - 1}} = - \frac{{R_{1}^{3}{{{\operatorname{sh} }}^{3}}{{\tau }_{1}}}}{2}\frac{{{{\tau }^{{2k - 1}}}}}{{(2k - 1)!}}Z( - 2k + 1)\zeta ( - 2k + 1,1 + {{\lambda }_{1}})$

Докажем, что $\mathop {lim}\limits_{\tau \to 0} {\kern 1pt} \left| {r_{{{{A}_{1}}}}^{{2l - 1}}{\text{/}}x_{{{{A}_{1}}}}^{{2l - 1}}} \right| = 0$. Для выражения:

(3.13)
$\begin{gathered} \left| {r_{{{{A}_{1}}}}^{{2l - 1}}} \right| = \frac{{R_{1}^{3}{{{\operatorname{sh} }}^{3}}{{\tau }_{1}}}}{2}\frac{1}{{2\pi }}{{\tau }^{{ - {{\sigma }_{{2l - 1}}}}}}\int\limits_{ - \infty }^\infty \left| {\Gamma ({{\sigma }_{{2l - 1}}} + it)Z\left( {{{\sigma }_{{2l - 1}}} + it} \right)\zeta \left( {{{\sigma }_{{2l - 1}}} + it,1 + {{\lambda }_{1}}} \right)} \right|dt, \\ - 2l < {{\sigma }_{{2l - 1}}} < - 2l + 1, \\ \end{gathered} $
была получена оценка [34]

$\left| {r_{{{{A}_{1}}}}^{{2l - 1}}} \right| = O\left( {{{\tau }^{{2l - 1 + 3}}}} \right)$

Тогда, учитывая, что

$\left| {x_{{{{A}_{1}}}}^{{2l - 1}}} \right| = O\left( {{{\tau }^{{2l - 1 + 3}}}} \right)$
можно доказать и более сильное утверждение

(3.14)
$\left| {r_{{{{A}_{1}}}}^{{2l - 1}}} \right| = o\left( {{{\tau }^{{2l - 1 + 3}}}} \right)$

Для этого заметим, что

$\left| {r_{{{{A}_{1}}}}^{{2l - 1}}} \right| = \left| {x_{{{{A}_{1}}}}^{{2l + 1}} + r_{{{{A}_{1}}}}^{{2l + 1}}} \right| \leqslant \left| {x_{{{{A}_{1}}}}^{{2l + 1}}} \right| + \left| {r_{{{{A}_{1}}}}^{{2l + 1}}} \right| = O\left( {{{\tau }^{{2l + 1 + 3}}}} \right),$
тогда
$\mathop {lim}\limits_{\tau \to 0} {\kern 1pt} \left| {\frac{{r_{{{{A}_{1}}}}^{{2l - 1}}}}{{x_{{{{A}_{1}}}}^{{2l - 1}}}}} \right| = 0$
и тем самым доказано, что разложение ${{A}_{1}}$ – асимптотическое по Пуанкаре. При этом ряд расходится для любых $\tau > 0$ и для вычислений нужно ограничиться конечным числом членов ряда.

Как отмечалось ранее [39], целесообразно ограничить суммирование асимптотического ряда при $m = \eta $, где $\eta $ находится из условия ${{\left. {d\left| {x_{{{{A}_{1}}}}^{m}} \right|{\text{/}}dm} \right|}_{\eta }}\sim 0$.

Определим асимптотику $x_{{{{A}_{1}}}}^{m}$ при больших значениях $m$. Учитывая тождество

$\zeta ( - m,a + 1) = \zeta ( - m,a) + {{a}^{m}}$
и формулу Гурвица [36]
$\zeta (1 - m,a) = 2\frac{{(m - 1)!}}{{{{{(2\pi )}}^{m}}}}\sum\limits_{n = 1}^\infty \frac{{cos\left( {2\pi na - \frac{1}{2}\pi m} \right)}}{{{{n}^{m}}}},\quad 1 \geqslant a \geqslant 0,\quad m \geqslant 1,$
для больших $m$ и при $0 \leqslant a \leqslant 2$ функцию $\zeta ( - m,a)$ можно аппроксимировать как
$\zeta ( - m,a) \approx 2\frac{{m!}}{{{{{(2\pi )}}^{{m + 1}}}}}cos\left( {2\pi a - \frac{\pi }{2}(m + 1)} \right)\sim 2\frac{{m!}}{{{{{(2\pi )}}^{{m + 1}}}}},$
тогда асимптотику $x_{{{{A}_{1}}}}^{m}$ можно оценить как

(3.15)
$\frac{{x_{{{{A}_{1}}}}^{m}}}{{{{p}^{3}}}}\sim 4\tau \sqrt {2\pi (m + 2)} {{\left( {\frac{{m + 2}}{{2{{\pi }^{2}}e}}\tau } \right)}^{{m + 2}}}$

Из условия ${{\left. {d\left| {x_{{{{A}_{1}}}}^{m}} \right|{\text{/}}dm} \right|}_{\eta }}\sim 0$ получаем $\eta \sim 2{{\pi }^{2}}{\text{/}}\tau $. Вблизи контакта, учитывая формулу (1.6), получим $\eta \sim 2{{\pi }^{2}}{\text{/}}\sqrt {2h{\text{/}}p} $. Аналогично вычисляются значения $\eta $ для всех других коэффициентов. При таком выборе $\eta $ погрешность имеет порядок ${{e}^{{ - \eta }}}$. Эта оценка подтверждается многочисленными численными расчетами.

3.4. Разложение по $h$ вблизи контакта. Для практических целей более удобно перейти от параметра $\tau = {{\tau }_{1}} + {{\tau }_{2}}$ к зазору $h$. Тогда разложение коэффициентов кинетической энергии принимает вид

(3.16)
$X = {{f}_{X}}(h) + {{g}_{X}}(h)ln\left( {\frac{h}{{2p}}} \right),\quad X = \{ {{A}_{i}},B,{{C}_{{ij}}},{{D}_{i}},E\} $

Необходимо найти 6 пар функций ${{f}_{X}}(h)$ и ${{g}_{X}}(h)$ для коэффициентов ${{A}_{1}}$, $B$, ${{C}_{{11}}}$, ${{C}_{{12}}}$, ${{D}_{1}}$, $E$, итого 12 независимых функций. Для остальных коэффициентов функции ${{f}_{X}}(h)$ и ${{g}_{X}}(h)$ получаются перестановкой индексов. Примечательно, что число независимых функций можно сократить до 10. Для этого докажем, что функции ${{g}_{X}}(h)$ для коэффициентов ${{A}_{1}}$ и $B$ совпадают и также совпадают функции ${{g}_{X}}(h)$ для коэффициентов ${{C}_{{11}}}$, ${{C}_{{21}}}$. Действительно, из формул (3.3) и (3.5) следует, что коэффициенты ${{g}_{{{{A}_{1}}}}}$, ${{g}_{B}}$ получаются из члена ${{c}^{3}}{\text{/}}(4\tau )ln\left( {\tau {\text{/}}2} \right)$, в котором аргумент $\tau $ надо выразить через $h$. Коэффициенты ${{g}_{{{{C}_{{11}}}}}}$, ${{g}_{{{{C}_{{21}}}}}}$ получаются аналогично из члена ${{c}^{3}}(\operatorname{ch} {{\tau }_{1}}$ – $1){\text{/}}(\tau {{\operatorname{sh} }^{2}}{{\tau }_{1}})ln\left( {\tau {\text{/}}2} \right)$. Функции ${{f}_{X}}(h)$ и ${{g}_{X}}(h)$ можно разложить по степеням $h$. Достаточная точность достигается кубическими полиномами вида:

(3.17)
$\begin{gathered} {{f}_{X}}(h) = f_{X}^{0} + f_{X}^{1}h + f_{X}^{2}{{h}^{2}} + f_{X}^{3}{{h}^{3}} + O({{h}^{4}}) \\ {{g}_{X}}(h) = g_{X}^{1}h + g_{X}^{2}{{h}^{2}} + g_{X}^{3}{{h}^{3}} + O({{h}^{4}}) \\ \end{gathered} $

Можно показать, что с точностью до перестановки индексов логарифмическая особенность определяется четырьмя полиномами. Их три первых коэффициента приведены в таблице 1.

Таблица 1.

Аналитический вид $g_{X}^{1}$, $g_{X}^{2}$, $g_{X}^{3}$ для коэффициентов кинетической энергии, ${{\alpha }_{i}} = {{R}_{i}}{\text{/}}\left( {{{R}_{1}} + {{R}_{2}}} \right)$

$X$ $g_{X}^{1}$ $g_{X}^{2}$ $g_{X}^{3}$
${{A}_{1}},B$ $\frac{{{{p}^{2}}}}{4}$ $\frac{{5p}}{{24}}\left( {\alpha _{1}^{2} - {{\alpha }_{1}}{{\alpha }_{2}} + \alpha _{2}^{2}} \right)$ $\frac{1}{{360}}\left( {13\alpha _{1}^{4} - 98\alpha _{1}^{3}{{\alpha }_{2}} + 183\alpha _{1}^{2}\alpha _{2}^{2} - 98{{\alpha }_{1}}\alpha _{2}^{3} + 13\alpha _{2}^{4}} \right)$
${{C}_{{11}}},{{C}_{{21}}}$ $\frac{{{{p}^{2}}}}{2}$ $\frac{p}{{12}}\left( {5\alpha _{1}^{2} - 5{{\alpha }_{1}}{{\alpha }_{2}} + 2\alpha _{2}^{2}} \right)$ $\frac{1}{{180}}\left( {13\alpha _{1}^{4} - 98\alpha _{1}^{3}{{\alpha }_{2}} + 123\alpha _{1}^{2}\alpha _{2}^{2} - 38{{\alpha }_{1}}\alpha _{2}^{3} - 2\alpha _{2}^{4}} \right)$
${{D}_{1}}$ $\frac{{{{p}^{2}}}}{4}$ $\frac{p}{{24}}\left( {5\alpha _{1}^{2} - 5{{\alpha }_{1}}{{\alpha }_{2}} - \alpha _{2}^{2}} \right)$ $\frac{{11}}{{720}} + \frac{1}{{48}}\alpha _{1}^{2}\left( {\alpha _{1}^{2} - 16{{\alpha }_{1}}{{\alpha }_{2}} + 4\alpha _{2}^{2}} \right)$
$E$ $\frac{{{{p}^{2}}}}{4}$ $\frac{p}{{24}}\left( {2\alpha _{1}^{2} - 5{{\alpha }_{1}}{{\alpha }_{2}} + 2\alpha _{2}^{2}} \right)$ $\frac{{11}}{{720}} - \frac{1}{{48}}\left( {\alpha _{1}^{2} - {{\alpha }_{1}}{{\alpha }_{2}} + \alpha _{2}^{2}} \right)\left( {\alpha _{1}^{2} + 9{{\alpha }_{1}}{{\alpha }_{2}} + \alpha _{2}^{2}} \right)$

Полиномы ${{f}_{X}}(h)$ имеют более громоздкий вид. Поэтому удобнее привести численные значения коэффициентов полиномов ${{f}_{X}}(h)$ при заданном отношении радиусов. Они приведены в таблицах 2–4 соответственно для отношений радиусов ${{R}_{2}}{\text{/}}{{R}_{1}}$ = {1, 3, 10}.

Таблица 2.

Численные значения $f_{X}^{0}$, $f_{X}^{1}$, $f_{X}^{2}$, $f_{X}^{3}$ для коэффициентов кинетической энергии при ${{R}_{2}}{\text{/}}{{R}_{1}} = 1$

$X$ $f_{X}^{0}{\text{/}}R_{1}^{3}$ $f_{X}^{1}{\text{/}}R_{1}^{3}$ $f_{X}^{2}{\text{/}}R_{1}^{3}$ $f_{X}^{3}{\text{/}}R_{1}^{3}$
${{A}_{1}}$ 0.19257 0.03834 –0.05783 –0.0064
$B$ 0.07513 –0.01375 –0.03339 –0.00841
${{A}_{2}}$ 0.19257 0.03834 –0.05783 –0.0064
${{C}_{{11}}}$ 0.07315 0.02403 –0.09609 0.00345
${{C}_{{12}}}$ 0.28191 –0.12419 –0.04413 –0.00127
${{C}_{{21}}}$ 0.28191 –0.12419 –0.04413 –0.00127
${{C}_{{22}}}$ 0.07315 0.02403 –0.09609 0.00345
${{D}_{1}}$ 1.05634 –0.02539 –0.02837 0.00549
$E$ 0.52088 –0.20799 0.02508 –0.00506
${{D}_{2}}$ 1.05634 –0.02539 –0.02837 0.00549
Таблица 3.

Численные значения $f_{X}^{0}$, $f_{X}^{1}$, $f_{X}^{2}$, $f_{X}^{3}$ для коэффициентов кинетической энергии при ${{R}_{2}}{\text{/}}{{R}_{1}} = 3$

$X$ $f_{X}^{0}{\text{/}}R_{1}^{3}$ $f_{X}^{1}{\text{/}}R_{1}^{3}$ $f_{X}^{2}{\text{/}}R_{1}^{3}$ $f_{X}^{3}{\text{/}}R_{1}^{3}$
${{A}_{1}}$ 0.22593 0.15456 –0.12096 –0.00727
$B$ 0.25356 0.03244 –0.08352 –0.00943
${{A}_{2}}$ 4.64004 0.05236 –0.0598 –0.02441
${{C}_{{11}}}$ 0.18871 0.14903 –0.22995 0.04843
${{C}_{{12}}}$ 0.65753 0.07208 –0.20445 –0.00445
${{C}_{{21}}}$ 1.81240 –0.59585 0.00243 –0.01
${{C}_{{22}}}$ 0.3404 0.06923 –0.13721 –0.03191
${{D}_{1}}$ 1.18701 –0.07682 –0.03699 0.01731
$E$ 2.32151 –0.45781 –0.00579 0.00787
${{D}_{2}}$ 27.21124 0.019 –0.08045 –0.00683
Таблица 4.

Численные значения $f_{X}^{0}$, $f_{X}^{1}$, $f_{X}^{2}$, $f_{X}^{3}$ для коэффициентов кинетической энергии при ${{R}_{2}}{\text{/}}{{R}_{1}} = 10$

$X$ $f_{X}^{0}{\text{/}}R_{1}^{3}$ $f_{X}^{1}{\text{/}}R_{1}^{3}$ $f_{X}^{2}{\text{/}}R_{1}^{3}$ $f_{X}^{3}{\text{/}}R_{1}^{3}$
${{A}_{1}}$ 0.25175 0.29173 –0.11741 –0.04509
$B$ 0.45156 0.20392 –0.1117 –0.04079
${{A}_{2}}$ 167.02413 0.16238 –0.09517 –0.03972
${{C}_{{11}}}$ 0.28907 0.33643 –0.31326 0.03108
${{C}_{{12}}}$ 0.98412 0.45188 –0.23408 –0.08365
${{C}_{{21}}}$ 8.51296 –1.12663 –0.13156 0.01537
${{C}_{{22}}}$ 0.77253 0.34336 –0.20516 –0.07911
${{D}_{1}}$ 1.35988 –0.10779 –0.0565 0.02402
$E$ 9.22154 –0.64576 –0.09002 0.012
${{D}_{2}}$ 1000.41854 0.18447 –0.10969 –0.03978

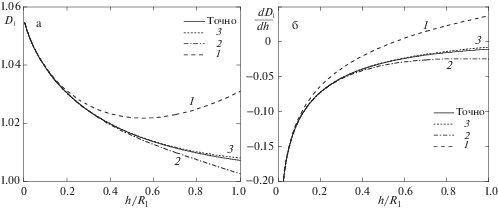
Сходимость приближений коэффициентов ${{A}_{1}}$ и ${{D}_{1}}$ полиномами первой (1), второй (2) и третьей степени (3) к точным зависимостям (жирная линия) показана на рис. 2а и 3а, а для их производных сходимость показана на рис. 2б и 3б. Как видно из рисунков с увеличением степени полинома наблюдается значительное повышение точности. рис. 3

Рис. 2.

Сходимость приближений (а) коэффициента ${{A}_{1}}$ и (б) производной $d{{A}_{1}}{\text{/}}dh$ полиномами первой (1), второй (2) и третьей степени (3) к точным зависимостям (сплошная линия).

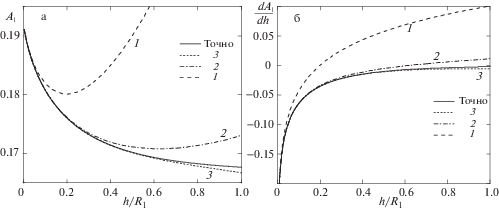
Рис. 3.

Сходимость приближений (а) коэффициента ${{D}_{1}}$ и (б) производной $d{{D}_{1}}{\text{/}}dh$ полиномами первой (1), второй (2) и третьей степени (3) к точным зависимостям (сплошная линия).

3.5. Гидродинамическая сила. Гидродинамическая сила, действующая на сферу, для произвольного расстояния между ними определяется по формуле Лагранжа:

(3.18)
${{F}_{1}} = - \frac{d}{{dt}}\frac{{\partial T}}{{\partial {{{\dot {z}}}_{1}}}} + \frac{{\partial T}}{{\partial {{z}_{1}}}} = \frac{d}{{dt}}\frac{{\partial T}}{{\partial {{u}_{1}}}} + \frac{{\partial T}}{{\partial r}} = \frac{d}{{dt}}\frac{{\partial T}}{{\partial {{u}_{1}}}} + \frac{{\partial T}}{{\partial h}}$

С помощью этой формулы и асимптотических разложений коэффициентов кинетической энергии можно получить разложение силы вблизи контакта с любой степенью точности по $h$. Главная асимптотика гидродинамической силы равна

(3.19)
$\frac{{{{F}_{1}}}}{{2\pi {{\rho }_{l}}}} = - \frac{d}{{dt}}\left( {\frac{1}{2}{{p}^{2}}hln\left( {\frac{h}{{2p}}} \right)\dot {h}} \right) + \frac{1}{4}{{p}^{2}}ln\left( {\frac{h}{{2p}}} \right){{\dot {h}}^{2}} + O({{h}^{0}}),$
где $p = {{R}_{1}}{{R}_{2}}{\text{/}}({{R}_{1}} + {{R}_{2}})$, $h = r - {{R}_{1}} - {{R}_{2}},$ $\dot {h} = - {\kern 1pt} ({{u}_{1}} + {{u}_{2}} + {{\dot {R}}_{1}} + {{\dot {R}}_{2}})$. Асимптотическое выражение (3.19) (совпадающая с ранее найденной методом тонкого слоя асимптотикой [40]) содержит логарифмическую особенность, которую трудно получить, если представлять кинетическую энергию в виде конечного разложения по обратным степеням расстояния между центрами пузырьков $r$.

В частом случае ${{u}_{2}} = {{\dot {R}}_{2}} = 0$, ${{R}_{2}} \to \infty $ (сфера у стенки) формула (3.19) принимает вид [31]

(3.20)
$\frac{{{{F}_{1}}}}{{2\pi {{\rho }_{l}}}} = - \frac{1}{4}R_{1}^{2}ln\left( {\frac{h}{{{{R}_{1}}}}} \right){{({{u}_{1}} + {{\dot {R}}_{1}})}^{2}} + O({{h}^{0}})$

При рассмотрении расширяющейся по закону $R = \beta {{t}^{{1/2}}}$ сферы, находящейся в контакте с плоскостью, ранее [41] было получено, что сила притяжения к плоскости равна $F = 0.29\pi {{\beta }^{4}}{{\rho }_{l}}$. Этот результат согласуется с силой $F = 0.288954\pi {{\beta }^{4}}{{\rho }_{l}}$, найденной по асимптотическим разложениям данной работы.

Таким образом, полученные разложения для сил взаимодействия двух сфер переменного радиуса обобщают все известные до сих пор результаты.

Заключение. Получено точное решение краевой задачи для функции тока в случае двух сфер переменных радиусов. Оно обобщает решение для твердых сфер. По найденной функции тока выведен новый вид кинетической энергии жидкости, в котором коэффициенты квадратичной формы представлены рядами. Показана тождественность новых рядов с ранее полученными рядами [20] и [21–23]. Преимущество новых рядов заключается в возможности их переразложения по зазору между сферами вместо обычно используемого расстояния между центрами пузырьков. Используя новую форму кинетической энергии, найдены асимптотические разложения коэффициентов кинетической энергии вблизи контакта. Доказано, что остаточный член разложения экспоненциально мал. Найденные асимптотические выражения обобщают все известные до сих пор результаты. Они необходимы для описания динамики сферических пузырьков вблизи контакта, а так же для анализа возможности их слияния (например, при акустическом воздействии на них).

Автор выражает благодарность Петрову А.Г. за полезные замечания и продуктивные обсуждения. Работа выполнена по теме государственного задания (№ госрегистрации АААА-А20-120011690138-6).

Список литературы

  1. Bjerknes V.F.K. Field of Force. New York: Columbia Univ. Press, 1906. 136 p.

  2. Zilonova E., Solovchuk M., Sheu T.W.H. Dynamics of bubble-bubble interactions experiencing viscoelastic drag // Phys. Rev. E. 2019. V. 99. № 2. P. 023109.

  3. Doinikov A.A., Bouakaz A. Theoretical model for coupled radial and translational motion of two bubbles at arbitrary separation distances // Phys. Rev. E. 2015. V. 92. № 4. P. 043001.

  4. Jiao J., He Y., Kentish S.E., Ashokkumar M., Manasseh R., Lee J. Experimental and theoretical analysis of secondary Bjerknes forces between two bubbles in a standing wave // Ultrasonics. 2015. V. 58. P. 35–42.

  5. Cleve S., Guédra M., Inserra C. et al. Surface modes with controlled axisymmetry triggered by bubble coalescence in a high-amplitude acoustic field // Phys. Rev. E. 2018. V. 98. № 3. P. 033115.

  6. Казанцев В.Ф. Движение газовых пузырьков в жидкости под действием сил Бьеркнеса, возникающих в акустическом поле // Докл. АН СССР. 1959. Т. 129. № 1. С. 64–67.

  7. Crum L.A. Bjerknes forces on bubbles in a stationary sound field // J. Acoust. Soc. America. 1975. V. 57. № 6. P. 1363–1370.

  8. Порфирьев Н.П. Силы взаимодействия между двумя осциллирующими в идеальной жидкости сферами // Динамика сплошной среды с нестационарными границами. ЧГУ, Чебоксары, 1984. С. 95–103.

  9. Воинов О.В., Петров А.Г. Движение сферы переменного объема в идеальной жидкости около плоской поверхности // Изв. АН СССР. МЖГ. 1971. № 5. С. 94–103.

  10. Буров А.В. О движении двух пульсирующих шаров в идеальной несжимаемой жидкости // Изв. АН СССР. МЖГ. 1983. Т. 3. С. 159 – 162.

  11. Кузнецов Г.Н., Щукин И.Е. Взаимодействие пульсирующих пузырьков в вязкой жидкости // Акустич. ж. 1972. Т. 18. № 4. С. 565–570.

  12. Doinikov A.A. Translational motion of two interacting bubbles in a strong acoustic field // Phys. Rev. E. 2001. T. 64. № 2. P. 026301.

  13. Harkin A., Kaper T.J., Nadim A.L.I. Coupled pulsation and translation of two gas bubbles in a liquid // J. Fluid Mech. 2001. V. 445. P. 377–411.

  14. Аганин A.A., Давлетшин А.И. Моделирование взаимодействия газовых пузырьков в жидкости с учетом их малой несферичности // Матем. модел. 2009. Т. 21. № 6. С. 89–102.

  15. Петров А.Г. Вынужденные колебания в жидкости двух газовых пузырей в окрестности их контакта // Изв. РАН МЖГ. 2011. № 4. С. 81–99.

  16. Jiao J., He Y., Leong T., Kentish S.E. et al. Experimental and theoretical studies on the movements of two bubbles in an acoustic standing wave field // J. Phys. Chem. B. 2013. V. 117. № 41. P. 12549–12555.

  17. Jiao J., He Y., Yasui K., Kentish S.E. et al. Influence of acoustic pressure and bubble sizes on the coalescence of two contacting bubbles in an acoustic field // Ultrason. Sonochem. 2015. V. 22. P. 70–77.

  18. Garbin V., Cojoc D., Ferrari E. et al. Changes in microbubble dynamics near a boundary revealed by combined optical micromanipulation and high-speed imaging // Appl. Phys. Lett. 2007. V. 90. P. 114103.

  19. Кобелев Ю.А., Островский Л.А., Сутин А.М. Эффект самопросветления для акустических волн в жидкости с пузырьками газа // Письма в ЖЭТФ. 1979. Т. 30. № 7. С. 423–425.

  20. Hicks W.M. On the motion of two spheres in a fluid // Phil. Trans. Roy. Soc. London. 1880. № 171. P. 455–492.

  21. Воинов О.В. Движение двух сфер переменных радиусов в идеальной жидкости // В сб.: Науч. конференция. Ин-т механ. МГУ. Тезисы докл. М.: МГУ, 1970. С. 10–12

  22. Воинов О.В. Движение идеальной жидкости около двух сфер с радиальными скоростями на поверхности // Вестн. МГУ. 1969. № 5. С. 83–88.

  23. Воинов О.В., Петров А.Г. Движение пузырей в жидкости // Итоги науки и техники. Механика жидкости и газа. 1976. Т. 10. С. 86–147.

  24. Hicks W.M. On the problem of two pulsating spheres in a fluid // Proc. Camb. Phil. Soc. 1879. vol. III.

  25. Hicks W.M. On the problem of two pulsating spheres in a fluid (part II) // Proc. Camb. Phil. Soc. 1879. vol. IV.

  26. Selby A.L. On two pulsating spheres in a liquid // London, Edinburgh, and Dublin Phil. Mag. & J. Sci. 1890. V. 29. № 176. P. 113–123.

  27. Jeffery G.B. On a form of the solution of Laplace’s equation suitable for problems relating to two spheres // Proc. Roy. Soc. London. Ser. A. 1912. V. 87. № 593. P. 109–120.

  28. Neumann C. Hydrodynamische untersuchungen: nebst einem Anhange über die Probleme der Elektrostatik und der magnetischen Induction. Leipzig: Druck und Verlag von B.G. Teubner, 1883. 318 pp.

  29. Bentwich M., Miloh T. On the exact solution for the two-sphere problem in axisymmetrical potential flow // J. Appl. Mech. 1978. V. 45. № 3. P. 463–468.

  30. Порфирьев Н.П. Движение шара в жидкости перпендикулярно к твердой стенке и к невозмущенному уровню свободной поверхности // Динамика сплошной среды с нестационарными границами. ЧГУ, Чебоксары, 1979. С. 80–100.

  31. Порфирьев Н.П. Взаимодействие пульсирующих в идеальной жидкости сферы с твердой стенкой // Проблемы гидродинамики больших скоростей. Чебоксары. 1993. С. 201–214.

  32. Воинов О.В. О движении двух сфер в идеальной жидкости // ПММ. 1969. Т. 33. № 4. С. 659–667.

  33. Сандуляну Ш.В., Петров А.Г. Трехчленные разложения коэффициентов кинетической энергии идеальной жидкости при движении в ней двух сфер вблизи их контакта // Докл. РАН. 2018. Т. 483. № 4. С. 389–393.

  34. Raszillier H., Guiasu I., Durst F. Optimal approximation of the added mass matrix of two spheres of unequal radii by an asymptotic short distance expansion // ZAMM. 1990. V. 70. № 2. P. 83–90.

  35. Ламб Г. Гидромеханика. М.: Гостехиздат, 1947. 928 с.

  36. Уиттекер Э.Т., Ватсон Д.Н. Курс современного анализа. Т. 1, 2. М.: Физматлит, 1963.

  37. Maksimov A.O., Yusupov V.I. Coupled oscillations of a pair of closely spaced bubbles // Europ. J. Mech.-B/Fluids. 2016. V. 60. P. 164–174.

  38. Maksimov A.O., Polovinka Y.A. Scattering from a pair of closely spaced bubbles // J. Acoust. Soc. America. 2018. V. 144. № 1. P. 104–114.

  39. Dingle R.B. Asymptotic Expansions: Their Derivation and Interpretation. London: Academic Press, 1973.

  40. Петров А.Г., Харламов А.А. Пространственные задачи гидродинамического взаимодействия тел в вязкой жидкости в окрестности их контакта // Изв. РАН. МЖГ. 2013. № 5. С. 14–25.

  41. Witze C.P., Schrock V.E., Chambre P.L. Flow about a growing sphere in contact with a plane surface // Intern. J. Heat and Mass Transfer. 1968. V. 11. № 11. P. 1637–1652.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал