1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 84, № 3, 2020

Прикладная математика и механика, 2020, T. 84, № 3, стр. 375-386

МОДЕЛИРОВАНИЕ ВОЛНОВЫХ ПРОЦЕССОВ В ГЕОЛОГИЧЕСКИХ ТРЕЩИНОВАТЫХ СРЕДАХ С ИСПОЛЬЗОВАНИЕМ МОДЕЛИ ШОНБЕРГА

П. В. Стогний 1, *, Н. И. Хохлов 2, **, И. Б. Петров 1, 2, ***

1 Московский физико-технический институт
Долгопрудный, Россия

2 Научно-исследовательский институт системных исследований РАН
Москва, Россия

* E-mail: stognii@phystech.edu
** E-mail: k_h@inbox.ru
*** E-mail: petrov@mipt.ru

Поступила в редакцию 29.11.2019
После доработки 11.03.2020
Принята к публикации 26.03.2020

Полный текст (PDF)

Аннотация

Для описания поведения геологических сред с наличием трещин Шонбергом была разработана механико-математическая модель, получившая применение в работах, связанных с сейсморазведкой нефтяных месторождений. В представленной работе предлагается использование этой модели при расчетах волновых процессов в геологических средах с помощью сеточно-характеристического метода. Искомыми функциями при этом являются компоненты вектора скорости и тензора напряжений в точках расчетной сетки на границе с трещиной. Проведены расчеты распространения сейсмического импульса в однородной упругой среде с трещиной для предельного случая полного отражения волнового фронта от границы трещины. Проведены сравнительные расчеты характеристик волнового поля с использованием моделей Шонберга и двухбереговой трещины с помощью сеточно-характеристического метода. Результаты расчетов показали удовлетворительное соответствие результатов, полученных по обеим используемым моделям.

Ключевые слова: сейсморазведка, трещины Шонберга, сеточно-характеристический метод

Сейсморазведка является широко используемым методом поиска залежей углеводородов [1]. Во время проведения сейсморазведочных работ, на дневной поверхности устанавливается система из источника и приемников сейсмического сигнала. Сигнал от источника отражается от геологических неоднородностей, что регистрируется приемниками, находящимися на дневной поверхности (амплитуды пришедших волн в определенные моменты времени). В дальнейшем при помощи расчетов волновых полей и сейсмограмм определяются местоположение, размер и другие характеристики залежей. Сейсмограммы также регистрируют отраженные волны от таких неоднородностей, как каверны, ледовые образования, границы между слоями в грунте, что затрудняет исследование “полезных” отраженных волн от залежей углеводородов, в результате чего процесс анализа сейсмограмм становится более сложным.

В представленной работе проводится численное моделирование динамического поведения геологического массива, в частности вычисляются значения тензора напряжений и вектора скорости в каждой расчетной точке. Численное решение задачи позволяет подробно изучить влияние различных неоднородностей (каверн, ледовых образований, поверхностей раздела сред) на вид сейсмограмм. Численное решение прямой динамической задачи позволяет с большей точностью интерпретировать данные натурных экспериментов, а также сокращать затраты на дальнейшие геологические работы на исследуемой территории. Математическое моделирование позволяет учитывать наличие различных неоднородностей, в частности, трещин [2], что позволяет получать достаточно точные волновые картины в геологической среде, а также более точно интерпретировать сейсмограммы.

В настоящее время существует несколько механико-математических моделей трещин, позволяющих учесть в расчетах их наличие в геологическом массиве. Например, модель тонкого вертикального пласта (TLM – thin layer model) [3], для реализации которой необходимо использовать очень подробные расчетные сетки, что требует значительных вычислительных затрат. В работе [4], авторы используют псевдоспектральный метод для моделирования распространения упругих волн в геологических средах с трещинами. В работах [5, 6] авторами построены континуальные модели слоистых сред с линейными и нелинейными контактными условиями проскальзывания и отрыва на межслойных границах, а также предложен алгоритм численного расчета распространения волн в таких средах [7, 8]. Также существует метод, использующий вспомогательные расчетные сетки для учета трещин в модели [9].

Еще одной широко известной математической моделью трещин является модель линейного проскальзывания (linear slip model, LSM) Шонберга [10]. В данной модели смещение на границе трещины пропорционально силе сцепления на поверхности трещины. Трещина в модели LSM характеризуется двумя параметрами – длиной и параметром раскрытости. Последний можно вычислить теоретически или с помощью лабораторного эксперимента [11, 12]. В настоящей работе предлагается использовать модель LSM с применением сеточно-характеристического метода.

Сеточно-характеристический метод хорошо зарекомендовал себя при решении задач сейсморазведки [13–16]. При проведении расчетов с его помощью могут быть использованы как регулярные, так и нерегулярные расчетные сетки.

В данной работе предлагается использовать модель трещины LSM при численном решении двумерных задач (расположение трещины представлено на рис. 1). В результате разработан и реализован алгоритм вычисления значений компонент вектора скорости и тензора напряжений в точках на границах трещины для линейно-упругой среды. Для проверки корректности разработанного алгоритма проводится тестовый расчет распространения волнового фронта в однородной среде с трещиной с параметрами, соответствующими полному отражению волны для продольной компоненты тензора напряжений Коши. Также проводится сравнение расчетов по предложенному алгоритму на основе модели LSM с расчетами по ранее разработанной модели двухбереговой бесконечно тонкой трещины [17–19] с использованием сеточно-характеристического метода.

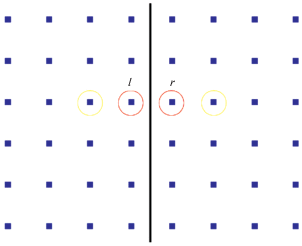
Рис. 1.

Схематичное изображение вычисления значений тензора напряжений и скорости в точках на границе трещины.

1. Численный метод и определяющие уравнения. Для расчета компонент тензора напряжений и вектора скорости в геологической среде с трещиной использовалась система уравнений теории упругости [14]:

(1.1)
$\begin{gathered} \rho \frac{\partial }{{\partial t}}v = {{(\nabla \cdot \sigma )}^{T}} \\ \frac{\partial }{{\partial t}}\sigma = \lambda (\nabla \cdot v)I + \mu ((\nabla \cdot v) + {{(\nabla \cdot v)}^{T}}) \\ \end{gathered} $

Здесь $\rho $ – плотность среды, $v$ – скорость распространения сейсмических волн, $\sigma $ – тензор напряжений Коши, t – время, $\lambda $ и $\mu $ – параметры Ляме, определяющие свойства упругого материала, I – единичный тензор.

Для решения системы (1.1) применялся сеточно-характеристический метод, для использования которого представим систему (1.1) в следующем виде:

(1.2)
$\frac{{\partial q}}{{\partial t}} + {{A}_{x}}\frac{{\partial q}}{{\partial x}} + {{A}_{y}}\frac{{\partial q}}{{\partial y}} = 0,$
где вектор искомого решения $q = \left\{ {{{\sigma }_{{xx}}},{{\sigma }_{{yy}}},{{\sigma }_{{xy}}},{{v}_{x}},{{v}_{y}}} \right\}$, матрицы Ax и Ay составлены из коэффициентов системы (1.1) и имеют следующий вид:

(1.3)
${{A}_{x}} = \left( {\begin{array}{*{20}{c}} 0&0&0&{ - \lambda - 2\mu }&0 \\ 0&0&0&{ - \lambda }&0 \\ 0&0&0&0&{ - \mu } \\ { - 1{\text{/}}\rho }&0&0&0&0 \\ 0&0&{ - 1{\text{/}}\rho }&0&0 \end{array}} \right),\quad {{A}_{y}} = \left( {\begin{array}{*{20}{c}} 0&0&0&0&{ - \lambda } \\ 0&0&0&0&{ - \lambda - 2\mu } \\ 0&0&0&{ - \mu }&0 \\ 0&0&{ - 1{\text{/}}\rho }&0&0 \\ 0&{ - 1{\text{/}}\rho }&0&0&0 \end{array}} \right)$

Применяем метод расщепления по пространственным координатам, получаем две одномерные системы уравнений:

(1.4)
$\frac{{\partial q}}{{\partial t}} + {{A}_{i}}\frac{{\partial q}}{{\partial i}} = 0,\quad i = x,y$

Рассмотрим систему (1.4) для координаты x:

(1.5)
$\frac{{\partial q}}{{\partial t}} + {{A}_{x}}\frac{{\partial q}}{{\partial x}} = 0$

В силу того, что система (1.5) является гиперболической, ее можно представить в следующем виде [20]:

(1.6)
$\frac{{\partial q}}{{\partial t}} + {{\Omega }_{x}}{{\Lambda }_{x}}\Omega _{x}^{{ - 1}}\frac{{\partial q}}{{\partial x}} = 0$

Здесь ${{\Omega }_{x}}$ – матрица из собственных векторов матрицы Ax, ${{\Lambda }_{x}}$ – диагональная матрица с собственными значениями на диагонали. Собственные значения как матрицы Ax, так и матрицы Ay, равны {–cp, cp, –cs, cs, 0}, где cp и cs – продольная и поперечная скорости звука, соответственно, которые можно вычислить по формулам:

(1.7)
${{c}_{p}} = \sqrt {(\lambda + 2\mu ){\text{/}}\rho } ,\quad {{c}_{s}} = \sqrt {\mu {\text{/}}\rho } $

Аналогично можно рассмотреть систему (1.4) для координаты y.

Далее делаем замену переменных $\omega = \Omega _{x}^{{ - 1}}q$, после чего система (1.6) принимает вид:

(1.8)
$\frac{{\partial \omega }}{{\partial t}} + {{\Lambda }_{x}}\frac{{\partial \omega }}{{\partial x}} = 0$

Система (1.8) состоит из пяти уравнений, каждое из которых можно решить при помощи разностной схемы. В данной работе уравнения из системы (1.8) решались сеточно-характеристическим методом 2-го порядка точности.

2. Использование модели LSM в сеточно-характеристическом методе. Рассмотрим алгоритм вычисления значений компонент тензора напряжений и вектора скорости на границе трещины подробнее. На рис. 1 представлено схематичное изображение расчетной сетки вблизи трещины. Индексами l и r обозначены узлы сетки слева и справа от трещины, соответственно. Для них вводятся граничные условия в соответствии с моделью LSM [10], которые выглядят следующим образом:

(2.1)
$\sigma _{{xx}}^{l} = \sigma _{{xx}}^{r}$
(2.2)
$\sigma _{{xy}}^{l} = \sigma _{{xy}}^{r}$
(2.3)
$\frac{{\partial {{\sigma }_{{xx}}}}}{{\partial t}} = {{K}_{T}}(v_{x}^{r} - v_{x}^{l})$
(2.4)
$\frac{{\partial {{\sigma }_{{xy}}}}}{{\partial t}} = {{K}_{N}}(v_{y}^{r} - v_{y}^{l})$

Уравнения (2.1), (2.2) означают равенство нормальной и касательной компонент тензора напряжений слева и справа от трещины. Уравнения (2.3) и (2.4) позволяют вычислить эти компоненты тензора напряжений. Для этого вводятся дополнительные параметры, характеризующие трещину – параметры раскрытости трещины KN и KT.

Сначала рассмотрим алгоритм вычисления значений тензора напряжений и вектора скорости в точках слева от трещины. Уравнения (2.3), (2.4) позволяют вычислить две из пяти составляющих неизвестного вектора q из (1.1), ${{\sigma }_{{xx}}}$ и ${{\sigma }_{{xy}}}$. В данной работе уравнения (2.3), (2.4) решались с помощью одношагового метода Эйлера:

(2.5)
$\sigma _{{xx}}^{{l,n + 1}} = \sigma _{{xx}}^{{l,n}} + {{K}_{T}}\Delta t(v_{x}^{{r,n}} - v_{x}^{{l,n}})$
(2.6)
$\sigma _{{xy}}^{{l,n + 1}} = \sigma _{{xy}}^{{l,n}} + {{K}_{N}}\Delta t(v_{y}^{{r,n}} - v_{y}^{{l,n}})$

Далее, для простоты обозначений индекс l везде опускается.

Для вычисления остальных компонент вектора q рассмотрим подробнее уравнение (1.8), которое записано для преобразованных переменных $\omega = \Omega _{x}^{{ - 1}}q$. Это уравнение состоит из 5 независимых уравнений:

$\frac{{\partial {{\omega }_{{{{\sigma }_{{xx}}}}}}}}{{\partial t}} + {{c}_{p}}\frac{{\partial {{\omega }_{{{{\sigma }_{{xx}}}}}}}}{{\partial x}} = 0$
$\frac{{\partial {{\omega }_{{{{\sigma }_{{yy}}}}}}}}{{\partial t}} - {{c}_{p}}\frac{{\partial {{\omega }_{{{{\sigma }_{{yy}}}}}}}}{{\partial x}} = 0$
(2.7)
$\frac{{\partial {{\omega }_{{{{\sigma }_{{xy}}}}}}}}{{\partial t}} + {{c}_{s}}\frac{{\partial {{\omega }_{{{{\sigma }_{{xy}}}}}}}}{{\partial x}} = 0$
$\frac{{\partial {{\omega }_{{{{v}_{x}}}}}}}{{\partial t}} - {{c}_{s}}\frac{{\partial {{\omega }_{{{{v}_{x}}}}}}}{{\partial x}} = 0$
$\frac{{\partial {{\omega }_{{{{v}_{y}}}}}}}{{\partial t}} = 0$

Далее, для простоты, вместо обозначений ${{\omega }_{{{{\sigma }_{{xx}}}}}}$, ${{\omega }_{{{{\sigma }_{{yy}}}}}}$, ${{\omega }_{{{{\sigma }_{{xy}}}}}}$, ${{\omega }_{{{{v}_{x}}}}}$, ${{\omega }_{{{{v}_{y}}}}}$ будут применяться обозначения ${{\omega }_{{xx}}}$, ${{\omega }_{{yy}}}$, ${{\omega }_{{xy}}}$, ${{\omega }_{x}}$, ${{\omega }_{y}}$, соответственно. Для решения уравнений (2.7) на границе с трещиной применяется следующая схема [21]:

$\omega _{{x{{x}_{i}}}}^{{n + 1}} = \omega _{{x{{x}_{i}}}}^{n} + \frac{{{{c}_{p}}\Delta t}}{{2h}}(\omega _{{x{{x}_{{i + 1}}}}}^{n} - \omega _{{x{{x}_{i}}}}^{n})$
$\omega _{{y{{y}_{i}}}}^{{n + 1}} = \omega _{{y{{y}_{i}}}}^{n} - \frac{{{{c}_{p}}\Delta t}}{{2h}}(\omega _{{y{{y}_{i}}}}^{n} - \omega _{{y{{y}_{{i - 1}}}}}^{n})$
(2.8)
$\omega _{{x{{y}_{i}}}}^{{n + 1}} = \omega _{{x{{y}_{i}}}}^{n} + \frac{{{{c}_{s}}\Delta t}}{{2h}}(\omega _{{x{{y}_{{i + 1}}}}}^{n} - \omega _{{x{{y}_{i}}}}^{n})$
$\omega _{{{{x}_{i}}}}^{{n + 1}} = \omega _{{{{x}_{i}}}}^{n} - \frac{{{{c}_{s}}\Delta t}}{{2h}}(\omega _{{{{x}_{i}}}}^{n} - \omega _{{{{x}_{{i - 1}}}}}^{n})$
$\omega _{{{{y}_{i}}}}^{{n + 1}} = \omega _{{{{y}_{i}}}}^{n},$
где h – шаг равномерной декартовой прямоугольной сетки. Значения $\omega _{{y{{y}_{i}}}}^{{n + 1}}$, $\omega _{{{{x}_{i}}}}^{{n + 1}}$ и $\omega _{{{{y}_{i}}}}^{{n + 1}}$ вычисляются с помощью известных значений в соответствующих точках на предыдущем шаге по времени. Остается найти значения $\omega _{{x{{x}_{i}}}}^{{n + 1}}$ и $\omega _{{x{{y}_{i}}}}^{{n + 1}}$, для вычисления которых используются условия (2.1), (2.2). Данные условия можно записать в следующем виде, учитывая, что $q = {{\Omega }_{x}}\omega $:

(2.9)
$\Omega _{{{{x}_{{{{\sigma }_{{xx}}}}}}}}^{l}{{\omega }^{l}} = \Omega _{{{{x}_{{{{\sigma }_{{xx}}}}}}}}^{r}{{\omega }^{r}}$
(2.10)
$\Omega _{{{{x}_{{{{\sigma }_{{xy}}}}}}}}^{l}{{\omega }^{l}} = \Omega _{{{{x}_{{{{\sigma }_{{xy}}}}}}}}^{r}{{\omega }^{r}}$

Здесь индексы ${{\sigma }_{{xx}}}$, ${{\sigma }_{{xy}}}$ у матрицы ${{\Omega }_{x}}$ обозначают строки матрицы ${{\Omega }_{x}}$, соответствующие компонентам ${{\sigma }_{{xx}}}$ и ${{\sigma }_{{xy}}}$ вектора q. Уравнения (2.9), (2.10), вместе с (2.5), (2.6), позволяют найти оставшиеся неизвестные $\omega _{{x{{x}_{i}}}}^{{n + 1}}$ и $\omega _{{x{{y}_{i}}}}^{{n + 1}}$ из (2.8).

Значения справа от трещины вычисляются аналогично, за исключением того, что значения ${{\sigma }_{{xx}}}$ и ${{\sigma }_{{xy}}}$, вычисленные слева, переносятся в соответствующие точки справа от трещины в связи с условиями (2.1), (2.2) .

В соответствии с сеточно-характеристическим методом, для вычисления искомых функций на n-м шаге по времени (при вычислении точек на шаге n + 1) вводятся дополнительный узел (“ghost”-узел [22]) i + 1 для сетки слева от трещины и дополнительный узел i – 1 для сетки справа от трещины независимо друг от друга. В данные узлы заносятся значения из соотношений (2.8). Таким образом, описанный алгоритм позволяет независимо проводить вычисления для расчетных сеток справа и слева от трещины за исключением необходимости обмена значениями ${{\sigma }_{{xx}}}$ и ${{\sigma }_{{xy}}}$ на границе.

3. Результаты тестовых расчетов распространения сейсмического импульса в геологической среде с трещиной с использованием модели шонберга. Для проверки корректности разработанного алгоритма на основе модели трещины LSM, был проведен расчет волнового поля от трещины с нулевыми параметрами раскрытости KN и KT, что соответствует случаю полного отражения волны для продольной компоненты тензора напряжений (sxx) от трещины. Размер геологической среды, в которой находилась трещина, был равен 4.5 × 6 м2. Физические свойства геологической среды были следующими: продольная скорость звука была равна 2 м/с, поперечная скорость звука – 1 м/c, плотность – 1 кг/м3. Трещина располагалась вертикально, параллельно оси y на координате x = 3 м.

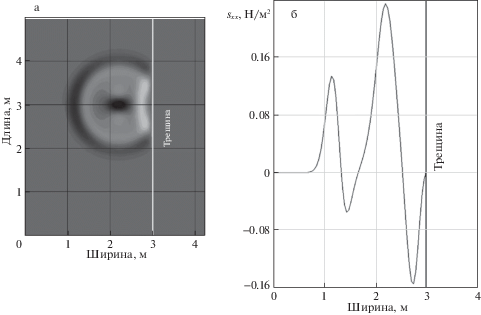
Проводилось моделирование распространения начального импульса, заданного следующими параметрами. В начальный момент времени скорость во всей области была равна нулю, значение продольной компоненты тензора напряжений было равно 1, значения всех остальных компонент тензора напряжений было равно нулю. В расчетах шаг по координатам x, y составлял 0.025 м, шаг по времени – 0.005 с. На рис. 2а–4а представлены карты продольной компоненты тензора напряжений в последовательные моменты времени (0 с, 0.025 с и 0.05 с, соответственно) в результате распространения сейсмической волны в однородной среде с трещиной (отмечена белой линией). На рис. 2б–4б представлены профили продольной компоненты тензора напряжений в моменты времени 0 с, 0.025 с и 0.05 с, соответственно. Из рис. 2–4 следует, что волна полностью отражается от трещины, причем значение амплитуды продольной компоненты тензора напряжений (sxx) отраженной волны совпадает со значением амплитуды до отражения от трещины (рис. 4б) с точностью до знака. Это качественно подтверждает применимость модели LSM трещины в дальнейших расчетах.

Рис. 2.

Карта (а) и профиль (б) продольной компоненты тензора напряжений sxx для момента времени t = 0 с.

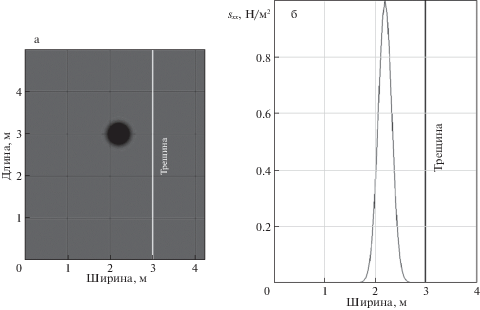
Рис. 3.

Карта (а) и профиль (б) продольной компоненты тензора напряжений sxx для момента времени t = 0.025 с.

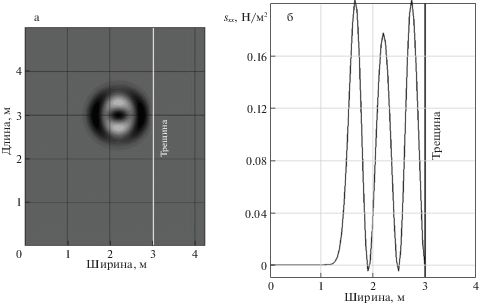
Рис. 4.

Карта (а) и профиль (б) продольной компоненты тензора напряжений sxx для момента времени t = 0.05 с.

4. Результаты сравнения разработанного алгоритма на основе модели трещины Шонберга с моделью двухбереговой бесконечно тонкой трещиной. Проводилось сравнение расчетов с использованием разработанного алгоритма на основе модели трещины LSM с расчетами с помощью модели двухбереговой бесконечно тонкой трещины (БТТ) с помощью сеточно-характеристического метода. Моделировалось распространение одиночного источника, заданного функцией Гаусса, в однородной среде с трещиной. Источник описывался следующими параметрами: скорость была равна нулю, значение продольной и поперечной компоненты тензора напряжений было равно 1, значение всех остальных компонент тензора напряжений было равно нулю. Физические свойства среды слева и справа от трещины были одинаковыми и описывались следующими параметрами: продольная скорость звука была равна 2 м/с, поперечная скорость звука – 1 м/с, плотность – 1 кг/м3. Параметры раскрытости для модели трещины LSM подбирались таким образом, чтобы максимально приблизиться к модели двухбереговой трещины [17]. Таким образом, значение параметра KN должно быть равным нулю, чтобы тангенциальные компоненты тензора напряжений слева и справа от трещины были равны нулю, а значение параметра KT должно стремиться к бесконечности, чтобы значения продольных компонент скорости были равны слева и справа от трещины. В модели LSM значение параметра KN полагалось равным нулю, KT = 100, 200, 400 для того, чтобы исследовать соответствие модели трещины LSM и модели БТТ. В расчетах шаг по координатам x, y составлял 1 м. Шаг по времени был равен 0.005 с при KT = 100, 0.0025 с при KT = 200 и 0.00125 с при KT = 400. Результаты сравнения волновых откликов (компоненты sxx) за вычетом волнового поля в отсутствие трещины для модели LSM при различных значениях KT и двухбереговой трещины представлены на рис. 5. По оси x отложена ширина модели, по оси y – значения продольной компоненты тензора напряжений sxx.

Рис. 5.

Результат моделирования волнового отклика от трещины для KT = 100 (а), 200 (б) и 400 (в). По оси y отложены значения компоненты sxx для двух моделей трещины (LSM и БТТ – двухбереговой трещины) в момент времени t = 0.5 с. Трещина расположена вертикально на значении x = 3 м.

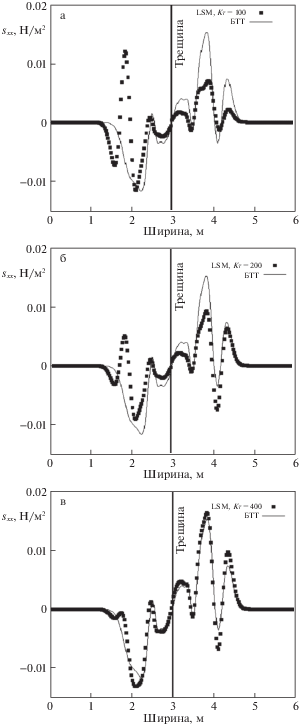
На рис. 5 сплошной линией показан волновой отклик от трещины, описанной моделью БТТ, пунктирными точками – моделью LSM. Из рис. 5 следует приближение волновых откликов от трещины при увеличении параметра раскрытости KT (рис. 5в), что соответствует уравнению (2.3). Также, результаты расчетов, полученные с использованием модели трещины LSM, имеют хорошее совпадение с моделью двухбереговой трещины. Для достижения максимального соответствия моделей необходимо устремить параметр раскрытости KT к бесконечности, что не представляется возможным.

Заключение. В данной работе представлен алгоритм применения модели трещины LSM Шонберга с использованием сеточно-характеристического метода. Разработан алгоритм расчета значений тензора напряжений и вектора скорости в точках на границе трещины, расположенной параллельно границам расчетной сетки, на структурированных сетках. Приведен метод расчета значений компонент вектора скорости и тензора напряжений в точках слева и справа от трещины для двумерного случая с помощью сеточно-характеристического метода. Дано описание “ghost”-узлов для использования представленного алгоритма в основной схеме расчета значений в точках вне границы с трещиной.

Проведены тестовые расчеты распространения импульса в однородной среде, содержащей трещину с заданной нулевой раскрытостью, для проверки правильности разработанного алгоритма. Как и предполагалось, наблюдалось полное отражение волнового фронта.

Проведено сравнение результатов расчетов с помощью модели трещины LSM (с соответствующими параметрами раскрытости) с результатами расчетов с использованием двухбереговой модели бесконечно тонкой трещины. Сравнение по значениям компоненты sxx показало соответствие результатов, полученных с использованием модели LSM и с использованием модели трещины БТТ. Модель LSM является обобщением модели бесконечно тонкой двухбереговой трещины, что позволит в дальнейшем рассматривать различные модели трещин, учитывая значения параметра раскрытости. Планируется разработка аналогичного алгоритма с использованием сеточно-характеристического метода для трещины, заданной моделью LSM Шонберга, в трехмерном случае.

Работа выполнена при финансовой поддержке РФФИ в рамках научного проекта № 19-01-00281.

Список литературы

  1. Курин Е.А. Сейсморазведка и суперкомпьютеры // Выч. мет. программирование. 2011. Т. 12. Вып. 1. С. 34–39.

  2. Khokhlov N., Stognii P. Novel approach to modelling the seismic waves in the areas with complex fractured geological structures // Minerals. 2020. V. 10. № 2.

  3. Zhan Q., Sun Q., Ren Q. et al. A discontinuous Galerkin method for simulating the effects of arbitrary discrete fractures on elastic wavepropagation // Geophys. Int. J. 2017. V. 210. № 2. P. 1219–1230.

  4. Carcione J. Scattering of elastic waves by a plane crack of finite width in a transversely isotropic medium // Int. J. Numer. Anal. Methods Geomech. 1998. V. 22. № 4. P. 263–275.

  5. Никитин И.С. Динамические модели слоистых и блочных сред с проскальзыванием, трением и отслоением // Изв. РАН. МТТ. 2008. № 4. С. 154–165.

  6. Nikitin I.S., Burago N.G., Nikitin A.D. Continuum model of the layered medium with slippage and nonlinear conditions at the interlayer boundaries // Solid State Phenom. 2017. V. 258. P. 137–140.

  7. Burago N.G., Zhuravlev A.B., Nikitin I.S. Continuum model and method of calculating for dynamics of inelastic layered medium// Math. Models &Comput. Simul. 2019. V. 11. № 3. P. 59–74.

  8. Nikitin I.S., Burago N.G., Golubev V.I., Nikitin A.D. Mathematical modeling of the dynamics of layered and block media with nonlinear contact conditions on supercomputers // J. Phys.: Conf. Ser. 2019. V. 1392. P. 012057.

  9. Zhang J., Gao H. Elastic wave modelling in 3-D fractured media: an explicit approach // Geophys. Intern. J. 2009. V. 177. № 3. P. 1233–1241.

  10. Schoenberg M. Elastic wave behavior across linear slip interfaces // J. Acoust. Soc. Amer. 1980. V. 68. № 5. P. 1516–1521.

  11. Rokhlin S., Wang Y. Analysis of boundary conditions for elastic wave interaction with an interface between two solids // J. Acoust. Soc. Amer. 1991. V. 89. № 2. P. 503–515.

  12. Santos J.E., Picotti S., Carcione J. Evaluation of the stiffness tensor of a fractured medium with harmonic experiments // Comput. Methods Appl. Mech. Eng. 2012. V. 247–248. P. 130–145.

  13. Petrov D.I. Application of grid-characteristic method to some seismic exploration problems in the Arctic // J. Phys.: Conf. Ser. 2018. V. 955.

  14. Golubev V.I. The usage of grid-characteristic method in seismic migration problems // Smart Innov., Syst. and Technol. 2019. V. 133. P. 143–155. https://doi.org/10.1007/978-3-030-06228-6_13

  15. Favorskaya A.V., Zhdanov M.S., Khokhlov N.I., Petrov I.B. Modelling the wave phenomena in acoustic & elastic media with sharp variations of physical properties using the grid-characteristic method // Geophys. Prosp. 2018. V. 66. № 8. P. 1485–1502.

  16. Khokhlov N.I., Golubev V.I. On the class of compact grid-characteristic schemes // Smart Innov., Systems & Technol. 2019. V. 133. P. 64–77. https://doi.org/10.1007/978-3-030-06228-6_7

  17. Golubev V., Khokhlov N., Grigorievyh D. et al. Numerical simulation of destruction processes by the grid-characteristic method // Proc. Comput. Sci. 2018. V. 126. P. 1281–1288. https://doi.org/10.1016/j.procs.2018.08.071

  18. Stognii P., Khokhlov N., Zhdanov M. Novel approach to modelling the elastic waves in a cluster of subvertical fractures // 81st EAGE Conference and Exhibition 2019.

  19. Stognii P., Khokhlov N., Grigorievih D. The comparison of two approaches to modelling the seismic reflection from the fractured media with the help of grid-characteristic method // 6th Scientific Conference. Tyumen 2019.

  20. Petrov I.B., Favorskaya A.V., Favorskaya M.N. et al. Development and application of computational methods // Smart Innov., Syst. & Technol. 2019. V. 133. P. 3–7.

  21. Петров И.Б., Лобанов А.И. Лекции по вычислительной математике. М.: Интернет-Университет информационных технологий, 2006.

  22. LeVeque R.J. Finite Volume Methods for Hyperbolic Problems. Cambridge Texts in Applied Mathematics. Cambridge: Univ. Press. 2002. P. 129–138.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал