Прикладная математика и механика, 2020, T. 84, № 3, стр. 341-361
ВЛИЯНИЕ ФОРМЫ ТЕЛА НА РЕШЕНИЕ НЕСВЯЗАННОЙ КВАЗИСТАТИЧЕСКОЙ ЦИКЛИЧЕСКОЙ ЗАДАЧИ ТЕРМОУПРУГОСТИ В ТЕРМИЧЕСКОМ СЛОЕ (НА ПРИМЕРЕ ТЕЛ ПРОСТОЙ ФОРМЫ)
1 МГТУ им. Н.Э. Баумана (Калужский филиал)
Калуга, Россия
* E-mail: max2901@mail.ru
Поступила в редакцию 11.12.2019
После доработки 26.03.2020
Принята к публикации 28.03.2020
Аннотация
Получены аналитические решения несвязанной квазистатической циклической задачи термоупругости для тел простой геометрической формы: полупространства, пластины, пространства с цилиндрическим каналом, цилиндра, пространства со сферической полостью, шара. Решения, представляющие собой тригонометрические ряды Фурье по времени, с помощью замены пространственной переменной преобразованы к виду, удобному для исследования колебаний температуры и термоциклических напряжений в термическом слое. Для найденных решений установлены простые асимптотические зависимости, пригодные при больших радиусах кривизны поверхности и размерах тела. Изучено влияние формы тела на колебания температуры и термоциклические напряжения в термическом слое.
1. Введение. В ряде технических устройств имеет место циклический теплообмен между их элементами и жидкой средой, в результате которого в деталях возбуждаются колебания температуры, сопровождающиеся термоциклическими напряжениями. Таким образом, колебания температуры деталей установки влияют не только на ее эффективность, но и надежность. Отдельный интерес представляют высокочастотные колебания температуры, которые быстро затухают с удалением от поверхности вглубь тела. Вызванные ими упругие термоциклические напряжения могут стать причиной многоциклового усталостного разрушения деталей, что подтверждается результатами экспериментальных исследований [1, 2]. Подобная проблема актуальна для рабочих лопаток газовых турбин, элементов двигателей внутреннего сгорания, трубопроводов атомных электростанций. Несмотря на успехи, связанные с уточнением модельных представлений о переносе теплоты и импульса в твердых телах [3–5], для инженерных приложений по прежнему приемлемо использование модели среды, в основе которой лежат феноменологические законы Фурье и Гука, о чем свидетельствуют работы [6, 7].
Строго говоря, не только изменение температуры приводит к деформации твердого тела, но имеет место и обратная связь, поскольку при деформировании выделяется или поглощается теплота, которая влияет на температуру. Однако в действительности влияние деформаций на поле температуры крайне мало, из-за чего им пренебрегают. Также ввиду малости обычно пренебрегают силами инерции, действующими на колеблющиеся частицы твердого тела при циклическом изменении температуры. В таком случае напряжения, вызванные колебаниями температуры, определяются с помощью несвязанной квазистатической задачи термоупругости, которая решается в два этапа. На первом этапе определяются колебания температуры из решения задачи теплопроводности. На втором этапе решается задача теории упругости с найденным на первом этапе неоднородным полем температуры.
Поверхностный слой материала, в котором происходит существенное затухание колебаний температуры и напряжений, называется термическим. Малая толщина термического слоя позволяет использовать для их расчета одномерные уравнения термоупругости. Одним из факторов, влияющих на величину термоциклических напряжений, является форма поверхности тела, определяемая в каждой своей точке главными кривизнами. Чтобы учесть влияние формы поверхности на термонапряженное состояние термического слоя, на практике обычно используют модели полупространства, цилиндра, пространства с цилиндрическим каналом, шара и пространства со сферической полостью. Для оценки влияния размеров тела на термоциклические напряжения в термическом слое применяют модель пластины. Решения циклических задач теплопроводности в указанных областях приведены в классических трудах [8, 9]. После их подстановки в уравнения теории упругости в перемещениях [10] могут быть найдены термоциклические напряжения и термоциклическое перемещение. Другим подходом к решению является использование термоупругого потенциала перемещений. С его помощью решена задача для полупространства в [11].
Использование в расчетах классических аналитических решений одномерных задач термоупругости вызывает сложности вычислительного характера в случаях, когда характерный линейный размер области существенно превосходит толщину термического слоя. Указанные трудности обусловлены поведением входящих в решения функций пространственной переменной, которые в одних случаях принимают слишком большие значения, а в других случаях – слишком малые. Кроме того, форма решений не позволяет в явном виде проследить за их поведением при неограниченном возрастании характерного линейного размера области R. Однако поведение решений достаточно просто установить, исходя из простых соображений: поскольку при $R \to \infty $ расчетная область может быть заменена полупространством, то характерные зависимости для колебаний температуры и термоциклических напряжений в термическом слое также можно получить из решения задачи термоупругости для полупространства. Автору известна лишь одна работа [8], в которой указанные соображения доказаны с использованием решения третьей краевой циклической задачи теплопроводности для пластины. Доказательство проведено с помощью замены пространственной переменной и предельного перехода в решении. При этом используемый в [8] подход нельзя признать рациональным, поскольку вычисление предела в классических решениях является довольно трудоемкой процедурой. Чтобы избежать отмеченных сложностей, требуются иные подходы, один из которых рассмотрен в представленной работе на примере решений несвязанных квазистатических циклических задач термоупругости для шести тел простой формы: полупространства, пластины, пространства с цилиндрическим каналом, цилиндра, пространства со сферической полостью, шара. При этом пластина имеет одинаковую с полупространством форму поверхности, что позволяет исследовать влияние размеров тела на термоциклические напряжения. Решение задач для тел правильной формы позволяет изучить влияние вида поверхности в случае двумерной и трехмерной геометрии. Для большей общности результатов решения задачи теплопроводности получены при граничных условиях I, II и III рода.
2. Классические решения задачи термоупругости. Для детального исследования термоупругих процессов в термическом слое необходимо располагать решениями несвязанной квазистатической циклической задачи термоупругости для интересующих нас областей. Поскольку в известной литературе представлены далеко не все решения рассматриваемых здесь задач, а среди имеющихся решений не все доведены до конечных расчетных формул, ниже с использованием единообразного подхода решения выводятся сразу для всех областей. Для изучения влияния формы поверхности на термоупругие процессы в термическом слое при различных условиях теплообмена задача теплопроводности решается для граничных условий I, II и III рода.
Для удобства поставим в соответствие первой краевой задаче теплопроводности $i = 1$, второй краевой задаче теплопроводности $i = 2$, третьей краевой задаче теплопроводности $i = 3$, полупространству $j = 0$, пластине $j = 1$, пространству с цилиндрическим каналом $j = 2$, цилиндру $j = 3$, пространству со сферической полостью $j = 4$, шару $j = 5$. Свяжем с $j$ номер системы координат $m = [j{\text{/2]}}$ и параметр ${\gamma } = {{\left( { - 1} \right)}^{{j + 1}}}$, причем в дальнейшем примем $m{\text{/}}\operatorname{sign} j \equiv 0$ при $j = 0$. Во всех решениях независимыми переменными будут: ${\eta }$ – обобщенная пространственная переменная, м; $t$ – время, с. Совокупность значений ${\eta }$ во внутренних точках области обозначим ${{\mathcal{D}}_{{\eta }}}$, а значение ${\eta }$ на границе области – ${{{\eta }}_{w}}$. Величина ${{{\eta }}_{w}}$ связана с номером $j$ зависимостью ${{{\eta }}_{w}} = R\operatorname{sign} j$, где $R$ – характерный линейный размер области, м. Основные параметры задачи для расчетных областей приведены в таблице 1, где $x$ – декартова координата, м; ${\rho }$ – полярный радиус, м; $r$ – радиальная координата, м; ${\kappa '} = {\gamma }\operatorname{sign} m{{R}^{{ - 1}}}$, ${\kappa ''} = {\gamma }\left( {m - \operatorname{sign} m} \right){{R}^{{ - 1}}}$ – главные кривизны поверхности, м–1.
Таблица 1
| j | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| m | 0 | 0 | 1 | 1 | 2 | 2 |
| η | x | x | ρ | ρ | r | r |
| ${{{\eta }}_{w}}$ | 0 | R | R | R | R | R |
| ${{\mathcal{D}}_{{\eta }}}$ | (0, ∞) | [0, R) | (R, ∞) | [0, R) | (R, ∞) | [0, R) |
| γ | –1 | 1 | –1 | 1 | –1 | 1 |
| κ' | 0 | 0 | –R–1 | R–1 | –R–1 | R–1 |
| κ'' | 0 | 0 | 0 | 0 | –R–1 | R–1 |
Для упрощения анализа перейдем к безразмерным переменным
Здесь $T = T\left( {{\eta },t;i,j} \right)$ – поле температуры твердого тела, К; $u = u\left( {{\eta },t;i,j} \right)$ – проекция колебательной составляющей вектора полного перемещения на ось ${\eta }$, м; ${\mathbf{\sigma }} = {\mathbf{\sigma }}\left( {{\eta },t;i,j} \right)$ – тензор напряжений, Па; ${{T}_{w}} = {{T}_{w}}\left( t \right)$ – температура поверхности тела, К; ${{q}_{w}} = {{q}_{w}}\left( t \right)$ – плотность теплового потока через поверхность тела, Вт/м2; ${{T}_{f}} = {{T}_{f}}\left( t \right)$ – температура жидкости, К; $\alpha = \alpha \left( t \right) > 0$ – коэффициент теплоотдачи, Вт/(м2 К); $h = \sqrt {a{\text{/}}\omega } $ – характерный линейный масштаб процесса, м; $\omega = 2\pi {\text{/}}\mathcal{T}$ – круговая частота процесса, с–1; $\mathcal{T}$ – период цикла, с; a – коэффициент температуропроводности, м2/с; λ – коэффициент теплопроводности, Вт/(м К); $E$ – модуль Юнга, Па; $\nu $ – коэффициент Пуассона; ${\beta }$ – коэффициент линейного термического расширения, К–1; $\Delta {{T}_{w}}$, $\Delta {{T}_{f}}$ – размахи колебаний ${{T}_{w}}$ и ${{T}_{f}}$, К; $\Delta {{q}_{w}}$ – размах колебаний ${{q}_{w}}$, Вт/м2; $\left\langle {{{T}_{w}}} \right\rangle $, $\left\langle {{{T}_{f}}} \right\rangle $ – средние за период значения ${{T}_{w}}$ и ${{T}_{f}}$, К; $\vartheta = T - \left\langle T \right\rangle $ – колебательная составляющая $T$, К; $\left\langle T \right\rangle $ – среднее за период значение $T$, К; Bi – критерий Био. По условию задачи краевые функции являются ограниченными и периодическими:
Кроме того, на размах колебаний ${{q}_{w}}$ накладывается условие
Поскольку в дальнейшем речь будет идти о безразмерных величинах, для удобства опустим все диакритические знаки, т.е. под обозначением некоторой размерной величины $b$ будем понимать ее безразмерное значение $\hat {b}$.
После приведения основных уравнений термоупругости [10] к безразмерному виду согласно принятым выше соотношениям запишем безразмерную несвязанную квазистатическую циклическую задачу термоупругости ($t > - \infty )$:
(2.1)
$\frac{{\partial \Theta }}{{\partial t}} = \frac{1}{{{{\eta }^{m}}}}\frac{\partial }{{\partial \eta }}\left( {{{\eta }^{m}}\frac{{\partial \Theta }}{{\partial \eta }}} \right),\quad \eta \in {{\mathcal{D}}_{\eta }},\quad i = \overline {1,3} ,\quad j = \overline {0,5} $(2.2)
$\Theta \left( {\eta ,t + 2\pi ;i,j} \right) = \Theta \left( {\eta ,t;i,j} \right),\quad \eta \in {{\mathcal{D}}_{\eta }},\quad i = \overline {1,3} ,\quad j = \overline {0,5} $(2.4)
$ - \gamma \frac{{\partial \Theta \left( {{{\eta }_{w}},t;2,j} \right)}}{{\partial \eta }} = {{q}_{w}},\quad j = \overline {0,5} $(2.5)
$ - \gamma \frac{{\partial \Theta \left( {{{\eta }_{w}},t;3,j} \right)}}{{\partial \eta }} = \operatorname{Bi} \left[ {\Theta \left( {{{{\hat {\eta }}}_{w}},t;3,j} \right) - {{\Theta }_{f}}} \right],\quad j = \overline {0,5} $(2.6)
$\mathop {\lim }\limits_{\eta \to \infty } \left( {{{\eta }^{m}}\frac{{\partial \Theta }}{{\partial \eta }}} \right) = 0,\quad i = \overline {1,3} ,\quad j = 0,2,4$(2.7)
$\frac{{\partial \Theta \left( {0,t;i,j} \right)}}{{\partial \eta }} = 0,\quad i = \overline {1,3} ,\quad j = 1,3,5$(2.8)
$\frac{\partial }{{\partial \eta }}\left[ {\frac{1}{{{{\eta }^{m}}}}\frac{{\partial ({{\eta }^{m}}u)}}{{\partial \eta }}} \right] = \frac{{\partial \vartheta }}{{\partial \eta }},\quad \eta \in {{\mathcal{D}}_{\eta }},\quad i = \overline {1,3} ,\quad j = \overline {0,5} $(2.9)
$u\left( {\eta ,t + 2\pi ;i,j} \right) = u\left( {\eta ,t;i,j} \right),\quad \eta \in {{\mathcal{D}}_{\eta }},\quad i = \overline {1,3} ,\quad j = \overline {0,5} $(2.10)
$\left( {1 - \nu } \right)\frac{{\partial u\left( {{{\eta }_{w}},t;i,j} \right)}}{{\partial \eta }} + m\nu \frac{{u\left( {{{\eta }_{w}},t;i,j} \right)}}{{{{\eta }_{w}}}} = \left( {1 - \nu } \right)\vartheta \left( {{{\eta }_{w}},t;i,j} \right),\quad i = \overline {1,3} ,\quad j = \overline {0,5} $Условие (2.6) выражает равенство нулю теплового потока через бесконечно удаленную от начала координат координатную поверхность. Условие (2.7) при $j = 1$ выражает симметрию поля температуры относительно $x = 0$, а при $j = 3$, 5 выражает ограниченность температуры при ${\eta } = 0$.
Используя обобщенный закон Дюамеля–Неймана и соотношения Коши, можно получить зависимости между компонентами тензора напряжений и вектора полного перемещения [10]. Воспользовавшись этими зависимостями для рассматриваемого случая и приведя их к безразмерному виду, получим для компонентов ${\mathbf{\sigma }}$ выражения
Два основных подхода к решению задачи теплопроводности заключаются в использовании конечного преобразования Фурье по переменной времени и интегрального преобразования по пространственной переменной [8, 9]. В первом случае решение будет представлено тригонометрическим рядом Фурье по переменной времени, а во втором – рядом Фурье по пространственной переменной для ограниченных областей и интегралом Фурье для частично ограниченных областей. Оба подхода позволяют решать классические задачи теплопроводности, в которых входящий в граничное условие III рода коэффициент теплоотдачи является постоянным. Однако нестационарность коэффициента теплоотдачи вызывает при решении сложности принципиального характера [12]. Разрешить их для циклической задачи теплопроводности при произвольной периодической зависимости коэффициента теплоотдачи от времени можно только в рамках первого подхода, что было показано ранее [13]. В связи с этим в дальнейшем будет использоваться первый подход.
Приведем основные обозначения, которые будут применяться в дальнейшем, на примере периодической с периодом $2{\pi }$ функции $f = f\left( t \right)$, удовлетворяющей условиям Дирихле. Разложение функции в тригонометрический ряд Фурье, записанный в комплексной форме, имеет вид
Обозначим среднее за период значение функции
размах колебаний функцииРешение краевой задачи (2.1)–(2.7) будем искать в виде
(2.13)
$\Theta = \mathop \sum \limits_{n = - \infty }^{n = + \infty } \,\mathcal{C}_{n}^{\Theta }{{e}^{{\operatorname{i} nt}}}$Непосредственной подстановкой можно убедиться, что функция вида (2.13) удовлетворяет условию (2.2). Подставив ряд (2.13) в уравнение (2.1) и условия (2.3)–(2.7), получим краевую задачу ($n \in \mathbb{Z}$):
(2.14)
$\frac{1}{{{{\eta }^{m}}}}\frac{d}{{d\eta }}\left( {{{\eta }^{m}}\frac{{d\mathcal{C}_{n}^{\Theta }}}{{d\eta }}} \right) - \operatorname{i} n\mathcal{C}_{n}^{\Theta } = 0,\quad \eta \in {{\mathcal{D}}_{\eta }},\quad i = \overline {1,3} ,\quad j = \overline {0,5} $(2.15)
$\mathcal{C}_{n}^{\Theta }\left( {{{\eta }_{w}};1,j} \right) = \mathcal{C}_{n}^{{{{\Theta }_{w}}}},\quad j = \overline {0,5} $(2.16)
$ - \gamma \frac{{d\mathcal{C}_{n}^{\Theta }\left( {{{\eta }_{w}};2,j} \right)}}{{d\eta }} = \mathcal{C}_{n}^{{{{q}_{w}}}},\quad j = \overline {0,5} $(2.17)
$ - \gamma \frac{{d\mathcal{C}_{n}^{\Theta }\left( {{{\eta }_{w}};3,j} \right)}}{{d\eta }} = \mathop \sum \limits_{k = - \infty }^{k = + \infty } \,\mathcal{C}_{{n - k}}^{{{\text{Bi}}}}\mathcal{C}_{k}^{\Theta }\left( {{{\eta }_{w}};3,j} \right) - \mathcal{C}_{n}^{{\operatorname{Bi} {{\Theta }_{f}}}},\quad j = \overline {0,5} $(2.18)
$\mathop {\lim }\limits_{\eta \to \infty } \left( {{{\eta }^{m}}\frac{{d\mathcal{C}_{n}^{\Theta }}}{{d\eta }}} \right) = 0,\quad i = \overline {1,3} ,\quad j = 0,2,4$(2.19)
$\frac{{d\mathcal{C}_{n}^{\Theta }\left( {0;i,j} \right)}}{{d\eta }} = 0,\quad i = \overline {1,3} ,\quad j = 1,3,5$Решение задачи (2.14)–(2.19) записывается как
При $i = 3$ постоянные интегрирования определяются из бесконечной системы линейных алгебраических уравнений
Здесь $\mathbb{N}$ – множество натуральных чисел;
Таблица 2
| j | ϕn | ψn |
|---|---|---|
| 0 | ${{e}^{{ - x\sqrt {\left| n \right|/2} }}}\cos \left( {x\sqrt {\left| n \right|{\text{/}}2} } \right)$ | $ - {{e}^{{ - x\sqrt {\left| n \right|/2} }}}\sin \left( {x\sqrt {\left| n \right|{\text{/}}2} } \right)$ |
| 1 | ${\text{ch}}\left( {x\sqrt {\left| n \right|{\text{/}}2} } \right)\cos \left( {x\sqrt {\left| n \right|{\text{/}}2} } \right)$ | ${\text{sh}}\left( {x\sqrt {\left| n \right|{\text{/}}2} } \right)\sin \left( {x\sqrt {\left| n \right|{\text{/}}2} } \right)$ |
| 2 | $\ker \left( {{\rho }\sqrt {\left| n \right|} } \right)$ | ${\text{kei}}\left( {{\rho }\sqrt {\left| n \right|} } \right)$ |
| 3 | ${\text{ber}}\left( {{\rho }\sqrt {\left| n \right|} } \right)$ | ${\text{bei}}\left( {{\rho }\sqrt {\left| n \right|} } \right)$ |
| 4 | $\frac{{{{e}^{{ - r\sqrt {\left| n \right|/2} }}}\cos \left( {r\sqrt {\left| n \right|{\text{/}}2} } \right)}}{{r\sqrt {\left| n \right|{\text{/}}2} }}$ | $ - \frac{{{{e}^{{ - r\sqrt {\left| n \right|/2} }}}\sin \left( {r\sqrt {\left| n \right|{\text{/}}2} } \right)}}{{r\sqrt {\left| n \right|{\text{/}}2} }}$ |
| 5 | $\frac{{{\text{sh}}\left( {r\sqrt {\left| n \right|{\text{/}}2} } \right)\cos \left( {r\sqrt {\left| n \right|{\text{/}}2} } \right)}}{{r\sqrt {\left| n \right|{\text{/}}2} }}$ | $\frac{{{\text{ch}}\left( {r\sqrt {\left| n \right|{\text{/}}2} } \right)\sin \left( {r\sqrt {\left| n \right|{\text{/}}2} } \right)}}{{r\sqrt {\left| n \right|{\text{/}}2} }}$ |
Следует заметить, что при $i = 2$ постановка краевой задачи теплопроводности не допускает непосредственного определения величины $\left\langle \Theta \right\rangle $, и для ее нахождения необходимо привлекать дополнительные сведения. Поскольку здесь рассматривается безразмерная колебательная составляющая температуры $\vartheta = \Theta - \left\langle \Theta \right\rangle $, которая определяется однозначно, в дальнейшем для удобства примем $\left\langle \Theta \right\rangle = 0$ при $i = 2$.
От комплексной формы ряда Фурье (2.13) можно перейти к действительной
Выражения для коэффициентов $\bar {A}_{n}^{{\Theta }}$ и $\bar {B}_{n}^{{\Theta }}$ ($\bar {A}_{0}^{{\Theta }} = \bar {B}_{0}^{{\Theta }} = 0$) приведены в таблице 3, причем для третьей краевой задачи решение дано при ${\text{Bi}} = {\text{const}}$.
Таблица 3
| i | 1 | 2 | 3 |
|---|---|---|---|
| $\bar {A}_{n}^{\Theta }$ | $\frac{{{{\Phi }_{n}}A_{n}^{{{{\Theta }_{w}}}} - {{\Psi }_{n}}B_{n}^{{{{\Theta }_{w}}}}}}{{\Phi _{n}^{2} + \Psi _{n}^{2}}}$ | $ - \gamma \frac{{{{\Lambda }_{n}}A_{n}^{{{{q}_{w}}}} - {{\Omega }_{n}}B_{n}^{{{{q}_{w}}}}}}{{\Lambda _{n}^{2} + \Omega _{n}^{2}}}$ | $\frac{{\left( {{{\Phi }_{n}} + \gamma {{\Lambda }_{n}}{\text{/Bi}}} \right)A_{n}^{{{{\Theta }_{f}}}} - \left( {{{\Psi }_{n}} + \gamma {{\Omega }_{n}}{\text{/Bi}}} \right)B_{n}^{{{{\Theta }_{f}}}}}}{{{{{\left( {{{\Phi }_{n}} + \gamma {{\Lambda }_{n}}{\text{/Bi}}} \right)}}^{2}} + {{{\left( {{{\Psi }_{n}} + \gamma {{\Omega }_{n}}{\text{/Bi}}} \right)}}^{2}}}}$ |
Автором было установлено [15], что в ряде случаев можно получить пригодное для инженерных расчетов приближенное решение третьей краевой задачи теплопроводности с нестационарным коэффициентом теплоотдачи путем специальной замены содержащего его граничного условия. При этом возможны два способа замены. В первом способе нестационарный коэффициент теплоотдачи заменяется эквивалентным стационарным, а во втором способе граничное условие III рода заменяется эквивалентным граничным условием II рода. Таким образом, нестационарность коэффициента теплоотдачи не приводит к возникновению принципиально новых эффектов, которые не могут быть исследованы при помощи классических решений задач теплопроводности.
Краевые задачи (2.8)–(2.12) достаточно просто интегрируются. Используя решение (2.8)–(2.12) определим напряжения. Искомые зависимости можно представить в виде
Здесь и далее переменная и индекс $h$ принимает значения
Подставив в них колебания температуры
Очевидно, что
Здесь ${{\mathcal{L}}_{h}}$ – интегральные операторы вида
Таблица 4
| j | ${{\mathcal{L}}_{1}}\left( {{{\phi }_{n}}} \right)$ | ${{\mathcal{L}}_{2}}\left( {{{\phi }_{n}}} \right)$ | ${{\mathcal{L}}_{3}}\left( {{{\phi }_{n}}} \right)$ | ${{\mathcal{L}}_{4}}\left( {{{\phi }_{n}}} \right)$ |
|---|---|---|---|---|
| 0 | 0 | $ - {{\phi }_{n}}$ | $ - {{\phi }_{n}}$ | ${{{\xi }}_{n}}$ |
| ${{\xi }_{n}} = {{e}^{{ - x\sqrt {n/2} }}}\left[ {\sin \left( {x\sqrt {n{\text{/}}2} } \right) - \cos \left( {x\sqrt {n{\text{/}}2} } \right)} \right]{\text{/}}\sqrt {2n} $ | ||||
| 1 | 0 | $ - {{\phi }_{n}}$ | $ - {{\phi }_{n}}$ | ${{{\xi }}_{n}}$ |
| ${{\xi }_{n}} = \left[ {\operatorname{sh} \left( {x\sqrt {n{\text{/}}2} } \right)\cos \left( {x\sqrt {n{\text{/}}2} } \right) + {\text{ch}}\left( {x\sqrt {n{\text{/}}2} } \right)\sin \left( {x\sqrt {n{\text{/}}2} } \right)} \right]{\text{/}}\sqrt {2n} $ | ||||
| 2 | $ - \frac{{{{\xi }_{n}} - {{\Xi }_{n}}}}{{{{\rho }^{2}}}}$ | $\frac{{{{{\xi }}_{n}} - {{{\Xi }}_{n}}}}{{{{{\rho }}^{2}}}} - {{\phi }_{n}}$ | $ - {{\phi }_{n}}$ | $\frac{{{{{\xi }}_{n}} - {{{\Xi }}_{n}}}}{{\rho }}$ |
| ${{\xi }_{n}} = \rho \operatorname{kei} '\left( {\rho \sqrt n } \right){\text{/}}\sqrt n $, ${{\upsilon }_{n}} = - \rho \ker '\left( {\rho \sqrt n } \right){\text{/}}\sqrt n $ | ||||
| 3 | $\frac{{{{{\Xi }}_{n}}}}{{{{R}^{2}}}} - \frac{{{{{\xi }}_{n}}}}{{{{{\rho }}^{2}}}}$ | $\frac{{{{{\Xi }}_{n}}}}{{{{R}^{2}}}} + \frac{{{{{\xi }}_{n}}}}{{{{{\rho }}^{2}}}} - {{\phi }_{n}}$ | $2{\nu }\frac{{{{{\Xi }}_{n}}}}{{{{R}^{2}}}} - {{\phi }_{n}}$ | $\left( {1 - 2{\nu }} \right){\rho }\frac{{{{{\Xi }}_{n}}}}{{{{R}^{2}}}} + \frac{{{{{\xi }}_{n}}}}{{\rho }}$ |
| ${{\xi }_{n}} = \rho \operatorname{bei} '\left( {\rho \sqrt n } \right){\text{/}}\sqrt n $, ${{\upsilon }_{n}} = - \rho \operatorname{ber} '\left( {\rho \sqrt n } \right){\text{/}}\sqrt n $ | ||||
| 4 | $ - 2\frac{{{{{\xi }}_{n}} - {{{\Xi }}_{n}}}}{{{{r}^{3}}}}$ | $\frac{{{{{\xi }}_{n}} - {{{\Xi }}_{n}}}}{{{{r}^{3}}}} - {{\phi }_{n}}$ | $\frac{{{{{\xi }}_{n}} - {{{\Xi }}_{n}}}}{{{{r}^{3}}}} - {{\phi }_{n}}$ | $\frac{{{{{\xi }}_{n}} - {{{\Xi }}_{n}}}}{{{{r}^{2}}}}$ |
| ${{\xi }_{n}} = {{e}^{{ - r\sqrt {n/2} }}}\left\{ {r\sqrt {n{\text{/}}2} \left[ {\sin \left( {r\sqrt {n{\text{/}}2} } \right) - \cos \left( {r\sqrt {n{\text{/}}2} } \right)} \right] + \sin \left( {r\sqrt {n{\text{/}}2} } \right)} \right\}{\text{/}}\sqrt {{{n}^{3}}{\text{/}}2} $ | ||||
| 5 | $2\left( {\frac{{{{{\Xi }}_{n}}}}{{{{R}^{3}}}} - \frac{{{{{\xi }}_{n}}}}{{{{r}^{3}}}}} \right)$ | $2\frac{{{{{\Xi }}_{n}}}}{{{{R}^{3}}}} + \frac{{{{{\xi }}_{n}}}}{{{{r}^{3}}}} - {{\phi }_{n}}$ | $2\frac{{{{{\Xi }}_{n}}}}{{{{R}^{3}}}} + \frac{{{{{\xi }}_{n}}}}{{{{r}^{3}}}} - {{\phi }_{n}}$ | $\frac{{2\left( {1 - 2\nu } \right)}}{{1 + \nu }}\frac{r}{{{{R}^{3}}}}{{\Xi }_{n}} + \frac{{{{\xi }_{n}}}}{{{{r}^{2}}}}$ |
| ${{\xi }_{n}} = \left\{ {r\sqrt {n{\text{/}}2} \left[ {{\text{ch}}\left( {r\sqrt {n{\text{/}}2} } \right)\cos \left( {r\sqrt {n{\text{/}}2} } \right) + {\text{sh}}\left( {r\sqrt {n{\text{/}}2} } \right)\sin \left( {r\sqrt {n{\text{/}}2} } \right)} \right] - } \right.\left. {{\text{ch}}\left( {r\sqrt {n{\text{/}}2} } \right)\sin \left( {r\sqrt {n{\text{/}}2} } \right)} \right\}{\text{/}}\sqrt {{{n}^{3}}{\text{/}}2} $ | ||||
Здесь $n \in \mathbb{N}$ и штрихом обозначена производная функции по аргументу Выражения для функций ${{\upsilon }_{n}}$ получаются заменой ${{\upsilon }_{n}} = {{\left. {{{\xi }_{n}}} \right|}_{{\begin{array}{*{20}{c}} {\sin \to \cos ,\cos \to - \sin ,\operatorname{sh} \to - \operatorname{ch} ,\operatorname{ch} \to - \operatorname{sh} } \end{array}}}},$ а коэффициентов ${{\mathcal{L}}_{h}}\left( {{{\psi }_{n}}} \right)$ заменой ${{\mathcal{L}}_{k}}\left( {{{\psi }_{n}}} \right) = {{\left. {{{\mathcal{L}}_{k}}\left( {{{\phi }_{n}}} \right)} \right|}_{{\begin{array}{*{20}{c}} {{{\phi }_{n}} \to {{\psi }_{n}},{{\xi }_{n}} \to {{\upsilon }_{n}},{{\Xi }_{n}} \to {{\Upsilon }_{n}}} \end{array}}}}$
Представленные классические решения циклических задач термоупругости достаточно тяжело поддаются анализу в том виде, в котором они были получены. Тем не менее, они позволяют легко установить следующие результаты ($i = \overline {1,3} $):
Использование приведенных зависимостей для дальнейшего изучения процессов в термическом слое вызывает затруднения.
3. Термоупругие процессы в термическом слое. Для задач термоупругости (2.1)–(2.12) можно показать, что при $R \to \infty $ решения в термическом слое всех областей будут идентичны. Для этого введем величину $s = \gamma \left( {{{\eta }_{w}} - \eta } \right)$, которая представляет собой безразмерное расстояние от поверхности тела до его точки (глубину), и проекцию колебательной составляющей вектора безразмерного полного перемещения на направление внутренней нормали к поверхности тела ${v} = - \gamma u$. Очевидно, что $s = x$ и ${v} = u$ при $j = 0$. Заменим ${\eta }$ и $u$ в (2.1)–(2.12) на $s$ и ${v}$ соответственно. В результате получим краевые задачи ($t > - \infty )$:
(3.1)
$\frac{{\partial \Theta }}{{\partial t}} = \frac{{{{\partial }^{2}}\Theta }}{{\partial {{s}^{2}}}} + \frac{m}{{s - \gamma {{\eta }_{w}}}}\frac{{\partial \Theta }}{{\partial s}},\quad s \in {{\mathcal{D}}_{s}},\quad i = \overline {1,3} ,\quad j = \overline {0,5} $(3.2)
$\Theta \left( {s,t + 2\pi ;i,j} \right) = \Theta \left( {s,t;i,j} \right),\quad s \in {{\mathcal{D}}_{s}},\quad i = \overline {1,3} ,\quad j = \overline {0,5} $(3.4)
$\frac{{\partial \Theta \left( {0,t;2,j} \right)}}{{\partial s}} = {{q}_{w}},\quad j = \overline {0,5} $(3.5)
$\frac{{\partial \Theta \left( {0,t;3,j} \right)}}{{\partial s}} = {\text{Bi}}\left[ {\Theta \left( {0,t;3,j} \right) - {{\Theta }_{f}}} \right],\quad j = \overline {0,5} $(3.6)
$\mathop {\lim }\limits_{s \to \infty } \left[ {{{{\left( {\operatorname{sign} j + \frac{s}{R}} \right)}}^{m}}\frac{{\partial \Theta }}{{\partial s}}} \right] = 0,\quad i = \overline {1,3} ,\quad j = 0,2,4$(3.7)
$\frac{{\partial \Theta \left( {R,t;i,j} \right)}}{{\partial s}} = 0,\quad i = \overline {1,3} ,\quad j = 1,3,5$(3.8)
$\frac{{{{\partial }^{2}}{v}}}{{\partial {{s}^{2}}}} + \frac{m}{{s - \gamma {{\eta }_{w}}}}\frac{{\partial {v}}}{{\partial s}} - \frac{{m{v}}}{{{{{\left( {s - \gamma {{\eta }_{w}}} \right)}}^{2}}}} = \frac{{\partial \vartheta }}{{\partial s}},\quad s \in {{\mathcal{D}}_{s}},\quad i = \overline {1,3} ,\quad j = \overline {0,5} $(3.9)
${v}\left( {s,t + 2\pi ;i,j} \right) = {v}\left( {s,t;i,j} \right),\quad s \in {{\mathcal{D}}_{s}},\quad i = \overline {1,3} ,\quad j = \overline {0,5} $(3.10)
$\left( {1 - \nu } \right)\frac{{\partial {v}\left( {0,t;i,j} \right)}}{{\partial s}} - \gamma m\nu \frac{{{v}\left( {0,t;i,j} \right)}}{{{{\eta }_{w}}}} = \left( {1 - \nu } \right)\vartheta \left( {0,t;i,j} \right),\quad i = \overline {1,3} ,\quad j = \overline {0,5} $Компоненты тензора безразмерных напряжений
(3.13)
${{\sigma }_{{ss}}} = \frac{1}{{1 - 2\nu }}\left[ {\left( {1 - \nu } \right)\frac{{\partial {v}}}{{\partial s}} + m\nu \frac{{v}}{{s - \gamma {{\eta }_{w}}}} - \left( {1 - \nu } \right)\vartheta } \right]$(3.14)
${{\sigma }_{{\tilde {n}\tilde {n}}}} = \frac{1}{{1 - 2\nu }}\left[ {\nu \frac{{\partial {v}}}{{\partial s}} + {{{\left( {1 - \nu } \right)}}^{{2 - m}}}\operatorname{sign} m\frac{{v}}{{s - \gamma {{\eta }_{w}}}} - \left( {1 - \nu } \right)\vartheta } \right]$(3.15)
${{\sigma }_{{\varsigma \varsigma }}} = \frac{1}{{1 - 2\nu }}\left[ {\nu \frac{{\partial {v}}}{{\partial s}} + {{\nu }^{{2 - m}}}\operatorname{sign} m\frac{{v}}{{s - \gamma {{\eta }_{w}}}} - \left( {1 - \nu } \right)\vartheta } \right]$Здесь $\Theta = \Theta \left( {s,t;i,j} \right)$, ${v} = {v}\left( {s,t;i,j} \right)$, $\vartheta = \vartheta \left( {s,t;i,j} \right)$, ${\mathbf{\sigma }} = {\mathbf{\sigma }}\left( {s,t;i,j} \right)$, причем ${{\sigma }_{{ss}}} = {{\sigma }_{{\eta \eta }}}$. Полагая все функции и их производные в уравнениях (3.1)–(3.15) ограниченными, выполним в них предельный переход при $R \to \infty $, в результате получим краевые задачи термоупругости и формулы для расчета напряжений, отвечающие полупространству. Поэтому можно ожидать, что с увеличением $R$ решения циклических задач термоупругости для $j = \overline {1,5} $ будут стремиться к соответствующим решениям для $j = 0$. Полученный вывод противоречит ранее установленным результатам, согласно которым ($i = \overline {1,3} $)
Причина противоречия может быть установлена при помощи анализа решений краевых задач.
Использование решений задач термоупругости в пределах термического слоя при $j = \overline {1,5} $ вызывает сложности вычислительного характера, обусловленные поведением ${{\phi }_{n}}\left( {R;j} \right)$ и ${{{\psi }}_{n}}\left( {R;j} \right)$ при больших значениях $R$: ${{\phi }_{n}}\left( {R;j} \right)$ и ${{{\psi }}_{n}}\left( {R;j} \right)$ являются неограниченными при $R \to \infty $ для $j = 1,3,5$; ${{\phi }_{n}}\left( {R;j} \right)$ и ${{{\psi }}_{n}}\left( {R;j} \right)$ являются бесконечно малыми при $R \to \infty $ для $j = 2,4$. Чтобы избежать указанных затруднений, следует преобразовать полученные решения таким образом, чтобы вместо ${{\phi }_{n}}\left( {R;j} \right)$ и ${{{\psi }}_{n}}\left( {R;j} \right)$ в них входили функции, принимающие конечные значения при $R \to \infty $. При этом преобразованные решения должны быть представлены в таком виде, который позволит явным образом установить их поведение при $R \gg 1$.
Преобразованные решения задачи теплопроводности, которые удовлетворяют указанным выше требованиям, были получены за счет приведения коэффициентов действительной формы ряда Фурье (2.25) $A_{n}^{{\Theta }}$ = $A_{n}^{{\Theta }}\left( {s;R,i,j} \right)$, $B_{n}^{{\Theta }}$ = $B_{n}^{{\Theta }}\left( {s;R,i,j} \right)$ к виду
Выражения для функций ${{{\tilde {\psi }}}_{n}}$ получаются заменой ${{\tilde {\psi }}_{n}} = - {{\left. {{{{\tilde {\phi }}}_{n}}} \right|}_{{\cos \to \sin }}}$. Постоянные интегрирования $\tilde {A}_{n}^{{\Theta }}$ и $\tilde {B}_{n}^{{{\hat {\Theta }}}}$ для $i = 1,2$ и $i = 3$ при ${\text{Bi}} = {\text{const}}$ выражены соотношениями, приведенными в таблице 3, где должны быть сделаны замены $\left( {{{{\Phi }}_{n}},{{{\Psi }}_{n}},{{{\Lambda }}_{n}},{{{\Omega }}_{n}}} \right)$ → → $\left( {{{{{\tilde {\Phi }}}}_{n}},{{{{\tilde {\Psi }}}}_{n}},{{{{\tilde {\Lambda }}}}_{n}},{{{{\tilde {\Omega }}}}_{n}}} \right)$. В общем случае ${\text{Bi}} \ne {\text{const}}$ постоянные интегрирования находятся из решения бесконечной системы уравнений
Здесь
Проанализируем полученные результаты. Прежде всего, отметим, что из них в явном виде следуют соотношения
Таким образом, колебания температуры вблизи поверхности слабо зависят от условий теплообмена на удаленной от нее границе области при $R \geqslant 3$. Данный вывод имеет важное практическое значение, поскольку он позволяет исключать из рассмотрения границу области произвольной формы, удаленную от рассматриваемой точки поверхности, даже в тех случаях, когда термический слой не образуется, и колебания температуры проникают на всю толщину детали $2R$, лишь бы было выполнено условие $R \geqslant 3$. В таких случаях на колебания температуры вблизи поверхности влияет только ее форма и заданные краевые условия теплообмена, что позволяет использовать модели тел простой формы. Из найденных соотношений также можно получить простые асимптотические зависимости при $~R \gg 1~$, $s{\text{/}}R \ll 1$
В них входит безразмерная средняя кривизна поверхности
Коэффициенты тригонометрических рядов Фурье функций ${{\sigma }_{{ss}}}$, ${{\sigma }_{{\tilde {n}\tilde {n}}}}$, ${{\sigma }_{{\varsigma \varsigma }}}$, ${v}$ были приведены к виду
Здесь $h = \left( {{{\sigma }_{{ss}}},{{\sigma }_{{\tilde {n}\tilde {n}}}},{{\sigma }_{{\varsigma \varsigma }}},{v}} \right)$, причем ${{\tilde {\mathcal{L}}}_{{{{\sigma }_{{ss}}}}}} = {{\tilde {\mathcal{L}}}_{{{{\sigma }_{{\eta \eta }}}}}}$; ${{\tilde {\mathcal{L}}}_{{v}}} = - \gamma {{\tilde {\mathcal{L}}}_{u}}$; ${{\tilde {\mathcal{L}}}_{u}}$, ${{\tilde {\mathcal{L}}}_{{{{\sigma }_{{\eta \eta }}}}}}$, ${{\tilde {\mathcal{L}}}_{{{{\sigma }_{{\tilde {n}\tilde {n}}}}}}}$, ${{\tilde {\mathcal{L}}}_{{{{\sigma }_{{\varsigma \varsigma }}}}}}$ – операторы, полученные из ${{\mathcal{L}}_{u}}$, ${{\mathcal{L}}_{{{{\sigma }_{{\eta \eta }}}}}}$, ${{\mathcal{L}}_{{{{\sigma }_{{\tilde {n}\tilde {n}}}}}}}$, ${{\mathcal{L}}_{{{{\sigma }_{{\varsigma \varsigma }}}}}}$ после замены в них переменной ${\eta }$ на $s$. Для рассматриваемых тел данные зависимости сведены в таблицу 5. Из анализа зависимостей для напряжений следует, что
Таблица 5
| j | ${{\tilde {\mathcal{L}}}_{1}}\left( {{{{\tilde {\phi }}}_{n}}} \right)$ | ${{\tilde {\mathcal{L}}}_{2}}\left( {{{{\tilde {\phi }}}_{n}}} \right)$ | ${{\tilde {\mathcal{L}}}_{3}}\left( {{{{\tilde {\phi }}}_{n}}} \right)$ | ${{\tilde {\mathcal{L}}}_{4}}\left( {{{{\tilde {\phi }}}_{n}}} \right)$ |
|---|---|---|---|---|
| 1 | 0 | $ - {{\tilde {\phi }}_{n}}$ | $ - {{\tilde {\phi }}_{n}}$ | $ - {{{\tilde {\xi }}}_{n}}$ |
| ${{\tilde {\xi }}_{n}} = - \frac{1}{{\sqrt {2n} }}\left\{ {{{e}^{{ - s\sqrt {n/2} }}}\left[ {\sin \left( {s\sqrt {n{\text{/}}2} } \right) - \cos \left( {s\sqrt {n{\text{/}}2} } \right)} \right] - } \right.$$\left. { - \;{{e}^{{ - 2R\sqrt {n/2} + s\sqrt {n/2} }}}\left[ {\sin \left( {2R\sqrt {n{\text{/}}2} - s\sqrt {n{\text{/}}2} } \right) - \cos \left( {2R\sqrt {n{\text{/}}2} - s\sqrt {n{\text{/}}2} } \right)} \right]} \right\}$ | ||||
| 2 | $ - \frac{{{{{\tilde {\xi }}}_{n}} - {{{\tilde {\Xi }}}_{n}}}}{{{{R}^{2}}{{{\left( {1 + s{\text{/}}R} \right)}}^{2}}}}$ | $\frac{{{{{\tilde {\xi }}}_{n}} - {{{\tilde {\Xi }}}_{n}}}}{{{{R}^{2}}{{{\left( {1 + s{\text{/}}R} \right)}}^{2}}}} - {{\tilde {\phi }}_{n}}$ | $ - {{\tilde {\phi }}_{n}}$ | $\frac{{{{{\tilde {\xi }}}_{n}} - {{{\tilde {\Xi }}}_{n}}}}{{R\left( {1 + s{\text{/}}R} \right)}}$ |
| ${{\tilde {\xi }}_{n}} = \frac{{R{{{\left( {1 + s{\text{/}}R} \right)}}^{{1/2}}}{{e}^{{ - s\sqrt {n/2} - {{{\bar {\bar {\iota }}}}_{n}}}}}}}{{\sqrt {2n} }}\left\{ {\left( {1 + \bar {\bar {\iota }}_{n}^{'}{\text{/}}\sqrt {n{\text{/}}2} } \right)\sin \left( {s\sqrt {n{\text{/}}2} - {{{\bar {\bar {\tau }}}}_{n}}} \right) - } \right.$$\left. { - \;\left( {1 - \bar {\bar {\tau }}_{n}^{'}{\text{/}}\sqrt {n{\text{/}}2} } \right)\cos \left( {s\sqrt {n{\text{/}}2} - {{{\bar {\bar {\tau }}}}_{n}}} \right) + \sin \left( {s\sqrt {n{\text{/}}2} - {{{\bar {\bar {\tau }}}}_{n}}} \right){\text{/}}\left[ {R\sqrt {2n} \left( {1 + s{\text{/}}R} \right)} \right]} \right\}$ | ||||
| 3 | $\frac{{{{{\tilde {\Xi }}}_{n}}}}{{{{R}^{2}}}} - \frac{{{{{\tilde {\xi }}}_{n}}{\text{/}}{{R}^{2}}}}{{{{{\left( {1 - s{\text{/}}R} \right)}}^{2}}}}$ | $\frac{{{{{\tilde {\Xi }}}_{n}}}}{{{{R}^{2}}}} + \frac{{{{{\tilde {\xi }}}_{n}}{\text{/}}{{R}^{2}}}}{{{{{\left( {1 - s{\text{/}}R} \right)}}^{2}}}} - {{\tilde {\phi }}_{n}}$ | $2\nu \frac{{{{{\tilde {\Xi }}}_{n}}}}{{{{R}^{2}}}} - {{\tilde {\phi }}_{n}}$ | $ - \left( {1 - 2\nu } \right)\frac{{1 - s{\text{/}}R}}{R}{{\tilde {\Xi }}_{n}} - $$ - \;\frac{{{{{\tilde {\xi }}}_{n}}{\text{/}}R}}{{1 - s{\text{/}}R}}$ |
| ${{\tilde {\xi }}_{n}} = - \frac{{R{{{\left( {1 - s{\text{/}}R} \right)}}^{{1/2}}}{{e}^{{ - s\sqrt {n/2} + {{\iota }_{n}}}}}}}{{\sqrt {2n} }}\left\{ {\left( {1 - \iota _{n}^{'}{\text{/}}\sqrt {n{\text{/}}2} } \right)\sin \left( {s\sqrt {n{\text{/}}2} + {{\tau }_{n}}} \right) - } \right.$$\left. { - \;\left( {1 + \tau _{n}^{'}{\text{/}}\sqrt {n{\text{/}}2} } \right)\cos \left( {s\sqrt {n{\text{/}}2} + {{\tau }_{n}}} \right) - \sin \left( {s\sqrt {n{\text{/}}2} + {{\tau }_{n}}} \right){\text{/}}\left[ {R\sqrt {2n} \left( {1 - s{\text{/}}R} \right)} \right]} \right\}$ | ||||
| 4 | $ - \frac{{2\left( {{{{\tilde {\xi }}}_{n}} - {{{\tilde {\Xi }}}_{n}}} \right)}}{{{{R}^{3}}{{{\left( {1 + s{\text{/}}R} \right)}}^{3}}}}$ | $\frac{{{{{\tilde {\xi }}}_{n}} - {{{\tilde {\Xi }}}_{n}}}}{{{{R}^{3}}{{{\left( {1 + s{\text{/}}R} \right)}}^{3}}}} - {{\tilde {\phi }}_{n}}$ | $\frac{{{{{\tilde {\xi }}}_{n}} - {{{\tilde {\Xi }}}_{n}}}}{{{{R}^{3}}{{{\left( {1 + s{\text{/}}R} \right)}}^{3}}}} - {{\tilde {\phi }}_{n}}$ | $\frac{{{{{\tilde {\xi }}}_{n}} - {{{\tilde {\Xi }}}_{n}}}}{{{{R}^{2}}{{{\left( {1 + s{\text{/}}R} \right)}}^{2}}}}$ |
| ${{\tilde {\xi }}_{n}} = \frac{{{{R}^{2}}\left( {1 + s{\text{/}}R} \right)}}{{\sqrt {2n} }}{{e}^{{ - s\sqrt {n/2} }}}\left[ {\sin \left( {s\sqrt {n{\text{/}}2} } \right) - \cos \left( {s\sqrt {n{\text{/}}2} } \right)} \right] + \frac{R}{n}{{e}^{{ - s\sqrt {n/2} }}}\sin \left( {s\sqrt {n{\text{/}}2} } \right)$ | ||||
| 5 | $\frac{{2{{{\tilde {\Xi }}}_{n}}}}{{{{R}^{3}}}} - \frac{{2{{{\tilde {\xi }}}_{n}}{\text{/}}{{R}^{3}}}}{{{{{\left( {1 - s{\text{/}}R} \right)}}^{3}}}}$ | $\frac{{2{{{\tilde {\Xi }}}_{n}}}}{{{{R}^{3}}}} + \frac{{{{{\tilde {\xi }}}_{n}}{\text{/}}{{R}^{3}}}}{{{{{\left( {1 - s{\text{/}}R} \right)}}^{3}}}} - {{\tilde {\phi }}_{n}}$ | $\frac{{2{{{\tilde {\Xi }}}_{n}}}}{{{{R}^{3}}}} + \frac{{{{{\tilde {\xi }}}_{n}}{\text{/}}{{R}^{3}}}}{{{{{\left( {1 - s{\text{/}}R} \right)}}^{3}}}} - {{\tilde {\phi }}_{n}}$ | $ - \frac{{2\left( {1 - 2\nu } \right)}}{{1 + \nu }}\frac{{1 - s{\text{/}}R}}{{{{R}^{2}}}}{{\tilde {\Xi }}_{n}} - $ $ - \;\frac{{{{{\tilde {\xi }}}_{n}}{\text{/}}{{R}^{2}}}}{{{{{\left( {1 - s{\text{/}}R} \right)}}^{2}}}}$ |
| ${{\tilde {\xi }}_{n}} = - \frac{{{{R}^{2}}\left( {1 - s{\text{/}}R} \right)}}{{\sqrt {2n} }}\left\{ {{{e}^{{ - s\sqrt {n/2} }}}\left[ {\sin \left( {s\sqrt {n{\text{/}}2} } \right) - \cos \left( {s\sqrt {n{\text{/}}2} } \right)} \right] + } \right.$$\left. { + \;{{e}^{{ - 2R\sqrt {n/2} + s\sqrt {n/2} }}}\left[ {\sin \left( {2R\sqrt {n{\text{/}}2} - s\sqrt {n{\text{/}}2} } \right) - \cos \left( {2R\sqrt {n{\text{/}}2} - s\sqrt {n{\text{/}}2} } \right)} \right]} \right\} + $$ + \;\frac{R}{n}\left[ {{{e}^{{ - s\sqrt {n/2} }}}\sin \left( {s\sqrt {n{\text{/}}2} } \right) - {{e}^{{ - 2R\sqrt {n/2} + s\sqrt {n/2} }}}\sin \left( {2R\sqrt {n{\text{/}}2} - s\sqrt {n{\text{/}}2} } \right)} \right]$ | ||||
Здесь ${{\tilde {\Xi }}_{n}} = {{\tilde {\xi }}_{n}}\left( {0;R,j} \right)$, ${{\tilde {\Upsilon }}_{n}} = {{\tilde {\upsilon }}_{n}}\left( {0;R,j} \right)$, $n \in \mathbb{N}$ и штрихом обозначена производная функции по аргументу. Выражения для функций ${{\tilde {\upsilon }}_{n}}$ получаются заменой ${{\tilde {\upsilon }}_{n}} = {{\left. {{{{\tilde {\xi }}}_{n}}} \right|}_{{\sin \to \cos ,\cos \to - \sin }}},$ а коэффициентов ${{\tilde {\mathcal{L}}}_{h}}\left( {{{{\tilde {\psi }}}_{n}}} \right)$ заменой ${{\tilde {\mathcal{L}}}_{h}}\left( {{{{\tilde {\psi }}}_{n}}} \right) = {{\left. {{{{\tilde {\mathcal{L}}}}_{h}}\left( {{{{\tilde {\phi }}}_{n}}} \right)} \right|}_{{{{{\tilde {\phi }}}_{n}} \to {{{\tilde {\psi }}}_{n}},{{{\tilde {\xi }}}_{n}} \to {{{\tilde {\upsilon }}}_{n}},{{{\tilde {\Xi }}}_{n}} \to {{{\tilde {\Upsilon }}}_{n}}}}}$
Найденные соотношения подтверждают результаты, полученные ранее с помощью предельного перехода в задаче термоупругости и зависимостях для напряжений. Формулы для напряжений в пластине показывают, что
Эти соотношения позволяют распространить на термоциклические напряжения ранее сделанный вывод о влиянии границы области, достаточно удаленной от рассматриваемой точки поверхности тела, на колебания температуры вблизи нее.
Предельный переход в зависимостях для колебаний перемещения подтверждает ранее полученный парадоксальный результат:
Интересно отметить, что предел функции ${v}$ при $R \to \infty $ ($i = \overline {1,3} $, $j = \overline {2,5} $) содержит два слагаемых, первое из которых не зависит от $s$ и не может вызывать напряжений, а второе представляет собой перемещение ${v}\left( {s,t;i,0} \right)$. Чтобы объяснить полученный парадокс, необходимо вспомнить, что граничные условия в любой краевой задаче, вообще говоря, носят предельный характер. Решим задачу термоупругости для ${v}$ в областях $j = \overline {2,5} $, но вместо (3.11), (3.12) используем граничное условие
Отсюда при ${{s}_{*}} \to \infty $ получим (3.11), а при ${{s}_{*}} \to R$ получим (3.12). В таком случае для $j = \overline {2,5} $ будем иметь
Из полученного выражения следует, что
Таким образом оказывается, что предельный переход в задаче термоупругости в перемещениях, вообще говоря, недопустим, и колебания нормального перемещения принципиальным образом зависят от формы поверхности тела и кинематических условий. В то же время, если бы задача термоупругости решалась в напряжениях, то в ней можно было бы выполнить предельный переход, что было показано ранее с помощью зависимостей для напряжений. Различное поведение решений задачи термоупругости для перемещения и напряжений при $R \to \infty $ связано с тем, что перемещения не определяются полностью напряжениями [17].
Из формул для термоциклических напряжений и колебаний перемещения можно установить асимптотические зависимости при $R \gg 1~$, $s{\text{/}}R \ll 1$ ($n \in \mathbb{N}$)
Выражения для функций ${{\tilde {\upsilon }}_{n}}$ получаются заменой ${{\tilde {\upsilon }}_{n}}$ = ${{\left. {{{{\tilde {\xi }}}_{n}}} \right|}_{{\begin{array}{*{20}{c}} {\sin \to \cos ,\cos \to - \sin } \end{array}}}}$, а коэффициентов ${{\tilde {\mathcal{L}}}_{h}}\left( {{{{\tilde {\psi }}}_{n}}} \right)$ заменой ${{\tilde {\mathcal{L}}}_{h}}\left( {{{{\tilde {\psi }}}_{n}}} \right)$ = ${{\left. {{{{\tilde {\mathcal{L}}}}_{h}}\left( {{{{\tilde {\phi }}}_{n}}} \right)} \right|}_{{{{{\tilde {\phi }}}_{n}} \to {{{\tilde {\psi }}}_{n}},{{{\tilde {\xi }}}_{n}} \to {{{\tilde {\upsilon }}}_{n}}}}}$. Анализируя полученные формулы, можно заключить, что в них параметры, зависящие от величин $j$ и $R$, которые однозначно определяют форму тела, не могут быть объединены в один комплекс, как это было в случае колебаний температуры. Таким образом, условия равенства параметра $\varkappa $ недостаточно, чтобы напряжения и перемещения в термическом слое двух тел с различной формой поверхности при прочих равных условиях были приближенно равны. Необходимым условием для этого является равенство главных кривизн поверхности, т.е. одинаковая форма тела. В то же время легко заметить, что в частично ограниченных областях основное влияние на термоциклические напряжения вблизи поверхности оказывает ее средняя кривизна, поскольку
4. Примеры. Для иллюстрации полученных результатов были проведены расчеты с использованием установленных зависимостей при простейших краевых функциях
Коэффициент Пуассона $\nu = 0,3$ соответствовал стали. Во всех рассматриваемых случаях $\vartheta \equiv \Theta $. В прочностных расчетах компонентам тензора напряжений принято ставить в соответствие некоторое эквивалентное напряжение, характеризующее прочность тела. Для оценки выносливости используют эквивалентный размах колебаний напряжений [18]
Наибольшие колебания температуры и термоциклические напряжения возникают на поверхности тела, поэтому они представляют основной интерес для изучения. Полагая $\Delta \vartheta = \Delta \vartheta \left( {s;i,j} \right)$ и $\Delta {{\sigma }_{e}} = \Delta {{\sigma }_{e}}\left( {s;i,j} \right)$, обозначим $\Delta {{\vartheta }_{w}} = \Delta \vartheta \left( {0;i,j} \right)$, $\Delta {{\sigma }_{{e.w}}} = \Delta {{\sigma }_{e}}\left( {0;i,j} \right)$.
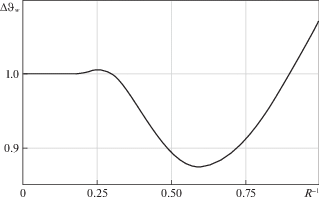
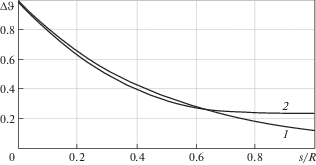
Влияние размеров тела на колебания температуры наглядно иллюстрирует рис. 1, на котором показана зависимость $\Delta \vartheta $ на поверхности пластины от величины $R$ при $i = 2$. Из нее следует, что $\Delta {{\vartheta }_{w}}$ при $R \geqslant 3$ отличается от $\Delta \vartheta $ на поверхности полупространства не более чем на 1.3%, хотя при $R = 3$ колебания температуры проникают на всю глубину пластины. Достаточно показательным является рис. 2, на котором приведены зависимости $\Delta \vartheta \left( s \right)$ для полупространства и пластины при $R = 3$. Сравнение двух зависимостей показывает, что для достаточно больших глубин $s \leqslant 2$ наибольшая разница между результатами составляет 7.1%, что вполне приемлемо для инженерных расчетов.
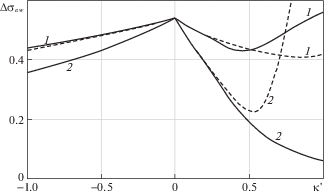
На рис. 3–8 приведено сравнение асимптотических зависимостей с точными решениями для тел, ограниченных цилиндрическими и сферическими поверхностями, при $i = \overline {1,3} $. Для сравнения использовались зависимости $\Delta {{\vartheta }_{w}}$ и $\Delta {{{\sigma }}_{{e.w}}}$ от $\kappa {\kern 1pt} '$, причем для $i = 1$ в связи с тривиальностью результата вместо $\Delta {{\vartheta }_{w}}$ рассчитывалась производная ${{\left( {d\Delta \vartheta {\text{/}}ds} \right)}_{w}}$ = $d\Delta \vartheta \left( {0;i,j} \right){\text{/}}ds$, которая характеризует интенсивность затухания колебаний температуры с увеличением глубины. Из представленных результатов следует, что асимптотические зависимости обеспечивают приемлемую для инженерных расчетов точность при $ - 1 \leqslant \kappa {\kern 1pt} ' \leqslant 0.4$. Наибольшие отклонения от точных результатов асимптотические зависимости дают при $\kappa {\kern 1pt} ' = 0.4$: отклонение от $\Delta {{\vartheta }_{w}}$ составляет –5.2% при $i = 2$, $j = 5$; отклонение от $\Delta {{\sigma }_{{e.w}}}$ составляет 12.6% при $i = 1$, $j = 5$. При $ - 1 \leqslant \kappa {\kern 1pt} ' \leqslant 0.3$ абсолютные отклонения от точных результатов не превышают 5%. Указанный диапазон изменения $\kappa {\kern 1pt} '$ охватывает достаточно широкий круг практически важных случаев, поэтому полученные асимптотические зависимости можно рекомендовать для приближенных вычислений.
Рис. 3.
Зависимости ${{\left( {d\Delta \vartheta {\text{/}}ds} \right)}_{w}}$ от κ' при $i = 1$ для тел, ограниченных цилиндрическими (1) и сферическими (2) поверхностями: сплошные линии – точные решения, штриховые линии – асимптотические зависимости.
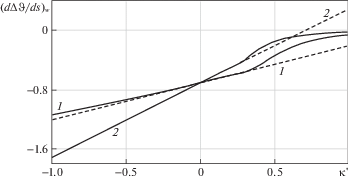
Рис. 4.
Зависимости $\Delta {{\vartheta }_{w}}$ от κ' при $i = 2$ для тел, ограниченных цилиндрическими (1) и сферическими (2) поверхностями: сплошные линии – точные решения, штриховые линии – асимптотические зависимости.
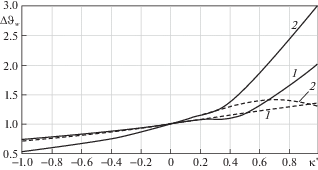
Рис. 5.
Зависимости $\Delta {{\vartheta }_{w}}$ от κ' при $i = 3$ для тел, ограниченных цилиндрическими (1) и сферическими (2) поверхностями: сплошные линии – точные решения, штриховые линии – асимптотические зависимости.
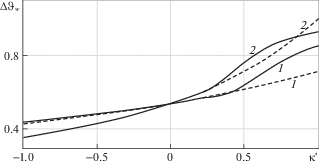
Рис. 6.
Зависимости $\Delta {{\sigma }_{{e.w}}}$ от κ' при $i = 1$ для тел, ограниченных цилиндрическими (1) и сферическими (2) поверхностями: сплошные линии – точные решения, штриховые линии – асимптотические зависимости
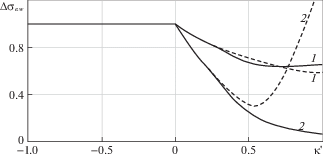
Рис. 7.
Зависимости $\Delta {{\sigma }_{{e.w}}}$ от κ' при $i = 2$ для тел, ограниченных цилиндрическими (1) и сферическими (2) поверхностями: сплошные линии – точные решения, штриховые линии – асимптотические зависимости.
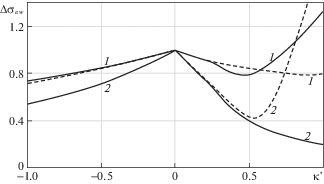
Рис. 8.
Зависимости $\Delta {{\sigma }_{{e.w}}}$ от κ' при $i = 3$ для тел, ограниченных цилиндрическими (1) и сферическими (2) поверхностями: сплошные линии – точные решения, штриховые линии – асимптотические зависимости.
Заключение. В ходе проведенного исследования рассмотрены несвязанные квазистатические циклические задачи термоупругости для тел простой формы. Получены классические решения указанных задач, которые приведены к форме, удобной для расчетов при больших безразмерных радиусах граничных поверхностей. С помощью найденных решений установлены асимптотические зависимости, упрощающие проведение инженерных расчетов при больших безразмерных радиусах граничных поверхностей. Показано, что при определенных условиях найденные зависимости обеспечивают приемлемую точность расчетов вблизи поверхности, даже когда колебания температуры проникают на всю глубину тела. Исследовано влияние формы тела на колебания температуры и термоциклические напряжения. Показано, что влияние формы тела на колебания температуры и вызванные ими термоциклические напряжения принципиальным образом различается: если основным параметром формы тела, влияющим на колебания температуры в термическом слое, является средняя кривизна поверхности, то на термоциклические напряжения существенным образом влияют обе главные кривизны.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-31-00090.
Список литературы
Zhu D., Miller R.A. Influence of high cycle thermal loads on thermal fatigue behavior of thick thermal barrier coatings // NASA Technical Paper TP-3676. Army Res. Lab. Techn. Rep. ARL-TR-1341, 1997. 51 p.
Wang Y., Charbal A., Hild F. et al. High cycle thermal fatigue of austenitic stainless steel // MATEC Web of Conferences. 2018. V. 165. № 19009. 6 p.
Wang L., Zhou X., Wei X. Heat Conduction: Mathematical Models and Analytical Solutions. Berlin: Springer, 2008. 515 p.
Шашков А.Г., Бубнов В.А., Яновский С.Ю. Волновые явления теплопроводности: Системно-структурный подход. М.: Едиториал УРСС, 2004. 296 с.
Encyclopedia of Thermal Stresses / Ed. by Hetnarski R.B. Dordrecht: Springer, 2014. 6643 p.
Chattopadhyay S. High cycle thermal fatigue crack growth in a semi-infinite plate // J. Therm. Stresses. 2009. V. 32. № 8. P. 839–846.
Kasahara N., Itoh T., Okazaki M. et al. Development of thermal fatigue evaluation methods of piping systems // E-J. Advanced Maintenance. 2014. V. 6. № 1. P. 14–23.
Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1967. 600 с.
Карслоу Г., Егер Д. Теплопроводность твердых тел. М.: Наука, 1964. 488 с.
Карташов Э.М., Кудинов В.А. Аналитическая теория теплопроводности и прикладной термоупругости. М.: Либроком, 2012. 656 с.
Паркус Г. Неустановившиеся температурные напряжения. М.: Физматгиз, 1963. 252 с.
Карташов Э.М. Аналитические методы в теории теплопроводности твердых тел. М.: Высшая школа, 2001. 550 с.
Минасян Р.С. Об одной периодической задаче теплопроводности в полом бесконечном цилиндре // ИФЖ. 1969. Т. 17. № 5. С. 880–891.
Канторович Л.В., Крылов В.И. Приближенные методы высшего анализа. М.; Л.: Физматлит, 1962. 708 с.
Supel’nyak M.I. Calculation of temperature oscillations in thermal layer of regular solids at unsteady coefficient of heat transfer // J. Phys.: Conf. Ser. 2019. V. 1382. № 012149. 10 p.
Ватсон Г.Н. Теория бесселевых функций. Часть I. М.: Изд-во иностранной литературы, 1949. 799 с.
Тимошенко С.П., Гудьер Дж. Теория упругости. М.: Наука, 1975. 576 с.
Биргер И.А., Мавлютов Р.Р. Сопротивление материалов. М.: Наука, 1986. 560 с.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика