1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 84, № 4, 2020

Прикладная математика и механика, 2020, T. 84, № 4, стр. 426-432

АНАЛИТИЧЕСКАЯ АППРОКСИМАЦИЯ ФУНКЦИОНАЛЬНЫХ ЗАВИСИМОСТЕЙ ПАРАМЕТРОВ ГЕОДЕЗИЧЕСКОЙ ЛИНИИ

П. А. Кучеренко 1, *, С. В. Соколов 2, **

1 Ростовский государственный университет путей сообщения
Ростов-на-Дону, Россия

2 Московский технический университет связи и информатики
Москва, Россия

* E-mail: pavelpost83@mail.ru
** E-mail: s.v.s.888@yandex.ru

Поступила в редакцию 04.12.2019
После доработки 19.02.2020
Принята к публикации 11.03.2020

Полный текст (PDF)

Аннотация

Рассмотрен синтез высокоточных аналитических аппроксимирующих функций зависимости геодезической долготы от приведенной широты на геодезической линии сфероида. Полученные аппроксимации актуальны как для задач геодезии, так и навигации при необходимости высокоточных расчетов.

Ключевые слова: ортодромическая траектория, сфероид, аппроксимация функциональной зависимости

Введение. Постоянный рост требований к точности современных навигационных систем приводит к необходимости решения проблемы компромисса между повышением точности описания текущих параметров движения объекта, неизбежно ведущим к усложнению навигационных алгоритмов, и снижением вычислительной сложности последних с целью обеспечения возможности решения навигационной задачи в реальном масштабе времени. Одним из путей решения первой задачи является использование при построении основных уравнений навигации сфероидальной модели Земли вместо сферической, а радикальным подходом к решению второй (сокращению размерности системы навигационных уравнений без потери точности решения задачи навигации) – использование функциональных зависимостей между навигационными переменными, в частности, между долготой и широтой, возникающих на отдельных видах траекторий. Подобные аналитические зависимости, выраженные в элементарных функциях, известны для локсодромической или ортодромической траекторий движения объекта по сферической Земле и для локсодромической траектории движения по сфероиду [1–5]. В [6] была получена аналогичная зависимость геодезической долготы от приведенной широты для геодезической линии на сфероиде в интегральной форме (затрудняющей ее применение в задачах геодезии и навигации) и показана возможность ее аппроксимации аналитической зависимостью, выраженной элементарными функциями. Точность полученной при этом аппроксимации составила единицы метров, что позволяет использовать ее при решении задачи позиционирования в навигационных системах среднего класса точности. Но для высокоточных систем навигации необходим уже сантиметровый (и менее) уровень ошибки аппроксимации, поэтому рассмотрим далее возможность построения с данной точностью зависимости геодезической долготы от приведенной широты на геодезической линии, выраженной в элементарных функциях.

1. Постановка задачи. Как показано в [6], точная зависимость геодезической долготы L от приведенной широты u (однозначно определяющей также и геодезическую широту В [7]) является интегральной:

(1.1)
$L(u) = {{L}_{0}} + \int\limits_{{{и}_{0}}}^и {\phi \frac{{\sqrt {1 - {{e}^{2}}{{{\cos }}^{2}}и} }}{{\cos и\sqrt {{{{\cos }}^{2}}и - {{\phi }^{2}}} }}} \,du,\quad \phi = \sin {{A}_{0}}\cos {{u}_{0}},$
где ${{u}_{0}}$ – приведенная широта начальной точки геодезической линии, ${{A}_{0}}$ – азимут геодезической линии в начальной точке, ${{L}_{0}}$ – геодезическая долгота начальной точки геодезической линии, е – второй эксцентриситет (для эллипсоида Красовского).

Это затрудняет ее непосредственное использование в задачах навигации и геодезии.

Графическое изображение этой зависимости, дающее представление об общем характере функции L(u) – непрерывном и монотонном, приведено также в [6]. Так как аналитическое вычисление интеграла (1.1) не представляется возможным, рассмотрим далее возможность его аналитической аппроксимации, обеспечивающей заявленную выше точность.

2. Решение задачи. Для построения искомой аппроксимации интеграла (1.1) рассмотрим возможность упрощения его подынтегрального выражения разложением в ряд функции $\sqrt {1 - {{e}^{2}}{{{\cos }}^{2}}и} $ по аргументу ${{e}^{2}}{{\cos }^{2}}и$ (в заданной точке ${{u}_{l}}$) с точностью до ${{\left( {{{e}^{2}}{{{\cos }}^{2}}и} \right)}^{4}}$ (что, как показано далее, достаточно для обеспечения точности аппроксимации существенно выше заявленной (сантиметровой) – в пределах ${{10}^{{ - 6}}}$ м):

(2.1)
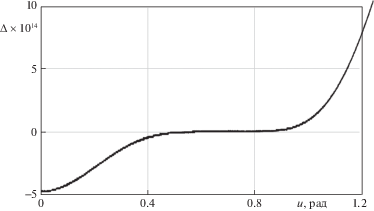
$\sqrt {1 - {{e}^{2}}{{{\cos }}^{2}}и} \approx {{\alpha }_{0}} + {{\alpha }_{1}}{{\cos }^{2}}и + {{\alpha }_{2}}{{\cos }^{4}}и + {{\alpha }_{3}}{{\cos }^{6}}и + {{\alpha }_{4}}{{\cos }^{8}}и$
где коэффициенты ${{\alpha }_{i}}$, $i = 0, \ldots ,4$ приведены в Приложении 1 .

Точность подобного разложения функции $\sqrt {1 - {{e}^{2}}{{{\cos }}^{2}}и} $ оказывается весьма высокой, что иллюстрирует приведенный на рис. 1 график изменения погрешности приближения Δ(u) в зависимости от приведенной широты u. Это, в свою очередь, позволяет использовать функцию (2.1) для последующего решения задачи.

Рис. 1.

Погрешность приближения Δ функции $\sqrt {1 - {{e}^{2}}{{{\cos }}^{2}}и} $ при ${{u}_{l}}$ = 0.7 рад.

При этом следует иметь в виду, что для области низких и высоких широт коэффициенты функции (2.1) существенно упрощаются:

− для района высоких широт – ${{и}_{0}} = \frac{\pi }{2}$ (при выборе точки аппроксимации в начале интервала, т.е. при ${{и}_{l}} = {{u}_{0}}$):

${{\alpha }_{0}} = 1,\quad {{\alpha }_{1}} = - \frac{{{{e}^{2}}}}{2},\quad {{\alpha }_{2}} = - \frac{{{{e}^{4}}}}{8},\quad {{\alpha }_{3}} = - \frac{{{{e}^{6}}}}{{16}},\quad {{\alpha }_{4}} = - \frac{{5{{e}^{8}}}}{{128}}$

− для района низких широт – ${{u}_{0}} = 0$ (также при ${{и}_{l}} = {{u}_{0}}$):

${{\alpha }_{n}} = \sqrt {1 - {{e}^{2}}} \sum\limits_{m \geqslant n}^4 {{{{\left( { - 1} \right)}}^{{n + m + 1}}}\frac{{{{e}^{{2m}}}}}{{{{{\left( {1 - {{e}^{2}}} \right)}}^{m}}}}{{\alpha }_{{nm}}}} ,\quad n = 0, \ldots ,4$
${{\alpha }_{{nm}}} = \left( {\begin{array}{*{20}{c}} { - 1}&{\frac{1}{2}}&{\frac{1}{8}}&{\frac{1}{{16}}}&{\frac{5}{{128}}} \\ 0&{\frac{1}{2}}&{\frac{1}{4}}&{\frac{3}{{16}}}&{\frac{5}{{32}}} \\ 0&0&{\frac{1}{8}}&{\frac{3}{{16}}}&{\frac{5}{{64}}} \\ 0&0&0&{\frac{1}{{16}}}&{\frac{5}{{32}}} \\ 0&0&0&0&{\frac{5}{{128}}} \end{array}} \right)$

При использовании функции (2.1) интеграл (1.1) распадается на сумму интегралов:

(2.2)
$L = {{L}_{0}} + \phi \cdot {{\alpha }_{0}}\int\limits_{{{u}_{0}}}^u {\frac{{du}}{{\cos и\sqrt {{{{\cos }}^{2}}и - {{\phi }^{2}}} }}} + \phi \sum\limits_{i = 1}^4 {{{\alpha }_{i}}} \int\limits_{{{u}_{0}}}^u {\frac{{{{{\cos }}^{{2i - 1}}}и}}{{\sqrt {{{{\cos }}^{2}}и - {{\phi }^{2}}} }}du} $

Первый из этих интегралов равен:

$\begin{gathered} \int\limits_{{{u}_{0}}}^u {\frac{{\phi {{\alpha }_{0}}}}{{\cos и\sqrt {{{{\cos }}^{2}}и - {{\phi }^{2}}} }}dи} = \phi {{\alpha }_{0}}k\int\limits_{{{u}_{0}}}^u {\frac{{dи}}{{\cos и\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} }}} = \\ = - \frac{1}{{2\kappa {\text{*}}}}\ln \left. {\frac{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} - k{\text{*}}\sin u}}{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} + k{\text{*}}\sin u}}} \right|_{{{{u}_{0}}}}^{u}\phi k{{\alpha }_{0}} \\ \end{gathered} $
${{k}^{2}} = {{\left( {1 - {{\phi }^{2}}} \right)}^{{ - 1}}},\quad k{\text{*}} = \sqrt {1 - {{k}^{2}}} $

Так как параметр $k{\text{*}} = \sqrt {1 - {{k}^{2}}} $ – комплексный, то представляя его в виде $k{\text{*}} = i{\nu }$, ${\nu } = \sqrt {\,{{k}^{2}} - 1} \,$преобразуем полученный логарифм следующим образом [8]:

$\begin{gathered} - \frac{1}{{2\kappa {\text{*}}}}\ln \frac{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} - k{\text{*}}\sin u}}{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} + k{\text{*}}\sin u}} = \\ = \frac{1}{\nu }{\text{arctg}}\frac{{{\nu }\sin u}}{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} }} = \frac{1}{{k\phi }}{\text{arctg}}\frac{{k\phi \sin u}}{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} }} \\ \end{gathered} $

С учетом данного преобразования окончательно определяем выражение для интеграла:

$\int\limits_{{{u}_{0}}}^u {\frac{{\phi {{\alpha }_{0}}}}{{\cos и\sqrt {{{{\cos }}^{2}}и - {{\phi }^{2}}} }}du} = {{\alpha }_{0}}\left[ {{\text{arctg}}\frac{{k\phi \sin u}}{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} }} - {\text{arctg}}\frac{{k\phi \sin {{u}_{0}}}}{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}{{и}_{0}}} }}} \right]$

Второй интеграл из (2.2) при замене переменных является табличным:

$\int\limits_{{{u}_{0}}}^u {\frac{{\phi {{\alpha }_{1}}\cos и}}{{\sqrt {{{{\cos }}^{2}}и - {{\phi }^{2}}} }}du} = \phi {{\alpha }_{1}}[(\arcsin (k\sin и) - \arcsin (k\sin {{и}_{0}})],$
а остальные интегралы
$\phi {{\alpha }_{n}}\int\limits_{{{u}_{0}}}^u {\frac{{{{{\cos }}^{{2n - 1}}}и}}{{\sqrt {{{{\cos }}^{2}}и - {{\phi }^{2}}} }}du} = \phi {{\alpha }_{n}}k\int\limits_{{{u}_{0}}}^u {\frac{{{{{\cos }}^{{2n - 1}}}и}}{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} }}} \,du,\quad n = 2,3,4$
могут быть определены из [8]:
$\begin{gathered} \phi k{{\alpha }_{n}}\int\limits_{{{u}_{0}}}^u {\frac{{{{{\cos }}^{{2n - 1}}}и}}{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} }}} \,du = \\ = \phi k{{\alpha }_{n}}\left\{ {\frac{{\sin u\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} }}{{{{k}^{{2(n - 1)}}}}}\sum\limits_{m = 0}^{n - 2} {{{{\left( {{{k}^{2}}{{{\sin }}^{2}}u} \right)}}^{m}}\sum\limits_{l = 0}^{n - m - 2} {{{{\left( { - 1} \right)}}^{{n + l}}}{{p}_{{nmk}}}{{k}^{{2l}}}} } } \right. + \\ + \;\left. {\left. {\frac{{\arcsin (k\sin u)}}{{{{k}^{{2n - 1}}}}}\sum\limits_{m = 0}^{n - 1} {{{{\left( { - 1} \right)}}^{{n - m - 1}}}{{q}_{{nm}}}{{k}^{{2m}}}} } \right\}} \right|_{{{{u}_{0}}}}^{u},\quad n = 2,3,4, \\ \end{gathered} $
где

$\begin{gathered} {{q}_{{20}}} = \frac{1}{2},\quad {{q}_{{21}}} = 1;\quad {{q}_{{30}}} = \frac{3}{8},\quad {{q}_{{31}}} = {{q}_{{32}}} = 1;\quad {{q}_{{40}}} = \frac{5}{{16}} \\ {{q}_{{41}}} = \frac{9}{8},\quad {{q}_{{42}}} = \frac{3}{2},\quad {{q}_{{43}}} = 1 \\ \end{gathered} $
$\begin{gathered} {{p}_{{200}}} = \frac{1}{2};\quad {{p}_{{300}}} = \frac{3}{8},\quad {{p}_{{301}}} = 1,\quad {{p}_{{310}}} = \frac{1}{4} \\ {{p}_{{400}}} = \frac{5}{{16}},\quad {{p}_{{401}}} = \frac{9}{8},\quad {{p}_{{402}}} = \frac{3}{2},\quad {{p}_{{410}}} = \frac{5}{{24}},\quad {{p}_{{411}}} = \frac{3}{4},\quad {{p}_{{420}}} = \frac{1}{6} \\ \end{gathered} $

С учетом соотношения

$\begin{gathered} \frac{{k\phi \sin {{u}_{0}}}}{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}{{и}_{0}}} }} = \frac{{\sin {{A}_{0}}\cos {{u}_{0}}\sin {{u}_{0}}}}{{\sqrt {1 - {{{(\sin {{A}_{0}}\cos {{u}_{0}})}}^{2}}} \sqrt {1 - \frac{{{{{\sin }}^{2}}{{u}_{0}}}}{{1 - {{{(\sin {{A}_{0}}\cos {{u}_{0}})}}^{2}}}}} }} = \\ = \frac{{\sin {{A}_{0}}\cos {{u}_{0}}\sin {{u}_{0}}}}{{\sqrt {{{{\cos }}^{2}}{{u}_{0}} - {{{(\sin {{A}_{0}}\cos {{u}_{0}})}}^{2}}} }} = \sin {{u}_{0}}\operatorname{tg} {{A}_{0}} \\ \end{gathered} $
и возможности представления в компактном виде суммы интегралов
$\begin{gathered} \phi \sum\limits_{n = 2}^4 {{{\alpha }_{n}}} \int\limits_{{{u}_{0}}}^u {\frac{{{{{\cos }}^{{2n - 1}}}и}}{{\sqrt {{{{\cos }}^{2}}и - {{\phi }^{2}}} }}du} = ({{\beta }_{0}} + {{\beta }_{1}}{{\sin }^{2}}и + {{\beta }_{2}}{{\sin }^{4}}и)\sin u\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} + \\ + \;{{{\beta }}_{3}}\arcsin (k\sin u) + {{{\beta }}_{4}}, \\ \end{gathered} $
где коэффициенты ${{{\beta }}_{n}}$, n = 0, …, 4 приведены в Приложении 2 , окончательно аппроксимация функциональной зависимости геодезической долготы от приведенной широты на геодезической линии принимает вид:

$\begin{gathered} L{\text{*}}(u) = {{L}_{0}} + {{\alpha }_{0}}\left[ {\operatorname{arctg} \frac{{k\phi \sin u}}{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} }} - \operatorname{arctg} (\sin {{u}_{0}}\operatorname{tg} {{A}_{0}})} \right] + \\ + \;\phi {{\alpha }_{1}}[(\arcsin (k\sin и) - \arcsin (k\sin {{и}_{0}})] + \\ \end{gathered} $
$\begin{gathered} + \;({{{\beta }}_{0}} + {{{\beta }}_{1}}{{\sin }^{2}}и + {{{\beta }}_{2}}{{\sin }^{4}}и)\sin u\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} + {{{\beta }}_{3}}\arcsin (k\sin u) + {{{\beta }}_{4}} = \\ = {{L}_{0}} + {{\alpha }_{0}}\operatorname{arctg} \frac{{k\phi \sin u}}{{\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} }} + ({{{\beta }}_{3}} + \phi {{\alpha }_{1}})\arcsin (k\sin u) + \\ \end{gathered} $
(2.3)
$\begin{gathered} + \;({{\beta }_{0}} + {{\beta }_{1}}{{\sin }^{2}}и + {{\beta }_{2}}{{\sin }^{4}}и)\sin u\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}и} + {{\beta }_{5}} \\ {{\beta }_{5}} = {{\beta }_{4}} - {{\alpha }_{0}}\operatorname{arctg} (\sin {{u}_{0}}\operatorname{tg} {{A}_{0}}) - \phi {{\alpha }_{1}}\arcsin (k\sin {{и}_{0}}) \\ \end{gathered} $

На рис. 2 приведен график характерного изменения погрешности аппроксимации ${\delta }(u) = L(u) - L{\text{*(}}u)$ в зависимости от широты u (для значений параметров ${{L}_{0}}$ = 0.3, ${{u}_{0}}$ = 0, ${{A}_{0}}$= 0.3 при ${{u}_{l}}$ = 0.7).

Рис. 2.

Погрешность аппроксимации ${\delta }$ для параметров ${{L}_{0}}$ = 0.3, ${{u}_{0}}$ = 0, ${{A}_{0}}$ = 0.3 при ${{u}_{l}}$ = 0.7 рад.

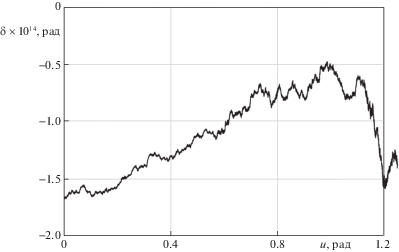
Как показали результаты моделирования, характер изменения и порядок значений среднеквадратических ошибок аппроксимации существенно не меняются при выборе различных интервалов изменения широты u и точек аппроксимации ${{u}_{l}}$ в пределах этих интервалов, что свидетельствует об общем характере полученной аппроксимации и возможности ее использования в высокоточных навигационных системах и геодезических расчетах.

В завершение рассмотрения данной аппроксимации следует отметить, что, учитывая известную связь приведенной и геодезической В широт

(2.4)
$\sin u = \frac{{\sin В}}{{\sqrt {1 + {{e}^{2}}{{{\cos }}^{2}}B} }}$
из (2.3), (2.4) можно легко получить следующую аппроксимацию связи геодезической долготы и геодезической широты B:
$\begin{gathered} L = {{L}_{0}} + {{\alpha }_{0}}\operatorname{arctg} \frac{{k\phi \sin В}}{{\sqrt {1 + {{e}^{2}} - ({{k}^{2}} + {{e}^{2}}){{{\sin }}^{2}}В} }} + \\ + \;({{\beta }_{3}} - \phi {{\alpha }_{1}})\arcsin \left( {k\frac{{\sin В}}{{\sqrt {1 + {{e}^{2}}{{{\cos }}^{2}}B} }}} \right) + \left( {{{\beta }_{0}} + {{\beta }_{1}}\frac{{{{{\sin }}^{2}}В}}{{1 + {{e}^{2}}{{{\cos }}^{2}}B}} + } \right. \\ + \;\left. {{{\beta }_{2}}\frac{{{{{\sin }}^{4}}В}}{{{{{(1 + {{e}^{2}}{{{\cos }}^{2}}B)}}^{2}}}}} \right)\frac{{\sin В}}{{1 + {{e}^{2}}{{{\cos }}^{2}}B}}\sqrt {1 - {{k}^{2}} + ({{e}^{2}} + {{k}^{2}}){{{\cos }}^{2}}B} + {{\beta }_{5}}, \\ \end{gathered} $
где коэффициенты ${{\alpha }_{i}}$, ${{{\beta }}_{i}}$, $i = 0,...,4$, приведенные в Приложениях 1, 2 пересчитываются аналогичным образом с учетом (2.4).

Заключение. Как показал вычислительный эксперимент, максимальная ошибка аппроксимации полученных аналитических аппроксимирующих функциональных зависимостей не превышает $2 \times {{10}^{{ - 13}}}$ рад ($1.5 \times {{10}^{{ - 6}}}$ м), что позволяет их эффективно использовать в высокоточных геодезических и навигационных расчетах.

ПРИЛОЖЕНИЕ 1 . Коэффициенты разложения в ряд функции $\sqrt {1 - {{e}^{2}}{{{\cos }}^{2}}и} $

${{\alpha }_{0}} = \sqrt {1 - {{e}^{2}}{{{\cos }}^{2}}{{и}_{l}}} + \frac{{{{e}^{2}}{{{\cos }}^{2}}{{и}_{l}}}}{{2\sqrt {1 - {{e}^{2}}{{{\cos }}^{2}}{{и}_{l}}} }} - \frac{{{{e}^{4}}{{{\cos }}^{4}}{{и}_{l}}}}{{8\sqrt {{{{(1 - {{e}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{3}}} }} + $
$ + \;\frac{{{{e}^{6}}{{{\cos }}^{6}}{{и}_{l}}}}{{16\sqrt {{{{(1 - {{e}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{5}}} }} - \frac{{5{{e}^{8}}{{{\cos }}^{8}}{{и}_{l}}}}{{128\sqrt {{{{(1 - {{e}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{7}}} }}$
${{\alpha }_{1}} = - \frac{{{{e}^{2}}}}{{2\sqrt {1 - {{e}^{2}}{{{\cos }}^{2}}{{и}_{l}}} }} + \frac{{{{e}^{4}}{{{\cos }}^{2}}{{и}_{l}}}}{{4\sqrt {{{{(1 - {{e}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{3}}} }} - $
$ - \;\frac{{3{{e}^{6}}{{{\cos }}^{4}}{{и}_{l}}}}{{16\sqrt {{{{(1 - {{e}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{5}}} }} + \frac{{5{{e}^{8}}{{{\cos }}^{6}}{{и}_{l}}}}{{32\sqrt {{{{(1 - {{e}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{7}}} }}$
${{\alpha }_{2}} = - \frac{{{{e}^{4}}}}{{8\sqrt {{{{(1 - {{e}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{3}}} }} + \frac{{3{{e}^{6}}{{{\cos }}^{2}}{{и}_{l}}}}{{16\sqrt {{{{(1 - {{e}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{5}}} }} - \frac{{15{{e}^{8}}{{{\cos }}^{4}}{{и}_{l}}}}{{64\sqrt {{{{(1 - {{e}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{7}}} }}$
${{\alpha }_{3}} = - \frac{{{{e}^{6}}}}{{16\sqrt {{{{(1 - {{e}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{5}}} }} + \frac{{5{{e}^{8}}{{{\cos }}^{2}}{{и}_{l}}}}{{32\sqrt {{{{(1 - {{e}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{7}}} }}$
${{\alpha }_{4}} = - \frac{{5{{e}^{8}}}}{{128\sqrt {{{{(1 - {{e}^{2}}{{{\cos }}^{2}}{{и}_{l}})}}^{7}}} }}$

ПРИЛОЖЕНИЕ 2 . Выражения для коэффициентов разложения ${{\beta }_{n}}$

${{\beta }_{0}} = \phi \frac{{24{{\alpha }_{2}}{{k}^{4}} + 6{{\alpha }_{3}}(8{{k}^{2}} - 3){{k}^{2}} + {{\alpha }_{4}}(72{{k}^{4}} - 54{{k}^{2}} + 15)}}{{48{{k}^{5}}}}$
${{\beta }_{1}} = - \phi \frac{{{{\alpha }_{4}}(18{{k}^{2}} - 5) + 6{{k}^{2}}{{\alpha }_{3}}}}{{24{{k}^{3}}}}$
${{\beta }_{2}} = \phi \frac{{{{\alpha }_{4}}}}{{6k}}$
${{\beta }_{3}} = \phi \frac{{{{\alpha }_{2}}(2{{k}^{2}} - 1)8{{k}^{4}} + {{\alpha }_{3}}(8{{k}^{4}} - 8{{k}^{2}} + 3)2{{k}^{2}} + {{\alpha }_{4}}(16{{k}^{6}} - 24{{k}^{4}} + 18{{k}^{2}} - 5)}}{{16{{k}^{6}}}}$
${{\beta }_{4}} = - ({{\beta }_{0}} + {{\beta }_{1}}{{\sin }^{2}}{{и}_{0}} + {{\beta }_{2}}{{\sin }^{4}}{{и}_{0}})\sin {{u}_{0}}\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}{{и}_{0}}} - {{\beta }_{3}}\arcsin (k\sin {{u}_{0}})$

Список литературы

  1. Серапинас Б.Б. Геодезические основы карт. М.: Изд-во МГУ, 2001. 132 с.

  2. Wei-Kuo Tseng, Michael A. Earle, Jiunn-Liang Guo Direct and inverse solutions with geodetic latitude in terms of longitude for rhumb line sailing // J. Navigation. 2012. V. 65. № 3. P. 549–559.

  3. Nihad E. Daidzic Long and short-range air navigation on spherical Earth // Intern. J. Aviation, Aeronautics and Aerospace. 2017. V. 4. № 1. P. 1–54.

  4. Соколов С.В. Аналитические модели пространственных траекторий для решения задач навигации // ПММ. 2015. Т. 79. Вып. 1. С. 24–30.

  5. Розенберг И.Н., Соколов С.В., Уманский В.И., Погорелов В.А. Теоретические основы тесной интеграции инерциально-спутниковых навигационных систем. М.: Физматлит, 2018. 306 с.

  6. Кучеренко П.А., Соколов С.В. Аналитическое решение задачи аппроксимации функциональных зависимостей параметров геодезической линии // Изв. РАН. МТТ. 2019. № 5. С. 104–112.

  7. Морозов В.П. Курс сфероидической геодезии. М.: Недра, 1979. 296 с.

  8. Градштейн И.С., Рыжик И.М. Таблицы интегралов. М.: Физматлит, 1963. 1100 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал